3.1立体几何平行垂直有关定理总结
- 格式:doc
- 大小:153.00 KB
- 文档页数:3

立体几何平行垂直8个定理哎,说起立体几何里的平行垂直那8个定理,简直就是我学生时代的一块心病啊!那时候,每次数学课讲到这儿,我就感觉自己的大脑像是被施了魔法,完全转不过来弯儿。
不过呢,现在回想起来,那段日子也挺有意思的,毕竟,谁能说学数学不是一场奇妙的冒险呢?首先啊,咱们得说说那个“平行公理”。
你知道吗,它就像是生活中的一条隐形规则,告诉你“过直线外一点,有且只有一条直线与已知直线平行”。
听起来挺绕的,但想象一下,你站在一条笔直的路上,想要找一条和这条路既不交叉也不重合的新路走,那你就只能选择平行于这条路的那一条,别无选择。
是不是觉得,数学有时候也挺有哲理的?接下来,就是那个“平行线的性质定理”了。
这个定理就像是平行线之间的秘密约定,告诉你“两直线平行,同位角相等”。
每次做题的时候,我就想象自己变成了侦探,在两条平行线之间寻找那些隐藏的“同位角”,然后像解开谜题一样,把它们一一对应起来。
那种成就感,简直比找到宝藏还要让人兴奋!还有那个“平行于同一条直线的两直线平行”,这个定理简直就是“物以类聚,人以群分”的数学版。
你想啊,如果两条直线都愿意和同一条直线做朋友,那它们之间肯定也合得来,对吧?这种逻辑上的简单明了,让我对数学又多了几分好感。
说到垂直,那“垂直平分线的性质定理”可就不能不提了。
它就像是足球场上的裁判,公正无私地告诉你“垂直平分线上的点到线段两端点的距离相等”。
每次看到这样的题目,我就感觉自己像是在进行一场公平的较量,只要我按照规则来,就一定能找到正确答案。
还有那个“直线垂直于平面的判定定理”,它就像是建筑工人手里的锤子,坚定地告诉你“一条直线如果垂直于平面内两条相交的直线,那么这条直线与这个平面垂直”。
每次想到这个定理,我就仿佛看到了那些高楼大厦拔地而起,每一块砖石都严丝合缝,让人不得不感叹数学的神奇。
“平面与平面垂直的判定定理”也挺有意思的,它就像是两个好朋友之间的默契,告诉你“如果一个平面过另外一个平面的垂线,那么这两个平面垂直”。

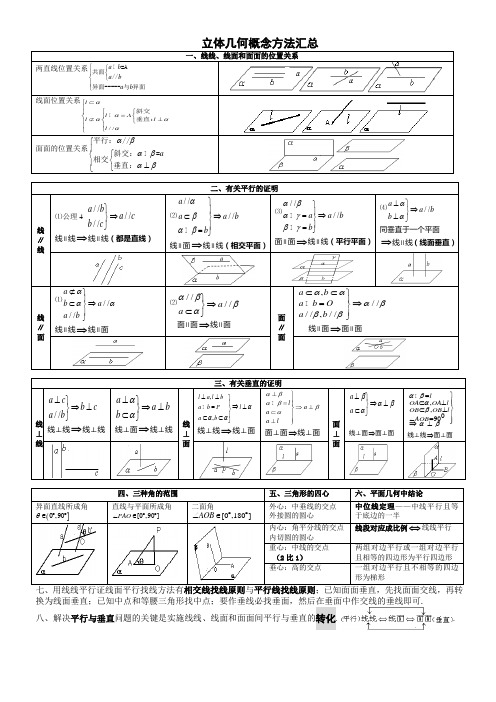
lmβααba立体几何的八大定理一、线面平行的判定定理:线线平行⇒线面平行文字语言:如果平面外.的一条直线与平面内.的一条直线平行,则这条直线与平面平行. 符号语言://a b a b αα⊄⎫⎪⊂⎬⎪⎭⇒//a α关键点:在平面内找一条与平面外的直线平行的线...................... 二、线面平行的性质定理:线面平行⇒线线平行文字语言:如果一条直线和一个平面平行,经过..这条直线的平面和这个平面相交..,那么这条直线就和交线..平行. 符号语言://l l m αβαβ⎫⎪⊂⎬⎪⋂=⎭⇒//l m关键点:需要借助一个经过已知直线的平面,接着找交线。
.......................... 三、面面平行的判定定理:线面平行⇒ 面面平行文字语言:如果一个平面内.有两.条相交..直线都平行..于另一个平面..,那么这两个平面平行. 符号语言://a b a b A a b αααβββ⊂⎫⎪⊂⎪⎪=⇒⎬⎪⎪⎪⎭∥∥ 关键点:在要证明面面平行的其中一个面内找两条相交直线和另一面线面平行。
................................... 四、面面平行的性质定理: 面面平行⇒线线平行、面面平行⇒线面平行 文字语言:如果两个平行平面同时..和第三..个.平面相交..,那么所得的两条交线..平行. 符号语言:////a a b b αβαγβγ⎫⎪⋂=⇒⎬⎪⋂=⎭关键点:找第三个平面与已知平面都相.................交,则交线平行.......文字语言:如果两个平面平行,那么其中一个平面内的任意..一条直线平行于另一个平面.符号语言://,//a a αβαβ⊂⇒ 关键:只要是其中一个平面内的直线就行..................nmAαaBA l βαaβα五、线面垂直的判定定理:线线垂直⇒线面垂直文字语言:如果一条直线和一个平面内.的两.条相交..直线垂直..,那么这条直线垂直于这个平面. 符号语言:,a ma n a m n A m n ααα⊥⎫⎪⊥⎪⇒⊥⎬⋂=⎪⎪⊂⊂⎭关键点:在平面内找两条相交直线与所要证的直线垂直........................ 六、线面垂直的性质定理:线面垂直⇒线线垂直文字语言:若一条直线垂直于一个平面,则这条直线垂直平面内的任意..一条直线. 符号语言:l l a a αα⊥⎫⇒⊥⎬⊂⎭关键点:往往线面垂直中的线线垂直需要用这个定理推出......................... 七、平面与平面垂直的判定定理:线面垂直⇒面面垂直文字语言:如果一个平面经过..另一个平面的一条垂线,则这两个平面互相垂直. (如果一条直线垂直于一个平面,并且有另一个平面经过这条直线,那么这两个平面垂直)符号表示:a a ααββ⊥⎫⇒⊥⎬⊂⎭关键点:....在需要证明的两个平面中找线面垂直................八、平面与平面垂直的性质定理:面面垂直⇒线面垂直文字语言:如果两个平面互相垂直,那么在一个平面内垂直..于它们的交线..的直线垂直于另一个平面.符号语言:l AB AB AB lαβαββα⊥⎫⎪=⎪⇒⊥⎬⊂⎪⎪⊥⎭关键点:先找交线,再在其中一个面内找与交线垂直的线。
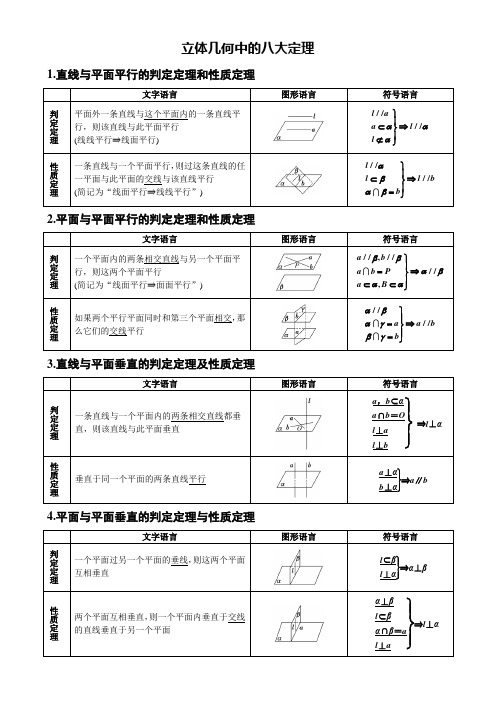
立体几何中的八大定理1.直线与平面平行的判定定理和性质定理文字语言图形语言符号语言判定定理平面外一条直线与这个平面内的一条直线平行,则该直线与此平面平行(线线平行⇒线面平行)////l aa llααα⎫⎪⊂⇒⎬⎪⊄⎭性质定理一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行(简记为“线面平行⇒线线平行”)////ll l bbαβαβ⎫⎪⊂⇒⎬⎪=⎭2.平面与平面平行的判定定理和性质定理文字语言图形语言符号语言判定定理一个平面内的两条相交直线与另一个平面平行,则这两个平面平行(简记为“线面平行⇒面面平行”)//,////,a ba b Pa Bββαβαα⎫⎪=⇒⎬⎪⊂⊂⎭性质定理如果两个平行平面同时和第三个平面相交,那么它们的交线平行////a a bbαβαγβγ⎫⎪=⇒⎬⎪=⎭3.直线与平面垂直的判定定理及性质定理文字语言图形语言符号语言判定定理一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直⎭⎪⎬⎪⎫a,b⊂αa∩b=Ol⊥al⊥b⇒l⊥α性质定理垂直于同一个平面的两条直线平行⎭⎪⎬⎪⎫a⊥αb⊥α⇒a∥b4.平面与平面垂直的判定定理与性质定理文字语言图形语言符号语言判定定理一个平面过另一个平面的垂线,则这两个平面互相垂直⎭⎪⎬⎪⎫l⊂βl⊥α⇒α⊥β性质定理两个平面互相垂直,则一个平面内垂直于交线的直线垂直于另一个平面⎭⎪⎬⎪⎫α⊥βl⊂βα∩β=al⊥a⇒l⊥α。

立体几何有关平行垂直定理总结 BHS
.
2.等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等。
3.推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等。
4.异面直线判定定理:用平面内一点与平面外一点的直线,与平面内不经过该点的直线是异面直线。
5.两异面直线所成的角:过空间任意一点引两条直线分别平行(或重合)于两条异面直线,它们所成的锐角(或直角)。
范围为 ( 0°,90°]
6.斜线线与平面所成的角:平面的一条斜线和它在这个平面内的射影所成的锐角。
直线和平面所成角的取值范围为 [0°,90°]
7.二面角的平面角:以二面角的棱上任意一点为端点,在两个面内
分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。
8.几何体的表面积和体积。
空间几何的平行与垂直关系知识点总结在空间几何中,平行与垂直关系是非常重要的概念,它们贯穿于整个几何学习的始终。
理解和掌握这些关系对于解决空间几何问题至关重要。
下面,我们就来详细总结一下空间几何中平行与垂直关系的相关知识点。
一、线线平行1、平行线的定义在同一平面内,不相交的两条直线叫做平行线。
2、线线平行的判定定理(1)同位角相等,两直线平行。
(2)内错角相等,两直线平行。
(3)同旁内角互补,两直线平行。
3、线线平行的性质定理(1)两直线平行,同位角相等。
(2)两直线平行,内错角相等。
(3)两直线平行,同旁内角互补。
4、空间中直线平行的传递性如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
二、线面平行1、线面平行的定义如果一条直线与一个平面没有公共点,那么这条直线与这个平面平行。
2、线面平行的判定定理如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行。
3、线面平行的性质定理如果一条直线与一个平面平行,经过这条直线的平面与这个平面相交,那么这条直线与交线平行。
三、面面平行1、面面平行的定义如果两个平面没有公共点,那么这两个平面平行。
2、面面平行的判定定理(1)如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行。
(2)如果两个平面都平行于同一条直线,那么这两个平面平行。
3、面面平行的性质定理(1)如果两个平面平行,那么其中一个平面内的直线平行于另一个平面。
(2)如果两个平行平面都和第三个平面相交,那么它们的交线平行。
四、线线垂直1、线线垂直的定义如果两条直线所成的角为直角,那么这两条直线互相垂直。
2、线线垂直的判定定理(1)如果一条直线垂直于一个平面,那么这条直线垂直于平面内的任意一条直线。
(2)如果两条平行线中的一条垂直于一条直线,那么另一条也垂直于这条直线。
五、线面垂直1、线面垂直的定义如果一条直线与一个平面内的任意一条直线都垂直,那么这条直线与这个平面垂直。
立体几何的概念、公理、定理(一)立体几何三公理公理1:如果一条直线上的两点在一个平面内,那么这条直线上的所有的点都在这个平面内。
公理2:如果两个平面有一个公共点,那么它们有且只有一条通过这个点的公共直线.,A a A a公理3:经过不在同一直线上的三点,有且只有一个平面。
A、B、C不在同一直线上有且只有一个平面α,使A∈α,B∈α,C∈α推论1:经过一条直线和这条直线外的一点,有且只有一个平面。
A a 有且只有一个平面,使推论2:经过两条相交直线,有且只有一个平面。
a∩b=A有且只有一个平面,使推论3:经过两条平行直线,有且只有一个平面。
a∥b=A有且只有一个平面,使(二)空间直线公理4 :平行于同一条直线的两条直线互相平行。
a∥bb∥c等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等。
推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等。
异面直线判定定理:用平面内一点与平面外一点的直线,与平面内不经过该点的直线是异面直线。
cbaaA∈a,B∈aA∈,B∈aA∈aababcba//a c////////AB A BAC A C///BAC B A CA∈PP(三)直线和平面直线和平面平行的判定定理:如果平面外一条直线和 这个平面内的一条直线平行,那么这条直线和这个平面平行。
直线和平面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
直线与平面垂直的判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面。
定理 :如果两条平行直线中的一条直线垂直于一个平面,那么另一条直线也垂直这个平面。
定理:一条直线垂直于两个平行平面中的一个平面, 它也垂直于另一个平面。
直线与平面垂直的性质定理:如果两条直线同垂直于一个平面, 那么这两条直线平行。
射影定理:从平面外一点向这个平面所引的垂线段和斜线段中, (1)射影相等的两条斜线段相等,射影较长的斜线段也较长; (2)相等的斜线段的射影相等,较长的斜线段的射影也较长; (3)垂线段比任何一条斜线段都短。