(完整版)解直角三角形》单元测试卷及答案,推荐文档
- 格式:pdf
- 大小:133.21 KB
- 文档页数:3

解直角三角形 单元检测试卷一、单选题(共10题;共30分)1.在△ABC 中,∠C=90°,BC=3,AC=4,则sinA 的值是( ) A. 34 B. 35 C. 45 D. 432.一个三角形的两边长分别是3和7,且第三边长为整数,这样的三角形周长最大的值为( )A. 15B. 16C. 18D. 19 3.为测量某河的宽度,小军在河对岸选定一个目标点A ,再在他所在的这一侧选点B ,C ,D ,使得AB ⊥BC ,CD ⊥BC ,然后找出AD 与BC 的交点E .如图所示,若测得BE=90m ,EC=45m ,CD=60m ,则这条河的宽AB 等于( )A. 120mB. 67.5mC. 40mD. 30m 4.等腰三角形的周长为20cm ,腰长为x cm ,底边长为y cm ,则底边长与腰长之间的函数关系式为( )A. y=20﹣x (0<x <10)B. y=20﹣x (10<x <20)C. y=20﹣2x (10<x <20)D. y=20﹣2x (5<x <10)5.一段拦水坝横断面如图所示,迎水坡AB 的坡度为i=1:√3 , 坝高BC=6m ,则坡面AB 的长度( )A. 12mB. 18mC. 6√3D. 12√3 6.汶川地震后,抢险队派一架直升飞机去A 、B 两个村庄抢险,飞机在距地面450米上空的P 点,测得A 村的俯角为30°,B 村的俯角为60°(如图)则A ,B 两个村庄间的距离是( )米.A. 300B. 900C. 300 √2D. 300 √37.如图,小明晚上由路灯A 下的点B 处走到点C 处时,测得自身影子CD 的长为1米,他继续往前走3米到达点E 处(即CE=3米),测得自己影子EF 的长为2米,已知小明的身高是1.5米,那么路灯A 的高度AB 是( )A. 4.5米B. 6米C. 7.2米D. 8米 8.一个三角形的两边长为2和6,第三边为偶数,则这个三角形的周长为( )A. 10B. 12C. 14D. 16 9.如图,斜面AC 的坡度(CD 与AD 的比)为1:2,AC=3 √5 米,坡顶有旗杆BC ,旗杆顶端B 点与A 点有一条彩带相连.若AB=10米,则旗杆BC 的高度为( )A. 5米B. 6米C. 8米D. (3+ √5 )米 10.如图,在□ABCD 中,AB ∶AD=3∶2,∠ADB=60°,那么cos A的值等于( )A. 3−√66B. √3+3√26C. 3+√66D. √3+2√26二、填空题(共10题;共33分)11.小凡沿着坡角为30°的坡面向下走了2米,那么他下降________米.12.已知一个等腰三角形的两边长分别为3和6,则该等腰三角形的周长是________. 13.如图是一个中心对称图形,A 为对称中心,若∠C=90°, ∠B=30°,AC=1,则BB′的长为________.14.如图,在直角坐标系中,P是第二象限的点,其坐标是(x,8),且OP与x轴的负半轴的夹角α的,则x=________,cosα=________.正切值是4315.在Rt△ABC中,∠C=90°,如果AC=4,sinB=2,那么AB=________316.高4 m的旗杆在水平地面上的影子长6 m,此时测得附近一个建筑物的影长24 m,则该建筑物的高是________m.17.tan________ °=0.7667.18.如图:∠DAE=∠ADE=15°,DE∥AB,DF⊥AB,若AE=8,则DF等于________.19.如图,将两块直角三角形的一条直角边重合叠放,已知AC=BC= √3+1,∠D=60°,则两条斜边的交点E到直角边BC的距离是________.x2+mx对应的函数值分别为y1,y2,y3,20.已知当x1=a,x2=b,x3=c时,二次函数y= 12若正整数a,b,c恰好是一个三角形的三边长,且当a<b<c时,都有y1<y2<y3,则实数m的取值范围是________.三、解答题(共8题;共57分)21.如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行多少海里与钓鱼岛A的距离最近?22.小宇想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB 与EF之间的距离为60米,求A、B两点的距离.23.如图,为了测量出楼房AC的高度,从距离楼底C处60 √3米的点D(点D与楼底C在同一水平上)出发,沿斜面坡度为i=l:√3的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53 °,求楼房AC的高度(参考数据:sin53 °= 45, cos53 °= 35, tan53°= 43,√3≈1.732,结果精确到0.1米)24.如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,求楼房CD的高度(√3=1.7).25.“蘑菇石”是我国著名的自然保护区梵净山的标志,小明从山脚B点先乘坐缆车到达观景平台DE观景,然后再沿着坡脚为29°的斜坡由E点步行到达“蘑菇石”A点,“蘑菇石”A点到水平面BC的垂直距离为1890m.如图,DE∥BC,BD=1800m,∠DBC=80°,求斜坡AE的长度.(结果精确到0.1m,可参考数据sin29°≈0.4848,sin80°≈0.9848,cos29°≈0.8746,cos80°≈0.1736)26.在一次数学活动课上,老师带领同学们去测量一座古塔CD的高度.他们首先从A处安置测倾器,测得塔顶C的仰角∠CFE=21°,然后往塔的方向前进50米到达B处,此时测得仰角∠CGE=37°,已知测倾器高1.5米,请你根据以上数据计算出古塔CD的高度.(参考数据:sin37°≈ 35,tan37°≈ 34,sin21°≈ 925,tan21°≈ 38)27.在一次课题学习中,老师让同学们合作编题.某学习小组受赵爽弦图的启发,编写了下面这道题,请你来解一解.如图,将矩形ABCD的四边BA、CB、DC、AD分别延长至E、F、G、H,使得AE=CG,BF=DH,连结EF、FG、GH、HE.(1)求证:四边形EFGH为平行四边形;(2)若矩形ABCD是边长为1的正方形,且∠FEB=45°,tan∠AEH=2,求AE的长.28.如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).答案解析部分一、单选题1.【答案】B【考点】锐角三角函数的定义【解析】【解答】解:在△ABC中,∠C=90°,∵AC=4,BC=3,∴AB= √32+42=5.∴sinA= 35,故答案为:B.【分析】先根据勾股定理算出AB,再根据正切定义得出结论。

沪科版九年级数学上册《第二十三章解直角三角形》单元测试卷-附答案学校:___________班级:___________姓名:___________考号:___________(满分150分,限时120分钟)一、选择题(本大题共10小题,每小题4分,满分40分)1.(2023安徽淮南模拟)如果Rt△ABC的各边长都扩大为原来的3倍,那么锐角A 的正弦值、余弦值()A.都扩大为原来的3倍B.都缩小为原来的13C.没有变化D.不能确定2.(2023安徽宿州埇桥期末)三角函数sin 30°、cos 16°、cos 43°之间的大小关系是()A.cos 43°>cos 16°>sin 30°B.cos 16°>sin 30°>cos 43°C.cos 16°>cos 43°>sin 30°D.cos 43°>sin 30°>cos 16°3.(2023安徽巢湖三中月考)若sin(70°-α)=cos 50°,则锐角α的度数是()A.50°B.40°C.30°D.20°4.在△ABC中,∠C=90°,tan A=2,则cos A的值为()A.√55B.2√55C.12D.25.(2023安徽阜阳质检)下列运算中,值为14的是() A.sin 45°×cos 45° B.tan 45°-cos230°C.tan30°cos60°D.(tan 60°)-16.如图,在Rt△ABC中,∠ACB=90°,∠B=β,CD⊥AB,垂足为D,那么下列线段的比值不一定等于sin β的是()A.ADBD B.ACABC.ADACD.CDBC7.(2023安徽池州月考)如图,将△ABC放在每个小正方形的边长均为1的网格中,点A,B,C均在格点上,则tan A的值是()A.√55B.12C.2D.√1058.【新考法】一配电房的示意图如图所示,它是一个轴对称图形,已知AB=3 m,∠ABC=α,则房顶A离地面EF的高度为()A.(4+3sin α)mB.(4+3tan α)mC.(4+3sinα)m D.(4+3tanα)m9.(2023安徽合肥庐江期末)如图,在△ABC中,sin B=12,AB=8,AC=5,且∠C 为锐角,cos C的值是()A.35B.45C.√32D.3410.【新情境·双翼闸机】下图是一个地铁站入口的双翼闸机示意图,它的双翼展开时,双翼边缘的端点A与B之间的距离为12 cm,双翼的边缘AC=BD=64 cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为()A.76 cmB.(64√2+12)cmC.(64√3+12)cmD.64 cm二、填空题(本大题共4小题,每小题5分,满分20分)11.如果tan α=1,那么锐角α=度.12.如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,BC=6,AC=8,设∠BCD=α,则tan α=.13.如图,已知tan O=4,点P在边OA上,OP=5,点M、N在边OB上,PM=PN,3如果MN=2,那么PM=.,BC=12,D是AB的中点,过点B 14.如图,在△ABC中,∠ACB=90°,cos A=35作线段CD的垂线,交CD的延长线于点E.(1)线段CD的长为;(2)cos∠DBE的值为.三、(本大题共2小题,每小题8分,满分16分) 15.计算:2cos 30°-tan 260°3tan45°+√(sin60°−1)2.16.(2023广西梧州模拟)构建几何图形解决代数问题是“数形结合”思想的重要体现,某数学兴趣小组在尝试计算tan 15°时,采用以下方法:如图,在Rt △ACB 中,∠C =90°,∠ABC =30°,延长CB 使BD =AB ,连接AD ,得∠D =15°,设AC =1,则AB =2,BC =√3,所以tan 15°=ACCD =2+√3=√3(2+√3)×(2−√3)=2-√3,类比这种方法,计算tan 22.5°的值(画出计算所需图形,并用文字、计算说明).四、(本大题共2小题,每小题8分,满分16分)17.(2021广东潮州中考)如图,在Rt△ABC中,∠A=90°,作BC的垂直平分线交AC于点D,延长AC至点E,使CE=AB.(1)若AE=1,求△ABD的周长;BD,求tan∠ABC的值.(2)若AD=1318.(2023安徽合肥瑶海期末)有一架长为6米的梯子AB,将它的上端A靠着墙面,下端B放在地面上,梯子与地面所成的角记为α,地面与墙面互相垂直(如图1所示).一般满足50°≤α≤75°时,人才能安全地使用这架梯子.(1)当梯子底端B距离墙面2.5米时,人是否能安全地使用这架梯子?(2)当人能安全地使用这架梯子,且梯子顶端A离地面最高时,梯子开始下滑,如果梯子顶端A沿着墙面下滑1.5米到墙面上的D点处停止,梯子底端B也随之向后平移到地面上的点E处(如图2所示),此时人是否能安全地使用这架梯子?请说明理由.(参考数据:sin 50°≈0.77,cos 50°≈0.64,sin 75°≈0.97,cos 75°≈0.26)五、(本大题共2小题,每小题10分,满分20分)19.如图,数学兴趣小组成员在热气球A上看到横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为53°和45°,已知大桥BC与地面在同一水平面上,其长度为75米,又知此时地面气温为20 ℃,海拔每升高100米,气温会下降约0.6 ℃,试求此时热气球(体积忽略不计)附近的温度.(参考数据:sin53°≈45,cos53°≈3 5,tan53°≈43)20.【方程思想】李老师给班级布置了一个实践活动,测量某广场纪念碑的高度,使用卷尺和测角仪测量.如图,纪念碑设在1.2 m的石台上,他们先在点B处测得纪念碑最高点A的仰角为22°,然后沿水平方向前进21 m,到达点N处,在点C 处测得点A的仰角为45°,BM=CN=1.7 m,求纪念碑的高度.(结果精确到0.1 m,参考数据:sin 22°≈0.37,cos 22°≈0.93tan 22°≈0.40,√2≈1.41)六、(本题满分12分)21.【主题教育·生命安全与健康】某校为检测师生体温,在校门安装了某型号测温门,如图,已知测温门AD的顶部A距地面2.2 m.某数学兴趣小组为了解测温门的有效测温区间,做了如下实践:身高为1.6 m的组员在地面N处时测温门开始显示额头温度,此时在额头B处测得A的仰角为20°,在地面M处时,测温门停止显示额头温度,此时在额头C处测得A的仰角为60°.求有效测温区间MN的长度.(参考数据:sin 20°≈0.34,cos 20°≈0.94,tan 20°≈0.36,√3≈1.73,额头到地面的距离以身高计,计算结果精确到0.1 m)七、(本题满分12分)22.如图,某大楼的顶部竖有一块广告牌CD,小明在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1∶√3,AB=16米,AE=24米.(1)求点B距水平面AE的高度BH;(2)求广告牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:√2≈1.414,√3≈1.732)八、(本题满分14分)23.(2022四川自贡中考)某数学兴趣小组自制测角仪到公园进行实地测量,活动过程如下:(1)[探究原理]制作测角仪时,将细线一端固定在量角器圆心O处,另一端系小重物G.测量时,使支杆OM、量角器90°刻度线ON与铅垂线OG相互重合(如图①),绕点O转动量角器,使观测目标P与直径两端点A、B共线(如图②),此时目标P的仰角∠POC=∠GON.请说明这两个角相等的理由;(2)[实地测量]如图③,公园广场上有一棵树,为测树高,同学们在观测点K处测得树顶端P 的仰角∠POQ=60°,观测点与树的距离KH为5米,点O到地面的距离OK为1.5米,求树高PH;(√3≈1.73,结果精确到0.1米)(3)[拓展探究]公园高台上有一凉亭,为测量凉亭顶端P 距地面的高度PH (如图④),同学们经过讨论,决定先在水平地面上选取观测点E 、F (E 、F 、H 在同一直线上),分别测得点P 的仰角为α、β,再测得E 、F 间的距离为m 米,点O 1、O 2到地面的距离O 1E 、O 2F 均为1.5米.求PH (用α、β、m 表示).参考答案与解析1.C Rt △ABC 的各边长都扩大为原来的3倍后,所得的三角形与Rt △ABC 是相似的,∴锐角A 的大小是不变的,∴锐角A 的正弦值、余弦值没有变化.2.C ∵sin 30°=cos 60°,16°<43°<60°,余弦值随着角度的增大而减小,∴cos 16°>cos 43°>sin 30°.3.C ∵sin(70°-α)=cos 50°,∴70°-α+50°=90°,解得α=30°.故选C.4.A 在△ABC 中,∠C =90°,设∠A 、∠B 、∠C 的对边分别为a 、b 、c ,因为tan A =ab =2,所以a =2b ,由勾股定理得c =√a 2+b 2=√5b所以cos A =bc =√5b =√55.5.Bsin 45°×cos 45°=√22×√22=12,故A 不符合题意;tan 45°-cos 230°=1-(√32)2=1-34=14,故B 符合题意;tan30°cos60°=√3312=23√3,故C 不符合题意;(tan 60°)-1=(√3)-1=√33,故D 不符合题意. 6.AAD BD不一定等于sin β,故A 符合题意;∵△ABC 是直角三角形,∴sin β=AC AB,故B 不符合题意; ∵CD ⊥AB ,∠ACB =90°,∴∠ACD +∠A =∠B +∠A =90°∴∠ACD =∠B ,∴sin β=ADAC,故C 不符合题意;∵△BCD 是直角三角形,∴sin β=CDBC,故D 不符合题意.7.B 如图,取格点D ,连接BD由题意得AD 2=22+22=8,BD 2=12+12=2,AB 2=12+32=10,∴AD 2+BD 2=AB 2 ∴△ABD 是直角三角形,∴∠ADB =90°,在Rt △ABD 中 AD =2√2,BD =√2,∴tan A =BDAD =√22√2=12. 8.A 过点A 作AD ⊥BC 于点D ,如图∵AD ⊥BC ,∠ABC =α,∴sin α=AD AB=AD3,∴AD =3sin α m ,∴房顶A 离地面EF 的高度=AD +BE =(4+3sin α)m .9.A 如图,过点A 作AD ⊥BC ,垂足为D∴∠ADB =∠ADC =90°在Rt △ABD 中,sin B =12,AB =8,∴AD =AB ·sin B =8×12=4在Rt △ADC 中,AC =5,∴CD =√AC 2−AD 2=√52−42=3,∴cos C =CD AC =35.10.A 如图所示,过A 作AE ⊥CP 于E ,过B 作BF ⊥DQ 于F ,在Rt △ACE 中,AE =12AC =12×64=32(cm),同理可得BF =32 cm ,∵点A 与B 之间的距离为12 cm ,∴通过闸机的物体的最大宽度为32+12+32=76(cm).11.45解析 ∵tan α=1,∴锐角α=45度. 12.34解析 ∵CD ⊥AB ,∠ACB =90°,∴∠α+∠B =∠A +∠B =90°,∴∠α=∠A ∴tan α=tan A =68=34.13.√17解析 如图,过P 作PD ⊥OB ,交OB 于点D∵tan O =PD OD =43,∴设PD =4x ,则OD =3x∵OP =5,由勾股定理得(3x )2+(4x )2=52,∴x =1(已舍负),∴PD =4 ∵PM =PN ,PD ⊥OB ,MN =2,∴MD =ND =12MN =1在Rt △PMD 中,由勾股定理得PM =√MD 2+PD 2=√17. 14.(1)152(2)2425解析 (1)在Rt △ABC 中,cos A =AC AB =35∴设AC =3x ,则AB =5x ,∴BC =√AB 2−AC 2=√(5x)2−(3x)2=4x ∵BC =12,∴4x =12,∴x =3,∴AB =15,AC =9,∵D 是AB 的中点 ∴CD =12AB =152.(2)∵∠ACB =90°,D 是AB 的中点,∴△CBD 的面积=12×△ABC 的面积,∴12CD ·BE =12×12AC ·BC ,∴152BE =12×9×12,∴BE =365,在Rt △BDE 中cos ∠DBE =BE BD=365152=2425.15.解析原式=2×√32-(√3)23×1+1-√32=√3-1+1-√32=√32. 16.解析 如图,在等腰直角△ABC 中,∠C =90°,延长CB 至点D ,使得AB =BD ,则∠BAD =∠D.∵∠ABC =45°=∠BAD +∠D =2∠D ,∴∠D =22.5° 设AC =1,则BC =1,AB =√2AC =√2 ∴CD =CB +BD =CB +AB =1+√2 ∴tan 22.5°=tan D =ACCD =1+√2=√2−1(1+√2)×(√2−1)=√2-1.17.解析 (1)如图,连接BD ,设BC 的垂直平分线交BC 于点F ,∴BD =CD ∴C △ABD =AB +AD +BD =AB +AD +DC =AB +AC. ∵AB =CE ,∴C △ABD =AC +CE =AE =1 故△ABD 的周长为1.(2)设AD =x ,∴BD =3x.∵BD=CD,∴AC=AD+CD=4x在Rt△ABD中,AB=√BD2−AD2=√(3x)2−x2=2√2x∴tan∠ABC=ACAB =2√2x=√2.18.解析(1)在Rt△AOB中,cos α=OBAB∴OB=AB·cos α当α=50°时,OB=AB·cos α≈6×0.64=3.84当α=75°时,OB=AB·cos α≈6×0.26=1.56.∵1.56<2.5<3.84∴此时人能安全地使用这架梯子.(2)此时人不能安全地使用这架梯子.理由如下:当∠ABO=75°时∵sin∠ABO=AOAB∴AO=AB·sin 75°≈6×0.97=5.82(米)∵梯子顶端A沿着墙面下滑1.5米到墙面上的D点∴OD=AO-AD=5.82-1.5=4.32(米).当∠ABO=50°时∵sin∠ABO=AOAB∴AO=AB·sin∠ABO≈6×0.77=4.62(米)∵4.32<4.62∴此时人不能安全地使用这架梯子.19.解析过A作AD⊥BC,交CB的延长线于点D,如图所示则∠ACD=45°,∠ABD=53°,在Rt△ACD中,tan∠ACD=ADCD∴CD=ADtan45°=AD1=AD在Rt△ABD中,tan∠ABD=ADBD ,∴BD=ADtan53°≈AD43=34AD由题意得AD-34AD=75,∴AD=300 m,∵此时地面气温为20 ℃,海拔每升高100米,气温会下降约0.6 ℃,∴此时热气球(体积忽略不计)附近的温度约为20-300100×0.6=18.2(℃).答:此时热气球(体积忽略不计)附近的温度约为18.2 ℃.20.解析延长BC交AF于E,延长AF交MN的延长线于D,如图则四边形BMNC、四边形BMDE是矩形∴BC=MN=21 m,DE=CN=BM=1.7 m∵∠AEC=90°,∠ACE=45°∴△ACE是等腰直角三角形∴CE=AE设AE=CE=x m∴BE=(21+x)m∵∠ABE=22°∴tan 22°=AE BE =x21+x≈0.40,解得x =14∴AE =14 m∴AD =AE +ED =14+1.7=15.7(m) ∴纪念碑的高度=15.7-1.2=14.5(m). 答:纪念碑的高度约为14.5 m . 21.解析 延长BC 交AD 于点E则DE =CM =BN =1.6 m ,BC =MN ,∠AEB =90° ∵AD =2.2 m∴AE =AD -DE =2.2-1.6=0.6(m) 在Rt △ACE 中,∠ACE =60° ∴CE =AE tan60°=√3≈0.35(m)在Rt △ABE 中,∠ABE =20° ∴BE =AE tan20°≈0.60.36≈1.67(m)∴MN =BC =BE -CE =1.67-0.35=1.32(m) ∴有效测温区间MN 的长度约为1.32 m .22.解析 (1)Rt △ABH 中,tan ∠BAH =√3=√33 ∴∠BAH =30°,∴BH =12AB =8米.(2)如图,过B 作BG ⊥DE 于G 由(1)得BH =8米,易得AH =8√3米∴BG=HE=AH+AE=(8√3+24)米,在Rt△BGC中,∠CBG=45°∴CG=BG=(8√3+24)米.在Rt△ADE中,∠DAE=60°,AE=24米,∴DE=√3AE=24√3米.∴CD=CG+GE-DE=8√3+24+8-24√3=32-16√3≈4.3(米).答:广告牌CD的高约为4.3米.23.解析(1)∵∠COG=90°,∠AON=90°∴∠POC+∠CON=∠GON+∠CON∴∠POC=∠GON.(2)由题意可得KH=OQ=5米,QH=OK=1.5米,∠PQO=90°,∠POQ=60°在Rt△PQO中,tan∠POQ=PQOQ∴tan 60°=PQ5∴PQ=5√3米∴PH=PQ+QH=5√3+1.5≈10.2(米)即树高PH约为10.2米.(3)由题意可得O1O2=m米,O1E=O2F=DH=1.5米,tan β=PDO2D ,tan α=PDO1D∴O2D=PDtanβ,O1D=PDtanα∵O1O2=O2D-O1D,∴m=PDtanβ-PD tanα∴PD=mtanα·tanβtanα−tanβ米,∴PH=PD+DH=(mtanα·tanβtanα−tanβ+1.5)米。
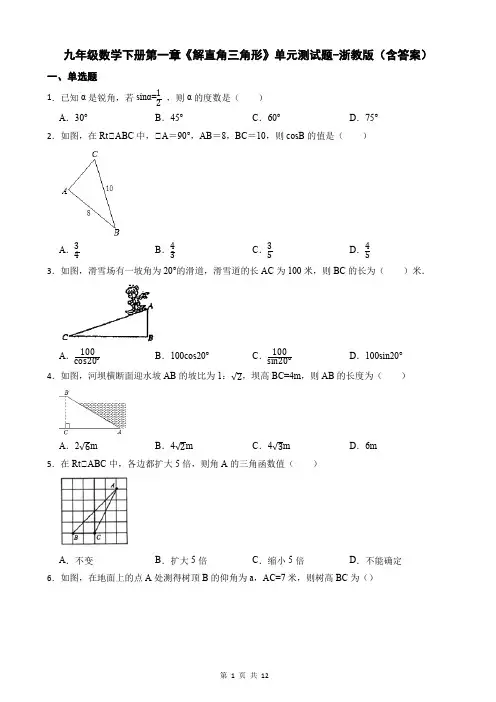
九年级数学下册第一章《解直角三角形》单元测试题-浙教版(含答案)一、单选题1.已知α是锐角,若sinα=12,则α的度数是()A.30°B.45°C.60°D.75°2.如图,在Rt△ABC中,△A=90°,AB=8,BC=10,则cosB的值是()A.34B.43C.35D.453.如图,滑雪场有一坡角为20°的滑道,滑雪道的长AC为100米,则BC的长为()米.A.100cos20°B.100cos20°C.100sin20°D.100sin20°4.如图,河坝横断面迎水坡AB的坡比为1:√2,坝高BC=4m,则AB的长度为()A.2√6m B.4√2m C.4√3m D.6m5.在Rt△ABC中,各边都扩大5倍,则角A的三角函数值()A.不变B.扩大5倍C.缩小5倍D.不能确定6.如图,在地面上的点A处测得树顶B的仰角为a,AC=7米,则树高BC为()A .7sina 米B .7cosa 米C .7tana 米D .7tana米 7.如图,在Rt△ABC 中,△C=90°,AB=13,AC=12,则△A 的正弦值为( )A .512B .1213C .125D .5138.如图,AB 是△O 的直径,且经过弦CD 的中点H ,已知cos△CDB =45,BD =5,则OH 的长为( )A .23B .56C .1D .769.如图是大坝的横断面,斜坡AB 的坡度 i 1 =1:2,背水坡CD 的坡度i 2=1:1,若坡面CD 的长度为6√2 米,则斜坡AB 的长度为( )A .4√3B .6√3C .6√5D .2410.如图,在△ABC 中,AB =AC ,BC =8,E 为AC 边的中点,线段BE 的垂直平分线交边BC 于点D.设BD =x ,tan△ACB =y ,则x 与y 满足关系式( )A .x ﹣y 2=3B .2x ﹣y 2=6C .3x ﹣y 2=9D .4x ﹣y 2=12二、填空题11.若cosα=0.5,则锐角α为 度.12.计算: |√3−2|+(12)−1+2sin60°= . 13.如图,在一次测绘活动中,小华同学站在点A 的位置观测停泊于B 、C 两处的小船,测得船B 在点A 北偏东75°方向900米处,船C 在点A 南偏东15°方向1200米处,则船B 与船C 之间的距离为 米.14.如图,正方形ABCD 的边长为4,P 是边CD 上的一动点,EF△BP 交BP 于G ,且EF 平分正方形ABCD 的面积,则线段GC 的最小值是 .三、计算题15.计算: |−5|+sin30∘−(π−1)016.计算: √8−4cos45°+(12)−1+|−2| 17.观察下列等式:①sin30°= 12 ,cos60°= 12; ②sin45°= √22 ,cos45°= √22; ③sin60°= √32 ,cos30°= √32. (1)根据上述规律,计算sin 2α+sin 2(90°﹣α)= .(2)计算:sin 21°+sin 22°+sin 23°+…+sin 289°.18.(1)√18 + |−√2| -(2012﹣π)0-4sin45°(2)解方程:x 2-10x +9=0.四、解答题19.如图,某商店营业大厅自动扶梯AB的倾斜角为31°,AB的长为12米,求大厅两层之间的距离BC的长.(结果精确到0.1米)(参考数据:sin31°=0.515,cos31°=0.857,tan31°=0.60)20.如图,锐角△ABC中,AB=10cm,BC=9cm,△ABC的面积为27cm2.求tanB的值.21.已知sinα+cosα=1713,且0°<α<45°,求sinα的值.22.已知:在Rt△ABC 中,△C=90°,sinA=23,AC=10,求△ABC的面积。

九年级数学下册《解直角三角形》试卷学校:__________ 姓名:__________ 班级:__________ 考号:__________题号一二三总分得分评卷人得分一、选择题1.(2分)三角形在正方形网格纸中的位置如图所示,则sinα的值是()A.34B.43C.35D.452.(2分)如图,在Rt△ABC中,∠C=90°,AC=3,AB=5.则cosB等于()A.34B.43C.35D.453.(2分) 如图,在300 m高的峭壁上测得一塔顶与塔基的俯角分别为 30°和 60°,则塔高 CD 约为()A.100m B.200m C.150m D.180m4.(2分)若把 Rt△ABC 的各边都扩大 3倍,则各边扩大后的cosB 与扩大前的cosB 的值之间的关系是()A.扩大3倍B.缩小3倍C.相等D.不能确定5.(2分)如图是某小区的一块三角形空地,准备在上面种植某种草皮以美化环境,已知这种草皮每平方米售价为m元,则购买这种草皮至少需要()A.450m元B.225m元C.150m元D.300m元6.(2分)在△ABC 中,∠C= 90°,如果∠B = 60°,那sinA+cosB=()A.14B.1 C12+D13+评卷人得分二、填空题7.(3分)某市为改善交通状况,修建了大量的高架桥.一汽车在坡度为30°的笔直高架桥点A 开始爬行,行驶了150米到达点B ,则这时汽车离地面的高度为 米. 8.(3分)已知正三角形的周长是 6,则它的面积为 .9.(3分)在直角三角形ABC 中,∠A=090,AC=5,AB=12,那么tan B = . 10.(3分) 如图所示,将两条宽度为 3cm 的纸带交叉叠放,若α已知,则阴影部分的面积为 .11.(3分)如图所示,某人在高楼A 处观测建筑物D 点,则它的俯角是 .12.(3分)一斜坡的坡比为 1:2,其最高点的垂直距离为 50m ,则该斜坡的长为 m . 13.(3分)Rt △ABC 中,斜边与一直角边比为25:7,则较小角的正切值为 . 14.(3分)计算:21()(12)4x x x −+÷−= .15.(3分)已知 CD 是 Rt △ABC 斜边上的高线,且 AB= 10,若 sin ∠ACD=45,则CD= . 评卷人 得分三、解答题16.(6分)又到了一年中的春游季节,某班学生利用周末到白塔山去参观“晏阳初博物馆”.下面是两位同学的一段对话: 甲:我站在此处看塔顶仰角为60 乙:我站在此处看塔顶仰角为30 甲:我们的身高都是1.5m乙:我们相距20m请你根据两位同学的对话,计算白塔的高度(精确到1米).17.(6分)如图,水坝的横断面是梯形,迎水坡BC的坡角30∠=°,背水坡AD的坡度为B1:2,坝顶DC宽25米,坝高CE是45米,求:坝底AB的长,迎风坡BC的长以及BC 的坡度.(答案可以带上根号)18.(6分)燕尾槽的横断面是等腰梯形.如图是一燕尾槽的横断面,其中燕尾角B是55,外口宽AD是16cm,燕尾槽的深度是6cm,求它的里口宽BC(精确到0.1cm).19.(6分)某科技馆座落在山坡M 处,从山脚A 处到科技馆的路线如图所示.已知A 处海拔高度为103.4m ,斜坡AB 的坡角为30,40m AB =,斜坡BM 的坡角为18,60m BM =,那么科技馆M 处的海拔高度是多少?(精确到0.1m )(参考数据:sin180.309= cos180.951= tan180.324=)20.(6分)随着社会的发展,人们对防洪的意识越来越强,今年为了提前做好防洪准备工作,某市正在长江边某处常出现险情的河段修建一防洪大坝,其横断面为梯形ABCD ,如图所示,根据图中数据计算坝底 CD 的宽度. (结果保留根号)21.(6分)下图为住宅区内的两幢楼,它们的高m CD AB 30==,现需了解甲楼对乙楼的采光的影响情况.当太阳光与水平线的夹角为30°时.试求: 1)若两楼间的距离m AC 24=时,甲楼的影子,落在乙楼上有多高? 2)若甲楼的影子,刚好不影响乙楼,那么两楼的距离应当有多远?甲 乙300BD22.(6分)Rt △ABC 中,∠C=90°,cosB=32,求a:b:c 等于多少?23.(6分)在Rt △ABC 中,∠C =900,AB =13,BC =5,求A sin , A cos ,A tan .24.(6分)化简:=−2)3(π .25.(6分)计算:322(3)a a −÷= .26.(6分)计算:(1))1)(1()2(2−+−+x x x (2))()23(3223ab ab b a b a ÷+−(3)262−−x x ÷ 4432+−−x x x27.(6分)已知等腰三角形的底边长为20,面积为10033,求这个等腰三角形的三个内角度数及腰长.28.(6分)如图所示,已知∠ACB=90° , AB=13 , AC=12 ,∠BCM=∠BAC,求cosB 及点B 到直线MN的距离.29.(6分)已知a、b、c是△ABC的三边,a、b、c满足等式2(2)4()()b c a c a=+−,且有5a-3c=0,求 sinB 的值.30.(6分)如图,在Rt△ABC 中,∠C= 90°,AC=5,BC=12,求B的正弦、余弦和正切的值.【参考答案】***试卷处理标记,请不要删除一、选择题1.C2.D 3.B 4.C 5.C 6.B二、填空题7.7589.125 10.9sin a11.∠EAD12. 13.247 14.1142x − 15.24三、解答题16.由题目可得:30CAB ∠=,60CBD ∠=,20m AB =, 1.5m AM BN DP ===.在ABC △中,CBD ACB CAB ∠=∠+∠,603030ACB ∴∠=−=,A M N PC B 乙 甲 6030 ACB CAB ∴∠=∠,20m BC AB ∴==.在Rt CBD △中,20m BC =,60CBD ∠=sin CD CBD BC ∠=,sin 6020CD∴=,320sin 6020103m CD ∴===103 1.519m CP CD DP ∴=+=≈.答:白塔的高度约为19米.17.解:452AF =∵452AF = 30tan 45=BE ,453BE =45225453AB =+∴(米),又451sin302BC ==∵° 90BC =(米),BC 的坡度为3.18.解:作AE BC DF BC ⊥⊥,,垂足分别为E ,F , 在Rt ABE △中,tan AEB BE=, ∴ tan AE BE B ==6tan 55. ∴6221624.4tan 55BC BE AD =+=⨯+≈(cm ). 答:燕尾槽的里口宽BC 约为24.4cm .19.解:过B 向水平线AC 作垂线BC ,垂足为C ,过M 向水平线BD 作垂线MD , 垂足为D ,则11402022BC AB ==⨯=. sin18MD BM =600.309=⨯18.54=.∴科技馆M 处的海拔高度是:103.42018.54141.94141.9(m)++=≈.20.在 Rt △ADF 中,∠D=60°,tan AFD DF =,∴3933tan 3AF DF D ==⨯=在 Rt △BEC 中,∵∠C=45°,∴△BEC 为等腰直角三角形∴EC= BE=9,在矩形 AFEB 中,FE=AB=10,∴DC DF FE EC ⋅=++331091933=+=+21.解:(1)设阳光照射在乙楼CD 的E 处,连结BD ,则BD=AC=24,∠D BE =30°,DE=33BD=83,∵AB=CD=30,∴CE=30-83;即阳光照射在乙楼离地面高30-83米处;(2)要使甲楼的影子不影响乙,则阳光刚好照射在乙楼C 处,在Rt △ABC 中,∠A BC =60°,AC=3AB=303,即两楼相距303米. 22.3:5:2. 23.135sin =A , 1312cos =A ,125tan =A . 24.3−π25.49a26.(1)54+x ;(2)2223b ab a +−;(3)42−x . 27.如图所示,AB=AC,∵BC=20,10033ABC S ∆=,∴1033AH =,∵BH=10,∴3tan 3B =∴∠B= 30°, ∴∠C= 30°, ∴∠BAC= 120°. Rt △ABH 中,20233AB AH ==,即△ABC 的三个内角分别为 30°, 30°,120°,腰长为2033. 28.如图过 B 作BH ⊥MNM 于H ,222213125BC AB AC =−=−=,5sin sin 13BC A BCH AB ===∠,5cos 13B = ∵sin 5BH BH BCH BC ∠==,∴2513BH =,即 B 到直线的距离为2513.29.由已知得222b c a =−,即222c a b =+,∴△ABC 是Rt △,∠C=90°, ∵530a c −=,∴35a c =. 设: a = 3k ,c= 5k ,∴b= 4k ,∴4sin 5b Bc ==. 30.5sin 13AC B AB ==,1213BC sB AB ∞==,5tan 12AC B BC ==。

华东师大版 九上数学 24章 《解直角三角形》单元测试卷(含解析)一. 选择题:(每小题2分,共20分)1. 在△EFG 中,∠G=90°,EG=6,EF=10,则cotE=( ) A.43 B.34 C. 53 D.35 2. 在△ABC 中,∠A=105°,∠B=45°,tanC 的值是( ) A. 21B.33 C. 1 D. 3 3. 在△ABC 中,若22cos =A ,3tan =B ,则那个三角形一定是( )A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等腰三角形4. 如图18,在△EFG 中,∠EFG=90°,FH ⊥EG ,下面等式中,错误的是( ) A.EG EF G =sin B. EF EHG =sinC. FGGH G =sinD. FGFH G =sin5. sin65°与cos26°之间的关系为( )A. sin65°<cos26°B. sin65°>cos26°C. sin65°=cos26°D. sin65°+cos26°=16. 已知30°<α<60°,下列各式正确的是( )A. B. C. D.7. 在△ABC 中,∠C=90°,52sin A ,则sinB 的值是( )A.32B.52 C.54 D. 521 8. 若平行四边形相邻两边的长分别为10和15,它们的夹角为60°,则平行四边形的面积是( )米2A. 150B.375 C. 9 D. 79. 如图19,铁路路基横断面为一个等腰梯形,若腰的坡度为i=2∶3,顶宽是3米,路基高是4米,则路基的下底宽是( )A. 7米B. 9米 C. 12米 D. 15米10. 如图20,两条宽度都为1的纸条,交叉重叠放在一起,且它们的交角为α,则它们重叠部分(图中阻影部分)的面积为( )A. αsin 1B. αcos 1C. αsinD. 1二. 填空题:(每小题2分,共10分)11. 已知0°<α<90°,当α=__________时,21sin =α,当α=__________时,Cota=3.12. 若,则锐角α=__________。

第一章直角三角形的边角关系综合测试卷 一、选择题(满分30分)1.在Rt△ABC 中,∠C=90°,如果cosA=,那么tanB 的值为( ) A .B .C .D .2.计算:cos 245°+tan60°•sin60°的值为( ) A . 1B . 2C .D .3.点M (﹣sin60°,cos60°)关于x 轴对称的点的坐标是( ) A .() B .(﹣) C .(﹣) D .(﹣) 4.每周一学校都要举行庄严的升国旗仪式,让我们感受到了国旗的神圣.某同学站在离国旗旗杆12米远的地方,当国旗升起到旗杆顶时,他测得视线的仰角为30°,若这位同学的目高1.6米,则旗杆的高度为( )A .米B .米C .米D .米5.如图,把两块相同的含30°角的三角尺按如图所示放置,若AD=,则三角尺的斜边的长为( )A . 6B .C . 10D . 126.已知α为锐角,下列结论:(1)sinα+cosα=1;(2)若α>45°,则sinα>cosα;(3)如果cosα>,则α<60°;(4)=1﹣sinα.其中正确结论的序号是( ) A .(1)(3)(4) B . (2)(4) C .(2)(3)(4)D .(3)(4)7.有人说,数学家就是不用爬树或者把树砍倒就能够知道树高的人.小敏想知道校园内一棵大树的高,如图,她测得BC=10米,∠ACB=50°,请你帮助她算出树高AB 约为( )米. (注:①树垂直于地面;②供选用数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.2)A . 7.7B . 8C . 6.4D . 128.如图,△ABC 中,∠C=90°,AD 是∠BAC 的角平分线,交BC 于点D ,那么=( )A . s in∠BA CB . c os∠BA CC . t an∠BA CD . c ot∠BAC9.将宽为2cm 的长方形纸条折叠成如图所示的形状,那么折痕PQ 的长是( )A .cm B .cm C .cm D . 2cm10.=( )A .B .C .D . 1二、填空题(满分30分)11.已知山坡的坡度i=1:,则坡角为____度.12.判定方程x 2﹣x •cos30°+cos60°=0的实数根情况.答:_________ .13.在正方形网格中,∠AOB 的位置如图所示,则cos∠AOB 的值是_________ .14.当锐角α_______时,有意义.15.在△ABC 中,∠A,∠B 都是锐角,cosA=,sinB=,则△ABC 的形状是_________.16.如图,小华为了测量所住楼房的高度,他请来同学帮忙,测量了同一时刻他自己的影长和楼房的影长分别是0.5米和15米.已知小华的身高为1.6米,那么他所住楼房的高度为________米.17.小明骑自行车以15千米/小时的速度在公路上向正北方向匀速行进,如图,出发时,在B 点他观察到仓库A 在他的北偏东30°处,骑行20分钟后到达C 点,发现此时这座仓库正好在他的东南方向,则这座仓库到公路的距离为 _________ 千米.(参考数据:≈1.732,结果保留两位有效数字)18.在数学活动课上,小敏,小颖分别画了△ABC和△DEF,AB=DE ,数据如图,如果把小敏画的三角形面积记作S △ABC′小颖画的三角形面积记作S △DEF ,那么你认为小敏和小颖画的两个三角形的面积的大小关系是S △ABC _________ S △DEF .(填“>,<,或=”)19.如图,将以A 为直角顶点的等腰直角三角形ABC 沿直线BC 平移得到△A′B′C′,使点B′与C 重合,连接A′B,则tan∠A′BC′的值为 _________ .20..公园里有一块形如四边形ABCD的草地,测得BC=CD=10米,∠B=∠C=120°,A=45°.则这块草地的面积为_______m2.三、解答题(共8小题,满分60分)21.(8分)计算:(1)2sin30°+cot60°﹣+(﹣cot45°)2008 (2)22.(7分)如图,某超市(大型商场)在一楼至二楼之间安装有电梯,天花板(一楼的楼顶墙壁)与地面平行,请你根据图中数据计算回答:小敏身高1.85米,他乘电梯会有碰头危险吗?(sin28°≈0.47,tan28°≈0.53)23.(7分)如图,两条笔直的公路AB、CD相交于点O,∠AOC为36°,指挥中心M设在OA路段上,与O地的距离为18千米,一次行动中,王警官带队从O地出发,沿OC方向行进.王警官与指挥中心均配有对讲机,两部对讲机只能在10千米之内进行通话,通过计算判断王警官在行进过程中能否实现与指挥中心用对讲机通话.(参考数据:sin36°=0.59,cos36°=0.81,tan36°=0.73)24.(10分)如图,小华家的住宅楼AB与北京奥运会主体育场鸟巢隔水相望且能看到鸟巢的最高处CD,两建筑物的底部在同一水平面上,视野开阔,但不能直接到达,小华为了测量鸟巢的最大高度CD,只能利用所在住宅楼的地理位置.现在小华仅有的测量工具是皮尺和测角仪(皮尺可测量长度,测角仪可测量仰角、俯角),请你帮助小华设计一个测量鸟巢的最大高度的方案.(1)要求写出测量步骤和必需的测量数据(用字母表示)并画出测量图形(测角仪高度忽略不计);(2)利用小华测量的数据(用字母表示),写出计算鸟巢最大高度CD的表达式.25.(8分)如图(1),先将一矩形ABCD置于直角坐标系中,已知AB=8,BC=6,使点A与坐标系的原点重合,边AB,AD分别落在x轴,y轴上,再将此矩形在坐标平面内按逆时针方向绕原点旋转30°,如图(2).请你利用三角函数知识求出矩形ABCD旋转前后点B的坐标和点C的坐标.26.(10分)如图(1),一架长4米的梯子AB斜靠在与地面OM垂直的墙ON上,梯子与地面的倾斜角α为60°.(1)求AO与BO的长;(2)若梯子顶端A沿NO下滑,同时底端B沿OM 向右滑行.如图(2),当A点下滑到A′点,B点向右滑行到B′点时,梯子AB的中点P也随之运动到P′点,若∠POP′=15°,试求AA′的长.27.(10分)一座建于若干年前的水库大坝的横断面如图所示,其中背水面的整个坡面是长为90米、宽为5米的矩形.现需将其整修并进行美化,方案如下:①将背水坡AB的坡度由1:0.75改为1:;②用一组与背水坡面长边垂直的平行线将背水坡面分成9块相同的矩形区域,依次相间地种草与栽花.(1)求整修后背水坡面的面积;(2)如果栽花的成本是每平方米25元,种草的成本是每平方米20元,那么种植花草至少需要多少元?第一章直角三角形的边角关系测试卷参考答案1.D 【解析】 设b=4x ,则c=5x ,a=3x ;∴tanB=.2.B 【解析】 原式==()2+•=+=2.3.B 【解析】先根据特殊三角函数值求出M 点坐标,再根据对称性解答.4.C 【解析】目高以上旗杆的高度h 1=12×tan30°=4(米),旗杆的高度h=h 1+1.6=1.6+4(米).5.D 【解析】根据题意,知△ABD 是等腰直角三角形,即可求得AB 的长,再根据30°的直角三角形的性质进行求解.6.C 【解析】(1)如果α=30°,那么sinα=,cosα=,sinα+cosα=≠1,错误;其余三个正确。

《解直角三角形》单元测试卷一、填空题:1、如下图,表示甲、乙两山坡的情况, _____坡更陡。
(填“甲”“乙”)αβ1213 34甲乙2、在Rt △ABC 中,∠C =90°,若AC =3,AB =5,则cosB 的值为__________。
3、在Rt △ABC 中,∠C=90°.若sinA=22,则sinB= 。
4、计算:tan 245°-1= 。
5、在△ABC 中,AB=AC=10,BC=16,则tanB=_____。
6、△ABC 中,∠C=90°,斜边上的中线CD=6,sinA=31,则S △ABC=______。
7、菱形的两条对角线长分别为23和6,则菱形较小的内角为______度。
8、如图2是固定电线杆的示意图。
已知:CD ⊥AB ,CD 33=m ,∠CAD=∠CBD=60°,则拉线AC 的长是__________m 。
9、升国旗时,某同学站在离旗杆底部24米处行注目礼,当国旗升至旗杆顶端时,该同学视线的仰角恰为30°,若双眼离地面1.5米,则旗杆的高度为______米。
(用含根号的式子表示)10、如图3,我校为了筹备校园艺术节,要在通往舞台的台阶上铺上红色地毯.如果地毯的宽度恰好与台阶的宽度一致,台阶的侧面如图所示,台阶的坡角为30,90BCA ∠=,台阶的高BC 为2米,那么请你帮忙算一算需要 米长的地毯恰好能铺好台阶.(结果精确到0.1m ,取2 1.414=,3 1.732=)11、如图4,如果△APB 绕点B 按逆时针方向旋转30°后得到△A'P 'B ,且BP=2,那么PP '的长为____________.(不取近似值. 以下数据供解题使用:sin15°=624-,cos 15°=624+)二、选择题:12、在ABC ∆中,︒=∠90C ,AB=15,sinA=13,则BC 等于( ) A 、45 B 、5 C 、15 D 、14513、李红同学遇到了这样一道题:3tan(α+20°)=1,你猜想锐角α的度数应是( ) A.40° B.30° C.20° D.10°14、身高相同的三个小朋友甲、乙、丙放风筝,他们放出的线长分别为300 m ,250 m ,200 m ;线与地面所成的角度分别为30°,45°,60°(假设风筝线是拉直的),则三人所放的风筝( )A.甲的最高B.乙的最低C.丙的最低D.乙的最高 15、在△ABC 中,若tanA=1,sinB=22,你认为最确切的判断是( ) A.△ABC 是等腰三角形 B.△ABC 是等腰直角三角形C.△ABC 是直角三角形D.△ABC 是一般锐角三角形16、如图5,某地夏季中午,当太阳移至房顶上方偏南时,光线与地面成80°角,房屋朝南的窗子高AB=1.8 m ,要在窗子外面上方安装水平挡光板AC ,使午间光线不能直接射入室内,那么挡光板的宽度AC 为( )A.1.8tan80°mB.1.8cos80°mC.︒80sin 8.1 m D.︒80tan 8.1 m17、如图6,四边形ABCD 中,∠A=135°,∠B=∠D=90°,BC=23,AD=2,则四边形ABCD 的面积是( ) A.42B.43C.4D.6三、解答题:18、计算:(1)3cos30°+2sin45° (2)6tan 2 30°-3sin 60°-2sin 45°19、根据下列条件,求出Rt △ABC(∠C=90°)中未知的边和锐角. (1)BC=8,∠B=60°; (2)AC=2,AB=2.20、如图7,在Rt △ABC 中,∠C=90°,AC=8,∠A 的平分线AD=3316,求∠B 的度数及边BC 、AB 的长.21、等腰三角形的底边长20 cm ,面积为33100c m 2,求它的各内角.22、同学们对公园的滑梯很熟悉吧!如图是某公园在“六•一”前新增设的一台滑梯,该滑梯高度AC =2m ,滑梯着地点B 与梯架之间的距离BC =4m 。

《解直角三角形》整章测试【1】一、选择题(每小题3分,共24分)1.在Rt △ABC 中, ∠C=90︒,AB=4,AC=1,则cos A 的值是( )(A )154(B)14(C)15 (D)42.计算:2)130(tan -︒=( )(A)331-(B)13- (C)133-(D )1-3 3.在ABC ∆中,,A B ∠∠都是锐角,且sinA =21, cosB =23,则ABC ∆的形状( ) (A )直角三角形(B )钝角三角形 (C )锐角三角形 (D )不能确定4.如图,在Rt ABC △中,3tan 2B =,23BC =,则AC 等于( )(A )3(B )4(C )43(D )65.如图,小颖利用有一个锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE 为5m ,AB 为1.5m (即小颖的 眼睛距地面的距离),那么这棵树高是( ) (A)(53332+)m (B)(3532+)m (C)533m (D)4m 6.因为1sin 302=,1sin 2102=-, 所以sin 210sin(18030)sin 30=+=-;因为2sin 452=,2sin 2252=-,所以sin 225sin(18045)sin 45=+=-,由此猜想,推理知:一般地当α为锐角时有sin(180)sin αα+=-,由此可知:sin 240=( )(A )12-(B)22-(C)32- (D)3-7.如图,客轮在海上以30km/h 的速度由B 向C 航行,在B 处测得 灯塔A 的方位角为北偏东80,测得C 处的方位角为南偏东25,航 行1小时后到达C 处,在C 处测得A 的方位角为北偏东20,则C 到A 的距离是( )(A)156km(B)152km (C)15(62)+km(D)5(632)+km北东ABC8.如图,在Rt ABC △中,906cm A AC ∠==,,8cm AB =,把AB 边翻折,使AB 边落在BC 边上,点A 落在点E 处,折痕为BD ,则sin DBE ∠的值为()(A)13(B)310(C)37373(D)1010二、填空题(每小题3分,共24分) 9.计算sin 60tan 45cos30-的值是.10. 用“>”或“<”号填空:1sin 50cos 402-0.(可用计算器计算) 11.在Rt ABC △中,90C ∠=,:3:4BC AC =,则cos A =. 12.如图,一架梯子斜靠在墙上,若梯子到墙的距离AC =3米,3cos 4BAC ∠=,则梯子AB 的长度为米.13.如图,一轮船由南向北航行到O 处时,发现与轮船相距40海里的A 岛在北偏东33方向.已知A 岛周围20海里水域有暗礁, 如果不改变航向,轮船(填“有”或“没有”)触暗礁 的危险.(可使用科学计算器)14. 如图,在菱形ABCD 中,DE ⊥AB ,垂足为E ,DE=6cm ,3sin 5A =,则菱形ABCD 的面积是__________2cm . 15.根据指令[s,A](s ≥0,0°≤A <360°)机器人在平面上能完成如下动作:先在原地逆时针旋转角度A ,再朝其面对的方向沿直线行走距离s .现在机器人在平面直角坐标系的原点,且面对y 轴的负方向,为使其移动到点(-3,3),应下的指令是.16. 有古诗“葭生池中”今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问: 水深、葭长各几何?(1丈=10尺)回答:水深,葭长. 17.(本题8分)计算:242(2cos 45sin 60)4︒-︒+. 18.(本题10分)某校数学兴趣小组在测量一座池塘边上A B ,两点间的距离时用了以下三种测量方法,如下图所示.图中a b c ,,表示长度,β表示角度.请你分别求出AB 的长度(用含有a b c β,,,字母的式子表示).(1)______AB = (2)______AB = (3)______AB =19.(本题10分)小强家有一块三角形菜地,量得两边长分别为40m ,50m ,第三边上的高为30m ,请你帮小强计算这块菜地的面积(结果保留根号). 20.(本题12分)海中有一个小岛P ,它的周围18海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A 测得小岛P 在北偏东60°方向上,航行12海里到达B 点,这时测得小岛P 在北偏东45°方向上.如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由. (1A C B a b(2AC B a β (3AC B aD Ec b A BCD EA BC21.(本题12分)如图,AC是某市环城路的一段,AE,BF,CD都是南北方向的街道,其与环城路AC的交叉路口分别是A,B,C.经测量花卉世界D位于点A的北偏东45°方向、点B的北偏东30°方向上,AB=2km,∠DAC=15°.(1)求B,D之间的距离;(2)求C,D之间的距离.四、附加题(本题20分)22.现代家居设计的“推拉式”钢窗,运用了轨道滑行技术,纱窗装卸时利用了平行四边形的不稳定性,操作步骤如下:(1)将矩形纱窗转化成平行四边形纱窗后,纱窗上边框嵌入窗框的上轨道槽(如图1).(2)将平行四边形纱窗的下边框对准窗框的下轨道槽(如图2).(3)将平行四边形纱窗还原成矩形纱窗,同时下边框嵌入窗框的下轨道槽(如图3).在装卸纱窗的过程中,如图所示α∠的值不得小于81,否则纱窗受损.现将高96cm的矩形纱窗恰好安装在上、下槽深分别为0.9cm,高96cm(上、下槽底间的距离)的窗框上.试求合理安装纱窗时α∠的sin810.987=0.990=sin830.993=0.995=cos90.987=0.990=0.993=0.995=章《解直角三角形》整章测试答案:~8 BABA ACDD三、17.解:2=原式2=-2=18.解:(1)AB=(2)tanAB aβ=(3)acABb=.19.解:分两种情况:(1)当ACB∠为钝角时,BD是高,90ADB∴∠=.在Rt BCD△中,40BC=,30BD=∴CD==.在Rt ABD△中,50AB=,ABC中山路文化路D和平路45°15°30°环城路EF 图1 2 图3∴40AD ==.40AC AD CD ∴=-=-,新课标第一网∴211(4030(600)22ABC S AC BD ==-⨯=-△. (2)当ACB ∠为锐角时, BD 是高,90ADB BDC ∴∠=∠=,在Rt ABD △中,5030AB BD ==,,40AD ∴==.同理CD ==∴(40AC AD CD =+=+,∴211(4030(600)22ABC S AC BD ==+⨯=+△.综上所述:2(600)ABC S =±△.20.解:有触礁危险.理由: 过点P 作PD ⊥AC 于D .设PD 为x ,在Rt △PBD 中,∠PBD=90°-45°=45°. ∴BD =PD =x .在Rt △PAD 中,∵∠PAD =90°-60°=30°,∴x .xAD 330tan =︒=∵BD ,AB AD +=∴x .x +=123 ∴)13(61312+=-=x .∵,<18)13(6+∴渔船不改变航线继续向东航行,有触礁危险.21. 解:(1)由题意得,∠EA D =45°,∠FBD=30°. ∴∠EAC=∠EA D +∠DA C =45°+15°=60°. ∵ AE∥BF∥CD,∴ ∠FBC=∠EAC =60°. ∴ ∠DBC=30°.又∵ ∠DBC=∠DAB+∠ADB, ∴ ∠ADB=15°.∴∠DAB=∠ADB.∴ BD=AB=2. 即B ,D 之间的距离为2km .(2)过B 作BO⊥DC,交其延长线于点O , 在Rt△DBO 中,BD=2,∠DBO=60°. ∴ DO=2×sin60°=2×323=,BO=2×cos60°=1. 在Rt△CBO 中,∠CBO=30°,CO=BOtan30°=33, ∴ CD=DO-CO=332333=-(km ). 即C ,D 之间的距离为332km . 22. 解:能够合理装上平行四边形纱窗时的最大高度:960.995.1-=(cm ) 能够合理装上平行四边形纱窗时的高:96sin α∠或96cos(90)α-∠·°当81α∠=°时,纱窗高:96sin81960.98794.75295.1=⨯=<° ∴此时纱窗能装进去,当82α∠=°时,纱窗高:96sin82960.99095.0495.1=⨯=<° ∴此时纱窗能装进去.当83α∠=°时,纱窗高:96sin83960.99395.32895.1=⨯=>° ∴此时纱窗装不进去.因此能合理装上纱窗时α∠的最大值是82°.。

2019年华师大版数学上册九年级《第24章解直角三角形》单元测试卷一.选择题(共15小题)1.具备下列条件的△ABC中,不是直角三角形的是()A.∠A+∠B=∠C B.∠A﹣∠B=∠CC.∠A:∠B:∠C=1:2:3D.∠A=∠B=3∠C2.如图,∠ACB=90°,CD⊥AB,垂足为D,下列结论错误的是()A.图中有三个直角三角形B.∠1=∠2C.∠1和∠B都是∠A的余角D.∠2=∠A3.如图,已知∠ACB=90°,CD⊥AB,垂足是D,则图中与∠A相等的角是()A.∠1B.∠2C.∠B D.∠1、∠2和∠B 4.如图,在直角三角形ABC中,AC≠AB,AD是斜边上的高,DE⊥AC,DF⊥AB,垂足分别为E、F,则图中与∠C(∠C除外)相等的角的个数是()A.3个B.4个C.5个D.6个5.Rt△ABC中,∠C=90°,∠B=54°,则∠A的度数是()A.66°B.36°C.56D.46°6.在Rt△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACD交AB于E,则下列结论一定成立的是()A.BC=EC B.EC=BE C.BC=BE D.AE=EC7.下列命题:(1)相等的角是对顶角.(2)同位角相等(3)直角三角形的两个锐角互余.(4)若两条线段不相交,则两条线段平行.其中正确的命题个数有()A.1个B.2个C.3个D.4个8.如果直角三角形的一个锐角是另一个锐角的4倍,那么这个直角三角形中一个锐角的度数是()A.9°B.18°C.27°D.36°9.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,如果AC=3,AB=6,那么AD 的值为()A.B.C.D.310.如图,△ABC中,点D在线段BC上,且∠BAD=∠C,则下列结论一定正确的是()A.AB2=AC•BD B.AB•AD=BD•BCC.AB2=BC•BD D.AB•AD=BD•CD11.已知,在Rt△ABC中,∠C=90°,AC=3,BC=4,则sin A的值为()A.B.C.D.12.当锐角A的cos A>时,∠A的值为()A.小于45°B.小于30°C.大于45°D.大于30°13.如果α是锐角,且sinα=,那么cos(90°﹣α)的值为()A.B.C.D.14.在Rt△ABC中,∠C=90°,sin B=,则tan A的值为()A.B.C.D.15.已知sin A=,则锐角A的度数是()A.30°B.45°C.60°D.75°二.填空题(共8小题)16.在Rt△ABC中,∠C=Rt∠,∠A=70°,则∠B=.17.在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1:2:3,③∠A=90°﹣∠B,④∠A=∠B=∠C中,能确定△ABC是直角三角形的条件有(填序号)18.已知:如图,在△ABC中,AD⊥BC,垂足为点D,BE⊥AC,垂足为点E,M为AB边的中点,连结ME、MD、ED.设AB=4,∠DBE=30°,则△EDM的面积为.19.如图,已知∠AON=40°,OA=6,点P是射线ON上一动点,当△AOP为直角三角形时,∠A=°.20.如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,DB=2,则CD的长为.21.如图,若CD是Rt△ABC斜边上的高,AD=3,CD=4,则BC=.22.在△ABC中,∠C=90°,sin A=,BC=4,则AB值是.23.比较大小:sin44°cos44°(填>、<或=).三.解答题(共3小题)24.如图,在△ABC中,CE,BF是两条高,若∠A=70°,∠BCE=30°,求∠EBF与∠FBC的度数.25.如图,在△ACB中,∠ACB=90゜,CD⊥AB于D.(1)求证:∠ACD=∠B;(2)若AF平分∠CAB分别交CD、BC于E、F,求证:∠CEF=∠CFE.26.在△ABC中,∠B、∠C均为锐角,其对边分别为b、c,求证:=.2019年华师大版数学上册九年级《第24章解直角三角形》单元测试卷参考答案与试题解析一.选择题(共15小题)1.具备下列条件的△ABC中,不是直角三角形的是()A.∠A+∠B=∠C B.∠A﹣∠B=∠CC.∠A:∠B:∠C=1:2:3D.∠A=∠B=3∠C【分析】由直角三角形内角和为180°求得三角形的每一个角,再判断形状.【解答】解:A中∠A+∠B=∠C,即2∠C=180°,∠C=90°,为直角三角形,同理,B,C均为直角三角形,D选项中∠A=∠B=3∠C,即7∠C=180°,三个角没有90°角,故不是直角三角形,故选:D.【点评】注意直角三角形中有一个内角为90°.2.如图,∠ACB=90°,CD⊥AB,垂足为D,下列结论错误的是()A.图中有三个直角三角形B.∠1=∠2C.∠1和∠B都是∠A的余角D.∠2=∠A【分析】在△ABC中,∠ACB=90°,CD⊥AB,因而△ACD∽△CBD∽△ABC,根据相似三角形的对应角相等,就可以证明各个选项.【解答】解:∵∠ACB=90°,CD⊥AB,垂足为D,∴△ACD∽△CBD∽△ABC.A、∵图中有三个直角三角形Rt△ACD、Rt△CBD、Rt△ABC;故本选项正确;B、应为∠1=∠B、∠2=∠A;故本选项错误;C、∵∠1=∠B、∠2=∠A,而∠B是∠A的余角,∴∠1和∠B都是∠A的余角;故本选项正确;D、∵∠2=∠A;故本选项正确.故选:B.【点评】本题主要考查了直角三角形的性质,直角三角形斜边上的高,把这个三角形分成的两个三角形与原三角形相似.3.如图,已知∠ACB=90°,CD⊥AB,垂足是D,则图中与∠A相等的角是()A.∠1B.∠2C.∠B D.∠1、∠2和∠B 【分析】根据直角三角形的两个锐角互余,以及同角的余角相等即可判断.【解答】解:∵∠ACB=90°,即∠1+∠2=90°,又∵直角△ACD中,∠A+∠1=90°,∴∠A=∠2.故选:B.【点评】本题考查了直角三角形的性质:直角三角形的两个锐角互余,以及余角的性质:同角的余角相等.4.如图,在直角三角形ABC中,AC≠AB,AD是斜边上的高,DE⊥AC,DF⊥AB,垂足分别为E、F,则图中与∠C(∠C除外)相等的角的个数是()A.3个B.4个C.5个D.6个【分析】由“直角三角形的两锐角互余”,结合题目条件,得∠C=∠BDF=∠BAD=∠ADE.【解答】解:∵AD是斜边BC上的高,DE⊥AC,DF⊥AB,∴∠C+∠B=90°,∠BDF+∠B=90°,∠BAD+∠B=90°,∴∠C=∠BDF=∠BAD,∵∠DAC+∠C=90°,∠DAC+∠ADE=90°,∴∠C=∠ADE,∴图中与∠C(除之C外)相等的角的个数是3,故选:A.【点评】此题考查了直角三角形的性质,余角的性质,掌握直角三角形的两锐角互余是解题的关键.5.Rt△ABC中,∠C=90°,∠B=54°,则∠A的度数是()A.66°B.36°C.56D.46°【分析】根据直角三角形的两个锐角互余,即可得出∠A的度数.【解答】解:∵Rt△ABC中,∠C=90°,∠B=54°,∴∠A=90°﹣∠B=90°﹣54°=36°;故选:B.【点评】本题考查了直角三角形的性质:直角三角形的两个锐角互余;熟练掌握直角三角形的性质,并能进行推理计算是解决问题的关键.6.在Rt△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACD交AB于E,则下列结论一定成立的是()A.BC=EC B.EC=BE C.BC=BE D.AE=EC【分析】根据同角的余角相等可得出∠BCD=∠A,根据角平分线的定义可得出∠ACE=∠DCE,再结合∠BEC=∠A+∠ACE、∠BCE=∠BCD+∠DCE即可得出∠BEC=∠BCE,利用等角对等边即可得出BC=BE,此题得解.【解答】解:∵∠ACB=90°,CD⊥AB,∴∠ACD+∠BCD=90°,∠ACD+∠A=90°,∴∠BCD=∠A.∵CE平分∠ACD,∴∠ACE=∠DCE.又∵∠BEC=∠A+∠ACE,∠BCE=∠BCD+∠DCE,∴∠BEC=∠BCE,∴BC=BE.故选:C.【点评】本题考查了直角三角形的性质、三角形外角的性质、余角、角平分线的定义以及等腰三角形的判定,通过角的计算找出∠BEC=∠BCE是解题的关键.7.下列命题:(1)相等的角是对顶角.(2)同位角相等(3)直角三角形的两个锐角互余.(4)若两条线段不相交,则两条线段平行.其中正确的命题个数有()A.1个B.2个C.3个D.4个【分析】此题考查的知识点多,用平行线的性质,对顶角性质,余角的定义等来一一验证,从而求解.【解答】解:①相等的角不一定是对顶角,故错误;②两直线同位角相等,故错误;③直角三角形两锐角互余,故正确;④在同一平面内,若两条直线不相交,则两直线平行,故错误.综上可得只有③正确.故选:A.【点评】本题考查了命题与定理的知识,涉及知识较多,请同学们认真阅读,最好借助图形来解答.8.如果直角三角形的一个锐角是另一个锐角的4倍,那么这个直角三角形中一个锐角的度数是()A.9°B.18°C.27°D.36°【分析】根据直角三角形的两个角互余即可求解.【解答】解:设较小的锐角是x度,则另一角是4x度.则x+4x=90,解得:x=18°.故选:B.【点评】本题主要考查了直角三角形的性质,两锐角互余.9.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,如果AC=3,AB=6,那么AD 的值为()A .B .C .D .3【分析】根据射影定理得到:AC 2=AD •AB ,把相关线段的长度代入即可求得线段AD 的长度.【解答】解:如图,∵在Rt △ABC 中,∠ACB =90°,CD ⊥AB , ∴AC 2=AD •AB , 又∵AC =3,AB =6,∴32=6AD ,则AD =. 故选:A .【点评】本题考查了射影定理.每一条直角边是这条直角边在斜边上的射影和斜边的比例中项.10.如图,△ABC 中,点D 在线段BC 上,且∠BAD =∠C ,则下列结论一定正确的是( )A .AB 2=AC •BD B .AB •AD =BD •BC C .AB 2=BC •BDD .AB •AD =BD •CD【分析】先证明△BAD ∽△BCA ,则利用相似的性质得AB :BC =BD :AB ,然后根据比例性质得到AB 2=BC •BD . 【解答】解:∵∠BAD =∠C , 而∠ABD =∠CBA , ∴△BAD ∽△BCA , ∴AB :BC =BD :AB , ∴AB 2=BC •BD . 故选:C .【点评】本题考查了射影定理:直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项;每一条直角边是这条直角边在斜边上的射影和斜边的比例中项.也考查了相似三角形的判定与性质.11.已知,在Rt△ABC中,∠C=90°,AC=3,BC=4,则sin A的值为()A.B.C.D.【分析】根据勾股定理,可得AB的长,根据角的正弦,等于角的对边比斜边,可得答案.【解答】解:由勾股定理得AB==5,sin A=,故选:D.【点评】本题考查了锐角三角函数的定义,先求出斜边,再求出正弦值.12.当锐角A的cos A>时,∠A的值为()A.小于45°B.小于30°C.大于45°D.大于30°【分析】明确cos45°=,余弦函数随角增大而减小进行分析.【解答】解:根据cos45°=,余弦函数随角增大而减小,则∠A一定小于45°.故选:A.【点评】熟记特殊角的三角函数值,了解锐角三角函数的增减性是解题的关键.13.如果α是锐角,且sinα=,那么cos(90°﹣α)的值为()A.B.C.D.【分析】根据互为余角三角函数关系,解答即可.【解答】解:∵α为锐角,,∴cos(90°﹣α)=sinα=.故选:B.【点评】本题考查了互为余角的三角函数值,熟记三角函数关系式,是正确解答的基础.14.在Rt△ABC中,∠C=90°,sin B=,则tan A的值为()A.B.C.D.【分析】根据一个角的余弦等于它余角的正弦,可得∠A的余弦,根据同角三角函数的关系,可得∠A的正弦,∠A的正切.【解答】解:由Rt△ABC中,∠C=90°,sin B=,得cos A=sin B=.由sin2A+cos2A=1,得sin A==,tan A===.故选:D.【点评】本题考查了互余两角三角函数的关系,利用一个角的余弦等于它余角的正弦得出∠A的余弦是解题关键.15.已知sin A=,则锐角A的度数是()A.30°B.45°C.60°D.75°【分析】根据30°角的正弦值等于解答.【解答】解:∵sin A=,∴A=30°.故选:A.【点评】本题考查了特殊角的三角函数值,需熟记.二.填空题(共8小题)16.在Rt△ABC中,∠C=Rt∠,∠A=70°,则∠B=20°.【分析】根据直角三角形两锐角互余列式计算即可得解.【解答】解:∵∠C=Rt∠,∠A=70°,∴∠B=90°﹣∠A=90°﹣70°=20°.故答案为:20°.【点评】本题考查了直角三角形两锐角互余的性质,是基础题,熟记性质是解题的关键.17.在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1:2:3,③∠A=90°﹣∠B,④∠A=∠B=∠C中,能确定△ABC是直角三角形的条件有①②③(填序号)【分析】根据有一个角是直角的三角形是直角三角形进行分析判断.【解答】解:①∵∠A+∠B=∠C,∠A+∠B+∠C=180°,∴2∠C=180°,∠C=90°,则该三角形是直角三角形;②∠A:∠B:∠C=1:2:3,∠A+∠B+∠C=180°,∴∠C=90°,则该三角形是直角三角形;③∠A=90°﹣∠B,则∠A+∠B=90°,∠C=90°.则该三角形是直角三角形;④∠A=∠B=∠C,则该三角形是等边三角形.故能确定△ABC是直角三角形的条件有①②③.【点评】此题要能够结合已知条件和三角形的内角和定理求得角的度数,根据直角三角形的定义进行判定.18.已知:如图,在△ABC中,AD⊥BC,垂足为点D,BE⊥AC,垂足为点E,M为AB边的中点,连结ME、MD、ED.设AB=4,∠DBE=30°,则△EDM的面积为.【分析】由条件知△ABE,三角形ADB是直角三角形,且EM,DM分别是它们斜边上的中线,证明∠EMD=2∠DAC=60°,从而可得三角形DME是边长为2的等边三角形可得到问题答案.【解答】解:∵在△ABC中,AD⊥BC,BE⊥AC,∴△ABE,△ADB是直角三角形,∴EM,DM分别是它们斜边上的中线,∴EM=DM=AB,∵ME=AB=MA,∴∠MAE=∠MEA,∴∠BME=2∠MAE,同理,MD=AB=MA,∴∠MAD=∠MDA,∴∠BMD=2∠MAD,∴∠EMD=∠BME﹣∠BMD=2∠MAE﹣2∠MAD=2∠DAC=60°,=.所以△DEM是边长为2的正三角形,所以S△DEM故答案为:.【点评】本题考查了直角三角形的性质以及等边三角形的判定和性质和等边三角形的面积计算,题目综合性很好.19.如图,已知∠AON=40°,OA=6,点P是射线ON上一动点,当△AOP为直角三角形时,∠A=50或90°.【分析】分别从若AP⊥ON与若PA⊥OA去分析求解,根据三角函数的性质,即可求得答案.【解答】解:当AP⊥ON时,∠APO=90°,则∠A=50°,当PA⊥OA时,∠A=90°,即当△AOP为直角三角形时,∠A=50或90°.故答案为:50或90.【点评】此题考查了直角三角形的性质,注意掌握数形结合思想与分类讨论思想的应用.20.如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,DB=2,则CD的长为4.【分析】根据射影定理得到:CD2=AD•BD,把相关线段的长度代入计算即可.【解答】解:∵在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,DB=2,∴CD2=AD•BD=8×2,则CD=4.故答案是:4.【点评】本题考查了射影定理.Rt△ABC中,∠BAC=90°,AD是斜边BC上的高,则有射影定理如下:①AD2=BD•DC;②AB2=BD•BC;AC2=CD•BC.21.如图,若CD是Rt△ABC斜边上的高,AD=3,CD=4,则BC=.【分析】由三角形的性质:直角三角形中,斜边上的高是两条直角边在斜边上的射影比例中项,即CD2=AD×BD,可将BD的长求出,然后在Rt△BCD中,根据勾股定理可将BC的边求出.【解答】解:∵若CD是Rt△ABC斜边上的高,AD=3,CD=4∴CD2=AD×BD,即42=3×BD解得:BD=在Rt△BCD中,∵BC2=CD2+BD2,∴BC===.故答案为:.【点评】本题主要考查三角形的性质及对勾股定理的应用.22.在△ABC中,∠C=90°,sin A=,BC=4,则AB值是10.【分析】根据正弦函数的定义得出sin A=,即=,即可得出AB的值.【解答】解:∵sin A=,即=,∴AB=10,故答案为:10.【点评】本题主要考查解直角三角形,熟练掌握正弦函数的定义是解题的关键.23.比较大小:sin44°<cos44°(填>、<或=).【分析】首先根据互余两角的三角函数的关系,得cos44°=sin46°,再根据正弦值随着角的增大而增大,进行分析.【解答】解:∵cos44°=sin46°,正弦值随着角的增大而增大,又∵44°<46°,∴sin44°<cos44°.故答案为<.【点评】本题考查了锐角三角函数的增减性:当角度在0°~90°间变化时,正弦值随着角度的增大(或减小)而增大(或减小);余弦值随着角度的增大(或减小)而减小(或增大);正切值随着角度的增大(或减小)而增大(或减小).同时考查了互余两角的三角函数的关系.三.解答题(共3小题)24.如图,在△ABC中,CE,BF是两条高,若∠A=70°,∠BCE=30°,求∠EBF与∠FBC的度数.【分析】在Rt△ABF中,∠A=70,CE,BF是两条高,求得∠EBF的度数,在Rt△BCF 中∠FBC=40°求得∠FBC的度数.【解答】解:在Rt△ABF中,∠A=70,CE,BF是两条高,∴∠EBF=20°,∠ECA=20°,又∵∠BCE=30°,∴∠ACB=50°,∴在Rt△BCF中∠FBC=40°.【点评】本题考查了直角三角形的性质,三角形内角和定理,熟练掌握直角三角形的性质是解题的关键.25.如图,在△ACB中,∠ACB=90゜,CD⊥AB于D.(1)求证:∠ACD=∠B;(2)若AF平分∠CAB分别交CD、BC于E、F,求证:∠CEF=∠CFE.【分析】(1)由于∠ACD与∠B都是∠BCD的余角,根据同角的余角相等即可得证;(2)根据直角三角形两锐角互余得出∠CFA=90°﹣∠CAF,∠AED=90°﹣∠DAE,再根据角平分线的定义得出∠CAF=∠DAE,然后由对顶角相等的性质,等量代换即可证明∠CEF=∠CFE.【解答】证明:(1)∵∠ACB=90゜,CD⊥AB于D,∴∠ACD+∠BCD=90°,∠B+∠BCD=90°,∴∠ACD=∠B;(2)在Rt△AFC中,∠CFA=90°﹣∠CAF,同理在Rt△AED中,∠AED=90°﹣∠DAE.又∵AF平分∠CAB,∴∠CAF=∠DAE,∴∠AED=∠CFE,又∵∠CEF=∠AED,∴∠CEF=∠CFE.【点评】本题考查了直角三角形的性质,三角形角平分线的定义,对顶角的性质,余角的性质,难度适中.26.在△ABC中,∠B、∠C均为锐角,其对边分别为b、c,求证:=.【分析】如图,过A作AD⊥BC于D,如果利用三角函数可以分别在△ABD和△ADC中可以得到sin sB,sin C的表达式,由此即可证明题目的结论.【解答】证明:过A作AD⊥BC于D,在Rt△ABD中,sin B=,∴AD=AB sin B,在Rt△ADC中,sin C=,∴AD=AC sin C,∴AB sin B=AC sin C,而AB=c,AC=b,∴c sin B=b sin C,∴=.【点评】本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.解题的关键是作辅助线把普通三角形转化为直角三角形解决问题.。
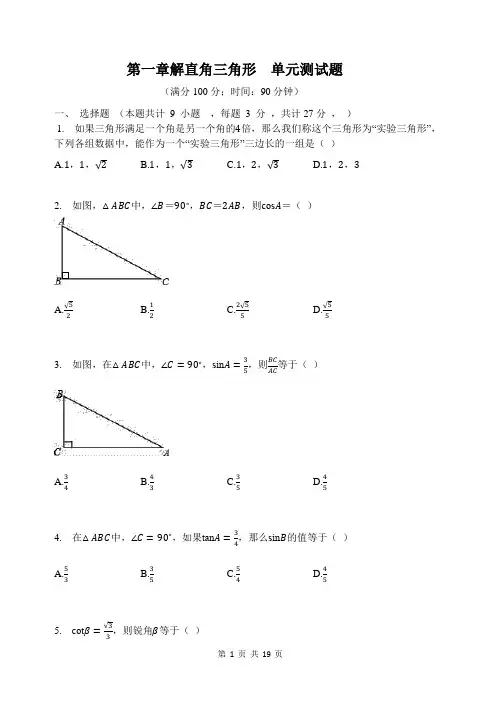
第一章解直角三角形 单元测试题(满分100分;时间:90分钟)一、 选择题 (本题共计 9 小题 ,每题 3 分 ,共计27分 , )1. 如果三角形满足一个角是另一个角的4倍,那么我们称这个三角形为“实验三角形”,下列各组数据中,能作为一个“实验三角形”三边长的一组是( )A.1,1,√2B.1,1,√3C.1,2,√3D.1,2,32. 如图,△ABC 中,∠B =90∘,BC =2AB ,则cos A =( )A.√52B.12C.2√55D.√553. 如图,在△ABC 中,∠C =90∘,sin A =35,则BC AC 等于( )A.34B.43C.35D.454. 在△ABC 中,∠C =90∘,如果tan A =34,那么sin B 的值等于( ) A.53 B.35 C.54 D.455. cot β=√33,则锐角β等于( )A.0∘B.30∘C.45∘D.60∘6. 如图是一台54英寸的大背投彩电放置在墙角的俯视图.设∠DAO=α,彩电后背AD平行于前沿BC,且与BC的距离为55cm,若AO=100cm,则墙角O到前沿BC的距离OE是()A.(55+100tanα)cmB.(55+100sinα)cmC.(55+100cosα)cmD.以上答案都不对7. 如果某人沿坡度为1:3的斜坡向上行走a米,那么他上升的高度为()A.√1010a米 B.√10a米 C.a3米 D.3a米8. 如图是一台54英寸的大背投彩电放置在墙角的俯视图(其中ABCD是矩形).设∠ADO=α,彩电后背AD与前沿BC的距离为60cm,若AO=100cm,则墙角O到前沿BC的距离OE是()A.(60+100sinα)cmB.(60+100cosα)cmC.(60+100tanα)cmD.(60−100sinα)cm9. 某校数学兴趣小组要测量摩天轮的高度.如图,他们在C处测得摩天轮的最高点A的仰角为45∘,再往摩天轮的方向前进50m至D处,测得最高点A的仰角为60∘.问摩天轮的高度AB约是()米(结果精确到1米,参考数据:√2≈1.41,√3≈1.73)A.120B.117C.118D.119二、填空题(本题共计11 小题,每题3 分,共计33分,)10. 如图,关于∠α与∠β的同一种三角函数值,有三个结论:①tanα>tanβ;②sinα>sinβ;③cosα>cosβ,正确的结论为________(填序号).11. 如图,在一次测绘活动中,某同学站在点A观测放置于B,C两处的标志物,数据显示点B在点A南偏东75∘方向20米处,点C在点A南偏西15∘方向20米处,则点B与点C的距离为________米..AC上有一点E,满足AE:CE= 12. 如图,已知AD是等腰△ABC底边上的高,且tan B=342:3.那么tan∠ADE的值是________.13. 如果在某建筑物的A处测得目标B的俯角为37∘,那么从目标B可以测得这个建筑物的A 处的仰角为________.14. 计算:sin60∘⋅cos30∘−tan45∘=________.15. 如图,要在宽AB为20米的瓯海大道两边安装路灯,路灯的灯臂CD与灯柱BC成120∘角,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线(即O为AB的中点)时照明效果最佳,若CD=√3米,则路灯的灯柱BC高度应该设计为________米.(计算结果保留根号).16. 茗茗在坡度为1:√3的坡面上走了100m,则茗茗上升了________m.17. 如图,我国一渔政船在A处,发现正东方向B处有一可疑船只,正以16海里/小时速度向西北方向航行,我渔政船立即往北偏东60∘方向航行,1.5小时后,在C处截获可疑船只,则我渔政船的航行路程AC=________海里(结果保留根号).18. 在Rt△ABC中,∠C=90∘,sin A=1,那么cos A=________.219. 如图,网格中的每个小正方形的边长都是1,△ABC每个顶点都在格点上,则sin A=________.20. 动手操作:今有一副三角板(如图1),中间各有一个直径为4cm的圆洞,现将三角形a的30∘角的那一头插入三角板b的圆洞内(如图2),则三角板a通过三角板b的圆洞的那一部分的最大面积为________cm2(不计三角板的厚度).三、解答题(本题共计6 小题,共计60分,)−√3⋅tan30∘.21. 计算:cos245∘+cos302sin60+122. 已知电线杆AB直立于地面,它的影子恰好照在土坡的坡面CD和地面BC上.如果CD与地面成45∘,∠A=60∘,CD=4√2米,BC=(4√3−4)米,求电线杆AB的长.23. 某数学兴趣小组要测量实验大楼部分楼体的高度(如图①所示,CD部分),在起点A处测得大楼部分楼体CD的顶端C点的仰角为45∘,底端D点的仰角为30∘,在同一剖面沿水平地面向前走20米到达B处,测得顶端C的仰角为60∘(如图②所示),求大楼部分楼体CD的高度为多少米?24. 在旧城改造中,要拆除一烟囱AB,在地面上事先划定以B为圆心,半径与AB等长的圆形危险区,现在从离B点21米远的建筑物CD顶端C测得A点的仰角为45∘,到B点的俯角为30∘,问离B点30米远的保护文物是否在危险区内?(√3约等于1.732)25. 如图,已知“中国渔政310”船(A)在南海执行护渔任务,接到陆地指挥中心(P)命令,得知出事渔船(B)位于陆地指挥中心西南方向,位于“中国渔政310”船正南方向,“中国渔政310”船位于陆地指挥中心北偏西60∘方向,距离为80海里的地方.而“中国渔政310”船最大航速为20海里/时.根据以上信息,请你求出“中国渔政310”船接到命令后赶往渔船出事地点最少需要多少时间(结果保留根号)?26. 我区在修筑渭河堤防工程时,欲拆除河岸边的一根电线杆AB.如图,已知距电线杆AB 水平距离14米处是河岸,即BD=14米,该河岸的坡面CD的坡度为1:0.5,岸高CF为2米,在坡顶C处测得杆顶A的仰角为30∘,D、E之间的宽是2米,请你通过计算说明在拆除电线杆AB时,为确保安全,是否将DE段封止?(在地面上以点B为圆心,以AB长为半径的圆形区域为危险区域)参考答案一、选择题(本题共计9 小题,每题 3 分,共计27分)1.【答案】B【解答】解:A、若三边为1,1,√2,由于12+12=(√2)2,则此三边构成一个等腰直角三角形,所以这个三角形不是“实验三角形”,所以A选项错误;B、由1,1,√3能构成,此三边构成一个等腰三角形,通过作底边上的高可得到底角为30∘,顶角为120∘,所以这个三角形是“实验三角形”,所以B选项正确;C、若三边为1,2,√3,由于12+(√3)2=22,则此三边构成直角三角形,最小角为30∘,所以这个三角形不是“实验三角形”,所以C选项错误;D、由1,2,3不能构成三角形,所以D选项错误.故选B.2.【答案】D【解答】∵∠B=90∘,BC=2AB,∴AC=√AB2+BC2=√AB2+(2AB)2=√5AB,∴cos A=ABAC =√5AB=√55.3.【答案】A【解答】解:∵sin A=35,设a=3x,则c=5x,结合a2+b2=c2得b=4x;∴tan A=BCAC =ab=3x4x=34,故选A.4.【答案】D【解答】解:由tan A=34,可设∠A的对边是3k,∠A的邻边是4k.则根据勾股定理,斜边是5k.∴sin B=4.故选D.5.【答案】D【解答】解:∵cotβ=√33,β为锐角,∴β=60∘.故选D.6.【答案】B【解答】解:设OE、AD相交于F,则EF=55,在直角三角形AFO中,∵∠DAO=α,AO=100cm,∴OF=100sinα,∵EF=55,∴OE=55+100sinαOE=55+100sinα.故选B.7.【答案】A【解答】解:如图:根据题意得:AC=a,i=1:3,∴i=AECE =13.设AE=x米,则CE=3x米,∴AC=√AE2+CE2=√10x(米),∴√10x=a,解得:x=√1010a,∴AE=√1010a米.即他上升的高度为√1010a米.故选A.8.【答案】B【解答】解:∵△AOD是直角三角形,∴∠OAD+∠ODA=90∘,∵△AOF是直角三角形,∴∠OAD+∠AOF=90∘,∴∠AOF=∠ADO=α,在Rt△AOF中,OF=AO⋅cosα=100cosα,∵EF=CD=60cm,∴OE=EF+OF=(60+100cosα)cm.故选B.9.【答案】C【解答】解:在Rt△ABC中,由∠C=45∘,得AB=BC,在Rt△ABD中,∵tan∠ADB=tan60∘=ABBD,∴BD=ABtan60∘=√3=√33AB,又∵CD=50m,∴BC−BD=50,即AB−√33AB=50,解得:AB≈118.即摩天轮的高度AB约是118米.故选:C.二、填空题(本题共计11 小题,每题 3 分,共计33分)10.【答案】①②【解答】解:根据图形得:∠α>∠β,∴tanα>tanβ,sinα>sinβ,cosα<cosβ.∴①②正确.故答案为①②.11.【答案】20√2【解答】解:根据题意得:∠BAC=90∘,AB=AC=20米,在R t△ABC中,BC=√AC2+AB2=√202+202=20√2,故答案是:20√2.12.【答案】89【解答】解:作EF⊥AD于F,如图,∵△ABC为等腰三角形,AD为高,∴∠B=∠C,∴tan C=34=ADDC设AD=3t,DC=4t,∴AC=√AD2+CD2=5t,而AE:CE=2:3,∴AE=2t,∵EF // CD,∴△AEF∽△ACD,∴EFCD =AFAD=AEAC,即EF4t=AF3t=2t5t,∴AF=65t,EF=85t,∴FD=AD−AF=95t,在Rt△DEF中,tan∠FDE=EFFD =85t95t=89∴tan∠ADE=89.故答案为89.13.【答案】37∘【解答】解:如图,∵某建筑物的A处测得目标B的俯角为37∘,∴目标B可以测得这个建筑物的A处的仰角为37∘,故答案为:37∘14.【答案】−1 4【解答】解:sin60∘⋅cos30∘−tan45∘=√32⋅√32−1=−14.故答案为:−14.15.8√3【解答】解:如图,延长OD,BC交于点P.∵∠ODC=∠B=90∘,∠P=30∘,OB=10米,CD=√3米,∴在直角△CPD中,DP=DC⋅tan60∘=3米,PC=CD÷sin30∘=2√3(米),∵∠P=∠P,∠PDC=∠B=90∘,∴△PDC∽△PBO,∴PDPB =CDOB,∴PB=PD⋅OBCD =3×10√3=10√3(米),∴BC=PB−PC=10√3−2√3=8√3(米).故答案为:8√3.16.【答案】50【解答】解:根据题意画图:AB=100,tan B=ACBC =1√3,设AC=x,BC=√3x,则x2+(√3x)2=1002,解得x=50,答:茗茗上升了50m.故答案为:50.17.24√2【解答】解:如图,作CD⊥AB于点D,垂足为D,∵在直角三角形BCD中,BC=16×1.5=24海里,∠CBD=45∘,∴CD=BC⋅sin45∘=24×√22=12√2海里,∴在直角三角形ACD中,AC=CDsin30∘=12√2×2=24√2海里,故答案为:24√2.18.【答案】√32【解答】∵在Rt△ABC中,∠C=90∘,sin A=12,∴∠A=30∘,∴cos A=√32.19.【答案】35【解答】解:如图所示:作CD⊥AB,则DC=3,AC=5,故sin A=DCAC =35.故答案为:35.20.【答案】 14.9【解答】解:如图,BC =4,∠BAC =30∘,作AD ⊥BC 于点D ,当点D 是BC 的中点时,△ABC 的面积最大,此时由中垂线的性质知,AB =AC ,∠B =75∘,S △ABC =12BC ⋅BD tan 75∘=12×4×2×3.732≈14.9cm 2.-----------------------故答案为:14.9三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )21.【答案】原式=(√22)2+√322×√32+1−√3×√33=12+3−√34−1 =1−√34.【解答】原式=(√22)2+√322×√32+1−√3×√33=12+3−√34−1 =1−√34.22.【答案】解:如图,延长AD交BC的延长线于点E,作DF⊥BE于F.∵在Rt△DCF中,∠CFD=90∘,∠DCF=45∘,CD=4√2,∴CF=DF=4.∵在Rt△DEF中,∠EFD=90∘,∠E=30∘,∴EF=DFtan∠E =4√33=4√3,∴BE=BC+CF+FE=4√3−4+4+4√3=8√3.∵在Rt△ABE中,∠B=90∘,∠E=30∘,∴AB=BE tan30∘=8√3×√33=8.故电线杆AB的长为8米.【解答】解:如图,延长AD交BC的延长线于点E,作DF⊥BE于F.∵在Rt△DCF中,∠CFD=90∘,∠DCF=45∘,CD=4√2,∴CF=DF=4.∵在Rt△DEF中,∠EFD=90∘,∠E=30∘,∴EF=DFtan∠E =4√33=4√3,∴BE=BC+CF+FE=4√3−4+4+4√3=8√3.∵在Rt△ABE中,∠B=90∘,∠E=30∘,∴AB=BE tan30∘=8√3×√33=8.故电线杆AB的长为8米.23.【答案】解:设楼高CE为x米,∵ 在Rt△AEC中,∠CAE=45∘,∴ AE=CE=x.∵ AB=20,∴ BE=x−20.在Rt△CEB中,CE=BE⋅tan60∘=√3(x−20),∴√3(x−20)=x,解得:x=30+10√3(米).=10√3+10,在Rt△DAE中,DE=AE⋅tan30∘=(30+10√3)×√33∴ CD=CE−DE=30+10√3−(10√3+10)=20(米).答:大楼部分楼体CD的高度为20米.【解答】解:设楼高CE为x米,∵ 在Rt△AEC中,∠CAE=45∘,∴ AE=CE=x.∵ AB=20,∴ BE=x−20.在Rt△CEB中,CE=BE⋅tan60∘=√3(x−20),∴√3(x−20)=x,解得:x=30+10√3(米).=10√3+10,在Rt△DAE中,DE=AE⋅tan30∘=(30+10√3)×√33∴ CD=CE−DE=30+10√3−(10√3+10)=20(米).答:大楼部分楼体CD的高度为20米.24.【答案】文物在危险区内.解:在Rt△AEC中,∠ACE=45∘,则CE=EA,∵DB=CE=21m,∴DB=EA=21m,在Rt△CEB中,∠BCE=30∘,则tan30∘=BE,即BE=EC tan30∘,EC=7√3m,∴BE=21×√33∴AB=AE+EB=(21+7√3)m,∵AB=(21+7√3)>30,∴文物在危险区内.【解答】此题暂无解答25.【答案】“中国渔政310”船接到命令后赶往渔船出事地点最少需要(2+2√3)小时.【解答】解:过点P作PD⊥AB于点D.在Rt△APD中,∵AP=80海里,∠APD=90∘−60∘=30∘,AP=40海里,PD=√3AD=40√3海里.∴AD=12在Rt△BDP中,PD=40√3海里,∠B=45∘,∴BD=PD=40√3海里,∴AB=AD+BD=(40+40√3)海里,=2+2√3(小“中国渔政310”船接到命令后赶往渔船出事地点最少需要的时间为40+40√320时).26.【答案】解:∵i=1:0.5,CF=2米=2,∴tan∠CDF=CFDF∴DF=1米,BG=2米,∵BD=14米,∴BF=GC=15米.=5√3≈8.66(米),在Rt△AGC中,AG=15tan30∘=15×√33∴AB=AG+BG=8.66+2=10.66米,BE=BD−DE=14−2=12(米),∵10.66<12,∴没有必要封止DE.【解答】解:∵i=1:0.5,CF=2米=2,∴tan∠CDF=CFDF∴DF=1米,BG=2米,∵BD=14米,∴BF=GC=15米.=5√3≈8.66(米),在Rt△AGC中,AG=15tan30∘=15×√33∴AB=AG+BG=8.66+2=10.66米,BE=BD−DE=14−2=12(米),∵10.66<12,∴没有必要封止DE.。
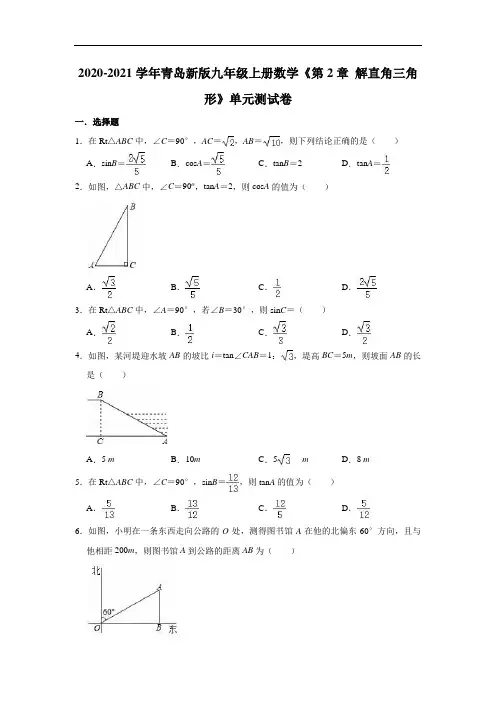
2020-2021学年青岛新版九年级上册数学《第2章解直角三角形》单元测试卷一.选择题1.在Rt△ABC中,∠C=90°,AC=,AB=,则下列结论正确的是()A.sin B=B.cos A=C.tan B=2D.tan A=2.如图,△ABC中,∠C=90o,tan A=2,则cos A的值为()A.B.C.D.3.在Rt△ABC中,∠A=90°,若∠B=30°,则sin C=()A.B.C.D.4.如图,某河堤迎水坡AB的坡比i=tan∠CAB=1:,堤高BC=5m,则坡面AB的长是()A.5 m B.10m C.5m D.8 m5.在Rt△ABC中,∠C=90°,sin B=,则tan A的值为()A.B.C.D.6.如图,小明在一条东西走向公路的O处,测得图书馆A在他的北偏东60°方向,且与他相距200m,则图书馆A到公路的距离AB为()A.100m B.100m C.100m D.m 7.重庆实验外国语学校坐落在美丽且有灵气的华岩寺旁边,特别是金灿灿的大佛让身高1.6米的小王同学很感兴趣,刚刚学过三角函数知识,他就想测一下大佛的高度,小王到A 点测得佛顶仰角为37°,接着向大佛走了10米来到B处,再经过一段坡度i=4:3,坡长为5米的斜坡BC到达C处,此时与大佛的水平距离DH=6.2米(其中点A、B、C、E、F在同一平面内,点A、B、F在同一条直线上),请问大佛的高度EF为()(参考数据:tan37°≈0.75,sin37°≈0.60,cos37°≈0.80).A.15米B.16米C.17米D.18米8.已知cosα=,则锐角α的取值范围是()A.0°<α<30°B.30°<α<45°C.45°<α<60°D.60°<α<90°9.在Rt△ABC中,已知∠C=90°,∠A=40°,AC=3,则BC的长为()A.3sin40°B.3sin50°C.3tan40°D.3tan50°10.人字折叠梯完全打开后如图1所示,B,C是折叠梯的两个着地点,D是折叠梯最高级踏板的固定点.图2是它的示意图,AB=AC,BD=140cm,∠BAC=40°,则点D离地面的高度DE为()A.140sin20°cm B.140cos20°cmC.140sin40°cm D.140cos40°cm二.填空题11.计算:tan15°•tan45°•tan75°=.12.如图,已知Rt△ABC中,斜边AB的长为m,∠B=40°,则直角边AC的长是.13.已知sinα=(α为锐角),则tanα=.14.小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B、C两点的俯角分别为45°、35°.已知大桥BC与地面在同一水平面上,其长度为100m,求热气球离地面的高度.(结果保留整数)(参考数据:sin35°=0.57,cos35°=0.82,tan35°=0.70)15.比较大小:(1)cos35°cos45°,tan50°tan60°;(2)若sinα=0.3276,sinβ=0.3274,则αβ.16.如果α是锐角,且sinα=cos20°,那么α=度.17.如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是海里.18.如图,AD是正五边形ABCDE的一条对角线,则∠BAD=.19.如图,在△ABC中,∠ACB=90°,D是AB的中点,DE⊥AB,交AC于E,若=,则tan∠A=.20.如图,某商场大厅自动扶梯AB的长为12m,它与水平面AC的夹角∠BAC=30°,则大厅两层之间的高度BC为m.三.解答题21.如图,在Rt△ABC中,∠C=90°,BC=5,AC=12,求∠A的正弦值、余弦值和正切值.22.求满足下列条件的锐角x.(1)cos x=(2)tan x﹣3=023.在Rt△ABC中,已知∠C=90°,a=19,c=19,解这个直角三角形.24.如图是某货站传送货物的平面示意图,为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4m.(1)求新传送带AC的长度;(2)如果需要在货物着地点C的左侧留出5m的通道,试判断距离B点4m的货物MNQP是否需要挪走,并说明理由.25.用计算器求下列各式的值:(1)sin59°;(2)cos68°42′.26.在△ABC中,AB=8,BC=6,∠B为锐角且cos B=.(1)求△ABC的面积.(2)求tan C.27.在△ABC中,已知∠C=90°,sin A+sin B=,求sin A﹣sin B的值.参考答案与试题解析一.选择题1.解:在Rt△ABC中,∠C=90°,∴BC==2,A、sin B===,本选项计算错误;B、cos A===,本选项计算正确;C、tan B===,本选项计算错误;D、tan A===2,本选项计算错误;故选:B.2.解:∵△ABC中,∠C=90o,∴tan A==2,∴设CB=2k,AC=k,∴AB==k,∴cos A===,故选:B.3.解:∵∠A=90°,∠B=30°,∴∠C=90°﹣30°=60°,∴sin C=sin60°=,故选:D.4.解:∵tan∠CAB===,∴在Rt△ABC中,∠BAC=30°,又∵BC=5m,∴AB=2BC=10m,故选:B.5.解:∵sin B==,∴设AC=12x,AB=13x,由勾股定理得:BC===5x,∴tan A===,故选:D.6.解:由题意得,∠AOB=90°﹣60°=30°,∴AB=OA=100(m),故选:A.7.解:过点C作CM⊥BF于点M,过点G作GN⊥EF于点N,∵斜坡BC的坡度i=4:3,BC=5米,∴设CM=4x,BM=3x,∴(4x)2+(3x)2=52,解得x=1,∴CM=4米,BM=3米,由题意可知四边形DHFM和四边形AGNF是矩形,∴DH=FM=6.2米,∵AB=10米,∴AF=GN=AB+BM+MF=10+3+6.2=19.2米,在Rt△ENG中,∵∠EGN=37°,∴tan37°=≈0.75,∴EN=0.75×NG=0.75×19.2=14.4米,∴EF=EN+NF=14.4+1.6=16米.故选:B.8.解:∵cos30°=,cos45°=,∵<<,∴30°<α<45°,故选:B.9.解:如图,在Rt△ABC中,∵∠C=90°,AC=3,∠A=40°,∴BC=AC•tan A=3tan40°,故选:C.10.解:∵∠BAC=40°,AB=AC,∴∠ACB=∠ABC=70°,∵DE⊥BC,∴∠DEB=90°,∴∠BDE=90°﹣70°=20°,∴DE=BD•cos20°=140cos20°,故选:B.二.填空题11.解:原式=tan15°•tan75°•tan45°=1×1=1.故答案为:1.12.解:在Rt△ABC中,sin B=,∴AC=AB•sin B=m sin40°,故答案为:m sin40°.13.解:∵sin2α+cos2α=1,∴cosα==,∴tanα===,故答案为:.14.解:作AD⊥BC交CB的延长线于D,设AD为x,由题意得,∠ABD=45°,∠ACD=35°,在Rt△ADB中,∠ABD=45°,∴DB=x,在Rt△ADC中,∠ACD=35°,∴tan∠ACD=,∴=,解得,x≈233.所以,热气球离地面的高度约为233米,故答案为:233米.15.解:(1)cos35°>cos45°,tan50°<tan60°;故答案为:>,<;(2)∵sinα=0.3276,sinβ=0.3274,则α>β.故答案为:>.16.解:∵sinα=cos20°,∴α=90°﹣20°=70°.故答案为:70.17.解:作BD⊥AC于点D,由题意得,∠CBA=25°+50°=75°,AB=20,则∠CAB=(90°﹣70°)+(90°﹣50°)=20°+40°=60°,∴∠ABD=30°,∴∠CBD=75°﹣30°=45°,在Rt△ABD中,BD=AB•sin∠CAB=20×sin60°=20×=10,在Rt△BCD中,∠CBD=45°,则BC=BD=10×=10,故答案为:10.18.解:∵正五边形ABCDE的内角和为(5﹣2)×180°=540°,∴∠E=×540°=108°,∠BAE=108°又∵EA=ED,∴∠EAD=×(180°﹣108°)=36°,∴∠BAD=∠BAE﹣∠EAD=72°,故答案为:72°.19.解:连接EB,∵D是AB的中点,DE⊥AB,∴DE是AB的垂直平分线,∴EA=EB,∵==,设EC=3k,则AE=BE=4k,AC=5k+3k=8k,在Rt△BCE中,BC==4k,在Rt△ABC中,tan∠A===,故答案为:.20.解;在Rt△ABC中,∠BAC=30°,AB=12m,∴BC=m,故答案为:6.三.解答题21.解:由勾股定理得,AB===13,则sin A==,cos A==,tan A==.22.解:(1)∵cos x=,∴x=30°;(2)tan x﹣3=0,∴tan x=3,∴tan x=,则x=60°.23.解:在Rt△ABC中,∠C=90°,a=19,c=19,∴b==19,∵tan A==1,∴∠A=45°,∴∠B=90°﹣∠A=45°,因此,b=19,∠A=∠B=45°.24.解:(1)在Rt△ABD中,∠ABD=45°,∴AD=AB=4,在Rt△ACD中,∠ACD=30°,∴AC=2AD=8,答:新传送带AC的长度为8m;(2)在Rt△ACD中,∠ACD=30°,∴CD=AB•cos∠ACD=4,在Rt△ABD中,∠ABD=45°,∴BD=AD=4,∴BC=CD﹣BD=4﹣4,∴PC=BP﹣BC=4﹣(4﹣4)=4<5,∴货物MNQP需要挪走.25.解:(1)sin59°≈0.857;(2)cos68°42′=cos68.7°≈0.363.26.解:(1)如图,过点A作AH⊥BC于H.∵cos B=,∴∠B=60°,∴BH=AB•cos B=4,AH=AB•sin B=4,∴S=•BC•AH=×6×4=12.△ABC(2)在Rt△ACH中,∵∠AHC=90°,AH=4,CH=BC﹣BH=7﹣4=2,∴tan C===2.27.解:∵sin A+sin B=,∴(sin A+sin B)2=,∴sin2A+sin2B+2sin A•sin B=,∵sin B=cos A,∴sin2A+cos2A+2sin A•sin B=,∴2sin A•sin B=,∴(sin A﹣sin B)2=1﹣=,∴sin A﹣sin B=±.。
图(1)图(2)第24章 解直角三角形单元测试卷姓名____________ 时间: 90分钟 满分:120分 总分____________ 一、选择题(每小题3分,共30分)1. 如图(1)所示,在△ABC 中,︒=∠90B ,AB BC 2=,则A cos 等于 【 】 (A )25 (B )21 (C )552 (D )552. 如图(2)所示,在Rt △ABC 中,︒=∠90BAC ,BC AD ⊥于点D ,如果α=∠ABC ,那么下列结论 错误的是 【 】 (A )αsin ACBC =(B )αtan ⋅=AD CD (C )αcos ⋅=AB BD (D )αcos ⋅=AD AC3. 如图(3)所示,在菱形ABCD 中,AB DE ⊥,2,53cos ==BE A ,则DBE ∠tan 的值是 【 】图(3)(A )21(B )2 (C )25 (D )554. 在Rt △ABC 中,︒=∠90C ,已知54sin =A ,则A cos 的值为 【 】 (A )54(B )1 (C )53 (D )525. 如图(4)所示,△ABC 的顶点是正方形网格的格点,则A sin 的值为 【 】图(4)CBA(A )21(B )55 (C )1010 (D )5526. 如图(5)所示,已知︒=∠60AOB ,点P 在边OA 上,,12=OP 点M 、N 在边OB 上,PN PM =,若2=MN ,则OM 等于 【 】A B图(5)N OPM(A )3 (B )4 (C )5 (D )67. 如图(6)所示,在矩形ABCD 中,点E 在AB 边上,沿CE 折叠矩形ABCD ,使点B 落在AD 边上的点F 处,若,5,4==BC AB 则AFE ∠tan 的值为 【 】图(6)D(A )54 (B )53 (C )43 (D )358. 如图(7)所示,在Rt △ABC 中,︒=∠90C ,︒=∠30A ,E 为AB 上一点,且1:4:=EB AE ,AC EF ⊥于点F ,连结FB ,则CFB ∠tan 的值等于【 】(A )33 (B )332 (C )335 (D )35 图(7)图(8)9. 小明利用测角仪和旗杆的拉绳测量学校旗杆的高度,如图(8)所示,旗杆P A 的高度与拉绳PB 的长度相等.小明将PB 拉到PB′的位置,测得α=∠C PB '(C B '为水平线),测角仪D B '的高度为1米,则旗杆P A 的高度为 【 】(A )αsin 11-米 (B )αsin 11+米(C )αcos 11-米 (D )αcos 11+米10. 如图(9)所示,要在宽为22米的九州大道两边安装路灯,路灯的灯臂CD 长2米,且与灯柱BC 成︒120角,路灯采用圆锥形灯罩,灯罩的轴线DO 与灯臂CD 垂直,当灯罩的轴线DO 通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC 的高度应该设计为 【 】A图(9)O DBC(A )()2211-米 (B )()22311-米 (C )()3211-米 (D )()4311-米二、填空题(每小题3分,共15分)11. 如图(10)所示,在△ABC 中,12,==BC AC AB ,BD 为高,M 为AB 的中点,且5=DM ,则△ABC 的面积为_________.图(10)图(11)MNBCAD12. 在△ABC 中,如果B A ∠∠、满足021cos 1tan 2=⎪⎭⎫⎝⎛-+-B A ,那么=∠C _________.13. 如图(11)所示,正方形ABCD 的边长为4,N 是DC 的中点,M 是AD 上异于D 的点,且MBC NMB ∠=∠,则=∠ABM tan _________.14. 一般地,当βα,为任意角时,()βα+sin 与()βα-sin 的值可以用下面的公式求得:()βαβαβαsin cos cos sin sin +=+,()βαβαβαsin cos cos sin sin -=-.例如:()4622223222145sin 30cos 45cos 30sin 4530sin 75sin +=⨯+⨯=︒︒+︒︒=︒+︒=︒类似地,可以求得=︒15sin __________.15. 如图(12)所示,已知点()0,35A ,直线b x y +=)0(>b 与y 轴交于点B ,连结AB ,若︒=75α,则=b _________.图(12)三、解答题(共75分)16. 计算:(每小题5分,共20分)(1)︒+︒45cos 360sin 2; (2)130sin 560cos 3-︒︒;(3)︒-︒-︒45tan 230cos 1245sin 22; (4)︒-︒-︒︒60cos 2345tan 60sin 230sin 2.17.(8分)先化简,再求值:1211222++-÷⎪⎭⎫ ⎝⎛+-x x x x x x ,其中︒=30sin x .18.(11分)如图(13)所示,在△ABC 中,AC BE BC AD ⊥⊥,,垂足分别为D 、E ,AD与BE相交于点F.(1)求证:△ACD∽△BFD;(2)当1=AC时,求BF的长.tan=∠ABD,3 Array图(13)19.(12分)如图(14)所示,在矩形ABCD中,点E是BC边上的点,AEAE⊥=,,垂足为点F,连结DE.BCDF(1)求证:DFAB=;(2)若,6=ABAD求EDF10=,tan的值.∠Array图(14)20.(12分)如图(15)所示,小强从自己家的阳台上看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,小强家与这栋楼的水平距离为42 m,这栋楼有多高?图(15)21.(12分)我们定义:等腰三角形中底边与腰的比叫做顶角的正对(记作sad ).如图1,在△ABC 中,AC AB =,顶角A 的正对记作sad A ,这时sad A ABBC==腰底边.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解答下列问题: (1)sad =︒60_________;(2)如图2,在△ABC 中,CA CB =,若sad C 56=,求B tan 的值; (3)如图3,在Rt △ABC 中,︒=∠90C ,若54sin =A ,试求sad A 的值.图 1BCA图 2BAC图 3C第24章 解直角三角形单元测试卷参考答案一、选择题(每小题3分,共30分)二、填空题(每小题3分,共15分)11. 48 12. ︒75 13.3114. 426- 15. 5 三、解答题(共75分)16. 计算:(每小题5分,共20分) (1)︒+︒45cos 360sin 2;解:原式223232⨯+⨯= 62626=+=(2)130sin 560cos 3-︒︒;解:原式1215213-⨯⨯=1= (3)︒-︒-︒45tan 230cos 1245sin 22; 解:原式223322222-⨯-⨯=292321-=--=(4)︒-︒-︒︒60cos 2345tan 60sin 230sin 2.解:原式21231232212⨯--⨯⨯=41324321343131-=-+=--=17.(8分)先化简,再求值:1211222++-÷⎪⎭⎫ ⎝⎛+-x x x x x x ,其中︒=30sin x .解:1211222++-÷⎪⎭⎫ ⎝⎛+-x x x x x x()()()()1111122-=-++⋅+=x x x x x x x x ……………………………………6分当2130sin =︒=x 时……………………………………7分 原式112121-=-=. ……………………………………8分 18.(11分)如图(13)所示,在△ABC 中,AC BE BC AD ⊥⊥,,垂足分别为D 、E ,AD 与BE 相交于点F . (1)求证:△ACD ∽△BFD ;(2)当1tan =∠ABD ,3=AC 时,求BF 的长.图(13)(1)证明:∵AC BE BC AD ⊥⊥, ∴︒=∠+∠︒=∠+∠902,901C C ……………………………………1分 ∴21∠=∠……………………………………2分 ∵︒=∠=∠90BDF ADC ,21∠=∠∴△ACD ∽△BFD ;……………………………………5分 (2)在Rt △ABD 中 ∵1tan =∠ABD ∴1=BDAD……………………………………7分 ∵△ACD ∽△BFD∴13,1===BFBD AD BF AC ∴3=BF .……………………………………9分 19.(12分)如图(14)所示,在矩形ABCD 中,点E是BC边上的点,AE DF BC AE ⊥=,,垂足为点F ,连结DE .(1)求证:DF AB =;(2)若,6,10==AB AD 求EDF ∠tan 的值.图(14)(1)证明:∵四边形ABCD 是矩形 ∴BC AD BC AD ABE =︒=∠,//,90 ……………………………………1分 ∴AEB DAF ∠=∠ ∵AE DF ⊥∴︒=∠=∠90ABE DFA ∵BC AE = ∴DA BC AE == 在△ABE 和△DF A 中∵⎪⎩⎪⎨⎧=∠=∠∠=∠DA AE DAF AEB DFA ABE ∴△ABE ≌△DF A (AAS )……………………………………5分 ∴DF AB =;(2)由(1)可知:△ABE ≌△DF A ∴6==DF AB……………………………………6分 ∵10=AD ∴10=AE在Rt △ABE 中,由勾股定理得:86102222=-=-=AB AE BE……………………………………9分 ∴8=FA∴2=-=FA AE EF……………………………………10分 ∴3162tan ===∠DF EF EDF . ……………………………………12分 20.(12分)如图(15)所示,小强从自己家的阳台上看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,小强家与这栋楼的水平距离为42 m,这栋楼有多高?解:由题意可知:42,=⊥AD BC AD m……………………………………1分 在Rt △ABD 中 ∵ADBDBAD =∠tan ∴3342=BD ∴314=BD m……………………………………6分 在Rt △ACD 中 ∵ADCDCAD =∠tan ∴360tan 42=︒=CD∴342=CD m……………………………………11分 ∴356=+=CD BD BC m……………………………………12分 答:这栋楼的高度为356m.21.(12分)我们定义:等腰三角形中底边与腰的比叫做顶角的正对(记作sad ).如图1,在△ABC 中,AC AB =,顶角A 的正对记作sad A ,这时sad A ABBC==腰底边.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解答下列问题:(1)sad =︒60_________;(2)如图2,在△ABC 中,CA CB =,若sad C 56=,求B tan 的值; (3)如图3,在Rt △ABC 中,︒=∠90C ,若54sin =A ,试求sad A 的值. 解:(1)1;……………………………………3分 (2)作AB CD ⊥.图 2∵CA CB =,AB CD ⊥ ∴AB BD 21=……………………………………4分∵sad C 56=∴56=BC AB 设x AB 6=,则x BC 5=∴x BD 3=在Rt △BCD 中,由勾股定理得:()()xx x BD BC CD 4352222=-=-=……………………………………5分 ∴3434tan ===x x BD CD B . ……………………………………6分 (3)延长AC 至E ,使AE AB =. ……………………………………8分图 3∵54sin =A ∴54=AB BC 设x AB x BC 5,4== ∴x AE 5=在Rt △ABC 中,由勾股定理得:()()xx x BC AB AC 3452222=-=-=……………………………………9分 ∴x AC AE CE 2=-= 在Rt △BCE 中,由勾股定理得:()()xx x CE BC BE 52242222=+=+=∴sad A 552552===x x AB BE .(12分)图 2 mm。
浙教版初中数学九年级下册第一单元《解直角三角形》(标准难度)(含答案解析)考试范围:第一单元; 考试时间:120分钟;总分:120分,第I卷(选择题)一、选择题(本大题共12小题,共36分。
在每小题列出的选项中,选出符合题目的一项)1. 如图,在Rt△ABC中,∠ACB=90°,BC=1,AB=2,则下列结论正确的是( )A. sinA=√32B. tanA=12C. cosB=√32D. tanB=√32. 如图,四边形ABCD内接于⊙O,AB为直径,AD=CD,过点D作DE⊥AB于点E,连接AC交DE于点F.若sin∠CAB=35,DF=5,则BC的长为( )A. 8B. 10C. 12D. 163. 如图,在Rt△BAD中,延长斜边BD到点C,使DC=12BD,连接AC,若tan B=53,则tan∠CAD的值为( )A. √33B. √35C. 13D. 154. 在实数π,13,√2,sin30°中,无理数的个数为( )A. 1B. 2C. 3D. 45. 如图,△ABC的三个顶点分别在正方形网格的格点上,下列三角函数值错误的是( )A. sinB=35B. cosB=45C. tanB=34D. tanA=436. 如图,CD是平面镜,光线从点A出发,经CD上点E反射后照射到点B.若入射角为α,AC⊥CD,BD⊥CD,垂足分别为点C,D,且AC=3,BD=6,CD=11,则tanα的值为( )A. 113B. 311C. 911D. 1197. 在Rt△ABC中,∠C=90∘,cosA=√32,∠B的平分线BD交AC于点D,若AD=16,则BC的长为( )A. 6B. 8C. 8√3D. 128. 如图,若锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),则下列三个结论:①sin∠C>sin∠D;②cos∠C>cos∠D;③tan∠C>tan∠D中,正确的结论为( )A. ①②;B. ②③;C. ①②③;D. ①③;9. 某简易房示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆AB的长为( )A. 95sinα米B. 95cosα米C. 59sinα米D. 59cosα米10. 如图,在△ABC中,∠B=45°,∠C=60°,AD⊥BC于点D,BD=√3.若E,F分别为AB,BC的中点,则EF的长为( )A. √33B. √32C. 1D. √6211. 如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内),已知AB=a,AD=b,∠BCO=α,则点A到OC的距离等于( )A. a⋅sinα+b⋅sinαB. a⋅cosα+b⋅cosαC. a⋅sinα+b⋅cosαD. a⋅cosα+b⋅sinα12. 如图,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸点A处,测得河的北岸边点B在其北偏东45∘方向然后向西走80米到达C点,测得点B在点C的北偏东60∘方向,则这段河的宽度为( )A. 80(√3+1)米B. 40(√3+1)米C. (120−40√3)米D. 40(√3−1)米第II卷(非选择题)二、填空题(本大题共4小题,共12分)13. 在Rt△ABC中,∠C=90°,AB=3,BC=2,则cosA的值是.14. 在菱形ABCD中,DE⊥AB,垂足是E,DE=6,sin A=3,则菱形ABCD的周长是.515. 若锐角α满足cosα<√2且tanα<√3,则α的范围是.216. 如图,在△ABC中,AB=AC=5cm,cosB=3.如果⊙O的半径为√10cm,且经过点B,5C,那么线段AO=cm.三、解答题(本大题共9小题,共72分。
解直角三角形 单元测试 (时间:100分钟 满分:150分)一、填空题(每题3分,共30分)1.若直角三角形两条直角边长分别为5和12,则斜边上的中线长为________. 2.若等腰直角三角形的一边长是2,则它的面积为___________. 3.△ABC 中,∠C =90°,a =6,b =8,则sinA =_____________. 4.在△ABC 中,∠C =90°,135sin =B ,则cosB =___________. 5.若23sin =a ,则锐角a =__________度. 6.Rt △ABC 中,∠C =90°,220,20==c a ,则∠B =_________度. 7.△ABC 中,∠C =90°,10,54sin ==AB A ,则AC =_________. 8.在离大楼15m 的地面上看大楼顶部仰角为60°,则大楼高约__________m(精确到lm). 9.在电线杆离地面8m 的地方向地面拉一条缆绳以固定电线杆,如果缆绳与地面成 60°角,那么需要缆绳__________m(忽略打结部分).10.一个斜坡的坡度是1:3,高度是4m ,则他从坡底到坡顶部所走的路程大约是___________m .二、选择题(每题4分,共20分)11.直角三角形的两条边长分别为3、4,则第三条边长为 ( ) A .5 B .7 C .7 D .5或712.如图,菱形ABCD 的对角线AC =6,BD =8,∠ABD =a ,则下列结论正确的是 ( ) A .54sin =a B .53cos =a C .34tan =a D .34cot =a第12题 第13题13.如图,在Rt △ABC 中,∠C =90°,BC =4,AC =3,CD ⊥AB 于D ,设∠ACD =a ,则cos a 的值为 ( )A .54B .43C .34D .5314.△ABC 中,∠C =90°,且a ≠b ,则下列式子中,不能表示△ABC 面积的是 ( )A .ab 21B .B ac sin 21C .A b tan 212D .B A c cos sin 212⋅15.如图,钓鱼竿AC 长6m ,露在水面上的鱼线BC 长23m ,某钓者想看看鱼钓上的情况,把鱼竿AC 转动到C A '的位置,此时露在水面上的鱼线C B ''为33,则鱼竿转过的角度是 ( )A .60°B .45°C .15°D .90°三、解答题(每题10分,共50分)16.计算(1)2cos30°+cot60°-2tan45°·tan60°(2)()︒-︒-︒⋅︒︒+︒30sin 60sin 330cot 30tan 45cos 45sin 2217.如图,求下列各直角三角形中字母的值.18.如图是直线y =-2x+5的图象,求锐角a 的四个三角函数值.19.如图,梯形ABCD 中,AB ⊥BC ,∠BAC =60°,∠ADC =135°,312 BC ,求梯形的面积和周长.20.身高相同的甲、乙、丙三人放风筝,各人放出的线长分别为300m、250m、200m,线与地平面所成的角分别为30°、45°、60°(假设风筝线是拉直的),问三人所放的风筝谁的最高?21.(本题15分)分别以直角三角形的三边为边长向外作图形,如图,甲是作三个正方形,乙是作三个正三角形,丙是作三个半圆,丁是作三个等腰直角三角形.分别探索这四个图形工、Ⅱ、Ⅲ的面积之间的关系,并证明。
第23章《解直角三角形》单元测试卷一、选择题(本大题共10小题,每小题3分,共30分)1.在Rt ABC ∆中,90C ∠=︒,6AC =,4sin 5A =,则AB 的值为()A.8B.9C.10D.122.如图,在ABC ∆中,90C ∠=︒,30A ∠=︒,则cos B 的值为()A.13B.12C.22D.323.如图,某游乐场山顶滑梯的高BC 为50米,滑梯的坡比为5:12,则滑梯的长AB 为()A.100米B.110米C.120米D.130米4.如图,ABC ∆的顶点都在正方形网格的格点上,则tan ACB ∠的值为()A.13B.35C.23D.125.下列各式中正确的是()A.sin 46cos 44︒>︒B.2sin 40sin 80︒=︒C.cos 44cos 46︒<︒D.22sin 44sin 461︒+︒=6.如图,在44⨯的正方形网格中,小正方形的顶点称为格点若ABC ∆的顶点都在格点上,则cos ABC ∠的值是()A.13B.12C.55D.2557.如图,在ABC ∆中,90ACB ∠=︒,点D 在AB 的延长线上,连接CD ,若2AB BD =,2tan 3BCD ∠=,则ACBC的值为()A.1B.2C.12D.328.如图,Rt ABC ∆中,90ABC ∠=︒,6AB =,8BC =,D 为AC 边上一动点,且1tan 2ABD ∠=,则BD 的长度为()A.1558B.25C.5D.5119.如图,AC 垂直于AB ,P 为线段AC 上的动点,F 为PD 的中点, 2.8AC m =, 2.4PD m =, 1.2CF m =,15DPE ∠=︒.若90PEB ∠=︒,65EBA ∠=︒,则AP 的长约为()(参考数据:sin 650.91︒≈,cos 650.42︒≈,sin 500.77︒≈,cos500.64)︒≈A.1.2B.1.3m C.1.5m D.2.0m10.如图,在Rt ABC ∆中,90C ∠=︒,30BAC ∠=︒,延长CA 到点D ,使AD AB =,连接BD .根据此图形可求得tan15︒的值是()A.23-B.23+C.36D.32二、填空题(本大题共8小题,每小题3分,共24分)11.如图,在ABC ∆中,90C ∠=︒,设A ∠,B ∠,C ∠所对的边分别为a ,b ,c ,则正确的是.A .sin a c A =⋅B .cos b c B =⋅C .tan a b A =⋅D .tan a b B=⋅12.有一斜坡AB ,坡顶B 离地面的高度BC 为30m ,斜坡的倾斜角是BAC ∠,若坡比为2:5,则此斜坡的水平距离AC 为.13.在Rt ABC ∆中,90BCA ∠=︒,CD 是AB 边上的中线,8BC =,5CD =,则tan ACD ∠=.14.如图所示,MON ∠是放置在正方形网格中的一个角,则tan MON ∠的值是.15.在ABC ∆中,22AB =,1tan 3B =,BC 边上的高长为2,则ABC ∆的面积为.16.某长江大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB 与水平桥面的夹角是30︒,拉索BD 与水平桥面的夹角是60︒,两拉索底端距离20AD =米,则立柱BC 的高为米.(结果保留根号)17.如图是一款利用杠杆原理设计的平衡灯,灯管AB 与支架AD ,砝码杆AC 均成120︒角,且40AB cm =,18AC cm =,6AD cm =,底座是半径为2cm 的圆柱体,点P 是杠杆的支点.如图1,若砝码E 在端点C 时,当杠杆平衡时,支架AD 垂直于桌面,则此时垂直光线照射到最远点M 到支点P 的距离PM 为cm .由于特殊设计,灯管的重力集中在端点B ,砝码杆重力集中在砝码E 上,支架AD 的重力忽略不计,由杠杆原理可知,平衡时重力保持垂直水平桌面向下,且1122G h G h ⋅=⋅,如图2.为了使得平衡时砝码杆与桌面平行,则砝码E 到离A 点的距离为cm .18.用一副如图1所示的七巧板,拼出如图2所示中间有一个空白正方形的“风车图”,则图2中tan ABC ∠=.三、解答题(本大题共8小题,共66分.)19.计算:22sin 456cos303tan 454sin 60︒-︒+︒+︒.20.如图,在Rt ABC ∆中,90C ∠=︒,10AB =,6BC =,求sin A ,cos A ,tan A 的值.21.如图,在ABC∆中,90C∠=︒,AB的垂直平分线分别交边AB、BC于点D、E,连接AE.(1)如果25B∠=︒,求CAE∠的度数;(2)如果2CE=,2sin3CAE∠=,求tan B的值.22.如图,在ABC∆中,已知ABC m∠=︒,ACB n∠=︒.090m n︒<︒+︒<︒,1AC=.(1)求AB及BC的长度(用m︒,n︒的三角函数表示);(2)试判断sin()sin cos cos sinm n m n m n︒+︒=︒︒+︒︒是否成立并说明理由.23.如图,梯子斜靠在与地面垂直(垂足为)O 的墙上.当梯子位于AB 位置时,它与地面所成的角60ABO ∠=︒,当梯子底端向右滑动0.5m (即0.5)BD m =到达CD 位置时,它与地面所成的角5118CDO ∠=︒',求梯子的长.(参考数据:sin 51180.780︒'=,cos 51180.625︒'=,tan 5118 1.248)︒'=24.如图,在Rt ABC ∆中,90A ∠=︒,作BC 的垂直平分线交AC 于点D ,延长AC 至点E ,使CE AB =.(1)若1AE =,求ABD ∆的周长;(2)若13AD BD =,求tan ABC ∠的值.25.在太原郁郁葱葱的西山上,环绕着一条蜿蜒曲折、鲜艳夺目的公路,它就是太原环城旅游公路暨公路自行车赛道,该赛道环西山而建,全长约136千米,将百余处景点串连成一条线.(1)周日,某自行车骑行团组织甲、乙两个赛队在该赛道进行骑行活动,他们从赛道同一端出发,甲队出发25分钟时乙队出发,结果乙队比甲队提前15分钟到达终点(即赛道的另一端).已知乙队骑行的平均速度为甲队的1.2倍.求甲、乙两个赛队此次活动骑行的平均速度.(2)该赛道一端附近是太原市的摄乐桥如图(1),摄乐桥是太原市第18座跨汾河大桥,也是太原市首座仅靠主塔及缆索承担桥面重量的跨河大桥.某数学兴趣小组的同学们为了测量摄乐桥主塔的高AB,在地面上选取测点C放置测倾仪,测得主塔顶端A的仰角45∠=︒,将测ADM倾仪向靠近主塔的方向前移10m至点E处,测得主塔顶端A的仰角47.7∠=︒,测量示意图AFM如图(2)所示.已知测倾仪的高度 1.5︒≈,=,求摄乐桥主塔的高AB.(参考数据:sin47.70.74CD m︒≈︒≈,tan47.7 1.10)cos47.70.6726.山西省隰县盛产香梨,被称为“隰县玉露香”.县政府运用“互联网+玉露香梨”的发展思路,探索“爱心助农精准脱贫”的方式,构建“隰县玉露香”电商生态圈,使隰县成为中国北方最大的电商孵化基地.2021年春节期间,“隰县玉露香”在网上热销,某电商看准商机,用10000元购进一批“隰县玉露香”,销量可观,于是又用18000元购进一批同款规格的“隰县玉露香”,但第二次的进价比第一次每箱上涨20元,第二次所购数量恰好是第一次的1.5倍.(1)求第一次购进的“隰县玉露香”每箱的价格.(2)政府为推进农村电商高质量可持续发展,在隰县新建一批移动信号发射塔,以提高农村互联网的传输效率.如图,是一个新建的移动信号发射塔AC ,其高15AC m =.用测角仪在山脚下的点B 处测得塔底C 的仰角36.9CBD ∠=︒,塔顶A 的仰角42ABD ∠=︒,点A ,C ,D 在同一条铅垂线上.果农要在山脚B 处修建房屋以方便管理梨园,按国家规定,通讯基站离居民居住地至少100m 就可不受信号塔辐射的影响.请判断在点B 处的房屋是否受信号塔塔顶A 发出的信号辐射的影响.(测角仪、房屋的高度忽略不计;结果精确到0.1m ;参考数据:sin 36.90.60︒≈,cos36.90.80︒≈,tan 36.90.75︒=,sin 420.67︒=,cos 420.74︒=,tan 420.90)︒≈答案一、选择题C .B .D .D .D .C .B .D .B .A .二、填空题11.A 、C .12.75m .13.43.14.1.15.7或5.16..17.165.18.3.三、解答题19.原式22()6314222=⨯-⨯+⨯+⨯2234=⨯-+13=-++4=.20.在Rt ACB ∆中,由勾股定理得:8AC ===,所以63sin 105BC A AB ===,84cos 105AC A AB ===,63tan 84BC A AC ===.21.(1)DE 垂直平分AB ,EA EB ∴=,25EAB B ∴∠=∠=︒.40CAE ∴∠=︒.(2)90C ∠=︒ ,∴2sin 3CE CAE AE ∠==.2CE = ,3AE ∴=,AC ∴=3EA EB == ,5BC ∴=,∴tan AC B BC ==.22.(1)作AD BC ⊥于点D ,在Rt ACD ∆中,1AC =,sin AD n AD AC ︒==,cos CD n CD AC︒==,在Rt ABD ∆中,sin AD m AB ︒=,sin sin sin AD n AB m m ︒∴==︒︒,cos BD m AB︒= ,sin cos cos sin n BD AB m m m ︒∴=⋅︒=︒︒.sin cos cos sin n BC BD CD m n m ︒∴=+=︒+︒︒.(2)成立,理由如下:作CE BA ⊥交BA 延长线于点E ,EAC ∠ 为ABC ∆的外角,EAC B ACB m n ∴∠=∠+∠=︒+︒,在Rt EBC ∆中,sin CE m BC︒=,sin sin (cos cos )sin sin cos cos sin sin n CE BC m m n m m n m n m ︒∴=⋅︒=︒+︒︒=︒︒+︒︒︒.23.设梯子的长为xm ,在Rt ABO ∆中,cos OBABO AB∠=1cos cos 602OB AB ABO x x ∴=∠=︒=在Rt CDO ∆中,cos ODCDO CD∠=cos cos51180.625OD CD CDO x x ∴=∠=︒'≈ .BD OD OB =- ,0.5BD m =10.6250.52x x ∴-=,解得4x =.故梯子的长是4米.24.(1)如图,连接BD ,设BC 垂直平分线交BC 于点F ,BD CD ∴=,ABD C AB AD BD∆=++AB AD DC=++AB AC =+,AB CE = ,1ABD C AC CE AE ∆∴=+==,故ABD ∆的周长为1.(2)设AD x =,3BD x ∴=,又BD CD = ,4AC AD CD x ∴=+=,在Rt ABD ∆中,AB ==.tanAC ABC AB ∴∠===.25.(1)设甲队骑行的平均速度为/xkm h,则乙队骑行的平均速度为1.2/xkm h.根据题意,得13613625151.26060x x-=+,解得:34x=.经检验,34x=是原方程的根.1.2 1.23440.8x∴=⨯=.答:甲队骑行的平均速度为34/km h,乙队骑行的平均速度为40.8/km h.(2)如图,过点D作DG AB⊥于点G,则DG过点F.由题意得 1.5BG EF CD m===,10DF m=.设FG a=m.在Rt ADG∆中,45ADG∠=︒,(10)AG DG a m∴==+.在Rt AFG∆中,tanAG AFGFG∠=,tan tan47.7 1.10() AG FG AFG a x m∴=⋅∠=︒≈,10 1.10a a∴+=,解得:100a≈,10100110()AG m∴=+=,110 1.5111.5()AB AG BG m∴=+=+=.答:摄乐桥主塔的高AB约为111.5m.26.(1)设第一次购进隰县玉露香的进价为x 元/箱,根据题意可得:10000180001.520x x ⨯=+,解得100x =,经检验,100x =是原方程的解,答:第一次购进的“隰县玉露香”每箱的价格为100元;(2)由题意得,90ADB ∠=︒,在Rt ABD ∆中,tan AD ABD BD∠=,tan 42AD BD ∴=⋅︒,在Rt BCD ∆中,tan CD CBD BD ∠=,tan 36.9CD BD ∴=⋅︒,AC AD CD =- ,15AC m =,15tan 42tan 36.9BD BD ∴=⋅︒-⋅︒,解得100BD m ≈,100135.1()cos 0.74BD AB m ABD ∴=≈≈∠,135.1100> ,∴在点B 处的房屋不会受信号塔塔顶A 发出的信号辐射的影响.。
九年级数学下册《解直角三角形》试卷学校:__________ 姓名:__________ 班级:__________ 考号:__________题号一二三总分得分评卷人得分一、选择题1.(2分)如图,小颖利用有一个锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5m,AB为1.5m (即小颖的眼睛距地面的距离),那么这棵树高是()A.(53332+)m B.(3532+)m C.533m D.4m2.(2分)如图,梯形护坡石坝的斜坡 AB 的坡度1:3i=,坝高 BC 为 2m,则斜坡AB 的长是()A.25m B.210 m C.45 m D.6m3.(2分)已知等腰三角形底边长为 10 cm,周长为36 cm,那么底角的余弦等于()A.513B.1213C.1013D.5124.(2分)如图所示,在高为 300 m 的山顶上,测得一建筑物顶端与底部俯角分别为 30°和60°,则该建筑物高为()A.200m B.lOOm C.1003 m D.30035.(2分)如图所示,在离地面 5m 处引拉线固定电信信号接收杆,若拉线与地面成 60°角,则拉线AB 的长是()A .53mB .53m C .103m D .lOm6.(2分)已知△ABC 中,∠C = Rt ∠,co sA=13,则sinB 的值等于 ( ) A .13B .1C .223D .30 7.(2分) 某人沿着倾斜角为α的斜坡前进了c 米,则他上升的高度为( ) A . csin αB .ctan αC . ccos αD .tan cα把Rt △ABC 各边的长度都扩大3倍得Rt △A ˊB ˊC ˊ,那么锐角A 、A ˊ的余弦值的关系为( ) A .cosA =cosA ˊB .cosA =3cosA ˊC .3cosA =cosA ˊD .不能确定9.(2分)如图,矩形ABCD 中,CE ⊥BD 于E ,若BC=4, DE=95,则tan ∠BCE 等于( ) A .35B .45C .34D .43评卷人得分二、填空题10.(3分)已知正三角形的周长是 6,则它的面积为 .11.(3分)如图所示,某河堤的横断面是梯形ABCD ,BC AD ∥,迎水坡AB 长13米,且12tan 5BAE ∠=,则河堤的高BE 为 米. 12.(3分)一斜坡的坡比为 1:2,斜面长为 l5m ,则斜面上最高点离地面的高度为 m . 13.(3分)如图所示,大坝的横断面是梯形 ABCD ,坝顶 AD=3,坝高 AE=4m ,斜坡 AB 的坡比是1:3,斜坡 DC 的坡角为∠C=45°,则坝底 BC 宽为 m .14.(3分)如图,学校在周一举行升国旗仪式,一位同学站在离旗杆20米处,随着国歌响起,五星红旗冉冉升起.当这位同学目视国旗的仰角为37时(假设该同学的眼睛距离地面的高度为1.6米),国旗距离地面约 米.(结果精确到0.1米). 15.(3分)若α为等腰直角三角形的锐角,则cos α= . 16.(3分)化简:35(2.510)(1.610)⨯⨯= .17.(3分)已知31a b ==,,则()()(2)a b a b b b +−+−= . 18.(3分)计算:11211 4.5352553−+−+−= . 19.(3分)在 Rt △ABC 中,若∠C= 90°,sinA =13,则cosB= . 20.(3分)若θ=60°,则cos θ= . 评卷人 得分三、解答题21.(6分)2008年初,我国南方部分省区发生了雪灾,造成通讯受损.如图,现有某处山坡上一座发射塔被冰雪从C 处压折,塔尖恰好落在坡面上的点B 处,在B 处测得点C 的仰角为38,塔基A 的俯角为21,又测得斜坡上点A 到点B 的坡面距离AB 为15米,求折断前...发射塔的高.(精确到0.1米)22.(6分)如图所示,某水库大坝的横断面是等腰梯形,坝顶宽 6m ,坝高 lOm ,斜坡AB 的坡度为 1:2,现要加高 2m ,在坝顶宽度和斜坡坡度均不变的情况下,加固一条长50m 的大坝,需要多少土?23.(6分)如图所示,杭州某公园入口处原有三级台阶,每级台阶高为 20 cm ,深为 30 cm .为方 便残疾人士,现拟将台阶改为斜坡,设台阶的起点为 A ,斜坡的起点为 C . 现将斜坡的坡角∠BCA 设为 12°,求 AC 的长度. (精确到1cm)24.(6分)已知,如图,在梯形 ABCD 中,AD ∥BC ,∠ABC=90°,∠C= 45°, BE ⊥CD 于点E ,AD= 1,CD=22,求 BE 的长.已知直角三角形两个锐角的正弦sin sin A B ,是方程222210x x −+=的两个根,求A B ∠∠,的度数.26.(6分)在Rt △ABC 中,∠C =900,AB =13,BC =5,求A sin , A cos ,A tan .27.(6分)计算:=⋅−20062005)31()3( .28.(6分)已知a 、b 、c 是△ABC 的三边,a 、b 、c 满足等式2(2)4()()b c a c a =+−,且有5a-3c=0,求 sinB 的值.29.(6分)如图所示,锐角α的顶点在坐标原点,一边在x 轴的正半轴上,另一边上有一点 P(2, y),若sin α=35,的值.30.(6分)如图,在Rt △ABC 中,∠C= 90°,AC=5,BC=12,求B 的正弦、余弦和正切的值.【参考答案】***试卷处理标记,请不要删除一、选择题1.A2.B3.A4.A5.C6.A7.A8.A9.D二、填空题1011.1212.13.7+14.16.715.2216.4210⨯17.118.11 515−19.1 320.12三、解答题21.解:作BD AC ⊥于D ,由已知得:38CBD ∠=,21ABD ∠=,15AB =米 在Rt ADB △中,sin ADABD AB∠=, sin 15sin 21 5.38AD AB ABD ∴=∠=⨯≈cos BDABD AB∠=,cos 15cos2114.00BD AB ABD ∴=∠=⨯≈ 在Rt BDC △中,tan CDCBD BD ∠=tan 14.00tan3810.94CD BD CBD ∴=∠⨯≈≈, cos BD CBD BC ∠=,14.0017.77cos cos38BD BC CBD ∴=∠≈≈ 5.3810.9417.7734.09AD CD BC ∴++++=≈34.1≈ 答:折断前发射塔的高约为34.1米.22.据题意作出加固后的坝体横断面(如图中等腰梯形 CFEP),过A 点作AH ⊥BC 于 H ,过E 点作 EM ⊥BC 于M ,则BH=2AH=20m.∴BC=2BH+AD=46m,1(646)102602AECD S =⨯+⨯=梯形(m 2), ∵EF=AD= 6 m,EM= 12 m, PM=24m.∴PC=54m,∴1(654)123602PCEF S =⨯+⨯=梯形(m 2),∴加的面积为 360—260=100(m 2),∴应增加100×50= 5000(m 3)土.23.过B 点作 BD ⊥CA ,垂足为 D 点,由已知得 BD= 20×3 =60 cm, AD=30×2=60 cm,60tan tan12o BD BCD CD CD∠===,∴CD= 282 cm, AC= 282- 60 = 222 (cm)答:AC 的长度为 222 cm.24.如图,过点 D 作DF ⊥AB ,交 BC 于F ,∵AD ∥BC,∴四边形 ABFD 是平行四边形,∴BF=AD=1,∵DF ∥AB,∴∠DFC=∠ABC=90°,Rt △DFC 中,∠C=45°,22CD =,cos CFC CD=,∴CF=2. BC=BF+FC=3,Rt △BEC 中,∠BEC=90°,sin BE C BC =,322BE =25.解:222210x x −+=,标准式为:21202x x −+= 202x ⎛−= ⎪⎝⎭∴,122x x ==∴ 2sin sin A B ==∵,45A B ∠=∠=∴° 26.135sin =A , 1312cos =A ,125tan =A .27.31−28.由已知得222b c a =−,即222c a b =+,∴△ABC 是Rt △,∠C=90°, ∵530a c −=,∴35a c =. 设: a = 3k ,c= 5k ,∴b= 4k ,∴4sin 5b Bc ==. 29.过点P 作x 轴的垂线段,M 为垂足,∵ PM=y ,OM= 2,∴24OP y =+,3sin 5PM a OP ==,∴2354y =+,∴32y ⋅=±∵y>0 ,∴32y =.30.5sin 13AC B AB ==,1213BC sB AB ∞==,5tan 12AC B BC ==。