第二章复变函数的积分
- 格式：doc
- 大小：372.00 KB
- 文档页数：6
下载文档原格式
合集下载
复变函数及积分变换第二章
x
arg z在负实 轴上不连续.
若z0=x0+iy0不是原点也不是负实轴及虚轴上的点
arctan( y / x),
arg z arctan( y / x) π,
arctan( y / x), arctan( y / x),
x0 0
lim
z z0
arg
z
lim
( x, y)( x0
,
y0
)
arctan(
) ，则说函数 f(z) 在点 z0 处连 内每一点都连续，那么称函
数f(z)在区域D内连续.
定理2.3 若 f(z)、g(z) 在点z0连续，则其和、差、积、 商（要求分母不为零）在点z0处连续.
(1)多项式 w a0 zn a1zn1 an1z an 在整个复平
面上连续；
(2)任何一个有理分式函数
例2.2 判断下列函数在原点处的极限是否存在，若存
在，试求出极限值：
(1) f (z)
z Re(z) ; z
(2) f (z)
Re( z
z
2
2
)
.
解： (1)方法一
因为
f (z)
z
Re(z) z
z
所以 0，取 ，当0 z 时，总有
f (z) 0 f (z) z
根据极限定义 lim f (z) 0 z0
解：dw lim f (z Δz) f (z) lim (z Δz)n zn
dz Δz0
Δz
Δz 0
Δz
Δlizm0(Cn1 zn1 Cn2 zn2Δz
C n1 n
zΔz
n2
Cnn Δz n1 )
Cn1zn1 nzn1,
第二章复变函数的积分
f (z)dz lim f (k )(zk zk1)
l
积分n函 数k1
积分路径 一般来说,复变函数的积分值与积分路径有关.
2、复变函数积分计算方法
n
f (z)dz lim f (k )(zk zk1) n k 1
l
1）将复变函数的路积分化为两个实变函数的线积分
2）参数积分法
若积分曲线的参数方程z=z(t) ( ),dz z'(t)dt
则
f (z)dz f [z(t)]z'(t)dt
l
（极坐标法，通常用来计算积分路径为圆弧时的情况）
通常思路：
积分路径l为圆弧： 宗量用指数形式表示：
z z0
z z0 ei
n
n
f (z)dz f (z)dz;l lk
l
k 1 lk
k 1
f (z)dz f (z)dz
lAB
lBA
f (z)dz
l
f (z) dz ; dz
dx2 dy2 ds
l
Ms; M f (z) , s l的长度
用来求积分的估计值
r
1
z3 z
2
dz
z3 z r 1 z2
dz
（1）
z3
z r 1 z2
dz M
dz M
z r
ds Ms
z r
（2）
由（1）（2）式，得：
z3 dz Ms
z r 1 z2
M
1
r
3
r
2
s ds 2 r z r
数学物理方法第二章复变函数的积分
1 1
一般而言,复变函数的积分不仅与起点和终点有 关, 同时还与路径有关。
§2.2 柯西（Cauchy）定理
——研究积分与路径之间的关系 （一）单连通域情形 单连通域： 在其中作任何简单闭合围线，围 线内的点都是属于该区域内的点。 单连通区域的Cauchy 定理 ：如果函数 f (z) 在闭 单连通区域 B 中单值且解析， 则沿 B 中任 何一个分段光滑的闭合曲线 l (也可以是 B 的 边界 l0 ), 函数的积分为零。
lim f( z z ) k)( k k 1
n
存在且与 k 的选取无关, 则这个和的极限称为 函数 f (z) 沿曲线 l 从 A 到 B 的路积分，记为
即
l
f (z) dz
n k k k 1
z ) d z lim f ( )( z z f(
l n k 1 max | z | 0 k
l 1 l 2
f (z)=Re (z)不是解析函数!
y i l2 o l1 1 l2
I1 Rez d z xd( x iy) 1 xd x i d y i 0 0 2 ( y = 0) (x=1)
1 1
1+i
l1 x
1 I 0 id y x d x 2 0 0 (x=0) ( y=i ) 2
l l l
v u u v d x d y i d x d y s s x y y x
又u、v 满足C-R条件 u v u v , x y y x
y
f ( z ) d z 0
l
B
l
o
一般而言,复变函数的积分不仅与起点和终点有 关, 同时还与路径有关。
§2.2 柯西（Cauchy）定理
——研究积分与路径之间的关系 （一）单连通域情形 单连通域： 在其中作任何简单闭合围线，围 线内的点都是属于该区域内的点。 单连通区域的Cauchy 定理 ：如果函数 f (z) 在闭 单连通区域 B 中单值且解析， 则沿 B 中任 何一个分段光滑的闭合曲线 l (也可以是 B 的 边界 l0 ), 函数的积分为零。
lim f( z z ) k)( k k 1
n
存在且与 k 的选取无关, 则这个和的极限称为 函数 f (z) 沿曲线 l 从 A 到 B 的路积分，记为
即
l
f (z) dz
n k k k 1
z ) d z lim f ( )( z z f(
l n k 1 max | z | 0 k
l 1 l 2
f (z)=Re (z)不是解析函数!
y i l2 o l1 1 l2
I1 Rez d z xd( x iy) 1 xd x i d y i 0 0 2 ( y = 0) (x=1)
1 1
1+i
l1 x
1 I 0 id y x d x 2 0 0 (x=0) ( y=i ) 2
l l l
v u u v d x d y i d x d y s s x y y x
又u、v 满足C-R条件 u v u v , x y y x
y
f ( z ) d z 0
l
B
l
o
第二章复变函数的积分
第二章 复变函数的积分在微积分学中，微分法与积分法是研究函数性质的重要方法。
同样，在复变函数中，积分法也跟微分法一样是研究复变函数性质十分重要的方法和解决实际问题的有力工具。
§2.1 复变函数积分的概念一、复变函数的积分设C 为平面上给定的一条光滑(或按段光滑)曲线。
若选定C 的两个可能方向中的一个作为正方向，那么就把C 理解为带有方向的曲线，称为有向曲线。
设曲线C 的两个端点为A 与B ，如果从A 到B 的方向作为C 的正方向，那么从B 到A 的方向就是C 的负方向，并把它记作-C 。
在今后的讨论中，常把两个端点中的一个作为起点，另一个作为终点。
除特殊声明外，正方向总是指从起点到终点的方向。
关于简单闭曲线的正方向是指当曲线上的点P 顺此方向沿该曲线前进时，临近P 点的曲线内部始终位于P 点的左方。
与之相反的方向就是曲线的负方向。
若光滑或逐段光滑的曲线C 的参数方程为)()()(t iy t x t z z +==，)(βα≤≤t （2.1） t 为实参数，则规定t 增加的方向为正方向，即由)(αz a =到)(βz b =的方向为正方向。
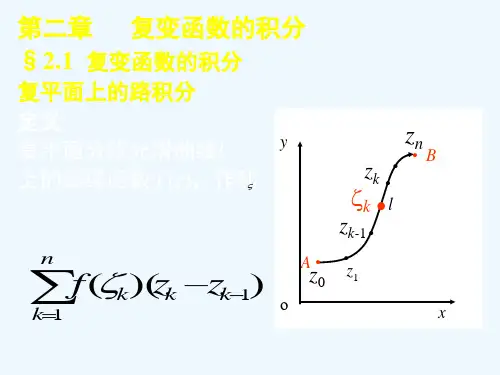
定义2.1 设函数)(z f w =定义在区域D 内，C 为区域D 内起点为A 终点为B 的一条光滑有向曲线，把曲线C 任意分成n 个弧段，设分点为：B z z z z z A n n ==-,...,,,1210 在每个小弧段上任取一点k ζ（图3.1），作和∑=∆=nk k k n z f S 1)(ζ其中1--=∆k k k z z z ，记=∆k s 的长度，}Δ{max 1k nk s δ≤≤=。
当n 无限增加，且δ趋于零时，如果不论对C 的分法及k ζ的取法如何，当n S 有唯一极限，那么称这个极限值为函数)(z f 沿曲线C 的积分，记作∑⎰=→=nk k kδCz ζf dz z f 1Δ)(lim )( （2.2）图2.1C 称为积分路径，⎰Cdz z f )(表示沿C 的正方向的积分，⎰-C dz z f )(表示沿C的负方向的积分。
数学物理方法第2章复变函数积分-2016方案
(2.1.3)
(2) 化为参数积分计算．设积分曲线L的参数方程为z(t)，
将z(t)及dz(t)＝z'(t)dt代入式(2.1.4)，可得
3
【例2.1.1】计算积分I=
其中曲线L是
(1)沿1+ i 到2+4 i 的直线，见图2.2(a)；
(2)沿1+ i 到2+i，再到2+4 i 的折线，见图2.2(b)；
§2.2.1 单通区域的柯西定理
定理 若函数f(z)在单通区域D 内解析，则f(z)在D内沿任意 闭曲线的积分为零
∮l f(z)dz = 0 (2.2.1)
证明 这个定理的严格证明比较复 杂, 为简单起见, 我们在“f(z)在D 内连续” 附加条件下证明这个定 理．
先将复变积分化为两个实变积 分的线性叠加
29
这就是解析函数的定积分公式，它与实变 函数中的牛顿-莱布尼茨公式具有相同的形 式。
通常把f(z)的原函数的集合
称f(z)的不定积分，式中C为复常数。
30
(2.2.8)
31
§2.2.3 复通区域的柯西定理
定理 若f(z)在闭复通区域 解析，则f(z)沿所
有内、外边界线(L=L0+ 之和为零
37
【2.2.2】试计算 其中积分回路分别(图2.11) (1) |z-i|＝2；(2) |z+i|＝2；(3) |z|＝3.
38
解 首先，将被积函数分解为部分分式(利用通 分可以凑出来)
≠0
=0
39
40
【例2.2.3】若f(z)=1/(z-a) 在z=a的无心邻域内 连续，积分回路是以a点为圆心的圆弧
由于a点在D内随意变动时，柯西公式依然成立， 有时分别用z和x代替式 (2.3.1)的a和z。将柯西公 式改写为
第二章 复变函数的积分chen
l
= ∫ [u( x , y )dx − v ( x , y )dy ] + i ∫ [u( x , y )dy + v ( x , y )dx ]
l l
结论： ※ 结论：复变函数的路积分可以归结为两个实变函数线 积分，它们分别构成路积分的实部和虚部。 积分，它们分别构成路积分的实部和虚部。
路积分的概念和性质
2
1
1 3 = 2 − + 2i = + 2i 2 2
路积分的计算例题
【例二】沿图所示的三条曲线分别计算复变函数 f ( z ) = Re z 从 O 到 B 的路积分。
∫
OAB
f ( z )dz = ∫
OAB
Re zdz = ∫ Re zdz + ∫ Re zdz
OA AB
OA段 z = iy , Re z = 0 dz = idy 段
C
C
f (z)dz
C
∫ [ f + g]dx = ∫
a
fdx + ∫ gdx
a
b
∫ [ f + g]dz = ∫
C
C
fdz + ∫ gdz
C
∫
b
a
f ( x)dx = −∫ f ( x)dx
b
a
∫
∫
C
f (z)dz = −∫ f (z)dz
f dz + ∫ f dz = ∫
C2 C1 ∪C2
∫
c
a
f dx + ∫ f dx = ∫ f dx
∫
l
f ( z )dz = ∫ [u( x , y )dx − v ( x , y )dy ] + i ∫ [v ( x , y )dx + u( x , y )dy ]
= ∫ [u( x , y )dx − v ( x , y )dy ] + i ∫ [u( x , y )dy + v ( x , y )dx ]
l l
结论： ※ 结论：复变函数的路积分可以归结为两个实变函数线 积分，它们分别构成路积分的实部和虚部。 积分，它们分别构成路积分的实部和虚部。
路积分的概念和性质
2
1
1 3 = 2 − + 2i = + 2i 2 2
路积分的计算例题
【例二】沿图所示的三条曲线分别计算复变函数 f ( z ) = Re z 从 O 到 B 的路积分。
∫
OAB
f ( z )dz = ∫
OAB
Re zdz = ∫ Re zdz + ∫ Re zdz
OA AB
OA段 z = iy , Re z = 0 dz = idy 段
C
C
f (z)dz
C
∫ [ f + g]dx = ∫
a
fdx + ∫ gdx
a
b
∫ [ f + g]dz = ∫
C
C
fdz + ∫ gdz
C
∫
b
a
f ( x)dx = −∫ f ( x)dx
b
a
∫
∫
C
f (z)dz = −∫ f (z)dz
f dz + ∫ f dz = ∫
C2 C1 ∪C2
∫
c
a
f dx + ∫ f dx = ∫ f dx
∫
l
f ( z )dz = ∫ [u( x , y )dx − v ( x , y )dy ] + i ∫ [v ( x , y )dx + u( x , y )dy ]
数学物理方法 第二章 复变函数的积分
wuxia@
证明： 1 dz 1 f (α )dz (1)已知f (α ) = f (α ) ⋅ ∫l z − α = 2πi ∫l z − α 2πi 1 f ( z )dz 1 f ( z ) − f (α ) 与f (α ) = 比较，只需证明 ∫l z − α ∫l z − α dz = 0即可. 2πi 2πi f ( z ) − f (α ) (2)因为z = α为 的奇点，因此，以α为圆心，取任意小 z −α f ( z ) − f (α ) ε为半径做小圆Cε , 这样在l及Cε 所围复通区域上 单值解析。 z −α f ( z ) − f (α ) 1 f ( z ) − f (α ) 1 根据柯西定理， ∫ dz = ∫Cε z − α dz l 2πi z −α 2πi 对于Cε 上的z有：z − α = εe iϕ , dz = iεeiϕ dϕ 于是, 有： 1 f ( z ) − f (α ) 1 2π f ( z ) − f (α ) iϕ 1 iεe dϕ = iϕ ∫l z − α dz = 2πi ∫0 εe 2πi 2π
wuxia@
∫
2π
0
[ f ( z ) − f (α )]dϕ
(3)现在需要对上式右端做估计 因为f ( z )连续，一定可以找到∆ > 0,当 | z − α |≤ ∆时， | f ( z ) − f (α ) |≤ ε ′ 因而有： 1 2π 1 2π 1 ∫0 [ f ( z ) − f (α )]dϕ ≤ 2π ∫0 | f ( z ) − f (α ) |⋅ | dϕ |< 2π 2π =ε 1 f ( z ) − f (α ) 1 f ( z) ∴ dz = 0, f (α ) = ∫l z − α ∫l z − α dz 2πi 2πi
证明： 1 dz 1 f (α )dz (1)已知f (α ) = f (α ) ⋅ ∫l z − α = 2πi ∫l z − α 2πi 1 f ( z )dz 1 f ( z ) − f (α ) 与f (α ) = 比较，只需证明 ∫l z − α ∫l z − α dz = 0即可. 2πi 2πi f ( z ) − f (α ) (2)因为z = α为 的奇点，因此，以α为圆心，取任意小 z −α f ( z ) − f (α ) ε为半径做小圆Cε , 这样在l及Cε 所围复通区域上 单值解析。 z −α f ( z ) − f (α ) 1 f ( z ) − f (α ) 1 根据柯西定理， ∫ dz = ∫Cε z − α dz l 2πi z −α 2πi 对于Cε 上的z有：z − α = εe iϕ , dz = iεeiϕ dϕ 于是, 有： 1 f ( z ) − f (α ) 1 2π f ( z ) − f (α ) iϕ 1 iεe dϕ = iϕ ∫l z − α dz = 2πi ∫0 εe 2πi 2π
wuxia@
∫
2π
0
[ f ( z ) − f (α )]dϕ
(3)现在需要对上式右端做估计 因为f ( z )连续，一定可以找到∆ > 0,当 | z − α |≤ ∆时， | f ( z ) − f (α ) |≤ ε ′ 因而有： 1 2π 1 2π 1 ∫0 [ f ( z ) − f (α )]dϕ ≤ 2π ∫0 | f ( z ) − f (α ) |⋅ | dϕ |< 2π 2π =ε 1 f ( z ) − f (α ) 1 f ( z) ∴ dz = 0, f (α ) = ∫l z − α ∫l z − α dz 2πi 2πi
数学物理方法第2章复变函数积分-2016
49
50
【例2.3.2】试计算积分，
积分回路L为x2 + y2=2x 解 (1) 积分回路的形状： (x-1)2+y2=1
(2)被积函数的奇点．
方程z4+1=0有四个根：z=exp[i (p+2kp)/4]， k=0,1,2,3，因此，被积函数有四个奇点，但仅有 z1与z4位于积分回路之内
51
2. 复通区域的柯西公式
设f (z)在闭复通区域D中解析，a为D的内点， 则 式中积分沿D的内外边界线的正方向．
32
证明 为了应用单通区域的柯西定理，作割线把外边界线 L0与内边界线连接起来，将闭复通区域变成闭单通区域。
33
推论3 在f(z)的解析区域中，积分回路连 续变形时，其积分值不变．
证明 取变形前后的积分回路 作为复通区域 的内外边界 线，如图2.9所示．由式 (2.2.21a) 可得
移项后，改变l2的积分方向，即有
复变积分性质(5)及式(2.2.34)，可证
43
由于e可任意地小，(q2-q1)为常量，式
(2.2.35)表明
可任意地小根据极限的定义，可得
44
2. 大圆弧引理
若j(z)在无穷远点的无心邻域内连续，在大 圆弧CR(z=Reiq, R→∞,q1<q<q2 )上
这两个引理为计算沿圆弧的积分带来方便． 2.3节将分别用来证明单通区域及无界区域的 柯西公式．
(3)按复通区域的柯西定理及柯西公式计算以小圆周c1 和c2分别包围奇点z1和z4 ，则被积函数在外边界线l 与内边界线c1 ， c2 所围的复通区域解析。按复通区 域的柯西定理，沿l的积分等于沿C1与C2积分之和， 后两个积分可按柯西公式算出，即
第二章 复变函数的积分
第二章 复变函数的积分
一.复变函数的积分
(复平面的路径积分) 复平面的路径积分)
∫ f (z )dz ≡ lim ∑ f (ξ )(z
l n →∞ k =1 k
l l
n
k
− z k −1 ) ≡ lim ∑ f (ξ k )dz k n→∞
k =1
n
∫ f (z )dz = ∫ u (x, y )dx − v(x. y )dy + i ∫ v(x, y )dx + u (x. y )dy
ez I =∫ 2 dz c ( z + 1) 2
z 2
2π i (n−1) f (ξ ) ∫ (ξ − z)n dξ = (n −1)! f (z) l
例:计算
z = a (> 1)
解:
I=∫
c1
e z /( z − i ) 2 e /( z + i) dz dz + ∫ 2 2 c2 ( z + i) ( z − i)
1
I 2 = ∫ xdz + ∫ xdz =
0
1
1+i
i
1 ∫ 0idy + ∫ xdx = 2 0 0
直线参数方程 : z = (1 + i)t或( y = x)
1
I 3 = ∫ t (1 + i )dt = 1 + i 2 0
(可见积分与路径有关)
例2
1+i
z 2 dz = ? 1)沿折线 0—1---1+i ∫
= 2π i [e z /( z + i) 2 ]′z =i + 2π i [e z /( z − i ) 2 ]′z = −i
一.复变函数的积分
(复平面的路径积分) 复平面的路径积分)
∫ f (z )dz ≡ lim ∑ f (ξ )(z
l n →∞ k =1 k
l l
n
k
− z k −1 ) ≡ lim ∑ f (ξ k )dz k n→∞
k =1
n
∫ f (z )dz = ∫ u (x, y )dx − v(x. y )dy + i ∫ v(x, y )dx + u (x. y )dy
ez I =∫ 2 dz c ( z + 1) 2
z 2
2π i (n−1) f (ξ ) ∫ (ξ − z)n dξ = (n −1)! f (z) l
例:计算
z = a (> 1)
解:
I=∫
c1
e z /( z − i ) 2 e /( z + i) dz dz + ∫ 2 2 c2 ( z + i) ( z − i)
1
I 2 = ∫ xdz + ∫ xdz =
0
1
1+i
i
1 ∫ 0idy + ∫ xdx = 2 0 0
直线参数方程 : z = (1 + i)t或( y = x)
1
I 3 = ∫ t (1 + i )dt = 1 + i 2 0
(可见积分与路径有关)
例2
1+i
z 2 dz = ? 1)沿折线 0—1---1+i ∫
= 2π i [e z /( z + i) 2 ]′z =i + 2π i [e z /( z − i ) 2 ]′z = −i
第二章复变函数的积分
数值测试有盲人摸象的感
觉，其实这些结果可以很
好地用柯西定理来解释。
21
单通区域的柯西定理
如果函数f(z)在闭单通区域(区域加境界线) B 上解 析，则沿 B 上任一分段光滑闭合曲线l (可以是边 界)，有：
条件可放宽为：
∫ f (z)dz = 0
l
在单通区域B上解析， 在闭单通区域B 上连续
无论沿顺时针还 是逆时针方向结 果均为0。由柯 西定理不难导出 解析函数路积分 的路径无关性。
1+i
1
∫ ∫ 积分值 = (x2 − y2 + 2xyi)dz = 2x2i(1+ i)dx
0
0
∫ =
2(i
1
−1)
x 2 dx
=
−
2
+
2
i
0
33
路径2结果和路径1积分结果相同。如果我们继续取 其他路径进行积分，仍然会得到相同结果。
11
3/17/2012
路积分与路径的关系
从上面的例子可以看到，某些路积分问题结 果与路径有关，而某些则与路径无关。
试计算以下路积分，积分路径如下图所示。积分 路径也是z=0至z=1+i。
I = ∫ z2dz l
这里被积函数z2是 一个解析函数。
3/17/2012
9
3/17/2012
路径1的情况
被积函数z2 = x2 − y2 + 2xyi
路径1的积分：
在0 → 1段，y = 0，我们有：
∫ ∫ 积分值 = 1 (x2 − y2 + 2xyi)dx = 1 x2dx = 1
∫
l
P(
x,
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二章：复变函数的积分第1节 复变函数的积分设()f z 在复平面上的光滑曲线l 上连续。
若将l 分成n 段，其中第k 小段为,1k k z z +⎡⎤⎣⎦。
在该小段上任取一点k ξ，若和式：()()11nkk k i f zz ξ+=-∑ （1）在当n →∞，()10k k z z +-→时的极限存在则这个和式的极限就称为()f z 在l 上的路积分。
记作：()()()110lim nk k k i lz f z dz f zz ξ+→∞=∆→=-∑⎰ （2）(),z x iy f z u iv =+=+∴()()()()()llf z dz u iv d x iy u iv dx idy =++=++⎰⎰⎰lludx vdy i vdx udy =-++⎰⎰（3）也分为实部和虚部其积分法可用实度函数积分法测：例1、试计算111Re l l I zdz xdz ==⎰⎰和22Re l I zdz =⎰。
其中1l 和2l 的路径如图。
起始点相同；解：''''''11111 1.l l l l I xdx idy =+=+⎰⎰⎰⎰11012xdx i dy i =-+=+⎰⎰ '"222l l I =+⎰⎰=100xdx +⎰⎰=12由此可见，一般在复变函数中，即使被积函数和积分起终点相同，但沿不同的路径，积分值是不一样的。
第2节 柯西定理以上，我们知道，一般复变函数的积分与路径有关。
但有特例——解析函数在“单通域”内积分就与路径无关 一、单通域与单通域柯西定理1、单通域（单连通域） 任意两点间连线上所有点均属于该域（无孔隙） 函数在闭域内的点上处处解析的域——单通域2、单通域的柯西定理若()f z 在单通域B 上解析，ρ是B 上一分常光滑闭合曲线，则：()0lf z dz =⎰ （1）证：()()()()()lllf z dz u iv d x iy u iv dx idy =++=++⎰⎰⎰lludx vdy i vdx udy =-++⎰⎰ （2）利用格林公式：l D Q P Pdx Qdy dxdy x y ⎛⎫∂∂+=- ⎪∂∂⎝⎭⎰⎰⎰ 则由（2）得：()lD D v u u v f z dz dxdy i dxdy x y x y ⎛⎫⎛⎫∂∂∂∂=-++- ⎪ ⎪∂∂∂∂⎝⎭⎝⎭⎰⎰⎰⎰⎰ （3） 又由C-R 条件：u v x y ∂∂=∂∂，v uxy ∂∂=-∂∂∴()0lf z dz =⎰二、复连通与复通通柯西定理1、复通域若域内存在奇点，可作一些半径适当的闭合曲线将这些奇点分离开，剩下的这些带孔的区域称为复连通区域。
简而言之，只要有一个有不属于闭合曲线所围区域内的点，这样的区域就称为复连通区域。
2、复通域的柯西定理若()f z 是闭复通域上的单值解析函数，l 为区域的外境界线，诸i l 为区域内境界线，则有：()()10i ni ll f z dz f z dz =+=∑⎰⎰ （4）其中，积分均沿境界线的正向进行。
境界线：规定：沿境界线正向前进时，区域总在观察者左方。
内境界线：即将奇点挖去的那些闭合曲线。
证明：以一个奇点的情况为例：（如图：）设'l 是挖去奇点的内境界线，l 为外境界线，若想用“剪子”沿AB 剪开，使内外境线相连，于是该多连通域就变为单连域了。
此时有（由单连域柯西定理）：()()()()''0ABll B Af z dz f z dz f z dz f z dz +++=⎰⎰⎰⎰ (5)但()()''ABB A f z dz f z dz =-⎰⎰（同一路径积分反向相反）∴()()'0ll f z dz f z dz +=⎰⎰ （6）与（4）吻合同理可证明挖去几个奇点的多连通域。
小结：1、闭单通域上的解析函数沿境界线（或域内任一单闭曲线）积分为零。
2、闭复通域上的解析函数沿所有内外境界线正方向闭积分和为零。
3、闭复通域上的解析函数沿外境界线积分等于所有内境界线沿逆时针方向闭积分之和4、解析函数在单通域或复通域上的积分与路径无关（只与起始、终点有关）。
第3节 不定积分一、不定积分的意义由上节第4点（小结），若始点固定、终点为任意的，则：在连通域上 ()()21z z F z f d ξξ=⎰（1）就定义了一个单值解析函数；并称()F z 是()f z 的一个原函数。
且有：()()()2121z z f d F z F z ξξ=-⎰（2）（2）式表明：解析函数的路径积分等于其原函数的改变量。
二、一个重要的积分： 考察积分：()nlI z dz α=-⎰ （1）其中：n =整数：2,1,0,1,2m m---此积分可分两种情况：1、l 不包围α点（即l 围域不含α点），则被积分函数()()nf z z ωα==-在l 所围区域是解析的,此时有()⎰=-02dz z α 2.若l 围域含有α，则又分两种情况：（1）当n >0时，()()2α-=z z f 在l 围域是解析函数：()⎰=0dz z f 。
()2当n <0时，()()2α-=z z f 在l 围域不是解析函数。
但由上节知识，可以α为圆心。
R 为半径作一回路c （将α挖去）。
于是上述积分可划为：()()⎰⎰-=-dz z dz z nc n lαα （2） 在c 上，ϕαi z Re =- ()ϕαϕϕd i d dz i i ReRe=+=()()⎰⎰-=-=∴lcnndz z dz z I αα()211.Re i n n in i n cR e i d iR ed πϕϕϕϕ++==⎰⎰ （a ）若.1-≠n 则：()ϕ111+++=n i n e n R I |020=π（b ）若,1-=n 则：()210i n I ie d πϕ+=⎰i综上所述：()()⎰-≠=-lnn dz z 1,0ϕ()()⎰⎩⎨⎧=-ll l i dz z ααπα不围，围0,21或：()⎰-≠=-ln n dz z 1,0i 21απ ()()⎰⎩⎨⎧=-l l l z dzi αααπ包围不包围,1,021ξ2.4 柯西公式一．柯西公式：若()f z 在闭单通区域B 上解析，l 为B 的边界线，a 为B 内的任一点，则有柯西公式：1()()2lf z f a dz iz aπ=-⎰（1）亦可写为：001()()2lf z f z dz iz z π=-⎰（2）二．证明： 由上节知：0()1()()22if a dz f a f a dz i z a iz aππ==--⎰⎰（3） 由（1）—（3）得：1()()02lf z f a dz iz aπ-=-⎰（4）显然若（4）成立，则（1）成立一般函数 ()()f z f a w z a-=-在z a =处不连续（a 是w 的奇点）所以可以a 为心（任意小）为半径作圆cξ由（第二节）柯西定律：1()()1()()22c f z f a f z f a dz dz iz a iz aξππ--=--⎰⎰（5）a b a b +≤+ ⇒20()()max f(z)-f(a)()()max ()()2i c f z f a f z f a dz dz e d f z f a z az a ξπϕξϕπξ--≤≤=---⎰⎰⎰若令z a →即0ξ→ ， ()()f z f a →lim max ()().20f z f a ξπ→-=即（5）左边=0 （而左边与ξ无关）. 所以（4）成立三．柯西公式的一般表示：由于a 是任意的，可令a z →。
此时z g →（作为积分变量），则柯西公式可表示为：1()()2lf g f z dg ig zπ=-⎰(6) 另：!()()()2()n nn nld n f g f z f z dg dz ig z π==-⎰（7） 柯西公式的一个重要应用是：（1） 式的右边，若被积函数可写为()f z z a -则积分可直接得出2()i f a π⋅ （被积函数是()g z 是只要能设法变换为()f z z a-即可用柯西公式求解）作业： （1）求：()nz a dz-⎰（2）求：22dz z a-⎰。