信息论与编码第5章 信源编码技术
- 格式:ppt
- 大小:1.55 MB
- 文档页数:77





第五章信源编码信息论基础第五章信源编码 本章主要讨论的问题:5.1 离散信源编码5.1.1 编码器5.1.2分组码5.1.3定长码5.1.4 变长码5.2 连续信源编码5.3 相关信源编码简介信源编码:以提高通信有效性为目的的编码。
通常通过压缩信源的冗余度来实现。
采用的方法是压缩每个信源符号的平均比特数或信源的码率。
即同样多的信息用较少的码率传送,使单位时间内传送的平均信息量增加,从而提高通信的有效性。
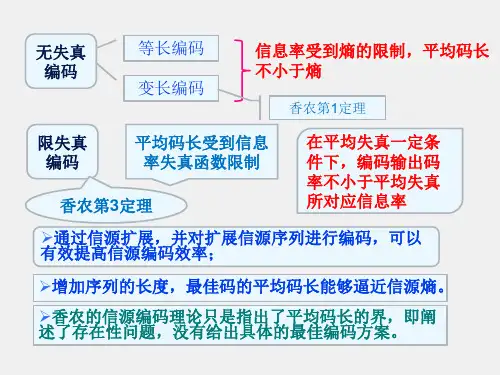
信源编码理论是信息论的一个重要分支,其理论基础是信源编码的两个定理。
–无失真信源编码定理:是离散信源/数字信号编码的基础;–限失真信源编码定理:是连续信源/模拟信号编码的基础,如语音、图像等信号。
信源编码的分类:离散信源编码、连续信源编码和相关信源编码三类。
–离散信源编码:独立信源编码,可做到无失真编码;–连续信源编码:独立信源编码,只能做到限失真信源编码;–相关信源编码:非独立信源编码。
编码器编码器可以看作这样一个系统,它的输入端为原始信源S ,其符号集为;而信道所能传输的符号集为。
编码器的功能是用符号集X 中的元素,将原始信源的符号变换为相应的码字符号,所以编码器输出端的符号集为称为码字,为码字的码元个数,称为码字的码字长度,简称码长。
码字的集合C 称为码书。
称为码元。
12{,,...,}q S S S S =12{,,...,}r X x x x =12{,,...,}q S s s s =12{,,...,}r X x x x =编码器12:{,,...,}q C W W W 12:{,,...,}q C w w w i S i w i w i L i w i w i x例:二元信道的信源编码器:码符号集X={0,1},如果要将信源通过二元信道传输,必须将信源编成二元码,这也是最常用的一种码。
等长码非等长码非奇异码非奇异码 等长码与变长码码中各个码字都是由同样多个码元构成的,称为等长码,反之,称为变长码。



信息论与编码第5章第五章信源编码(第⼗讲)(2课时)主要内容:(1)编码的定义(2)⽆失真信源编码重点:定长编码定理、变长编码定理、最佳变长编码。
难点:定长编码定理、哈夫曼编码⽅法。
作业:5。
2,5。
4,5。
6;说明:本堂课推导内容较多,枯燥平淡,不易激发学⽣兴趣,要注意多讨论⽤途。
另外,注意,解题⽅法。
多加⼀些内容丰富知识和理解。
通信的实质是信息的传输。
⽽⾼速度、⾼质量地传送信息是信息传输的基本问题。
将信源信息通过信道传送给信宿,怎样才能做到尽可能不失真⽽⼜快速呢?这就需要解决两个问题:第⼀,在不失真或允许⼀定失真的条件下,如何⽤尽可能少的符号来传送信源信息;第⼆,在信道受⼲扰的情况下,如何增加信号的抗⼲扰能⼒,同时⼜使得信息传输率最⼤。
为了解决这两个问题,就要引⼊信源编码和信道编码。
⼀般来说,提⾼抗⼲扰能⼒(降低失真或错误概率)往往是以降低信息传输率为代价的;反之,要提⾼信息传输率常常⼜会使抗⼲扰能⼒减弱。
⼆者是有⽭盾的。
然⽽在信息论的编码定理中,已从理论上证明,⾄少存在某种最佳的编码或信息处理⽅法,能够解决上述⽭盾,做到既可靠⼜有效地传输信息。
这些结论对各种通信系统的设计和估价具有重⼤的理论指导意义。
§3.1 编码的定义编码实质上是对信源的原始符号按⼀定的数学规则进⾏的⼀种变换。
讨论⽆失真信源编码,可以不考虑⼲扰问题,所以它的数学描述⽐较简单。
图 3.1是⼀个信源编码器,它的输⼊是信源符号},,, {21q s s s S =,同时存在另⼀符号},,,{21r x x x X =,⼀般来说,元素xj 是适合信道传输的,称为码符号(或者码元)。
编码器的功能就是将信源符号集中的符号s i (或者长为N 的信源符号序列)变换成由x j (j=1,2,3,…r)组成的长度为l i 的⼀⼀对应的序列。
输出的码符号序列称为码字,长度l i 称为码字长度或简称码长。
可见,编码就是从信源符号到码符号的⼀种映射。


第五章无失真信源编码定理与编码5.1.1 信源编码和码的类型1.信源编码2.码的类型若码符号集中符号数r=2称为二元码,r=3称为三元码,……,r元码。
若分组码中所有码字的码长都相同则称为等长码,否则称为变长码。
若分组码中所有码字都不相同则称为非奇异码,否则称为奇异码。
若每个码符号x i∈X的传输时间都相同则称为同价码,否则称为非同价码。
若分组码的任意一串有限长的码符号只能被唯一地译成所对应的信源符号序列则称为唯一可译码,否则称为非唯一可译码。
若分组码中,没有任何完整的码字是其他码字的前缀,则称为即时码(又称非延长码或前缀条件码),否则称为延长码。
本章主要研究的是同价唯一可译码.5.1.2 即时码及其树图构造法即时码(非延长码或前缀条件码)是唯一可译码的一类子码。
即时码可用树图法来构造。
构造的要点是:(1)最上端为树根A,从根出发向下伸出树枝,树枝总数等于r,树枝的尽头为节点。
(2)从每个节点再伸出r枝树枝,当某节点被安排为码字后,就不再伸枝,这节点为终端节点。
一直继续进行,直至都不能伸枝为止。
(3)每个节点所伸出的树枝标上码符号,从根出发到终端节点所走路径对应的码符号序列则为终端节点的码字。
即时码可用树图法来进行编码和译码。
从树图可知,即时码可以即时进行译码。
当码字长度给定,即时码不是唯一的。
可以认为等长唯一可译码是即时码的一类子码。
5.1.3 唯一可译码存在的充要条件(1)对含有q个信源符号的信源用含r个符号的码符号集进行编码,各码字的码长为l1,l2,…,l q的唯一可译码存在的充要条件是,满足Kraft不等式5.1.4 唯一可译码的判断法唯一可译码的判断步骤:首先,观察是否是非奇异码.若是奇异码则一定不是唯一可译码。
其次,计算是否满足Kraft不等式。
若不满足一定不是唯一可译码。
再次,将码画成一棵树图,观察是否满足即时码的树图的构造,若满足则是唯一可译码。
或用Sardinas和Patterson设计的判断方法:计算出分组码中所有可能的尾随后缀集合F,观察F中有没有包含任一码字,若无则为唯一可译码;若有则一定不是唯一可译码.上述判断步骤中Sardinas和Patterson设计的判断方法是能确切地判断出是否是唯一可译码的方法,所以可以跳过前三个步骤直接采用该判断法。