当前位置：文档之家 › 小学奥数等差数列PPT课件

小学奥数等差数列PPT课件

  • 格式：ppt
  • 大小：2.52 MB
  • 文档页数：20

下载文档原格式

  / 20

合集下载

学而思四年级奥数等差数列进阶PPT

学而思四年级奥数等差数列进阶PPT
第1个数：1=1 第3个数4=2+2=1+1+2 第2个数：2=1+1 第4个数7=3+4=1+1+2+3
第5个数11=4+7=4+1+1+2+3=1+1+2+3+4 第6个数16=5+11=5+1+1+2+3+4=1+1+2+3+4+5。。。。 第n个数：1+1+2+3+4+5+…+(n-1)
第101个数为：1+1+2+3+4+5+。。。++（101-1）=1+1+1+2+3+4+5+6
作业为课后练习1,2,3,4 5，6 加油！
谢谢 再见
101=20402
练习：8个连续自然数的和是164，其中最 小的数是多少？
求和速算
例1.计算： 1+3+5+7+9= 1+3+5+7+9+11= 1+2+3+4+5+6+7+8+9+10+11+......+99+100= 练习1：2+4+6+8+10+12+......+98+100= 练习2：99+97+95+93+91+......+3+1= 拓展练习1：5+10+15+20+......95+100=

【四升五】小学数学奥数第10讲：等差数列-课件

【四升五】小学数学奥数第10讲：等差数列-课件

练习三
有一个等差数列的第1项是2.4，第7项是26.4， 求它的第5项。
a7a6da16d
a12.4，a7 26.4代入上式，
2.4 62.46d， d 4， a 5 a 1 4 d 2 .4 4 4 1.4 8
答：第5项是18.4。
例题四
游乐园的智慧梯最高一级宽60厘米，最低一级宽 150厘米，中间还有9级，各级的宽度成等差数列，求 正中间一级的宽。
首项 项数
通项公式：
ana1(n1)d
第n项
公差
例题三
一批货箱，上面的标号是按等差数列排列的， 第一项是3.6，第五项是12，求它的第2项。
a5a4da14d
a13.6，a5 12代入上式，
123.64d， d2.1 a 2 a 1 d 3 .6 2 .1 5 .7
答：第二项是5.7。
580 8n4, n=（580+4）÷8=73
答：580是第73项。
练习二
等差数列3，9，15，21，…中，381是第几项？
a1 3, d936,
an a1 (n 1)d
3(n1)6
6n3
我们把381代入
a
，
n
381 6n3, n=（381+3）÷6=64
答：381是第64项。
小结
等差数列：
ana1(n1)d
通项公式
例题一
求等差数列3，8，13，18，…的第38项和第69项。
a1 3, d835,
an a1 (n 1)d 3(n1)5 5n2
a3853 82188 a69569 2343
答：第38项是188，第69项是343。
练习一
等差数列1，4，7，10，13，…的第20项和第89项。

等差数列课件ppt课件

等差数列课件ppt课件
等差数列课件 ppt
contents
目录
• 等差数列的定义 • 等差数列的性质 • 等差数列的通项公式 • 等差数列的求和公式 • 等差数列的应用 • 等差数列的习题与解析
01
CATALOGUE
等差数列的定义
等差数列的文字定义
总结词
等差数列是一种特殊的数列，其中任意两个相邻项的差是一 个常数。
详细描述
等差数列是一种有序的数字排列，其中任意两个相邻项之间 的差是一个固定的值，这个值被称为公差。在等差数列中， 首项和末项是固定的，而其他项则可以通过首项、末项和公 差进行计算。
等差数列的数学公式定义
总结词
等差数列的数学公式可以用来表 示任意一项的值。
详细描述
等差数列的数学公式是 a_n = a_1 + (n-1)d，其中 a_n 是第 n 项的值，a_1 是首项，d 是公差 ，n 是项数。这个公式可以帮助 我们快速计算出等差数列中的任 意一项。
04
CATALOGUE
等差数列的求和公式
公式推导
公式推导方法一
利用等差数列的性质，通过累加法推 导得出求和公式。
公式推导方法二
利用等差数列的通项公式，通过代数 运算推导得出求和公式。
公式应用
应用场景一
计算等差数列的和，例如计算 1+2+3+...+n的和。
应用场景二
解决与等差数列相关的实际问题，例 如计算存款的本金和利息之和。
，公差是多少？
进阶习题
进阶习题1
进阶习题2
题目：已知一个等差数列的前三项依次为 a-d, a, a+d，如果该数列的第2008项为 2008，那么它的第10项是什么？

小学奥数-等差数列PPT课件

小学奥数-等差数列PPT课件
(85-1) ÷3+1 =29（人）
CHENLI
15
• 有一组数列如下：5、9、13、17、21、 …325、329你能求出这组数列共有多少个 数吗？
项数=（末项-首项） ÷ 公差+1 (329-5) ÷4+1 =82
• 拓展1. 39个连续奇数的和是1989,其中最大 的一个奇数是多少
• 答：因为39个连续奇数之和为1989,所以中间一个数是这39个数的
第二行：（2+51） × 50 ÷ 2=1325 第三行：（3+51） × 50 ÷ 2=1375
…… 第四十九行：（49+98） × 50 ÷ 2=36 第五十行：（50+99） × 50 ÷ 2=3725 方阵所有数之和： 1275+1325+1375+……+3675+3725 =（1275+3725） × 50 ÷ 2
=4+3 ×(20-1)=61
（2）298是这个数列中的第几项？
项数=（末项-首项） ÷ 公差+1 (298-4) ÷3+1 =99
CHENLI
8
求 和 ： 和 = （首项+末项）×项数÷2
1 + 2 + 3 + 4 + 5 + … …+ 99 =（1+99）×99÷2 = 9900÷2 = 4950
平均数,1989÷39=51,
• 比51大的另外19个奇数为:53,55,57,…,87,89.或用末项=首项+公差 × （项数-1）
• 51+19×2=51+38=89.所以其中最大的一个奇数为89.
CHENLI

四年级上册数学课件_奥数 高斯求和(等差数列)全国通用版PPT23页

四年级上册数学课件_奥数 高斯求和(等差数列)全国通用版PPT23页
Thank you
6、最大的骄傲于最大的自卑都表示心灵的最软弱无力。——斯宾诺莎 7、自知之明是最难得的知识。——西班牙 8、勇气通往天堂，怯懦通往地狱。——塞内加 9、有时候读书是一种巧妙地避开思考的方法。——赫尔普斯 10、阅读一切好书如和过去最杰出的人谈话。——笛卡儿
四年级上册数学课件_奥数 高斯求和 (等差数列)全国通用版
46、法律有权打破平静。——马·格林 47、在一千磅法律里，没有一盎司仁 爱。— —英国
48、法律一多，公正就少。——托·富 勒 49、犯罪总是以惩罚相补偿；只有处 罚才能 使犯罪 得到偿 还。— —达雷 尔
50、弱者比强者更能得到法律的保护 。—— 威·厄尔

等差数列概念及通项公式PPT课件

等差数列概念及通项公式PPT课件
(1) 1, 1, 1, 1 , 1, (2) 1, 0, 1, 0, 1 . (3) -3, -2, -1, 1, 2. (4) 4, 7, 10, 13, 16.
首项为a1 ,公差为d的等差数列｛an｝的通项公式:
an = a1 + (n－1)d.
证:因为｛an｝为等差数列, 所以当n≥2时,有
3.在等差数列｛an｝中,a10= 100,
a19=10,
a1+an=0 , 求n的值.
课堂小结
1. 等差数列的概念及通项公式.
(1)数列｛an｝为等差数列 : an－ an-1 = d (n≥2) 或 an+1－ an = d
(2)通项公式an = a1 + (n－1)d. an = am + (n－m)d.
n值为( )
A.667 B.668 C.669 D.670
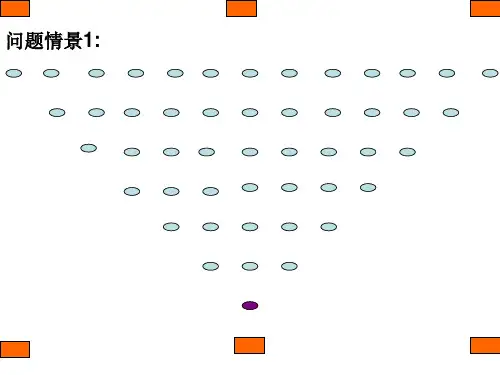
观察上面的数列有什么共同的特点?
一般地,如果一个数列从第二项起, 每一项减去它 的前一项所得的差都等于同一个常数, 那么这个数列就 叫做等差数列,这个常数叫做等差数列的公差,公差通常 用d表示.
数学表达式: an－ an-1 = d (n≥2) an+1－ an = d
练习: 判断下列数列是否为等差数列.若是,指出首项和公差.
a2－a1=d,
a3－a2=d,
……
叠加法
an－an-1=d,
将上面n-1个等式的两边分别相加,
得an－a1= (n-1)d,
所以, an= a1+(n-1)d, 当n=1时,上面的等式显然成立.
例1.在等差数列｛an｝中,已知a3=10, a9=28,求a12 .
等差数列的通项公式一般形式: an = am + (n－m)d.

小学奥数等差数列完美版PPT

小学奥数等差数列完美版PPT

实战演练2
• 观察与分析下面各列数的排列规律，然后填空
。
21 25
• 〔1〕5，9，13，17，25 ， 36。
• 〔2〕1，4，9，16， ， 35。 67
• 〔3〕4，5，7，11，19， ， 。
• 找出以下各数列的规律，在横线上，填出适当的数。
• 〔1〕5，15，45，135， 405， • 〔2〕60，63，68，75， 84，
12。15 9。5
• 〔3〕180，155，131，108， 86， 6。5
• 〔4〕0，1，1，2，3，5， 8 ， 1。3
一、定义：
一般地，如果一个数列从第2项起，后一项与它的前一项的
等差数列 81,64,49,36,( ),( )
去求项数和差公差等的式于子,这同两个一公式个常数，那麽这个数列就叫做
项
首
末
项
项
实战演练1
• 数列：2，3，5，8，13，……，89
• 首项是：
2
• 末项是：
89
• 项数是：
9
• 55在这个数列当中是第 8 项
• 1、按数列中项的个数来分类：
– 有限数列：
• 如：0，1，1，2，4，7，13，24，44
– 无限数列：
• 如：1，3，5，7，9，11，13，……
• 2、按数列中项的变化规律来分类：
象这样按照一定的规律排列的一组数,我们称为数列,其中
每个数都叫做数列的项,排在第一列的叫第一项,(也叫首项)一
般用a 1 表示,第二列的叫第二项,用a 2表示,……排在第N列的
数叫第N项,用a n表示.
认识数列
• 观察：1，3，5，7，9，……，19
项数

全国通用四年级上册奥数培训精品课件等差数列求和共35张PPT

全国通用四年级上册奥数培训精品课件等差数列求和共35张PPT
分析：首项=2 公差=3
解：（1）第10项： （2）第98项：
2+3 ×（10-1）=29 2+3 ×（98-1）=293
例2 已知数列2、5、8、11、14、 17，......122,这个数列有多少项。
规律：末项比首项多的公差的个数，再加上1，就得到 这个数列的项数。
等差数列的项数= 公差个数 + 1 =（末项-首项）÷公差 + 1
这个数列的项数= （122-2）÷3+1=41
小结：
等差数列项的有关规律
等差数列的某一项=首项+公差×（项数-1） 等差数列的每1项除以它的公差，余数相同。 等差数列的项数=（末项-首项）÷公差+1
练习
1、一串数：1、3、5、7、9、……49。 （1）它的第21项是多少? （2）这串数共有多少个？
解：原数列之和=（6+38）×9÷2 =44×9÷2 =198
等差数列的和=（首项+末项）×项数÷2
例2：计算1 + 6+ 11 + 16 + 21+ 26 +......+ 276
等差数列的和=（首项+末项）×项数÷2 ？
等差数列的项数=（末项-首项）÷公差+1
解：等差数列的项数： （276-1）÷5+1=56（项）
原数列之和=（1+276）×56÷2 = 277×28 =7756
等差数列二
复习
1、计算
（1）7+10+13+16+...+37 （2）7+11+15+19+......+403 （3）9+19+29+39+......+99 （4）1+3+5+7+......+99

四年级上册数学课件-奥数 高斯求和(等差数列)全国通用版(共21张PPT)

四年级上册数学课件-奥数 高斯求和(等差数列)全国通用版(共21张PPT)
7+7+7+7+ 7+7= 42 （1+6）×6÷3;‥‥‥+99+100= (1+100）×100÷2=5050 （首项+末项）×项数÷2
2+4+6+8+10+12+14+16+18= 18+16+14+12+10+8+6+4+2=
（2+18）×项数÷2
项数=（末项－首项）÷公差＋1（末项大于首项） 项数=（首项－末项）÷公差＋1（首项大于末项）
德国著名数学家高斯，被誉 为”数学王子”。在他童年 时代，他就显露出聪明的才 智。有一天老师出了一道题 让同学们计算：1＋2＋3＋… ＋100＝？当全班同学都在埋 头计算时，10岁的小高斯已 经计算出了答案。
1、2、3、4、5、6、7、 2、4、6、8、10、12、 3、7、11、15、19 2、9、16、23、30
你学会了吗？
1
11+2+3+440+‥‥+19+20=
2
2
39、40
3
139+18+1387-+-4+0‥‥+2+1=
‥ ‥ ‥ ‥ ‥ ‥ 第一张 可能性 详细、
19
1290×202=24--0-400 21
19
22--40
20
20
21--40 22
18
23--40
23
17
24--40
‥‥ ‥‥ ‥‥
连续自然数的和怎么求 （首项+末项）×项数÷2 （1+19）×19÷2=190 （1+20）×20÷2=210

等差数列ppt课件

等差数列ppt课件

等差数列的表示方法
通项公式
an = a1 + (n-1)d，其中an是第n项 ，a1是首项，d是公差。
前n项和公式
Sn = n/2 * (2a1 + (n-1)d)，其中Sn 是前n项和，a1是首项，d是公差。
等差数列的性质
01
02
03
公差性质
公差d是任意两个相邻项 的差，即an - a(n-1) = d 。
04
等差数列的应用
在数学中的应用
基础概念理解
等差数列是数学中的基础 概念，对于理解数列、函 数等其他数学概念有着重 要作用。
数学运算
等差数列的特性使其在数 学运算中有着广泛的应用 ，例如求和、求差等。
解决数学问题
等差数列可以用来解决一 些复杂的数学问题，例如 求解方程、不等式等。
在物理中的应用
综合练习题
题目：已知一个等差数列的前4项 和为40，前8项和为64，求这个 等差数列的前12项和。
答案：88
解析：根据等差数列的求和公式 ，得到前4项和$S_4 = frac{4}{2} times (2a_1 + (4-1)d) = 40$， 前8项和$S_8 = frac{8}{2} times (2a_1 + (8-1)d) = 64$。解这个 方程组得到首项$a_1=13$，公差 $d=-2$。然后根据等差数列的求 和公式，得到前12项和$S_{12} = frac{12}{2} times (2 times 13 + (12-1) times (-2)) = 88$。
等差数列在日常生活和科学研究中有着广泛的应用，如计算 存款利息、解决几何问题等。
公式中的参数意义
01
02

等差数列公式ppt课件

等差数列公式ppt课件

下节课预告
• 下节课我们将学习等差数列在实际生活中的应用，以及如何利 用等差数列解决实际问题。同时，我们还将学习等差数列的性 质，进一步加深对等差数列的理解。
感谢观看
THANKS
一般形式
等差数列的通项公式可以 表示为an=kn+b，其中k 和b是常数，n是项数。
特殊形式
当k=0时，等差数列变为 常数列；当b=0时，等差 数列变为等差序列。
扩展形式
通过变换通项公式，我们 可以得到其他形式的等差 数列。
等差数列通项公式的应用
数学问题求解
数学建模
利用通项公式可以求解等差数列中的 未知数。
日常计数
在日常生活中，我们经常使用等差 数列来计数物品，例如按顺序排列 的电话号码、门牌号等。
等差数列在数学领域中的应用
数学分析
在数学分析中，等差数列是研究 函数和级数的重要工具，可以用
于证明一些数学定理和性质。
几何学
在几何学中，等差数列可以用于 计算一些几何形状的周长、面积
和体积等。
组合数学
在组合数学中，等差数列可以用 于计算组合数的公式和性质。
通过建立数学模型，我们可以利用通 项公式解决实际问题。
实际应用
等差数列在日常生活和科学研究中有 着广泛的应用，例如在统计学、物理 学等领域。
03
等差数列的求和公式
等差数列求和公式的推导
01
通过对等差数列的性质进行归纳 和演绎，利用倒序相加法推导出 等差数列的求和公式。
02
倒序相加法的原理是将等差数列 的前n项和与后n项和相加，再除 以2得到n项和的公式。
等差数列求和公式还可以用于解决一 些实际问题，例如计算存款的本金和 利息、计算工资等。

《等差数列》PPT课件

《等差数列》PPT课件
解： 因为
an 是等差数列，它的公差为d.所以有
= (a1 d ) d a1 2d
两边都等于a1 ，
a2 a1 d
a3 a2 d
a4 a3 d (a1 2d ) d 当 a1 n 3 d 1时，等式 a5 a4 d (a1 3d ) d a1 4d
2.2.0 引理：
1. 在现实生活中，我们经常这样数数， 从0开始，每隔5数一次，可以得到数 列：0, 5,____,____,____,____,….
2. 2000年，在澳大利亚悉尼举行的奥 运会上，女子举重被正式列为比赛项 目.该项目共设置了7个级别.其中较轻 的4个级别体重组成数列(单位：kg)： 48，53，58，63.
练习６
a4 6、等差数列{an }中，
则
3a1 , ak 9a1
k 13
小结：
1、等差数列的概念：
an an 1 d (n 2, n N ）
或

an 1 an d （n N ）

2、等差数列的通项公式：
an a1 (n 1)d
an , a1 , n ,d 这四个变量 ， 知道其中三
例后思考：
等差数列的通项公式
例后思考
an = a1+(n-1)d 中 ，
an , a1 , n ,d 这四个变 量 ， 知道其中三个量
就可以求余下的一个
量.
例题2
在等差数列
a
n
a5 10, a12 31 , 中，
求 首项 a1 与公差
解：
d
.

a5 a1 4d 10 a12 a1 11d 31

人教版四年级上册数学奥数——等差数列(课件)

人教版四年级上册数学奥数——等差数列(课件)
的两个数的和都是101.一共有100个101相加，所得的和就是所求数列的和的2
倍，再除以2.就是所求数列的和。
1+2+3+…+99+100=（1+100）×100÷2=5050
上面的数列是一个等差数列，经研究发现，所有的等差数列都可以用下面的
公式求和：
等差数列总和=（首项+末项）×项数÷2
这个公式也叫做等差数列求和公式。
实践与应用
【练习1】 P83
求等差数列3，7，11，…的第4项，第7项和第10项。
【例2】有一堆粗细均匀的圆木堆成梯形，最上面一层有6根圆木，每向下一层增
加1根，一共堆了28层，最下面一层有多少根圆木？
【分析与解答】
将每层圆木的根数写出来:6,7,8,9,10,…可以看出这是一个等差数列。在这个
【思路导航】
容易看出这是一个等差数列，公差为6，首项是4，末项是52.要求项数，
可直接带入项数公式进行计算。
项数=（52－4）÷6＋1=9，即这个数列共有9项。
【例题2】
有一等差数列：3,7,11,15,……，这个等差数列的第100项是多少？
【思路导航】
这个等差数列的首项是3.公差是4，项数是100。
等差数列中，已知首项(1 )是6，公差（d)是1，项数(n)是28，求最下面一层是
多少，也就是求这个等差数列的第28项是多少。
我来解答：6+1×(28-1)=33(根)
小结与提示
在解答这道题时，将每层的圆木根数抽象成等差数列是关键。
实践与应用
【练习2】 P83
一个剧场设置了22排座位，第一排有36个座位，后面每排都比前一排多
2个座位，第22排有多少个座位？
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
⒉ 等差数列1，3，5，……中， 第401项是多少？
末项=首项+公差 × （项数-1） =1+2 × (401-1)=801
求项数
共几项？
1949，1950，1951，……，1999，2000 4 , 7 , 10 , 13 … … 25 , 28
练习：
1，有这样一个数列：3，7，11，15，19，23……问 （1）这个数列中的第50项是几？ 3+4 ×(50-1) =199 （2）139是这 个数列中的第几项？
项数=（末项-首项） ÷ 公差+1 (70-1) ÷3+1 =24
练习2 有一列数1、5、9、13、17、21、…… 他的 第100个数是多少？
答：这个数列为等差数列，首项为1，公差为4 数列的通项可以表示为为an=（n-1）×4+1 所以a100=（100-1） × 4+1=397 即第100项为397 这100个数和是多少？ 等差数列的总和=（首项+末项） ×项数÷ 2 （1+397） ×100 ÷2=19900
=125000
SUCCESS
THANK YOU
2019/8/2
求 公差 ：
在19和91之间插入5个数，使这7个数构成一个 等差数列。写出插入的5个数。
(91-19) ÷(7-1)=12 依次为31、43、55、67、79
• 下面这组数是按一定规律排列的，你能求 出这组数列的第48个数是几吗？
• 54、58、62、66、70、74、78、82、 86…
54+4 × （48-1）=242
• 6和26插入三个数，使它们每两个相邻数的 差相等，这三个数分别是多少？
（26-6） ÷ （5-1）=5 依次为11、16、21
练习1 小明往棋盘上放棋子，他在第一格放1枚，在 第二格放4枚，第三格放7枚……这样以后每格都 比前一格多放3枚棋子，小明在棋盘的最后一格放 了70枚棋子，则这个棋盘共有多少格？
求和 4 + 5 + … …+ 99 =（1+99）×99÷2 = 9900÷2 = 4950
求下列方阵中所有各数的和：
解： 每一横行数列之和：
第一行：（1+50） ×50 ÷ 2=1275
1、2、3、4、……49、50； 2、3、4、5、……50、51； 3、4、5、6、……51、52；
…… 49、50、51、52、……97、98； 50、51、52、53、……98、99。
第二行：（2+51） × 50 ÷ 2=1325 第三行：（3+51） × 50 ÷ 2=1375
…… 第四十九行：（49+98） × 50 ÷ 2=36 第五十行：（50+99） × 50 ÷ 2=3725 方阵所有数之和： 1275+1325+1375+……+3675+3725 =（1275+3725） × 50 ÷ 2
项数=（末项-首项） ÷ 公差+1 (139-3) ÷4+1 =35
2， 有一个等差数列4，7，10，13……，问 （1）这个数列中的20项是几？ 末项=首项+公差 × （项数-1）
=4+3 ×(20-1)=61
（2）298是这个数列中的第几项？
项数=（末项-首项） ÷ 公差+1 (298-4) ÷3+1 =99
找出规律后填出下面数列中括号里的数：
(1) 1， 2， 3，4， ( )， 6， 7， ( )，… (2) 1， 4， 7， 10， ( )， 16， 19， … (3) 1， 3， 5， 7， 9， ( )，13，…
规律：从第二项起，每 一项与前一项的差为‘1’
等差数列：一个数列，从第 个2数开始，依次与前一个 数的差相同，这样的数列叫 等差数列
(85-1) ÷3+1 =29（人）
• 有一组数列如下：5、9、13、17、21、 …325、329你能求出这组数列共有多少个 数吗？
项数=（末项-首项） ÷ 公差+1 (329-5) ÷4+1 =82
• 拓展1. 39个连续奇数的和是1989,其中最大 的一个奇数是多少
• 答：因为39个连续奇数之和为1989,所以中间一个数是这39个数的
一套书有5本，每隔5年出版一本，第三本是1998年 出版的。其他几本书分别是哪年出版的？
1986
1992
1998
2004
2010
这个数列有几个数
公 差：2
项数：6
练习：
⒈在数列5，6，7，8，9，……，94，95，96中， 第40个数是多少？ 末项=首项+公差 × （项数-1）
=5+1 ×(40-1)= 44
知识点： 1、数列：按一定顺序排成的一列数叫做数列。数列中的每一个数都叫做 项，第一项称为首项，最后一项称为末项。数列中共有的项的个数叫做项 数。 2、等差数列与公差：一个数列，从第二项起，每一项与与它前一项的差
都相等，这样的数列的叫做等差数列，其中相邻两项的差叫做公差。 3、常用公式
等差数列的总和=（首项+末项） ×项数÷ 2 项数=（末项-首项） ÷ 公差+1 末项=首项+公差 × （项数-1） 首项=末项-公差 × （项数-1） 公差=（末项-首项） ÷ （项数-1） 等差数列（奇数个数）的总和=中间项× 项数
平均数,1989÷39=51, • 比51大的另外19个奇数为:53,55,57,…,87,89.或用末项=首项+公差 ×
（项数-1） • 51+19×2=51+38=89.所以其中最大的一个奇数为89.
拓展2. 在1~200这二百个数中能被9整除的数的和是多少? 答：在1~200这二百个数中能被9整除的数构成了一个以9为首项,公差为9的等差数 列:9,18,27,36,…,189,198,
一共有(198-9)÷9+1=22项.
它们的和为: 等差数列的总和=（首项+末项） ×项数÷ 2 (9+198)×22÷2 =207×22÷2 =2277.
• 一座塔挂满了彩灯，最顶层挂了7盏彩灯， 下面一层挂了12盏，再下一层挂了17盏 ……以后每下一层都比上一层多挂5盏灯， 最底层是72盏灯，这座塔共多少层？
项数=（末项-首项） ÷ 公差+1 (72-7) ÷5+1 =14
一群小朋友玩报数游戏，第一个小朋友报1， 第二个小朋友报4，第三个小朋友报7…… 后一个小朋友比前一个小朋友多报3，后一 个小朋友报85，有多少个小朋友在做游戏 ？