电磁场与电磁兼容习题答案与详解_第2章
- 格式:doc
- 大小:378.00 KB
- 文档页数:6

第二章习题解答【习题2.1】101929=.=101.6102.0810e qR R mq e Cp m Ce e 解:电偶极矩p 其中 1.3可得电偶极矩p 的大小其方向为从负电荷指向正电荷,即从氯离子指向氢离子。
---´== =醋【习题2.2】解1解:由例2.2得,电偶极子所产生的电场为533()1[]4e e P R RP E RRπε=-0()R R << ……………………①其中 0e P qR = ,0R方向从负电荷指向正电荷,R是从电偶极子指向电场中任一点的矢量,起点在正负电荷连线的中点。
(如图)本题 100 1.310R m -=⨯ 1010010R m -=⨯满足 0R R << .将①式整理:32013[()]4e e E P R R P RRπε=-令 ()e m k P R R P =-(23k R=)则 304m E Rπε=…………………………②欲求E的最大值,求出m最大值即可.222222[()]()2()()e e e e e e m k P R R P k P R R P k P R P R =-=+- 2222(2)()e e k R k P R P =-+2224296()()e e R P R P R R=-+ 2223()e e P R P R=+其中 00cos e P R qR R qR R θ== , (θ是0R 和R之间的夹角)易见,当cos 1θ=,即0θ=时,2m可取最大值22222m ax 234e e e m R P P P R=+=则 m=2e P 代入②式得 m a x33m ax042e P mERRπεπε==将习题2.1中的结论 e P=2.082910c m -⨯⋅ 代入得29112103max2.08102 3.148.910(10010)EV m ----⨯=⋅⨯⨯⨯⨯⨯513.710V m-≈⨯⋅距离自由电子处的电场 191712121020 1.6101.41044 3.148.910(10010)e E V mV mRπε-----⨯==⋅≈⨯⋅⨯⨯⨯⨯⨯故 距离电偶极子处的电场最大值为 513.710V m -⨯⋅ 距离自由电子处的电场为 711.410V m -⨯⋅【习题2.2】解2解:设矢量0R e的方向从电荷C L -指向电荷H +R n 是从由C L - H +构成的电偶极子指向电场中的任一点的矢量,起点在正负电荷连线的中点,且0R 〈〈R. ( e , n 为单位矢量,θ是e , n的夹角)(1)003303cos 1[]4qR qR E n e R R θπε=- (41P )由向量减法的三角形法则及余弦定理得:=03024qR R πε⎛⎫⎪⎝⎭E =由上题得290( 2.110)e p qR cm -==⨯因此,当0θ=或θπ=时E有最大值, 03024qR E R πε==50302 3.7104qR V M R πε=⨯ (2)7201() 1.4104q R VE M R R πε==⨯【习题2.3】证明: 电偶极距qRe p =其方向为从负电荷指向正电荷。

第一章PdBW=10lgP、 UdBV=20lgU、IdBA=20lgI第二章 2、电磁干扰的三要素是什么?答:骚扰源、耦合通道、敏感单元3、常见的电磁骚扰源有哪些?如何分类?答:(1)从来源分:自然骚扰和人为骚扰(2)从骚扰属性分:功能性骚扰和非功能性骚扰(3)从耦合方式分:传导骚扰和辐射骚扰(4)从频谱宽度分:宽频骚扰和窄频骚扰(5)从频率范围分:甚低频骚扰、工频与音频骚扰、载频骚扰、射频及视频骚扰、微波骚扰6、电磁骚扰的传播主要有哪些途径?答:传导耦合、磁场耦合、电场耦合、辐射耦合7、为什么要对电流返回路径格外重视?答:(1)任何电流都要返回其源,对于高频电流,如果我们能给他提供一个通路,他就可能(主要)沿着这条通路走,如果不提供这种通路,他就会自己找到通路(不在控制之中)。
(2)电流总是沿着最小阻抗路线走12、影响磁场耦合的通路有哪些?如何减小其影响?答:(1)-jwBscosθ、被干扰电路中的源阻抗和负载阻抗、正弦磁通密度、角频率、闭合回路面积、磁通密度与回路面的夹角(2)降低骚扰电流的频率、减小回路之间的互感、减小被干扰回路的负载阻抗13、影响电场耦合的因素有哪些?如何减小其影响?答:(1)骚扰源的频率、骚扰电压、骚扰电路、耦合电容、被干扰回路的源阻抗和负载阻抗。
(2)减小骚扰电压、降低骚扰电压频率、减小被干扰回路中源阻抗和负载阻抗的并联、减小电路之间的耦合电容,可适当增大电路间距离、采取屏蔽措施。
第三章屏蔽按其机理可分为电场屏蔽、磁场屏蔽、电磁场屏蔽、编织带屏蔽。
1、静电屏蔽的原理是什么?答:导体置于静电场中并到达静电平衡后,该导体是一个等位体,内部电场为零,导体内部没有静电荷,电荷只能分布在导体表面。
若该导体内部有空腔,空腔中也没有电场,空腔导体起到了隔绝外部静电场的作用。
如将带电体置于空腔导体内部,会在空腔导体表面感应出等量电荷。
如果把空腔导体接地,不会在导体外部产生电场。
2、磁屏蔽的原理是什么?答:利用高导磁材料进行磁场屏蔽,是利用其低阻特性,对骚扰磁场进行分路,使被屏蔽体包围区域内的磁场大大减弱。

电磁场与电磁波》(第四版 )答案二章习题解答2.1 一个平行板真空二极管内的电荷体密度为$\rho=-\frac{4\epsilon U}{d}-4\times 10^{-3}x-2\times 10^{-3}$,式中阴极板位于$x=9$,阳极板位于$x=d$,极间电压为$U$。
如果$U=40V$,$d=1cm$,横截面$S=10cm^2$,求:(1)$x$和$x=d$区域内的总电荷量$Q$;(2)$x=d/2$和$x=d$区域内的总电荷量$Q'$。
解(1)$Q=\int\limits_{0}^{9}\rhoSdx+\int\limits_{d}^{9}\rho Sdx=-4.72\times 10^{-11}C(3d)$2)$Q'=\int\limits_{d/2}^{d}\rho Sdx=-0.97\times 10^{-11}C$2.2 一个体密度为$\rho=2.32\times 10^{-7}Cm^3$的质子束,通过$1000V$的电压加速后形成等速的质子束,质子束内的电荷均匀分布,束直径为$2mm$,束外没有电荷分布,试求电流密度和电流。
解:质子的质量$m=1.7\times 10^{-27}kg$,电量$q=1.6\times 10^{-19}C$。
由$1/2mv^2=qU$得$v=2mqU=1.37\times 10^6ms^{-1}$,故$J=\rho v=0.318Am^2$,$I=J\pi (d/2)^2=10^{-6}A$2.3 一个半径为$a$的球体内均匀分布总电荷量为$Q$的电荷,球体以匀角速度$\omega$绕一个直径旋转,求球内的电流密度。
解:以球心为坐标原点,转轴(一直径)为$z$轴。
设球内任一点$P$的位置矢量为$r$,且$r$与$z$轴的夹角为$\theta$,则$P$点的线速度为$v=\omega\times r=e_\phi \omegar\sin\theta$。


电磁场与电磁波第二章课后答案本页仅作为文档封面,使用时可以删除This document is for reference only-rar21year.March第二章 静电场重点和难点电场强度及电场线等概念容易接受,重点讲解如何由物理学中积分形式的静电场方程导出微分形式的静电场方程,即散度方程和旋度方程,并强调微分形式的场方程描述的是静电场的微分特性或称为点特性。
利用亥姆霍兹定理,直接导出真空中电场强度与电荷之间的关系。
通过书中列举的4个例子,总结归纳出根据电荷分布计算电场强度的三种方法。
至于媒质的介电特性,应着重说明均匀和非均匀、线性与非线性、各向同性与各向异性等概念。
讲解介质中静电场方程时,应强调电通密度仅与自由电荷有关。
介绍边界条件时,应说明仅可依据积分形式的静电场方程,由于边界上场量不连续,因而微分形式的场方程不成立。
关于静电场的能量与力,应总结出计算能量的三种方法,指出电场能量不符合迭加原理。
介绍利用虚位移的概念计算电场力,常电荷系统和常电位系统,以及广义力和广义坐标等概念。
至于电容和部分电容一节可以从简。
重要公式真空中静电场方程:积分形式:⎰=⋅SS E 0d εq⎰=⋅ll E 0d微分形式:ερ=⋅∇E0=⨯∇E已知电荷分布求解电场强度:1,)()(r r E ϕ-∇=; ⎰''-'=V Vd )(41)(|r r |r r ρπεϕ2,⎰'''-'-'=V V 3d |4))(()(|r r r r r r E περ3,⎰=⋅SS E 0d εq高斯定律介质中静电场方程:积分形式:q S=⋅⎰ d S D⎰=⋅ll E 0d微分形式:ρ=⋅∇D0=⨯∇E线性均匀各向同性介质中静电场方程:积分形式:εqS=⋅⎰ d S E⎰=⋅ll E 0d微分形式:ερ=⋅∇E0=⨯∇E静电场边界条件:1,t t E E 21=。

电磁场与电磁波第四版第二章部分答案习题二无限长线电荷通过点且平行于z轴,线电荷密度为ρ?,试求点P(x,y,x)处的电场强度E。
解:线电荷沿z方向为无限长,故电场分布与z无关,设P位于z=0的平面上。
则R=ex x?6 +ey y?8 , R = (x?6)2+(y?8)2ex x?6 +ey y?8 ReR== R (x?6)2+(y?8)2则P点的E为ρ?ρ?ex x?6 +ey y?8 RE=eR=?=? 222πε0RR2πε0R2πε0(x?6)+(y?8)2.10半径为a的一个半圆环上均匀分布着线电荷ρ?,如图所示。
试求垂直于半圆环所在轴线的平面上z=a处的电场强度E(0,0,a)。
解:′P(0,0,a)的位置矢量是 =eza,电荷元ρ?dl=ρ?ad?, =eacos?+x′rrρ?eyasin?′′′ ? =ea?eacos??easin? zxy′rr= a2+ acos?′ 2+ asin?′ 2= 2aez? exacos?′+eyasin?′ dE=d?=d?4πε0 2a 3a8 2 πε0ρ?E 0,0,a = dE = =ρ?8 2 aπε0? ρ?a rr′ez? exacos?′+eyasin?′ d? π2π?2ρ?(ezπ?ex2)8 2 aπε0一个很薄的无限大导体带电平面,其上的面电荷密度为ρs。
试证明:垂直于平面的z轴上z=z0处的电场强度中,有一半是平面上半径为 3z0的圆内的电荷产生的。
解:取面积元ds′=r′d?′dr′,dq=ρsds′=ρsr′d?′dr′,电荷元在z=z0处产生的电场强度dE=ρsr′d?′dr′4πε0ezz0+err′ z0322+r′ 2 d?′整个平面在z=z0处的电场强度为E=ρsz0=?ez2ε0当r ∞时,E=exρs2ε0ρs4πε0r2πezz0+err′′′rdr 3002z02+r′ 21 z02+r2ρs1+ez2ε02,当r= 3z0时,E′=ezρs4ε0=E21半径为a的导体球形体积内充满密度为ρ r 的体电荷。


电磁场与电磁波第2章课后答案2-1.已知真空中有四个点电荷q C 11=,q C 22=,q C 34=,q C 48=,分别位于(1,0,0),(0,1,0),(-1,0,0,),(0,-1,0)点,求(0,0,1)点的电场强度。
解:z y r z x r z y r z xr ??;??;??;??4321+=+=+-=+-=ρρρρ 84?15?6?3)(41024442333222221110πεπεz y xr r q r r q r r q r r q E ++=+++=ρ2-2.已知线电荷密度为ρl 的均匀线电荷围成如图所示的几种形状,求P 点的电场强度。
题2-2图解:(a) 由对称性04321=+++=E E E E E ρρρρρ(b) 由对称性0321=++=E E E E ρρρρ(c) 两条半无限长线电荷产生的电场为yay x y x a E E E ll a ?2)}??()??{(40021περπερ-=+--=+=ρρρ 半径为a 的半圆环线电荷产生的电场为y aE lb ?20περ=ρ总电场为0=+=b a E E E ρρρ2-3.真空中无限长的半径为a 的半边圆筒上电荷密度为ρs ,求轴线上的电场强度。
解:在无限长的半边圆筒上取宽度为?ad 的窄条,此窄条可看作无限长的线电荷,电荷线密度为?ρρad s l =,对?积分,可得真空中无限长的半径为a 的半边圆筒在轴线上的电场强度为y d x y a d r a E ss s ?)?cos ?sin (22?00000??-=--==πππερπερπε?ρρ 题2-3图题2-4图2-4.真空中无限长的宽度为a 的平板上电荷密度为ρs ,求空间任一点上的电场强度。
解: 在平板上'x 处取宽度为'dx 的无限长窄条,可看成无限长的线电荷,电荷线密度为'dx s l ρρ=,在点),(y x 处产生的电场为ρρρπε'?21),(0dx y x E d s =ρ其中 22)'(y x x +-=ρ;22)'(??)'(?yx x y y xx x +-+-=ρ对'x 积分可得无限长的宽度为a 的平板上的电荷在点),(y x 处产生的电场为)}2/2/(2?)2/()2/(ln ?{4),(2222y a x arctg y a x arctg y y a x y a x x y x E s --+++-++=περρ2-5.已知真空中电荷分布为ρ=≤>r a r ar a220;;ρs b r a ==;r 为场点到坐标原点的距离,a ,b 为常数。

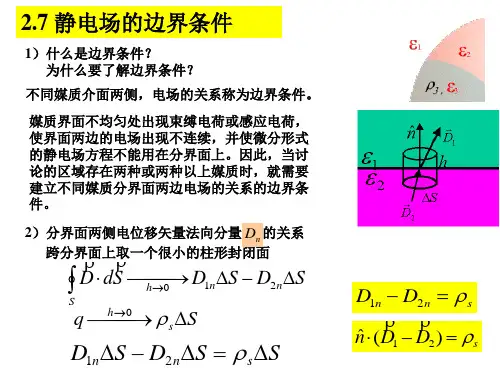

电磁场与电磁兼容习题答案与详解-第2章第2章:电磁场基础知识1.题目:电场强度的方向与电荷正负有关吗?答案:是的,电场强度的方向与电荷的正负有关。
正电荷的电场强度方向指向远离电荷的方向,负电荷的电场强度方向指向靠近电荷的方向。
详解:电场强度的方向由正电荷指向负电荷,这是由于电荷之间存在相互作用力。
根据库仑定律,同性电荷之间的相互作用力是斥力,异性电荷之间的相互作用力是吸引力。
电场强度的方向就是这种相互作用力的方向。
2.题目:什么是电场线?答案:电场线是描述电场强度方向的线条。
在电场中,电场线的方向与电场强度的方向一致,电场线之间不会相交。
详解:电场线是静电场中电场强度方向的图形表示。
它可以用来表示电场强度的大小和方向。
电场线的方向由正电荷指向负电荷,线的密度表示电场强度的大小。
电场线之间不会相交,这是因为在相交点上电场强度有多个值,与实际不符。
3.题目:什么是电场强度?答案:电场强度是描述电场对单位正电荷施加的力的大小和方向。
详解:电场强度是电场的物理量,它表示电场对单位正电荷施加的力的大小和方向。
电场强度的单位是牛顿/库仑。
电场强度的方向由正电荷指向负电荷。
4.题目:电场强度与电场线之间的关系是什么?答案:电场强度和电场线是相互对应的。
电场强度的方向与电场线的方向一致,电场线的密度表示电场强度的大小。
详解:电场强度和电场线是相互对应的。
电场强度的方向由正电荷指向负电荷,电场线的方向也是由正电荷指向负电荷。
电场线的密度表示电场强度的大小,密度越大,表示电场强度越大。
5.题目:电场强度的大小与电荷量有关吗?答案:是的,电场强度的大小与电荷量有关。
在距离电荷越远的地方,电场强度越小;在距离电荷越近的地方,电场强度越大。
详解:电场强度的大小与电荷量有关。
根据库仑定律,电场强度与电荷量成正比,与距离的平方成反比。
在距离电荷越远的地方,电场强度越小;在距离电荷越近的地方,电场强度越大。
第2章习题解答2.2已知半径为a 、长为l 的圆柱体内分布着轴对称的体电荷,已知其电荷密度()0V a ρρρρ=,()0a ρ≤≤。
试求总电量Q 。
解:2π200002d d d d π3laV VQ V z la aρρρρρϕρ===⎰⎰⎰⎰2.3 半径为0R 的球面上均匀分布着电荷,总电量为Q 。
当球以角速度ω绕某一直径(z 轴)旋转时,试求其表面上的面电流密度。
解:面电荷密度为 24πS QR ρ=面电流密度为 00200sin sin sin 4π4πS S S Q Q J v R R R R ωθρρωθωθ=⋅=== 2.4 均匀密绕的螺旋管可等效为圆柱形面电流0S S J e J ϕ=。
已知导线的直径为d ,导线中的电流为0I ,试求0S J 。
解:每根导线的体电流密度为 00224π(/2)πI I J d d ==由于导线是均匀密绕,则根据定义面电流密度为 04πS IJ Jd d ==因此,等效面电流密度为 04πS IJ e dϕ=2.6 两个带电量分别为0q 和02q 的点电荷相距为d ,另有一带电量为0q 的点电荷位于其间。
为使中间的点电荷处于平衡状态,试求其位置。
当中间的点电荷带电量为-0q 时,结果又如何? 解:设实验电荷0q 离02q 为x ,那么离0q 为x d -。
由库仑定律,实验电荷受02q 的排斥力为12214πq F x ε=实验电荷受0q 的排斥力为02214π()q F d x ε=-要使实验电荷保持平衡,即21F F =,那么由00222114π4π()q q x d x εε=-,可以解得d d x 585.0122=+=如果实验电荷为0q -,那么平衡位置仍然为d d x 585.0122=+=。
只是这时实验电荷与0q 和02q 不是排斥力,而是吸引力。
2.7 边长为a 的正方形的三个顶点上各放置带电量为0q 的点电荷,试求第四个顶点上的电场强度E 。
第二章静电场重点和难点电场强度及电场线等概念容易接受,重点讲解如何由物理学中积分形式的静电场方程导出微分形式的静电场方程,即散度方程和旋度方程,并强调微分形式的场方程描述的是静电场的微分特性或称为点特性。
利用亥姆霍兹定理,直接导出真空中电场强度与电荷之间的关系。
通过书中列举的4个例子,总结归纳出根据电荷分布计算电场强度的三种方法。
至于媒质的介电特性,应着重说明均匀和非均匀、线性与非线性、各向同性与各向异性等概念。
讲解介质中静电场方程时,应强调电通密度仅与自由电荷有关。
介绍边界条件时,应说明仅可依据积分形式的静电场方程,由于边界上场量不连续,因而微分形式的场方程不成立。
关于静电场的能量与力,应总结出计算能量的三种方法,指出电场能量不符合迭加原理。
介绍利用虚位移的概念计算电场力,常电荷系统和常电位系统,以及广义力和广义坐标等概念。
至于电容和部分电容一节可以从简。
重要公式真空中静电场方程:E d S q积分形式: E d l 0S l微分形式:E E 0已知电荷分布求解电场强度:1,E(r)( r ) ;1( r) ( r ) d V4 0V | r r|(r)( r r)2,E(r) d VV 4 0| r r|33,E d S q高斯定律S介质中静电场方程:积分形式:D d S q E d l0S l微分形式:D E0线性均匀各向同性介质中静电场方程:积分形式:E d S qE d l 0S l微分形式:E E0静电场边界条件:1,E1 t E 2 t。
对于两种各向同性的线性介质,则D1t D2 t122,D2 n D 1n s 。
在两种介质形成的边界上,则D1 n D2 n对于两种各向同性的线性介质,则1 E1 n 2E2 n3,介质与导体的边界条件:e n E0 ;e n D S若导体周围是各向同性的线性介质,则E n S;Sn 静电场的能量:1 Q21孤立带电体的能量: W e Q2 C2离散带电体的能量: W e n1i Q i i 12分布电荷的能量:W e11S d S1V 2d V l d lS 2l 21静电场的能量密度:w e D E212对于各向同性的线性介质,则w e E2电场力:库仑定律: Fq q2err4常电荷系统: Fd W eq 常数d ldW e常电位系统: F常数d l题解2-1 若真空中相距为d的两个电荷q1及q2的电量分别为q点电荷q 位于q1及q2的连线上时,系统处于平衡状态,试求及 4 q ,当q的大小及位置。
第二章 静电场重点和难点电场强度及电场线等概念容易接受,重点讲解如何由物理学中积分形式的静电场方程导出微分形式的静电场方程,即散度方程和旋度方程,并强调微分形式的场方程描述的是静电场的微分特性或称为点特性。
利用亥姆霍兹定理,直接导出真空中电场强度与电荷之间的关系。
通过书中列举的4个例子,总结归纳出根据电荷分布计算电场强度的三种方法。
至于媒质的介电特性,应着重说明均匀和非均匀、线性与非线性、各向同性与各向异性等概念。
讲解介质中静电场方程时,应强调电通密度仅与自由电荷有关。
介绍边界条件时,应说明仅可依据积分形式的静电场方程,由于边界上场量不连续,因而微分形式的场方程不成立。
关于静电场的能量与力,应总结出计算能量的三种方法,指出电场能量不符合迭加原理。
介绍利用虚位移的概念计算电场力,常电荷系统和常电位系统,以及广义力和广义坐标等概念。
至于电容和部分电容一节可以从简。
重要公式真空中静电场方程:积分形式:⎰=⋅SS E 0d εq⎰=⋅ll E 0d微分形式:ερ=⋅∇E0=⨯∇E已知电荷分布求解电场强度:1,)()(r r E ϕ-∇=; ⎰''-'=V Vd )(41)(|r r |r r ρπεϕ2,⎰'''-'-'=V V 3d |4))(()(|r r r r r r E περ3,⎰=⋅SS E 0d εq高斯定律介质中静电场方程:积分形式:q S=⋅⎰ d S D⎰=⋅ll E 0d微分形式:ρ=⋅∇D0=⨯∇E线性均匀各向同性介质中静电场方程:积分形式:εqS=⋅⎰ d S E⎰=⋅ll E 0d微分形式:ερ=⋅∇E0=⨯∇E静电场边界条件:1,t t E E 21=。
对于两种各向同性的线性介质,则2211εεttD D =2,s n n D D ρ=-12。
在两种介质形成的边界上,则n n D D 21=对于两种各向同性的线性介质,则n n E E 2211εε=3,介质与导体的边界条件:0=⨯E e n ; S n D e ρ=⋅若导体周围是各向同性的线性介质,则ερS n E =;ερϕS n -=∂∂静电场的能量:孤立带电体的能量:Q C Q W e 21212Φ== 离散带电体的能量:∑==ni i i e Q W 121Φ分布电荷的能量:l S V W l l S S Ve d 21d 21d 21ρϕρϕρϕ⎰⎰⎰===静电场的能量密度:E D ⋅=21e w 对于各向同性的线性介质,则2 21E w e ε=电场力:库仑定律:rrq q e F 2 4πε'=常电荷系统:常数=-=q e lW F d d常电位系统:常数==ϕlW F e d d题 解2-1 若真空中相距为d 的两个电荷q 1及q 2的电量分别为q 及4q ,当点电荷q '位于q 1及q 2的连线上时,系统处于平衡状态,试求q '的大小及位置。
电磁场与电磁兼容习题答案与详解
第二章
麦克斯韦方程组:
.在均匀的非导电媒质(0=σ,1=r μ)中,已知时变电磁场为
()V /m 3
4cos 300⎪
⎭⎫ ⎝⎛-=y t z ωπa E ,()
A/m 34cos 10⎪⎭⎫ ⎝
⎛
-=y t x ωa H ,利用麦克斯韦方程
组求出ω和r ε。
解:将E 和H 用复数表示:
由复数形式的麦克斯韦方程,有:
比较(1)与(3),(2)与(4),得 :
…
由此得:
16
/108==r s
rad εϖ
.已知无源空间中的电场为()()
()V/m 106cos 100.1sin 9
z t x y βππ-⨯=a E , 利用麦克斯韦
方程求H 及常数β。
解:E 复数形式:
由复数形式麦克斯韦方程
&
将上式与题给的电场E 相比较,即可得:
而磁场的瞬时表达式为:
高斯定理:
.两个相同的均匀线电荷沿x 轴和y 轴放置,电荷密度μc/m l 20=ρ,求点(3,3,3)处的电位移矢量D 。
【
解:设x 轴上线电荷在P (3,3,3)点上产生的电位移矢量为D 1,x 轴上线电荷在P (3,3,3)点上产生的电位移矢量为D 2。
D 122y z + D 222
x z 因为以x 轴为轴心,32l ds D ρ=
⋅⎰
1
l D ρπ=⋅⋅2321 即π
μπμ23102
32201=
⋅=
D
同理π
μ23102=
D
z y x z y x a a a a a a D D D π
μπμπμπ
μ3103535)22
12
1(
231021++=
++
=
+=
.μc/m l 30=ρ的均匀线电荷沿z 轴放置,以z 轴为轴心另有一半径为2m 的无限长圆柱面,其上分布有密度为2μc/m 41.5
π
ρ-=s 的电荷,利用高斯定理求各区域内的电位移矢量D 。
解:建立圆柱坐标系,以z 轴为轴心,设一单位长度的圆柱面 (1) 》
(2) 当r<2m 时 因为⎰
=⋅l ds D ρ,所以l r D ρπ=⋅2
故r D l πρ2=
,D =l l l a r
u
a r ππρ152=
(2)当r>2m 时1221⋅⋅⋅+⋅=
⋅⎰
πρρs l ds D
故c u c u c u r D ⋅⋅=⋅⋅-⋅⋅=⋅5.285.1302π 所以l a r
c
u D π25.28⋅⋅=
安培定律:
.半径为a 的实心圆柱导体,电流I 在其截面上均匀分布,求磁场强度H 。
解:根据⎰
=⋅I u dl B 0可知
当a ≤ρ时,I a
I a I 22
2
2ρππρ==' ]
I
a u B dl B 22
02ρπρϕ=⋅=⋅⎰
所以202a
I u B πρ
ϕ=
当a >ρ时,πρ
ϕ20I
u B =
|
.求半径为a 的圆形电流回路中心轴上的磁场H ,并给出回路中心的磁场。
y
解:取圆柱坐标,使z 轴与圆环的轴线相合,并使圆环在z=0的平面上,中心轴上任一点的坐标为(0,0,z ),并且ϕa 是ϕ的函数,即ρϕϕ
a a -=∂∂
根据比-萨定理得
⎰⨯=
2
04R a dl I u B R
π (1)
ϕϕad a dl = (2) ααρcos sin z R a a a +-= (3)
22z a R += (4)
(2),(3),(4)代入(1)中得 【
⎰++-⨯=220)cos sin (4z a a a d a Ia u B z ααϕπρϕ
=ϕααπρd a a z a Ia
u z )cos sin ()
(4220⎰++ =
⎪⎭⎫ ⎝
⎛++⎰⎰ππρϕαϕαπ20202204d cos a d sin a )z a (Ia u z 括号中的第二项积分为零,因为ρa 是φ的函数,在[0,2π]的范围内各个单位矢量互相抵消,积分为零。
=
z a sin )
z a (Ia
u ⋅+αππ242
20
=
z
a
)
z
a(
Ia
u
2
3
2
2
2
2+
在中心点处
z=0,所以
z
a
a
I
u
B
2
=
边界条件:
.在两导体平板(分别位于z=0和z=d处)之间的空气中,已知电场强度为
()()
V/m
cos
sin
x
k
t
z
d
E
x
y
-
⎪
⎭
⎫
⎝
⎛
=ω
π
a
E,式中
E和
x
k为常数。
试求:(1)磁场强度H;(2)两导体表面上的电流密度J s。
#
解:(1 )将E表示为复数形式,由复数形式的麦克斯韦方程,得磁场的复数形式:
磁场的瞬时表达式为:
(2)z=0处的导体表面的电流密度为:
z=d处的导体表面的电流密度为
电磁场的能量:
2.19 电场强度和磁场强度分别为()e t ϕω+=cos 0E E 和()m t ϕω+=cos 0H H ,证明其坡
印廷矢量的平均值为:()m e ϕϕ-⨯=cos 2
1
00H E S av 。
解:⎰⎰
++⨯=⨯=T m e T
av
dt t t H E T
dt H E T
S 00
)cos()cos()(1
)(1ϕωϕω (1)
设αϕω=+e t ;βϕω=+m t 且[])cos()cos(2
1
cos cos βαβαβα++-=
⋅ (2) 将(2)代入(1)中得
[]dt t H E T
S T m e m e av ⎰+++-⨯=
000)2cos()cos()(21
ϕϕωϕϕ
=dt t H E T
H E T m e m e ⎰++⨯+⨯-00000)2cos()(21
))(cos(21ϕϕωϕϕ
=)cos()(2
1
00m e H E ϕϕ-⋅⨯。