合肥市包河区48中八年级上模块三测试

合肥48中数学全等三角形达标检测（Word 版 含解析） 一、八年级数学轴对称三角形填空题（难）1．在直角坐标系中，O 为坐标原点，已知点 A （1，2），点 P 是 y 轴正半轴上的一点，且△AOP 为等腰三角形，则点 P 的坐标为_____________．【答案】5(0,5),(0,4),0,4⎛⎫ ⎪⎝⎭【解析】【分析】有三种情况：①以O 为圆心，以OA 为半径画弧交y 轴于D ，求出OA 即可；②以A 为圆心，以OA 为半径画弧交y 轴于P ，求出OP 即可；③作OA 的垂直平分线交y 轴于C ，则AC ＝OC ，根据勾股定理求出OC 即可．【详解】有三种情况：①以O 为圆心，以OA 为半径画弧交y 轴于D ，则OA ＝OD ＝22125+=；∴D （0，5）；②以A 为圆心，以OA 为半径画弧交y 轴于P ，OP ＝2×y A =4，∴P （0，4）；③作OA 的垂直平分线交y 轴于C ，则AC ＝OC ，由勾股定理得：OC ＝AC ＝()2212OC +-，∴OC ＝54， ∴C （0，54）； 故答案为：5(0,5),(0,4),0,4⎛⎫ ⎪⎝⎭．【点睛】本题主要考查对线段的垂直平分线，等腰三角形的性质和判定，勾股定理，坐标与图形性质等知识点的理解和掌握，能求出符合条件的所有情况是解此题的关键．2．如图，在锐角△ABC中，AB=5，∠BAC=45°，∠BAC的平分线交BC于点D，M，N分别是AD，AB上的动点，则BM+MN的最小值是______．【答案】5【解析】【分析】作BH⊥AC，垂足为H，交AD于M点，过M点作MN⊥AB，垂足为N，则BM+MN为所求的最小值，再根据AD是∠BAC的平分线可知MH=MN，再由等腰直角三角形的性质即可得出结论．【详解】如图，作BH⊥AC，垂足为H，交AD于M点，过M点作MN⊥AB，垂足为N，则BM+MN 为所求的最小值．∵AD是∠BAC的平分线，∴MH=MN，∴BH是点B到直线AC的最短距离（垂线段最短）．∵AB=5，∠BAC=45°，∴BH==5．∵BM+MN的最小值是BM+MN=BM+MH=BH=5．故答案为5．【点睛】本题考查了轴对称﹣最短路线问题，解答此类问题时要从已知条件结合图形认真思考，通过角平分线性质，垂线段最短，确定线段和的最小值．3．如图，已知△ABC和△ADE都是正三角形，连接CE、BD、AF，BF=4,CF=7,求AF的长_________ .【答案】3【解析】【分析】过点A作AF⊥CE交于I，AG⊥BD交于J,证明CAE≅BAD，再证明CAI≅BAJ，求出°7830∠=∠=，然后求出12IF FJ AF==，，通过设FJ x=求出x ，即可求出AF的长.【详解】解：过点A作AF⊥CE交于I，AG⊥BD交于J在CAE和BAD中AC ABCAE BADAE AD=⎧⎪∠=∠⎨⎪=⎩∴CAE≅BAD∴ICA ABJ∠=∠∴BFE CAB∠=∠（8字形）∴°120CFD∠=在CAI和BAJ中°90ICA ABJCAI BJACA BA∠=∠⎧⎪∠=∠=⎨⎪=⎩∴CAI ≅BAJ,AI AJ CI BJ ==∴°60CFA AFJ ∠=∠=∴°30FAI FAE ∠=∠=在RtAIF 和RtAJF 中°30FAI FAE ∠=∠=∴12IF FJ AF ==设FJ x = 7,4CF BF ==则47x x +=-32x ∴=2AF FJ =AF ∴=3【点睛】此题主要考查了通过做辅助线证明三角形全等，得出相关的边相等，学会合理添加辅助线求解是解决本题的重点.4．等腰三角形顶角为30°，腰长是4cm ，则三角形的面积为__________【答案】4【解析】如图，根据30°角所对直角边等于斜边的一半的性质，可由等腰三角形的顶角为30°，腰长是4cm ，可求得BD=12AB =4×12=2，因此此三角形的面积为：S=12AC•BD=12×4×2=8×12=4（cm 2）．故答案是：4．5．如图，己知30MON ∠=︒，点1A ，2A ，3A ，…在射线ON 上，点1B ，2B ，3B ，…在射线OM 上，112A B A ∆，223A B A ∆，334A B A ∆，…均为等边三角形，若12OA =，则556A B A ∆的边长为________.【答案】32【解析】【分析】根据底边三角形的性质求出130∠=︒以及平行线的性质得出112233////A B A B A B ，以及22122A B B A =，得出332212244A B A B B A ===，441288A B B A ==，551216A B B A =⋯进而得出答案．【详解】解：△112A B A 是等边三角形，1121A B A B ∴=，341260∠=∠=∠=︒，2120∴∠=︒，30MON ∠=︒，11801203030∴∠=︒-︒-︒=︒，又360∠=︒，5180603090∴∠=︒-︒-︒=︒，130MON ∠=∠=︒，1112OA A B ∴==，212A B ∴=，△223A B A 、△334A B A 是等边三角形，111060∴∠=∠=︒，1360∠=︒，41260∠=∠=︒，112233////A B A B A B ∴，1223//B A B A ， 16730∴∠=∠=∠=︒，5890∠=∠=︒，22122242A B B A =∴==，33232B A B A =，33312428A B B A ∴===，同理可得:444128216A B B A ===，⋯∴△1n n n A B A +的边长为2n ，∴△556A B A 的边长为5232=．故答案为：32．【点睛】本题考查了等边三角形的性质以及30°直角三角形的性质，根据已知得出33124A B B A =，44128A B B A =，551216A B B A =进而发现规律是解题关键．6．如图，在△ABC 中，P ，Q 分别是BC ，AC 上的点，PR ⊥AB ，PS ⊥AC ，垂足分别是R ，S ，若AQ PQ =，PR PS =，那么下面四个结论：①AS AR =；②QP //AR ；③△BRP ≌△QSP ；④BRQS ，其中一定正确的是（填写编号）_____________.【答案】①，②【解析】【分析】连接AP ，根据角平分线性质即可推出①，根据勾股定理即可推出AR=AS ，根据等腰三角形性质推出∠QAP=∠QPA ，推出∠QPA=∠BAP ，根据平行线判定推出QP ∥AB 即可；在Rt △BRP 和Rt △QSP 中，只有PR=PS ．无法判断△BRP ≌△QSP 也无法证明BRQS ．【详解】解：连接AP①∵PR ⊥AB ，PS ⊥AC ，PR=PS ，∴点P 在∠BAC 的平分线上，∠ARP=∠ASP=90°，∴∠SAP=∠RAP ，在Rt △ARP 和Rt △ASP 中，由勾股定理得：AR 2=AP 2-PR 2，AS 2=AP 2-PS 2，∵AP=AP ，PR=PS ，∴AR=AS ，∴①正确；②∵AQ=QP，∴∠QAP=∠QPA，∵∠QAP=∠BAP，∴∠QPA=∠BAP，∴QP∥AR，∴②正确；③在Rt△BRP和Rt△QSP中，只有PR=PS，不满足三角形全等的条件，故③④错误；故答案为：①②.【点睛】本题主要考查了角平分线的性质与勾股定理的应用，熟练掌握根据垂直与相等得出点在角平分线上是解题的关键.7．如图，在△ABC中，AB=AC，D、E是△ABC内的两点，AE平分∠BAC，∠D=∠DBC=60°，若BD=5cm，DE=3cm，则BC的长是 ______cm．【答案】8．【解析】【分析】作出辅助线后根据等边三角形的判定得出△BDM为等边三角形，△EFD为等边三角形，从而得出BN的长，进而求出答案．【详解】解：延长DE交BC于M，延长AE交BC于N，作EF∥BC于F，∵AB=AC，AE平分∠BAC，∴AN⊥BC，BN=CN，∵∠DBC=∠D=60°，∴△BDM为等边三角形，∴△EFD为等边三角形，∵BD=5，DE=3，∴EM=2，∵△BDM为等边三角形，∴∠DMB=60°，∵AN⊥BC，∴∠ENM=90°，∴∠NEM=30°，∴NM=1，∴BN=4，∴BC=2BN=8（cm），故答案为8．【点睛】本题考查等边三角形的判定与性质；等腰三角形的性质．8．如图，在四边形ABCD中，∠A+∠C＝180°，E、F分别在BC、CD上，且AB＝BE，AD ＝DF，M为EF的中点，DM＝3，BM＝4，则五边形ABEFD的面积是_____．【答案】12【解析】【分析】延长BM至G，使MG＝BM，连接FG、DG，证明△BME≌△GMF（SAS），得出FG＝BE，∠MBE＝∠MGF，证出AB＝FG，证明△DAB≌△DFG（SAS），得出DB＝DG，由等腰三角形的性质即可得DM⊥BM，由五边形ABEFD的面积＝△DBG的面积，可求解．【详解】延长BM至G，使MG＝BM＝4，连接FG、DG，如图所示：∵M 为EF 中点，∴ME ＝MF ，在△BME 和△GMF 中，BM MG BME GMFME MF =⎧⎪∠=∠⎨⎪=⎩， ∴△BME ≌△GMF （SAS ），∴FG ＝BE ，∠MBE ＝∠MGF ，S △BEM ＝S △GFM ，∴FG ∥BE ，∴∠C ＝∠GFC ，∵∠A +∠C ＝180°，∠DFG +∠GFC ＝180°，∴∠A ＝∠DFG ，∵AB ＝BE ，∴AB ＝FG ，在△DAB 和△DFG 中，AB FG A DFGAD DF =⎧⎪∠=∠⎨⎪=⎩， ∴△DAB ≌△DFG （SAS ），∴DB ＝DG ，S △DAB ＝S △DFG ，∵MG ＝BM ，∴DM ⊥BM ，∴五边形ABEFD 的面积＝△DBG 的面积＝12×BG ×DM ＝12×8×3＝12， 故答案为：12．【点睛】本题考查了全等三角形的判定与性质、平行线的性质、等腰三角形的判定与性质等知识；熟练掌握等腰三角形的判定由性质，证明三角形全等是解题的关键．9．如图，过边长为1的等边三角形ABC 的边AB 上一点P ，作PE ⊥AC 于点E ，Q 为BC 延长线上一点，当AP ＝CQ 时，PQ 交AC 于D ，则DE 的长为______．【答案】1 2【解析】过点Q作AD的延长线的垂线于点F.因为△ABC是等边三角形，所以∠A=∠ACB=60°.因为∠ACB=∠QCF，所以∠QCF=60°.因为PE⊥AC，QF⊥AC，所以∠AEP=∠CFQ=90°，又因为AP=CQ，所以△AEP≌△CFQ，所以AE=CF，PE=QC.同理可证，△DEP≌△DFQ，所以DE=DF.所以AC=AE+DE+CD=DE+CD+CF=DE+DF=2DE，所以DE=12AC=12.故答案为1 2 .10．如图，在△ABC中，AB=AC，AB边的垂直平分线DE交AC于点D．已知△BDC的周长为14，BC=6，则AB=___．【答案】8【解析】试题分析：根据线段垂直平分线的性质，可知AD=BD，然后根据△BDC的周长为BC+CD+BD=14，可得AC+BC=14，再由BC=6可得AC=8，即AB=8.故答案为8.点睛：此题主要考查了线段的垂直平分线的性质，解题时，先利用线段的垂直平分线求出BD=AD ，然后根据三角形的周长互相代换，即可其解.二、八年级数学轴对称三角形选择题（难）11．如图，已知一条线段的长度为a ，作边长为a 的等边三角形的方法是：①画射线AM ；②连结AC 、BC ；③分别以A 、B 为圆心，以a 的长为半径作圆弧，两弧交于点C ；④在射线AM 上截取AB ＝a ；以上画法正确的顺序是（ ）A ．①②③④B ．①④③②C ．①④②③D ．②①④③【答案】B【解析】【分析】 根据尺规作等边三角形的过程逐项判断即可解答.【详解】解：已知一条线段的长度为a ，作边长为a 的等边三角形的方法是：①画射线AM ；②在射线AM 上截取AB ＝a ；③分别以A 、B 为圆心，以a 的长为半径作圆弧，两弧交于点C ；④连结AC 、BC ．△ABC 即为所求作的三角形．故选答案为B ．【点睛】本题考查了尺规作图和等边三角形的性质，解决本题的关键是理解等边三角形的作图过程.12．如图，30MON ∠=︒．点1A ，2A ，3A ，⋯，在射线ON 上，点1B ，2B ，3B ，⋯，在射线OM 上，112A B A ∆，223A B A ∆，334A B A ∆，⋯均为等边三角形，若11OA =，则201920192020A B A ∆的边长为（ ）A ．20172B ．20182C ．20192D ．20202【答案】B【解析】【分析】根据等边三角形的性质和30MON ∠=︒，可求得1130∠=︒OB A ，进而证得11OA B ∆是等腰三角形，可求得2OA 的长，同理可得22OA B ∆是等腰三角形，可得222=A B OA ，同理得规律333、、=⋅⋅⋅=n n n A B OA A B OA ，即可求得结果． 【详解】解：∵30MON ∠=︒，112A B A ∆是等边三角形，∴11260∠=︒B A A ，1112A B A A =∴1111230∠=∠-∠=︒OB A B A A MON ，∴11∠=∠OB A MON ，则11OA B ∆是等腰三角形，∴111=A B OA ，∵11OA =，∴11121==A B A A OA =1，21122=+=OA OA A A ，同理可得22OA B ∆是等腰三角形，可得222=A B OA =2，同理得23342==A B 、34482==A B ，根据以上规律可得：2018201920192=A B ，即201920192020A B A ∆的边长为20182，故选：B ．【点睛】本题属于探索规律题，主要考查了等边三角形的性质、等腰三角形的判定与性质，掌握等边三角形的三个内角都是60°、等角对等边和探索规律并归纳公式是解题的关键．13．如图，在锐角△ABC 中，AC ＝10，S △ABC ＝25，∠BAC 的平分线交 BC 于点 D ，点 M ，N 分别是 AD 和 AB 上的动点，则 BM ＋MN 的最小值是（ ）A ．4B ．245C ．5D ．6【答案】C【解析】试题解析：如图，∵AD是∠BAC的平分线，∴点B关于AD的对称点B′在AC上，过点B′作B′N⊥AB于N交AD于M，由轴对称确定最短路线问题，点M即为使BM+MN最小的点，B′N=BM+MN，过点B作BE⊥AC于E，∵AC=10，S△ABC=25，∴12×10•BE=25，解得BE=5，∵AD是∠BAC的平分线，B′与B关于AD对称，∴AB=AB′，∴△ABB′是等腰三角形，∴B′N=BE=5，即BM+MN的最小值是5．故选C．14．如图钢架中，∠A=a,焊上等长的钢条P1P2, P2P3, P3P4, P4P5……来加固钢架.著P1A= P1P2,且恰好用了4根钢条,则α的取值范圈是( )A．15°≤ a <18°B．15°< a ≤18°C．18°≤ a <22.5°D．18° < a ≤ 22.5°【答案】C【解析】【分析】由每根钢管长度相等，可知图中都是等腰三角形，利用等腰三角形底角一定是锐角，可推出取值范围.【详解】∵AB=BC=CD=DE=EF∴∠P1P2A=∠A=a由三角形外角性质，可得∠P 2P 1P 3=2∠A=2a同理可得，∠P 1P 3P 2=∠P 2P 1P 3=2a ，∠P 3P 2P 4=∠P 3P 4P 2=∠A+∠P 1P 3P 2=3a ，∠P 4P 3P 5=∠P 4P 5P 3=∠A+∠P 3P 4P 2=4a ，在△P 4P 3P 5中，∠P 3P 4P 5=180°-2∠P 4P 3P 5=180°-8a当∠P 5P 4B ≥90°即∠P 5P 4A ≤90°时，不能再放钢管，∴3180890+-≤a a ，解得a ≥18°又∵等腰三角形底角只能是锐角，∴4a ＜90°，解得a ＜22.5∴1822.5οο≤<a故选C.【点睛】本题考查等腰三角形的性质，掌握等腰三角形的底角只能是锐角是关键.15．如图，△ABC 是等边三角形，AQ ＝PQ ，PR ⊥AB 于点R ，PS ⊥AC 于点S ，PR ＝PS ，则下列结论：①AP ⊥BC ；②AS ＝AR ；③QP ∥AR ；④△BRP ≌△QSP .正确的有( )A ．1个B ．2个C ．3个D ．4个【答案】D【解析】【分析】 根据到角的两边的距离相等的点在角的平分线上可得AP 平分∠BAC ，根据等腰三角形“三线合一”的性质判断出①正确；根据HL 证明Rt △APR ≌Rt △APS ，即可判断②正确；根据等边对等角的性质可得∠APQ =∠PAQ ，根据三角形外角的性质得到然后得到∠PQC =2∠PAC =60°=∠BAC ，然后根据同位角相等两直线平行可得QP ∥AB ，从而判断出③正确，④由③易证△QPC 是等边三角形，得到PQ =PC ，等量代换得到BP =PQ ，用HL 证明Rt △BRP ≌Rt △QSP ，即可得到④正确．【详解】∵△ABC 是等边三角形，PR ⊥AB ，PS ⊥AC ，且PR =PS ，∴P 在∠A 的平分线上．∵AB =AC ，∴AP ⊥BC ，故①正确；∵PA =PA ，PR =PS ，∴Rt △APR ≌Rt △APS ，∴AS =AR ，故②正确；∵AQ =PQ ，∴∠APQ =∠PAQ ，∴∠PQC =2∠PAC =60°=∠BAC ，∴PQ ∥AR ，故③正确； 由③得：△PQC 是等边三角形，∴△PQS ≌△PCS ，∴PQ =PC ．又∵AB =AC ，AP ⊥BC ，∴BP =PC ，∴BP =PQ ．∵PR =PS ，∴Rt △BRP ≌Rt △QSP ，故④也正确．∵①②③④都正确．故选D．【点睛】本题考查了等腰三角形的性质、全等三角形的判定与性质以及等边三角形的判定与性质，准确识图并熟练掌握全等三角形的判定方法与性质是解题的关键．16．如图，点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点，点P从顶点A，点Q从顶点B同时出发，且速度都为1cm/s，连接AQ、CP交于点M，下面四个结论:①BP＝CM；②△ABQ≌△CAP；③∠CMQ的度数不变，始终等于60°；④当第43秒或第83秒时，△PBQ为直角三角形，正确的有几个 ( )A．1 B．2 C．3 D．4【答案】C【解析】【分析】①等边三角形ABC中，AB=BC，而AP=BQ，所以BP=CQ．②根据等边三角形的性质，利用SAS证明△ABQ≌△CAP；③由△ABQ≌△CAP根据全等三角形的性质可得∠BAQ=∠ACP，从而得到∠CMQ=60°；④设时间为t秒，则AP=BQ=tcm，PB=（4-t）cm，当∠PQB=90°时，因为∠B=60°，所以PB=2BQ，即4-t=2t故可得出t的值，当∠BPQ=90°时，同理可得BQ=2BP，即t=2（4-t），由此两种情况即可得出结论．【详解】①在等边△ABC中，AB=BC．∵点P、Q的速度都为1cm/s，∴AP=BQ，∴BP=CQ．只有当CM=CQ时，BP=CM．故①错误；②∵△ABC是等边三角形∴∠ABQ=∠CAP，AB=CA，又∵点P、Q运动速度相同，∴AP=BQ，在△ABQ与△CAP中，∵ABCA ABQ CAP AP BQ ⎧⎪∠∠⎨⎪⎩＝＝＝， ∴△ABQ ≌△CAP （SAS ）．故②正确；③点P 、Q 在运动的过程中，∠QMC 不变．理由：∵△ABQ ≌△CAP ，∴∠BAQ=∠ACP ，∵∠QMC=∠ACP+∠MAC ，∴∠CMQ=∠BAQ+∠MAC=∠BAC=60°．故③正确；④设时间为t 秒，则AP=BQ=tcm ，PB=（4-t ）cm ，当∠PQB=90°时，∵∠B=60°，∴PB=2BQ ，即4-t=2t ，t=43， 当∠BPQ=90°时，∵∠B=60°，∴BQ=2BP ，得t=2（4-t ），t=83， ∴当第43秒或第83秒时，△PBQ 为直角三角形． 故④正确．正确的是②③④，故选C ．【点睛】 此题是一个综合性题目，主要考查等边三角形的性质、全等三角形的判定与性质等知识．熟知等边三角形的三个内角都是60°是解答此题的关键．17．已知等边△ABC 中，在射线BA 上有一点D ，连接CD ，并以CD 为边向上作等边△CDE ，连接BE 和AE ，试判断下列结论：①AE=BD ； ②AE 与AB 所夹锐夹角为60°；③当D 在线段AB 或BA 延长线上时，总有∠BDE-∠AED=2∠BDC ；④∠BCD=90°时，CE 2+AD 2=AC 2+DE 2 ，正确的序号有（ ）A ．①②B ．①②③C ．①②④D ．①②③④【答案】C【解析】【分析】由∠BCD=∠ACD+60°，∠ACE=∠ACD+60°可得∠BCD=∠ACE，利用SAS可证明△BCD≌△ACE，可得AE=BD，①正确；∠CBD=∠CAE=60°，进而可得∠EAD=60°，②正确，当∠BCD=90°时，可得∠ACD=∠ADC=30°，可得AD=AC，即可得CE2+AD2=AC2+DE2，④正确；当D点在BA延长线上时，∠BDE-∠BDC=60°，根据△BCD≌△ACE可得∠AEC=∠BDC，进而可得∠BDC+∠AED=∠AEC+∠AED=∠CED=60°，即可证明∠BDE-∠BDC=∠BDC+∠AED，即∠BDE-∠AED=2∠BDC，当点D在AB上时可证明∠BDE-∠AED=120°，③错误，综上即可得答案.【详解】∵∠BCA=∠DCE=60°，∴∠BCA+∠ACD=∠DCE+∠ACD，∴∠BCD=∠ACE，又∵AC=BC，CE=CD，∴△BCD≌△ACE，∴AE=BD，∠CBA=∠CAE=60°，∠AEC=∠BDC，①正确，∴∠BAE=120°，∴∠EAD=60°，②正确，∵∠BCD=90°，∠BCA=60°，∴∠ACD=∠ADC=30°，∴AC=AD，∵CE=DE，∴CE2+AD2=AC2+DE2，④正确，当D点在BA延长线上时，∠BDE-∠BDC=60°，∵∠AEC=∠BDC，∴∠BDC+∠AED=∠AEC+∠AED=∠CED=60°，∴∠BDE-∠BDC=∠BDC+∠AED∴∠BDE-∠AED=2∠BDC，如图，当点D在AB上时，∵△BCD≌△∠ACE，∴∠CAE=∠CBD=60°，∴∠DAE=∠BAC+∠CAE=120°，∴∠BDE-∠AED=∠DAE=120°，③错误故正确的结论有①②④，故选C.【点睛】此题主要考查等边三角形的性质和全等三角形的判定与性质等知识点的理解和掌握18．如图，已知，点A（0，0）、B（43，0）、C（0，4），在△ABC内依次作等边三角形，使一边在x轴上，另一个顶点在BC边上，作出的等边三角形分别是第1个△AA1B1，第2个△B1A2B2，第3个△B2A3B3，…则第2017个等边三角形的边长等于（）A 3B3C3D3【答案】A【解析】【分析】【详解】根据锐角三函数的性质，由OB=3OC=1，可得∠OCB=90°，然后根据等边三角形的性质，可知∠A1AB=60°，进而可得∠CAA1=30°，∠CA1O=90°，因此可推导出∠A2A1B=30°，同理得到∠CA2B1=∠CA3B2=∠CA4B3=90°，∠A2A1B=∠A3A2B2=∠A4A3B3=30°，故可得后一个等边三角形的边长等于前一个等边三角形的边长的一半，即OA1=OCcos∠CAA1=3B1A2=1232⨯2017个等边三角形的边长为：2017201513()4322⨯=.故选A.【点睛】此题主要考查了等边三角形的性质，属于规律型题目，解题关键是仔细审图，得出：后一个等边三角形的边长等于前一个等边三角形的边长的一半.19．如图所示，把腰长为1的等腰直角三角形折叠两次后，得到的一个小三角形的周长是（）A．1+2B．1+22C．2-2D．2-1【答案】B 【解析】第一次折叠后，等腰三角形的底边长为1，腰长为22；第一次折叠后，等腰三角形的底边长为22，腰长为12，所以周长为112212222++=+.故答案为B.20．如图，在平面直角坐标系中，A(1，2)，B(3，2)，连接AB，点P是x轴上的一个动点，连接AP、BP，当△ABP的周长最小时，对应的点P的坐标和△ABP的最小周长分别为( )A．(1，0)，224+ B．(3，0)，224+ C．(2,0), 25D．(2,0),252+【答案】D【解析】作A关于x轴的对称点N（1，-2），连接BN与x轴的交点即为点P的位置，此时△ABP的周长最小.设直线BN的解析式为y kx b=+，∵N (1，-2)，B (3，2)，∴232k b k b +=-⎧⎨+=⎩ ， 解得24k b =⎧⎨=-⎩， ∴24y x =-，当0y =时，240x -=，解得，2x =，∴点P 的坐标为（2，0）；∵A (1，2)，B (3，2)，∴AB //x 轴，∵AN ⊥x 轴，∴AB ⊥x 轴，在Rt △ABC 中，AB ＝2，AN ＝4，由勾股定理得，BN==∵AP =NP , ∴△ABP 的周长最小值为：AB +BP +AP =AB +BP +PN =AB +BN故选D.点睛：本题考查最短路径问题.利用轴对称作出点P 的位置是解题的关键.。

2024届安徽省合肥市第四十八中学物理八上期末预测试题注意事项：1．答卷前，考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。

用2B铅笔将试卷类型（B）填涂在答题卡相应位置上。

将条形码粘贴在答题卡右上角"条形码粘贴处"。

2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。

答案不能答在试题卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。

不按以上要求作答无效。

4．考生必须保证答题卡的整洁。

考试结束后，请将本试卷和答题卡一并交回。

一、选择题1．小明洗水果时，发现不同的水果在水中静止时所处位置是不一样的。

葡萄在水中下沉后静止在容器底部；苹果漂着，大约有14体积露出水面；青枣也漂着，约有910体积在水中，如图所示。

他的四个小伙伴看到后，一人说了一句话，其中正确的是( )A．小刚说“苹果漂浮在水面上，说明苹果受到的浮力比苹果受到的重力大”B．小华说“葡萄沉在容器的底部，葡萄受到的浮力不一定比葡萄受到的重力小”C．小强说“青枣和苹果相比，青枣的密度更接近水的密度”D．小峰说“苹果的密度比葡萄密度大”2．下列现象发生的过程中，吸收热量的一组是（）①春天，皑皑的白雪开始消融；②夏天，青青的小草挂上露珠；③秋天，浓浓的白雾慢慢散去；④冬天，静静的池塘覆上薄冰A．①②B．②④C．①③D．③④3．下列数据中，最符合实际情况的是A．人的心跳频率大约为1.2Hz B．正常洗澡水的温度大约为60℃C．人的正常体温为35℃D．让人感觉舒适的环境声强级为90dB-100dB4．由我国成功发射的世界首颗量子科学实验卫星被命名为“墨子号”．墨子第一次用科学方法解释了光沿直线传播，启发了量子通信．如图所示各选项中光现象的原理与墨子的这一解释相符的是A．日食现象B．雨后“彩虹”C．水中“倒影”D．放大镜把字“放大”5．下列各组物态变化现象中，都放热的是（）A．春天冰封的湖面逐渐解冻；家里冰箱中形成冰霜B．工人用铁水浇铸成工件；太阳出来，湖面上的水雾消失了C．夏天剥开包装的冰棍周围冒“白气”；冬天玻璃窗上出现冰花D．洒在地面上的水很快就干了；家中衣箱内的樟脑球逐渐变小6．如图使用共享单车需要用手机摄像头扫描二维码，当手机扫描二维码时，下列选项正确的是A．摄像头相当于凹透镜B．二维码位于摄像头的二倍焦距以外C．二维码是光源D．二维码中黑色部分发生漫反射，白色部分发生镜面反射7．下列现象中，属于光的反射的是A．开凿隧道时，利用激光束引导掘进方向B．用凸面镜扩大视野C．放大镜使光会聚D．手影的形成8．关于声现象，下列说法中正确的是A．一切正在发声的物体都在振动B．声音在真空中传播的速度最大C．音调越高说明声源振动的幅度越大D．市区内要求汽车“禁止鸣笛”是在声音的传播过程减弱噪声9．以下研究方法与“研究蒸发快慢与温度的关系”方法相同的是（）A．研究物体的运动时将运动分为直线运动和曲线运动B．通过蜡烛火焰晃动的情况来判断声音是否可以传递能量C．研究声音响度与振幅的关系时，控制钢尺长度不变D．研究光的直线传播时引入光线10．在室温下，用绷紧的橡皮膜把一个空锥形瓶的瓶口封上，然后把瓶子放进热水中，橡皮膜会凸起来。

安徽省合肥市包河区48中学2024届中考三模语文试题注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、积累与运用1．下列文学文化常识说法正确的一项是（）A．安徒生，19世纪丹麦童话作家，代表作有《皇帝的新装》《丑小鸭》《卖火柴的小女孩》《白雪公主》等。

B．序，文体名，一般用以陈述创作主旨、创作经过等，《送东阳马生序》是一篇赠序。

C．下列文章按写作年代排列，依次为：《马说》、《桃花源记》、《儒林外史》、《岳阳楼记》。

D．始龀，指七八岁；加冠，指二十岁；不惑之年，指三十岁；而立之年，指四十岁。

2．下列句子加点词语使用不正确的一项是( )A．文艺创作者应该创作出更多令人喜闻乐见．．．．的文艺节目,弘扬真善美,鞭挞假恶丑,不能依靠低俗段子哗众取宠。

B．虽然网络媒体是新兴阅读方式,但在浮光掠影．．．．式的阅读下,我们更倾向于将其作为一种文化快餐。

C．从1958年参加工作开始,黄旭华一直战斗在核潜艇研制领域,孜孜不倦．．．．、呕心沥血,为我国核潜艇事业奉献了毕生心血,被誉为“中国核潜艇之父”。

D．有了这些在假日中坚守岗位的劳动者的无悔付出,我们才能够外出饱览美景,和家人、朋友共享天伦之乐．．．．。

3．下列各句中，加点的成语使用恰当一项是（）A．发展低碳经济首当其冲．．．．的是要坚持节约资源、保护环境的基本国策，协调资源利用和环境保护的关系，实现可持续发展。

B．乔布斯的生活片断被无限放大，他的话受到人们的热捧，甚至“不要为别人而活’’这样的话也被一些年轻人断．章取义．．．，奉为“创业宝典”。

C．语文课上，王老师将《智取生辰纲》里面的故事讲得惟妙惟肖．．．．，同学们都沉浸在其中。

2022年安徽省合肥市包河区中考数学三模试卷一、选择题（本大题共10小题，共40.0分。

在每小题列出的选项中，选出符合题目的一项）1. −3的相反数是( )A. −3B. 3C. −13D. 132. 下列运算正确的是( )A. (ab)2=ab2B. 2a÷3a=−aC. 3a⋅2a=6a2D. 3a+2b=5ab3. 2021年我国农产品加工工业收入超过232000亿元，数值232000亿用科学记数法表示正确的是( )A. 2.32×105B. 2.32×109C. 2.32×1012D. 2.32×10134. 某立体图形的展开图如所示，则该立体图形是( )A. 三棱锥B. 圆锥C. 三棱柱D. 长方体5. 不等式x−23<x−12的解集是( )A. x<−1B. x>2C. x>−1D. x<26. 如图，已知点A、B、C、D在⊙O上，弦AB、CD的延长线交⊙O外一点E，∠BCD=25°，∠E=39°，则∠APC的度数为( )A. 64°B. 89°C. 90°D. 94°7. 某兴趣小组6位同学进行理化实验模拟测试，成绩统计如表所示．人数(人)123分数6910那么该兴趣小组6位同学理化实验模拟测试成绩的中位数和方差分别是( )A. 10、2B. 10、1C. 9.5、2D. 9.5、18. 受疫情反弹的影响，某景区今年3月份游客人数比2月份下降了40%，4月份又比3月份下降了50%，随着疫情逐步得到控制，预计5月份游客人数将比2月份翻一番(即是2月份的2倍)，设5月份与4月份相比游客人数的增长率为x，则下列关系正确的是( )A. (1−40%−50%)(1+x)=2B. (1−40%−50%)(1+x)2=2C. (1−40%)(1−50%)(l+x)2=2D. (1−40%)(1−50%)(1+x)=29. 如图，已知AB⊥BC、DC⊥BC，AC与BD相交于点O，作OM⊥BC于点M，点E是BD的中点，EF⊥BC于点G，交AC于点F，若AB=4，CD=6，则OM−EF值为( )A. 75B. 125C. 35D. 2510. 已知二次函数y=ax2+(b−1)x+c+1的图象如图所示，则在同一坐标系中y1= ax2+bx+1与y2=x−c的图象可能是( )A.B.C.D.二、填空题（本大题共4小题，共20.0分）11. 化简：√8−√2=______．12. 因式分解：2m2−8mn+8n2=______．13. 如图，直线x=1交反比例函数y=kx (x>0)的图象于点A，交y=4x(x>0)的图象于点B，点C的坐标为(2,0)，△ABC的面积为3，则k的值为______．14. 如图，在矩形ABCD中，AD=3，AB=4，E是边AB上一点，△BCE与△FCE关于直线CE 对称，连接BF并延长交AD于点G，请完成下列探究：(1)设BE=a，则AG=______(用含a的代数式表示)；(2)若点F为BG中点，则BE的长为______．三、解答题（本大题共9小题，共90.0分。

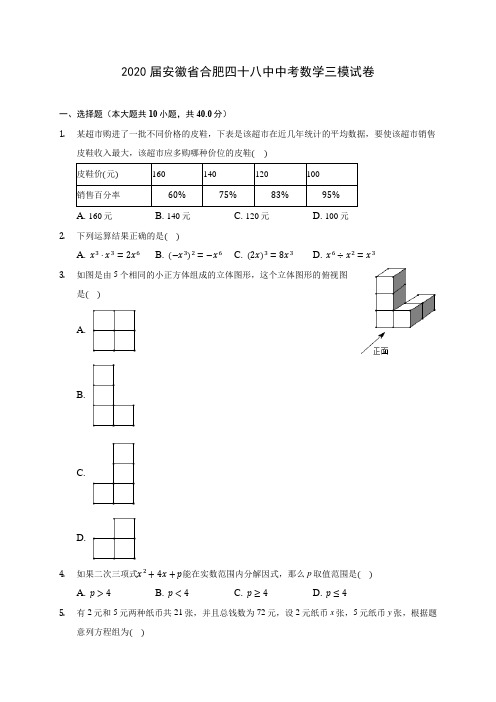
2020届安徽省合肥四十八中中考数学三模试卷一、选择题（本大题共10小题，共40.0分）1.某超市购进了一批不同价格的皮鞋，下表是该超市在近几年统计的平均数据，要使该超市销售皮鞋收入最大，该超市应多购哪种价位的皮鞋()皮鞋价(元)160140120100销售百分率60%75%83%95%A. 160元B. 140元C. 120元D. 100元2.下列运算结果正确的是()A. x3⋅x3=2x6B. (−x3)2=−x6C. (2x)3=8x3D. x6÷x2=x33.如图是由5个相同的小正方体组成的立体图形，这个立体图形的俯视图是()A.B.C.D.4.如果二次三项式x2+4x+p能在实数范围内分解因式，那么p取值范围是()A. p>4B. p<4C. p≥4D. p≤45.有2元和5元两种纸币共21张，并且总钱数为72元，设2元纸币x张，5元纸币y张，根据题意列方程组为()A. {x +y =215x +2y =72B. {x +y =212x +5y =72 C. {2x +5y =21x +y =72D. {5x +2y =21x +y =72 6. 下列说法正确的是( ) A. “明天降雨的概率是50%”表示明天有半天都在降雨B. 数据4，4，5，5，0的中位数和众数都是5C. 要了解一批钢化玻璃的最少允许碎片数，应采用普查的方式D. 一组数据5，6，7，8，9的方差是27. 如图，将边长为2的等边三角形ABC 绕点C 旋转120°，得到△DCE ，连接BD ，则BD 的长为( )A. 2B. 2.5C. 3D. 2√3 8. 如图，AB 是⊙O 的直径，点C ，D 在⊙O 上，且点C 是弧BD 的中点．过点C 作AD 的垂线EF 交直线AD 于点E.若⊙O 的半径为2.5，AC 的长度为4，则CE 的长度为( )A. 3B. 203C. 125D. 1659. 某公司在销售一种智能机器人时发现，每月可售出100个，当定价每降价1元时，每月可多售出5个．如果定价降价x 元，那么每月可售出机器人的个数是( ) A. 5x B. 100+5x C. 100+x D. 100+15x 10. 二次函数y =mx 2−4x +m 有最小值−3，则m 等于( )A. 1B. −4C. 1或−4D. −1或4二、填空题（本大题共4小题，共20.0分）11. 将数607000用科学记数法表示为______．12.不等式x+52−1>3x+23的解集为______ ．13.如图，在直角坐标系中有菱形OABC，A点的坐标为(10,0)，对角线OB、AC相交于点D，双曲线y=kx(x>0)经过点D，交BC的延长线于点E，且OB⋅AC=160，则点E的坐标为____．14.如图，在△ABC中，AB=AC=5，BC=6，点D在边AB上，且∠BDC=90°.如果△ACD绕点A顺时针旋转，使点C与点B重合，点D旋转至点D1，那么线段DD1的长为______．三、计算题（本大题共3小题，共30.0分）15.计算：2tan30°−|1−√3|+(√2+π)0+√13．16.如图，一架无人机在距离地面高度为21.4米的点B处，测得地面点A的俯角为47°，接着，这架无人机从点B沿仰角为37°的方向继续飞行20√6米到达点C，此时测得点C恰好在地面点D的正上方，且A，D两点在同一水平线上，求A，D两点之间的距离．(结果精确到1米；参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，sin47°≈0.73，cos47°≈0.68，tan47°≈1.07，√6≈2.45)17.一个不透明的口袋中装有4个完全相同的小球，分别标有数字1，2，3，4，另外有一个可以自由旋转的圆盘，被分成面积相等的3个扇形区域，分别标有数字1，2，3(如图所示)．(1)从口袋中摸出一个小球，所摸球上的数字大于2的概率为多少？(2)小龙和小东想通过游戏来决定谁代表学校参加歌咏比赛，游戏规则为：一人从口袋中摸出一个小球，另一人转动圆盘，如果所摸球上的数字与圆盘上转出数字之和小于5，那么小龙去；否则小东去．你认为游戏公平吗？请用树状图或列表法说明理由．四、解答题（本大题共6小题，共60.0分）18. 某工地有72m2的墙面需要粉刷．若安排4名一级技工粉刷一天，结果还剩12m2墙面未能刷完；同样时间内安排6名二级技工去粉刷，则刚好全部刷完．已知每名一级技工比二级技工一天多粉刷3m2墙面．设每一名一级技工一天粉刷墙面xm2．(1)每名二级技工一天粉刷墙面______m2(用含x的式子表示)；(2)求每名一级技工、二级技工一天分别能粉刷多少m2墙面？(3)每名一级技工一天的施工费是300元，每名二级技工一天的施工费是200元．若另一工地有540m2的墙面需要粉刷，要求一天完工且施工总费用不超过10600元，则至少需要______名二级技工(直接写出结果)．19. 如图，矩形ABCD中，AD=3，AB=4，点P是对角线AC上一动点(不与A，C重合)，连接BP，作PE⊥PB，交射线DC于点E，以线段PE，PB为邻边作矩形BPEF.过点P作GH⊥CD，分别交AB、CD于点G、H．(1)求证：△PGB∽△EHP；(2)求PE的值；PB(3)求矩形BPEF的面积的最小值．20. 已知1+2+3+⋯+n的和的个位数字是3，十位数字是0，百位数字不是0，求n最小值．(x<0)的图象相交21. 如图，直线y1=kx+b与反比例函数y2=k′x于点A、点B，与x轴交于点C，其中点A的坐标为(−2,4)，点B的横坐标为−4．(1)试确定反比例函数和直线AB的解析式；(2)求△AOB的面积．(3)观察图象，请直接写出当y1>y2时，x的取值范围．22. 如图所示正方形区域ABCD是某公园健身广场示意图，公园管理处想在其四个角的三角形区域内种植草皮加以绿化(阴影部分)，剩余部分安装健身器材作为市民健身活动场所(四边形EFGH)其中AB=100米，且AE=AH=CF=CG.则当AE的长度为多少时，市民健身活动场所的面积达到最大？23. 已知：如图，AB为⊙O的弦，OD⊥AB，垂足为点D，DO的延长线交⊙O于点C.过点C作CE⊥AO，．分别与AB、AO的延长线相交于E、F两点．CD=8，sin∠A=35求：(1)弦AB的长；(2)△CDE的面积．【答案与解析】1.答案：B解析：解：设每种皮鞋a只．四种皮鞋的销售额分别为：a×160×60%=96a；a×140×75%=105a；a×120×83%=99.6a；a×100×95%=95a.可见应多购140元的皮鞋．故选：B．此题的实质是求每种皮鞋的销售额．本题是实际问题，需要同学们有读表能力，才能准确理解题意．2.答案：C解析：解：A、x3⋅x3=x6，故此选项错误；B、(−x3)2=x6，故此选项错误；C、(2x)3=8x3，故此选项正确；D、x6÷x2=x4，故此选项错误；故选：C．直接利用同底数幂的乘除运算法则以及积的乘方运算法则、幂的乘方运算法则分别计算得出答案．此题主要考查了同底数幂的乘除运算以及积的乘方运算、幂的乘方运算，正确掌握相关运算法则是解题关键．3.答案：D解析：解：这个立体图形的俯视图是：故选：D．根据组合体的形状即可求出答案．本题考查了学生的思考能力和对几何体三种视图的空间想象能力．解题的关键是根据组合体的形状进行判断．4.答案：D解析：解：∵二次三项式x2+4x+p能在实数范围内分解因式，∴△=16−4p≥0，解得：p≤4，故选：D．根据多项式能分解因式，得到多项式为0时方程有解，确定出p 的范围即可．此题考查了实数范围内分解因式，熟练掌握一元二次方程根的判别式的意义是解本题的关键． 5.答案：B解析：解：设2元纸币x 张，5元纸币y 张，根据题意列方程组为：{x +y =212x +5y =72． 故选：B ．根据等量关系：2元纸币的张数+5元纸币的张数=21，2元纸币的钱数+5元纸币的钱数=72列出方程组即可．本题主要考查了由实际问题抽象出二元一次方程组，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程组．6.答案：D解析：解：A 、“明天降雨的概率是50%”表示明天降雨的机会是50%，故选项错误；B 、数据4，4，5，5，0的中位数是4，众数是4和5，故选项错误；C 、要了解一批钢化玻璃的最少允许碎片数，应采用抽查的方式，故本选项错误；D 、这组数据的平均数是15(5+6+7+8+9)=7，方差是15[(5−7)2+(6−7)2+(7−7)2+(8−7)2+(9−7)2]=2，故本选项正确；故选：D ．根据概率是表示事件发生机会大小，以及众数、中位数，方差的意义即可作出判断．本题考查利用频率估计概率．大量反复试验下频率稳定值即概率．注意随机事件发生的概率在0和1之间． 7.答案：D解析：本题考查的是等边三角形的性质及旋转的性质，熟知图形旋转后的图形与原图形全等的性质是解答此题的关键．连接AD 构建菱形ABCD ，根据等边三角形的性质得到AB =DC =BC =DE =2，∠ABC =∠ACB =∠DCE =∠E =60°，推出四边形ABCD 为菱形，根据菱形的性质得到∠DBE =12∠ABC =30°，在Rt △BDE 中利用勾股定理即可得出BD 的长．解：连接AD ，由题意知，△ABC≌△EDC，∠ACE=120°，又∵△ABC是等边三角形，∴AB=DC=BC=DE=2，∠ABC=∠ACB=∠DCE=∠E=60°，∴∠ACE+∠ACB=120°+60°=180°，∴B、C、E三点在一条直线上．∴AB//DC，∴四边形ABCD为菱形，∴∠DBE=12∠ABC=30°，∵∠DBE+∠BDE+∠E=180°，∴∠BDE=90°，∴BE=4，∴BD=√BE2−DE2=√42−22=2√3．故选D．8.答案：C解析：解：连接BC，∵点C是弧BD的中点，∴∠EAC=∠CAB，又∵AB为直径，AE⊥EF，∴∠AEC=∠ACB=90°，∴△EAC∽△CAB，∴ACAB =ECBC，∴EC=AC⋅BCAB =4×√52−425=125．故选：C．根据直径所对的角是90°和等弧对等角判定相似，然后根据相似三角形的性质结合勾股定理求出CE 的长度．本题主要考查圆周角定理、相似三角形的判定和性质和圆心角、弧、弦的关系，关键是在圆中寻找相等的角判定相似．9.答案：B解析：解：由题意可得，定价降价x元，每月可售出机器人的个数是：100+5x，故选：B．根据某公司在销售一种智能机器人时发现，每月可售出100个，当定价每降价1元时，每月可多售出5个，可以用含x的代数式表示出定价降价x元，每月可售出机器人的个数．本题考查列代数式，解答本题的关键是明确题意，列出相应的代数式．10.答案：A解析：解：∵二次函数有最小值，∴m>0且4m2−164m=−3，解得m=1．故选：A．根据二次函数的最值公式列式计算即可得解．本题考查了二次函数的最值问题，熟记最大(小)值公式是解题的关键．11.答案：6.07×105解析：解：将数607000用科学记数法表示为6.07×105，故答案为：6.07×105．科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数，确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值>1时，n是正数；当原数的绝对值<1时，n是负数．此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n 为整数，表示时关键要正确确定a的值以及n的值．12.答案：x<53解析：利用不等式的基本性质，先去分母，再去括号，然后移项、合并同类项、化系数为1即可求出不等式的解集．解不等式依据不等式的基本性质，在不等式的两边同时加上或减去同一个数或整式不等号的方向不变；在不等式的两边同时乘以或除以同一个正数不等号的方向不变；在不等式的两边同时乘以或除以同一个负数不等号的方向改变．特别是在系数化为1这一个过程中要注意不等号的方向的变化．解：去分母得3x+15−6>6x+4，移项合并同类项得3x<5，化系数为1得x<53．所以不等式x+52−1>3x+23的解集为x<53．13.答案：(4,8)解析：解：过点C作CF⊥x轴于点F，如下图所示：∵OB⋅AC=160，A点的坐标为(10,0)，OA=AB=BC=OC=10，∴OA⋅CF=12OB⋅AC═12×160=80，∴CF=8，在Rt△OCF中，∵OC=10，CF=8，∴OF=√OC2−CF2=√102−82=6，∴C(6,8)，∵点D 是线段AC 的中点， ∴D 点坐标为(10+62,82)，即(8,4)，∵双曲线y =k x (x >0)经过D 点， ∴4=k8，即k =32，∴双曲线的解析式为：y =32x(x >0)，∵CF =8，∴直线CB 的解析式为y =8，∴{y =8y =32x解得：{x =4y =8，∴E 点坐标为(4,8)， 故答案为(4,8)．过点C 作CF ⊥x 轴于点F ，根据面积求出CF ，即可知道C 点坐标，通过D 是AC 的中点，就能求出D 点坐标，带入双曲线y =kx(x >0)求出反比例函数的解析式，最后通过双曲线y =kx(x >0)与直线BC 的方程，就能求出E 的坐标．本题考查了反比例函数在菱形的性质中的应用，熟练掌握菱形的性质以及反比例函数的性质是解答此题的关键．14.答案：4225解析：本题考查了旋转的性质、等腰三角形的性质、相似三角形的判定和性质，解题的关键是证明△ABC∽△ADD 1.作AE ⊥BC 于E.根据等腰三角形三线合一的性质得出BE =EC =12BC =3，利用勾股定理求出AE =4.根据三角形的面积得出CD =BC⋅AE AB=245，那么AD =√AC 2−CD 2=75.再根据旋转的性质可知AD =AD 1，∠CAD =∠BAD 1，那么△ABC∽△ADD 1，利用相似三角形的性质可求出DD 1． 解：如图，作AE ⊥BC 于E ．∵AB=AC=5，BC=6，∴BE=EC=12BC=3，∴AE=√AB2−BE2=4．∵S△ABC=12AB⋅CD=12BC⋅AE，∴CD=BC⋅AEAB =6×45=245，∴AD=√AC2−CD2=75．∵△ACD绕点A顺时针旋转，使点C与点B重合，点D旋转至点D1，∴AD=AD1，∠CAD=∠BAD1，∵AB=AC，∴△ABC∽△ADD1，∴BCDD1=ABAD，∴6DD1=575，∴DD1=4225．故答案为4225．15.答案：解：2tan30°−|1−√3|+(√2+π)0+√13=2×√33−(√3−1)+1+√33=2解析：此题主要考查了实数的运算，要熟练掌握，解答此题的关键是要明确：在进行实数运算时，和有理数运算一样，要从高级到低级，即先算乘方、开方，再算乘除，最后算加减，有括号的要先算括号里面的，同级运算要按照从左到右的顺序进行．另外，有理数的运算律在实数范围内仍然适用．首先计算乘方、开方和乘法，然后从左向右依次计算，求出算式的值是多少即可．16.答案：解：如图，过点B作BE⊥CD于点E，过点A作AF⊥BE于点F，由题意可知：CD⊥AD，∴四边形AFED是矩形，∴AD=EF，在Rt△BCE中，BC=20√6，∠CBE=37°，∴BE=BC⋅cos37°=20√6×0.80≈39.2，在Rt△ABF中，AF=21.4，∠ABF=47°，∴BF=AFtan47∘=21.41.07≈20，∴EF=BE−BF≈39.2−20≈19，∴AD=EF≈19(米)．答：A，D两点之间的距离约为19米．解析：过点B作BE⊥CD于点E，过点A作AF⊥BE于点F，由题意可得，四边形AFED是矩形，然后根据三角函数求出BE和BF的长，进而即可求出A、D两点之间的距离．本题考查了解直角三角形的应用−方向角问题，解决本题的关键是掌握方向角定义．17.答案：[解](1)口袋中装有4个完全相同的小球，球上的数字大于2的球有两个，占球的个数的一半，所以所求概率是2/4=1/2，即从口袋中摸出一个小球，所摸球上的数字大于2的概率为1/2．(2)游戏公平．列举所有等可能的结果12个：1234123452345634567由表可知：所摸球上的数字与圆盘上转出数字之和小于5可能的情况有6种，∴所摸球上的数字与圆盘上转出数字之和小于5的概率为P=即所摸球上的数字与圆盘上转出数字之和不小于5的概率也为1/2，故可知游戏公平．解析：[解析](1)利用概率公式的求解方法就可求出．(2)本题用列表法比较简单，通过表格可清楚看出两种事件的概率，由于两种事件的概率相同，故可知游戏公平．[类型题]概率——求概率、概率的应用18.答案：(x −3) 5解析：解：(1)由题意得，每名二级技工一天粉刷墙面(x −3)m 2； 故答案为：(x −3) (2)依题意列方程：72−124x=726(x−3)；解得x =15，经检验x =15是原方程的解，即每名一级技工和二级技工一天分别能粉刷15m 2、12m 2墙面； (3)设需要m 名一级技工，需要n 名二级技工， 根据题意得，{15m +12n =540300m +200n =10600，解得：{m =32n =5，答：至少需要5名二级技工， 故答案为：5．(1)根据题意列出代数式即可；(2)根据题意列分式方程，解方程即可得到结论；(3)设需要m 名一级技工，需要n 名二级技工，根据题意列方程组即可得到结论． 本题考查了分式方程的应用，一元二次方程组的应用，正确的理解题意是解题的关键．19.答案：(1)证明：∵∠PGB =∠EHP =∠BPE =90°，∴∠PBG +∠GPB =∠GPB +∠EPH =90°， ∴∠PBG =∠EPH(同角的余角相等)， ∴△PGB∽△EHP ； 解：(2)连接BE ，∵PE⊥PB，∴∠BPE=90°，∵∠BCE=90°，∴∠BCE+∠BPE=180°，∴P，B，E，C四点共圆，∴∠PBE=∠PCE，在Rt△BPE与Rt△CDA中，∠BPE=∠D=90°，∠PBE=∠ACD，∴Rt△BPE∽Rt△CDA，∴PEAD =PBDC，即PEPB =ADDC=34；(3)方法一：设AP的长为x．∵BC=AD=3，AB=4，∴Rt△ABC中，由勾股定理可得：AC=√AB2+BC2=√32+42=5，∵cos∠GAP=AGAP =ABAC=45，∴AG=45AP=45x.同理，sin∠GAP=GPAP =BCAC=35，则GP=35x.在Rt△PBG中，PB2=BG2+PG2=(4−45x)2+(35x)2=x2−325x+16，∵PEPB =ADDC=34．∴PE=34PB，∴S 矩形BPEF =PB ⋅PE =34PB 2=34(x 2−325x +16)=34(x −165)2+10825，∵0<x <5， ∴x =165时，S 有最小值10825． 方法二：设BP =x ，x >0，由(2)得PE =34PB =34x ， ∴矩形BPEF 的面积为S =34x 2，由二次函数性质可知x >0时，S 随着x 的增大而增大， ∴，当x ，即BP 取最小值时，矩形BPEF 的面积S 取得最小值， 由题可知P 在对角线AC 上移动，(不与A 、C 重合)， ∴当BP ⊥AC 时，BP 最短，(垂线段最短)， 此时Rt △ABC 中，AB =4，BC =3，∴AC =5， ∴S △ABC =12AB ·BC =12AC ·BP ， BP =AB·BC AC=3×45=125，∴矩形BPEF 的面积S 的最小值为34×(125)2=10825．解析：本题考查了相似综合题，需要掌握矩形的性质、相似三角形的判定和性质、勾股定理、锐角三角函数以及二次函数等知识；熟练掌握矩形的性质和勾股定理，证明三角形相似是解决问题的关键．(1)由∠PGB =∠EHP =∠BPE =90°，利用同角的余角相等证得∠PBG =∠EPH ，即可证得结论； (2)证得P 、B 、E 、C 四点共圆，即可得∠PBE =∠PCE ，即可证得△BPE∽△CDA ，通过相似三角形相似比即可得解；(3)方法一：设AP =x ，利用锐角三角函数定义表示出AG 、GP 、GB ，进而利用勾股定理用x 表示出PB 2，根据矩形面积公式得出二次函数，再利用二次函数的性质求最值，即可解决问题． 方法二：设PB =x ，则矩形BPEF 的面积为S =34x 2，可知当BP ⊥AC 时PB 取得最小值，则S 取得最小值，利用等面积法求出此时的PB 长，即可得解．20.答案：解：设1+2+3+⋯+n =100a +10b +c ，由题意可知：b =0，c =3， 即1+2+3+⋯+n =100a +3，∵1+2+3+⋯+n =n(n+1)2，∴n(n+1)2=100a +3，∴n(n +1)=200a +6，∵两个连续的自然数相乘，个位数为6的只有自然数的个位是2和3或7和8． ∴n 的个位数可能是2，7， 当n =12时，n(n+1)2=78(不合题意，舍去)， 当n =17时，n(n+1)2=153(不合题意，舍去)， 当n =22时，n(n+1)2=253(不合题意，舍去)， 当n =27时，n(n+1)2=378(不合题意，舍去)， 当n =32时，n(n+1)2=528(不合题意，舍去)， 当n =37时，n(n+1)2=703(不合题意，舍去)．∴n 最小的值是37．解析：首先设1+2+3+⋯+n =100a +10b +c ，根据题意可得b =0，c =3，又由1+2+3+⋯+n =n(n+1)2，可得n(n +1)=200a +6，由两个连续的自然数相乘，可得n 的个位数可能是2，7，然后分类讨论即可求得答案．此题考查了数的十进制问题．此题难度较大，注意由题意得到n 的个位数可能是2，7是解此题的关键，注意分类讨论思想的应用．21.答案：解：(1)∵点A(−2,4)在反比例函数y 2=k′x 的图象上，∴k′=−2×4=−8，∴反比例函数解析式为y 2=−8x ．B 在反比例函数y 2=−8x 的图象上，且点B 的横坐标为−4，∴点B 的坐标为(−4,2)．将A(−2,4)、B(−4,2)代入y 1=kx +b ， {−2k +b =4−4k +b =2，解得：{k =1b =6， ∴直线AB 的解析式为y =x +6．(2)过点B作BD//x轴交OA于点D，如图所示．设直线OA的解析式为y=mx，将A(−2,4)代入y=mx，4=−2m，解得：m=−2，∴直线OA的解析式为y=−2x．且BD//x轴，点B与点D纵坐标相同，B(−4,2)，∴点D的坐标为(−1,2)，∴BD=−1−(−4)=3．∴S△AOB=S△ABD+S△OBD=12×3×(4−2)+12×3×(2−0)=6．(3)观察函数图象可知：当−4<x<−2时，一次函数图象在反比例函数图象上方，∴当y1>y2时，x的取值范围为−4<x<−2．解析：(1)由点A的坐标利用反比例函数图象上点的坐标特征即可得出反比例函数解析式，由点B的横坐标结合反比例函数图象上点的坐标特征即可得出点B的坐标，再根据点A、B的坐标利用待定系数法即可求出一次函数解析式；(2)过点B作BD//x轴交OA于点D，由点A的坐标利用待定系数法即可求出直线OA的解析式，结合点B的坐标即可得出点D的坐标，再根据三角形的面积公式即可求出△AOB的面积；(3)观察函数图象，根据两函数图象的上下位置关系即可得出当y1>y2时x的取值范围．本题考查了反比例函数与一次函数的交点问题、反比例(一次)函数图象上点的坐标特征、待定系数法求一次函数解析式以及三角形的面积，解题的关键是：(1)根据点的坐标利用待定系数法求出函数解析式；(2)利用分割图形求面积法求出△AOB的面积；(3)根据函数图象的上下位置关系找出不等式的解集．22.答案：解：∵四边形ABCD是正方形，∴AB=BC=CD=AD，∠A=∠B=∠C=∠D=90°．∵AE=AH=CF=CG，∴BE=BF=DG=DH，∴△AHE，△BEF，△CGF，△DCH都是等腰直角三角形；∴设AE=x米，则BE=(100−x)米．设四边形EFGH的面积为S，则S=100×100−2×12x2−2×12(100−x)2=−2x2+200x(0<x<100)．∵S=−2(x−50)2+5000．∵−2<0，当x=50时，S有最大值为5000．答：当AE=50米时，市民健身活动场所的面积达到最大．解析：根据正方形的性质得到AB=BC=CD=AD，∠A=∠B=∠C=∠D=90°推出△AHE，△BEF，△CGF，△DCH都是等腰直角三角形；设AE=x米，则BE=(100−x)米．设四边形EFGH的面积为S，根据图形的面积公式即可得到结论．本题考查了二次函数的应用，正方形和矩形的性质，等腰直角三角形的性质，图形的面积的计算，二次函数的性质，正确的识别图形是解题的关键．23.答案：解：(1)设⊙O的半径OA=r，则OD=CD−OC=8−r．∵OD⊥AB，∴∠ADO=90°．∵在Rt△AOD中，sin∠A=ODOA =35．∴8−rr =35．解得：r=5，∴OA=5，OD=3．利用勾股定理，得：AD=√OA2−OD2=4，∵OD⊥AB，O为圆心，∴AB=2AD=8；(2)∵CE⊥AO，∴∠AFE=∠CDE=90°．∴∠A+∠E=90°，∠C+∠E=90°，∴∠A=∠C，又∵∠ADO=∠CDE=90°，∴△AOD∽△CED．∴S△AODS△CDE =AD2CD2=14，∵S△ACD=12AD⋅OD=12×4×3=6，∴S△CDE=4S△ACD=24．解析：(1)首先设⊙O的半径OA=r，那么OD=8−r.由OD⊥AB，得∠ADO=90°.于是由在Rt△AOD中，sin∠A=ODOA =35，可得8−rr=35.继而求得r的长，然后由垂径定理，求得弦AB的长；(2)易证得△AOD∽△CED，然后由相似三角形面积的比等于相似比的平方，求得△CDE的面积．。

2021-2022中考数学模拟试卷注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）1．若实数m 满足22210⎛⎫++= ⎪⎝⎭m m ，则下列对m 值的估计正确的是（ ） A ．﹣2＜m ＜﹣1 B ．﹣1＜m ＜0 C ．0＜m ＜1 D ．1＜m ＜22．2017上半年，四川货物贸易进出口总值为2 098.7亿元，较去年同期增长59.5%，远高于同期全国19.6%的整体进出口增幅．在“一带一路”倡议下，四川同期对以色列、埃及、罗马尼亚、伊拉克进出口均实现数倍增长．将2098.7亿元用科学记数法表示是（ ）A ．2.098 7×103B ．2.098 7×1010C ．2.098 7×1011D ．2.098 7×10123．为了尽早适应中考体育项目，小丽同学加强跳绳训练，并把某周的练习情况做了如下记录：周一(160个)，周二(160个)，周三(180个)，周四(200个)，周五(170个).则小丽这周跳绳个数的中位数和众数分别是( ) A ．180个，160个B ．170个，160个C ．170个，180个D ．160个，200个4．在方格纸中，选择标有序号①②③④中的一个小正方形涂黑，与图中阴影部分构成中心对称图形．该小正方形的序号是（ ）A ．①B ．②C ．③D ．④5．已知e 是一个单位向量，a 、b 是非零向量，那么下列等式正确的是（ ）A ．a e a =B ．e b b =C ．1a e a =D ．11a b a b= 6．点A(x 1，y 1)、B(x 2，y 2)、C(x 3，y 3)都在反比例函数3y=x -的图象上，且x 1＜x 2＜0＜x 3，则y 1、y 2、y 3的大小关系是（ ）A ．y 3＜y 1＜y 2B ．y 1＜y 2＜y 3C ．y 3＜y 2＜y 1D ．y 2＜y 1＜y 37．改革开放40年以来，城乡居民生活水平持续快速提升，居民教育、文化和娱乐消费支出持续增长，已经成为居民各项消费支出中仅次于居住、食品烟酒、交通通信后的第四大消费支出，如图为北京市统计局发布的2017年和2018年我市居民人均教育、文化和娱乐消费支出的折线图．说明：在统计学中，同比是指本期统计数据与上一年同期统计数据相比较，例如2018年第二季度与2017年第二季度相比较；环比是指本期统计数据与上期统计数据相比较，例如2018年第二季度与2018年第一季度相比较．根据上述信息，下列结论中错误的是（）A．2017年第二季度环比有所提高B．2017年第三季度环比有所提高C．2018年第一季度同比有所提高D．2018年第四季度同比有所提高8．如图，A、B、C是⊙O上的三点，∠B=75°，则∠AOC的度数是（）A．150°B．140°C．130°D．120°9．某城市几条道路的位置关系如图所示，已知AB∥CD，AE与AB的夹角为48°，若CF与EF的长度相等，则∠C 的度数为（）A．48°B．40°C．30°D．24°10．如图1所示，甲、乙两车沿直路同向行驶，车速分别为20 m/s和v(m/s)，起初甲车在乙车前a (m)处，两车同时出发，当乙车追上甲车时，两车都停止行驶．设x(s)后两车相距y (m)，y与x的函数关系如图2所示．有以下结论：①图1中a的值为500；②乙车的速度为35 m/s；；③图1中线段EF应表示为5005x④图2中函数图象与x轴交点的横坐标为1．其中所有的正确结论是（）A．①④B．②③C．①②④D．①③④二、填空题（共7小题，每小题3分，满分21分）11．把直线y＝－x＋3向上平移m个单位后，与直线y＝2x＋4的交点在第一象限，则m的取值范围是_________________.12．如图，正方形ABCD中，E是BC边上一点，以E为圆心，EC为半径的半圆与以A为圆心，AB为半径的圆弧外切，则sin∠EAB的值为．13．已知一次函数y＝ax+b，且2a+b＝1，则该一次函数图象必经过点_____．14．在由乙猜甲刚才想的数字游戏中，把乙猜的数字记为b且，a，b是0，1，2，3四个数中的其中某一个，若|a﹣b|≤1则称甲乙”心有灵犀”．现任意找两个人玩这个游戏，得出他们”心有灵犀”的概率为_____．15．如果关于x的方程x2+2ax﹣b2+2=0有两个相等的实数根，且常数a与b互为倒数，那么a+b=_____．16．平面直角坐标系中一点P（m﹣3，1﹣2m）在第三象限，则m的取值范围是_____．17．分解因式：m2n﹣2mn+n= ．三、解答题（共7小题，满分69分）18．（10分）如图，在△ABC中，∠ACB=90°，BC的垂直平分线DE交BC于D，交AB于E，F在DE上，且AF=CE=AE．（1）说明四边形ACEF是平行四边形；（2）当∠B满足什么条件时，四边形ACEF是菱形，并说明理由．19．（5分）观察下列等式：①1×5+4=32；②2×6+4=42；③3×7+4=52；…（1）按照上面的规律，写出第⑥个等式：_____；（2）模仿上面的方法，写出下面等式的左边：_____=502；（3）按照上面的规律，写出第n个等式，并证明其成立．20．（8分）如图，△ABC是⊙O的内接三角形，AB是⊙O的直径，OF⊥AB，交AC于点F，点E在AB的延长线上，射线EM经过点C，且∠ACE+∠AFO=180°.求证：EM是⊙O的切线；若∠A=∠E,BC=3，求阴影部分的面积.（结果保留 和根号）.21．（10分）问题探究(1)如图①，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，则线段BE、EF、FD之间的数量关系为；(2)如图②，在△ADC中，AD=2，CD=4，∠ADC是一个不固定的角，以AC为边向△ADC的另一侧作等边△ABC，连接BD，则BD的长是否存在最大值？若存在，请求出其最大值；若不存在，请说明理由；问题解决(3)如图③，在四边形ABCD中，AB=AD，∠BAD=60°，2，若BD⊥CD，垂足为点D，则对角线AC的长是否存在最大值？若存在，请求出其最大值；若不存在，请说明理由．22．（10分）计算：2sin30°﹣（π﹣2）0+|3﹣1|+（12）﹣123．（12分）如图，在等边△ABC中，点D是AB边上一点，连接CD，将线段CD绕点C按顺时针方向旋转60°后得到CE，连接AE．求证：AE∥BC．24．（14分）如图,已知□ABCD的面积为S，点P、Q时是▱ABCD对角线BD的三等分点，延长AQ、AP，分别交BC，CD于点E，F，连结EF。

合肥包河四十八分校2023-2024学年八上月考预测物理作业试卷（含答案）本卷沪科版2.1～2.4、共4页四大题25小题，满分100分，时间90分钟一、填空题（每空2分，共32分）1、完整的科学探究方法应该包括提出问题、设计实验与制定计划、进行实验与收集证据、分析与论证、评估、交流与合作等七个环节．2、某次测量如图所示，被测物体的长度是 m．分度值是 cm．第 2 题第 3 题第 4 题第 5 题3、如图所示神舟七号载人飞船进入运行轨道后，飞行员翟志刚出舱进行了中国人第一次太空漫步，若以地球为参照物，翟志刚是的。

（选填“运动”或“静止”）4、甲乙两辆车同时向西行驶，它们的s-t图象如图所示，若以甲车为参照物，乙车向（选填“东”或“西”）行驶，甲、乙两车的速度之比为。

5、在研究气泡运动规律的实验中，小明每隔10s记录的气泡位置如图所示，则气泡上升时速度大小的变化情况是（填“一直变大”、“一直变小”或“先变大后不变”）；小明用刻度尺测出A、B间的距离s=80cm，则气泡通过AB段的平均速度v= m/s．6、向同一方向运动，它们运动的图象如图所示，由图象可知，运动速度相同的两是；经过5s跑在最前面的与紧跟其后的相距米。

第 6 题第 7 题7，小明在马路边上拍街景照片，先后连续拍了两张照片，如图甲、乙所示，若以卡车为参照物，则小汽车是向运动的，自行车是向运动的（两空均填“左”或“右”）8、做匀速直线运动的甲、乙两个物体，他们通过的路程之比是3：2，所用的时间之比是2：3，则他们的速度之比是。

9、小刚测得班上同学小丽的一组数据，但忘了写上单位，请你帮忙补上：正常步行的速度是4.1 ；它所表示的物理意义是。

10、小明在上学的路上，先以υ1的速度走完前一半路程，又以υ2走完后一半路程，则他在上学的全程中平均速度为二、选择题（本大题10小题，每小题3分，满分30分）11、由匀速直线运动公式svt可知，匀速直线运动的速度（）A．速度与路程成正比 B．速度与时间成正比C．速度随路程和时间的变化而变化 D．速度与路程和时间无关12、下列关于运动和静止的说法正确的是（）A．地球同步卫星围绕地球飞行，以地面为参照物，卫星是运动的B.飞机在空中加油时，以地面为参照物，受油机是静止的，C．卡车和联合收割机收割庄稼时，它们是相对运动的，D．“天宫一号”与“神州八号”对接成功时，它们是相对静止的。

安徽省合肥市第四十八中学2022-2023学年八年级上学期期中考试数学试卷学校:___________姓名：___________班级：___________考号：___________一、单选题．．C．．．如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知添加以下的哪个条件仍不能判定△ABE≌△ACDA ．∠B =∠C B ．AD =AE C ．BD =CE D ．BE =CD 7．在平面直角坐标系中，将直线y ＝kx ﹣6沿x 轴向左平移3个单位后恰好经过原点，则k 的值为（）A ．﹣2B ．2C ．﹣3D ．38．已知等腰三角形的周长为19，一边长为8，则该等腰三角形的腰长为（）A ．3B ．8C ．3或8D ．8或5．59．如图所示，一次函数y kx b =+（k ，b 是常数，且0k ≠）与正比例函数y mx =（m 是常数，且0m ≠）的图象相交于点()1,2M ，下列判断不正确的是（）A ．关于x 的方程mx kx b =+的解是1x =B ．关于,x y 的方程组00mx y kx y b -=⎧⎨-+=⎩的解是12x y =⎧⎨=⎩C ．当0x <时，函数y kx b =+的值比函数y mx =的值大D ．关于x 的不等式()m k x b ->的解集是1x <10．如图，已知在 ABC 中，AB ＝AC ，点D 沿BC 自B 向C 运动，作BE ⊥AD 于E ，CF ⊥AD 于F ，则BE +CF 的值y 与BD 的长x 之间的函数图象大致是（）A ．B ．C ．D ．二、填空题11．已知点(1,3)P a a +-在y 轴上，则a 等于_______．12．已知三角形的三个外角的度数比为2:3:4，则它的最大内角的度数为______．13．如图，AB CD ⊥，且AB CD =．E 、F 是AD 上两点，,CE AD BF AD ⊥⊥．若6,3,2CE BF EF ===，则AD 的长为_____．14．直线23y kx k =-+恒过一定点，则该点的坐标是______．平面直角坐标系中有三点(1,0),(2,3),(5,0)A B C -，若该直线23y kx k =-+将ABC 分成左右面积之比为1∶2的两部分，则k 的值是_______．三、解答题15．已知点(2,28)P a a -+，请分别根据下列条件求出点P 的坐标：(1)点Q 的坐标为(1,5)，直线PQ y ∥轴；(2)点P 到x 轴、y 轴的距离相等．16．已知2y -与4x +成正比例，且当2x =时5y =．(1)求y 与x 之间的函数解析式；(2)若点(),3M a -在这个函数的图象上，求a 的值．17．在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形顶点是网格线的交点的三角形）ABC 的顶点A ，C 的坐标分别为()4,5-，(1,3)-．(1)请在如图所示的网格内作出的面积；(2)求出ABC先向下平移(3)请作出将ABC18．如图，点D在AB上，点(1)画出A，B，C三点并求直线AB的解析式；(1)点B的坐标为________，点C表示的实际意义是________；(2)求S甲的函数表达式，并注明自变量的取值范围；(3)若用S乙表示乙距出发点的路程s与x之间的关系，请在图②中画出S乙的图象．。

2022-2023学年八上物理期末模拟试卷注意事项：1．答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。

2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。

3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、单选题1．下列数据最接近实际的是（）A．适宜学习的环境应控制噪声不超过90dBB．正常人的体温为39 ℃C．正常人安静状态下心跳一次时间约0.9sD．人正常步行速度约5m/s2．质量和体积都相同的三个空心球，它们的材料分别是铝、铜和铅，则空心部分最大的是（）A．铝球B．铜球C．铅球D．无法判断3．人类在新材料探索的道路上总在进行着不懈的努力．世界上密度最小的固体“气凝胶”就是新材料探索的重要成果．该物质的坚固耐用程度不亚于钢材，且能承受1400℃的高温，而密度只有1kg/m1．一架用钢材（ρ钢=7、9×101kg/m1）制成的质量约160吨的大型飞机，如果用“气凝胶”做成，其质量相当于（）A．一片鸡毛的质量B．一只鸡蛋的质量C．一个成年人的质量D．一台大卡车的质量4．要想尽可能准确地一次性测出100g密度为0.8×103kg/m3的某种油的体积，请从以下给定的量筒中选出你认为最适当的量筒（）A．50mL，5mL B．100mL，2mLC．250mL，5mL D．500mL，10mL5．“安全用电，珍惜生命”是每个公民应有的意识，下列有关安全用电的说法正确的是A．有时可在电线上晾晒衣服B．手机充电器可以永久插在电源插座上C．在未断开电源的情况下更换灯泡D．发现有人触电时应先切断电源再施救6．元旦文艺晚会结束后班主任组织照合影，摄影师发现最边上的几位同学没有进入取景框内，下列关于摄影师的做法正确的是（）A．照相机靠近同学，镜头向前伸B．照相机靠近同学，镜头向后缩C．照相机远离同学，镜头向前伸D．照相机远离同学，镜头向后缩7．如图是太阳能无人机Aquila，它使用碳纤维制造以减轻重量，主要利用了碳纤维的（）A．硬度大B．密度小C．易导电性D．可塑性强8．沿同一条直线向同一方向运动的物体甲、乙，运动时相对同一参考点O的距离s随时间t变化的图象如图示。

2025届安徽合肥包河区四十八中学物理八年级第一学期期末检测试题注意事项1．考生要认真填写考场号和座位序号。

2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。

第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。

3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、选择题1．平静的明湖湖面上映出了正在空中飞翔的一只小鸟，正在湖边散步的小红说：“快来看，小鸟和鱼在水中比赛呢！”她看到的“鸟”和“鱼”实际上是（）A．鱼和鸟都是虚像B．鸟是虚像，鱼是实像C．鱼和鸟都是实像D．鸟是实像，鱼是虚像2．一瓶矿泉水喝掉一半后，剩余水的（）A．密度变小，体积变小，质量变小B．密度不变，体积变小，质量变小C．密度不变，体积不变，质量变大D．密度变小，体积变小，质量变大3．下列措施中，能使蒸发减慢的是A．用干手器将手上的水吹干B．把湿衣服晾在通风向阳处C．用扫把将地面上的水扫开D．把新鲜的樱桃装入保鲜盒放在冰箱内4．学生使用的橡皮，用过一段时间后，没有发生变化的是（）A．形状B．质量C．密度D．体积5．如图是一种沙漠里能收集空气中水分的甲虫．清晨，空气中水蒸气含量高，甲虫从洞穴中走出爬上沙丘，迎着风整个身体呈倒立的姿势，很快空气中的水蒸气在背部凝结成水珠，水珠越聚越多，顺着背部流入甲虫的嘴里．科学家利用该原理制造了沙漠集水器，实现沙漠淡水的补给，能让沙漠变成一块块绿洲．甲虫能收集到空气中的水蒸气，说明它背部的温度比外界气温A．一定高B．一定低C．一定相同D．无法确定6．如图所示的图象中，描述的是同一种运动形式的是（）A．A与B B．A与C C．C与D D．B与C7．将规格都是“220 V 180 W”的一台电冰箱、一台电风扇和一床电热毯，分别接入同一家庭电路中，若通电时间相同，则产生热量最多的是A．电冰箱B．电风扇C．电热毯D．一样多8．有一支用过后未甩的体温计，其示数为39℃。

用这支体温计先后去测两个体温分别是38℃和40℃的病人的体温，体温计显示的示数分别是（）A．38℃，39℃B．39℃，40℃C．38℃，40℃D．39℃，38℃9．下列物体中属于光源的是A．平面镜B．月亮C．放电影时看到的银幕D．收看电视时看到的电视机屏幕10．下图中所列仪器不是用来测量物体长度的是（）A．卷尺B．游标卡尺C．千分尺D．机械停表11．分别用两个完全相同的“热得快”，同时给质量和温度相同的A、B两种液体加热，它们的温度随时变化的图像如图所示，则两种液体的比热大小应是（）A ．c A = cB B ．c A >c BC ．c A <c BD ．无法确定12．一个瓶子正好能装满1kg 的水，它一定能装下1kg 的（ ）（ρρρρ<<<酒油水酱油） A ．酱油 B ．花生油C ．白酒D ．茶籽油二、填空题13．冬天，0℃以下冰冻的衣服也会干，这是_________现象；寒冷的冬夜，门窗玻璃_______（选填“内”或“外”）侧出现冰花，这是_________现象，这个过程需要_________热量．14．为了保护环境，北京市城区冬季取暖锅炉房不许烧煤，改烧油或气。