当前位置：文档之家 › 高等数学中两个重要极限

高等数学中两个重要极限

  • 格式：ppt
  • 大小：1.00 MB
  • 文档页数：64

下载文档原格式

  / 64

合集下载

两个重要极限

两个重要极限

高等数学 两个重要极限 (Two important limits)
advanced mathematics
sin x 1. lim =1 x0 x
1 0.75 0.5 0.25
f ( x)
5
s i nx x
10 15
-15
-10
-5
o
-0.25 -0.5
高等数学 两个重要极限 (Two important limits)
例10
解
求极限
2x 3 x lim( ) . x 2 x 1
2x 3 x 2 l i m( ) l i m(1 )x x 2 x 1 x 2x 1
2 x 1 2 x 2 2 x 1
2 lim(1 ) x 2x 1
2 lim(1 ) x 2x 1
2 x 1 1 2 2
e
2x x 2 x 1 lim
e.
2 (1 ) 2x 1 lim 1 x 2 2 (1 ) 2x 1
2 x 1 2
e.
高等数学
advanced mathematics
3 1 另解: 2x 3 x 2x )x l i m( ) l i m( x 2 x 1 x 1 1 2x 3 x 3 x l i m(1 ) (1 ) x 2x 2 x lim x 1 x 1 x l i m(1 ) (1 ) x 2x 2x


4x 1 5 x
解
4 2 (2)求 lim(1 ) x 3x 3x 3x 4 2 4 4 2 e2 lim(1 ) lim(1 ) x x 3x 3x
e .3 x

两个重要极限

两个重要极限

x
元
。
现在若以天为单位计算复利，则x年末资金变为：
Q
1
r 365
365
x
元
；
若以
1 n
年为单位计算复利，则x年末末资金变为：Q
1
r n
nx
元
；
若令 n ，即每时每刻计算复利（称为连续复利）则x年末末资金为：
lim
n
Q
1
r n
nx
=
Q
lim
n
1
r n
n r
rx
=Q erx 元 。
高等数学
或若
lim
xa
x
0
a可以是有限数x 0
， ，
则
1
1
x
x
lim1 x lim 1 x e 。
xa
x0
例1.5 求
lim
x
1
2 x
x
。
解 令 2 t ，则 x 2 当 x 时 t 0 ，于是
x
t
lim
x
1
2 x
x
lim t0
1 t
2 t
ltim0
1 t
1 2 t
x0 x
t0 sint
两个重要极限
1.2 第二个重要极限：
lim
x
1
1 x
x
e
注意：这个重要极限也可以变形和推广：
(1) 令 1，则t x
时 x 代入后得t 到 0
1
lim1 t t
t0
e
；
(2) 若limxa Nhomakorabeax
a可以是有限数x 0
， ， 则

高等数学极限存在准则

高等数学极限存在准则

x x0 ( x )
x x0 ( x )
那末 lim f ( x)存在, 且等于A. x x0 ( x)
A
A
A
（（ 1 x0
y h( x) y f (x) y g(x)
x0
）） 2
x0
准则 Ⅰ和准则 Ⅰ'称为夹逼准则. 问题: 1. 怎样使用数列夹逼准则？
回答：关键是构造数列 yn和 zn，使得对于一切正整
于是有sin x BD, x 弧 AB, tan x AC,
sin x x tan x, 即 cos x sin x 1, x
上式对于 x 0也成立. 2
当 0 x 时,
2
0 cos x 1 1 cos x
2sin2 x 2
2( x)2
x2 ,
22
lim x 2 0, lim(1 cos x) 0,
x x
3. lim xsin 1 _0___ ;
x0
x
作业
2. lim xsin 1 __1__ ;
x
x
4. lim (1 1)n _e___1;
n n
P55 1 (4)，(5)，(6) ; 2 (2)，(3)，(4) ; 4 (4) , (5)
第七节 目录 上页 下页 返回 结束
xn
存在.
xn1
3 xn ,
xn21 3 xn ,
lim
n
x2 n1
lim(3
n
xn ),
A2 3 A, 解得 A 1 13 , A 1 13 (舍去)
2
2
lim n
xn
1
2
13 .
二、两个重要极限
(1) lim sin x 1 x0 x

高数两个重要极限的使用条件

高数两个重要极限的使用条件

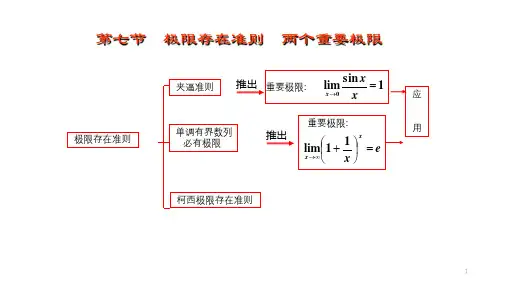
高数两个重要极限的使用条件在高等数学的世界里，有两个极限可以说是超级明星，走到哪里都能吸引目光。

没错，就是那个著名的“1 + 1/n”极限和“sin(x)/x”极限。

这两个小家伙就像数学界的老友记，无论你是刚入门的小白，还是资深的高数玩家，它们都能在你的学习旅程中起到意想不到的作用。

首先说说“1 + 1/n”这个极限。

每当n趋近于无穷大时，1 + 1/n就像小猫咪一样，温柔地挤进了1这个温暖的怀抱。

你说，这个极限有什么用呢？它可不光是用来秀个数学公式的。

想象一下，做一些概率统计的时候，尤其是涉及到大数法则的情况。

你会发现，这个极限像个老实巴交的邻居，总是能在你需要的时候出现，给你一种踏实感。

记得有一次我在做统计的时候，老是搞不明白一个复杂的分布。

结果一看，这个极限就像闪电一样击中了我！它告诉我，随着样本数量的增加，样本均值会越来越接近于真实均值。

这种感觉，真是爽得不要不要的，简直像喝了冰镇饮料一样清爽！再说说“sin(x)/x”这个极限。

它的神奇之处在于，不管你把x带到哪里，它总是默默地在0这个点上守护着自己。

想象一下，有一个忠诚的小狗，走到哪儿都跟着你，无论风雨。

这可不是普通的小狗，它可以随着x的变化而变化，但只要x接近0的时候，它就是1！在信号处理和物理学中，这个极限就像一位超级英雄，救你于水深火热之中。

比如说，在进行傅里叶变换的时候，这个极限就像那把钥匙，帮你打开了通往频域的大门。

没错，有时候这就是数学的魅力，越复杂的公式，背后越简单的道理。

常常会有人说，高数就是一个大海，深不可测，似乎总是有些波澜起伏。

但偶尔跳出水面的，不就是这两个极限吗？它们用自己简洁的形式告诉你：别怕，数学其实也可以很简单。

应用这两个极限的时候，你一定要注意一些小细节。

就好比在吃火锅的时候，千万别把调料放得太多，不然就太咸了，影响口感。

同样，使用极限的时候，要确保满足它们的使用条件。

否则，你可能会像往火锅里放盐一样，得不偿失。

高等数学中的两个重要极限

高等数学中的两个重要极限
x
1 x lim (1 ) ? x x
1000 10000 100000 …
2.717 2.718
-1000 -10000
2.71827
-100000 …
X
x
-10
-100
1 2.868 2.732 (1 ) x
2.720 2.7183
2.71828
1 x lim (1 ) e x x
sin t 所以 , 原式 5lim 5 1 5 t 0 t
注：在运算熟练后可不必代换，直接计算：
sin 5 x sin 5 x lim 5lim 5 1 5 x 0 x 0 5x x
推广： 设 为某过程中的无穷小量 ,
某过程
lim
sin

1
练习1. 求下列极限:
x 0 u0
u0
2 x

2 u
1 u 2
lim[(1 u) ]
[lim(1 u) ]
u0 1 u 2
e 2
方法二 掌握熟练后可不设新变量
lim 1 x lim[(1 x ) ]2
x 0 x 0 1 x 2 2 x
1 x
[lim(1 x )
O x B
C D A
sin x lim 1. ＋ x 0 x
tan x 例 1 求 lim x0 x tan x sin x 1 解 lim lim( ) x 0 x 0 cos x x x sin x 1 lim( ) x 0 x cos x sin x 1 lim lim x 0 x 0 cos x x
当 x 时 1 0 且 | sin x | 1 x

高等数学 第1章 第七节 极限存在准则 两个重要极限

高等数学 第1章 第七节 极限存在准则 两个重要极限

则
lim
n
x n1
lim n
6 xn ,
A
6 A,
解得 A 3或A 2,（舍去）
lim n
xn
3.
14
3.两个重要极限的应用
例6： 求 lim tan x 1
x0 x
可作为公式
lim
x
s
in u x ux
1
lim ux 0
x
解： lim tan x lim sin x 1 lim sin x lim 1 11 1 x0 x x0 x cos x x0 x x0 cos x
1 n2 1
n2
1
22
n2
1
n2
n n2 1
,
1
lim 1 0, n 2n
lim n n n2 1
lim n
n
1
1
由夹逼定理知：
n2
0 0, 10
lim n
n
1 2
1
n2
1 22
n2
1 n2
存在, 且
lim n
n
1 2
1
n2
1
22
n2
1
n2
0.
8
例2 用夹逼准则证明：
lim sin x 1.
1yn xn zn n 1,2,3,,
2
lim
n
yn
a,
lim
n
z
n
a,
则数列x
n
的
极
限
存
在,
且
lim
n
xn
a.
准则1 若
1当x
U
x

大一高等数学 第一章第六节 极限存在准则 两个重要极限

大一高等数学 第一章第六节 极限存在准则 两个重要极限

lim f (x) A
(
x x
x0 )
( 利用定理1及数列的夹逼准则可证 )
二、 两个重要极限证:Leabharlann 当x(0,
π 2
)
时，
△AOB 的面积＜
圆扇形AOB的面积
BD
1
x O
C
A
＜△AOD的面积
即 亦故即有 显然有
1 2
sin
x
1 2
tan
x
sin x x tan x
(0
x
π 2
)
cos x sin x 1 x
有
lim
n
f
(xn
)
A.
法1 找一个数列
xn x0 ,
使
lim
n
f
(xn
)
不存在
.
法2 找两个趋于
的不同数列 xn 及 xn , 使
lim
n
f
(xn )
lim
n
f
(xn )
例1. 证明
不存在 .
证: 取两个趋于 0 的数列
xn
1 2n π
及
xn
1 2n π
π 2
(n 1, 2,)
有 lim sin 1 lim sin 2n π 0 n xn n
3. lim xsin 1 __0__ ;
x0
x
2. lim xsin 1 _1___ ;
x
x
4. lim (1 1)n _e__1_; n n
作业
P56 1 (4)，(5)，(6) ;
(4) ;
2
(2)，(3)，
4
(4) , (5)

高等数学1.6极限存在准则、两个重要极限

高等数学1.6极限存在准则、两个重要极限

二、两个重要极限
例4
1 cos x 求 lim . 2 x0 x
2 x x 2 sin 2sin 2 1 lim 2 解 原式 lim 2 x 0 2 x x 0 x 2 2 2
0 0
sin x lim 1 x 0 x
lim cos x 1,
x 0
x x0 x x0
lim f ( u ) A， 则 lim f [ g ( x )] A lim f ( u )
u a
证明
lim(1 x ) e
x 0
1 x
x x0 1 x
u a
1 1 令 x , lim(1 )t ＝ lim(1 x ) t t t x0
x x0 ( x ) x x0 ( x )
f ( x) lim h( x ) A, 那末 xlim x
( x)
0
存在, 且等于 A 上述两准则称为两边夹准则.
例1 求 lim( n 解：
1 n 1
2

1 n 2
2

1 n n
2
).
n n n
2
n
x 1 sin x 1, cos x 1 sin x cos x x
A
下面证 lim cos x 1,
x0
2 x x x 2 2 1 cos x 2 sin 2( ) , 2 2 2
0 cos x 1 x2 lim 0, lim(1 cos x ) 0, x0 x0 2 sin x lim cos x 1, lim1 1, lim x 0 x0 x0 x
(2)
1 x lim (1 ) e x x

高教社2024高等数学第五版教学课件-1.3 两个重要极限

高教社2024高等数学第五版教学课件-1.3 两个重要极限
则若有函数()在0 的某邻域内恒有
() ≤ () ≤ ()，
那么当 → 0 时，有 ≤ () ≤ ()，
即
故
≤ () ≤ ，
() = .
→0
= 1.
(−)
证：因为
−
−
−

=
=
，

所以我们只需讨论 → 0+ 的情形，

→∞
→∞ 2 + 1
1+
= 1 +
→∞
方法二
2 + 3

→∞ 2 + 1
=
2
2+1
2
2+1
3
1+
2
=
1
→∞
1+
2
+1

→∞

→∞
1+
1+
3
2
1
2
2 3
3 ×2
1
2×2
2+1
2
2+1
2
⋅ 1+
2
2+1
∙ 1 +
→∞
1
2
2
2+1
1
2
= ⋅ 1 = .
+1
∙ 1+
∙ 1+
3
2
1
2
=
3
2
×1
1
2
×1
=


→0
例3 计算
解
≠ 0， ≠ 0）






→0

=

高等数学 第六节 极限存在准则 两个重要极限

高等数学 第六节 极限存在准则 两个重要极限

1 + 2 +⋯+ n < I n 2 2 2 n +n n +n n +n < 1 + 2 +⋯+ n , n2 + 1 n2 + 1 n2 + 1
+ 即 1 + 22 ⋯ + n < In < 1 + 2 + ⋯ + n , n +n n2 + 1
n(n + 1) n(n + 1) < In < , 2 2 2(n + 1) 2(n + n)
n
或 lim(1+ x)
x→0
1 x
=e .
e = 2.7182818284 59045⋯ (无理数 ⋯ )
sin x =1 . 2) . lim x→0 x
弦长 AB = 2 sin x , 弧长 AB = 2 x , 切线长 CD = 2 tan x .
F
A C
x
B
E
D
7
sin x < x < tan x . ( x > 0)
∀ε > 0 , ∃ N1 , 当 n > N1 时, A − ε < yn < A + ε ;
∃ N 2 , 当 n > N 2 时, A − ε < zn < A + ε , 从而 , 当 n > max{ N1 , N 2 } 时 ,
A − ε < yn ≤ xn ≤ z n < A + ε
n→∞
13
uk + uk uk −1 − uk −1 − uk −1uk uk uk−1 = − (1 + uk ) (1 + uk −1 ) 1+ uk 1+ uk−1 uk − uk −1 = > 0 ⇒ uk +1 > uk , { un } 单调增加 . (1 + uk ) (1 + uk −1 )

高等数学 第二章 极限与连续 2.6 两个重要极限

高等数学 第二章 极限与连续 2.6 两个重要极限
sin kx kx k lim sin kx kx
k 1 k .
解： 原式 k lim x 0
kx 0
例4
求
2 sin x
2 2 x 2
解： 原式 lim 例5 求
x 0
sin lim x 2 x 0 2
1
x 2

2

1 2
1
2
解： 令 t
例11
求 x
lim (
x 2
x
2
2
x 1
)
x
x x x x 解： lim ( 2 ) lim lim x x x x 1 x 1 x 1 x 1 x 1
x
x
x
x
1 1 lim 1 1 x x 1 x 1
x,
OAB 的高为 BD ,
于是有
sin x BD ,
tan x AC ,
C
二、两个重要极限
B
(1)
lim
sin x x
x 0
1
0 0
型
x
o
D
A
△AOB 的面积＜圆扇形AOB的面积＜△AOD的面积
即
1 2
sin x

1 2
tan x
(0 x

2

2
sin x x tan x ,
单调减少
定理2.12
准则Ⅱ
单调有界数列必有极限.
几何解释:
m
x1
x 2 x 3x n x n 1
A
M
x
C

高等数学第3章第4节两个重要的极限

高等数学第3章第4节两个重要的极限
（2） （3） 先利用数列极限 证明（2）式成立． 为此，作定义在上的两个阶梯函数如下：
， ，
，
， 易见增（第二章§3习题4）且有上界,减（第二章§3习题9）且有下
界．故据上节习题2， 与皆存在．于是，由归结原则（取）得到
另一方面，当
时有 以及 ，
即有 ，．
从而根据迫敛性，定理（2）式得证． 现证（3）式．为此作代换，则
§４ 两个重要的极限
一、证明 证 如图：由可导出如下不等式
（）． 除以
，得到，由此得
在（１）式中用
代替
时，（１）式不变，故 （１）式当 时也成立，从而它对一切满足不等式 的
都成立． 由 及函数极． 求. 例2． 求. 注：利用归结原则，可求数列极限。如求，直接利用是不严格的； 但已知，故取，则，从而由归结原则. 例3． 求. 二、 证明或. 证 所求证的极限等价于同时成立以下两个极限
， 且当 时，从而有
以后还常用到的另一种极限形式： （4）
事实上，令，则，所以
例1． 求. 例2． 求.
例3． 求.
作业：p58. 1(2), (5), (8), (9), (10) ， 2(1), (3), (5), (6), 3.

《高等数学》两个重要极限

《高等数学》两个重要极限

两个重要极限1.6.1第一重要极限1sin lim0=→xxx几何说明：单位圆中 特征：（1）是“”型极限； （2）无论x 趋于何值，只要0)(→x α，就有1)()(sin lim 0)(=→x x x ααα。

【例1】 求下列极限（1）x x x sin lim0→； （2）x xx tan lim 0→； （3）x x x arcsin lim 0→；（4）x x x 5sin 3tan lim 0→； （5）20cos 1lim x x x -→； （6）203cos cos lim xxx x -→； （7）xx xx x 2sin 2sin lim 0+-→。

解：（1）x xx sin lim0→1sin lim 1sin 1lim 00===→→xxx x x x （2）x x x x x x x cos 1sin lim tan lim 00⋅=→→ 1cos 1lim sin lim 00=⋅=→→x x x x x（3）令t x =arcsin ，，则t x sin =，且0→x 时，0→t ，于是1sin lim arcsin lim 00==→→tt x x t x （4）535sin 5lim 33tan lim 535sin 55333tan lim 5sin 3tan lim 0000=⋅=⋅⋅=→→→→x x x x x x x x x x x x x x（5）220202sin 2limcos 1lim x x x x x x →→=- 2022sin 21lim ⎪⎪⎪⎪⎭⎫ ⎝⎛⋅=→x x x 2112122sin lim 21202=⋅=⎪⎪⎪⎪⎭⎫ ⎝⎛=→x x x （6）4sin 222sin lim 2)sin(2sin 2lim 3cos cos lim 02020=⋅⋅=--=-→→→x xx x xx x x x x x x x （7）31212122sin 2122sin 21lim 2sin 12sin 1lim 2sin 2sin lim000-=+-=⋅+⋅-=+-=+-→→→xx x x x x x x x x x x x x x 注：（1）、（2）的结果可以作为公式使用，同样还有公式：1tan lim0=→xxx 。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
x
X -10 -100
(1 1 ) x 2.868 2.732 x
-1000 -10000
2.720 2.7183
-100000 …
2.71828
li( m 11)xe x x
li(m 11)xe (1 )
x x
令t 1,
lim (1
1
)
x
lim(1
1
t)t
e
x x
x
t 0
1
lim(1 t)t e (1 )
1 x 1 ,
sinx coxs
CD
即coxs sinx1. x
sin x lim 1.
x x0＋
Ox BA
例 1 求 lim tan x x 0 x
解
limtanxlim (sinx1)
x 0 x x 0 cosx x
sinx 1 lim( )
x0 x cosx
limsinxlim 1 x0 x x0 cosx
0.001 …. 0.9999998
X －1 －0.5
sin x
0.84147 0.95885
x
－0.1 0.99833
－0.01 0.99998
－0.001 …. 0.9999998
lim six n1 x 0 x
证明 limsinx1. x x0＋
证
即sinxxtanx
各 式 同 除 以 s i n x ( 因 为 s i n x 0 ) ,得
t0
1
推 广 为 某 过 程 中 的 无 穷 小 量 ,lim (1) e 某过程
使 用lim (11)xe 须 注 意 : x x
(1)类 型 :
1 型
1
(2)推广形式: lim(1) e 某过程
极限limsinx x0 x
极限xl im(11x)x
❖预备知识
1.有关三角函数的知识
tan x sin x cos x
sin00 cos0=1 |sinx|1 |cosx|1
2.有关对数函数的知识
lnxlogex
以e为底的指数函数y=ex的反函数 y = logex， 叫做自然对数，在工程技术中经常被运用，常简
lim s in 5 x 5limsin5x515
x 0 x
x0 5x
sin
推 广 ： 设 为 某 过 程 中 的 无 穷 小 量 ,某li过m程
1
练习1. 求下列极限:
（ 1） lim s in 3 x x 0 x
解 ： limsin3xlim3sin3x 3lim sin 3x 313
x 0 x x 0 3x
例 4 求 lim xsin 1
x
x
解
lim x sin 1
lim
sin
1 x
x
x x 1
1
x
思考题
lim sin x lim 1 s in x
x x
x x
当 x 时 1 0 且 | sin x|1 x
故 limsinx 0 x x
lim six n1 x 0 x
练习3：下列等式正确的是（ B ）
f (x) 1sinx ，当 x
x 0
时，
f ( x) 为无穷小量．
练习8. limxsinx___1 ___
x x
练习9. limxsinx__0____
x0 x
❖第二个重要极限 lim (11)x ?
x x
X 10 100 1000 10000 100000 … (1 1 ) x 2.594 2.705 2.717 2.718 2.71827
A. limsin x 1; x x
1
C. limxsin 1;
x0
x
B. limxsin1 1;
x
x
sin 1
D. lim x 1 ．
x x
练习4：下列等式不正确的是（ D ）
A lim sinx 1; B lim x 1;
x0 x
x0 sinx
C limxsin1 1;
x
x
D
limxsin1 1
x0 3x
（ 2） lim sin 5 x x 0 3 x
解 ： limsin5xlim (sin5x)(5) 1 5 5 x 0 3x x 0 5x 3 3 3
使 用lim sinx1时 须 注 意 : x 0 x
(1)类 型 ：
0型
0
(2)推广形式:
lim sin 1 某过程
（ lim0 ） 某过程
5.极限的运算法则
(1 )lim (f(x ) g (x )) lim f(x ) lim g (x )
( 2 ) l i m [ f ( x ) g ( x ) ] l i m f ( x ) l i m g ( x )
(3)若lim g(x)0， lim
f (x) g(x)
limf (x) limg(x)
.
( 4 )l i m [ c f ( x ) ] c l i m f ( x )
( 5 )lim [f( x ) ] k [ lim f( x ) ] k
❖第一个重要极限 limsinx?
x0 x
X
1
0.5
sin x
0.84147 0.95885
x
0.1 0.99833
0.01 0.99998
x0
x
练习5. 下列极限计算正确的是（ B ）
x A. lim 1
x0 x
C. limxsin1 1
x0
x
x B. lim 1
x x0
D. limsinx 1 x x
A 练习6. 已知
f (x) x 1 tanx
当（
f (x) 为无穷小量.
）时，
A. x0
C. x
B. x1
D. x
练习7. 已知
(3)等 价 形 式 ：limx 1 x 0 sinx
例3
求
sin(x1)
lim
x1
x2 1
解
lxi m 1sin x(2x 11)lxi m 1(xsi n1 ()x(x 1 )1)lxi m1[sinx(x11)
1] x1
lx i1m sixnx 1 (1)lx i1m x1 11111
1 2
111
这个结果可以作为公式使用 limtanx 1 x0 x
例 2 求 limsin5x x0 x
解： limsin5x lim 5sin 5x 5lim sin 5x
x0 x
x0 5x
x0 5x
令 5 x t,当 x 0 时 ,有 t 0
所以,原式5limsint 515
t0 t
注：在运算熟练后可不必代换，直接计算：
记为 y = ln x.
数 e 是一个无理数，它的前八位数是： e = 2.718 281 8
3.有关指数运算的知识
(ab)nanbn anmanam anm an m
4.无穷小量 定义 在某个变化过程中，以0为极限的变量称 为在这个变化过程中的无穷小量，常用字母 a,b,g等 表 示 。 性质 无穷小量与有界变量的乘积仍为无穷小量.