空间曲线及其方程

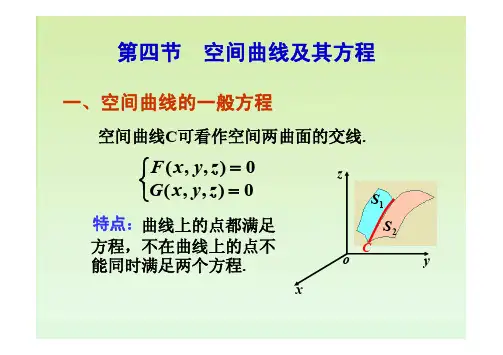
1第四节空间曲线及其方程⎩⎨⎧==0),,(0),,(z y x G z y x F 曲线上的点都满足方程，不在曲线上的点不能同时满足两个方程.xozy1S 2S C空间曲线C 可看作空间两曲面的交线.特点：一、空间曲线的一般方程2方程组表示怎样的曲线？⎩⎨⎧=++=+6332122z y x y x 解122=+y x 表示圆柱面，6332=++z y x 表示平面，⎩⎨⎧=++=+6332122z y x y x 交线为椭圆.例13方程组表示怎样的曲线？⎪⎩⎪⎨⎧=+---=4)2(222222a y a x y x a z 解222yx a z --=上半球面,4)2(222a y a x =+-母线平行于z 轴的圆柱面,交线如图.例2Oxyz准线为xOy 面上的圆, 圆心在点.2),0,2(a a 半径为4⎩⎨⎧==0),,(0),,(z y x G z y x F 消去变量z 后得：0),(=y x H 曲线关于的投影柱面xoy 设空间曲线的一般方程：以此空间曲线为准线，垂直于所投影的坐标面.投影柱面的特征：二、空间曲线在坐标面上的投影如图:投影曲线的研究过程.投影柱面空间曲线投影曲线56类似地：可定义空间曲线在其他坐标面上的投影⎩⎨⎧==00),(x z y R ⎩⎨⎧==00),(y z x T 面上的投影曲线,yoz 面上的投影曲线,xoz ⎩⎨⎧==00),(z y x H 空间曲线在面上的投影曲线xoy7求曲线在坐标面上的投影.⎪⎩⎪⎨⎧==++211222z z y x （1）消去变量z 后得,4322=+y x 在面上的投影为xoy ,04322⎪⎩⎪⎨⎧==+z y x 解例38求曲线在坐标面上的投影.⎪⎩⎪⎨⎧==++211222z z y x 解例3所以在面上的投影为线段.xoz ;23||,021≤⎪⎩⎪⎨⎧==x y z （3）同理在面上的投影也为线段.yoz .23||,021≤⎪⎩⎪⎨⎧==y x z (2) 因为曲线在平面上，21=z9求曲线⎪⎩⎪⎨⎧+=--=)(342222y x z yx z 在xOy 面上的投影.消去z 得：122=+y x ,所求投影为圆周⎩⎨⎧==+0122z y x . 注：所围立体在xy 面上的投影为：122≤+y x .即上半球面与圆锥面的交线.解例4。

第四讲Ⅰ 授课题目§7.4 空间曲线及其方程Ⅱ 教学目的与要求1、掌握空间曲线的一般方程及参数方程；2、掌握空间曲线在坐标面上的投影。

Ⅲ 教学重点与难点重点：空间曲线的一般方程及参数方程。

难点：空间曲线在坐标面上的投影。

Ⅳ 讲授内容：一、空间曲线的一般空间曲线可以看作两个曲面的交线. 设F (x , y , z )=0和G (x , y , z )=0是两个曲面方程, 它们的交线为C . 因为曲线C 上的任何点的坐标应同时满足这两个方程, 所以应满足方程组⎩⎨⎧==0),,(0),,(z y x G z y x F . 反过来, 如果点M 不在曲线C 上, 那么它不可能同时在两个曲面上, 所以它的坐标不满足方程组. 因此, 曲线C 可以用上述方程组来表示. 上述方程组叫做空间曲线C 的一般方程.例1 方程组⎩⎨⎧=+=+632122z x y x 表示怎样的曲线? 解 方程组中第一个方程表示母线平行于z 轴的圆柱面, 其准线是xOy 面上的圆, 圆心在原点O , 半行为1. 方程组中第二个方程表示一个母线平行于y 轴的柱面, 由于它的准线是zOx 面上的直线, 因此它是一个平面. 方程组就表示上述平面与圆柱面的交线.例2 方程组⎪⎩⎪⎨⎧=+---=222222)2()2(a y a x y x a z 表示怎样的曲线? 解 方程组中第一个方程表示球心在坐标原点O , 半行为a 的上半球面. 第二个方程表示母线平行于z 轴的圆柱面, 它的准线是xOy 面上的圆, 这圆的圆心在点)0 ,2(a , 半行为2a . 方程组就表示上述半球面与圆柱面的交线.例2 方程组⎩⎨⎧=+---=222222)(4a y a x y x a z 表示怎样的曲线? 解 方程组中第一个方程表示球心在坐标原点O , 半行为2a 的上半球面. 第二个方程表示母线平行于z 轴的圆柱面, 它的准线是xOy 面上的圆, 这圆的圆心在点(a , 0) , 半行为a . 方程组就表示上述半球面与圆柱面的交线.二、空间曲线的参数方程空间曲线C 的方程除了一般方程之外, 也可以用参数形式表示, 只要将C 上动点的坐标x 、y 、z 表示为参数t 的函数:⎪⎩⎪⎨⎧===)()()(t z z t y y t x x .当给定t =t 1时, 就得到C 上的一个点(x 1, y 1, z 1); 随着t 的变动便得曲线C 上的全部点. 方程组(2)叫做空间曲线的参数方程.例3 如果空间一点M 在圆柱面x 2+y 2=a 2 上以角速度ω绕z 轴旋转, 同时又以线速度v 沿平行于z 轴的正方向上升(其中ω、v 都是常数), 那么点M 构成的图形叫做螺旋线. 试建立其参数方程.解 取时间t 为参数. 设当t =0时, 动点位于x 轴上的一点A (a , 0, 0)处. 经过时间t , 动点由A 运动到M (x , y , z ) . 记M 在xOy 面上的投影为M ', M '的坐标为x , y ,0. 由于动点在圆柱面上以角速度ω 绕 z 轴旋转, 所以经过时间t ,∠AOM '= ω t . 从而x =|OM '|cos ∠AOM '=a cos ω t ,y =|OM '|sin ∠AOM '=a sin ω t ,由于动点同时以线速度v 沿平行于 z 轴的正方向上升, 所以z =MM '=vt .因此螺旋线的参数方程为⎪⎩⎪⎨⎧===vtz t a y t a x ωωsin cos ,也可以用其他变量作参数; 例如令θ=ω t , 则螺旋线的参数方程可写为⎪⎩⎪⎨⎧===θθθb z a y a x sin cos , 其中ωv b =, 而参数为θ . *曲面的参数方程曲面的参数方程通常是含两个参数的方程, 形如⎪⎩⎪⎨⎧===),() ,() ,(t s z z t s y y t s x x .例如空间曲线Γ⎪⎩⎪⎨⎧===)()()(t z t y t x ωψϕ (α≤t ≤β),绕z 轴旋转, 所得旋转曲面的方程为⎪⎪⎩⎪⎪⎨⎧=+=+=)(sin )]([)]([cos )]([)]([2222t z t t y t t x ωθψϕθψϕ (α≤t ≤β, 0≤θ≤2π). (4)这是因为, 固定一个t , 得Γ上一点M 1(ϕ(t ), ψ(t ), ω(t )), 点M 1绕z 轴旋转, 得空间的一个圆, 该圆在平面z =ω(t )上, 其半径为点M 1到z 轴的距离22)]([)]([t t ψϕ+, 因此, 固定t 的方程(4)就是该圆的参数方程. 再令t 在[α, β]内变动, 方程(4)便是旋转曲面的方程.例如直线⎪⎩⎪⎨⎧===tz t y x 21绕z 轴旋转所得旋转曲面的方程为⎪⎩⎪⎨⎧=+=+=t z t y t x 2sin 1cos 122θθ.(上式消t 和θ, 得曲面的直角坐标方程为41222z y x +=+) 又如球面x 2+y 2+z 2=a 2可看成zOx 面上的半圆周⎪⎩⎪⎨⎧===ϕϕcos 0sin a z y a x (0≤ϕ≤π)绕z 轴旋转所得, 故球面方程为⎪⎩⎪⎨⎧===ϕθϕθϕcos sin sin cos sin a z a y a x (0≤ϕ≤π, 0≤θ≤2π).三、空间曲线在坐标面上的投影以曲线C 为准线、母线平行于z 轴的柱面叫做曲线C 关于xOy 面的投影柱面, 投影柱面与xOy 面的交线叫做空间曲线C 在xOy 面上的投影曲线, 或简称投影(类似地可以定义曲线C 在其它坐标面上的投影).设空间曲线C 的一般方程为⎩⎨⎧==0),,(0),,(z y x G z y x F . 设方程组消去变量z 后所得的方程H (x , y )=0 ,这就是曲线C 关于xOy 面的投影柱面.这是因为: 一方面方程H (x , y )=0表示一个母线平行于z 轴的柱面, 另一方面方程H (x , y )=0是由方程组消去变量z 后所得的方程, 因此当x 、y 、z 满足方程组时, 前两个数x 、y 必定满足方程H (x , y )=0 , 这就说明曲线C 上的所有点都在方程H (x , y )=0所表示的曲面上, 即曲线C 在方程H (x , y )=0表示的柱面上. 所以方程H (x , y )=0表示的柱面就是曲线C 关于xOy 面的投影柱面. 曲线C 在xOy 面上的投影曲线的方程为:⎩⎨⎧==00),(z y x H . 讨论: 曲线C 关于yO z 面和zOx 面的投影柱面的方程是什么? 曲线C 在yO z 面和zOx 面上的投影曲线的方程是什么?例4 已知两球面的方程为x 2+y 2+z 2=1, (5)和x 2+(y -1)2+(z -1)2=1, (6)求它们的交线C 在xOy 面上的投影方程.解 先将方程x 2+(y -1)2+(z -1)2=1化为x 2+y 2+z 2-2y -2z =1,然后与方程x 2+y 2+z 2=1相减得y +z =1.将 z =1-y 代入x 2+y 2+z 2=1 得x 2+2y 2-2y =0.这就是交线C 关于xOy 面的投影柱面方程. 两球面的交线C 在xOy 面上的投影方程为⎩⎨⎧==-+002222z y y x . 例5 求由上半球面224y x z --=和锥面)(322y x z +=所围成立体在xOy 面上的投影.解 由方程224y x z --=和)(322y x z +=消去z 得到x 2+y 2=1. 这是一个母线平行于z 轴的圆柱面, 容易看出, 这恰好是半球面与锥面的交线C 关于xOy 面的投影柱面, 因此交线C 在xOy 面上的投影曲线为⎩⎨⎧==+0122z y x . 这是xOy 面上的一个圆, 于是所求立体在xOy 面上的投影, 就是该圆在xOy 面上所围的部分:x 2+y 2≤1.Ⅴ 小结与提问小结：1、空间曲线的一般方程及参数方程。

曲面与空间曲线的总结椭圆柱面；12222=+yx 122=-y x曲面与空间曲线一.曲面及其方程：1.曲面方程的一般概念： 定义：若曲面上的点的坐标(x,y,z)都满足方程F(x,y,z)=0，而满足此方程的点都在曲面上，则称此方程为 该曲面的方程，而曲面称为此方程的‘图形’。

例1：求与A(2,3,1)和B(4,5,6)等距离的点的运动规迹。

解： 设M(x,y,z)为动点的坐标，动点应满足的条件是 |AM|=|BM|由距离公式得此即所求点的规迹方程，为一平面方程。

2.坐标面及与坐标面平行的平面方程： ①坐标平面xOy 的方程：z=0②过点（a,b,c)且与xOy 面平行的平面方程：z=c③坐标面yOz 、坐标面zOx 以及过（a,b,c)点且分别与之平行的平面方程：x=0; y=0; x=a; y=b 3. 球面方程：①球面的标准方程：以M0(x0,y0,z0)为球心，R 为半径 的球面方程为(x-x0)2+(y-y0)2+(z-z0)2=R2 ②球面的一般方程：x2+y2+z2+Ax+By+Cz+D=0球面方程的特点：平方项系数相同；没有交叉项。

例2：求x2+y2+z2+2x-2y-2=0表示的曲面 解：整理得： (x+1)2+(y-1)2+z2=22故此为一个球心在（-1,1,0)，半径为2的球。

4.母线平行于坐标轴的柱面方程：一般我们将动直线l 沿定曲线c 平行移动所形成的轨迹 称为柱面。

其中直线l 称为柱面的母线，定曲线c 称为柱面 的准线。

本章中我们只研究母线平行于坐标轴的柱面方程。

此时有以下结论：若柱面的母线平行于z 轴，准线c 是xOy 面上的一条曲线，其方程为F(x,y)=0，则该柱面的方程为F(x,y)=0; 同理，G(x,z)=0,H(y,z)=0在空间中分别表示母线平行于y 轴和x 轴的柱面。

分析：母线平行于坐标轴的柱面的特点为：平行于某轴，则在其方程中无此坐标项。

空间曲线及其方程空间曲线的一般方程空间曲线的参数方程空间曲线在坐标面上的投影空间曲线的一般方程定义称⎩⎨⎧==0),,(0),,(z y x G z y x F 为空间曲线C 的一般方程. xyzOC1∑2∑例 讨论方程组⎩⎨⎧=+=+632122z x y x 表示的曲线.解221x y +=236x z +=xyzOΓ例 讨论方程组⎪⎩⎪⎨⎧=+---=222222)2()2(a y a x y x a z 表示的曲线. 解zyxa空间曲线的参数方程定义 称方程组⎪⎩⎪⎨⎧===)()()(t z z t y y t x x 为空间曲线的参数方程.例 如果空间一点M 在圆柱面x 2+y 2=a 2上以角速度ω绕z 轴旋转,同时又以线速度v 沿平行于z 轴的正方向上升(ω,v 都是参数),那么点M 构成的图形叫做螺旋线.试建立其参数方程.yz OhPMM 't ωx空间曲线——圆柱螺线P圆柱面222x y a +=yz0xax =y =z =a cos ωt vta sin ωt M螺线从点P →Q当t 从0 →2π，QtωM '空间曲线在坐标面上的投影定义 设空间曲线C 的一般方程为⎩⎨⎧==0),,(0),,(z y x G z y x F ，消去z 后得方程：H (x,y )=0称此方程为曲面C 关于xOy 面的投影柱面,投影柱面与xoy 面的交线叫做空间曲线C 在xOy 面上的投影曲线,简称投影.xyzOC'Γ即空间曲线C 在xOy 面上的投影曲线方程为：⎩⎨⎧==0),(z y x H 同理,空间曲线C 在yOz 面与xOz 面上的投影曲线方程分别为00),(⎩⎨⎧==x z y R 和 (,)0T x z y =⎧⎨=⎩例 已知两球面的方程为x 2+y 2+z 2=1和x 2+(y －1)2+(z －1)2=1,求它们的交线C 在xOy 面上的投影方程.解消去z 后,得柱面方程x 2+2y 2－2y =0,于是两球面的交线在xOy 面上的投影方程是：⎩⎨⎧==-+002222z y y xzyx1OC例 设立体由上半球面z =224y x --和锥面z =)(322y x +所围成,求它在xOy 面上的投影.解 上半球面和锥面的交线C ：⎪⎩⎪⎨⎧+=--=)(342222y x z y x z 消去z 后,得投影曲线的方程为: ⎩⎨⎧==+0122z y x消去z 后,得投影曲线的方程为: ⎩⎨⎧==+0122z y x从而所求立体在xOy 面上的投影为: x 2+y 2≤1.zxy1CO空间曲线及其方程1.掌握空间曲线的一般形式、参数方程形式.2.会根据一般方程讨论其所表示的曲线.3.理解空间曲线在坐标面上的投影的概念.4.会求特殊空间曲线在坐标面上的投影的形状和方程。

江西理工大学理学院第 4 节曲面、空间曲线及其方程江西理工大学理学院一、曲面方程的概念曲面的实例： 水桶的表面、台灯的罩子面等． 曲面在空间解析几何中被看成是点的几何轨迹． 曲面方程的定义：如果曲面 S 与三元方程 F ( x , y , z ) = 0 有下述关系：（1）曲面 S 上任一点的坐标都满足方程； （2）不在曲面 S 上的点的坐标都不满足方程；那么，方程 F ( x , y , z ) = 0 就叫做曲面 S 的方程， 而曲面 S 就叫做方程的图形．江西理工大学理学院以下给出几例常见的曲面.例 1 建立球心在点 M 0 ( x 0 , y0 , z 0 ) 、半径为 R 的球面方程.解设 M ( x , y , z ) 是球面上任一点，根据题意有| MM 0 |= R2 22 2 2( x − x0 )2+ ( y − y0 ) + ( z − z 0 ) = R2所求方程为 ( x − x0 ) + ( y − y0 ) + ( z − z0 ) = R 特殊地：球心在原点时方程为 x + y + z = R2 2 22江西理工大学理学院例 2 求与原点O 及 M 0 ( 2,3,4)的距离之比为1 : 2 的 点的全体所组成的曲面方程.解设 M ( x , y , z ) 是曲面上任一点，| MO | 1 = , 根据题意有 | MM 0 | 2 x2 + y2 + z2( x − 2) + ( y − 3) + (z − 4)2 221 = , 222⎞ 4 ⎞ 116 2 ⎛ ⎛ . 所求方程为 ⎜ x + ⎟ + ( y + 1) + ⎜ z + ⎟ = 3⎠ 3⎠ 9 ⎝ ⎝2江西理工大学理学院例 3 已知 A(1,2,3) ， B( 2,−1,4)，求线段 AB 的 垂直平分面的方程.解设 M ( x , y , z ) 是所求平面上任一点，根据题意有 | MA |=| MB |,( x − 1) + ( y − 2 ) + ( z − 3 )2 22( x − 2)2 + ( y + 1)2 + ( z − 4)2 , =化简得所求方程 2 x − 6 y + 2 z − 7 = 0.江西理工大学理学院2 2 例4 方程 z = ( x − 1) + ( y − 2) − 1的图形是怎样的？解根据题意有 z ≥ −1用平面 z = c 去截图形得圆：z( x − 1)2 + ( y − 2) 2 = 1 + c (c ≥ −1)当平面 z = c 上下移动时， 得到一系列圆coxy圆心在(1,2, c )，半径为 1 + c半径随c 的增大而增大. 图形上不封顶，下封底．江西理工大学理学院以上几例表明研究空间曲面有两个基本问题： （1）已知曲面作为点的轨迹时，求曲面方程． （讨论旋转曲面） （2）已知坐标间的关系式，研究曲面形状． （讨论柱面、二次曲面）江西理工大学理学院二、旋转曲面定义 以一条平面 曲线绕其平面上的 一条直线旋转一周 所成的曲面称为旋 转曲面. 这条定直线叫旋转 曲面的轴．播放 播放江西理工大学理学院旋转过程中的特征： 如图设 M ( x , y , z ),z⋅ M ( 0, y , z ) ⋅ Md1 1 1(1) z = z1（2）点 M 到 z 轴的距离o x2 2f ( y, z ) = 0yd=x + y =| y1 |2 2将 z = z1 , y1 = ± x + y 代入f ( y1 , z1 ) = 0江西理工大学理学院z = z1 , y1 = ± x 2 + y 2 代入 f ( y1 , z1 ) = 0 将得方程f (± x + y , z = 0,2 2)yoz 坐标面上的已知曲线 f ( y , z ) = 0 绕 z 轴旋转一周的旋转曲面方程.同理： yoz 坐标面上的已知曲线 f ( y , z ) = 0 绕 y 轴旋转一周的旋转曲面方程为f y, ±(x 2 + z 2 = 0.)江西理工大学理学院例 5 直线 L绕另一条与 L相交的直线旋转一周， 所得旋转曲面叫圆锥面．两直线的交点叫圆锥面 ⎛ 0 < α < π ⎞ 叫圆锥面的 的顶点，两直线的夹角 α ⎜ ⎟ 2⎠ ⎝ 半顶角．试建立顶点在坐标原点，旋转轴为 z 轴， 半顶角为α 的圆锥面方程． z解yoz 面上直线方程为 z = y cot α2 2⋅ αoM 1 (0, y1 , z1 )y圆锥面方程z = ± x + y cot αxM ( x , y, z )江西理工大学理学院例6 将下列各曲线绕对应的轴旋转一周，求 生成的旋转曲面的方程．⎧ x2 z2 ⎪ 2 − 2 =1 （1）双曲线 ⎨ a 分别绕 x 轴和 z 轴； c ⎪ y=0 ⎩x2 y2 + z2 绕 x 轴旋转 − =1 2 2 a c x +y z − 2 =1 绕 z 轴旋转 2 a c2 2 2旋 转 双 曲 面⎧ y2 z2 ⎪ 2 + 2 =1 （2）椭圆 ⎨ a 绕 y 轴和 z 轴； c ⎪x = 0 ⎩ y2 x2 + z2 旋 绕 y 轴旋转 + =1 2 2a c x +y z + 2 =1 绕 z 轴旋转 2 a c2 2 2江西理工大学理学院转 椭 球 面⎧ y 2 = 2 pz （3）抛物线 ⎨ 绕 z 轴； ⎩x = 0x 2 + y 2 = 2 pz旋转抛物面江西理工大学理学院三、柱面定义 平行于定直线并沿定曲线 C 移动的直线 L 所形成的曲面称为柱面. 这条定曲线 C 叫柱面的准线 ，动直线 L 叫 柱面的母线. 观察柱面的形 成过程:播放 播放江西理工大学理学院柱面举例zzy = 2x2平面o xo xyyy= x抛物柱面江西理工大学理学院从柱面方程看柱面的特征：只含 x, y 而缺 z 的方程 F ( x , y ) = 0 ，在 空间直角坐标系中表示母线平行于 z 轴的柱 面，其准线为 xoy 面上曲线C . （其他类推）实 例y z + 2 = 1 椭圆柱面 // x 轴 2 b c x2 y2 − 2 = 1 双曲柱面 // z 轴 2 a b 2 抛物柱面 // y 轴 x = 2 pz22江西理工大学理学院四、空间曲线的一般方程空间曲线C可看作空间两曲面的交线.⎧F ( x, y, z ) = 0 ⎨ ⎩G ( x , y , z ) = 0空间曲线的一般方程 特点：曲线上的点都满足 方程，满足方程的点都在 曲线上，不在曲线上的点 不能同时满足两个方程.zS1 S2oxCy江西理工大学理学院⎧ x2 + y2 = 1 例7 方程组 ⎨ 表示怎样的曲线？ ⎩2 x + 3 y + 3z = 6解x 2 + y 2 = 1 表示圆柱面，2 x + 3 y + 3 z = 6 表示平面，⎧ x2 + y2 = 1 ⎨ ⎩2 x + 3 y + 3z = 6交线为椭圆.江西理工大学理学院⎧z = a2 − x2 − y2 ⎪ 2 表示怎样的曲线？ 例8 方程组 ⎨ a 2 a 2 ⎪( x − ) + y = ⎩ 2 4解z = a2 − x2 − y2上半球面,a 2 a2 2 圆柱面, (x − ) + y = 2 4交线如图.江西理工大学理学院五、空间曲线的参数方程⎧ x = x(t ) ⎪ ⎨ y = y( t ) 空间曲线的参数方程 ⎪ z = z( t ) ⎩当给定 t = t1 时，就 得到曲线上的一个点( x1 , y1 , z1 )，随着参数的变化可得到曲线上的全部点.,0αb +空间曲线投影柱面。