下载文档原格式
重庆大学动力工程学院2008年级硕士研究生1班《高等流体力学》考题答案学号： 姓名：1. （10分）试证明：()()()0a b c b c a c a b ⨯⨯+⨯⨯+⨯⨯= 解：原式[]0)()()()(m in =-+-+--=---=++=jk in jn ik ij kn in kj ki jn kn ji k j i mkn ijm mjn kim jkm k j i kmnijm j i k jmn kim i k j imn jkm k j i c b a c b a b a c a c b c b a δδδδδδδδδδδδεεεεεεεεεεεε2. （20分）流体在弯曲的变截面细管中流动，设A 为细管的横截面积，在A 截面上流动参数均匀分布，试证明对该细管连续方程可写为：0)(=∂∂+∂∂Au s t A ρρ 式中u 是沿管轴线的速度，δs 是沿流动方向的微元弧长。
证明：取ds 长的细管如图，取两端面A 1 、A 2 及侧面∑所围之体积为控制体。
引用积分形式的连续方程⎰⎰=⋅+∂∂A ndA u d t 0ρτρτ对于上述控制体有τρτd t ⎰∂∂≈Ads t ∂∂ρ⎰⎰⎰⎰⋅+⋅+⋅=⋅∑A A A ndA u ndA u ndA u ndA u 12ρρρρ =ds sAu Au Au ∂∂≈-)()()(12ρρρ 代入连续方程得3. （25分）试利用边界层简化方法将不可压缩平壁边界层的耗散函数ij ij s s μ2=Φ简化为2⎪⎪⎭⎫ ⎝⎛∂∂=Φy u μ 其中，⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=i j j i ij x u x u s 21解：在不可压缩平壁边界层流动中不为零的应变率张量分量是xu s ∂∂=11，)(212112x v y u s s ∂∂+∂∂==，y v s ∂∂=22 由于U u ~，L x ~，δ~y ，y v x u ∂∂∂∂~ ⇒ δv L U ~ ⇒ L U v δ~，于是应变率张量各分量的量级可估计如下，LU L U x u δδ=∂∂~ δU y u ~∂∂ 2)(~LU L L U x v δδδ=∂∂ LU y v δδ~∂∂ 显然y u ∂∂量级最大，其余各量中的最大者与y u ∂∂的比值为L δ，均可忽略，于是222)(])(41)(41[22yu y u y u s s ij ij ∂∂=∂∂+∂∂==Φμμμ4. （25分）设某边界层外边界的势流速度分布为3/1kx U =，设)(23ηνψf x k m =，3/132x y k νη=，试证明边界层方程可转换为常微分方程：021)(212''"'=+-+f ff f 证明：由于31kx U =有3231-=kx dx dU ，3123-=x k dx dU U ，则边界层方程 22yu dx dU U y u v x u u ∂∂+=∂∂+∂∂ν 可改写为333122223yx k y x y x y ∂∂+=∂∂∂∂-∂∂∂∂∂-ψνψψψψ 由3132x y k νη=，)(23ηνψf x k m =可得 )3(23'1mf f x k x m +-=∂∂-ηνψ '31f kx ym -=∂∂ψ )])31(31[('''342f m f kx y x m -+-=∂∂∂-ηψ ''322232f x k k y m -=∂∂νψ '''123332f x k ym -=∂∂νψ 将以上各式代入边界层方程并加以整理，得f f x mk f f x k f x k m f f x k m m m m ''3522'''35222'3522'''35223)()31(31ηηη-----+-+- ='''1212323f x k x k m --+ 上式左侧第一项和第三项相互抵消，2k 也可以从整个方程中约去，则微分方程简化为031)()31(3212'352'''352'''1=+-++----x f x m f f mx f x m m m 为了得到相似解，x 变量不应在方程中出现，即x 的指数必须为零，313521-=-=-m m ⇒ 32=m 将其代入微分方程即得，021)(212''''''=+-+f ff f5. （20分）试根据不可压缩流动的N-S 方程，导出其紊流流动下的时均流动的雷诺方程。
高等流体力学考题权威版（陈小榆）1、 柱坐标下V V ⋅∇的表达式（112233V V e V e V e =++）：()()()()()()2211i i i i i i j i i j i i j j j j j j i j j i j j i i i i i i i i i j j j j j i i j j i j i i iV e V e V V V e e V e e e V h q h q q V VV V VV h V e V e V V e e i j i j e e i j h q h q h q h q h h q h q ⎡⎤⎡⎤∂⎛⎫∂∂⎢⎥⋅∇=⋅=⋅+⎢⎥ ⎪ ⎪∂∂∂⎢⎥⎢⎥⎝⎭⎣⎦⎣⎦∂∂∂∂∂∂=+≠+==+≠+∂∂∂∂∂∂对于柱坐标系：1321231,;,,h h h r q r q q z ε======2121122222121311323332133dV V dV dV V dV V dV dV V V =V ++V e +V ++V +e dr r d dz r dr r d dz r dV dVdV V +V ++V e drd dz V V r εεε∴⋅∇⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭⎛⎫ ⎪⎝⎭2、 利用哈密尔顿算子证明以下各式： (1) ()a =0∇⋅∇⨯()()2222221233132231121222331213a j j i i i j i j ijk ki ii j i j i j a e x aaaa =e e e e e e e e x x x xx x x x aa ae e e e e e x x x x x x a e ⎛⎫∂∂⨯ ⎪ ⎪∂∇⨯∂⎛⎫⎛⎫∂∂∂⎝⎭∇⋅∇⨯⋅=⋅=⋅⨯=⨯⋅=⋅ ⎪ ⎪ ⎪ ⎪∂∂∂∂∂∂∂∂⎝⎭⎝⎭∂∂∂=⋅+⋅+⋅∂∂∂∂∂∂∂+22331232121213132a ae e e e e x x x x x x ∂∂⋅+⋅+⋅=∂∂∂∂∂∂(2) ()0ψ∇⨯∇=()()22222123313223213232121311121222213331323212i i jijk ki i j i j =e e e e e x x x x x e e e e e e x x x x x x e e e e e e x x x x x x ψψψψψψψψψψ⎛⎫∂∇⨯∂∂∇⨯∇⨯=⨯= ⎪ ⎪∂∂∂∂∂⎝⎭∂∂∂=++∂∂∂∂∂∂∂∂∂+++=∂∂∂∂∂∂(3) ()()()a b a b b a ∇⋅⨯=∇⨯⋅-∇⨯⋅()()()()i iiii i iiia b a b a b a b e e b a e b e a a b b a x x x x x ∂⨯⎛⎫∂∂∂∂∇⋅⨯=⋅=⋅⨯+⨯=⨯⋅-⨯⋅=∇⨯⋅-∇⨯⋅⎪∂∂∂∂∂⎝⎭(4) ()()()a b a b a b b a b a ∇⋅=⨯∇⨯+⋅∇+⋅∇+⨯∇⨯()()iii ii ia b a ba b e eb e a a b b a x x x ∂∂⋅∇⋅=⋅+⋅=∇⋅+∇⋅∂=∂∂∂ 又：()()b b b b ba a i i i i ii i i i i a b e e a e e a a e b a a b x x x x x ⎛⎫⎛⎫⎛⎫∂∂∂∂∂⨯∇⨯=⨯⨯=⋅-⋅=⋅-⋅=∇⋅-⋅∇ ⎪ ⎪ ⎪∂∂∂∂∂⎝⎭⎝⎭⎝⎭()()i i i i ii i i i i a a a a ab a b e b e b e e b b e a b b a x x x x x ⎛⎫⎛⎫⎛⎫∂∂∂∂∂⨯∇⨯=⨯⨯=⋅-⋅=⋅-⋅=∇⋅-⋅∇ ⎪ ⎪ ⎪∂∂∂∂∂⎝⎭⎝⎭⎝⎭3、 如果n 为闭曲面A 上的微元面dA 的单位外法线向量，12,ϕϕ是闭曲面满足20ϕ∇=的两个不同的解，试证明：（38页，6） (1)AndA=0⎰⎰(2)2112AAdA dA nnϕϕϕϕ∂∂=∂∂⎰⎰⎰⎰ 证明：（1）1AndA=d 0ττ∇=⎰⎰⎰⎰⎰（2）()()()()()()211221122112212212122121221221120AA A AdA dA n n dAnnn n dA d d d τττϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕτϕϕϕϕϕϕϕϕτϕϕϕϕτ∂∂-=⋅∇-⋅∇∂∂⎡⎤=⋅∇-⋅∇=∇⋅∇-∇⎣⎦=∇+∇∇-∇-∇∇=⋅⋅=∇-∇⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰4、 有两族平面正交曲线()(),,,x y c x y d ζη==，已知22,2x y y ζ=-=时4x η=，求()x,y η，（40页，10） 解：,=0x x y yζηζηζη∂∂∂∂∴+∂∂∂∂正交， 即2x2y =0x yηη∂∂-∂∂ 40y y =22x 4-22x ηη∂∂=⋅⨯=∂∂当时，，代入得22yx xy c ηη∂∴=⇒=+∂2402y x c xy ηη===∴=由时，知，5、 求半径为a 的四分之一圆的垂直平面上流体的总的作用力F 和压力中心C 的位置，已知0x 与流体自由水平面重合，自由面上压力为零。
2023年大学流体力学期末考试复习题总结（最新版汇总）一、选择题1.连续介质假设意味着 B 。
(A)流体分子互相紧连 (B) 流体的物理量是连续函数(C) 流体分子间有空隙 (D) 流体不可压缩2.流体的体积压缩系数βp 是在 B 条件下单位压强变化引起的体积变化率。
(A) 等压 (B) 等温 (C) 等密度3.水的体积弹性模数 C 空气的弹性模数。
(A) 小于 (B) 近似等于 (C) 大于4.静止流体 A 剪切应力。
(A) 不能承受 (B) 可以承受 (C) 能承受很小的 (D)具有粘性时可承受5.温度升高时，空气的粘性系数 B 。
(A) 变小 (B) 变大 (C) 不变6.运动粘性系数的单位是 B 。
(A)s/m2 (B) m2/s (C)N ·s/m2 (D) N ·m/s7.动力粘性系数μ与运动粘性系数ν的关系为μ= A 。
(A)ρν (B)ν/ρ (C) ν/p (D) pν8.流体的粘性与流体的 D 无关。
(A) 分子内聚力 (B) 分子动量交换 (C) 温度 (D) 速度梯度9.毛细液柱高度h 与 C 成反比。
(A) 表面张力系数 (B) 接触角 (C) 管径 (D) 粘性系数10．流体受压，体积缩小，密度增大 的性质，称为流体的压缩性 ；流体受热，体积膨胀，密度减少 的性质，称为流体的热胀性 。
压缩系数β的倒数称为流体的弹性模量 ，以E 来表示11．流体静压强的方向必然是沿着作用面的内法线方向。
12．通过描述物理量在空间的分布来研究流体运动的方法称为欧拉法。
13． 流线不能相交（驻点处除外），也不能是折线，因为流场内任一固定点在同一瞬间只能有一个速度向量，流线只能是一条光滑的曲线或直线。
14．液体质点的运动是极不规则的，各部分流体相互剧烈掺混，这种流动状态称为紊流。
15．由紊流转变为层流的临界流速k v 小于 由层流转变为紊流的临界流速kv '，其中kv '称为上临界速度，k v 称为下临界速度。
2011年1月流体力学试题一、单项选择题（本大题共10小题，每小题2分，共20分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.不可压缩流体是指( )A.平衡流体B.运动流体C.无粘性流体D.忽略密度变化的流体2.如题2图所示，用U形水银压差计测量水管A、B两点的压强差，水银面高差h p=10cm，p A-p B 为( )A.13.33kPaB.12.35kPaC.9.8kPaD.6.4kPa3.关于水流流向的正确说法是( )A.水一定是从高处往低处流题2图B.水一定是从流速大处往流速小处流C.水一定是从机械能大处往机械能小处流D.水一定是从测压管水头高处往测压管水头低处流4.实际液体的水力坡度J为( )A.J<0B.J=0C.J>0D.J=J p5.如题5图所示，排水管的断面平均流速v=2.0m/s，则管道出口的局部水头损失为( )A.0.102mB.0.204mC.0.306mD.0.408m题5图6.欲使水力最优梯形断面渠道的水深和底宽相等，则渠道的边坡系数m应为( )A.1／4B.1／2C.3／4D.17.棱柱形渠道发生M2型水面曲线时，水流的特性为( )A.Fr<l h>h cB.Fr>l h>h cC.Fr<l h<h cD.Fr>l h<h c8.宽顶堰的淹没系数随淹没程度h g／H的增大而( )sA.减小B.增大C.先减小后增大D.先增大后减小9.地下水渐变渗流的浸润线，沿程变化为( )A.下降B.保持水平C.上升D.前述情况都可能10.桥墩绕流的模型设计应采用( )A.雷诺准则B.马赫准则C.欧拉准则D.弗劳德准则二、填空题（本大题共10小题，每小题2分，共20分）请在每小题的空格中填上正确答案。
错填、不填均无分。
11.已知某流体的粘性切应力为5.0N／m2，动力粘度为0.1Pa·s，则其剪切变形速率为_______。
一、选择题1．按连续介质的概念，流体质点是指A .流体的分子； B. 流体内的固体颗粒； C . 无大小的几何点； D. 几何尺寸同流动空间相比是极小量，又含有大量分子的微元体。
2．作用在流体的质量力包括A. 压力；B. 摩擦力；C. 重力；D. 惯性力。
3．单位质量力的国际单位是：A . N ； B. m/s ； C. N/kg ； D. m/s 2。
4．与牛顿内摩擦定律直接有关系的因素是Ａ. 切应力和压强； B. 切应力和剪切变形速率； C. 切应力和剪切变形。
5．水的粘性随温度升高而A . 增大； B. 减小； C. 不变。
6．气体的粘性随温度的升高而 A. 增大；Ｂ. 减小；Ｃ. 不变。
7．流体的运动粘度υ的国际单位是Ａ. m 2/s ；B. N/m 2 ； C. kg/m ；D. N ·s/ｍ2 8．理想流体的特征是Ａ. 粘度是常数；B. 不可压缩；C. 无粘性； D. 符合pV=RT 。
9．当水的压强增加１个大气压时，水的密度增大约为Ａ. 200001； Ｂ. 100001；Ｃ. 40001 。
10．水力学中，单位质量力是指作用在Ａ. 单位面积液体上的质量力；Ｂ. 单位体积液体上的质量力； Ｃ. 单位质量液体上的质量力；Ｄ. 单位重量液体上的质量力 11．以下关于流体粘性的说法中不正确的是Ａ. 粘性是流体的固有属性；Ｂ. 粘性是在运动状态下流体具有抵抗剪切变形速率能力的量度Ｃ. 流体的粘性具有传递运动和阻滞运动的双重作用；Ｄ. 流体的粘性随温度的升高而增大。
12．已知液体中的流速分布µ－y 如图所示，其切应力分布为 Ａ.τ＝０；Ｂ.τ＝常数； Ｃ. τ＝ky (k 为常数)。
13．以下关于液体质点和液体微团的正确论述是Ａ. 液体微团比液体质点大；Ｂ. 液体微团包括有很多液体的质点； Ｃ. 液体质点没有大小，没有质量；Ｄ. 液体质点又称液体微团。
14．液体的汽化压强随温度升高而 Ａ. 增大；Ｂ. 减小；Ｃ. 不变；15．一封闭容器盛以水，当其从空中自由下落时（不计空气阻力），其单位质量力为 Ａ. 0 ； Ｂ. -g ； Ｃ. mg ；Ｄ. –mg 。
一、选择题（每题2分，共计30分）1、在（ ）参考系中给出各个流体质点的空间位置随时间的变化:000(,,,)r r x y z t =，而把相关的物理量表示为流体质点和时间的函数。
a. 拉格朗日 b. 欧拉 c. 黎曼 d. 连续介质2. 流体质点的某一物理量η随时间的变化率为：()D u Dt tηηη∂=+∇∂，其中t η∂∂称为（ ）。
a. 随体导数 b. 质点导数 c. 当地导数d. 对流导数3. 若速度场在任意空间点都满足0u ∇⨯=，则该速度场为（ ）流场。
a. 无旋 b. 定常 c. 层流 d. 均匀4. 应力张量ij σ与应变率张量ij s 之间的关系称为本构方程，下面叙述不正确的选项是（ ）。
a. 应力ij σ张量是对称张量b. 应变率张量ij s 是对称张量c. 理想流体本构关系为：ij ij p σδ=-d. 静止流体本构关系为：ij p σ=-5. 若速度场在任意空间点都满足（ ），则该速度场为不可压缩流场。
a.0t ρ∂=∂ b. ()0u ρ∇=c. 0u ∇=d. 0dudt=6.已知：平面不可压缩流动，其y 方向的速度v=v 0( t )，忽略重力，则x 方向的N-S 方程可以写为：a. 221u u p ut y x y νρ∂∂∂∂+=-+∂∂∂∂b. 202()u u p uv t t y x y ν∂∂∂∂+=+∂∂∂∂c. 2021()u u p u v t t y x y νρ∂∂∂∂+=-+∂∂∂∂d. 202()u u u v t t y yν∂∂∂+=∂∂∂7.根据开尔文定理，正压、理想流体在质量力有势的情况下，如果某时刻部分流体无旋，则这部分流体在（ ）。
a.该时刻以前无旋，该时刻以后可能有旋。
b. 该时刻以前无旋，该时刻以后也无旋。
c.该时刻以前可能无旋，该时刻以后可能有旋。
d. 该时刻以前可能有旋，该时刻以后也可能有旋。
8.如图1所示，假设河水是理想不可压缩匀质、定常无旋流动，且外力只考虑重力，则（ ）。
高等流体力学考试题
每题20分，请用答题纸答题一、牛顿提出流体粘性
定律依据如图的实验，
但在实验过程中即使经
过仔细的处理，仍会带
来误差。
比如通过减小
上面平板的比重使其漂
浮在流体上，但总有一
部分平板会浸入到液体
中；另外，当平板运动
时，其前部的液体会发生堆积，后部的液体会被拖曳，使液面产生如图的变化而带来附加阻力。
请思考回答，你认为可以通过什么办法使测量误差减小到最小，并设计新的测量办法来实现减小测量误差。
二、在理想流体中，由涡丝组
成的两个涡环，两种情况分别
如图中的(a)和(b)所示。
假设两
个涡环强度相等，方向如图，
涡环直径同为D，间距为L，
初始时刻两涡环的整体运动速
度都为零。
请分析并图示画出
两种情况涡环组的运动趋势。
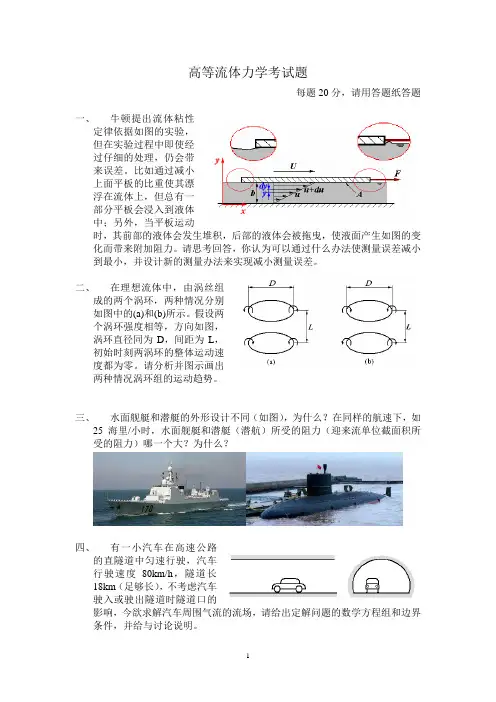
三、水面舰艇和潜艇的外形设计不同（如图），为什么？在同样的航速下，如
25海里/小时，水面舰艇和潜艇（潜航）所受的阻力（迎来流单位截面积所受的阻力）哪一个大？为什么？
四、有一小汽车在高速公路
的直隧道中匀速行驶，汽车
行驶速度80km/h，隧道长
18km（足够长），不考虑汽车
驶入或驶出隧道时隧道口的
影响，今欲求解汽车周围气流的流场，请给出定解问题的数学方程组和边界条件，并给与讨论说明。
五、任何流体都是有粘性的，为什么我们还要引入理想流体的概念？在什么
情况下我们可以把流动问题的研究对象当作理想流体考虑？如下图所示，给出你所认为的合理的流场分析方法。
以上问题没有标准答案，可以讨论，请大家独立完成。
下学期开学后第二周周二交卷。
《高等流体力学》复习题一、基本概念1． 什么是流体，什么是流体质点？2． 什么是流体粘性，静止的流体是否具有粘性，在一定压强条件下，水和空气的粘性随着温度的升高是如何变化的？3． 什么是连续介质模型？在流体力学中为什么要建立连续介质这一理论模型？4． 给出流体压缩性系数和膨胀性系数的定义及表达式。
5． 简述系统与控制体的主要区别。
6． 流体静压强的特性是什么？绝对压强s p 、计示压强（压力表表压）p 、真空v p 及环境压强（一般为大气压）a p 之间有什么关系？7． 什么是理想流体，正压流体，不可压缩流体？8． 什么是定常场，均匀场，并用数学形式表达。
9． 分别用数学表达式给出拉格朗日法和欧拉法的流体加速度表达式。
10． 流线和迹线有何区别，在什么条件下流场中的流线和迹线相重合？11． 理想流体运动时有无切应力？粘性流体静止时有无切应力？静止时无切应力是否无粘性？为什么？12． 试述伯努利方程()22p V Z C g gψρ++=中各项的物理意义，并说明该方程的适用条件。
13． 流体有势运动指的是什么？什么是速度势函数？无旋运动与有势运动有何关系？14． 什么是流函数？存在流函数的流体具有什么特性？（什么样的流体具有流函数？）15． 平面流动中用复变位势描述的流体具有哪些条件（性质）？16． 伯努利方程22p V Z Const g gρ++=对于全流场均成立需要基于那些基本假设？ 17． 什么是第一粘性系数和第二粘性系数？在什么条件下可以不考虑第二粘性系数？stokes 假设的基本事实依据是什么？18． 为推出牛顿流体的本构方程，Skokes 提出了3条基本假设，分为是什么？19． 作用在流体微团上的力分为那两种？表面应力ij τ的两个下标分别表示？ij τ的正负如何规定？20． 从分子运动学观点看流体与固体比较有什么不同？21． 试述流体运动的Helmhottz 速度分解定律并给出其表达式。
22． 流体微团有哪些运动形式？它们的数学表达式是什么？23． 描述流体运动的基本方法有哪两种？分别写出其描述流体运动的速度、加速度的表达式。
24． 什么是随体导数（加速度）、局部导数（加速度）及位变导数（加速度）？分别说明0=dt v d ，0=∂∂tv 及()0=∇⋅v v 的物理意义？25． 什么是流体的速度梯度张量？试述其对称和反对称张量的物理意义。
26． 流体应力张量的物理意义是什么？它有什么性质？27． 某平面上的应力与应力张量有什么关系？nm mn p p =的物理含义是什么？28． 流体微团上受力形式有哪两种？它们各自用什么形式的物理量来表达？29． 什么是广义的牛顿流体和非牛顿流体？30． 试述广义牛顿内摩擦定律的物理意义及相应的数学表达式？31． 粘性流动和理想流动的壁面边界条件有何不同？32． 简述N-S 方程是如何得到的，以不可压流动的N-S 方程2d p f dt υνυρ∇=-+∇为例，说明其各项的物理意义。
33． 在理想有势的流动假设条件下，绕流物体产生的升力主要受那些因素的影响，有何规律？34． 什么是层流运动、湍流运动、雷诺数和临界雷诺数？35． 圆管中定常不可压层流和湍流运动的速度分布规律是什么？36． 流动相似的条件是什么？简述π定理的内容。
37． 什么是马赫数？其物理意义是什么？38． 什么是雷诺数？其物理意义是什么？39． 给出当量直径（水力直径）的表达式并说明各项的意义。
40． 流体的阻力可分为哪几种？管路中因阻力引起的损失通常分为哪几种？影响管路损失系数的主要因素有那些？41． 何谓管道流动的水击现象，如何减轻水击造成的危害？42． 怎样判断流动是否有旋，涡度与速度环量有何关系，流动是否有旋与流体质点的运动轨迹有关吗？43． 试说明粘性流体流动的三个基本特征，它们与理想流体运动相比有何不同？44． 什么是涡管？涡管模型的特点是什么？45． 使流体涡量产生变化的因素有哪些？其中哪些是流体运动的内在因素，哪些是外在因素？46． 螺旋流、偶极子流和绕圆柱体有环流动分别是由那些基本势流叠加而成？47． 何谓空化现象？何谓空蚀现象？48． 试说明层流边界层和湍流边界层的速度分布特征。
49． 分别给出不可压流动平板边界层的位移（排挤）厚度和动量损失厚度的表达式。
50． 试述雷诺应力j i u u ''-ρ的物理意义及其与分子粘性应力的异同。
51． 试述平板湍流边界层的结构及其速度分布特征。
52． 边界层理论的基本思想是什么？平板不可压定常层流边界层的厚度主要受那些因素的影响？53． 边界层分离的概念和原因是什么？分离点处的流动特征是什么（用表达式）？54． 求解平板边界层动量积分方程时原则上需要补充那几个方程？55． 以圆柱绕流为例，简述卡门涡街现象，并对涡街引发圆柱振动作简要说明。
56． 简述卡门涡街流量计测量流量的基本原理。
57． 大涡模拟的基本思想是什么？58． 简述湍流的特点、湍流模型的概念和主要分类。
59． 什么是Prantl 混合长度？雷诺应力的定义表达式是什么？雷诺应力有何特征？60． 什么是壁面函数？引入壁面函数的意义何在？61． 粘性流动的动能方程()()2:2D V f V T V pV p V T dt ρρε⎛⎫=⋅+∇⋅⋅-∇⋅+∇⋅- ⎪⎝⎭中右边5项的物理意义依次为？62． 完整的CFD 数学模型主要包括那些内容？63． 利用CFD 技术求解流动问题主要包括那三个环节？各环节主要完成那些工作？64． 为提高CFD 计算的效率和精度，计算网格应具备那些特点。
65． 给出速度矢量的随体导数表达式并说明各项的物理意义。
66． 什么是声速，理想气体的声速大小与那些因素有关？67． 在流场中出现扰动时，亚声速气流和超声速气流的流动状态有何本质上的区别？68． 什么是压气机的喘振现象，喘振和旋转失速有何关系？69． 什么是压气机的堵塞现象，产生堵塞的原因是什么？70． 什么是喷管的壅塞的现象，为什么会出现这种现象？71． 什么是激波，激波在什么条件下才会出现，激波通常分为那三种？72． 激波是压缩波还是膨胀波，激波前后的流动参数速度、压力和密度是如何变化的，激波前后的流动一般看作等熵过程还是绝热过程？二、推导及证明1．根据质量守恒定律推导连续性方程。
2．根据动量定律推导出微分形式的运动方程。
3．试推导理想流体平面二维运动欧拉微分方程式。
4．从N-S 方程出发，试推导出Bernoulli 公式()22p V z C g gψρ++=，其中ψ表示流线。
5．试利用N-S 方程证明不可压平面层流的流函数(,,)x y z ψ满足：22222()t y x x y ψψψψψμψρ∂∂∂∂∂∇+∇-∇=∇∇∂∂∂∂∂ 其中：444224224()2x x y y ∂∂∂∇∇=++∂∂∂∂。
6．进行圆管中流体摩擦试验时，发现圆管中沿轴向的压降p ∆是流速u 、密度ρ、粘性系数μ、管长l 、 管内径d 及管壁粗糙度d h k ∆=的函数，而且p ∆与l 成正比。
试用因次分析方法证明221u d l p ρλ=∆，其中()Re ,k λλ=为无因次系数。
7．从不可压流动的N-S 方程出发，推导出平板定常不可压二维层流的Prantl 边界层方程。
8．以平面二维问题为例，证明动量方程：1yx x xx x d f dt x y τυσρ∂⎛⎫∂=++ ⎪∂∂⎝⎭，1y yy xy y d f dt y x υστρ∂∂⎛⎫=++ ⎪∂∂⎝⎭。
9．如图所示，已知不可压射流初速为0υ，流量为V q ，平板向着射流以等速υ运动，试推导出平板运动所需要的功率N 的表达式。
10． 流体在弯曲的变截面细管中流动，设A 为细管的横截面积，在A 截面上流动参数均匀分布，试证明对该细管连续方程可写为：()0A Au t s ρρ∂∂+=∂∂式中u 是沿管轴的速度，s ∂是沿流动方向的微元弧长。
11．写出理想不可压缩流体定常平面流动的动量方程（忽略质量力），如果是密度分层流动，则流体密度ρ 将是,x y 的函数。
试证明如令,u v **==，式中0ρ是一个参考密度，为常数，则上述方程可转换为速度u * 和v * 、流体密度为0ρ的平面流动的动量方程。
12．证明方程()()ij j j k j k i u u u f t x x σρρρ∂∂∂+=+∂∂∂可化简为j j ij k j k iu u u f t x x σρρρ∂∂∂+=+∂∂∂。
13．对于不可压缩流体，证明速度矢量u 和涡量矢量Ω之间有下述关系式成立。
[]221()()()2u u u u u u ∇⋅⋅∇=∇⋅-⋅∇-Ω⋅Ω 14．证明对于理想流体，当质量力有势时有下式成立。
31D u p Dt ρρρρ⎛⎫⎛⎫ΩΩ=⋅∇+∇⨯∇ ⎪ ⎪⎝⎭⎝⎭15．设某定常层流边界层外边界的流体速度分布为13U kx =，设()m f ψη=，其中η= 试证明边界层方程可转换为常微分方程()211022f ff f ''''+-+=。
三、计算题 1．已知23xy yz ϕ=+，求ϕ在点M （2,-1,1）处沿向量22l i j k =+-方向的方向导数。
2．设流场的速度分布为：2224y x y t u x +-=；222yx x u y +=。
求（1）当地加速度的表达式；（2）t =0时在点（1，1）处流体质点的加速度。
3．在柱坐标系下，2cos r v r θ=，2sin rv θθ=，0=r v ，求流线族。
4．在直角坐标系下，t x u +=，t y v +-=，0=w ，求流线族和迹线族。
5．在直角坐标系下，t x u +=，v y t =+，0=w ，求流线族和迹线族。
6．一速度场用1x u t =+，21y v t =+，31z w t=+描述，（1）求加速度的欧拉描述；（2）先求矢径表示式000(,,,)r r x y z t =，再求此加速度的拉格朗日描述；（3）求流线。
7．已知流体质点的空间位置表示如下：0x x =，200(1)t y y x e -=+-，300(1)t z z x e -=+-。
求（1）速度的欧拉表示；（2）加速度的欧拉和拉格朗日表示；（3）过点(1,1,1)的流线及t =0时在(x , y , z ) = (1,1,1)处的流体质点的迹线；（4）散度、旋度及涡线；（5）应变率张量和旋转张量。
8．如图所示，一个圆柱形水箱放置在电梯中，水箱直径为D ，水箱底面附近有一出水管，出水直径为d ，水箱中自由面与出水管轴线间水深为h 。
当电梯以等加速度a 垂直上升时打开出水管水龙头，试确定瞬间的出流速度。
