微纳系统仿真大作业
- 格式:doc
- 大小:780.50 KB
- 文档页数:11

微机电系统器件设计模型仿真及实验验证微机电系统(MEMS)技术是一种集成了机械、光学、电子和计算机技术的新型技术,逐渐应用于各个领域,包括医疗、通信、能源等。
在MEMS器件设计中,模型仿真和实验验证是非常重要的步骤,可以验证器件设计的可行性和性能表现,优化设计方案,提高研发效率。
本文将介绍MEMS器件设计模型仿真及实验验证的流程和方法,并探讨其在实际应用中的意义。
首先,MEMS器件设计的模型仿真是一种基于计算机模型的仿真技术,通过建立数学模型和使用相应的软件工具,对器件的结构和性能进行预测和分析。
常用的仿真软件包括ANSYS、COMSOL等。
模型仿真可以帮助设计人员快速建立和修改器件结构,优化材料选择和几何参数,预测器件的力学、光学、热学等性能指标。
仿真结果可以减少研发时间和成本,提高设计的准确性和可靠性。
其次,实验验证是将设计的MEMS器件制作成实际样品,并通过实验测试来验证器件的性能和功能。
实验验证可以分为两个阶段:样品制作和测试验证。
样品制作包括器件工艺流程的设计与实施,包括光刻、湿法腐蚀、离子刻蚀等工序。
测试验证包括对器件性能的定量测量和质量评估,例如使用扫描电子显微镜(SEM)观察器件结构的形貌和表面粗糙度,使用光学显微镜观察器件是否工作正常,使用激光干涉仪测试其位移或力学性能等。
在实际应用中,MEMS器件设计模型仿真和实验验证具有重要的意义。
首先,通过仿真可以提前预测器件的性能和功能,避免不必要的实验测试,减少研发时间和成本。
其次,仿真可以进行多次参数优化和设计方案的比较,最终选定性能最佳的器件方案。
而实验验证可以验证仿真结果的准确度和可靠性,确保器件在实际制造和使用过程中的性能符合设计要求。
此外,实验验证还可以发现和解决仿真无法考虑到的一些问题,如器件工艺可行性、制造工艺的复杂度等。
当然,MEMS器件设计模型仿真和实验验证也面临一些挑战。
首先,MEMS器件设计的模型仿真在建模过程中需要准确的物理特性参数和材料参数,而这些参数通常需要进行实验测试,并可能受到误差的影响。

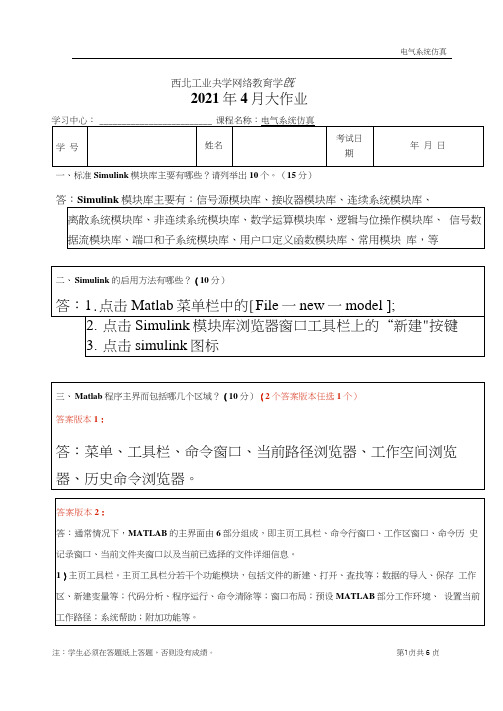
西北工业夬学网络教育学旣2021年4月大作业一、标准Simulink模块库主要有哪些?请列举出10个。
(15分)答:Simulink模块库主要有:信号源模块库、接收器模块库、连续系统模块库、MATLAB关系运算符关系运算符描述< 小于(3)逻辑运算MATLAB提供了3种逻辑运算符:&(与八1(或)和~(非)。
在算术.关系、逻辑运算中,算术运算优先级最高,逻辑运算优先级最低。
答案版本2:MATLAB屮包括三种矩阵运算类型:矩阵的代数运算、矩阵的关系运算和矩阵的逻辑运算。
其屮,矩阵的代数运算应用最广泛。
根据不同的应用II的, 矩阵的代数运算乂包含两种审要的运算形式:按矩阵整体进行运算的矩阵运算、按矩阵单个元素进行运算的元素群运算。
五.如何淸理Matlab I作区窗口的变量?(10分)(2个答案版本任选1个)答案版本1:答:选择主页•清除工作区•变量,即可消除工作区的变量。
或者在命令窗口中用clear命令,在提示符后键入:clear,回车即可。
答案版本2:答:使用“clear”命令,可以将工作区窗口的所有变量删除。
六、简述电力系统分析元件Powergui模块的功能。
(15分)(2个答案版本任选1个)答案版本1:七、SimPowerSystems 库中提供了哪几种简化同步发电机模块?有何不同?(15分)答:SimPowerSystems 库中提供了两种简化同步电机模块,其图标如图4-2所示。
图4-2(a)为标幺制单 位(p ・u ・)下的简化同步电机模块,图4・2(b)为国际单位制(SI)下的简化同步电机模块。
简化同步电机的两种模块本质上是一致的,唯一的不同在于参数所选用的单位。
(2个答案版本任选1个)答案版本1:(a) (b)图4-2简化同步电机模块图标(J 标幺制;(b)国际单位制答案版本2:答:提供了2种简化同步发电机模块:标幺制单位下的简化同步电机模块.国 际单位制下的简化同步电机模块.2种简化同步电机模块本质上是-样的,唯- 的不同在于参数所选用的单位。

微纳机电系统的设计与模拟分析引言近年来,微纳机电系统成为了科技领域的热门研究方向之一。
作为微型机械结构和电子元件的有机结合,微纳机电系统在电子通信、医疗健康、能源环保等领域具有广泛的应用前景。
本文将探讨微纳机电系统的设计与模拟分析,从理论到实践,系统地介绍微纳机电系统的设计原理、建模方法以及模拟分析技术。
一、微纳机电系统的设计原理微纳机电系统是通过集成微型机械结构和电子元件,通过微纳加工技术实现的一种微型化系统。
在设计微纳机电系统时,需要考虑以下几个关键原理。
1.机械结构的设计原理微纳机电系统是由微型机械结构组成的,对于机械结构的设计原理需要兼顾结构刚度、质量和可靠性等方面。
在设计时,可以借鉴力学原理,如应力分析、振动分析等,以保证机械结构的性能满足系统的需求。
2.电子元件的集成原理微纳机电系统中,电子元件的集成是实现系统功能的重要途径。
通过将传感器、执行器等电子元件集成到微型机械结构中,可以实现多个功能模块间的高效协同工作。
因此,在设计中需要考虑电子元件的布局、连接等问题。
3.微纳加工技术的应用原理微纳机电系统的制造离不开微纳加工技术的支持。
微纳加工技术包括光刻、电子束曝光、化学蚀刻等,可以实现对微型机械结构和电子元件的精确加工。
在设计过程中,需要充分考虑微纳加工技术的限制和特点,以确保设计方案的可实现性。
二、微纳机电系统的建模方法为了更好地理解微纳机电系统的行为和性能,需要对系统进行建模和仿真分析。
下面介绍几种常用的微纳机电系统建模方法。
1.有限元法建模有限元法是一种广泛应用于工程领域的建模方法,适用于对微纳机电系统进行结构力学和振动分析。
通过将微纳机电系统离散为多个有限元,利用平衡方程和边界条件求解节点的位移和应力分布,从而得到系统的结构响应。
2.多物理场耦合建模微纳机电系统往往涉及多个物理场的相互作用,如结构力学、热学、电磁学等。
在建模时,可以使用多物理场耦合的方法,将物理量耦合方程集成到一个综合模型中,从而综合考虑各个物理场的影响。

微纳流体力学仿真与智能微流控系统设计引言微纳流体力学是研究微观尺度下流体行为及其相关现象的学科领域,其应用广泛,涵盖了生物医学、化学分析、能源等多个领域。
在微纳尺度下,流体行为的特性与宏观尺度存在明显差异,因此需要针对微纳尺度下的流体行为进行仿真和研究。
智能微流控系统是利用微纳流体力学原理,通过精确控制微流道中的流体流动,实现样品的分离、混合、反应等操作的系统。
该系统具有高效、快速、精准等特点,可以用于生物医学分析、化学合成、环境监测等领域。
本文将对微纳流体力学仿真与智能微流控系统设计进行详细介绍,包括仿真方法、系统设计原理、应用案例等内容。
微纳流体力学仿真方法微纳流体力学仿真是研究微流道中流体行为的重要手段。
目前常用的微纳流体力学仿真方法主要包括有限元法、边界元法和蒙特卡洛法。
有限元法有限元法是一种常用的数值解法,可以对微纳尺度下的流体行为进行精确的仿真。
它通过将流域划分为有限个小单元,利用有限元法的基本原理,求解流体的速度、压力分布等参数。
边界元法边界元法是一种将边界上的条件转化为数学表达式进行求解的方法。
它通过在流体边界上建立边界元,利用边界元法的基本原理,求解流体的速度、压力等参数。
蒙特卡洛法蒙特卡洛法是一种通过随机抽样来模拟流体行为的方法。
它通过随机生成微观颗粒的位置和速度,利用概率分布函数来求解浓度、压力等参数。
智能微流控系统设计原理智能微流控系统设计是将微纳流体力学仿真的研究成果应用到实际的流控系统中。
其设计原理主要包括微流道设计、外部控制和自动化控制。
微流道设计微流道设计是智能微流控系统的核心,其主要任务是实现流体的分离、混合和反应等操作。
微流道的设计需要考虑流体行为、材料选择、表面处理等因素。
外部控制外部控制是智能微流控系统的关键环节,通过控制外部的压力、温度等参数,实现对微流道中流体的精确控制。
外部控制可以通过电动阀、温控器等设备来实现。
自动化控制自动化控制是将智能微流控系统与计算机等设备进行连接,实现对流体流动过程的自动监控和控制。

微纳流体力学仿真与微流控芯片设计1. 引言微纳流体力学是研究微尺度下流体行为的学科领域,它涵盖了从微观到纳米尺度的流体流动、传热和传质等现象。
近年来,微纳流体力学在医学诊断、生物分析、化学合成等领域得到了广泛的应用。
为了更好地理解和设计微纳流体系统,开展仿真和设计工作显得尤为重要。
本文将介绍微纳流体力学仿真的基本原理和方法,并探讨了微流控芯片的设计与制造过程。
2. 微纳流体力学仿真2.1 离散粒子动力学 (Lattice Boltzmann Method)离散粒子动力学方法是一种基于分子动力学原理的流体力学仿真方法,它通过将流体系统离散为许多粒子,并模拟粒子之间的相互作用,从而研究流体的运动行为。
在微纳尺度下,离散粒子动力学方法具有高效、准确和可靠的优势,被广泛应用于微纳流体力学仿真中。
2.2 多尺度模拟由于微纳流体系统的尺度差异,采用单一的仿真方法往往不能满足需求。
多尺度模拟是一种将不同尺度的仿真方法结合起来,通过耦合不同模型和方法,实现对复杂流动现象的分析与预测。
目前,常用的多尺度模拟方法包括分子动力学与连续介质力学的耦合仿真、多尺度网格方法等。
2.3 流体-结构耦合仿真在微流体系统中,流体与结构的相互作用对流动行为有着重要影响。
流体-结构耦合仿真是一种将流体力学仿真和结构力学仿真相结合的方法,能够模拟流体与结构之间的相互作用和耦合效应。
流体-结构耦合仿真在微纳流体力学领域中具有重要的应用价值,可以用于分析微通道的变形行为、流动对结构的影响等问题。
3. 微流控芯片设计3.1 微流控芯片基本结构微流控芯片是一种集成了微流体器件和微电子器件的芯片,通过精确控制微流体的流动和混合,实现对样品的操控和分析。
微流控芯片的基本结构包括微通道、微阀门、微泵和微感应器等组成部分。
其中,微通道是微流控芯片的核心,其形状和尺寸的设计直接影响流体的流动行为。
3.2 微流控芯片设计流程微流控芯片的设计流程一般包括以下几个步骤:•设计目标确定:根据实际需求确定微流控芯片的设计目标,包括流体流动参数、操控方法等;•结构设计:根据目标要求,设计微通道、微阀门等器件的结构和尺寸;•流场分析:通过数值仿真方法,对微通道内的流场进行模拟和分析,评估设计的可行性和效果;•制造工艺设计:根据设计结果,确定微流控芯片的制造工艺和流程,包括材料选择、薄膜制备、图案化和封装等;•制造与测试:根据制造工艺,制备微流控芯片,并进行相关的测试和评价;•优化和改进:根据测试结果,对设计进行优化和改进,以满足实际需求。
微纳机械系统的设计与模拟分析随着科技的不断进步,微纳机械系统在诸多领域中的应用日益广泛。
微纳机械系统是指尺度在微米至纳米级别的机械结构,具有非常小的尺寸和质量,能够完成微小的机械功能。
例如,微纳机械系统可以用于精确操控细胞、制造微型机器人、构建纳米级传感器等。
在微纳机械系统的设计与开发过程中,模拟分析是至关重要的一步,它可以帮助工程师和科研人员评估设计方案的可行性、性能和效果。
微纳机械系统的设计与模拟分析通常包括以下几个步骤:建立模型、进行数值模拟、分析模拟结果和优化设计。
首先,建立模型是模拟分析的基础。
微纳机械系统通常由一系列微小的结构组成,如悬臂梁、薄膜和微型齿轮等。
为了进行模拟分析,必须对这些结构进行准确的建模。
传统的建模方法包括有限元方法和多体动力学方法等,而近年来,机器学习等新兴技术也被应用于微纳机械系统的模型建立。
在建立模型之后,接下来进行数值模拟。
数值模拟是通过计算机仿真的方式,对微纳机械系统的行为进行预测和分析。
在数值模拟过程中,需要考虑多个因素,如材料力学性质、结构几何形状、环境条件等。
通过对这些因素进行合理的参数设置和模拟计算,可以获得微纳机械系统在不同工作条件下的响应,如位移、应力和振动等。
分析模拟结果是设计与模拟分析的重要一环。
根据模拟结果,可以评估设计方案的可行性和性能。
例如,可以通过模拟分析来判断微纳机械系统是否满足预期的运动精度、工作稳定性和可靠性要求。
同时,分析模拟结果还可以帮助寻找设计方案中的潜在问题和改进空间。
通过对模拟结果的仔细分析和解读,可以为后续的优化设计提供指导和参考。
优化设计是微纳机械系统设计与模拟分析的最终目标。
通过优化设计,可以进一步改进设计方案,使其在性能、效率和成本等方面得到最佳平衡。
优化设计可以基于模拟分析结果,采用一系列的优化算法和方法,寻找最优的设计参数。
例如,可以通过改变材料的选择、结构的布局和尺寸的变化等,来提高微纳机械系统的性能和效果。
微纳卫星测控系统链路预算与仿真1. 内容概述本文档旨在详细介绍微纳卫星测控系统链路预算与仿真的相关知识和技术。
随着微纳卫星技术的不断发展,其在通信、导航、遥感等领域的应用越来越广泛。
为了提高微纳卫星的性能和可靠性,对其测控系统的链路预算与仿真进行研究具有重要意义。
本文档首先介绍了微纳卫星测控系统的基本概念和组成,包括通信链路、控制链路、数据链路等。
然后详细阐述了链路预算的概念和方法,包括链路预算的计算步骤、参数设置、性能评估等。
本文对微纳卫星测控系统的链路预算与仿真进行了实例分析,通过具体的实验数据和仿真结果,验证了链路预算方法的有效性。
本文档还讨论了微纳卫星测控系统中的关键技术,如信道编码、多址接入、干扰抑制等,并提出了相应的解决方案。
本文对微纳卫星测控系统链路预算与仿真的未来发展趋势进行了展望,包括采用新型算法、优化设计方法、提高仿真精度等方面的研究。
1.1 研究背景与意义随着航天技术的迅速发展,微纳卫星作为一种低成本、高效率的航天器解决方案,已成为当今航天领域的研究热点。
微纳卫星具有体积小、质量轻、研制周期短等特点,广泛应用于科研实验、通信技术、地球观测等多个领域。
而微纳卫星测控系统作为保障微纳卫星正常运行的关键组成部分,其性能优劣直接影响到微纳卫星的任务执行效果。
在当前复杂的航天环境中,微纳卫星测控系统面临着诸多挑战,如通信链路不稳定、能源管理困难、控制精度要求高等。
为了解决这些问题,对微纳卫星测控系统的链路预算与仿真研究显得尤为重要。
通过对测控系统的链路进行全面预算,可以评估系统性能,预测潜在问题,并优化资源配置。
仿真技术的运用能够在不实际制造卫星的情况下模拟测控系统的运行情况,从而验证设计的合理性和可行性,降低研发风险。
深入研究微纳卫星测控系统的链路预算与仿真技术具有十分重要的意义。
这不仅有助于提升微纳卫星的整体性能,还能推动航天测控技术的进步,为未来的航天事业发展提供有力支撑。
1.2 国内外研究现状随着微纳卫星技术的飞速发展,微纳卫星测控系统及其链路预算在空间探索领域受到了越来越多的关注。
微纳流体力学特性的多尺度模拟与实验验证近年来,微纳流体力学已经成为研究领域中备受关注的热点之一。
微纳流体力学主要研究微尺度下流体的运动和传输特性,具有广泛的应用前景,例如微流控芯片、生物医学领域的药物输送系统等。
为了深入理解和掌握微纳流体力学特性,研究人员不断探索多尺度模拟和实验验证的方法。
多尺度模拟是研究微纳流体力学特性的重要手段之一。
由于微尺度下流体的运动和传输过程受到分子间相互作用力的影响,传统的宏观流体力学理论不能直接适用于微纳尺度。
因此,研究人员通过分子动力学(MD)模拟和介观动力学(MD)模拟等方法,对微纳流体力学进行多尺度建模和模拟。
通过这些模拟方法,研究人员可以获得微尺度下流体的精细结构和动力学行为,进而揭示微纳流体力学的一些重要特性,如流体的流动规律、分子传输的机制等。
然而,多尺度模拟也存在一些局限性。
首先,由于微纳尺度下流体的分子数目巨大,模拟过程需要耗费大量的计算资源和时间。
其次,多尺度模拟中的参数选择和模型构建也是一个挑战,需要考虑到精度和计算效率的平衡。
此外,模拟结果的可靠性和准确性也需要通过实验验证来进行验证。
实验验证是研究微纳流体力学特性不可或缺的一部分。
通过实验,研究人员可以直接观察和测量微纳尺度下流体的运动和传输行为,从而验证模拟结果的准确性。
例如,通过显微镜观察微流控芯片中的流体流动情况,可以验证模拟结果中的流动规律和流体的微观行为。
此外,利用纳米颗粒追踪技术,可以实时观察和测量微纳尺度下颗粒的运动轨迹,进一步验证模拟结果中的颗粒传输机制。
然而,实验验证也存在一些困难和限制。
首先,由于微纳尺度下流体的运动和传输过程很小,需要使用高分辨率的仪器和设备进行观测和测量。
其次,实验过程中会受到环境因素的影响,如温度、压力等,需要进行相应的修正和校正。
此外,实验结果的可重复性和可靠性也需要进行多次实验和统计分析来进行验证。
综上所述,微纳流体力学特性的研究需要结合多尺度模拟和实验验证的方法。
微纳尺度MEMS传感器制备和模型仿真技术表征与测试微纳尺度MEMS(Micro Electro-Mechanical Systems,微机电系统)传感器是一种基于微纳技术制备的具有微机电一体化功能的传感器。
它具有尺寸小、功耗低、响应速度快、精度高等特点,广泛应用于工业控制、医疗设备和消费电子等领域。
在微纳尺度MEMS传感器的制备和模型仿真技术方面,表征与测试的重要性不可忽视。
首先,微纳尺度MEMS传感器的制备是保证其性能的关键。
微纳技术的发展为传感器的制备提供了一种精确控制器件尺寸和结构的方法。
制备过程中,需要采用高精度的光刻技术、扩散、沉积、蚀刻等工艺步骤来实现传感器的微纳尺度结构。
此外,传感器材料的选择也是制备过程中需要考虑的重要因素。
常用的材料有硅、玻璃和聚合物等。
通过不同的制备工艺和材料选择,可以实现不同类型和功能的微纳尺度MEMS传感器。
其次,模型仿真技术对于微纳尺度MEMS传感器的设计和性能分析具有重要意义。
借助仿真软件,可以对传感器的结构、材料和工艺参数进行模拟和优化。
通过建立传感器的数学模型,可以预测其在不同工作条件下的性能表现。
仿真结果可以为传感器设计提供重要参考,帮助工程师优化传感器的结构和工艺参数,提高其灵敏度、精度和可靠性。
第三,对微纳尺度MEMS传感器进行表征与测试是验证其性能的关键环节。
传感器性能的表征与测试包括静态和动态性能测试。
静态性能测试主要包括灵敏度、线性度、分辨率和稳定性等指标的测试。
而动态性能测试则关注传感器在响应时间、频率响应和抗干扰等方面的表现。
表征与测试的过程需要采用适当的测试设备和方法,如静电力和压力测量系统、微机电系统测试平台等。
通过表征和测试,可以全面了解传感器的性能特性,评估其是否满足设计要求。
在微纳尺度MEMS传感器制备和模型仿真技术表征与测试中,还有一些挑战需要克服。
首先,微纳尺度制备技术要求高度精确,制备过程容易受到环境和材料的干扰。
这要求研究人员采用高精度的设备和工艺控制方法,提高制备的一致性和可重复性。
1. 用有限差分法和有线元方法把以下问题变成数值方程,并说明两种方法的异同:
2(,)0x y ϕ∇= 边界条件:
(,0)(,1)0;(0,)(1,)1;
x x y y ϕϕϕϕ==== 解:
(1) 有限差分法 2(,)0x y ϕ∇= 即为20xx yy u u u ∇=+=,其中(),u x y ϕ=
将定义域等分,步长均为h ,则
()()()()()()222,,,,4,u x h y u x h y u x y h u x y h u x y u O h h
++-+++--∇=+ 略去高阶无穷小,由20xx yy u u u ∇=+=得
()()()()(),,,,4,0u x h y u x h y u x y h u x y h u x y ++-+++--=
定义域离散,离散点为(),i j x y ,则上式可化为
()()()()(),,,,4,0i j i j i j i j i j u x h y u x h y u x y h u x y h u x y ++-+++--=
定义域为01,01x y ≤≤≤≤,因为本题只是为了说明原理,故将其简单等分为33⨯单元,节点编号从()()0,02,2到。
则
1,1,,1,1,40i j i j i j i j i j u u u u u +-+-+++-=
其位移矢量为
()()()()()()()()()0,00,10,21,01,11,22,02,12,24110141101410141101411011410141011410140u u u u u u u u u ⎡⎤⎢⎥-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦
由边界条件 (,0)(,1)0;(0,)(1,)1;
x x y y ϕϕϕϕ==== 可知()()()()0,00,22,02,2,,,u u u u 有冲突,可以区位均值即()()()()0,00,22,02,20.5u u u u ====,而()()1,11,20u u ==,()()0,12,10u u ==,带入化简即可求得()1,1u
(2) 有限元法
使用有限元法的计算流程为:
求解区域离散化;
构造插值函数形成分段光滑的坐标函数系;
用 Ritz 方法求解微分方程
对2(,)0x y ϕ∇=构造函数
()221,2x y dxdy x x ϕϕϕ⎡⎤∂∂⎛⎫⎛⎫∏=+⎡⎤⎢⎥ ⎪ ⎪⎣⎦∂∂⎝⎭⎝⎭⎢⎥⎣⎦
⎰⎰ 首先将整个区域离散为三角形的子区域如下图, 三角形微小子区域中的值由三 角形节点值的插值结果表示,即
(),i i j j k k x y N N N ϕϕϕϕ=++
其中,,i j k N N N 为三角形的节点插值函数, ,,i j k ϕϕϕ为函数(),x y ϕ在节点 ,,i j k 处的函数值。
可知每一个三角形子区域中泛函可由节点插值函数和节点函数值表示, 那么对于整个求解区域的泛函表达式为
()[]123,,,...n x y ϕϕϕϕϕ∏=∏⎡⎤⎣⎦
由变分原理可知
12...0n
ϕϕϕ∂∏∂∏∂∏====∂∂∂ 计算这 n 个方程即可得到整个求解区域的值
(3) 有限元法与差分法的区别
• 区域离散化要与坐标轴一致,所以大多是正方形或矩形的离散结构,表述边界的误差较大
• 有限元单元的形状没有限制,可以做到单元形状与边界重合,处理无规边界的问题
• 有限元统一对待区域内的节点与边界上的节点,因此个节点的计算精度总体上协调;而有限差分必须分别处理微分方程与定解条件
2. 请看Microrobot的说明文件(这个文件可以在COMSOL
3.5中打开Model Library----→ Thermal Structure Interaction---→Microrobot 3D),详细看懂说明书该问题的分析,用自己熟悉的3D工具进行建模,用COMSOL更高版本进行仿真。
解:
微型机器人腿构造如下:
原理:热源加热使得局部温度升高,由于所使用有机物的热膨胀系数较高,故加热有有机物体积膨胀大,V型槽上部体积膨胀高于下部,故硅腿会向下弯曲。
Comsol仿真:
建模时V型槽薄板不画出,仿真设定V型面为shell单元。
模型如下图:
图1.1 Robot leg 3D模型
计算结果:
图1.2 Robot leg 位移图
图1.3 Robot leg 温度图
分析:从位移变形图可以看出,腿向下弯曲,这与实际情况一致;从根部至末端,位移逐渐增大;末端最大为51.8110m -⨯ 即18.1um 。
从温度变形图可以看出,V 型槽温度最高,为305K ,腿根部温度最低,为275K ,散热效果良好
3. 请学习COMSOL
4.4的COMSOL Reference Manual中Deformed Geometry and Moving Mesh的使用方法,用COMSOL4.4 仿真流体与结构的相互作用(问题描述请见文件:fluid_structure_interaction.pdf)。
解:
原理:流体以一定流速流过通道时,会与通道中物体产生相互作用了,在该作用力的作用下,物体会产生应力和形变。
Comsol仿真:流体从六面体前表面流进inlet,后表面流出outlet,其他便面设定为wall,中间固定物体下表面为fix constrain。
在comsol5.0中流速采用例子中所给的
16*u_max*y*(width-y)*z*(height-z)/(width^2*height^2)无法求解,具体原因不详,因此设定inlet为恒定速度1.5/
m s。
模型如下图:
图2.1 Fluid structure 3D模型
计算结果:
图2.2 Fluid structure 位移图
图2.3 Fluid structure 应力图
分析:从位移和应力图可以看出,流体与柱状体表面作用使得柱状体弯曲,与实际情况相符;顶端点为位移最大,应力最小,位移为55.293510m -⨯ 即52.935um ,
应力为382.465Pa
;根部位移最小,应力最大,位移为0um ,应力为621.1704710/N m ⨯ 即1.17047Mpa 。
4. 微型层流混合器
(1)请看COMSOL4.4 中Model Libraries—MEMS Module –Micromixers---Lamella mixer PDF说明书,用SOLIDWOKS工具建模,用COMSOL仿真;
(2)自己设想一种可能的更有效的微型流体混合结构;
(3)试试用其他的软件进行仿真并比较说明
解:
原理:
经过微型流体混合机构,微流体从不同的小通道汇聚到大通道中
首先要进行3D建模,微型流体混合器的3D模型如下图:
图3.1 Lamella mixer 3D模型
Comsol计算结果
图3.2 Lamella mixer 速度图
图3.3 Lamella mixer 浓度图
分析
流体从微小通道汇聚到大通道后流速会降低,且浓度会保持分层趋势,仿真结果与实际情况符合。
通过对速度图分析可知最高流体速度为31.2810/m s -⨯ ,最小速度为零;分析浓度图可知,流体在校通道中浓度不变,汇聚到大通道后浓度混合,但上层浓度明显要高于下层。
ANSYS CFX 计算
在ANSYS 分析中,没有严格按照Comsol 中的速度及浓度定义,设定入口速度分别为5m/s 和10m/s ,其余均为默认值,分析结果如下:
图3.4 CFX 分析结果-速度
图3.5 CFX分析结果-压力
两种分析结果对比分析
ANSYS CFX中后处理的可选项相对Comsol比较少,但是操作流程基本相同
微纳系统仿真
5. 谈谈使用COMSOL进行多场耦合仿真的体会。
以上2、3、4道需要大家安装COMSOL软件。
Comsol可以很方便的进行多场仿真,包含了相当多的常用模块,想要添加场时只需要简单的添加相应模块并设定初值和边界条件即可。
和Ansys比起来comsol的一大优点是,可以看到计算的微分方程模型。
这一功能对于初学者来说虽然意义不大,因为初学者没有足够的知识储备去理解这些方程,但是如果真正的从事研究工作,Comsol是非常好用的计算仿真工具。
第11页。