第十一章本章优化总结

第十一章约束最优化问题的可行方向法§1 Frank-Wolf方法一、问题形式（11.1）其中为矩阵，，。

记并设一阶连续可微。

二、算法基本思想是一个凸多面体，任取，将在处线性展开用或（11.2）逼近原问题，这是一个线性规划问题，设是其最优解。

1）若，则也是线性规划问题（11.2）的最优解，此时可证为原问题的K-T点。

2）若，则由是（11.2）的最优解，故必有从而即为在处的下降方向，沿此方向作有约束的一维搜索设最佳步长因子为，令当充分小时用取代，重复以上计算过程。

三、算法迭代步骤1）给定初始点，允许误差，。

2）求解线性规划问题，得最优解。

3）若，Stop,；否则go to 4)。

4）进行一维搜索，得最优步长因子；令，，go to 2)四、算法收敛性定理设非线性规划问题（11.1）的最优解存在，且对算法产生的点列，线性规划问题（11.3）的最优解总存在。

则1）若迭代到某步，有，则为问题（11.1）的K-T点；2）若情形1）总不发生，则算法产生一有界无穷点列，其任意极限点都是原问题（11.1）的K-T点。

证明：若情形1）出现，则也是问题（11.3）的最优解，故满足（11.3）的K-T条件：（11.4）而(11.1)的K-T条件：（11.5）（11.4）表明，，一起满足K-T条件（11.5），故是原问题的K-T点。

2）由点列包含在的极点的凸组合中，而均为的极点，故、均为有界点列。

设为的任一极限点，即存在子列，使得：注意到点列满足：考虑点列、、，不失一般性，设，，否则，可以通过反复抽取子序列，使上式对某个子序列成立。

由是的最优解，故，有且再由及取极限，有（11.6）不等式组（11.6）等价于：（11.7）若能证明即为问题的最优解，由本定理的第一部分可知，为原问题K-T点。

下证：，若不然，由（11.7）即知必有故为处的下降方向，因而当充分小时，有进而有：（11.8）但为单调下降的有界序列，故存在而且即与（11.8）矛盾，故必有。

高中物理必修三第十一章知识点总结高中物理必修三第十一章主要涉及到电流和电阻的相关知识。

本章内容包括电流、电阻的定义和性质、欧姆定律、串联和并联电阻的计算、电功率和电能的计算等。

一、电流电流是电荷的流动，是电荷在导体中的移动形成的。

电流的单位是安培（A），1A等于1库仑/秒。

电流的方向由正电荷的流动方向决定。

二、电阻电阻是导体阻碍电流通过的程度，是导体抵抗电流流动的特性。

电阻的单位是欧姆（Ω）。

电阻与导体材料、导体的长度和截面积有关。

三、欧姆定律欧姆定律是描述电流、电压和电阻之间关系的定律。

它表明在恒温下，电流与电压成正比，与电阻成反比。

数学表达式为：I = U/R。

四、串联电阻串联电阻是指多个电阻依次连接，电流依次流过各个电阻的情况。

串联电阻的总电阻等于各个电阻之和，即R = R1 + R2 + ... + Rn。

五、并联电阻并联电阻是指多个电阻同时连接在电路中，电流在各个电阻中分流的情况。

并联电阻的总电阻满足倒数之和等于倒数和，即1/R = 1/R1 + 1/R2 + ... + 1/Rn。

六、电功率电功率是电流通过电路时所做的功，表示电能转化的速率。

电功率的单位是瓦特（W），1W等于1焦耳/秒。

电功率可以通过电流和电压计算得到，P = UI。

七、电能电能是电流通过电路时所转化的能量，是电功率与时间的乘积。

电能的单位是瓦特时（Wh），1Wh等于1瓦特乘以1小时。

电能可以通过电功率和使用时间计算得到，E = Pt。

总结：本章主要介绍了电流和电阻的基本概念和性质，以及与之相关的欧姆定律、串联和并联电阻的计算、电功率和电能的计算等知识。

了解这些知识可以帮助我们理解电流和电阻在电路中的作用和计算方法，为解决相关问题提供了基础。

同时，通过掌握这些知识，我们也可以更好地理解和应用电路中的其他内容，为进一步学习和研究电路提供了基础。

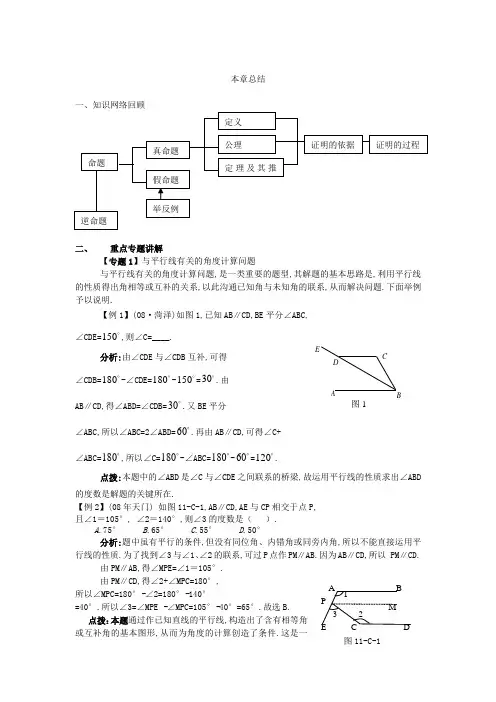
本章总结一、知识网络回顾二、 重点专题讲解【专题1】与平行线有关的角度计算问题与平行线有关的角度计算问题,是一类重要的题型,其解题的基本思路是,利用平行线的性质得出角相等或互补的关系,以此沟通已知角与未知角的联系,从而解决问题.下面举例予以说明.【例1】(08·菏泽)如图1,已知AB ∥CD,BE 平分∠ABC,∠CDE= 150,则∠C=____.分析:由∠CDE 与∠CDB 互补,可得∠CDB= 180-∠CDE= 180- 150= 30.由AB ∥CD,得∠ABD=∠CDB= 30.又BE 平分∠ABC,所以∠ABC=2∠ABD=60.再由AB ∥CD,可得∠C+∠ABC= 180,所以∠C= 180-∠ABC= 180- 60= 120.点拨:本题中的∠ABD 是∠C 与∠CDE 之间联系的桥梁,故运用平行线的性质求出∠ABD 的度数是解题的关键所在.【例2】(08年天门) 如图11-C-1,AB ∥CD,AE 与CP 相交于点P,且∠1＝105°, ∠2＝140°,则∠3的度数是（ ）.A .75°B .65°C .55°D .50°分析:题中虽有平行的条件,但没有同位角、内错角或同旁内角,所以不能直接运用平行线的性质.为了找到∠3与∠1、∠2的联系,可过P 点作PM ∥AB.因为AB ∥CD,所以 PM ∥CD.由PM ∥AB,得∠MPE=∠1＝105°.由PM ∥CD,得∠2+∠MPC=180°, 所以∠MPC=180°-∠2=180°-140° =40°.所以∠3=∠MPE -∠MPC=105°-40°=65°.故选B. 点拨：本题通过作已知直线的平行线,构造出了含有相等角或互补角的基本图形,从而为角度的计算创造了条件.这是一 A B C D E 图1 A B C D P M 1 2 3 E 图11-C-1种常用的解题技巧,希望同学们能够认真体会.【专题2】数学思想方法（一）分类思想分类思想方法是一种重要的数学思想方法,正确、合理、严谨的分类,可将一个复杂的问题简单化,达到化繁为简、化难为易、分而治之的目的。

必修三第十一章知识点总结本章主要讲述了社会主义初级阶段的理论和实践，探讨了社会主义初级阶段的基本特征、基本矛盾和基本任务，深入分析了我国社会主义初级阶段的基本国情和基本状况，以及在这种基本国情和基本状况下，社会主义初级阶段的总路线和基本纲领，指出了全党全军全国各族人民团结奋斗、坚持稳定、密切联合、以经济建设为中心的方针，处理好社会主义初级阶段的各种矛盾。

一、本章要点（一）社会主义初级阶段1、社会主义初级阶段的基本特征社会主义初级阶段是指进入社会主义制度的国家在生产力不发达、经济文化落后的情况下，必须经历的一个相对长的历史时期。

它的主要特征是：我国是世界上最大的发展中国家，人口众多，还处于城乡差距大、区域发展不平衡、生产力比较薄弱、物质文明和精神文明都比较落后的国情。

因此它是在我国国情和国际条件下确立的历史阶段。

2、社会主义初级阶段的基本矛盾社会主义初级阶段的基本矛盾是**生产关系和生产力之间的矛盾**。

生产关系和生产力的矛盾，在经济基础中具体表现为：我国经济社会的总体生产力比较落后，同生产关系发展的需要不相适应，出现了严重的矛盾。

3、社会主义初级阶段的基本任务关于社会主义初级阶段的基本任务，既要坚持马克思主义的基本原则，又要根据我国具体国情，以发展生产力为中心。

我国的基本国情是我国是世界上最大的发展中国家，人口众多，粮食短缺任务繁、生产力落后，还处于城乡差距大、区域发展不平衡、物质文明和精神文明都比较落后的国情。

因此，发展生产力仍然是解放生产力，解决人民日益增长的需要的根本动力。

（二）社会主义初级阶段的总路线和基本纲领1、社会主义初级阶段的总路线社会主义初级阶段的总路线是：在社会主义初级阶段，发展社会主义社会生产力，解决人民日益增长的物质和文化需要，发展社会主义的先进文化，建设社会主义的先进政治制度。

这是在我国社会主义初级阶段总路线的基础上提出的基本纲领。

它概括了我国社会主义初级阶段发展的战略任务。

八年级数学上册第十一章梯形知识点总
结 (新版)新人教版
1. 梯形的定义
梯形是指有两条平行边的四边形。

其中，较长的两边叫做上底和下底，两条连接上底和下底的斜边叫做腰，而两条腰的交点叫做顶点。

2. 梯形的分类
根据上底和下底的长度关系，梯形可以分为以下几类：
- 等腰梯形：上底和下底长度相等的梯形。

- 直角梯形：腰和底边之间有直角的梯形。

- 一般梯形：除了等腰梯形和直角梯形以外的其他梯形。

3. 梯形的性质
- 梯形的对边平行：一条边和与之不共顶点的另一条边平行。

- 梯形的底角和顶角互补：底边的两个邻角和顶边的两个邻角互补，即它们的和为180度。

- 等腰梯形的性质：等腰梯形的底角相等，顶角相等，且底边中点连线与顶边中点连线平行。

4. 梯形的面积计算
梯形的面积可以用以下公式计算：
面积 = [(上底 + 下底) ×高] ÷ 2
5. 梯形的周长计算
梯形的周长可以用以下公式计算：
周长 = 上底 + 下底 + 两条腰的长度
以上是八年级数学上册第十一章梯形的基本知识点总结，希望对您的研究有所帮助！。

论语第十一章先进篇心得总结的第十一章先进篇，读来真让我感触颇多。

这一章里，孔子和他弟子们的言行举止，就像是一幅幅生动的画面，在我眼前不断展开。

先来说说这一章中的一些具体内容吧。

里面提到了颜回的安贫乐道，子路的直率勇敢，还有孔子对于不同弟子的评价和教导。

这让我不禁想到了自己生活中的点点滴滴。

就拿我身边的一个朋友小宁来说吧。

小宁啊，那可真是个特别的人，跟颜回有点相似之处呢。

小宁的家庭条件不算好，但是他从来没有抱怨过，每天都是乐呵呵的。

他住在一个小小的出租屋里，房间简陋得很，一张旧床，一个掉了漆的书桌，还有一把坐上去嘎吱嘎吱响的椅子。

可他却把那小房间收拾得干干净净，还在墙上贴了自己写的励志话语。

有一次我去他那里，一进门就被那股积极向上的氛围给感染了。

他正在那张书桌上认真地学习，台灯的光洒在他专注的脸上。

我好奇地问他：“小宁，你这条件这么艰苦，咋还这么有劲头呢？”他抬起头，笑着对我说：“这算啥艰苦呀，能有个地方让我安安静静学习，我就很满足啦。

”他的眼神里透着坚定，那一刻，我突然明白了颜回那种“一箪食，一瓢饮，在陋巷，人不堪其忧，回也不改其乐”的境界。

小宁在学习上也特别刻苦。

每天早上天不亮就起来背单词，晚上我们都出去玩了，他还在那里做练习题。

记得有一次，我们几个朋友约好一起去看电影，大家都到齐了，就差小宁。

打电话一问，他居然还在图书馆查资料，为了一道难题在那钻研呢。

等他赶到电影院的时候，电影都快结束了。

我们都埋怨他，他却一脸不好意思地说：“哎呀，那道题我要是不弄明白，心里就不踏实。

”还有一次，学校组织了一场知识竞赛。

小宁毫不犹豫地报了名。

比赛前的那几天，他几乎是废寝忘食，把所有的时间都花在了准备上。

我们都劝他别太拼了，可他却说：“这是个难得的机会，我得好好把握。

”比赛那天，他在台上镇定自若，对答如流，最终赢得了比赛的冠军。

那一刻，他站在领奖台上，笑容灿烂得像阳光一样。

再回过头来看中的先进篇，我觉得孔子对于弟子们的教导，其实就是在告诉我们，人生的道路上，无论处于何种境遇，都要有自己的坚守和追求。

初中物理第十一章知识点总结归纳第一节电流的概念与电路图符号电流是流经导体的电荷数量。

用字母I表示，单位是安培（A）。

在电路图中，电流用箭头表示，箭头指向表示电流的方向。

第二节电流的方向与电子的运动方向电流方向是指正电荷（正离子）的运动方向，与电子的运动方向相反。

第三节电流的测量电流可以使用安培表进行测量，将安培表连接在待测电路的路径上，读数即为电流值。

第四节电阻的概念与测量电阻是物体阻碍电流通过的特性。

用字母R表示，单位是欧姆（Ω）。

电阻可以使用欧姆表进行测量，将欧姆表连接在待测电阻两端，读数即为电阻值。

第五节常用导体与非导体的特性常用导体如铜、铝等，它们具有低电阻，能够很好地传导电流。

非导体如橡胶、塑料等，它们具有高电阻，不易传导电流。

第六节串联电路与并联电路串联电路是指电流从一个元件流过，再流向下一个元件。

在串联电路中，总电阻等于各个元件电阻之和。

并联电路是指电流同时通过多个元件。

在并联电路中，总电阻等于各个元件电阻的倒数之和的倒数。

第七节电压的概念与测量电压是电荷在电路中的能量转换，也称为电势差。

用字母U表示，单位是伏特（V）。

电压可以使用电压表进行测量，将电压表连接在待测电路的两点之间，读数即为电压值。

第八节电阻与电压的关系根据欧姆定律，电阻与电压成正比，电流与电压成正比。

公式为：U = I * R。

其中，U表示电压，I表示电流，R表示电阻。

第九节欧姆定律的应用欧姆定律可以应用于解决电路中的电流、电压和电阻之间的关系问题。

通过欧姆定律，我们可以计算出电流、电压或电阻的未知值。

第十节电功与功率电功是电能转换的体现，用字母W表示，单位是焦耳（J）。

功率是电功转化的速率，用字母P表示，单位是瓦特（W）。

功率等于电流乘以电压，即P = I * U。

第十一节并联电路中的电流计算在并联电路中，总电流等于各个元件所受电压之和除以总电阻。

第十二节串联电路中的电压计算在串联电路中，总电压等于各个元件电压之和。

第十一章三角形11.1.与三角形有关的线段11.1.1.三角形的边1、三角形的概念由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。

组成三角形的线段叫做三角形的边；相邻两边的公共端点叫做三角形的顶点；相邻两边所组成的角叫做三角形的内角，简称三角形的角。

三角形用符号“∆”表示，顶点是A、B、C的三角形记作“∆ABC”，读作“三角形ABC”。

2、三条边都不相等的三角形叫做不等边三角形三条边都相等的三角形叫做等边三角形有两条边相等的三角形叫做等腰三角形。

相等的两条边叫做腰，另一条边叫做底边，两腰的夹角叫做顶角，腰与底边的夹角叫做底角3、三角形的分类三角形按边分类如下：三边都不相等的三角形三角形底和腰不相等的等腰三角形等腰三角形等边三角形三角形按角的关系分类如下：直角三角形（有一个角为直角的三角形）三角形锐角三角形（三个角都是锐角的三角形）斜三角形钝角三角形（有一个角为钝角的三角形）4、三角形的三边关系定理及推论（1）三角形三边关系定理：三角形的两边的和大于第三边。

（2）推论：三角形的两边的差小于第三边。

11.1.2三角形的高、中线与角平分线1、三角形的高：经过三角形的一个顶点向它对边所在的直线画垂线，这个点和垂足之间的线段叫做三角形的高高的表示方法;（1）AD 是三角形ABC 的高（2）AD 是BC 边上的高（3）AD ⊥BC 于点D（4）∠ADB=∠ADC=90°2、三角形的中线：连接三角形的一个顶点和它对边中点的线段叫做三角形的中线。

中线的表示方法：（1）AE 是三角形ABC 的中线（2）BE=CE（3）BE=21BC （4）BC=2BE 或BC=2CE3、三角形的角平分线：三角形的一个角的平分线与它的对边相交，这个点和交点间的线段叫做三角形的角平分线。

角平分线的表示方法：（1）AF 是三角形ABC 的角平分线（2）∠BAF=∠CAF（3）∠BAC=2∠BAF（4）∠BAF=21∠BAC 4、三角形的三条中线相交于一点，三角形三条中线的交点叫做三角形的重心。

高中数学第十一章-概率考试内容：随机事件的概率．等可能性事件的概率．互斥事件有一个发生的概率．相互独立事件同时发生的概率．独立重复试验． 考试要求：（1）了解随机事件的发生存在着规律性和随机事件概率的意义．（2）了解等可能性事件的概率的意义，会用排列组合的基本公式计算一些等可能性事件的概率。

（3）了解互斥事件、相互独立事件的意义，会用互斥事件的概率加法公式与相互独立事件的概率乘法公式计算一些事件的概率．（4）会计算事件在n 次独立重复试验中恰好发生κ次的概率．§11. 概率 知识要点1. 概率：随机事件A 的概率是频率的稳定值，反之，频率是概率的近似值.2. 等可能事件的概率：如果一次试验中可能出现的结果有年n 个，且所有结果出现的可能性都相等，那么，每一个基本事件的概率都是n1，如果某个事件A 包含的结果有m 个，那么事件A 的概率nm P(A)=. 3. ①互斥事件：不可能同时发生的两个事件叫互斥事件. 如果事件A 、B 互斥，那么事件A+B 发生(即A 、B 中有一个发生)的概率，等于事件A 、B 分别发生的概率和，即P(A+B)=P(A)+P(B)，推广：)P(A )P(A )P(A )A A P(A n 21n 21+++=+++ .②对立事件：两个事件必有一个发生的互斥事件．．．．．．．．．．．．．．．叫对立事件. 例如：从1～52张扑克牌中任取一张抽到“红桃”与抽到“黑桃”互为互斥事件，因为其中一个不可能同时发生，但又不能保证其中一个必然发生，故不是对立事件.而抽到“红色牌”与抽到黑色牌“互为对立事件，因为其中一个必发生.注意：i.对立事件的概率和等于1：1)A P(A )A P(P(A)=+=+.ii.互为对立的两个事件一定互斥，但互斥不一定是对立事件.③相互独立事件：事件A(或B)是否发生对事件B(或A)发生的概率没有影响.这样的两个事件叫做相互独立事件. 如果两个相互独立事件同时发生的概率，等于每个事件发生的概率的积，即P(A·B)=P(A)·P(B). 由此，当两个事件同时发生的概率P （AB ）等于这两个事件发生概率之和，这时我们也可称这两个事件为独立事件.例如：从一副扑克牌（52张）中任抽一张设A ：“抽到老K”；B ：“抽到红牌”则 A 应与B 互为独立事件[看上去A 与B 有关系很有可能不是独立事件，但261P(B)P(A),215226P(B),131524P(A)=⋅====.又事件AB 表示“既抽到老K 对抽到红牌”即“抽到红桃老K 或方块老K”有261522B)P(A ==⋅，因此有)B P(A P(B)P(A)⋅=⋅.推广：若事件n 21,A ,,A A 相互独立，则)P(A )P(A )P(A )A A P(A n 21n 21 ⋅=⋅.注意：i. 一般地，如果事件A 与B 相互独立，那么A 与A B ,与B ，A 与B 也都相互独立. ii. 必然事件与任何事件都是相互独立的.互斥对立iii. 独立事件是对任意多个事件来讲，而互斥事件是对同一实验来讲的多个事件，且这多个事件不能同时发生，故这些事件相互之间必然影响，因此互斥事件一定不是独立事件. ④独立重复试验：若n 次重复试验中，每次试验结果的概率都不依赖于其他各次试验的结果，则称这n 次试验是独立的. 如果在一次试验中某事件发生的概率为P ，那么在n 次独立重复试验中这个事件恰好发生k 次的概率：kn k k n n P)(1P C (k)P --=. 4. 对任何两个事件都有)()()()(B A P B P A P B A P ⋅-+=+第十二章-概率与统计考试内容：抽样方法.总体分布的估计． 总体期望值和方差的估计． 考试要求：（1）了解随机抽样了解分层抽样的意义，会用它们对简单实际问题进行抽样． （2）会用样本频率分布估计总体分布． （3）会用样本估计总体期望值和方差．§12. 概率与统计 知识要点一、随机变量.1. 随机试验的结构应该是不确定的.试验如果满足下述条件： ①试验可以在相同的情形下重复进行；②试验的所有可能结果是明确可知的，并且不止一个；③每次试验总是恰好出现这些结果中的一个，但在一次试验之前却不能肯定这次试验会出现哪一个结果.它就被称为一个随机试验.2. 离散型随机变量：如果对于随机变量可能取的值，可以按一定次序一一列出，这样的随机变量叫做离散型随机变量.若ξ是一个随机变量，a ，b 是常数.则b a +=ξη也是一个随机变量.一般地，若ξ是随机变量，)(x f 是连续函数或单调函数，则)(ξf 也是随机变量.也就是说，随机变量的某些函数也是随机变量.设离散型随机变量ξ可能取的值为： ,,,,21i x x xξ取每一个值),2,1(1 =i x 的概率i i p x P ==)(ξ，则表称为随机变量ξ的概率分布，简称ξ的121i 注意：若随机变量可以取某一区间内的一切值，这样的变量叫做连续型随机变量.例如：]5,0[∈ξ即ξ可以取0～5之间的一切数，包括整数、小数、无理数.3. ⑴二项分布：如果在一次试验中某事件发生的概率是P ，那么在n 次独立重复试验中这个事件恰好发生k 次的概率是：kn k k n qp C k)P(ξ-==[其中p q n k -==1,,,1,0 ] 于是得到随机变量ξ的概率分布如下：我们称这样的随机变量ξ服从二项分布，记作ξ～B（n·p ），其中n ，p 为参数，并记p)n b(k;qp C k n k k n ⋅=-. ⑵二项分布的判断与应用.①二项分布，实际是对n 次独立重复试验.关键是看某一事件是否是进行n 次独立重复，且每次试验只有两种结果，如果不满足此两条件，随机变量就不服从二项分布.②当随机变量的总体很大且抽取的样本容量相对于总体来说又比较小，而每次抽取时又只有两种试验结果，此时可以把它看作独立重复试验，利用二项分布求其分布列.4. 几何分布：“k =ξ”表示在第k 次独立重复试验时，事件第一次发生，如果把k 次试验时事件A 发生记为k A ，事A 不发生记为q )P(A ,A k k =，那么)A A A A P(k)P(ξk 1k 21-== .根据相互独立事件的概率乘法分式：))P(A A P()A )P(A P(k)P(ξk 1k 21-== ),3,2,1(1 ==-k p q k 于是得我们称ξ服从几何分布，并记p q p)g(k,1k -=，其中 3,2,1.1=-=k p q5. ⑴超几何分布：一批产品共有N 件，其中有M （M ＜N ）件次品，今抽取)N n n(1≤≤件，则其中的次品数ξ是一离散型随机变量，分布列为)M N k n M,0k (0CC C k)P(ξnNkn MN k M -≤-≤≤≤⋅⋅==--.〔分子是从M 件次品中取k 件，从N-M 件正品中取n-k 件的取法数，如果规定m ＜r 时0C rm=，则k 的范围可以写为k=0，1，…，n.〕 ⑵超几何分布的另一种形式：一批产品由 a 件次品、b 件正品组成，今抽取n 件（1≤n≤a+b ），则次品数ξ的分布列为n.,0,1,k CC C k)P(ξnba kn bk a =⋅==+-.⑶超几何分布与二项分布的关系.设一批产品由a 件次品、b 件正品组成，不放回抽取n 件时，其中次品数ξ服从超几何分布.若放回式抽取，则其中次品数η的分布列可如下求得：把b a +个产品编号，则抽取n 次共有nb a )(+个可能结果，等可能：k)(η=含kn k k n b a C -个结果，故n ,0,1,2,k ,)ba a (1)b a a (C b)(a ba C k)P(ηkn k k n nk n k k n =+-+=+==--，即η～)(b a a n B +⋅.[我们先为k 个次品选定位置，共k n C 种选法；然后每个次品位置有a 种选法，每个正品位置有b 种选法] 可以证明：当产品总数很大而抽取个数不多时，k)P(ηk)P(ξ=≈=，因此二项分布可作为超几何分布的近似，无放回抽样可近似看作放回抽样.二、数学期望与方差.n n 2211期望反映了离散型随机变量取值的平均水平.2. ⑴随机变量b a +=ξη的数学期望：b aE b a E E +=+=ξξη)( ①当0=a 时，b b E =)(，即常数的数学期望就是这个常数本身.②当1=a 时，b E b E +=+ξξ)(，即随机变量ξ与常数之和的期望等于ξ的期望与这个常数的和.③当0=b 时，ξξaE a E =)(，即常数与随机变量乘积的期望等于这个常数与随机变量期望的乘积.⑵单点分布：c c E =⨯=1ξ其分布列为：c P ==)1(ξ. ⑶两点分布：p p q E =⨯+⨯=10ξ，其分布列为：（p + q = 1）⑷二项分布：∑=⋅-⋅=-np q p k n k n k E k n k )!(!!ξ 其分布列为ξ～),(p n B .（P 为发生ξ的概率）⑸几何分布：pE 1=ξ 其分布列为ξ～),(p k q .（P 为发生ξ的概率） 3.方差、标准差的定义：当已知随机变量ξ的分布列为),2,1()( ===k p x P k k ξ时，则称+-++-+-=n n p E x p E x p E x D 2222121)()()(ξξξξ为ξ的方差. 显然0≥ξD ，故σξξσξ.D =为ξ的根方差或标准差.随机变量ξ的方差与标准差都反映了随机变量ξ取值的稳定与波动，集中与离散的程度.ξD 越小，稳定性越高，波动越小．．．．．．．．．．．．．.． 4.方差的性质.⑴随机变量b a +=ξη的方差ξξηD a b a D D 2)()(=+=.（a 、b 均为常数） ⑵单点分布：0=ξD 其分布列为p P ==)1(ξ⑶两点分布：pq D =ξ 其分布列为：（p + q = 1）⑷二项分布：npq D =ξ ⑸几何分布：2p q D =ξ5. 期望与方差的关系.⑴如果ξE 和ηE 都存在，则ηξηξE E E ±=±)(⑵设ξ和η是互相独立的两个随机变量，则ηξηξηξξηD D D E E E +=+⋅=)(,)(⑶期望与方差的转化：22)(ξξξE E D -= ⑷)()()(ξξξξE E E E E -=-（因为ξE 为一常数）0=-=ξξE E .三、正态分布.（基本不列入考试范围）1.密度曲线与密度函数：对于连续型随机变量ξ，位于x 轴上方，ξ落在任一区间),[b a 内的概率等于它与x 轴.直线a x =与直线b x =（如图阴影部分）的曲线叫ξ的密度曲线，以其作为 图像的函数)(x f 叫做ξ的密度函数，由于“),(+∞-∞∈x ”是必然事件，故密度曲线与x 轴所夹部分面积等于1.2. ⑴正态分布与正态曲线：如果随机变量ξ的概率密度为：2221)(σσπ-=ex f . （σμ,,R x ∈为常数，且0 σ），称ξ服从参数为σμ,的正态分布，用ξ～),(2σμN 表示.)(x f 的表达式可简记为),(2σμN ，它的密度曲线简称为正态曲线.⑵正态分布的期望与方差：若ξ～),(2σμN ，则ξ的期望与方差分别为：2,σξμξ==D E . ⑶正态曲线的性质.①曲线在x 轴上方，与x 轴不相交. ②曲线关于直线μ=x 对称.③当μ=x 时曲线处于最高点，当x 向左、向右远离时，曲线不断地降低，呈现出“中间高、两边低”的钟形曲线.④当x ＜μ时，曲线上升；当x ＞μ时，曲线下降，并且当曲线向左、向右两边无限延伸时，以x 轴为渐近线，向x 轴无限的靠近.⑤当μ一定时，曲线的形状由σ确定，σ越大，曲线越“矮胖”.表示总体的分布越分散；σ越小，曲线越“瘦高”，表示总体的分布越集中.3. ⑴标准正态分布：如果随机变量ξ的概率函数为)(21)(22+∞-∞=- x ex x πϕ，则称ξ服从标准正态分布. 即ξ～)1,0(N 有)()(x P x ≤=ξϕ，)(1)(x x --=ϕϕ求出，而P （a ＜ξ≤b ）的计算则是)()()(a b b a P ϕϕξ-=≤ .注意：当标准正态分布的)(x Φ的X 取0时，有5.0)(=Φx 当)(x Φ的X 取大于0的数时，有5.0)( x Φ.比如5.00793.0)5.0(=-Φσμ则σμ-5.0必然小于0，如图.⑵正态分布与标准正态分布间的关系：若ξ～),(2σμN 则ξ的分布函数通 常用)(x F 表示，且有)σμx (F(x)x)P(ξ-==≤ϕ.4.⑴“3σ”原则.假设检验是就正态总体而言的，进行假设检验可归结为如下三步：①提出统计假设，统计假设里的变量服从正态分布),(2σμN .②确定一次试验中的取值a 是否落入范围)3,3(σμσμ+-.③做出判断：如果)3,3(σμσμ+-∈a ，接受统计假设. 如果)3,3(σμσμ+-∉a ，由于这是小概率事件，就拒绝统计假设.⑵“3σ”原则的应用：若随机变量ξ服从正态分布),(2σμN 则 ξ落在)3,3(σμσμ+-内的概率为99.7％ 亦即落在)3,3(σμσμ+-之外的概率为0.3％，此为小概率事件，如果此事件发生了，就说明此种产品不合格（即ξ不服从正态分布）.S 阴=0.5S a =0.5+S。