劈尖干涉matlab程序
- 格式：docx
- 大小：12.82 KB
- 文档页数：1
文档推荐
-
干涉条纹图数字图像处理页数:5
-
光干涉条纹图的中心线提取算法页数:5
-
干涉条纹图数字图像处理页数:6
-
相位拼接闭合条纹干涉图处理技术页数:6
-
干涉条纹图的数字图像处理页数:6
-
干涉条纹图数字图像处理页数:5
下载文档原格式
合集下载
基于MATLAB与C_混合编程实现光的干涉仿真_栾国杰
（2 ）
（3a ） E0= 姨E10+E20+2E10E20cos(Φ20-Φ10) ， E10sinΦ10+E20sinΦ20 。 （3b ） Φ0=arctan E10cosΦ10+E20cosΦ20 在 一 定 时 间 内 观 察 到 的 平 均 光 强I与 光 矢 量 的 平 方 的 平 均值成正比 （4 ） I=aE0=a ［E10+E20+2E10E20cos(Φ20-Φ10) ］， 其中 a 是比例系数 。 对于普通光源 ， 两光波之间的相位差 Φ
20 2 2 2
-Φ10 是随机变化的 ， 平均值为零 ， 因此 I=aE10+aE20=I1+I2 。
2 2
（5 ） 这就是光的非相干叠加 ， 总光强等于两束光各自照射时 的光强之和 。 如果两束光的相位差恒定 ， 则合成光强为 （6a ） I=I1+I2+2 姨I1I2 cos△Φ ， 其中 ΔΦ=Φ20-Φ10 ， 第三项是干涉项 。 这就是光的相干叠 加 。 如果 I1=I2 ， 则合成光强为 更不能充门面供参观所用 ， 应真正为教学一线服务 。 “ 再穷不 能 穷 教 育 ”， 应 结 合 当 地 的 经 济 和 学 校 财 力 ， 鼓 励 民 营 经 济 参 与办教育 ， 多方筹资 ， 完善网络教育基础设施 。 4.4 重 视 网络 信息 资 源 的 普 及和 长 效 机 制 建 设 。 网络教育通过网络的协作学习系统 、 网络讲座 、 网络辅导 与答疑 、 网上在线交谈等 ， 使得师生之间的交互跨越了时空的 限制 。 西部农村中小学应该试点建设网络教室 ， 购买计算机和 电脑设备及配套软件 ， 然后这种做法逐步地向全国普及 。 应该 加 强 制 度 建 设 ，增 强 责 任 感 ，狠 抓 落 实 ，完 善 “以 县 为 主 ”的 管 理制度 ， 增加投入 ， 完善经费保障机制 。 建设类似于美国的网 络教室和网络设备管理制度 ， 以保证网络教室的经常开放和 网络设备的正常运转 ， 并让教师和学生有足够的时间进入网 络教室 。 参考文献 ： ［1 ］ 曾祥翊 ，庄秀丽 ，刘德亮.我国中小学网络教育教学的现 状 、 问题 、 对策及其发展趋势 ［J ］. 电化教育研究 ，2004.9 ：57-60. ［2 ］ 沈 洪 . 中 小 学 网 络 教 育 资 源 建 设 现 状 和 策 略 研 究 ［J ］. 图书馆工作与研究 ，2010.7 ：107-108. ［3 ］ 司 晓 宏 ， 杨 令 平 . 当 前 我 国 西 部 地 区 农 村 义 务 教 育 形 势分析 ［J ］. 教育研究 ，2010.8 ：13-19. ［4 ］ 国家教育发展研究中心.2009年中国教育绿皮书— —— 中 国教育政策年度分析报告 ［M］.北京 ：教育科学出版社 ，2009.9. ［5 ］ 郭 炯 ， 郭 绍 青 . 西 部 农 村 中 小 学 教 育 信 息 化 发 展 中 存 在的问题及对策 ［J ］. 现代远距离教育 ，2004.6 ：14-16. ［6 ］ 钱玲 ， 库文 颖 ， 李 中 华 . 发 达 国 家 中 小 学 网 络 教 育 比 较 研究 ［J ］. 世界教育信息 ，2006.1:24-26.
光的干涉和衍射的matlab模拟
光的干涉和衍射的matlab模拟摘要：运用matlab强大的计算和绘图能力，对光的双缝干涉、单缝夫琅禾费衍射、双缝衍射和衍射光栅的光谱进行仿真。
仿真程序可以显示单色光入射时的光谱图样和光强分布曲线，并可输入实验参数，观察在不同条件下图像及光强曲线，并分析了它们各自的特点。
关键字：干涉衍射matlab 模拟1引言光的干涉与衍射现象是光波动性的实验基础。
对任何一个物理专业或涉及光学方面专业的人士来讲，认识干涉与衍射现象的图样特征，理解它们的理论推导，辨别它们之间的联系与区别是必须的。
为了使学生比较容易地接受光栅衍射的知识，同时更能对干涉与衍射的区别与联系有深刻的理解，仔细推导杨氏双缝干涉实验、单缝夫琅和费衍射实验、双缝衍射实验和有关衍射光栅光谱在形成条件，光谱特点及光强分布函数的联系与区别是必要的。
同时将上述干涉，衍射图样用计算机模拟的方式表现出来必将有助于加深对干涉与衍射在形成条件，光谱特点上的联系与区别的理解。
数学软件matlab 具有强大的数值计算功能和高级可视化图形功能，而且可以生成用户自己的图像控制界面，所以运用MATLAB软件，在计算机上编制相应的程序，模拟仿真以上四种不同干涉或衍射的光谱图样，并编制可输入参数的用户界面，尝试在不同参数输入情况下它们图样间的光滑过渡成为可能[1-3]。
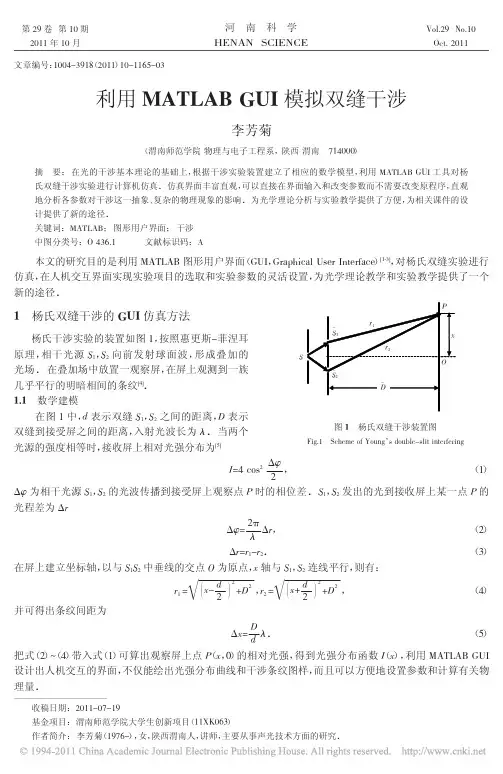
2杨氏双缝干涉杨氏双缝实验是揭开光的波动本性的一把钥匙，如图1所示，同一波面上的光波被分成两束，然后在光屏pp’上叠加形成干涉条纹。
在这里，双缝的宽度必须非常小，即的情况。
在这个前提下每一束光的传播可以用几何光学来处理。
由叠加原理光屏上任一点的光强等于由两缝的光强的叠加。
由同方向，同频率两波动的叠加公式得：,在两缝宽度相同时，即时：光强。
其中为两缝到屏上P点的相位差，当时，对应的极大光强为，即各级明纹的亮度时相同的。
在输入波长550纳米，双缝宽度0.2毫米，观察屏距双缝一米的情况下，可得明暗相间干涉条纹,即为光强分布曲线。
用matlab实现杨氏双缝干涉实验仿真
用MATLAB实现杨氏双缝干涉实验仿真摘要：实验室中，做普通光学实验，受到仪器和场所的限制；实验参数的改变引起干涉图样的改变不明显，难以体现实验的特征。
本文利用MATLAB仿真杨氏双缝干涉实验，创建用户界面，实现人机交互，输入不同实验参数，使干涉现象直观表现出来。
关键词：MATLAB；杨氏双缝干涉实验；用户界面设计；程序编写；仿真。
1. 引言：在计算机迅猛发展的今天，光学实验的仿真越来越多的受科研工作者和教育工作者关注。
其应用主要有两个方面：一是科学计算方面，利用仿真实验的结果指导实际实验，减少和避免贵重仪器的损害；二是在光学教学方面，将抽象难懂的光学概念和规律，由仿真实验过程直观的描述，使学生对学习感兴趣。
在科学计算方面，国外的光学实验仿真是模拟设计和优化光学系统的过程中发展起来的，在这方面美国走在最前，其中最具代表性的是劳伦斯利和弗莫尔实验光传输模拟计算机软件Prop92及大型总体优化设计软件CHAINOP和PROPSUITE；另外法国也开发完成其具有自身特点的光传输软件Miro。
在光学教学方面，国外已有相关的配有光盘演示光学实验的教材。
我国用于科学研究的光学实验计算机数值仿真软件随开发较晚，但也已经取得了显著成绩。
特别是1999年，神光——III原型装置TLL分系统集成实验的启动为高功率固体激光驱动器的计算机数值模拟的研究创造了条件。
目前已基本完成SG99光传输模拟计算软件的开发，推出的标准版本基本能稳定运行。
目前该软件已经应用于神光——III主机可行性论证的工作中。
计算机仿真具有观测方便，过程可控等优点，可以减少系统对外界条件对实验本身的限制，方便设置不同的参数，借助计算机的高数运算能力，可以反复改变输入的实验条件系统参数，大大提高实验效率。
MATLAB是MatlabWorks公司于1982年推出的一套高性能的数值计算和可视化软件。
具有可扩展性，易学易用性，高效性等优势。
通过对目前计算机仿真光学实验的现状和相关研究的分析，本文将用Matlab编程实现杨氏双缝干涉实验的仿真。
光的干涉MATLAB程序
M(:,ot(4,1,2) %选子图
image(M) %画绿色干涉条纹
axis off %隐轴
dx=0.002; %明纹之间的距离
xm=k*dx; %劈尖的长度
x=linspace(0,xm,1000); %劈尖的长度向量
theta=lambda(1)/2/n/dx; %劈尖的夹角
%劈尖的等厚干涉条纹
clear %清除变量
lambda=[750,540,440]*1e-9; %波长
n=1.5; %劈尖的折射率
k=10; %明纹最高级次
M(:,:,1)=i1; %矩阵的红色页赋值
figure %开创图形窗口
subplot(4,1,1) %选子图
image(M) %画红色干涉条纹
title('劈尖的等厚干涉绿色条纹','FontSize',fs)%标题
i3=cos(pi*(2*n*e/lambda(3)+1/2)).^2; %蓝色反射光的相对光强
M=zeros(1,length(x),3); %1行若干列3页全零矩阵
M(:,:,3)=i3; %矩阵的蓝色页赋值
e=x*tan(theta); %劈尖的厚度向量
i1=cos(pi*(2*n*e/lambda(1)+1/2)).^2; %红色反射光的相对光强
M=zeros(1,length(x),3); %1行若干列3页全零矩阵
axis off %隐轴
title('劈尖的等厚干涉彩色条纹','FontSize',fs)%标题
subplot(4,1,3) %选子图
image(M) %画蓝色干涉条纹
image(M) %画绿色干涉条纹
axis off %隐轴
dx=0.002; %明纹之间的距离
xm=k*dx; %劈尖的长度
x=linspace(0,xm,1000); %劈尖的长度向量
theta=lambda(1)/2/n/dx; %劈尖的夹角
%劈尖的等厚干涉条纹
clear %清除变量
lambda=[750,540,440]*1e-9; %波长
n=1.5; %劈尖的折射率
k=10; %明纹最高级次
M(:,:,1)=i1; %矩阵的红色页赋值
figure %开创图形窗口
subplot(4,1,1) %选子图
image(M) %画红色干涉条纹
title('劈尖的等厚干涉绿色条纹','FontSize',fs)%标题
i3=cos(pi*(2*n*e/lambda(3)+1/2)).^2; %蓝色反射光的相对光强
M=zeros(1,length(x),3); %1行若干列3页全零矩阵
M(:,:,3)=i3; %矩阵的蓝色页赋值
e=x*tan(theta); %劈尖的厚度向量
i1=cos(pi*(2*n*e/lambda(1)+1/2)).^2; %红色反射光的相对光强
M=zeros(1,length(x),3); %1行若干列3页全零矩阵
axis off %隐轴
title('劈尖的等厚干涉彩色条纹','FontSize',fs)%标题
subplot(4,1,3) %选子图
image(M) %画蓝色干涉条纹
基于matlab的光的干涉演示
光的干涉的研究问题：利用MA TLAB 仿真程序验证两束频率相同的单色光在空间某点相遇时，讨论光强和干涉条纹的分布规律，更加直观地让学生理解光的干涉现象。
相关词：MA TLAB 光的干涉工具：MA TLAB光的双缝干涉两束频率相同的单色光在空间某点相遇时，讨论光强和干涉条纹的分布规律。
[数学模型]根据波的叠加理论，两束同频率单色光在空间某一点光矢量的大小为E 1 = E 10cos(ωt + φ10)，E 2 = E 20cos(ωt + φ20)， (7.1.1)其中，E 10和E 20分别是两个光矢量的振幅，φ10和φ20分别是初相。
如果两个光矢量的方向相同，合成的光矢量为E = E 0cos(ωt + φ0)， (7.1.2)其中，振幅和初相分别为0E =， (7.1.3a)10102020010102020sin sin arctan cos cos E E E E ϕϕϕϕϕ+=+。
(7.1.3b) 在一定时间内观察到的平均光强I 与光矢量的平方的平均值成正比2220102010202010[2cos()]I aE a E E E E ϕϕ==++-， (7.1.4)其中a 是比例系数。
对于普通光源，两光波之间的相位差φ20 – φ10是随机变化的，平均值为零，因此22102012I aE aE I I =+=+。
(7.1.5)这就是光的非相干叠加，总光强等于两束光各自照射时的光强之和。
如果两束光的相位差恒定，则合成光强为12I I I ϕ=++∆， (7.1.6a)其中Δφ = φ20 – φ10，第三项是干涉项。
这就是光的相干叠加。
如果I 1 = I 2，则合成光强为2112(1cos )4cos 2I I I ϕϕ∆=+∆=。
(7.1.6b) [讨论]①当Δφ = 2k π时(k = 0, ±1, ±2,…)，满足这样条件的空间各点的光强最大2M 12I I I =++=， (7.1.7a)或 I M = 4I 1。
利用MATLABGUI模拟双缝干涉
［4］ 徐志东， 陈世涛． 大学物理实验 ［M］ ． 成都： 西南交通大学出版社， 2003． ［5］ 姚启钧． 光学教程 ［M］ ． 北京： 高等教育出版社， 1981．
The Simulation of Double-Slit Interference Based on M ATLAB GUI
Li Fangju
（Department of Physics and Electronic Engineering ，Weinan Teachers University，Wainan 714000，Shaanxi China ）
Abstract：According to the basic theory of optical interference and experimental device ， we set up a mathematical model of the interference experiment ， which can realize the simulation of Young’ s double slit interference experiment based on MATLAB GUI. The GUI （Graphical User Interfaces ）is beautiful and intuitive， the user can directly input the parameters on the GUI， also do not alter the primary procedure ， making the user able to analyze the par- ameters influencing the result． It makes it easy to teach optical theory and experiment ， and offers a new way to design the related CAI． Key words：MATLAB； graphical user interface； interference
基于Matlab的波的干涉实验仿真研究
第３２卷第４期大学物理实验Ｖｏｌ.３２Ｎｏ.４２０１９年８月ＰＨＹＳＩＣＡＬＥＸＰＥＲＩＭＥＮＴＯＦＣＯＬＬＥＧＥＡｕｇ.２０１９收稿日期:２０１９￣０３￣２２∗通讯联系人文章编号:１００７￣２９３４(２０１９)０４￣００７６￣０３基于Ｍａｔｌａｂ的波的干涉实验仿真研究史㊀严∗ꎬ牛宽宽(石家庄铁道大学数理系ꎬ河北石家庄㊀０５００４３)摘要:利用计算机和Ｍａｔｌａｂ方法对大学物理实验中的波的干涉实验进行了仿真研究ꎬ并进行了适当的计算和作图ꎬ此方法可以大大简化实验条件ꎬ并能加深学生对物理实验内涵的理解ꎮ关键词:计算机技术ꎻＭａｔｌａｂ软件ꎻ波的干涉实验中图分类号:Ｏ４￣３９文献标志码:ＡＤＯＩ:１０.１４１３９/ｊ.ｃｎｋｉ.ｃｎ２２￣１２２８.２０１９.０４.０２１㊀㊀在传统的大学物理实验中ꎬ通常需要使用大量的实验仪器㊁装置ꎬ需要在特定的物理实验室中进行操作ꎬ并且需要一定的环境条件ꎬ如:温度㊁湿度㊁压力㊁外场等[１]ꎮ随着计算机技术的发展ꎬ越来越多的新技术㊁新方法被引入到大学物理实验的科研和教学环节中[２]ꎬ其中使用Ｍａｔｌａｂ程序方法进行大学物理和实验的仿真研究是一个热点[３￣７]ꎬ利用这个方法既可以使学生深刻理解物理实验的内涵ꎬ又可以减少对实验条件的依赖ꎬ有很大的发展空间ꎮ本文使用Ｍａｔｌａｂ方法详细研究了波的干涉实验ꎮ１㊀波的干涉实验的强度和图样研究１.１㊀物理模型及分析设空间中两个相干波源ꎬ其角频率都为ｗꎬ初相位分别是φ１和φ２ꎬ两个波源之间的距离是２ａꎬ假设空间任意一点Ｐꎬ两列波在Ｐ点产生的振动是ｕ１＝Ａ１ｃｏｓ(ｗｔ＋φ１－２πｒ１/λ)ｕ２＝Ａ２ｃｏｓ(ｗｔ＋φ２－２πｒ２/λ)其中ꎬＡ１和Ａ２分别是两列波在Ｐ点的振幅ꎻｒ１和ｒ２是两个波源到Ｐ点的距离ꎮ则Ｐ点的合振动是ｕ＝ｕ１＋ｕ２＝Ａｃｏｓ(ｗｔ＋φ)其中Ａ＝Ａ２１＋Ａ２２＋２Ａ１Ａ２ｃｏｓΔφφ＝ａｒｃｔａｎＡ１ｓｉｎ(φ１－２πｒ１/λ)＋Ａ２ｓｉｎ(φ２－２πｒ２/λ)Ａ１ｃｏｓ(φ１－２πｒ１/λ)＋Ａ２ｃｏｓ(φ２－２πｒ２/λ)Δφ称为相位差Δφ＝φ２－φ１－２πｒ２－ｒ１λ其中ꎬδ＝ｒ２－ｒ１称为波程差ꎮ波的强度与振幅的平方成正比ꎬ所以波的强度是Ｉ＝Ｉ１＋Ｉ２＋２Ｉ１Ｉ２ｃｏｓΔφ当Δφ＝２κπ时(ｋ＝０ꎬ１ꎬ－１ꎬ )满足这样条件的点干涉振幅最大ꎬ称为干涉相长ꎻ当Δφ＝(２κ＋１)π时(ｋ＝０ꎬ１ꎬ－１ꎬ )ꎬ满足这样条件的点干涉振幅最小ꎬ称为干涉相消ꎮ１.２㊀编程思想取Ａ１为振幅单位ꎬ则合振幅可表示如下Ａ＝Ａ１１＋Ａ∗２２＋２Ａ∗２ｃｏｓΔφ其中ꎬＡ∗２＝Ａ２/Ａ１ꎬ取Ｉ１＝Ａ２１为波的强度单位ꎬ则波的总强度可表示如下Ｉ＝Ｉ１(１＋Ｉ∗２２Ｉ∗２ｃｏｓΔφ)其中ꎬＩ∗２＝Ｉ２/Ｉ１＝Ａ∗２２ꎮ可限定０<Ａ∗２<１ꎬ或者取Ａ２为振幅单位ꎮ波的振幅和强度随Ａ∗２值不同而不同ꎮ取分振幅之比为参数向量ꎬ取相差为自变量向量ꎬ形成矩阵ꎬ即可计算相对合振幅和相对强度ꎮ１.３㊀作图及分析取干涉相长的级数为２ꎬ则有５个干涉相长位置ꎬ４个干涉相消位置ꎬ取四个不同的分振幅之比０.１㊁０.４㊁０.７㊁１ꎬ绘制相对合振幅如图１ꎮ图１㊀两列相干波干涉的振幅分布同样的数据ꎬ绘制两列波干涉的相对强度ꎬ如图２所示ꎮ图２㊀两列相干波干涉的强度分布根据图１可知ꎬ随着振幅比的增大ꎬ相对振幅的大小范围急剧变化ꎬ但整体上还是有余弦函数的趋势ꎮ由图２可以看出ꎬ相对强度是相差的余弦函数ꎬ随着振幅比增大ꎬ干涉相长增强ꎬ干涉相消减弱ꎮ２㊀水波的干涉实验图样研究２.１㊀物理模型及分析两列相干的水波相遇ꎬ仿真模拟其形成的干涉图样ꎮ假设两列相干水波的振幅都为Ａ０ꎬ频率相同ꎬ振动方向相同ꎬ令它们的初相位均是零ꎬ则它们在Ｐ点叠加的合振幅和初相位分别是Ａ＝２Ａ０ｃｏｓ(πｒ１－ｒ２λ)φ＝ａｒｃｔａｎ－ｓｉｎ(２πｒ１/λ)－ｓｉｎ(２πｒ２/λ)ｃｏｓ(２πｒ１/λ)＋ｃｏｓ(２πｒ２/λ)由此可得ꎬ在干涉相长线上ꎬ不同的点的相位一般也是不同的ꎮ根据振动方程可以确定各点的位移值ꎮ２.２㊀编程思想取波长为单位ꎬ则水波的合振幅可表示如下Ａ∗＝Ａ∗０２ｃｏｓπ(ｒ∗２－ｒ∗１)[]初相位可表示为φ＝ａｒｃｔａｎ－ｓｉｎ(２πｒ∗１)＋ｓｉｎ(２πｒ∗２)[]ｃｏｓ(２πｒ∗１)＋ｃｏｓ(２πｒ∗２)其中ꎬＡ∗０＝Ａ０/λꎬＡ∗＝Ａ/λꎬ波程ｒ∗１＝ｘ∗２＋(ｙ∗－ａ∗)２ｒ∗２＝ｘ∗２＋(ｙ∗＋ａ∗)２其中ꎬｘ∗＝ｘ/λꎬｙ∗＝ｙ/λꎮＰ点的振动方程可表示如下ｕ∗＝Ａ∗ｃｏｓ(ｔ∗＋φ)其中ｔ∗＝ｗｔ表示无量纲的时间ꎮ２.３㊀作图根据各点位移的大小ꎬ用曲面ｓｕｒｆ指令画出水波的初始干涉图样ꎬ变换各点的坐标数值ꎬ连续扫描ꎬ形成波的传播的动画ꎬ显示稳定的干涉图样ꎬ设置俯视角即可得两列水波的干涉图样ꎮ如图３所示图３㊀水波的干涉图样效果图３㊀总㊀结在大学物理实验的教学和科研中ꎬ计算机技７７基于Ｍａｔｌａｂ的波的干涉实验仿真研究术都提供了很大的帮助ꎬ在科研中主要进行数值分析和模拟㊁复杂的演算和推导ꎬ在教学中是重要的辅助工具ꎬ可以帮助学生处理实验数据㊁解决物理问题和作图等ꎮ对于大学物理和实验中的问题ꎬ应用计算机程序解决物理问题是一个新的思想ꎬ未来有很大的应用前景ꎮ参考文献:[１]㊀王振彪ꎬ刘虎ꎬ郑乔ꎬ等.大学物理实验[Ｍ].中国铁道出版社ꎬ２００９.[２]㊀隋成华ꎬ魏高尧ꎬ等.大学物理实验[Ｍ].高等教育出版社ꎬ２０１６.[３]㊀李海涛ꎬ苏艳丽ꎬ等.ＭＡＴＬＡＢＧＵＩ在光学实验教学中的应用[Ｊ].大学物理实验ꎬ２０１７ꎬ３０(６). [４]㊀周群益.ＭＡＴＬＡＢ可视化大学物理学[Ｍ].清华大学出版社ꎬ２００１.[５]㊀彭芳麟.理论力学计算机模拟[Ｍ].清华大学出版社ꎬ２００２.[６]㊀张志涌.精通ｍａｔｌａｂ[Ｍ].北京航空航天大学出版社ꎬ２０００.[７]㊀ＮｉｃｈｏｌａｓＪ.ＧｉｏｒｄａｎｏꎬＣｏｍｐｕｔａｔｉｏｎａｌＰｈｙｓｉｃｓ[Ｍ].清华大学出版社ꎬ２０１１.ＳｉｍｕｌａｔｉｏｎＲｅｓｅａｒｃｈｏｎＩｎｔｅｒｆｅｒｅｎｃｅＥｘｐｅｒｉｍｅｎｔｏｆＷａｖｅＢａｓｅｄｏｎＭａｔｌａｂＳＨＩＹａｎ∗ꎬＮＩＵＫｕａｎｋｕａｎ(ＤｅｐａｒｔｍｅｎｔｏｆＭａｔｈｓａｎｄＰｈｙｓｉｃｓꎬＳｈｉｊｉａｚｈｕａｎｇＴｉｅｄａｏＵｎｉｖｅｒｓｉｔｙꎬＳｈｉｊｉａｚｈｕａｎｇ０５００４３ꎬＣｈｉｎａ)Ａｂｓｔｒａｃｔ:ＵｓｉｎｇＭａｔｌａｂｍｅｔｈｏｄꎬｗｅｓｉｍｕｌａｔｅｄａｎｄｓｔｕｄｉｅｄｔｈｅｉｎｔｅｒｆｅｒｅｎｃｅｅｘｐｅｒｉｍｅｎｔｏｆｗａｖｅｉｎｃｏｌｌｅｇｅｐｈｙｓ￣ｉｃｓｅｘｐｅｒｉｍｅｎｔ.Ｔｈｉｓｍｅｔｈｏｄｃａｎｓｉｍｐｌｉｆｙｔｈｅｅｘｐｅｒｉｍｅｎｔｃｏｎｄｉｔｉｏｎａｎｄｄｅｅｐｅｎｔｈｅｓｔｕｄｅｎｔｓ'ｕｎｄｅｒｓｔａｎｄｉｎｇｏｆｐｈｙｓｉｃｓｃｏｎｔｅｎｔ.Ｋｅｙｗｏｒｄｓ:ｃｏｍｐｕｔｅｒｔｅｃｈｎｏｌｏｇｙꎻＭａｔｌａｂｓｏｆｔｗａｒｅꎻｉｎｔｅｒｆｅｒｅｎｃｅｅｘｐｅｒｉｍｅｎｔｏｆｗａｖｅ８７基于Ｍａｔｌａｂ的波的干涉实验仿真研究。
多光束干涉原理及MATLAB实现
text(-3,0.1,'rho=0.8')%显示该位置字符串，下同 text(5,0.2,'rho=0.5') text(7,0.44,'rho=0.6') text(12,0.5,'rho=0.01') text(16,0.65,'rho=0.4') text(20,0.89,'rho=0.23') xlabel('角变量') ylabel('反射光强') figure(2) for i=1:11 y2=1./(1+(1-rho(i))^2./(4*rho(i)*sin(phi/2).^2));%透射光强 plot(phi,y2)%绘图 hold on end text(-3,0.1,'rho=0.8')%显示该位置字符串，下同 text(5,0.2,'rho=0.5') text(7,0.44,'rho=0.6') text(12,0.5,'rho=0.01') text(16,0.65,'rho=0.4') text(20,0.89,'rho=0.23') xlabel('角变量') ylabel('透射光强') 思路已由百分号标明
’ 0
A0 (1 )e i 1 e i
2
IT
UT
2
A0 (1 ) 2 （ 1 e i）（ 1 e -i）
2 （ 1 ） 4 sin 2 2 2 I A0 为入射光强 IT 2 1 2 （ 1 ） 4 sin 2 I
n A2
matlab gui在迈克尔孙干涉实验中的应用
文章标题：MATLAB GUI在迈克尔孙干涉实验中的应用1.引言迈克尔孙干涉实验是一种重要的光学实验，用于测量光的相位差，常用于薄膜厚度的测量。
MATLAB GUI（图形用户界面）作为一种强大的工具，可以有效地帮助实验者进行数据处理和分析，提高实验效率和精度。
2.迈克尔孙干涉实验简介迈克尔孙干涉实验是利用迈克尔孙干涉仪观察透明物体的厚度和折射率变化。
通过干涉条纹的移动或者变化，可以计算出光的相位差，进而得到物体的厚度和折射率信息。
3.MATLAB GUI在迈克尔孙干涉实验中的应用3.1 数据采集在实验中，利用MATLAB GUI可以快速采集干涉条纹的图像数据，包括干涉条纹的位置、强度等信息。
通过图像处理和分析算法，可以实现自动化数据采集和处理，提高数据的准确性和可靠性。
3.2 数据处理利用MATLAB GUI可以进行干涉条纹的图像处理，包括背景去除、噪声滤波、条纹识别等，同时还可以进行干涉条纹的数据分析和拟合，得到干涉条纹的参数信息。
3.3 结果展示结果展示是实验的重要部分，利用MATLAB GUI可以将实验数据直观地展示出来，包括干涉条纹的图像、参数曲线等，使得实验结果更加清晰和可视化。
4.个人观点和理解通过MATLAB GUI的应用，可以极大地提高迈克尔孙干涉实验的效率和精度，实现数据的自动化采集、处理和展示。
MATLAB GUI还为实验者提供了一个灵活且强大的评台，可以根据实际需求进行定制化的数据处理和分析。
我认为MATLAB GUI在迈克尔孙干涉实验中具有重要的应用前景。
5.总结本文从数据采集、数据处理和结果展示等方面探讨了MATLAB GUI 在迈克尔孙干涉实验中的应用，同时共享了个人观点和理解。
通过MATLAB GUI的应用，可以提高实验效率和精度，为光学实验提供了一种新的解决方案。
希望本文对于迈克尔孙干涉实验的研究和实践能够有所帮助。
以上是我的初步撰写，希望对您有所帮助。
6. MATLAB GUI在迈克尔孙干涉实验中的实际操作在实际操作中，使用MATLAB GUI进行迈克尔孙干涉实验的数据采集和处理非常方便。
matlab的几个干涉实验模拟
基于matlab 的几个干涉实验模拟------------吴旭普摘要：根据干涉原理对牛顿环，杨氏双缝和迈克尔逊干涉仪原理进行分析得到各种参数的关系，采用计算机模拟方法并通过软件matlab 编程并运行得到干涉图样 关键词：干涉 matlab 牛顿环 杨氏干涉 迈克尔逊干涉仪 一．牛顿环干涉模拟 1.建模如图，牛顿环是一种分振幅法产生干涉的装置，由一光平玻璃和一曲率很大的平凸透镜构成，平玻璃和平凸透镜之间形成了一个空气劈尖，且其等厚轨迹是以接触点为圆心的一系列同心圆，所以干涉条纹的形状也是明暗相间的同心圆。
在编制程序之前，我们需要对决定干涉条纹特征的光程差、相位差与干涉条纹半径r ，光波波长和平凸透镜的曲率半径R 之间的曲率半径R 之间的关系。
对于形成牛顿环干涉处的空气层厚度e ，两相干光的光程差为: 22e λ∆=+由几何关系：因为R>>e ,所以略去故得:所以两相干光的相位差为：=两相干光的干涉光强为：其中分别是反射光1和反射光2的光强，为使问题简单化设平凸透镜和平板玻璃的反射率均为15%，并且设两反射光的光强近似相等，均设为最终牛顿环干涉的光强为2.程序编写Clear all %清除内存lamd=600e-9; %设定入射光波长 R=10; %设定牛顿环曲率 rm=1e-2; %设定干涉条纹区域 x=0:0.0001:rm; y=rm:-0.0001:0; [X,Y]=meshgrid(x,y); r2=X.^2+Y.^2;phi=2*pi*(r2/R+lamd/2)/lamd; %相位差I=4*cos(phi./2).^2; %第一象限干涉光强 N=255; %设定灰度等级Ir2=(I/4.0)*N; %最大光强为最大灰度Ir1=fliplr(Ir2); %矩阵对称操作Ir3=flipud(Ir1);Ir4=flipud(Ir2);Ir=[Ir1 Ir2;Ir3 Ir4]; %构造图像矩阵figureimage(Ir,'XData',[-0.02,0.02],'YData',[0.02,-0.02]); %画干涉条纹colormap(gray(N));axis squareTitle（“牛顿环干涉光强”）3．运行程序与结果分析如图2，模拟结果与实验一致，通过以上推倒可知牛顿环条纹与相位差有很大联系。