电力系统分析第14章(电力系统暂态稳定)

电力系统暂态稳定性分析电力系统暂态稳定性分析8、5 简单电力系统暂态稳定性暂态稳定性的概念：指在某个运行情况下突然受到大的干扰后，能否经过暂态过程达到新的稳定运行状态或回复到原来的状态。

大干扰：一般指大型负荷的投入和切除、突然断开线路或发电机、短路故障及切除等。

一般伴随着系统结构的变化。

分析方法：不同于静态稳定问题的分析，不能做线性化处理，暂态稳定问题研究（1）暂态稳定性与按否和原来运行方式及干扰种类有关。

（2）系统暂态稳定过程是一个电磁暂态过程和机电暂态过程汇合在一起的复杂的运动过程，它们互相作用、互相影响。

暂态稳定性分析中的基本假设：（1）发电机采用简化的数学模型采用x d 后的E ' 为发电机的模型。

E ' 与无限大系统母线电压相量之间夹角为δ' ，见图8、2（2）在定量分析中不考虑原动机调速器的作用即 P T =C 认为原动机的输入机械功率为恒定不变。

8、5、1 暂态稳定的物理过程分析分析所用的电力系统：*正常运行时，发电机经由变压器和输电线向无限大系统送电，等值电路如图所示。

假设为状态ⅠG T1 L T2V 发电机与无限大系统的等值电抗为：X I=X d +X T 1+l +X T 2发电机发出的电磁功率为：E ' V P I =sin δ*若在一回输电线始端发生不对称短路（对应状态Ⅱ），按照正序增广网络理论，只需在正序网络（即正常运行状态）的基础上，在故障点接一附加电抗。

用此附加电抗区分不同的短路类型。

为求发电机的电磁功率，需要求解E ‘和V 之间的等值电抗XX II =(X d +X T 1) +(+X T 2) +2(X d +X T 1)(+X T 2)P ∏=sin δ* 故障发生后，保护动作跳开故障线路两端的开关，将故障线路切除，等值V X III =X d +X T 1+X l +X T 2 E ' V P III =sin δ上述三种运行状态，显然有：I >P III >P IIa ：正常运行状态，在a 点处某一时刻发生不对称故障，等值电抗增大，P E (δ) 变为（II ），由于转子惯性，δ不突变，所以运行点转移到b 点。

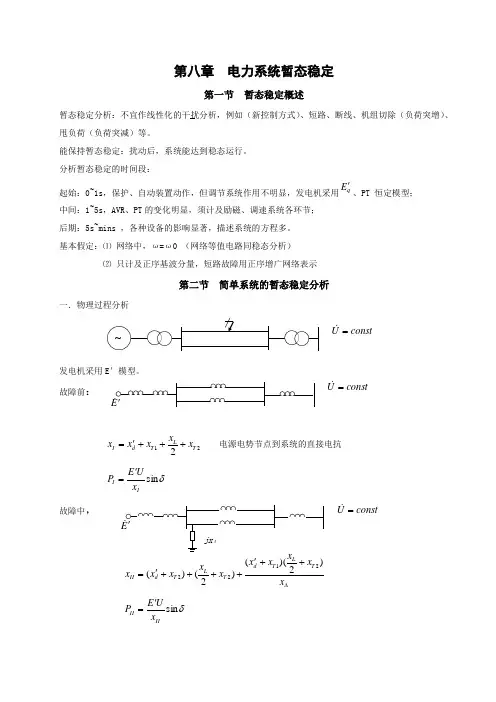
第八章 电力系统暂态稳定第一节 暂态稳定概述暂态稳定分析：不宜作线性化的干扰分析，例如（新控制方式）、短路、断线、机组切除（负荷突增）、甩负荷（负荷突减）等。

能保持暂态稳定：扰动后，系统能达到稳态运行。

分析暂态稳定的时间段：起始：0~1s ，保护、自动装置动作，但调节系统作用不明显，发电机采用qE '、PT 恒定模型；中间：1~5s ，AVR 、PT 的变化明显，须计及励磁、调速系统各环节； 后期：5s~mins ，各种设备的影响显著，描述系统的方程多。

基本假定：⑴ 网络中，ω=ω0 （网络等值电路同稳态分析） ⑵ 只计及正序基波分量，短路故障用正序增广网络表示第二节 简单系统的暂态稳定分析一．物理过程分析发电机采用E ’模型。

故障前：221T LT dI x x x x x +++'= 电源电势节点到系统的直接电抗 δsin II x UE P '= 故障中，∆++'++++'=x xx x x x x x x T LT dT LT dII )2)(()2()(2122δsin IIII x UE P '=故障切除后：功角特性曲线为故障发生后的过程为：运行点变化 原因 结果a →b 短路发生 PT>PE, 加速，ω上升，δ增大 b →c ω上升，δ增大 ω>ω0 ,动能增加c →e 故障切除 PT<PE, 开始减速，但ω>ω0 ，δ继续增大 e →f 动能释放 减速，当ωf =ω0，动能释放完毕，δm 角达最大 f →k PT<PE, 减速δ，减小 经振荡后稳定于平衡点k 结论： 若最大摇摆角h m δδ<，系统可经衰减的振荡后停止于稳定平衡点ｋ，系统保持暂态稳定，反之，系统不能保持暂态稳定。

暂态稳定分析与初始运行方式、故障点条件、故障切除时间、故障后状态有关。

电力系统暂态稳定分析是计算电力系统故障及恢复期间内各发电机组的功率角i δ的变化情况（即δ–ｔ曲线），然后根据i δ角有无趋向恒定（稳定）数值，来判断系统能否保持稳定，求解方法是非线性微分方程的数值求解。

电⼒系统静态稳定暂态稳定实验报告电⼒系统静态、暂态稳定实验报告⼀、实验⽬的1．了解和掌握对称稳定情况下，输电系统的各种运⾏状态与运⾏参数的数值变化范围；2．通过实验加深对电⼒系统暂态稳定内容的理解3．通过实际操作，从实验中观察到系统失步现象和掌握正确处理的措施⼆、原理与说明实验⽤⼀次系统接线图如图1所⽰：图1. ⼀次系统接线图实验中采⽤直流电动机来模拟原动机，原动机输出功率的⼤⼩，可通过给定直流电动机的电枢电压来调节。

实验系统⽤标准⼩型三相同步发电机来模拟电⼒系统的同步发电机，虽然其参数不能与⼤型发电机相似，但也可以看成是⼀种具有特殊参数的电⼒系统的发电机。

发电机的励磁系统可以⽤外加直流电源通过⼿动来调节，也可以切换到台上的微机励磁调节器来实现⾃动调节。

实验台的输电线路是⽤多个接成链型的电抗线圈来模拟，其电抗值满⾜相似条件。

“⽆穷⼤”母线就直接⽤实验室的交流电源，因为它是由实际电⼒系统供电的，因此，它基本上符合“⽆穷⼤”母线的条件。

为了进⾏测量，实验台设置了测量系统，以测量各种电量（电流、电压、功率、频率）。

为了测量发电机转⼦与系统的相对位置⾓（功率⾓），在发电机轴上装设了闪光测⾓装置。

此外，台上还设置了模拟短路故障等控制设备。

电⼒系统静态稳定问题是指电⼒系统受到⼩⼲扰后，各发电机能否不失同步恢复到原来稳定状态的能⼒。

在实验中测量单回路和双回路运⾏时，发电机不同出⼒情况下各节点的电压值，并测出静态稳定极限数值记录在表格中。

电⼒系统暂态稳定问题是指电⼒系统受到较⼤的扰动之后，各发电机能否过渡到新的稳定状态，继续保持同步运⾏的问题。

在各种扰动中以短路故障的扰动最为严重。

正常运⾏时发电机功率特性为：P1＝（Eo×Uo）×sinδ1/X1；短路运⾏时发电机功率特性为：P2＝（Eo×Uo）×sinδ2/X2；故障切除发电机功率特性为：P3＝（Eo×Uo）×sinδ3/X3；对这三个公式进⾏⽐较，我们可以知道决定功率特性发⽣变化与阻抗和功⾓特性有关。

电力系统分析第二版(孟祥萍著)课后答案下载电力系统分析(第2版)内容介绍第一篇电力系统的稳态分析第1章电力系统的基本概念1.1 电力系统的组成和特点1.2 电力系统的电压等级和规定1.3 电力系统的接线方式1.4 电力线路的结构小结思考题与习题第2章电力网各元件的参数和等值电路2.1 输电线路的参数2.2 输电线路的等值电路2.3 变压器的等值电路及参数2.4 标么制小结思考题与习题第3章简单电力系统的潮流计算3.1 基本概念3.2 开式网络电压和功率分布计算3.3 简单闭式网络的电压和功率分布计算小结思考题与习题第4章电力系统的有功功率平衡与频率调整 4.1 概述4.2 自动调速系统4.3 电力系统的频率特性4.4 电力系统的频率调整4.5 电力系统中有功功率的平衡小结思考题与习题第5章电力系统的无功功率平衡与电压调整 5.1 电压调整的必要性5.2 电力系统的无功功率平衡5.3 电力系统的电压管理5.4 电压调整的措施小结思考题与习题第6章电力系统的经济运行6.1 电力系统负荷和负荷曲线6.2 电力系统有功功率负荷的经济分配6.3 电力网中的电能损耗6.4 降低电力网电能损耗的措施小结思考题与习题第二篇电力系统的电磁暂态第7章同步发电机的基本方程7.1 同步发电机的原始方程7.2 d、q、0坐标系统的发电机基本方程7.3 同步电机的稳态运行小结思考题与习题第8章电力系统三相短路的暂态过程8.1 短路的基本概念8.2 无限大功率电源供电系统的三相短路分析8.3 无阻尼绕组同步发电机突然三相短路的分析 8.4 计及阻尼绕组的同步电机突然三相短路分析 8.5 强行励磁对同步电机三相短路的影响小结思考题与习题第9章电力系统三相短路电流的实用计算9.1 交流分量电流初始值的计算9.2 起始次暂态电流和冲击电流的计算9.3 计算曲线法9.4 转移阻抗及电流分布系数小结思考题与习题第10章电力系统各元件的序阻抗和等值电路 10.1 对称分量法10.2 对称分量法在不对称故障分析中的应用10.3 同步发电机的负序和零序电抗10.4 异步电动机的负序电抗和零序电抗10.5 变压器的零序电抗10.6 架空输电线的零序阻抗10.7 电缆线路的零序阻抗10.8 电力系统的序网络小结思考题与习题第11章电力系统简单不对称故障的分析和计算 11.1 单相接地短路11.2 两相短路11.3 两相短路接地11.4 正序等效定则的应用11.5 非故障处电流和电压的计算11.6 非全相运行的分析计算小结思考题与习题第三篇电力系统的机电暂态第12章电力系统稳定性概述12.1 概述12.2 同步发电机组的转子运动方程12.3 简单电力系统的功角特性12.4 复杂电力系统的功角特性12.5 同步发电机自动调节励磁系统小结思考题与习题第13章电力系统静态稳定13.1 简单电力系统的静态稳定13.2 负荷的静态稳定13.3 小干扰法分析电力系统静态稳定13.4 自动调节励磁系统对静态稳定的影响 13.5 提高电力系统静态稳定的措施小结思考题与习题第14章电力系统暂态稳定14.1 电力系统暂态稳定概述14.2 简单电力系统的暂态稳定14.3 复杂电力系统暂态稳定的分析计算 14.4 提高电力系统暂态稳定性的措施14.5 电力系统的异步运行小结思考题与习题第四篇电力系统计算的计算机算法第15章电力网络的数学模型15.1 电力网络的基本方程式15.2 节点导纳矩阵及其算法15.3 节点阻抗矩阵及其算法小结思考题与习题第16章电力系统故障的计算机算法16.1 概述16.2 对称故障的计算机算法16.3 简单不对称故障的计算机算法小结思考题与习题第17章电力系统潮流计算的计算机算法 17.1 概述17.2 潮流计算的基本方程17.3 牛顿-拉夫逊法潮流计算17.4 pq分解法潮流计算小结思考题与习题第18章电力系统稳定的计算机算法18.1 简化模型的暂态稳定计算18.2 简化模型的静态稳定计算小结思考题与习题附录附录1 程序清单1.1 形成节点导纳矩阵1.2 形成节点阻抗矩阵1.3 对称故障的计算1.4 用计算曲线计算对称故障1.5 简单不对称故障的计算1.6 牛顿-拉夫逊法潮流计算1.7 户口分解法潮流计算1.8 分段法确定发电机转子摇摆曲线1.9 小干扰法判断系统的静态稳定附录2 短路电流周期分量计算曲线数字表参考文献电力系统分析(第2版)目录《电力系统分析(第2版)》是教育科学“十五”国家规划课题研究成果之一。

电力系统的暂态稳定性分析电力系统是现代社会不可或缺的基础设施之一，它的稳定运行对于保障电力供应的可靠性和质量至关重要。

而暂态稳定性分析则是电力系统运行中的一个重要方面，它主要研究电力系统在发生故障或突发负荷变化时的动态响应和稳定恢复能力。

暂态稳定性是指电力系统在遭受外界扰动后，能够在一定时间内恢复到新的稳定工作状态的能力。

它是电力系统运行安全性的重要指标，也是电力系统规划、设计和运行的关键问题之一。

暂态稳定性分析的目的就是评估系统在遭受各种故障或负荷变化时的稳定性，并采取相应的措施来提高系统的稳定性。

在进行暂态稳定性分析时，首先需要建立电力系统的数学模型。

这个模型通常是基于电力系统的节点和支路参数，包括发电机、变压器、线路和负荷等。

然后，通过对这个模型进行求解和仿真，可以得到系统在不同故障情况下的动态响应和稳定恢复过程。

暂态稳定性分析的核心是对系统的动态稳定性进行评估。

这个评估通常包括两个方面的内容：一是判断系统是否能够在故障后恢复到稳定工作状态；二是评估恢复过程中的稳定性和动态性能。

为了实现这个评估，通常需要考虑系统的暂态稳定极限、暂态稳定域和暂态稳定边界等指标。

在实际的电力系统运行中，暂态稳定性分析可以帮助运营人员预测系统在故障发生后的动态响应，并采取相应的措施来保障系统的稳定运行。

例如，当系统遭受短路故障时，暂态稳定性分析可以帮助运营人员判断故障是否会导致系统崩溃，并提供相应的补偿措施，如调整发电机励磁系统或采取控制措施来稳定系统。

此外，暂态稳定性分析还对电力系统的规划和设计具有重要意义。

通过对系统的暂态稳定性进行评估，可以确定系统的容量和配置，以满足系统在故障或负荷变化时的稳定要求。

同时，暂态稳定性分析还可以帮助设计师评估不同方案的优劣，选择最优的方案来提高系统的暂态稳定性。

总之，电力系统的暂态稳定性分析是电力工程中一个重要的研究领域。

它关注系统在面临故障或负荷变化时的动态响应和稳定恢复能力，对于保障电力系统的安全可靠运行具有重要意义。

实验二电力系统暂态稳定分析实验目的本次实验旨在通过分析电力系统暂态稳定性，理解电力系统中的稳定性问题，并掌握电力系统的建模和计算方法。

实验原理电力系统暂态稳定性主要是指电力系统在发生大幅度干扰后，是否能够恢复到稳定状态。

因此，暂态稳定性分析主要是对电力系统对外干扰的响应进行预测和评估。

电力系统暂态稳定性分析一般采用时间域仿真方法和频率域方法，其中，时间域仿真法主要是通过对电力系统的微分方程进行数值求解，得到电力系统的动态响应；而频率域方法则是将电力系统的微分方程用拉普拉斯变换转化成复数域的代数方程，通过对这些代数方程进行解析求解，得到电力系统的频率响应。

实验步骤1. 电力系统建模电力系统建模是电力系统暂态稳定性分析的基础，具体步骤如下：•确定电力系统的拓扑结构；•确定电力系统的各个元件（发电机、变压器、线路等）的参数和运行状态；•根据电力系统的拓扑结构和元件参数，列出微分方程或代数方程，得到电力系统的数学模型。

2. 干扰信号的设计在进行暂态稳定分析之前，需要确定干扰信号，在此实验中，我们选择加入一个突然的三相短路干扰信号。

3. 稳定性分析3.1 时间域仿真法•利用Matlab或其他仿真软件，实现电力系统的微分方程求解，得到电力系统随时间的响应；•分析电力系统的响应，判断其是否能够恢复到稳定状态。

3.2 频率域方法•将电力系统的微分方程用拉普拉斯变换转化成复数域的代数方程；•对代数方程进行解析求解，得到电力系统的频率响应；•分析电力系统的频率响应，判断其是否具有稳态解。

4. 结果分析根据时间域仿真法和频率域方法得到的结果，对电力系统的稳定性进行评估和分析。

实验通过本次实验，我们深入了解了电力系统暂态稳定性的原理和计算方法，通过对电力系统的建模和仿真分析，可以有效提高电力系统的稳定性和可靠性。

参考资料•《电力系统分析教程》•《电力系统稳定分析与控制》•《电力系统稳定性分析》。

实验⼆电⼒系统暂态稳定分析实验⼆电⼒系统暂态稳定分析⼀、实验⽬的1. 通过实验加深对电⼒系统暂态稳定内容的理解，使理论教学与实践结合，提⾼学⽣的感性认识；2. 学⽣通过实际操作，从试验中观察到系统失步现象和掌握正确处理的措施。

⼆、实验原理电⼒系统的暂态稳定问题是指电⼒系统受到较⼤的扰动之后，各发电机能否继续保持同步运⾏的问题，在各种扰动中，以短路故障的扰动最为严重。

在故障发⽣时及故障切除通过强励磁增加发电机的电势，可⽤于提⾼系统的稳定性。

由于电⼒系统发⽣瞬间单相接地故障较多，发⽣瞬间单相故障时采⽤⾃动重合闸，使系统进⼊正常⼯作状态。

这两种⽅法都有利于提⾼系统的稳定性。

暂态稳定是指电⼒系统在某个运⾏情况下突然受到⼤的⼲扰后，能否经过暂态过程达到新的稳态运⾏状态或则恢复到原来的状态。

这⾥所谓的⼤⼲扰是相对⼩⼲扰来说的，⼀般指短路故障，突然断开线路或则发电机等。

如果收到⼲扰后系统能够回到稳态运⾏，就说系统在这种运⾏情况下是暂态稳定。

反之，各发电机组转⼦间⼀直有相对运动，相对⾓不断变化，系统的功率、电流、电压都不断振荡，导致系统不能继续运⾏下去，则称系统在这种运⾏情况下不能保持暂态稳定。

⼀个系统的暂态稳定情况和系统原来的运⾏⽅式及⼲扰⽅式有关，同⼀个系统在某个运⾏⽅式下和某种⼲扰下系统是暂态稳定，⽽在另⼀个运⾏⽅式和另外⼀种⼲扰下它也可能是不稳定的。

⼲扰最严重的是三相短路故障，单相接地故障⽐较多。

系统的暂态时间有些可以在1S内都失去同步，有些可以维持⼏分钟。

模拟电⼒系统暂态稳定性实验接线图⼀般采⽤发电机-变压器-双回线路-⽆穷⼤系统。

以下我们来分析⼀下发电机在正常运⾏-短路故障-故障切除三种状态下功率特性曲线。

如下图：原动机输出的机械功率⽤PT表⽰，发电机向系统送的电磁功率⽤P0表⽰。

正常运⾏的时候PT= P0。

假设不计故障之后⼏秒钟调速器的作⽤，机械功率始终保持P0，图中a表⽰发电机正常运⾏点在曲线PⅠ上，发⽣短路后功率特性降为PⅡ，由于转⼦的惯性，转⼦⾓度不会⽴刻变化，运⾏点有a变⾄b点，电磁功率显著减⼩，⽽原动机PT 不变，三相短路时PⅡ曲线越低，此时将加速，其相对速度和相对⾓度（同步）增加，有b点向c点移动，如果故障⼀直存在，则始终存在过剩功率，发电机⼀直加速，直到系统失去同步。

电力系统分析目录第一部分电力系统稳态分析第一章电力系统的基本概念第二章电力系统的元件参数及等值电路第三章简单电力系统的计算和分析第四章电力系统潮流的计算机算法第五章电力系统的有功功率和频率调整第六章电力系统的无功功率和电压调整第二部分电力系统暂态分析第七章电力系统故障分析的基本知识第八章同步发电机突然三相短路分析第九章电力系统三相短路的实用计算第十章对称分量法及元件的各序参数和等值电路第十一章不对称故障的分析、计算第十二章电力系统各元件的机电特性第十三章电力系统静态稳定第十四章电力系统暂态稳定第十五章研究生入学考试试题附录第一部分电力系统稳态分析电力系统稳态分析,研究的内容分为两类,一类是电力系统稳态运行状况下的分析与潮流分布计算，另一类是电力系统稳态运行状况的优化和调整。

第一章电力系统的基本概念1—1 什么叫电力系统、电力网及动力系统？电力系统为什么要采用高压输电？1-2 为什么要规定额定电压？电力线、发电机、变压器和用电设备的额定电压是如何确定的?1—3 我国电网的电压等级有哪些？1—4 标出图1—4电力系统中各元件的额定电压。

1—5 请回答如图1－5所示电力系统中的二个问题:⑴ 发电机G 、变压器1T 2T 3T 4T 、三相电动机D 、单相电灯L 等各元件的额定电压。

⑵ 当变压器1T 在+2。

5％抽头处工作，2T 在主抽头处工作，3T 在-2。

5%抽头处工作时，求这些变压器的实际变比。

1-6 图1—6中已标明各级电网的电压等级.试标出图中发电机和电动机的额定电压及变压器的额定变比。

1-7 电力系统结线如图1—7所示，电网各级电压示于图中.试求：⑴发电机G 和变压器1T 、2T 、3T 高低压侧的额定电压。

⑵设变压器1T 工作于+2。

5％抽头， 2T 工作于主抽头，3T 工作于—5%抽头，求这些变压器的实际变比。

习题1-4图1-8 比较两种接地方式的优缺点，分析其适用范围.1-9 什么叫三相系统中性点位移?它在什么情况下发生？中性点不接地系统发生单相接地时，非故障相电压为什么增加3倍?1—10 若在变压器中性点经消弧线圈接地，消弧线圈的作用是什么？ 1—11 什么叫分裂导线、扩径导线？为什么要用这种导线？1-12 架空线为什么要换位？规程规定，架空线长于多少公里就应进行换位？1—13 架空线的电压在35kV 以上应该用悬式绝缘子,如采用X —4。

精品文档1．采用分裂导线的目的是（ A ）A.减小电抗B.增大电抗C.减小电纳D.增大电阻2．下列故障形式中对称的短路故障为（ C ）A.单相接地短路B.两相短路C.三相短路D.两相接地短路3．简单系统静态稳定判据为（ A ）A.>0B.<0C.=0D.都不对4．应用等面积定则分析简单电力系统暂态稳定性，系统稳定的条件是（ C ）A.整步功率系数大于零B.整步功率系数小于零C.最大减速面积大于加速面积D.最大减速面积小于加速面积5．频率的一次调整是（ A ）A.由发电机组的调速系统完成的B.由发电机组的调频系统完成的C.由负荷的频率特性完成的D.由无功补偿设备完成的6.系统备用容量中，哪种可能不需要( A )A.负荷备用B.国民经济备用C.事故备用D.检修备用7．电力系统中一级负荷、二级负荷和三级负荷的划分依据是用户对供电的（A ）A.可靠性要求B.经济性要求C.灵活性要求D.优质性要求9．中性点不接地系统发生单相接地短路时，非故障相电压升高至（ A ）A.线电压B.1.5倍相电压C.1.5倍线电压D.倍相电压10.P-σ曲线被称为( D )A.耗量特性曲线B.负荷曲线C.正弦电压曲线D.功角曲线11.顺调压是指( B )A.高峰负荷时，电压调高，低谷负荷时，电压调低B.高峰负荷时，允许电压偏低，低谷负荷时，允许电压偏高C.高峰负荷，低谷负荷，电压均调高D.高峰负荷，低谷负荷，电压均调低12.潮流方程是( D )A.线性方程组B.微分方程组C.线性方程D.非线性方程组13.分析简单电力系统的暂态稳定主要应用( B )A.等耗量微增率原则B.等面积定则C.小干扰法D.对称分量法14.电力线路等值参数中消耗有功功率的是（A）A.电阻B.电感C.电纳D.电容15.一般情况，变压器的负序电抗X T（2）与正序电抗X T（1）的大小关系为（C）精品文档A.X T（1）>X T(2)B.X T（1）<X T(2)C.X T（1）=X T(2)D.X T（1）>>X T(2)16.电力系统分析中，有功功率的单位常用（B）A.VARB.MWC.MVAD.V17.在下列各种故障类型中，属于纵向故障的是（D）A.两相短路B.两相断线C.单相接地短路D.两相短路接地18.利用P—Q分解法和牛顿—拉夫逊法进行潮流计算，二者的收敛速度是（C）A.P—Q分解法高于牛顿—拉夫逊法B.无法比较C.牛顿拉夫逊法高于P—Q分解法D.两种方法一样19.电力系统的综合供电负荷加上厂用电之和，称为（A）A.发电负荷B.供电负荷C.用电负荷D.工业负荷20.构成电力网的主要设备有（B）A.变压器，用户B.变压器，电力线路C.电缆，架空线D.电阻，电容21.系统发生两相接地短路故障时，复合序网的连接方式为（A）A.正序、负序、零序并联B.正序、负序并联、零序网开路C.正序、零序并联、负序开路D.零序、负序并联，正序开路22.系统发生两相短路故障时，复合序网的连接方式为（B）A.正序、负序、零序并联B.正序、负序并联、零序网开路C.正序、零序并联、负序开路D.零序、负序并联，正序开路23.系统发生单接地短路故障时，复合序网的连接方式为（A）A.正序、负序、零序串联B.正序、负序并联、零序网开路C.正序、零序并联、负序开路D.零序、负序并联，正序开路24.二相断线时的复合序网是在断口处( A )。

稳态与暂态状态下电力系统稳定性分析电力系统（power system）作为一个由发电、输电、变电和供电部分组成的整体，其运行状态的稳定性一直是电力工程师们所关注的问题。

一个稳定的电力系统能够维持正常的电压和频率，同时能够满足用户的用电需求，在各种异常情况下能够保持正常的运转，而一个不稳定的电力系统则会导致电网的瘫痪和能源的短缺。

因此，分析电力系统的稳定性，既是电力工程师的基本功，也是维护电网安全稳定运行的重要手段。

电力系统的稳态和暂态是两个概念。

稳态状态是指在不受外界干扰的情况下，电力系统内各部分电参数（如电压、频率、电流）能够保持在一个相对稳定的水平。

稳态状态下，电力系统的运行特点是稳定可控的，因此长期稳态方程（即电力系统的潮流计算）是电力系统分析的基础。

相比之下，暂态状态下电力系统的运行特点则是动态不稳定的。

暂态状态下，电力系统内的各种电参数可能发生急剧变化，如电压骤升或骤降、电流突变等，因此暂态分析考虑的是电力系统在受到干扰后的响应能力。

而暂态分析通常用于评估电力系统的远距离输电线路、变电站、短路故障等情况下的稳定性。

为了使电力系统保持稳定，电力工程师们通常需要对电力系统进行全面的分析和仿真，分析出稳态和暂态下的电力系统稳定性。

对于稳态分析，我们通常采用潮流计算法（load flow calculation）来计算电力系统的各参数数量，例如电压、电流、功率等等。

该方法通过对电力系统内各分支线路电参数进行计算和矫正，以达到使得各节点电压和线路功率处于最合适的状态的目的，从而维持整个电力系统的运行和分配。

而对于暂态分析，我们通常使用传递函数法（transfer function method）来进行分析。

传递函数法考虑电源系统，负载系统和干扰因素之间相互作用，并对系统行为进行数学建模、仿真和测试。

通过分析系统电源、扰动幅度、负载响应等因素，可以评估电力系统在不同条件下的响应能力和鲁棒性。

总之，对于电力系统来说，稳定性是相当重要的因素。

暂态能量函数法是基于一个古典的力学概念发展而来的，该概念中指出：“对于一个自由的（无外力作用的）动态系统，若系统的总能量V （V （X）＞0，X为系统状态量）随时间变化率恒为负，则系统总能量不断减少，直至最终达到一个最小值，即平衡状态，则此系统是稳定的”。

图9-1所示的滚球系统在无扰动时，球位于稳定平衡点（stable equilibrium point, SEP）;受扰后，小球在扰动结束时位于高度h处（以SEP为参考点），并具有速度V。

该质量为m的小球，总能量V由动能jmv2及势能mgh（g为重力加速度）的和组成，即1 2V mv mgh 0若小球与壁有摩擦力，则受扰后能量在摩擦力作用下逐步减少；设小球所在容器的壁高为H （以SEP为参考点），当小球位于壁沿上，且速度为零时（即处于不稳定平衡状态），相应的势能为mgH,称此位置为不稳定平衡点（unstable equilibrium point，UEP），相应的势能为系统临界能量V c r，即根据运动原理，我们知道，若忽略容器壁摩擦，在扰动结束时小球总能量V大于临界能量乂「时，则小球最终将滚出容器，而失去稳定性；反之V ：：：V“，则小球将在摩擦力作用下，能量逐步减少，最终静止于SEP。

而V二V“为临界状态，显然可根据（V cr -V）判别稳定裕度。

对于一个实际系统要解决两个关键问题：一是对于一个实际系统如何构造（定义）一个合理的暂态能量函数，它的大小应能正确地反映系统失去稳定的严重性；二是如何确定和系统临界稳定相对应的函数值，即临界能量，从而可通过对扰动结束时暂态能量函数值（即上例中的1mv2mgh ）和临界值（即上例中的mgH）的比较来判别稳定性或确定稳定域。

这种判别稳定的方法统称为暂态能量函数法（transien tenergy function TEF法）。

它的特点是从能量的观点来判别稳定性，而不是根据系统运动的轨迹（物理量随时间变化的曲线）来判别稳定性，从而计算量少，速度快。

第一章1.短路的概念和类型概念：指一切不正常的相与相与地（对于中性点接地的系统）之间发生通路或同一绕组之间的匝间非正常连通的情况。

类型：三相短路、两相短路、两相接地短路、单相接地短路。

2.电力系统发生短路故障会对系统本身造成什么危害？1）短路故障是短路点附近的支路中出现比正常值大许多倍的电流，由于短路电流的电动力效应，导体间将产生巨大的机械应力，可能破坏导体和它们的支架。

2）比设备额定电流大许多倍的短路电流通过设备，会使设备发热增加，可能烧毁设备。

3）短路电流在短路点可能产生电弧，引发火灾。

4）短路时系统电压大幅度下降，对用户造成很大影响。

严重时会导致系统电压崩溃，造成电网大面积停电。

5）短路故障可能造成并列运行的发电机失去同步，破坏系统稳定，造成大面积停电。

这是短路故障的最严重后果。

6）发生不对称短路时，不平衡电流可能产生较大的磁通在邻近的电路内感应出很大的电动势，干扰附近的通信线路和信号系统，危及设备和人身安全。

7）不对称短路产生的负序电流和电压会对发电机造成损坏，破坏发电机的安全，缩短发电机的使用寿命。

3．同步发电机三相短路时为什么进行派克变换？目的是将同步发电机的变系数微分方程式转化为常系数微分方程式，从而为研究同步发电机的运行问题提供了一种简捷、准确的方法。

4.同步发电机磁链方程的电感系数矩阵中为什么会有变数、常数或零？变数：因为定子绕组的自感系数、互感系数以及定子绕组和转子绕组间的互感系数与定子绕组和转子绕组的相对位置θ角有关，变化周期前两者为π，后者为2π。

根本原因是在静止的定子空间有旋转的转子。

常数：转子绕组随转子旋转，对于其电流产生的磁通，其此路的磁阻总不便，因此转子各绕组自感系数为常数，同理转子各绕组间的互感系数也为常数，两个直轴绕组互感系数也为常数。

零：因为无论转子的位置如何，转子的直轴绕组和交轴绕组永远互相垂直，因此它们之间的互感系数为零。

5.同步发电机三相短路后，短路电流包含哪些分量？各按什么时间常数衰减？1）定子短路电流包含二倍频分量、直流分量和交流分量；励磁绕组的包含交流分量和直流分量；D轴阻尼绕组的包含交流分量和直流分量；Q轴阻尼包含交流分量。