第二章对偶问题一般题答案
- 格式:doc
- 大小:475.00 KB
- 文档页数:7

第2章 对偶问题判断下列说法是否正确:对偶问题的对偶问题一定是原问题;根据对偶问题的性质,当原问题为无界解时,其对偶问题无可行解,反之,当对偶问题无可行解时,其原问题具有无界解; 已知*i y 为线性规划的对偶问题的最优解,若*i y >0,说明在最优生产计划中的i 种资源已完全耗尽;已知*i y 为线性规划的对偶问题的最优解,若*i y =0,说明在最优生产计划中第i 种资源一定有剩余;若某种资源的影子价格等于k ,在其它条件不变的情况下,当改种资源增加5个单位时,相应的目标函数值将增大5k ; 在线性规划问题的最优解中,如某一变量j x 为非基变量,则在原来问题中,无论改变它在目标函数中的系数j c 或在各约束中的相应系数ij a ,反映到最终单纯形表中,除该列数字有变化外,将不会引起其它列数字的变化。
简答题、试述对偶单纯形法的优点及其应用上的局限性。
、试述对偶单纯形法的步骤。
、试解释对偶解的经济含义和影子价格在市场决策中的作用。
、什么是资源的影子价格?同相应的市场价格之间有何区别?以及研究影子价格的意义是什么?:判断下列说法是否正确,为什么?(a )如果线性规划的原问题存在可行解,则其对偶问题也一定存在可行解; (b )如果线性规划的对偶问题存在可行解,则其原问题也一定无可行解;(c )在互为对偶的一对原问题和对偶问题中,不管原问题是求极大或极小,原问题可行解的目标函数都一定不超过其对偶问题可行解的目标函数。
若某种资源的影子价格等于k ,在其他条件不变的情况下,当该种资源增加5个单位时,相应的目标函数最大值将增加5k 吗? 已知*i y 为某线性规划问题的对偶问题最优解中的第i 分量,若*i y =0,能否肯定在最优生产计划种第i 种资源一定有剩余?写出对偶问题写出下列线性规划问题的对偶问题123max 102Z x x x =++123123123420,,0x x x x x x ++≤≥写出下列线性规划问题的对偶问题1234max 23Z x x x x =+++12341231341324252341,0,,x x x x x x x x x x x x x x +++≤-+=--+≥≥无约束写出下列线性规划问题的对偶问题1234min 3234Z x x x x =+-+1234234123414232343345237420,0,,x x x x x x x x x x x x x x x -++≤++≥----=≥≤无约束写出下列线性规划问题的对偶问题123min 567Z x x x =---123123123123531556102050,0,x x x x x x x x x x x x -+-≥--+≤--=-≤≥无约束写出下列线性规划问题的对偶问题123max 25Z x x x =++12312313123235237365,,0x x x x x x x x x x x ++≤++≤+≤≥写出下列线性规划问题的对偶问题123max Z x x x =++1231312327664,,0x x x x x x x x ++=+≥≥写出下列线性规划问题的对偶问题123min 423Z x x x =++123123131232562742,0,0x x x x x x x x x x x ++≤++=+≥≤≥无约束写出下列线性规划问题的对偶问题:1231231231231232242352373..465,,0MinZ x x x x x x x x x s t x x x x x x =++++≥⎧⎪++≤⎪⎨++≤⎪⎪≥⎩写出下列线性规划问题的对偶问题:12312312312312323231325..34,,0,MinZ x x x x x x x x x s t x x x x x x =--+-=⎧⎪-+≥-⎪⎨-+≤⎪⎪≥⎩无限制写出下列线性规划问题的对偶问题:123123123131232423134..40,0,MaxZ x x x x x x x x x s t x x x x x =++++≥⎧⎪-+≤⎪⎨+=⎪⎪≥≤⎩无限制写出下列线性规划问题的对偶问题:1234512345123451~45275354625..232690,MaxZ x x x x x x x x x x s t x x x x x x x =++++++++=⎧⎪++++=⎨⎪≥⎩无限制写出下面线性规划问题的对偶问题12max 52z x x =-+1212123235,0x x x x x x -+≤-+≤≥写出下面线性规划问题的对偶问题12max 56z x x =+12122553x x x x +=-+≥1x 无限制2,0x ≥设有原始问题123max 325z x x x =++约束条件:12313121232560324204400,,0x x x x x x x x x x ++≤+≤+≤≥写出以上原始问题的对偶问题。

对偶问题习题● 证明题(选做)1. 证明下面的线性规划问题要么无解,要么最优目标函数值为零,其中C 为n 维向量,b 为m 维向量,A 为m n ⨯矩阵。
min ..0,0yb cxAx bs t yA c x y -≤⎧⎪≥⎨⎪≥≥⎩证明 把问题拆成两个问题(A)max ..0z cxAx b s t x =≤⎧⎨≥⎩ 和 (B)min ..0w ybyA c s t y =≥⎧⎨≥⎩显然两个问题为原问题和对偶问题,分四种情形讨论:情形1 如果两个问题都有可行解,那么两个问题都有最优解,且最优目标函数值相等。
根据对偶理论,由于有cx yb ≤,因此0yb cx -≥。
而**y b cx -=0,因而该情形下有解,且最优解为0。
情形2 如果问题A 有解但为无穷解,那么B 问题一定无解,也就是yA c ≥不成立,从而该情形下无解。
情形3 如果问题B 有解但为无穷解,那么A 问题一定无解,也就是Ax b ≤不成立,从而该情形下无解。
情形4 如果问题A 和问题B 均无解,那么Ax b ≤和yA c ≥都不成立,从而该情形下也无解。
综合上述,根据对偶理论只可能有如上情形,从而命题成立。
2. 设线性规划问题1是11max ..0(1)nj jj nij ji j jz c x a x b s t x j n 1== =⎧≤⎪⎨⎪≥≤≤⎩∑∑ 其中***12(,,,)m y y y 是其对偶问题的最优解。
又设线性规划问题2是11max ..0(1)nj jj nij ji i j jz c x a x b k s t x j n 2== =⎧≤+⎪⎨⎪≥≤≤⎩∑∑ 其中i k 是给定的常数,求证*211max()max()mi ii z z k y=≤+∑证明 问题1的对偶问题为11221min ...,1,2,...,..0m mmij i j i iw b y b y b y a y c j ns t y = =+++⎧≥=⎪⎨⎪≥⎩∑问题2的对偶问题为1112221min ()()...(),1,2,...,..0m m mmij i j i iw b k y b k y b k y a y c j ns t y = =++++++⎧≥=⎪⎨⎪≥⎩∑既然***12(,,,)m y y y 是问题1的对偶问题最优解,那么必有 ***11122max()...m mz b y b y b y =+++ 又由于***12(,,,)m y y y 是问题1的对偶问题的可行解,那么有***2111222******11221122***11122max()()()...() ...(...) max()(...)m m mm m m m m m z b k y b k y b k y b y b y b y k y k y k y z k y k y k y ≤++++++=+++++++=++++ 3. 设线性规划问题1是11min (1)..0(1)nj jj nij ji j jz c x a x b i m s t x j n 1== =⎧=≤≤⎪⎨⎪≥≤≤⎩∑∑ 又设线性规划问题2是*11min ()(1,)..0(1)nj k kj jj nij ji j jz c y a x a x b i m i k s t x j n 2== =-⎧≤≤≤≠⎪⎨⎪≥≤≤⎩∑∑ 设***12(,,,)n x x x 是线性规划问题1的最优解,***12(,,,)m y y y 为其对偶问题的最优解,请证明***12(,,,)n x x x 也是问题2的最优解。


第二章线性规划的对偶问题习题2.1写出下列线性规划问题的对偶问题(1)maxz=10x1+x2+2x3(2)maxz=2x1+x2+3x3+x4st.x1+x2+2x3≤10st.x1+x2+x3+x4≤54x1+x2+x3≤202x1-x2+3x3=-4x j ≥0(j=1,2,3)x1-x3+x4≥1xj≥0(j=1,2,3,4)其对偶问题的最优解y1*=4;y2*=1,试根据对偶问题的性质,求出原问题的最优解。
2.5考虑线性规划问题maxz=2x1+4x2+3x3st.3x1+4x2+2x3≤602x1+x2+2x3≤40x 1+3x2+2x3≤80xj≥0(j=1,2,3)(1)写出其对偶问题(2)用单纯形法求解原问题,列出每步迭代计算得到的原问题的解与互补的对偶问题的解;仅供个人学习参考(3)用对偶单纯形法求解其对偶问题,并列出每步迭代计算得到的对偶问题解及与其互补的对偶问题的解;(4)比较(2)和(3)计算结果。
2.6已知线性规划问题maxz=10x1+5x2st.3x1+4x2≤95x1+2x2≤8xj≥0(j=1,2)(1)给出a,b,c,d,e,f,g的值或表达式;(2)指出原问题是求目标函数的最大值还是最小值;(3)用a+?a,b+?b分别代替a和b,仍然保持上表是最优单纯形表,求?a,?b满足的范围。
仅供个人学习参考仅供个人学习参考2.9某文教用品厂用原材料白坯纸生产原稿纸、日记本和练习本三种产品。
该厂现有工人100人,每月白坯纸供应量为30000千克。
已知工人的劳动生产率为:每人每月可生产原稿纸30捆,或日记本30打,或练习本30箱。
已知原材料消耗为:每捆原稿纸用白坯纸310千克,每打日记本用白坯纸340千克,每箱练习本用白坯纸380千克。
又知每生产一捆原稿纸可获利2元,生产一打日记本获利3元,生产一箱练习本获利1元。
试确定:(1)现有生产条件下获利最大的方案;(2)如白坯纸的供应数量不变,当工人数不足时可招收临时工,临时工工资支出为每人每月40元,则该厂要不要招收临时工?如要的话,招多少临时工最合适?2.10某厂生产甲、乙两种产品,需要A 、B 两种原料,生产消耗等参数如下表(表中2.12试从经济上解释对偶问题及对偶变量的含义。


第二章 对偶问题与灵敏度分析一、写出下列线性规划的对偶问题1、P89,2.1(a)321422m in x x x Z ++=s.t ⎪⎪⎩⎪⎪⎨⎧≥=++≤++≥++.,0,;534;332;243321321321321无约束x x x x x x x x x x x x解:原模型可化为321422m in x x x Z ++=s.t ⎪⎪⎩⎪⎪⎨⎧≥=++≥≥++.,0,;534;3-3--2-;243321321321321321无约束x x x y y y x x x x x x x x x 于是对偶模型为321532m ax y y y W +-=s.t ⎪⎪⎩⎪⎪⎨⎧≥≤+-≤+-≤+-.,0,;4334;243;22321321321321无约束y y y y y y y y y y y y2、P89,2.1(b)321365m ax x x x Z ++=s.t ⎪⎪⎩⎪⎪⎨⎧≤≥≤++≥-+-=++.0,0,;8374;35;522321321321321x x x x x x x x x x x x 无约束解:令033≥-='x x 原模型可化为321365m ax x x x Z '-+=s.t ⎪⎪⎩⎪⎪⎨⎧≥'≥≤'+≤'='+.0,0,;83-74;3--5-;52-2321321321321321x x x y y y x x x x x x x x x 无约束于是对偶模型为321835m in y y y W +-=s.t ⎪⎪⎩⎪⎪⎨⎧≥-≥---≥+-=++.0,,;332;6752;54321321321321y y y y y y y y y y y y 无约束 或⎪⎪⎩⎪⎪⎨⎧≥≤++≥+-=++.0,,;332;6752;54321321321321y y y y y y y y y y y y 无约束二、灵敏度分析1、P92, 2.11线性规划问题213m ax x x Z += s.t ⎪⎩⎪⎨⎧≥≤+≤+0,1025;74212121x x x x x x最优单纯形表如下试用灵敏度分析的方法,分析:(1) 目标函数中的系数21,c c 分别在什么范围内变化,最优解不变? (2) 约束条件右端常数项21,b b 分别在什么范围内变化,最优基保持不变? 解:(1) 1c 的分析:要使得最优解不变,则需⎪⎪⎩⎪⎪⎨⎧≤⨯-⨯+=≤⨯+⨯-=034131003513201413c c σσ 即 ⎪⎩⎪⎨⎧≤≥42511c c 所以:4251≤≤c 时可保持最优解不变。

习题二2.1 写出下列线性规划问题的对偶问题(1) max z =10x1+x2+2x3(2) max z =2x1+x2+3x3+x4st. x1+x2+2 x3≤10 st. x1+x2+x3 +x4≤54x1+x2+x3≤20 2x1-x2+3x3=-4x j≥0 (j=1,2,3)x1-x3+x4≥1x1,x3≥0,x2,x4无约束(3) min z =3x1+2 x2-3x3+4x4(4) min z =-5 x1-6x2-7x3st. x1-2x2+3x3+4x4≤3 st. -x1+5x2-3x3≥15x2+3x3+4x4≥-5 -5x1-6x2+10x3≤202x1-3x2-7x3 -4x4=2=x1-x2-x3=-5 x1≥0,x4≤0,x2,,x3无约束x1≤0,x2≥0,x3无约束2.2 已知线性规划问题max z=CX,AX=b,X≥0。
分别说明发生下列情况时,其对偶问题的解的变化:(1)问题的第k个约束条件乘上常数λ(λ≠0);(2)将第k个约束条件乘上常数λ(λ≠0)后加到第r个约束条件上;(3)目标函数改变为max z=λCX(λ≠0);'x代换。
(4)模型中全部x1用312.3 已知线性规划问题min z=8x1+6x2+3x3+6x4st. x1+2x2+x4≥33x1+x2+x3+x4≥6x3 +x4=2x1 +x3 ≥2x j≥0(j=1,2,3,4)(1) 写出其对偶问题;(2) 已知原问题最优解为x*=(1,1,2,0),试根据对偶理论,直接求出对偶问题的最优解。
2.4 已知线性规划问题min z=2x1+x2+5x3+6x4 对偶变量st. 2x1 +x3+x4≤8 y12x1+2x2+x3+2x4≤12 y2x j≥0(j=1,2,3,4)对偶问题的最优解y1*=4;y2*=1,试对偶问题的性质,求出原问题的最优解。
2.5 考虑线性规划问题max z=2x1+4x2+3x3st. 3x1+4 x2+2x3≤602x1+x2+2x3≤40x1+3x2+2x3≤80x j≥0 (j=1,2,3)4748(1)写出其对偶问题(2)用单纯形法求解原问题,列出每步迭代计算得到的原问题的解与互补的对偶问题的解;(3)用对偶单纯形法求解其对偶问题,并列出每步迭代计算得到的对偶问题解及与其互补的对偶问题的解;(4)比较(2)和(3)计算结果。

第二章线性规划的对偶理论2.1 写出下列线性规划问题的对偶问题max z=2x1+2x2-4x3x1 + 3x2 + 3x3 ≤304x1 + 2x2 + 4x3≤80x1、x2,x3≥0解:其对偶问题为min w=30y1+ 80y2y1+ 4y2≥23y1 + 2y2 ≥23y1 + 4y2≥-4y1、y2≥02.2 写出下列线性规划问题的对偶问题min z=2x1+8x2-4x3x1 + 3x2-3x3 ≥30-x1 + 5x2 + 4x3 = 804x1 + 2x2-4x3≤50x1≤0、x2≥0,x3无限制解:其对偶问题为max w=30y1+80 y2+50 y3y1-y2 + 4 y3≥23y1+5y2 + 2y3≤8-3y1 + 4y2-4y3 =-4y1≥0,y2无限制,y3≤02.3已知线性规划问题max z=x1+2x2+3x3+4x4x1 + 2x2 + 2x3 +3x4≤202x1 + x2 + 3x3 +2x4≤20x1、x2,x3,x4≥0其对偶问题的最优解为y1*=6/5,y2*=1/5。
试用互补松弛定理求该线性规划问题的最优解。
解:其对偶问题为min w=20y1+ 20y2y1 + 2y2≥1 (1)2y1 + y2 ≥2 (2)2y1 +3y2≥3 (3)3y1 +2y2≥4 (4)y1、y2≥0将y1*=6/5,y2*=1/5代入上述约束条件,得(1)、(2)为严格不等式;由互补松弛定理可以推得x1*=0,x2*=0。
又因y1*>0,y2*>0,故原问题的两个约束条件应取等式,所以2x3*+3x4* = 203x3* +2x4* = 20解得x3* = x4* = 4。
故原问题的最优解为X*=(0,0,4,4)T2.4用对偶单纯形法求解下列线性规划min z=4x1+2x2+6x32x1 +4x2 +8x3 ≥244x1 + x2 + 4x3≥8x1、x2,x3≥0解将问题改写成如下形式max(-z)=-4x1-2x2-6x3-2x1-4x2 -8x3 + x4=-24-4x1-x2-4x3+x5 =-8x1、x2,x3,x4,x5≥0显然,p4、p5可以构成现成的单位基,此时,非基变量在目标函数中的系数全为负数,因此p4、p5构成的就是初始正侧基。

第二章.对偶理论与灵敏度分析1. 已知线性规划问题:332211m a xx c x c x c z ++= ⎪⎩⎪⎨⎧=≥⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡)5,,1(01001.2154323132221212111 j x b b x x x a a x a a x a a st j 用单纯形法求解得最终单纯形表如下表所示: (a ) 求232221131211,,,,,a a a a a a 和21,b b321,,c c c 8,4,7,5,8,2,4,1,1,2/5,2/932121231322122111===========c c c b b a a a a a a2. 已知矩阵A 及其逆矩阵1-A 如下:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=104020012A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=-11202/1004/12/11A试根据改进单纯形法中求逆矩阵的方法原理求下述矩阵B 的逆矩阵1-B,已知⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=144210152B答:先设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=144010052C ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-∙-72/14/114151A∴⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=∙⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=--16201002/52/1114002002/11111A C ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=144210152B 有 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡∙-1322/111211C∴⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----=∙⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=--26/226/1226/426/426/226/826/1126/126/913/10013/21026/110111C B3. 已知线性规划的原问题与对偶问题分别为:(P )原问题:CX z =max (D)对偶问题:Yb w =min⎩⎨⎧≥≤0.X b AX st ⎩⎨⎧≥≥0Y C YA st若*Y 为对偶问题最优解,又原问题约束条件右端项用b 替换之后其最优解为X ,试证明有b Y X C *≤证明:原问题右端项b 用b 替换后,新的原问题'P 及对偶问题'D 为::'P ⎩⎨⎧≥≤=0.'m a x Z b AZ st CZz :'D ⎩⎨⎧≥≤=0.min 'Y C YA st bY w设'D 的最优解为Y ,因有b Y Z C =,有*Y 是'D 的可行解,故有b Y b Y *≤,由此b Y Z C *≤4. 已知下表为求解某线性规划问题的最终单纯形表,表中54,x x 为松弛变量,问题的约束(b) 直接由表写出对偶问题的最优解。
对偶问题一般习题答案● 一般题目内容1:根据原规划,写出对偶规划 1.1 写出下面线性规划问题的对偶问题(a.) 2341234123412341234max 2343567358..12999200,0,0,z x x x x x x x x x x x x s t x x x x x x x x =+++-+--=⎧⎪++-≥⎪⎨--+≤⎪⎪≥≥≤⎩无约束 (b.) 111111111max (1,)(1)..0(1,)1nj jj nij j i j n ij j i j j j z c x a x b i m m m a x b m i m s t x j n n n x n j n=== =⎧≤ ≤≤≤⎪⎪⎪⎪= +≤≤⎨⎪⎪≥ ≤≤≤⎪+≤≤⎪⎩∑∑∑无约束,当 内容2:根据对偶问题,判定原问题有最优解、无解、有无穷大解 2.1 应用对偶理论, 证明线性规划问题有最优解。
12121212max 32243214..301,2j z x x x x x x s t x x x j =+-+≤⎧⎪+≤⎪⎨-≤⎪⎪≥ =⎩提示:找到原问题和对偶问题的一个可行解,那么就能说明原问题有最优解。
2.2 应用对偶理论, 证明线性规划问题是可行的,但无最优解。
12313123max 4..1401,2,3jz x x xx x s t x x x x j =-+⎧-≥⎪-+≥⎨⎪≥ =⎩提示:说明对偶问题无解,再根据原问题有可行解,就说明原问题为无穷解,所以没有最优解。
2.3 应用对偶理论, 证明线性规划问题无解。
12121212max 5241..23101,2j z x x x x x x s t x x x j =+-≥⎧⎪+≤⎪⎨-≤⎪⎪≥ =⎩提示:说明对偶问题有无穷解,就说明原问题无解。
内容3:由原问题的最优解得到对偶问题的最优解 3.1 课本2.11题。
(a )写出最优单纯形表由最优单纯形表对于2x 有 []2311/2*(1/2)*4c c c -+-=-对于2x 有 []43141/2*(1/6)*4(0)c c c c -+-=-= 对于5x 有 []53150*(1/3)*2(0)c c c c -+=-=可得1c 、2c 和3c 的值由于11/201/61/3B -⎛⎫=⎪-⎝⎭ 13112321a a B a a ⎛⎫= ⎪⎝⎭且1*B B I -=那么可求得11a 、21a 、13a 和23a由于121221/2*1/2a B a -⎛⎫⎛⎫= ⎪ ⎪-⎝⎭⎝⎭那么可求得12a 和22a3.2 原规划为121212max 332212416..51501,2j z x x x x x s t x x j =++≤⎧⎪≤⎪⎨≤⎪⎪≥ =⎩引入松弛变量后为 121231425max 332212416..51501,2,3,4,5j z x x x x x x x s t x x x j =+++=⎧⎪+=⎪⎨+=⎪⎪≥ =⎩对偶规划为1231213min 121615243..25301,2,3jw y y yy y s t y y y j =++⎧+≥⎪+≥⎨⎪≥ =⎩已知对偶规划的最优解为(3/2, 0, 0), 试完成原规划的最优单纯形表(不用单纯形求解,并写出具体思路)。
第二章线性规划的对偶理论2.1 写出下列线性规划问题的对偶问题max z=2x1+2x2-4x3x1 + 3x2 + 3x3 ≤304x1 + 2x2 + 4x3≤80x1、x2,x3≥0解:其对偶问题为min w=30y1+ 80y2y1+ 4y2≥23y1 + 2y2 ≥23y1 + 4y2≥-4y1、y2≥02.2 写出下列线性规划问题的对偶问题min z=2x1+8x2-4x3x1 + 3x2-3x3 ≥30-x1 + 5x2 + 4x3 = 804x1 + 2x2-4x3≤50x1≤0、x2≥0,x3无限制解:其对偶问题为max w=30y1+80 y2+50 y3y1-y2 + 4 y3≥23y1+5y2 + 2y3≤8-3y1 + 4y2-4y3 =-4y1≥0,y2无限制,y3≤02.3已知线性规划问题max z=x1+2x2+3x3+4x4x1 + 2x2 + 2x3 +3x4≤202x1 + x2 + 3x3 +2x4≤20x1、x2,x3,x4≥0其对偶问题的最优解为y1*=6/5,y2*=1/5。
试用互补松弛定理求该线性规划问题的最优解。
解:其对偶问题为min w=20y1+ 20y2y1 + 2y2≥1 (1)2y1 + y2 ≥2 (2)2y1 +3y2≥3 (3)3y1 +2y2≥4 (4)y1、y2≥0将y1*=6/5,y2*=1/5代入上述约束条件,得(1)、(2)为严格不等式;由互补松弛定理可以推得x1*=0,x2*=0。
又因y1*>0,y2*>0,故原问题的两个约束条件应取等式,所以2x3*+3x4* = 203x3* +2x4* = 20解得x3* = x4* = 4。
故原问题的最优解为X*=(0,0,4,4)T2.4用对偶单纯形法求解下列线性规划min z=4x1+2x2+6x32x1 +4x2 +8x3 ≥244x1 + x2 + 4x3≥8x1、x2,x3≥0解将问题改写成如下形式max(-z)=-4x1-2x2-6x3-2x1-4x2 -8x3 + x4=-24-4x1-x2-4x3+x5 =-8x1、x2,x3,x4,x5≥0显然,p4、p5可以构成现成的单位基,此时,非基变量在目标函数中的系数全为负数,因此p4、p5构成的就是初始正侧基。
第2章 对偶问题02100011:T 02100021:F 02100031:T 02100041:F 02100051:F 02100061:F 02100071:T 02200011:略 02200021:略 02200031:略 02200041:略 02200051解:(a )不对(b )不对(c )不对02200061 解:不一定。
应考虑其他资源的拥有量。
02200071解:无法 肯定。
由互补松弛性知。
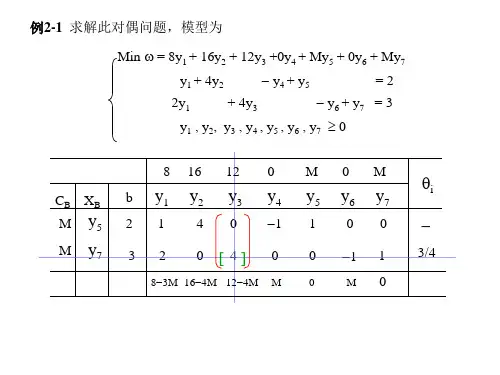
023*******min 1020W y y =+ 023********min 54W y y y =-+12121212410122,y y y y y y y y +≥+≥+≥≥ 12312123131322213310,0,y y y y y y y y y y y y y ++≥-=+-≥+=≥≤无约束023********max 352W y y y =-+ 023********max 15205W y y y =+-1212312312312323232337344440,0,y y y y y y y y y y y y y y +≤-+-=+-=-+-≥≤≥无约束1231231231235556631070,0,y y y y y y y y y y y y --+≥---≤--+-=-≥≤无约束023********min 235W y y y =++ 02301061 123m i n 1264W y y y =++ 12312123123232315765,,0y y y y y y y y y y y ++≥+≥++≥≥12312123123212157610,,y 0y y y y y y y y y y ++≥+≥++≥≥≤无约束023********max W 642y y y =++1231212312324225730,,0y y y y y y y y y y y ++=+≥++≤≤≥无约束02301081:02301091123123123123123235232342..5764,,0MaxW y y y y y y y y y s t y y y y y y =----≤⎧⎪--≤⎪⎨--≤⎪⎪≥⎩ 123123123123123542312..3233,0,0MaxW y y y y y y y y y s t y y y y y y =-+++≥⎧⎪--≥-⎪⎨-+-=-⎪⎪≤≥⎩无限制 023010101 02301111123123121231234323231..40,0,MinW y y y y y y y y s t y y y y y y =++++≥⎧⎪-≤⎪⎨++=⎪⎪≤≥⎩无限制12121212125922537..45,MinW y y y y y y s t y y y y =++≥⎧⎪+≥⎪⎨+≥⎪⎪⎩无限制 02301121 解:略02301131 解:略 02301141解:略02301152 解:11max m ni ijm ji j w a y b y+===+∑∑约束条件:i m j ij y y c ++≥ 1,,;1,,i m j n ==k y 无约束 1,,k m n =+02301162解:原始问题最优解:()*0,10,0,12,0,4X = 而minz=maxw=2602302011最优解为*2110(,)1313T X =,最优值为*31min 13Z =; 02302021最优解为*(1.5,0.125,0)TX =,最优值为*min 14Z =; 02302031最优解为*(9,4)TX =,最优值为*min 610Z =; 02302041最优解为*(6,2,0)TX =,最优值为*min 10Z =; 02302051最优解为*(4,1,0)TX =,最优值为*min 6Z =-; 02302061最优解为*(3,0,0,0)TX =,最优值为*min 9Z =;02302071解:最优解:()*0,10,0,12,0,4X = 而minz=maxw=26 02302081用对偶单纯形法求解:12min 23z x x =+12121212233021005,0x x x x x x x x +≤+≥-≥≥≥解:最优解为*55,2X ⎛⎫= ⎪⎝⎭minz=35/202302091 解:()**0,2/3,1,36TX z ==023021011212121212(1)30405552..263,0MinW y y y y y y s t y y y y =++≥⎧⎪-≥⎪⎨-≥⎪⎪≥⎩无限制 **12(2)5;0;min 150y y w ===02302011:最优解是()*0,20,0X = minz=120 02302121****123****1234(,,)(2/3,2,0)MinZ=22/33,0MinW=9Tx x x x x x x x ======(1)最优解:;最优值:(2)最优解:;最优值:02302131.略02302141解:(1)最优解为*55,2X ⎛⎫= ⎪⎝⎭02302152解:最优解()*5,0Y = Minw=15002302162解:(2)根据互补松弛定理求得*43,,1,055TY ⎛⎫= ⎪⎝⎭02302171 解略。
第二章线性规划的对偶理论2.1 写出下列线性规划问题的对偶问题max z=2x1+2x2-4x3x1 + 3x2 + 3x3 ≤304x1 + 2x2 + 4x3≤80x1、x2,x3≥0解:其对偶问题为min w=30y1+ 80y2y1+ 4y2≥23y1 + 2y2 ≥23y1 + 4y2≥-4y1、y2≥02.2 写出下列线性规划问题的对偶问题min z=2x1+8x2-4x3x1 + 3x2-3x3 ≥30-x1 + 5x2 + 4x3 = 804x1 + 2x2-4x3≤50x1≤0、x2≥0,x3无限制解:其对偶问题为max w=30y1+80 y2+50 y3y1-y2 + 4 y3≥23y1+5y2 + 2y3≤8-3y1 + 4y2-4y3 =-4y1≥0,y2无限制,y3≤02.3已知线性规划问题max z=x1+2x2+3x3+4x4x1 + 2x2 + 2x3 +3x4≤202x1 + x2 + 3x3 +2x4≤20x1、x2,x3,x4≥0其对偶问题的最优解为y1*=6/5,y2*=1/5。
试用互补松弛定理求该线性规划问题的最优解。
解:其对偶问题为min w=20y1+ 20y2y1 + 2y2≥1 (1)2y1 + y2 ≥2 (2)2y1 +3y2≥3 (3)3y1 +2y2≥4 (4)y1、y2≥0将y1*=6/5,y2*=1/5代入上述约束条件,得(1)、(2)为严格不等式;由互补松弛定理可以推得x1*=0,x2*=0。
又因y1*>0,y2*>0,故原问题的两个约束条件应取等式,所以2x3*+3x4* = 203x3* +2x4* = 20解得x3* = x4* = 4。
故原问题的最优解为X*=(0,0,4,4)T2.4用对偶单纯形法求解下列线性规划min z=4x1+2x2+6x32x1 +4x2 +8x3 ≥244x1 + x2 + 4x3≥8x1、x2,x3≥0解将问题改写成如下形式max(-z)=-4x1-2x2-6x3-2x1-4x2 -8x3 + x4=-24-4x1-x2-4x3+x5 =-8x1、x2,x3,x4,x5≥0显然,p4、p5可以构成现成的单位基,此时,非基变量在目标函数中的系数全为负数,因此p4、p5构成的就是初始正侧基。
第二章 对偶问题 一、选择1. 如果原问题有最优解,则其对偶问题也一定具有最优解,且有(A )。
A maxZ=minW B maxZ<minW C maxZ>minW D maxZ 与minW 无关2. 影子价格B c Y B 1*-=是(C )A 、对偶可行解B 、对偶基本可行解C 、对偶最优解D 无可行解3.原问题有可行解,其对偶问题有非可行解,则目标函数值( B )A 、最优B 、z <zmax C 、z >zmax D无可行解4. 影子价格是一种(C )A 、实际价格B 、市场价格C 、边际价格D 产品价格5. 资源的市场价格是已知数,相对比较稳定,而它的影子价格则有赖于(c ),是未知 数A 市场的定价B 买卖的多少C 资源的利用情况D 购买力6. 如果原问题(对偶问题)具有无界解,则其对偶问题(原问题)(D )。
A 唯一最优解B 无穷多最优解C 无界解D 无可行解 7. 影子价格是一种边际价格,实际上又是一种(A )。
A 机会成本B 实际成本 C 市场价格 D 产品价格9.如果),,1(n j x j K =-是原问题的可行解,),,1(m j y iK =-是其对偶问题的可行解,则恒有( A )A ∑∑=-=-≤mi ii nj j j y b x c 11B ∑∑=-=-=mi ii nj j j y b x c 11C∑∑=-=-≥mi iin j jjy b x c 11D 无法确定10. 如果),,1(n j x j K =∧是原问题的可行解,),,1(m j y iK =∧是其对偶问题的可行解,且有( B ),则),,1(n j x j K =∧是原问题的最优解,),,1(m j y iK =∧是其对偶问题的最优解A ∑∑=∧=∧≤mi ii nj j j y b x c 11B ∑∑=∧=∧=mi ii nj j j y b x c 11C∑∑=∧=∧≥mi iin j jjy b x c 11D ∧∧=y xij11.如果∑=∧∧=>n j i j ij ib x a y 1,0则,其符合(D )定理A 强对偶性B 弱对偶性C 最优性D 互补松弛性 12.如果有0,1=>∧=∧∑x c y a j mi j iij 则,其符合(D )定理A 强对偶性B 弱对偶性C 最优性D 互补松弛性 13. 如果∑=∧∧=>mi j iij j c y a x 1,0则,其符合(D )定理A 强对偶性B 弱对偶性C 最优性D 互补松弛性14. 如果有0,1=<∧=∧∑y b x a in j i j ij 则,其符合(D )定理A 强对偶性B 弱对偶性C 最优性D 互补松弛性15.在单纯形法中,最终单纯形表,原问题的变量对应着对偶问题的( A ) A 松弛变量B 剩余变量C 变量D 最优解16. 在单纯形法中,最终单纯形表,原问题的松弛变量对应着对偶问题的(C ) A 松弛变量B 剩余变量C 变量D 最优解17. 在单纯形法中,最终单纯形表中,对偶问题的最优解由(B )的值组成。
对偶问题一般习题答案
● 一般题目
内容1:根据原规划,写出对偶规划 1.1 写出下面线性规划问题的对偶问题
(a.) 234
1234123412341
234m a x 2343567358
..12999200,0,0,z x x x x x x x x x x x x s t x x x x x x x x =+++-+--=⎧⎪
++-≥⎪⎨
--+≤⎪
⎪≥≥≤⎩无约束
(b.) 1
111
11111m a x (1,)(1)
..0(1,)1n
j j
j n
ij j i j n ij j i j j j
z c x a x b i m m m a x b m i m s t x j n n n x n j n === =
⎧
≤ ≤≤≤⎪⎪⎪⎪
= +≤≤⎨⎪
⎪≥ ≤≤≤⎪
+≤≤⎪⎩∑
∑∑无约束,当
内容2:根据对偶问题,判定原问题有最优解、无解、有无穷大解 2.1 应用对偶理论, 证明线性规划问题有最优解。
12
12121
2m a x 3224
3214
..301,2j
z x x x x x x s t x x x j =+-+≤⎧⎪
+≤⎪⎨
-≤⎪⎪≥ =⎩ 提示:找到原问题和对偶问题的一个可行解,那么就能说明原问题有最优解。
2.2 应用对偶理论, 证明线性规划问题是可行的,但无最优解。
123
13123m a x 4
..14
01,2,3j
z x x x x x s t x x x x j =-+⎧-≥⎪
-+≥⎨⎪
≥ =⎩
提示:说明对偶问题无解,再根据原问题有可行解,就说明原问题为无穷解,所以没有最优解。
2.3 应用对偶理论, 证明线性规划问题无解。
12
12121
2m a x 5241
..23101,2j
z x x x x x x s t x x x j =+-≥⎧⎪
+≤⎪⎨
-≤⎪⎪≥ =⎩ 提示:说明对偶问题有无穷解,就说明原问题无解。
内容3:由原问题的最优解得到对偶问题的最优解 3.1 课本2.11题。
(a )写出最优单纯形表
由最优单纯形表
对于2x 有 []2311/2*(1/2)*4c c c -+-=- 对于2x 有 []43141/2*(1/6)*4(0)c c c c -+-=-= 对于5x 有 []53150*(1/3)*2(0)c c c c -+=-=
可得1c 、2c 和3c 的值
由于 11/201/6
1/3B -⎛⎫=
⎪-⎝⎭ 13
1123
21a a B a a ⎛⎫
= ⎪⎝⎭
且1*B B I -=
那么可求得11a 、21a 、13a 和23a
由于 121
221/2*1/2a B
a -⎛⎫⎛⎫= ⎪ ⎪-⎝
⎭⎝⎭ 那么可求得12a 和22a
3.2 原规划为
12
1212
m a x 332212416
..51501,2j
z x x x x x s t x x j =++≤⎧⎪
≤⎪⎨
≤⎪⎪≥ =⎩ 引入松弛变量后为 12
123142
5m a x 332212416
..51501,2,3,4,5j
z x x x x x x x s t x x x j =+++=⎧⎪
+=⎪⎨
+=⎪⎪≥ =⎩ 对偶规划为
123
1213m in 121615243..253
01,2,3j
w y y y y y s t y y y j =++⎧+≥⎪
+≥⎨⎪
≥ =⎩
已知对偶规划的最优解为(3/2, 0, 0), 试完成原规划的最优单纯形表(不用单纯形求解,并写出具体思路)。
第一步:先给出原问题的初始单纯形表
第二步:根据对偶问题的最优解(3/2, 0, 0),得到下图
第三步:由于只能是5x 、1x 和2x 为基变量,那么3x 40x ==,立即可得
14x =,22x =,55x =,且可得下表
第四步:预指定1x 为第一行的基变量,那么2x 为第三行的基变量,有下表
检验1x 是否为第一行的基变量。
根据表3的第一行和14416x x +=,立即可验证1x 确实是第一行的基变量。
第五步:在表4中,对于4x 有0=0-(3*1/4+0*5/4+3*34a ),因而可得
第六步:根据1*B B I -=,可得
1
23
01/405/411/21/4
0B
a -⎛⎫ ⎪=
⎪ ⎪-⎝
⎭ 20240001
5B ⎛⎫
⎪= ⎪ ⎪⎝
⎭
内容4:计算影子价格和隐含成本 4.1 课本(2.12)。
(略)
内容5:会使用对偶单纯形法 5.1 用对偶单纯形法解下列问题
(a.) 1234
12342341
234m in 6735563412
5610
..25801,2,3,4j
z x x x x x x x x x x x s t x x x x x j =++++-+≥⎧⎪
+-≥⎪⎨
+++≥⎪⎪≥ =⎩
引入松弛变量转化为下式
123412345234612347m a x 67355634125610
..25801,2,3,4,5,6,7j
z x x x x x x x x x x x x x s t x x x x x x j =------+-+=-⎧⎪
--++=-⎪⎨
----+=-⎪
⎪≥ =⎩ (b ) 123
1231231
23m in 2242352373
..46501,2,3j
z x x x x x x x x x s t x x x x j =---++≥⎧⎪
++≤⎪⎨
++≤⎪⎪≥ =⎩
引入松弛变量转化为下式
123123412351
236m a x 2242352373
..46501,2,3j
z x x x x x x x x x x x s t x x x x x j =++---+=-⎧⎪
+++=⎪⎨
+++=⎪⎪≥ =⎩ 令1236546x x x x =---代入上式得
23623
236234236235m a x 2(546)242(546)352
..3(546)73
02,3,4,5,6j
z x x x x x x x x x x x s t x x x x x x x j =---++⎧------+=-⎪
---+++=⎨⎪
≥ =⎩ 即
236
23642365m a x 585728
..1111312
02,3,4,5,6j
z x x x x x x x s t x x x x x j =---⎧+++=⎪
---+=-⎨⎪
≥ =⎩ (c ) 123
123131231
3m in 2332384
..226
24701,2,3j z x x x x x x x x s t x x x x x x j =--+⎧--+≥-⎪
+≤⎪⎪
+-≤⎨⎪
+≤⎪⎪≥ =⎩
(略)
(d)
122
122
123
123
m in974
575
3484
..
2686
01,2,3
j
z x x x
x x x
x x x
s t
x x x
x j
=-+
++≤
⎧
⎪
++=
⎪
⎨
++≥
⎪
⎪≥ =
⎩
(略)
内容6:能进行敏感性分析
6.1 课本2.9题(略)
内容7:会解参数规划
7.1 课本2.10题中(a)和(d)(略)。