当前位置：文档之家 › 第二章对偶问题

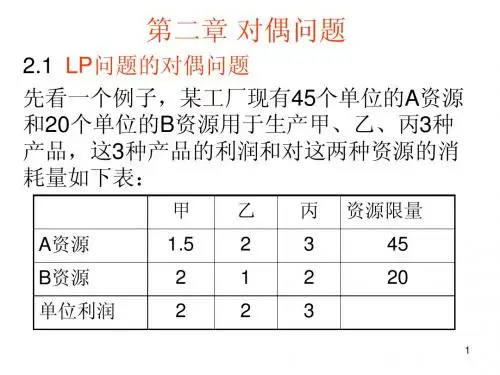
第二章对偶问题

  • 格式：ppt
  • 大小：1.05 MB
  • 文档页数：55

下载文档原格式

  / 55

合集下载

第2章 对偶问题

第2章 对偶问题

第2章 对偶问题判断下列说法是否正确：对偶问题的对偶问题一定是原问题；根据对偶问题的性质，当原问题为无界解时，其对偶问题无可行解，反之，当对偶问题无可行解时，其原问题具有无界解； 已知*i y 为线性规划的对偶问题的最优解，若*i y >0，说明在最优生产计划中的i 种资源已完全耗尽；已知*i y 为线性规划的对偶问题的最优解，若*i y ＝0，说明在最优生产计划中第i 种资源一定有剩余；若某种资源的影子价格等于k ，在其它条件不变的情况下，当改种资源增加5个单位时，相应的目标函数值将增大5k ； 在线性规划问题的最优解中，如某一变量j x 为非基变量，则在原来问题中，无论改变它在目标函数中的系数j c 或在各约束中的相应系数ij a ，反映到最终单纯形表中，除该列数字有变化外，将不会引起其它列数字的变化。

简答题、试述对偶单纯形法的优点及其应用上的局限性。

、试述对偶单纯形法的步骤。

、试解释对偶解的经济含义和影子价格在市场决策中的作用。

、什么是资源的影子价格？同相应的市场价格之间有何区别？以及研究影子价格的意义是什么？:判断下列说法是否正确，为什么？（a ）如果线性规划的原问题存在可行解，则其对偶问题也一定存在可行解； （b ）如果线性规划的对偶问题存在可行解，则其原问题也一定无可行解；（c ）在互为对偶的一对原问题和对偶问题中，不管原问题是求极大或极小，原问题可行解的目标函数都一定不超过其对偶问题可行解的目标函数。

若某种资源的影子价格等于k ，在其他条件不变的情况下，当该种资源增加5个单位时，相应的目标函数最大值将增加5k 吗？ 已知*i y 为某线性规划问题的对偶问题最优解中的第i 分量，若*i y ＝0，能否肯定在最优生产计划种第i 种资源一定有剩余？写出对偶问题写出下列线性规划问题的对偶问题123max 102Z x x x =++123123123420,,0x x x x x x ++≤≥写出下列线性规划问题的对偶问题1234max 23Z x x x x =+++12341231341324252341,0,,x x x x x x x x x x x x x x +++≤-+=--+≥≥无约束写出下列线性规划问题的对偶问题1234min 3234Z x x x x =+-+1234234123414232343345237420,0,,x x x x x x x x x x x x x x x -++≤++≥----=≥≤无约束写出下列线性规划问题的对偶问题123min 567Z x x x =---123123123123531556102050,0,x x x x x x x x x x x x -+-≥--+≤--=-≤≥无约束写出下列线性规划问题的对偶问题123max 25Z x x x =++12312313123235237365,,0x x x x x x x x x x x ++≤++≤+≤≥写出下列线性规划问题的对偶问题123max Z x x x =++1231312327664,,0x x x x x x x x ++=+≥≥写出下列线性规划问题的对偶问题123min 423Z x x x =++123123131232562742,0,0x x x x x x x x x x x ++≤++=+≥≤≥无约束写出下列线性规划问题的对偶问题：1231231231231232242352373..465,,0MinZ x x x x x x x x x s t x x x x x x =++++≥⎧⎪++≤⎪⎨++≤⎪⎪≥⎩写出下列线性规划问题的对偶问题：12312312312312323231325..34,,0,MinZ x x x x x x x x x s t x x x x x x =--+-=⎧⎪-+≥-⎪⎨-+≤⎪⎪≥⎩无限制写出下列线性规划问题的对偶问题：123123123131232423134..40,0,MaxZ x x x x x x x x x s t x x x x x =++++≥⎧⎪-+≤⎪⎨+=⎪⎪≥≤⎩无限制写出下列线性规划问题的对偶问题：1234512345123451~45275354625..232690,MaxZ x x x x x x x x x x s t x x x x x x x =++++++++=⎧⎪++++=⎨⎪≥⎩无限制写出下面线性规划问题的对偶问题12max 52z x x =-+1212123235,0x x x x x x -+≤-+≤≥写出下面线性规划问题的对偶问题12max 56z x x =+12122553x x x x +=-+≥1x 无限制2,0x ≥设有原始问题123max 325z x x x =++约束条件：12313121232560324204400,,0x x x x x x x x x x ++≤+≤+≤≥写出以上原始问题的对偶问题。

对偶问题

对偶问题
12
②若P问题是无界解,则D问题就是无可行解. ③若P问题有可行解,而其D问题却无可行解, 则P问题就是无界解. 2、强对偶定理:若P问题和D问题都有可行解, 则它们都有最优解,并且它们的最优解的目 标函数值相等. 于是得到如下最优解判定定理: 最优解判定定理 若P问题的某个可行解X0的 目标函数值与其D问题的某个可行解Y0的目 标函数值相等,则X0和Y0分别是相应问题的 最优解.
max f 2 x1 2 x2 3 x3 1.5 x1 2 x2 3 x3 45 s.t 2 x1 x2 2 x3 20 x1 , x2 , x3 0
2
现在问题却是这样的：由于产品结构调整， 工厂需要将这些资源卖出去，然后转产生 产其它产品，那么对资历源A和B如何定价， 才能是让买卖双方都能接受。 作为厂方来说，当然希望价格越高越好，但 太高了买方肯定不能接受，要想能卖出去， 就只能定低价,但低到什么程度,底线是多少? 这里利润c1、c2和c3就是考虑的依据.即出售 资源的价格应该考虑其利润不比用这些资 源组织生产所产生的利润低.设y1和y2分别 表示资源源A和B的价格,按产品原料配套来 卖,则应该有关系:
-7
0 1 0 0 1 0 0 1 -1 -1
0
-1 0 -10000 -1 0 -1.5 -0.5 0.5 -2 -1
0
0 -1 -7 0 -1 -7 0 -1 -6 1
-10000
1 0 0 1 0 -9998.5 0.5 -0.5 -9998 1
y2
2
0
1
2
1
-2
-1
19
去掉人工变量后,D问题的第一个可行基解 正好是最优解.
单位利润
2

线性规划的对偶问题

线性规划的对偶问题
第9页
(二)非对称型对偶问题
max z c1x1 c2x2 c3x3 c3x3 s.t. a11x1 a12 x2 a13x3 a13x3 b1
a21x1 a22 x2 a23x3 a23x3 b2 a2a1x21x1 a2a2 x222x2 a2a3x233x3 a2a3x233x3 b2b2 a31x1 a32x2 a33x3 a33x3 b3
min w b1y1 b2 y2 b3 y3 s.t. a11 y1 a21 y2 a31 y3 c1
a12 y1 a22 y2 a32 y3 c2
a13 y1 a23 y2 a33 y3 c3 y1 0，y2无约束，y3 0
第11页
(二)非对称型对偶问题
对偶问题（原问题）
目标函数 min
约束条件右端常数
目标函数的系数
3个
≥0
变
≤0
量
无符号限制
23个
约
≥
束
≤
条 件
=
第13页
二、原问题与对偶问题的对应关系
原问题（对偶问题）
目标函数 max
目标函数的系数
约束条件右端常数
约 m个
束≤
条 件
≥
=
n个
变
≥0
量
≤0
无符号限制
对偶问题（原问题）
目标函数 min
约束条件右端常数
第8页
(二)非对称型对偶问题
max z = c1x1 + c2x2 + c3x3 s.t. a11x1 + a12x2 + a13x3 ≤ b1
a21x1 + a22x2 + a23x3 = b2 a31x1 + a32x2 + a33x3 ≥ b3 x1≥0, x2≤0, x3无约束 分析：化为对称形式。令 x2 x2，x3 x3 x3 (x3 0, x3 0)

第二章 对偶问题

第二章 对偶问题

（不一定为最优解），它所对应的基矩阵为 B , 决策变量 X T 和松弛变量 X T S 所对应的检验数分别为：
1
，
C C B B 1 A 和 CB B （不一定满足“≤0”条件）。
令
Y C B B 1
这时两组检验数分别为：
C Y*A
和
Y
再根据问题（2），这两组检验数可分别记为
m
ˆ i c j时 ， 必 有 ˆ j 0；j 1,2,, n 当 aij y x
i 1
m
利用互补松弛定理,在已知一个问题的最优解的情况下, 可以不要列单纯形表求出另一个的最优解.
例4：已知线性规划问题
min Z 2 x1 x 2 2 x3 x1 x 2 x3 4 x1 x 2 x3 6 x 0, x 0, x 无 约 束 2 3 1
0 6 1 1 0 1. 得到原问题的基本可 A 行解的同时，其检验 5 2 1 0 1
例： max( ) 15y1 松弛变量 24 y2 5 y 0 y 4 0 y5 3 ←→ 决策变量
5 x2 15 ←→剩余变量 6 y2 y 4y 2 6 y2 2决策变量 3 y 4 3y 6 x 1 2 x2 24 基变量 ←→非基变量 y12 y2 y y y 1 5 y15 y y 1 2 3 5 2 3 5 x x 5 2 1 非基变量 ←→ 基变量 y 0 , i 1 , 2 , , 5 i 0, i 1, 2, ,5 y i x1 , x2 0
引例 1 生产计划问题 max Z 2 x1 3 x2 原问题 某工厂用三台设备生产两种产品，已知的条 2 x1 2 x2 12 x 2x 8 件如表所示，试制订总利润最大的生产计划 1 2

b第二章 对偶问题

b第二章 对偶问题
为提高计算效率，利用单纯形法的矩阵表示，提出改 进单纯形法。
第二章：对偶问题（1）
对偶问题的提出: 复习典型引例： 某工厂在计划期内安排甲，乙两种产品，已知生 产单位产品所消耗资源以及产生的利润如下表：
甲产品 设备 原材料A 原材料B 产生的利润 1 4 0 2元
乙产品 2 0 4 3元
资源量 8 台时 16公斤 12公斤
YA--Ys=C Y,Ys ≥0
则原问题单纯形表的松弛变量的检验数对应对偶问题的一个解
第二章：对偶问题（1）
性质1的证明： 求证: 对称性 对偶问题的对偶是原问题。
证明：原问题 ：
Max CX， AX ≤ b， X ≥0 对偶： Min Y b， YA ≥ C， Y ≥0 即 Max -Y b， -YA ≤ - C， Y ≥0 对偶问题的对偶： Min - CX， - AX ≥ - b， X ≥0
对偶性质的应用二例： 例1：用对偶理论证明线性规划无最优解 (p60) Max Z= X1 +X2
MaxZ=CX AX<=b X ≥0 Min w=Y b YA≥C Y ≥0
- X1+X2+X3 <=2
- 2X1+X2-X3 <=1 X1,X2,X3>=0 对偶:
思路：利用约束 条件的矛盾证明 线性规划无解
Y*Xs=0 和 YsX*=0 ， 当且仅当 X*.Y* 为最 优解。
（Y3 ， Y4 ， Y5 ， Y6 ， Y7 ）
第二章：对偶问题（2）
所以Y* 是使目标值最小的可行解，因此Y*是最优解
同理， X*是最优解
性质5 的证明：
对偶定理 若原问题有最优解，则对偶问题也有最优解，且 目标函数值相等。 证明：P58 设X* 是原问题最优解，B 是最优基，

运筹学课件第二章对偶问题

运筹学课件第二章对偶问题

第二章线性规划的对偶理论与灵敏度分析一、学习目的与要求 1、掌握对偶理论及其性质 2、掌握对偶单纯形法3、熟悉灵敏度分析的概念和内容4、掌握限制常数与价值系数、约束条件系数的变化对原最优解的影响5、掌握增加新变量和增加新的约束条件对原最优解的影响，并求出相应因素的灵敏度范围6、了解参数线性规划的解法 二、课时 6学时第一节 线性规划的对偶问题一、对偶问题的提出定义：一个线性规划问题常伴随着与之配对的、两者有密切联系的另一个线性规划问题，我们将其中一个称为原问题，另一个就称为对偶问题，在求出一个问题的解时，也同时给出了另一问题的解。

应用：在某些情况下，解对偶问题比解原问题更加容易；对偶变量有重要的经济解释(影子价格)；作为灵敏度分析的工具；对偶单纯形法(从一个非可行基出发，得到线性规划问题的最优解)；避免使用人工变量(人工变量带来很多麻烦，两阶段法则增加一倍的计算量)。

例：某家具厂木器车间生产木门与木窗；两种产品。

加工木门收入为56元/扇，加工木窗收入为30元/扇。

生产一扇木门需要木工4小时，油漆工2小时；生产一扇木窗需要木工3小时，油漆工1小时；该车间每日可用木工总共时为120小时，油漆工总工时为50小时。

问：(1)该车间应如何安排生产才能使每日收入最大？(2)假若有一个个体经营者，手中有一批木器家具生产订单。

他想利用该木器车间的木工与油漆工来加工完成他的订单。

他就要考虑付给该车间每个工时的价格。

他可以构造一个数学模型来研究如何定价才能既使木器车间觉得有利可图而愿意为他加工这批订单、又使自己所付的工时费用最少。

解(1)：设该车间每日安排生产木门x1扇，木窗x2扇，则数学模型为⎪⎩⎪⎨⎧≥≤+≤++=-0502120343056max 21212121x x x x x x x zX*=(15,20)’ Z*=1440元解(2)：设y 1为付给木工每个工时的价格，y 2为付给油工每个工时的价格⎪⎩⎪⎨⎧≥≥+≥++=-0303562450120min 21212121y y y y y y y wY*=(2,24)’ W*=1440元将上述问题1与问题2称为一对对偶问题，两者之间存在着紧密的联系与区别：它们都使用了木器生产车间相同的数据，只是数据在模型中所处的位置不同，反映所要表达的含义也不同。

第2章对偶问题

第2章对偶问题第⼆章对偶问题⼀、选择1. 如果原问题有最优解，则其对偶问题也⼀定具有最优解，且有（A ）。

A maxZ=minW B maxZminW D maxZ 与minW ⽆关2. 影⼦价格B c Y B 1*-=是（C ）A 、对偶可⾏解B 、对偶基本可⾏解C 、对偶最优解D ⽆可⾏解3．原问题有可⾏解，其对偶问题有⾮可⾏解，则⽬标函数值（ B ）A 、最优B 、zmax C 、z >zmax D⽆可⾏解4. 影⼦价格是⼀种（C ）A 、实际价格B 、市场价格C 、边际价格D 产品价格5. 资源的市场价格是已知数，相对⽐较稳定，⽽它的影⼦价格则有赖于（c ），是未知数A 市场的定价B 买卖的多少C 资源的利⽤情况D 购买⼒6. 如果原问题（对偶问题）具有⽆界解，则其对偶问题（原问题）（D ）。

A 唯⼀最优解B ⽆穷多最优解 C ⽆界解 D ⽆可⾏解7. 影⼦价格是⼀种边际价格，实际上⼜是⼀种（A ）。

A 机会成本B 实际成本 C 市场价格 D 产品价格9.如果),,1(n j x j =-是原问题的可⾏解，),,1(m j y i=-是其对偶问题的可⾏解，则恒有（ A ）A ∑∑=-=-≤mi ii nj j j y b x c 11B ∑∑=-=-=mi ii nj j j y b x c 11C∑∑=-=-≥mi iin j jjy b x c 11D ⽆法确定10. 如果),,1(n j x j =∧是原问题的可⾏解，),,1(m j y i=∧是其对偶问题的可⾏解，且有（ B ），则),,1(n j x j =∧是原问题的最优解，),,1(m j y i=∧是其对偶问题的最优解A ∑∑=∧=∧≤mi ii nj j j y b x c 11B ∑∑=∧=∧=mi ii nj j j y b x c 11C∑∑=∧=∧≥mi iin j jjy b x c 11D ∧∧=y xij11.如果∑=∧∧=>n j i j ij ib x a y 1,0则，其符合（D ）定理A 强对偶性B 弱对偶性C 最优性D 互补松弛性 12.如果有0,1=>∧=∧∑x c y a j mi j iij 则，其符合（D ）定理A 强对偶性B 弱对偶性C 最优性D 互补松弛性 13. 如果∑=∧∧=>mi j iij j c y a x 1,0则，其符合（D ）定理A 强对偶性B 弱对偶性C 最优性D 互补松弛性 14. 如果有0,1=<∧=∧∑y b x a inj i j ij 则，其符合（D ）定理A 强对偶性B 弱对偶性C 最优性D 互补松弛性15.在单纯形法中，最终单纯形表，原问题的变量对应着对偶问题的（ A ） A 松弛变量B 剩余变量C 变量D 最优解16. 在单纯形法中，最终单纯形表，原问题的松弛变量对应着对偶问题的（C ） A 松弛变量B 剩余变量C 变量D 最优解17. 在单纯形法中，最终单纯形表中，对偶问题的最优解由（B ）的值组成。

运筹学第二章对偶问题


DUAL PRICES
1.500000 0.125000 0.000000
影子价格 （对 偶问题的解）
迭代（旋转）次数 NO. ITERATIONS= 2
用软件分析
目标不变下要素的变化范围 RANGES IN WHICH THE BASIS IS UNCHANGED:
目标系数的变化范围
VARIABLE
CB XB b y1 y2 y3 y4 y5 y6ቤተ መጻሕፍቲ ባይዱy7
i
M y5 2 1 4 0 1 1 0 0
M y7 3 2
0 [ 4] 0
0 1 1
3/4
83M 164M 124M M 0
M0
8 16 12 0 M 0 M
CB XB b y1 y2 y3 y4 y5 y6 y7
i
M y5 2 1
4 0 1 1 0 0
M0
3 M－3
8 16 12 0 M 0 M
CB XB b y1 y2 y3 y4 y5 y6 y7
i
M y5 2
1 [ 44 ] 0 1 1
0 0 1/2
12 y3 3/4 1/2 0 1
0 0 1/4 1/4 －
2-M 16-4M 0
M0
3 M－3
8 16 12 0 M 0 M
CB XB b y1 y2 y3 y4 y5 y6 y7
两边乘以“1”
5x1 3x2 + x3 200 5x1 3x2 + x3 200
Max z = 3x1 +4x2 +6x3 St. 2x1 +3x2 +6x3 440 6x1 +4x2 + x3 100 对偶 5x1 3x2 + x3 200 5x1 +3x2 x3 200 x1 ，x2 ，x3 0

第二章对偶理论


3 5
x1 , x2 , x3 0
解：首先将原式变形
max Z 2 x1 3 x2 4 x3
2 x 3 x2 5 x3 2
3 x1 x2 7 x3 3
x1 4 x2 6 x3
5
x1 , x2 , x3 0
注意：以后不强调等式右段项 b≥0，原因在对偶单
纯型表中只保证 而j 不0 保证
=（1.1），分别是
（P_）_ 和__（D）的可行解。Z=10 ，W=40，故有
C X ＜ Y b ，弱对偶定理成立。由推论⑴可知，W 的最
小值不能小于10，Z 的最大值不能超过40。
例二、已知
p : max Z x1 2x2
D : minW 2 y1 y2
x1 x2 x3 2
2x1 x2 x3 1
n
j 1
aij
yi
cj
（对偶问题）
yi 0
目标函数 约束条件
原问题
对偶问题
max
min
≤
≥
变量数量 约束条件个数
约束条件个数 变量数量
例三、
23
x1
x2
原问题
12 y1 2
2
≤ 12
8
y2
1
2
≤
8
16 y3 4 0 ≤ 16 12 y4 0 4 ≤ 12
对偶问题 2 3
二、线性规划的对偶理论
原问题 问题无界
无可 行解
对偶问题 无可 行解
问题无界
（对）
y1 y1
y1
y2 y2 0, y2
2 1 0
无可 行解
推论⑶.在一对对偶问题（P）和（D）中，若一个可 行（如P），而另一个不可行，（如D），则该可行的 问题无界。

第二章 线性规划的对偶理论1-对偶问题


矩阵表达形式：
min w Y b AY C Y 0
对偶的经济解释
1、原问题是利润最大化的生产计划问题
总利润（元）
单位产品的利润（元/件）
产品产量（件）
max z c1 x1 c2 x2 cnx n b1 s.t. a11 x1 a12 x2 a1n xn xn 1 xn 2 b2 a21 x1 a22 x2 a2 n xn xn m bm am1 x1 am 2 x2 amn xn x1 x2 xn xn 1 xn 2 xn m ≥ 0 消耗的资源（吨）
第二章 对偶理论与灵敏度分析
第一节 线性规划的对偶问题
每一个线性规划问题都存在一个与其对偶的问题，在求出
一个问题的解的时候，同时也给出了另一问题的解。
例：某公司计划生产甲、乙两种产品，已知各生产一件时 分别占用的设备A、B的台时、调试时间和调试工序每天可用于 这两种产品的能力、各销售一件时的获利情况，如下表所示。 问该公司应生产两种产品各多少件，使获取的利润为最大。
A
b
约束系数矩阵
约束条件右端项向量
约束系数矩阵的转置
目标函数中价格系数向量
C
目标函数
目标函数中价格系数向量
max z
约束条件右端项向量
min w
c
j 1
n
j
xj
b
i 1
m
i
yi
变量 xj (j=1,·,n) · ·
约束条件有n个
xj ≥0
xj ≤0 xj 无约束 约束条件有m个 ≤bi ≥bi =bi
min z 2 x1 3x 2 5 x3 x 4
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

对称形式的对应关系
原问题 max z n个决策变量 m个约束条件 约束条件“≤”型
决策变量≥0
对偶问题 min w n个约束条件 m个决策变量 决策变量≥0
约束条件“≥”型
对偶问题的对偶是原问题，即对偶关系是 相互对称的关系
非对称形式下的对偶关系
原问题（对偶问题） max z n个决策变量 m个约束条件 约束条件“≤”型 约束条件“≥”型 约束条件“=”型 决策变量≥0 决策变量≤0 决策变量无约束 对偶问题（原问题） min w n个约束条件 m个决策变量 决策变量≥0 决策变量≤0 决策变量无约束 约束条件“≥”型 约束条件“≤”型 约束条件“=”型
y4 2 y1 2 y2 3 y1 y2 y3 y4 4 y3 y 4 1 y4 0
第三节 影子价格
* ( j 1 , , n ) y 设 x* 和 j i (i 1, , n) 分别是原问题和 对偶问题的最优解，则由对偶性质，有
例 用对偶单纯形法求解如下的LP问题
min z 15x1 24x2 5 x3 6 x2 x3 2 5 x1 2 x2 x3 1 x1 , x2 , x3 0
化成标准形式
m ax w 15x1 24x2 5 x3 6 x2 x3 x4 2 5 x1 2 x2 x3 x5 1 x1 , x2 , x3 0
•最优性 若原问题一个可行解目标函数等于对偶问题的 某个可行解的目标函数,则这两个可行解分别 是原问题和对偶问题的最优解 •强对偶性 若原问题和对偶问题都有可行解,则它们都有 最优解,且最优解的目标函数值相等 •互补松弛性 在线性规划问题的最优解中,如果对应某一约 束条件的对偶变量值非零,则其对应的约束条 件取等式;反之若一个约束条件为严格的不等 式,则其对应的对偶变量为零
将各约束条件两端同乘“-1”得
m ax w 15x1 24x2 5 x3 6 x2 x3 x4 2 5 x1 2 x2 x3 x5 1 x1 , x2 , x3 0
用对偶单纯形法求解得
-15 Cb Xb 0 x4 0 x5 b -2 -1 x1 0 -5 -15 x2 -6 -2 -24
CN XN
N CN CN XN B-1N CN –CBB-1N
0 XS
I 0 0 XS B-1 –CBB-1
• 在初始单纯形表中单位矩阵经过迭代后变为基 矩阵B的逆 • 在初始单纯形表给出的解中基变量Xs=b,而在迭 代后的表给出的解中基变量 XB=B-1b • 系数矩阵的变化: [A, I]B-1[A, I] • 在初始单纯形表中变量xj的系数为Pj经过迭代 后变为Pj′,并且Pj′=B-1 Pj • 若迭代后的单纯形表为最终表则题的对称形式
• 变量：所有变量均具有非负约束 • 约束条件： 最大化问题 所有约束条件都是“≤” 型的 最小化问题 所有约束条件都是“≥” 型的
对称形式下的对偶关系
项目 A b C 目标函数 约束条件 决策变量 原问题 约束条件系数矩阵 约束条件右端项向量 目标函数系数向量 max z=CX AX≤b X≥0 对偶问题 约束条件系数矩阵转置 目标函数的系数向量 约束条件的右端项向量 min w=Yb’ A’Y ≥C’ Y ≥0
单纯形法的矩阵表示
m ax z CX
AX b X 0
XB X , A B X N C CB C N N ,
max z CX 0 X s
添加松 弛变量XS
AX IX S b X 0
BX B NX N IX S b X 0, X 0 N B
• 资源的影子价格随企业的生产任务、产品结构 的改变而改变 • 影子价格是资源的边际价格 • 资源的影子价格也可视为一种机会成本 • 在生产过程中若某种资源未得到充分利用则其 影子价格为零；只有在资源得到充分利用时， 其影子价格才可能非零 • 利用影子价格可以说明：单纯形法中的检验数 可以看成生产某种产品的产值与隐含成本的差 • 可以利用影子价格确定企业内部的核算价格， 以便控制有限资源的使用和考核下属企业经营 的好坏。
y4
y5
y1 y3
0 1
对偶 问题 最终 单纯 形表
对偶问题剩余变量
y2
y3
y1
y2 y3 1/4 1/2 -5/4 15/2
y2
1 0
y4
-1/4 1/2
y5
1/4 -3/2
σj
15/2
0
0
7/2
3/2
原问题松弛变量
原问题变量
x3
x4
x5
x1
x2
原本在对偶关系中，原问题的变量对应着对偶问题 的约束条件，原问题的约束条件对应着对偶变量。 但在分别添加了松弛变量和剩余变量后，也可以建 立原问题变量与对偶问题变量之间的对应关系
max z C B X B C N X N 0 X s
将XB的系数 矩阵化为单 位矩阵
原来 BX B NX N IX S b 1 1 1 IX B B NX N B X S B b
初 始 单 纯 形 表
迭 代 后 的 单 纯 形 表
CB XB
0 XS b B CB CB XB CB XB B-1b I 0
互补松弛性的另一种表述
在线性规划问题的最优解中,如果对应某一约 束条件的对偶变量值非零,则该约束条件中松 弛变量等于零;反之若一个约束条件中松弛变 量非零,则其对应的对偶变量为零。
例（p76.7） 原问题 max z 2 x1 4 x2 x3 x4 x1 3 x2 x4 8 2 x x 6 1 2 x2 x3 x4 6 x1 x2 x3 9 x 0, j 1,2,3,4 j
问题 美佳公司愿意以多大的代价出让自己所 拥有的生产资源？
设y1,y2和y3分别表示出让资源A，B和调试 工序的单价，则美佳公司同意出让的条件 将是 同意出让生产产品I的资源 6 y 2 y3 2 同意出让生产产品II的资源 5 y1 2 y2 y3 1
购买者希望用最少的代价获得这些资源， 因此
例1
6x1+2x2 =24
资源的变化： 设备B的可用 时间从增加 一小时
Max z=2x1+x2
s.t. 5x2≤15
6x1+2x2 ≤24
x1+x2 ≤5
可行域 x2=3 最优解
x1,x2≥0
最优目标 函数值的 变化：8.5 变到8.75， 增加1/4
x1+x2 =5
参考文献：
李慧：资源影子价格分析与经营管理决策， 系统工程理论与实践，2003年4月号，22-26
对偶问题基可行解 （检验数非正）
原问题基可行 解
• 保持对偶问题有基可行解,而原问题只是 基本解,通过迭代,使后者的负分量个数减 少，一旦成为基可行解,则原问题与对偶 问题同时实现最优解.
对偶单纯形法计算步骤
• 适应于求解这样的LP问题：标准化后不 含初始基变量，但将某些约束条件两端 乘以“-1”后，即可找出初始基变量。 • 要求：初始单纯形表中的检验数满足最 优性条件
对满足上述条件的LP问题，对偶单纯形法的 步骤是： •作出初始单纯形表（注意要求） •检查b列的数据是否非负，若是，表中已经 给出最优解；否则转下一步 •确定换出变量：取b列最小的数对应的变量 为换出变量 •确定换入变量：用检验数去除以换出变量行 的那些对应的负系数，在除得的商中选取其 中最小者对应的变量为换入变量 •旋转运算。然后回到第2步。
对偶问题 min w 8 y1 6 y2 6 y3 9 y4 y4 2 y1 2 y2 3 y1 y2 y3 y4 4 y3 y 4 1 y1 y3 1 y 0, i 1,2,3,4 i 将原问题最优解X*=(2,2,4,0)代入原问题约束条件中得 第一个约束条件：2+6=8，为等式 第二个约束条件：4+2=6，为等式 第三个约束条件：2+4=6，为等式 第四个约束条件：2+2+4<9，为不等式，故y4 = 0
* z* c j x * b y i i w* j j 1 i 1
n
m
式中bi是线性规划原问题约束条件的右端 项，它代表第i种资源的拥有量；对偶变 量yi的意义代表在资源最优利用的条件下 对第i种资源的估价。这种估价不是资源 的市场价格，而是根据资源在生产中作 出的贡献而作的估价，为区别起见，称 为影子价格。
min z 15y1 24y2 5 y3
这样得到一个新的线性规划问题
min w 15y1 24y2 5 y3 6 y 2 y3 2 5 y1 2 y2 y3 1 y1 , y2 , y3 0
称这一问题是原来的LP问题的对偶线性规 划问题或对偶问题，原来的LP问题也称为 原问题。
而由x1=2>0, 得 而由x2=2>0, 得 而由x3=4>0, 得 于是得到方程组
y1 2 y2 y4 2 3 y1 y2 y3 y4 4 y3 y4 1
4 3 得对偶问题最优解为 y1 , y2 , y3 1, y4 0 5 5
注：原问题与对偶问题最优目标函数值都是 z*=4+8+4=16
0 1 0
1/4 -1 1/2 -1 1/2
例1 原问 题最 终单 纯形 表
项目
原问题变量
原问题松弛变量
x1
x3 15/2 x1 7/2 x2 3/2 - σj 0 1 0 0
x2
0 0 1 0
x3
1 0 0 0