潮流计算报告

电力系统分析实验报告实验一：潮流计算的计算机算法>> clear;n=10;nl=10;isb=1;pr=0.00001;B1=[120.03512+0.08306i0.13455i10;230.0068+0.18375i0 1.023811;140.05620+0.13289i0.05382i10;450.00811+0.24549i0 1.023811;160.05620+0.13289i0.05382i10;460.04215+0.09967i0.04037i10;670.0068+0.18375i0 1.023811;680.02810+0.06645i0.10764i10;8100.00811+0.24549i011;890.03512+0.08306i0.13455i10] B2=[00 1.1 1.101;001002;00.343+0.21256i1002;001002;00.204+0.12638i1002;001002;00.306+0.18962i1002;001002;0.50 1.1 1.103;00.343+0.21256i1002]Y=zeros(n);e=zeros(1,n);f=zeros(1,n);V=zeros(1,n);sida=zeros(1,n);S1=zeros(nl);for i=1:nlif B1(i,6)==0p=B1(i,1);q=B1(i,2);elsep=B1(i,2);q=B1(i,1);endY(p,q)=Y(p,q)-1./(B1(i,3)*B1(i,5));Y(q,p)=Y(p,q);Y(q,q)=Y(q,q)+1./(B1(i,3)*B1(i,5)^2)+B1(i,4)./2;Y(p,p)=Y(p,p)+1./B1(i,3)+B1(i,4)./2;enddisp('导纳矩阵Y=');disp(Y)%----------------------------------------------------------G=real(Y);B=imag(Y);for i=1:ne(i)=real(B2(i,3));f(i)=imag(B2(i,3));V(i)=B2(i,4);endfor i=1:nS(i)=B2(i,1)-B2(i,2);B(i,i)=B(i,i)+B2(i,5);endP=real(S);Q=imag(S);ICT1=0;IT2=1;N0=2*n;N=N0+1;a=0;while IT2~=0IT2=0;a=a+1;for i=1:nif i~=isbC(i)=0;D(i)=0;for j1=1:nC(i)=C(i)+G(i,j1)*e(j1)-B(i,j1)*f(j1);%Σ(Gij*ej-Bij*fj)D(i)=D(i)+G(i,j1)*f(j1)+B(i,j1)*e(j1);%Σ(Gij*fj+Bij*ej) endP1=C(i)*e(i)+f(i)*D(i);Q1=C(i)*f(i)-e(i)*D(i);V2=e(i)^2+f(i)^2;if B2(i,6)~=3DP=P(i)-P1;DQ=Q(i)-Q1;for j1=1:nif j1~=isb&j1~=iX1=-G(i,j1)*e(i)-B(i,j1)*f(i);X2=B(i,j1)*e(i)-G(i,j1)*f(i);X3=X2;X4=-X1;p=2*i-1;q=2*j1-1;J(p,q)=X3;J(p,N)=DQ;m=p+1;J(m,q)=X1;J(m,N)=DP;q=q+1;J(p,q)=X4;J(m,q)=X2;elseif j1==i&j1~=isbX1=-C(i)-G(i,i)*e(i)-B(i,i)*f(i);X2=-D(i)+B(i,i)*e(i)-G(i,i)*f(i);X3=D(i)+B(i,i)*e(i)-G(i,i)*f(i);X4=-C(i)+G(i,i)*e(i)+B(i,i)*f(i);p=2*i-1;q=2*j1-1;J(p,q)=X3;J(p,N)=DQ;m=p+1;J(m,q)=X1;q=q+1;J(p,q)=X4;J(m,N)=DP;J(m,q)=X2;endendelseDP=P(i)-P1;DV=V(i)^2-V2;for j1=1:nif j1~=isb&j1~=iX1=-G(i,j1)*e(i)-B(i,j1)*f(i);X2=B(i,j1)*e(i)-G(i,j1)*f(i);X5=0;X6=0;p=2*i-1;q=2*j1-1;J(p,q)=X5;J(p,N)=DV;m=p+1;J(m,q)=X1;J(m,N)=DP;q=q+1;J(p,q)=X6;J(m,q)=X2;elseif j1==i&j1~=isbX1=-C(i)-G(i,i)*e(i)-B(i,i)*f(i);X2=-D(i)+B(i,i)*e(i)-G(i,i)*f(i);X5=-2*e(i);X6=-2*f(i);p=2*i-1;q=2*j1-1;J(p,q)=X5;J(p,N)=DV;m=p+1;J(m,q)=X1;J(m,N)=DP;q=q+1;J(p,q)=X6;J(m,q)=X2;endendendendendfor k=3:N0k1=k+1;N1=N;for k2=k1:N1J(k,k2)=J(k,k2)./J(k,k);endJ(k,k)=1;if k~=3k4=k-1;for k3=3:k4for k2=k1:N1J(k3,k2)=J(k3,k2)-J(k3,k)*J(k,k2);endJ(k3,k)=0;endif k==N0break;endfor k3=k1:N0for k2=k1:N1J(k3,k2)=J(k3,k2)-J(k3,k)*J(k,k2);endJ(k3,k)=0;endelsefor k3=k1:N0for k2=k1:N1J(k3,k2)=J(k3,k2)-J(k3,k)*J(k,k2);endJ(k3,k)=0;endendendfor k=3:2:N0-1L=(k+1)./2;e(L)=e(L)-J(k,N);k1=k+1;f(L)=f(L)-J(k1,N);endfor k=3:N0DET=abs(J(k,N));if DET>=prIT2=IT2+1;endendICT2(a)=IT2;ICT1=ICT1+1;enddisp('迭代次数：');disp(ICT1);disp('没有达到精度要求的个数：');disp(ICT2);for k=1:nV(k)=sqrt(e(k)^2+f(k)^2);sida(k)=atan(f(k)./e(k))*180./pi;E(k)=e(k)+f(k)*j;enddisp('各节点的实际电压标幺值E为(节点号从小到大排列)：');disp(E);disp('-----------------------------------------------------');disp('各节点的电压大小V为(节点号从小到大排列)：');disp(V);disp('-----------------------------------------------------');disp('各节点的电压相角sida为(节点号从小到大排列)：');disp(sida);for p=1:nC(p)=0;for q=1:nC(p)=C(p)+conj(Y(p,q))*conj(E(q));endS(p)=E(p)*C(p);enddisp('各节点的功率S为(节点号从小到大排列)：');disp(S);disp('-----------------------------------------------------');disp('各条支路的首端功率Si为(顺序同输入B1时一致)：');for i=1:nlp=B1(i,1);q=B1(i,2);if B1(i,6)==0Si(p,q)=E(p)*(conj(E(p))*conj(B1(i,4)./2)+(conj(E(p)*B1(i,5))...-conj(E(q)))*conj(1./(B1(i,3)*B1(i,5))));Siz(i)=Si(p,q);elseSi(p,q)=E(p)*(conj(E(p))*conj(B1(i,4)./2)+(conj(E(p)./B1(i,5))...-conj(E(q)))*conj(1./(B1(i,3)*B1(i,5))));Siz(i)=Si(p,q);enddisp(Si(p,q));SSi(p,q)=Si(p,q);ZF=['S(',num2str(p),',',num2str(q),')=',num2str(SSi(p,q))];disp(ZF);disp('-----------------------------------------------------');enddisp('各条支路的末端功率Sj为(顺序同输入B1时一致)：');for i=1:nlp=B1(i,1);q=B1(i,2);if B1(i,6)==0Sj(q,p)=E(q)*(conj(E(q))*conj(B1(i,4)./2)+(conj(E(q)./B1(i,5))...-conj(E(p)))*conj(1./(B1(i,3)*B1(i,5))));Sjy(i)=Sj(q,p);elseSj(q,p)=E(q)*(conj(E(q))*conj(B1(i,4)./2)+(conj(E(q)*B1(i,5))...-conj(E(p)))*conj(1./(B1(i,3)*B1(i,5))));Sjy(i)=Sj(q,p);enddisp(Sj(q,p));SSj(q,p)=Sj(q,p);ZF=['S(',num2str(q),',',num2str(p),')=',num2str(SSj(q,p))];disp(ZF);disp('-----------------------------------------------------');enddisp('各条支路的功率损耗DS为(顺序同输入B1时一致)：');for i=1:nlp=B1(i,1);q=B1(i,2);DS(i)=Si(p,q)+Sj(q,p);disp(DS(i));DDS(i)=DS(i);ZF=['DS(',num2str(p),',',num2str(q),')=',num2str(DDS(i))];disp(ZF);disp('-----------------------------------------------------');endfigure(1);subplot(1,2,1);plot(V);xlabel('节点号');ylabel('电压标幺值');grid on;subplot(1,2,2);plot(sida);xlabel('节点号');ylabel('电压角度');grid on;figure(2);subplot(2,2,1);P=real(S);Q=imag(S);bar(P);xlabel('节点号');ylabel('节点注入有功');grid on;subplot(2,2,2);bar(Q);xlabel('节点号');ylabel('节点注入无功');grid on;subplot(2,2,3);P1=real(Siz);Q1=imag(Siz);bar(P1);xlabel('支路号');ylabel('支路首端注入有功');grid on;subplot(2,2,4);bar(Q1);xlabel('支路号');ylabel('支路首端注入无功');grid on;B1 =1.00002.0000 0.0351 + 0.0831i 0 + 0.1346i 1.0000 02.00003.0000 0.0068 + 0.1838i 0 1.0238 1.00001.0000 4.0000 0.0562 + 0.1329i 0 + 0.0538i 1.0000 04.00005.0000 0.0081 + 0.2455i 0 1.0238 1.00001.0000 6.0000 0.0562 + 0.1329i 0 + 0.0538i 1.0000 04.0000 6.0000 0.0422 + 0.0997i 0 + 0.0404i 1.0000 06.00007.0000 0.0068 + 0.1838i 0 1.0238 1.00006.0000 8.0000 0.0281 + 0.0664i 0 + 0.1076i 1.0000 08.0000 10.0000 0.0081 + 0.2455i 0 1.0000 1.00008.0000 9.0000 0.0351 + 0.0831i 0 + 0.1346i 1.0000 0 B2 =0 0 1.1000 1.1000 0 1.00000 0 1.0000 0 0 2.00000 0.3430 + 0.2126i 1.0000 0 0 2.00000 0 1.0000 0 0 2.00000 0.2040 + 0.1264i 1.0000 0 0 2.00000 0 1.0000 0 0 2.00000 0.3060 + 0.1896i 1.0000 0 0 2.00000 0 1.0000 0 0 2.0000 0.5000 0 1.1000 1.1000 0 3.00000 0.3430 + 0.2126i 1.0000 0 0 2.0000导纳矩阵Y=Columns 1 through 69.7177 -22.8591i -4.3185 +10.2135i 0 -2.6996 + 6.3834i 0 -2.6996 + 6.3834i-4.3185 +10.2135i 4.5104 -15.3311i -0.1964 + 5.3083i 0 0 00 -0.1964 + 5.3083i 0.2011 - 5.4347i 0 0 0-2.6996 + 6.3834i 0 0 6.4271 -18.7292i -0.1313 + 3.9744i -3.5993 + 8.5110i0 0 0 -0.1313 + 3.9744i 0.1344 - 4.0690i 0-2.6996 + 6.3834i 0 0 -3.5993 + 8.5110i 0 11.8891 -32.7444i0 0 0 0 0 -0.1964 + 5.3083i0 0 0 0 0 -5.3984 +12.7660i0 0 0 0 0 00 0 0 0 0 0Columns 7 through 100 0 0 00 0 0 00 0 0 00 0 0 00 0 0 0-0.1964 + 5.3083i -5.3984 +12.7660i 0 00.2011 - 5.4347i 0 0 00 9.8514 -26.9275i -4.3185 +10.2135i -0.1344 + 4.0690i0 -4.3185 +10.2135i 4.3185 -10.1462i 00 -0.1344 + 4.0690i 0 0.1344 - 4.0690i迭代次数：4没有达到精度要求的个数：17 18 17 0各节点的实际电压标幺值E为(节点号从小到大排列)：Columns 1 through 61.1000 1.0757 - 0.0207i 1.0050 - 0.0780i 1.0772 - 0.0175i 1.0171 - 0.0631i 1.0762 - 0.0152iColumns 7 through 101.0112 - 0.0666i 1.0778 - 0.0051i 1.0996 + 0.0304i 1.0177 - 0.0814i-----------------------------------------------------各节点的电压大小V为(节点号从小到大排列)：1.1000 1.0759 1.0080 1.0773 1.0191 1.0763 1.0134 1.0778 1.1000 1.0209-----------------------------------------------------各节点的电压相角sida为(节点号从小到大排列)：0 -1.1046 -4.4373 -0.9283 -3.5503 -0.8106 -3.7665 -0.27181.5822 -4.5707各节点的功率S为(节点号从小到大排列)：Columns 1 through 60.7165 + 0.2587i 0.0000 + 0.0000i -0.3430 - 0.2126i -0.0000 + 0.0000i -0.2040 - 0.1264i -0.0000 + 0.0000iColumns 7 through 10-0.3060 - 0.1896i -0.0000 + 0.0000i 0.5000 + 0.0089i -0.3430 - 0.2126i-----------------------------------------------------各条支路的首端功率Si为(顺序同输入B1时一致)：0.3485 + 0.0932iS(1,2)=0.3485+0.093157i-----------------------------------------------------0.3441 + 0.2420iS(2,3)=0.34409+0.24201i-----------------------------------------------------0.1904 + 0.0760iS(1,4)=0.19038+0.07599i-----------------------------------------------------0.2044 + 0.1400iS(4,5)=0.20445+0.13999i-----------------------------------------------------0.1777 + 0.0895iS(1,6)=0.17767+0.089525i------------------------------------------------------0.0163 - 0.0055iS(4,6)=-0.016305-0.0054856i-----------------------------------------------------0.3069 + 0.2128iS(6,7)=0.30686+0.21281i------------------------------------------------------0.1477 - 0.0234iS(6,8)=-0.14767-0.02338i-----------------------------------------------------0.3443 + 0.2509iS(8,10)=0.34427+0.25091i------------------------------------------------------0.4925 - 0.1508iS(8,9)=-0.49251-0.15077i-----------------------------------------------------各条支路的末端功率Sj为(顺序同输入B1时一致)：-0.3441 - 0.2420iS(2,1)=-0.34409-0.24201i------------------------------------------------------0.3430 - 0.2126iS(3,2)=-0.343-0.21256i------------------------------------------------------0.1881 - 0.1345iS(4,1)=-0.18815-0.13451i------------------------------------------------------0.2040 - 0.1264iS(5,4)=-0.204-0.12638i------------------------------------------------------0.1755 - 0.1482iS(6,1)=-0.17551-0.14815i-----------------------------------------------------0.0163 - 0.0413iS(6,4)=0.016326-0.041272i------------------------------------------------------0.3060 - 0.1896iS(7,6)=-0.306-0.18962i-----------------------------------------------------0.1482 - 0.1001iS(8,6)=0.14824-0.10014i------------------------------------------------------0.3430 - 0.2126iS(10,8)=-0.343-0.21256i-----------------------------------------------------0.5000 + 0.0089iS(9,8)=0.5+0.0089402i-----------------------------------------------------各条支路的功率损耗DS为(顺序同输入B1时一致)：0.0044 - 0.1488iDS(1,2)=0.0044095-0.14885i-----------------------------------------------------0.0011 + 0.0294iDS(2,3)=0.0010897+0.029445i-----------------------------------------------------0.0022 - 0.0585iDS(1,4)=0.0022306-0.058518i-----------------------------------------------------0.0004 + 0.0136iDS(4,5)=0.00044972+0.013613i-----------------------------------------------------0.0022 - 0.0586iDS(1,6)=0.0021584-0.058629i-----------------------------------------------------0.0000 - 0.0468iDS(4,6)=2.1344e-005-0.046758i-----------------------------------------------------0.0009 + 0.0232iDS(6,7)=0.00085804+0.023186i-----------------------------------------------------0.0006 - 0.1235iDS(6,8)=0.00056584-0.12352i-----------------------------------------------------0.0013 + 0.0384iDS(8,10)=0.001267+0.038353i-----------------------------------------------------0.0075 - 0.1418iDS(8,9)=0.0074931-0.14183i----------------------------------------------------- >>。

一、系统结构图：二、网络参数：、支路参数：1网络装机导线的技术参数电压支路容量类型b等级1xr编号（Ω）（Ω） (MW)11）（kV （） 1-2 13.6 125.5 67.8552.24 130.5 1-3 8.321100环 74.993-5128.810.2220网28.36 8.5 105.4 2-351.45 7.579 129.6 1-42.78 13.84 4-5125.31——42——1-22、节点参数：4+2i 0 2辐6+3.2i 3 0射3+1.44i 4 0网4+3.2i 5 02+1.1i6:三、潮流计算流程图四、matlab程序：clear;输入所需的额定电压%请输入'Un:'); Un=input(PQ=[无功有功 %节点电压Un 0 0Un 4 2Un 6 3.2Un 3 1.44Un 4 3.2．Un 2 1.1];FT=[末端%首端 4 33 26 55 22 1];RX=[% R X4 83 64 41 22 4];节点数%NN=size(PQ,1);支路数数NB=size(FT,1); %初始电压相量%V V=PQ(:,1);maxd=1k=1 maxd>0.0001whilek=k+1;每一次迭代各节点的注入有功和无功相同 PQ2=PQ; % PL=0.0;i=1:NB for前推始节点号% kf=FT(i,1);前推终节点号% kt=FT(i,2);A平方计算沿线电流 / x=(PQ2(kf,2)^2+PQ2(kf,3)^2)/V(kf)/V(kf);% /MW 计算线路有功损耗 losss(i,1)=RX(i,1)*x; %/MW 计算线路无功损耗losss(i,2)=RX(i,2)*x; %/MW RX(i,1)*R%计算支路首端有功PQ1(i,1)=PQ2(kf,2)+RX(i,1)*x;/MW RX(i,2)*X%计算沿支路的无功 PQ1(i,2)=PQ2(kf,3)+RX(i,2)*x;PQ2(kt,2)= PQ2(kt,2)+PQ1(i,1); %用PQ1去修正支路末端节点的有功P 单MW位PQ2(kt,3)= PQ2(kt,3)+PQ1(i,2); %用PQ1去修正支路末端节点的有功Q 单Mvar位endangle(1)=0.0; i=NB:-1:1for回代始节点号 kf=FT(i,2); %回代终节点号kt=FT(i,1); % dv1=(PQ1(i,1)*RX(i,1)+PQ1(i,2)*RX(i,2))/V(kf); %计算支路电压损耗的dv1纵分量 dv2=(PQ1(i,1)*RX(i,2)-PQ1(i,2)*RX(i,1))/V(kf); %计算支路电压损耗的dv2横分量/kV计算支路末端电压 V2(kt)=sqrt((V(kf)-dv1)^2+dv2^2); %计算支路% angle(kt)=angle(kf)+atand(dv2/(V(kf)-dv1));end maxd=abs(V2(2)-V(2));V2(1)=V(1); i=3:1:NN for abs(V2(i)-V(i))>maxd;ifmaxd=abs(V2(i)-V(i));end end计算线路总损耗 fullloss(1,1)=0;% fullloss(1,2)=0;finalPQ=max(PQ1); i=1:NB for fullloss(1,1)=fullloss(1,1)+losss(i,1);fullloss(1,2)=fullloss(1,2)+losss(i,2);end)''辐射网迭代次数：disp(k) 辐射网系统电压差精度：'disp('maxd)'disp('辐射网系统末端节点有功和无功：MVA 即支路首端潮流%finalPQ 潮流分布)辐射网系统总功率损耗：''disp(MVA线路总损耗%fullloss)辐射网系统各支路功率损耗：'disp('MVA%各支路损耗losss)辐射网系统各节点电压幅值：'disp('kV%节点电压模计算结果V=V2)辐射网系统各节点电压相角：'disp('节点电压角度计算结果单位度angle %endclc)'disp('辐射网迭代次数：k) 'disp('辐射网系统电压差精度：maxd)'/MVA：disp('辐射网系统末端节点有功和无功MVA 即支路首端潮流%FinPQ=finalPQ(1,1)+finalPQ(1,2)*j潮流分布)：'disp('辐射网系统总功率损耗/MVA MVA%线路总损耗Fulloss=fullloss(1,1)+fullloss(1,2)*j)'辐射网系统各支路功率损耗/MVA：disp('(a=1:5)for MVA各支路损耗LOSS=losss(a,1)+losss(a,2)*j %end)'/KV'辐射网系统各节点电压幅值：disp(kV节点电压模计算结果V=V2 %)'辐射网系统各节点电压相角：disp('节点电压角度计算结果单位度angle %');节点数%input('n=5;');支路数nl=6; %input('');平衡母线节点号isb=1; %input('pr=');误差精度：pr=0.000001; %input('B1=[1,2,13.6+125.5i,0.00006785i,1,0;1,3,8.321+130.5i,0.00005224i,1,0;3,5,10.2+128.8i,0.00007499i,1,0;2,3,8.5+105.4i,0.00002836i,1,0;1,4,7.579+129.6i,0.00005145i,1,0;');%input('由支路参数形成的矩阵4,5,13.84+125.31i,0.0000278i,1,0];B2=[-FinPQ,0,Un,0,0,1;100,0,Un,Un,0,3;0,15+9.4i,Un,0,0,2;0,27+6i,Un,0,0,2;');各节点参数形成的矩阵0,35.5+25.5i,Un,0,0,2]; %input('Y=zeros(n);e=zeros(1,n);f=zeros(1,n);V=zeros(1,n);sida=zeros(1,n);S1=对各矩阵置零%zeros(nl);－－－－－－－修改部分－－－－－－－－－－－－%ym=1;定义视在功率和电压基值%SB=100;UB=Un; 若不是标幺值%if ym~=0定义导纳标幺值 YB=SB./UB./UB; % BB1=B1; BB2=B2;i=1:nl for切换为阻抗标幺值% B1(i,3)=B1(i,3)*YB;切换为导纳标幺值 B1(i,4)=B1(i,4)./YB; %end);B1=' disp('支路矩阵 sparseB1=sparse(B1);B1输出标幺值稀疏矩阵disp(sparseB1) %);'-----------------------------------------------------' disp( i=1:n for切换为视在功率标幺值% B2(i,1)=B2(i,1)./SB;切换为视在功率标幺值% B2(i,2)=B2(i,2)./SB;切换为电压标幺值 B2(i,3)=B2(i,3)./UB; %切换为电压标幺值B2(i,4)=B2(i,4)./UB; %切换为视在功率标幺值B2(i,5)=B2(i,5)./SB; %end);B2=' disp('节点矩阵 sparseB2=sparse(B2);B2输出标幺值稀疏矩阵disp(sparseB2) %end);disp('-----------------------------------------------------'% % %---------------------------------------------------支路数% i=1:nlfor侧左节点处于%1if B1(i,6)==0p=B1(i,1);q=B1(i,2);else使左节点处于低压侧% p=B1(i,2);q=B1(i,1);end求解非对角元导纳 Y(p,q)=Y(p,q)-1./(B1(i,3)*B1(i,5)); %对角元两侧对称Y(q,p)=Y(p,q); %侧KY(q,q)=Y(q,q)+1./(B1(i,3)*B1(i,5)^2)+B1(i,4)./2; %对角元侧%对角元1Y(p,p)=Y(p,p)+1./B1(i,3)+B1(i,4)./2;end求导纳矩阵%); Y=''导纳矩阵disp(sparseY=sparse(Y);输出导纳稀疏矩阵%disp(sparseY));disp('-----------------------------------------------------'%---------------------------------------------------------- %分解出导纳阵的实部和虚部G=real(Y);B=imag(Y);i=1:n for节点初始电压的实部i给定e(i)=real(B2(i,3)); %节点初始电压的虚部if(i)=imag(B2(i,3)); %给定节点电压给定模值V(i)=B2(i,4); %PV end %给定各节点注入功率for i=1:n SG-SL 节点注入功率%i S(i)=B2(i,1)-B2(i,2);节点无功补偿量 B(i,i)=B(i,i)+B2(i,5); %iend%===================================================================定义有功功率和无功功率%P=real(S);Q=imag(S);ICT1=0;IT2=1;N0=2*n;N=N0+1;a=0; %定义迭代次数ICT1和不满足精度要求的IT2节点个数．仍有不满足精度要求的节点 IT2~=0 %while置零IT2=0;a=a+1; %IT2 i=1:n for %非平衡节点ifi~=isbC(i)=0;D(i)=0; j1=1:n forC(i)=C(i)+G(i,j1)*e(j1)-B(i,j1)*f(j1);%Σ(Gij*ej-Bij*fj)D(i)=D(i)+G(i,j1)*f(j1)+B(i,j1)*e(j1);%Σ(Gij*fj+Bij*ej)endP1=C(i)*e(i)+f(i)*D(i);%节点功率P计算eiΣ(Gij*ej-Bij*fj)+fi(Gij*fj+Bij*ej)Σ Q1=C(i)*f(i)-e(i)*D(i);%节点功率Q计算fiΣ(Gij*ej-Bij*fj)-ei(Gij*fj+Bij*ej)ΣP',Q' %求电压模平方 V2=e(i)^2+f(i)^2; % =========Jacobi矩阵元素以下针对非PV节点来求取功率差及%=========节点%非PV if B2(i,6)~=3节点有功功率差 DP=P(i)-P1; % %节点无功功率差DQ=Q(i)-Q1;=================%=============== 以上为除平衡节点外其它节点的功率计算===================矩阵%================= 求取Jacobi j1=1:n for&非对角元非平衡节点 j1~=isb&j1~=i if%X1=-G(i,j1)*e(i)-B(i,j1)*f(i); %X1=N(i,j1)=dDP(i)/de(j1)．X2=B(i,j1)*e(i)-G(i,j1)*f(i); %X2=H(i,j1)=dDP(i)/df(j1)X3=X2; %X2=H(i,j1)=dDP(i)/df(j1)=X3=M(i,j1)=dDQ(i)/de(j1)X4=-X1; %X1=N(i,j1)=dDP(i)/de(j1)=-X4=-L(i,j1)=-dDQ(i)/df(j1)p=2*i-1;q=2*j1-1;Q扩展列△ J(p,q)=X3;J(p,N)=DQ;m=p+1;%P扩展列△ J(m,q)=X1;J(m,N)=DP;q=q+1;%矩阵赋值对%JacobiJ(p,q)=X4;J(m,q)=X2;&对角元elseif j1==i&j1~=isb %非平衡节点X1=-C(i)-G(i,i)*e(i)-B(i,i)*f(i);%X1=N(i,i)=dDP(i)/de(i) X2=-D(i)+B(i,i)*e(i)-G(i,i)*f(i);%X2=H(i,i)=dDP(i)/df(i) X3=D(i)+B(i,i)*e(i)-G(i,i)*f(i); %X3=M(i,i)=dDQ(i)/de(i) X4=-C(i)+G(i,i)*e(i)+B(i,i)*f(i);%X4=L(i,i)=dDQ(i)/df(i)Q扩展列△p=2*i-1;q=2*j1-1;J(p,q)=X3;J(p,N)=DQ;% m=p+1;P%扩展列△J(m,q)=X1;q=q+1;J(p,q)=X4;J(m,N)=DP;矩阵赋值JacobiJ(m,q)=X2; %对endendelse===========矩阵的元素Jacobi节点来求取PV下面是针对%===============节点有功误差 DP=P(i)-P1; % PV节点电压误差DV=V(i)^2-V2; % PV j1=1:n for非对角元%非平衡节点&if j1~=isb&j1~=iX1=-G(i,j1)*e(i)-B(i,j1)*f(i); %X1=N(i,j1)=dDP(i)/de(j1)X2=B(i,j1)*e(i)-G(i,j1)*f(i); %X2=H(i,j1)=dDP(i)/df(j1) X5=0;X6=0; %X5=R(i,j1)=X6=S(i,j1)=0V%p=2*i-1;q=2*j1-1;J(p,q)=X5;J(p,N)=DV;扩展列△ m=p+1;P%扩展列△ J(m,q)=X1;J(m,N)=DP;q=q+1;J(p,q)=X6;矩阵赋值对JacobiJ(m,q)=X2; %对角元%非平衡节点&elseifj1==i&j1~=isbX1=-C(i)-G(i,i)*e(i)-B(i,i)*f(i);%X1=N(i,i)=dDP(i)/de(i) X2=-D(i)+B(i,i)*e(i)-G(i,i)*f(i);%X2=H(i,i)=dDP(i)/df(i)% X5=R(i,i)=-2e(i) X5=-2*e(i); % X6=F(i,i)=-2f(i) X6=-2*f(i);V扩展列△ p=2*i-1;q=2*j1-1;J(p,q)=X5;J(p,N)=DV;%m=p+1;P% J(m,q)=X1;J(m,N)=DP;q=q+1;J(p,q)=X6;扩展列△矩阵赋值%对Jacobi J(m,q)=X2;endendendendend=====================%========= 以上为求雅可比矩阵的各个元素fork=3:N0 % N0=2*n （从第三行开始，第一、二行是平衡节点）Q、△ N=2*n+1扩展列△P k1=k+1;N1=N; % N=N0+1 即Q 、△扩展列△P for k2=k1:N1 %非对角元规格化 J(k,k2)=J(k,k2)./J(k,k); %end对角元规格化 J(k,k)=1; %不是第三行 k~=3 %if%============================================================k4=k-1;行消去k4k3行从第三行开始到当前行前的用for k3=3:k4 % 行后各行下三角元素 k2=k1:N1 for% k3消去运算 J(k3,k2)=J(k3,k2)-J(k3,k)*J(k,k2);%endJ(k3,k)=0;endk==N0 if;breakend%========================================== k3=k1:N0fork2=k1:N1for消去运算% J(k3,k2)=J(k3,k2)-J(k3,k)*J(k,k2);endJ(k3,k)=0;endelsek3=k1:N0fork2=k1:N1 for消去运算J(k3,k2)=J(k3,k2)-J(k3,k)*J(k,k2);%endJ(k3,k)=0;endendend%====上面是用线性变换方式将Jacobi矩阵化成单位矩阵(利用线性代数求解电压实部)=====与虚部 k=3:2:N0-1 for L=(k+1)./2;修改节点电压实部%e(L)=e(L)-J(k,N);k1=k+1;修改节点电压虚部% f(L)=f(L)-J(k1,N);end-----------修改节点电压%------ k=3:N0forDET=abs(J(k,N));电压偏差量是否满足要求 DET>=pr %if1不满足要求的节点数加IT2=IT2+1; %endendICT2(a)=IT2; ICT1=ICT1+1;end睜??屖用高斯消去法解%);''迭代次数disp(disp(ICT1););没有达到精度要求的个数''disp(disp(ICT2););disp('-----------------------------------------------------' k=1:n for计算实际电压大小 V(k)=sqrt(e(k)^2+f(k)^2); %计算实际电压相角% sida(k)=atan(f(k)./e(k))*180./pi;计算实际电压相量% E(k)=e(k)+f(k)*j; end ===========================计算各输出量%===============);：'为(节点号从小到大排列)'disp(各节点的实际电压标幺值E sparseE=sparse(E);disp(sparseE);EE=E*UB;);disp('-----------------------------------------------------');'：)节点号从小到大排列(为EE各节点的实际电压'disp(sparseEE=sparse(EE);disp(sparseEE););disp('-----------------------------------------------------');'节点号从小到大排列)：disp('各节点的电压标幺值幅值V为(sparseV=sparse(V);disp(sparseV););'-----------------------------------------------------'disp(VV=V*UB;);')：VV为(节点号从小到大排列'disp(各节点的电压幅值sparseVV=sparse(VV);disp(sparseVV););disp('-----------------------------------------------------');')(节点号从小到大排列：disp('各节点的电压相角为sparsesida=sparse(sida);disp(sparsesida));'-----------------------------------------------------'disp( p=1:n for C(p)=0; q=1:n for计算电流的共轭C(p)=C(p)+conj(Y(p,q))*conj(E(q));%end计算节点的视在功率% S(p)=E(p)*C(p);end);'：)节点号从小到大排列(为S各节点的功率标幺值'disp(sparseS=sparse(S);disp(sparseS););'-----------------------------------------------------'disp();'节点号从小到大排列)：disp('各节点的功率实际值SS为(SS=S*SB;sparseSS=sparse(SS);disp(sparseSS););'-----------------------------------------------------'disp();：'为(顺序支路参数矩阵顺序一致)SS disp('各条支路的功率损耗S标幺值和实际值HDDS=0;i=1:nl for p=B1(i,1);q=B1(i,2);Si(p,q)=E(p)*(conj(E(p))*conj(B1(i,4)./2)+(E(p)-E(q))*(conj(E(p))-conj(E(q)))*conj(1./(B1(i,3))))+E(q)*(conj(E(q))*conj(B1(i,4)./2));,num2str(Si(p,q))];')=',num2str(p),',',num2str(q), ZF1=['S(' disp(ZF1);SSi计算各条支路的消耗功率实际值 SSi(p,q)=Si(p,q)*SB;%HDDS=HDDS+SSi(p,q);,num2str(SSi(p,q))];')='',''SS(',num2str(p),,num2str(q),ZF=[ disp(ZF);end);环网总网损为；'disp(',num2str(HDDS)];'HDDS='ZH=[环网总网耗%disp(ZH);ZSS=HDDS+Fulloss;);'disp('总网损为：ZSS五、额定电压不同时对系统参数的分析：（1）额定电压为240V：辐射网：环网：（2）额定电压为220V：辐射网：环网：（3）额定电压为200V：辐射网：环网：结果分析：240V时总损耗为0.8856KVA 220V时为0.95KVA 200V时为0.9828KVA电压等级越高，损耗越小。

一、实验目的1. 理解电力系统潮流计算的基本原理和方法。

2. 掌握MATLAB/Simulink在电力系统仿真中的应用。

3. 通过仿真实验，验证潮流计算的正确性和实用性。

二、实验原理与内容1. 潮流计算的基本原理潮流计算是电力系统分析的重要手段，用于计算电力系统各节点的电压、相角、功率等参数。

其基本原理如下：（1）根据电力系统的网络结构和参数，建立节点方程和支路方程。

（2）利用节点方程和支路方程，求解节点电压和相角。

（3）根据节点电压和相角，计算各节点的有功功率和无功功率。

2. 仿真实验内容本次仿真实验采用MATLAB/Simulink搭建一个简单的2机5节点电力系统模型，并利用PowerGUI进行潮流计算。

（1）建立电力系统模型首先，在MATLAB/Simulink中搭建电力系统模型，包括发电机、负荷、线路等元件。

根据实验要求，设置发电机参数、负荷参数和线路参数。

（2）潮流计算利用PowerGUI进行潮流计算，设置求解器参数，如迭代次数、收敛精度等。

运行潮流计算，得到各节点的电压、相角、有功功率和无功功率等参数。

（3）结果分析对潮流计算结果进行分析，验证潮流计算的正确性和实用性。

比较不同运行方式下的潮流计算结果，分析系统稳定性。

三、实验方法1. 利用MATLAB/Simulink搭建电力系统模型。

2. 利用PowerGUI进行潮流计算。

3. 对潮流计算结果进行分析。

四、实验步骤1. 启动MATLAB/Simulink，新建一个仿真模型。

2. 在仿真模型中，添加发电机、负荷、线路等元件，设置相应参数。

3. 将搭建好的电力系统模型连接起来，形成一个完整的系统。

4. 打开PowerGUI，选择潮流计算模块。

5. 在潮流计算模块中，设置求解器参数，如迭代次数、收敛精度等。

6. 运行潮流计算，得到各节点的电压、相角、有功功率和无功功率等参数。

7. 对潮流计算结果进行分析，验证潮流计算的正确性和实用性。

五、实验结果与分析1. 潮流计算结果本次仿真实验中，潮流计算结果如下：（1）节点电压：U1=1.02p.u., U2=1.05p.u., U3=1.03p.u., U4=1.00p.u., U5=1.01p.u.（2）节点相角：δ1=0.5°, δ2=1.0°, δ3=0.7°, δ4=0.0°, δ5=0.6°（3）有功功率：P1=100MW, P2=100MW, P3=100MW, P4=100MW, P5=100MW（4）无功功率：Q1=20Mvar, Q2=20Mvar, Q3=20Mvar, Q4=20Mvar, Q5=20Mvar2. 结果分析（1）节点电压和相角在合理范围内，说明潮流计算正确。

PSS/E实验报告实验名称：潮流计算（一）班级：XXXXXXX 班姓名：XXX学号：XXXXXXX任课教师：XXXX实验老师：XXXX实验时间：2018年11月17日成绩：实验二潮流计算（1）一．实验目的（5分）通过对9 节点 3 机系统的潮流计算，掌握PSS/E 软件的基本操作方法，提高对电力系统分析的感性认识，学会PSS/E 潮流分布图的绘制方法，并为今后的实验提供数据基础。

二．实验预习要求(5分)实验前请完成以下预习要求：1)简述动态仿真和静态仿真的区别；动态仿真：电力系统遭受一些大的扰动，如短路故障等，系统的结果和参数发生重大改变时，对系统进行潮流计算分析。

静态仿真：静态仿真不涉及元件的动态特性和电力系统动态过程，本质上是系统运行的稳态分析。

2)简述高斯—塞德尔法解潮流和牛顿—拉夫逊法解潮流的步骤；高斯塞德尔法：1.设各节点电压初值，并给定迭代误差判据2.对每一个PQ节点以前一次迭代的电压值来计算新值3.求平衡节点注入功率4.求支路功率分部和支路功率损耗牛顿-拉夫逊法：1.形成节点导纳矩阵2.给各节点电压初值3.求修正方程的常数项向量4.求雅克比矩阵元素5.求解修正方程是式，求修正量6.求取节点电压新值7.检查是否收敛8.计算功率分布，PV节点无功功率和平衡节点注入功率3)简述牛顿—拉夫逊法解潮流问题。

1.稀疏矩阵表示法2.高斯消去法3.节点的优化编号4.牛顿拉夫逊法的收敛性三．实验内容和步骤(60分)1）打开已建立的原始数据文件①打开软件，点击File>>New>>Case Data②打开数据如图所示③潮流计算前节点电压和发电机功率记录在表2-1表2-1 潮流计算前的节点电压和发电机功率节点电压发电机功率（MW/Mvar）V1=1.5 V2=1.3 V3=1.025 Pgen1=0 Qgen1=0 Qmin gen1=-9999 V4=1.00 V5=1.00 V6=1.00 Pgen2=163 Qgen2=0 Qmin gen2=-9999 V7=1.00 V8=1.00 V9=1.00 Pgen3=85 Qgen3=0 Qmin gen3=-99992）进行潮流计算Newton-Raphson法①选择菜单栏>>Power Flow>>Solution>>Solve选项，得到如图的对话框，可以看到PSS/E使用的不同的潮流解法，Newton法和Gauss法。

一、实训目的本次实训旨在通过实际操作，加深对电力系统潮流计算理论和方法的理解，掌握电力系统潮流计算的基本步骤和常用算法，提高解决实际电力系统运行问题的能力。

二、实训内容1. 实训背景实训选取我国某地区典型电力系统进行潮流计算，该系统包含若干发电厂、变电站、输电线路和负荷，采用双绕组变压器和单相交流系统。

2. 实训步骤（1）建立电力系统模型根据实训提供的系统参数，建立电力系统节点、支路和设备模型，包括节点电压、支路阻抗、变压器变比、负荷等。

（2）选择潮流计算方法本实训采用牛顿-拉夫逊法进行潮流计算，该方法适用于大型电力系统计算，收敛速度快，精度高。

（3）编写潮流计算程序利用编程语言（如MATLAB、Python等）编写潮流计算程序，实现牛顿-拉夫逊法的基本步骤，包括计算雅可比矩阵、求解修正方程等。

（4）进行潮流计算运行潮流计算程序，对电力系统进行潮流计算，得到各节点电压、支路电流、功率损耗等数据。

（5）分析计算结果对计算结果进行分析，包括节点电压是否满足要求、支路电流是否越限、功率损耗是否合理等。

3. 实训结果（1）节点电压通过潮流计算，得到各节点电压值，并与设计要求进行比较。

结果显示，大部分节点电压满足要求，但部分节点电压略低于设计值，需进一步分析原因。

（2）支路电流计算各支路电流，并与额定电流进行比较。

结果显示，大部分支路电流未超过额定电流，但部分支路电流接近额定值，需注意运行安全。

（3）功率损耗计算系统总功率损耗，并与设计值进行比较。

结果显示，系统功率损耗略高于设计值，需优化运行方式，降低损耗。

三、实训总结1. 实训收获通过本次实训，我对电力系统潮流计算有了更深入的理解，掌握了牛顿-拉夫逊法的基本原理和编程实现方法。

同时，提高了分析电力系统运行问题的能力。

2. 实训体会（1）电力系统潮流计算是电力系统运行、规划、设计等方面的重要基础，掌握潮流计算方法对电力系统工作人员具有重要意义。

（2）编程能力在电力系统潮流计算中发挥着重要作用，熟练掌握编程语言有助于提高工作效率。

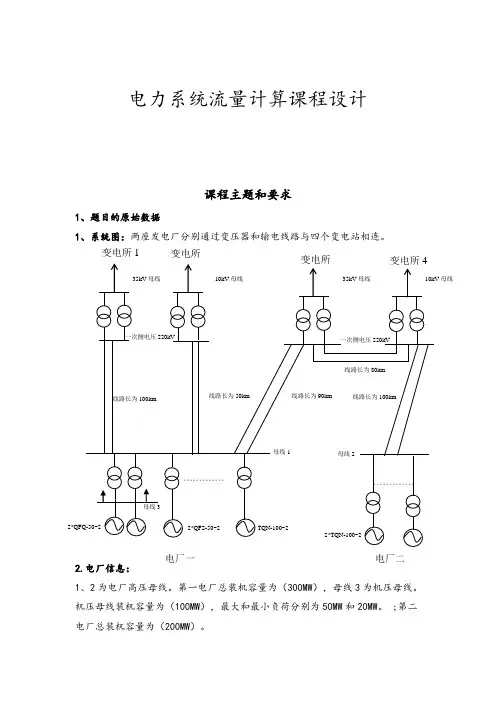
电力系统流量计算课程设计课程主题和要求1、题目的原始数据1、系统图：两座发电厂分别通过变压器和输电线路与四个变电站相连。

2.电厂信息：1、2为电厂高压母线。

第一电厂总装机容量为（300MW ），母线3为机压母线。

机压母线装机容量为（100MW ），最大和最小负荷分别为50MW 和20MW 。

;第二电厂总装机容量为（200MW ）。

变电所1变电所母线电厂一 电厂二3、变电站信息：(一) 1、2、3、4变电站低压母线电压等级为：35KV 10KV 35KV 10KV (二)变电站负荷为：60MW 40MW 40MW 50MW (三) 各变电站功率因数cos φ=0.85；(四)1、3变电站分别配备两台容量为75MVA 的变压器，短路损耗为414KW ，短路电压（%）=16.7；变电站2、变电站4分别配备两台容量为63MVA 的变压器，短路损耗为245KW ，短路电压（%）=10.5；4、输电线路信息：电厂与变电站之间输电线路的电压等级和长度如图所示，Ω17.0单位长度电阻为 ，单位长度电抗Ω0.402为 ，单位长度电纳为S -610*2.78。

二、 课程设计的基本内容：1. 给定网络，并画出等效电路图。

2. 输入各支路数据，在变电站一定负荷条件下，通过给定程序计算各节点数据，并对计算结果进行分析。

3. 跟随变电站负荷按一定比例变化，进行潮流计算分析。

1) 4个变电站负荷同时增加2%； 2) 4个变电站负荷同时降低2%3) 1、4号变电站负荷同时下降2%，2、3号变电站负荷同时上升2%； 4. 在不同的负载条件下，分析潮流计算的结果，如果每条母线的电压不符合要求，则调整电压。

（变电站低压母线电压10KV 需要在9.5-10.5之间调整；35KV 电压需要在35-36之间调整）5. 断开支路双回线路之一，分析潮流分布。

（好几根树枝断了好几次）6. 使用DDRTS 软件，绘制系统图，分析上述各种情况的流程，并比较结果。

南昌大学实验报告学生姓名：学号：专业班级：实验类型：□验证□综合■设计□创新实验日期：实验成绩：一、实验项目名称直流潮流计算实验二、实验目的与要求：目的：电力系统分析的潮流计算是电力系统分析的一个重要的部分。

通过对电力系统潮流分布的分析和计算，可进一步对系统运行的安全性，经济性进行分析、评估，提出改进措施。

电力系统潮流的计算和分析是电力系统运行和规划工作的基础。

潮流计算是指对电力系统正常运行状况的分析和计算。

通常需要已知系统参数和条件，给定一些初始条件，从而计算出系统运行的电压和功率等；潮流计算方法很多：高斯-塞德尔法、牛顿-拉夫逊法、P-Q分解法、直流潮流法，以及由高斯-塞德尔法、牛顿-拉夫逊法演变的各种潮流计算方法。

本实验采用直流潮流算法进行电力系统分析的潮流计算程序的编制与调试，获得电力系统中各个支路的有功分布，为进一步进行电力系统分析作准备。

通过实验教学加深学生对电力系统潮流计算原理的理解和计算，初步学会运用计算机知识解决电力系统的问题，掌握潮流计算的过程及其特点。

熟悉各种常用应用软件，熟悉硬件设备的使用方法，加强编制调试计算机程序的能力，提高工程计算的能力，学习如何将理论知识和实际工程问题结合起来。

要求：编制调试电力系统潮流计算的计算机程序。

程序要求根据已知的电力网的数学模型（节点导纳矩阵）及各节点参数，完成该电力系统的潮流计算，要求计算出节点电压、功率等参数。

三、实验基本原理（一）、直流潮流的介绍在电力系统稳态分析课程中，我们已经学习过有关高斯-塞德尔和牛顿-拉夫逊等潮流计算方法，它们所面对的是个非线性方程组求解问题。

虽然这些方法都具有一定的精度，但计算量较大，这显然不适应形成电网规划方案时多次而反复的潮流计算要求。

直流潮流模型是把非线性电力潮流问题简化为线形电路问题，从而使分析计算非常方便，直流潮流专门用于研究电网中有功潮流的分布。

（二）、直流潮流算法的形成过程对下图所示等值电路图，对于之路（i,j ），如果忽略其并联支路，例如忽略线路的充电电容。

PSASP 潮流计算一、实验目的理解电力系统分析中潮流计算的相关概念，掌握用PSASP 软件对系统潮流进行计算的过程。

学会在文本方式下和图形方式下的对潮流计算结果进行分析。

二、预习要求复习《电力系统分析》中有关潮流计算的内容，了解有关潮流计算的功能，理解常用潮流计算方法，了解PQ、PV和Vθ（平衡节点，在PSASP中称为Slack节点）的设置。

三、实验内容（一） PSASP 潮流计算概述潮流计算是根据给定的电网结构、参数和发电机、负荷等元件的运行条件，确定电力系统各部分稳态运行状态参数的计算。

通常给定的运行条件有系统中各电源和负荷点的功率、枢纽点电压、平衡点的电压和相位角。

待求的运行状态参量包括电网各母线节点的电压幅值和相角，以及各支路的功率分布、网络的功率损耗等。

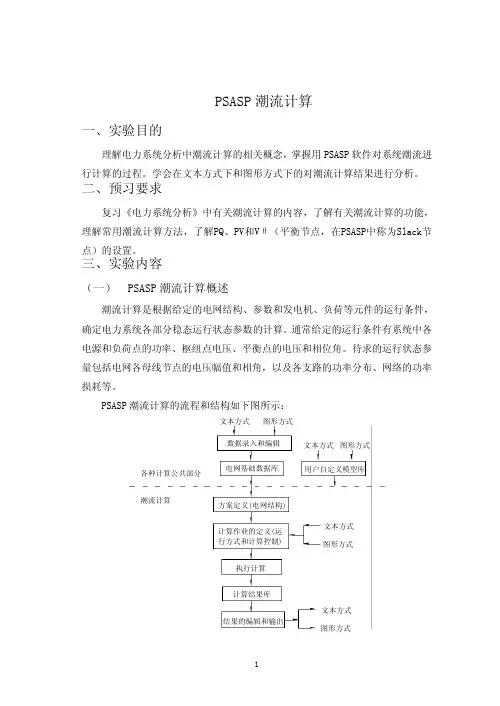
PSASP 潮流计算的流程和结构如下图所示：潮流计算各种计算公共部分文本方式图形方式结果的编辑和输出计算结果库执行计算图形方式文本方式计算作业的定义(运行方式和计算控制)方案定义(电网结构)文本方式图形方式用户自定义模型库电网基础数据库图形方式文本方式数据录入和编辑以一个图所示9节点系统为例，计算其在常规、规划两种运行方式下的潮流。

规划运行方式即在常规运行方式下，其中接于一条母线（STNB-230）处的负荷增加，对原有电网进行改造后的运行方式，具体方法为：在母线GEN3-230和STNB-230之间增加一回输电线，增加发电机3的出力及其出口变压器的容量，新增或改造的元件如下图虚线所示。

（二） 数据准备1. 指定数据目录及基准容量双击PSASP图标，弹出PSASP封面后，按任意键，即进入PSASP主画面：在该画面中，要完成的工作如下：(1) 指定数据目录第一次可通过“创建数据目录” 按钮，建立新目录，如：C:\CLJS。

以后可通过“选择数据目录”按钮，选择该目录。

(2) 给定系统基准容量系统基准容量项中，键入该系统基准容量，如100MVA。

一、实验背景与目的电力系统潮流计算是电力系统分析中的一个重要环节，它通过对电力系统网络中功率和电压的分布进行计算，以评估系统的运行状态。

本实验旨在通过实际操作，加深对电力系统潮流计算原理和方法的理解，并掌握使用PSASP、ETAP等软件进行潮流计算的基本技能。

二、实验原理与方法1. 基本原理潮流计算主要基于基尔霍夫电流定律和基尔霍夫电压定律，通过求解电力系统网络中的功率和电压分布，得到各节点电压、线路电流和设备功率等参数。

2. 计算方法常用的潮流计算方法包括牛顿-拉夫逊法、快速分解法、迭代法等。

本实验采用牛顿-拉夫逊法进行潮流计算。

3. 实验步骤（1）建立电力系统网络模型，包括节点、线路、变压器等元件；（2）设置各节点电压初始值和负荷功率；（3）计算网络中各支路功率和节点电压，判断是否满足功率平衡和电压平衡；（4）根据功率平衡和电压平衡条件，修正节点电压，重复步骤（3）直至满足收敛条件。

三、实验过程与结果分析1. 实验数据本实验采用某实际电力系统网络进行计算，网络包括10个节点、15条线路和3个变压器。

2. 实验步骤（1）根据实验数据，建立电力系统网络模型；（2）设置各节点电压初始值和负荷功率；（3）使用PSASP软件进行潮流计算；（4）分析计算结果，包括节点电压、线路电流和设备功率等。

3. 结果分析（1）节点电压分布合理，各节点电压满足运行要求；（2）线路电流分布均匀，线路负载率在合理范围内；（3）设备功率分配合理，满足电力系统运行需求。

四、实验总结与讨论1. 实验总结本实验通过实际操作，加深了对电力系统潮流计算原理和方法的理解，掌握了使用PSASP软件进行潮流计算的基本技能。

2. 讨论（1）实验中，节点电压初始值设置对计算结果有较大影响，需要根据实际情况进行设置；（2）潮流计算结果受网络拓扑结构、元件参数和负荷分布等因素的影响，需要综合考虑；（3）在实际工程应用中，应根据具体情况选择合适的潮流计算方法，以保证计算结果的准确性和可靠性。

Beijing Jiaotong University电力系统潮流计算仿真报告…姓名：TYP班级：电气0906学号：指导老师：吴俊勇完成日期：一、实验内容电力系统潮流计算是研究电力系统稳态运行情况的一种基本电气计算。

它的任务是根据给定的运行条件和网路结构确定整个系统的运行状态，如各母线上的电压（幅值及相角）、网络中的功率分布以及功率损耗等。

电力系统潮流计算的结果是电力系统稳定计算和故障分析的基础。

对于简单系统，可以将其分为开式网络和闭式网络手工计算。

对于复杂电力系统，根据定解条件，应用牛顿—拉夫逊法进行计算，在手工计算中，由于涉及大量变量、微分方程、矩阵计算，求解很烦琐，而且容易出错，计算不同系统时需要重新计算。

故而我们可以借助计算机来进行潮流计算，方便快捷且准确率高。

二、计算机潮流计算方法@我们常用牛顿—拉夫逊法来进行潮流计算。

牛顿—拉夫逊法(简称牛顿法)在数学上是求解非线性代数方程式的有效方法，其要点是把非线性方程式的求解过程变成反复地对相应的线性方程式进行求解的过程，即通常所称的逐次线性化过程。

1、基本原理从几何意义上，牛顿—拉夫逊法实质上就是切线法，是一种逐步线性化的方法。

2、牛顿—拉夫逊法潮流求解过程以下讨论的是用直角坐标形式的牛顿—拉夫逊法潮流的求解过程。

当采用直角坐标时，潮流问题的待求量为各节点电压的实部和虚部两个分量，由于平衡节点的电压向量是给定的，因此待求量共2(n-1)需要2(n-1)个方程式。

事实上，除了平衡节点的功率方程式在迭代过程中没有约束作用以外，其余每个节点都可以列出两个方程式。

求解过程大致可以分为以下步骤：！(1)形成节点导纳矩阵；(2)将各节点电压设初值；(3)将节点初值代入相关求式，求出修正方程式的常数项向量；(4)将节点电压初值代入求式，求出雅可比矩阵元素；(5)求解修正方程，求修正向量；(6)求取节点电压的新值；(7)检查是否收敛，如不收敛，则以各节点电压的新值作为初值自第3步重新开始进行狭义次迭代，否则转入下一步；(8)计算支路功率分布，PV节点无功功率和平衡节点功率。

一、实训目的本次电力网潮流计算实训旨在使学生掌握电力系统潮流计算的基本原理和方法，提高学生对电力系统运行状态的分析能力，培养学生运用所学知识解决实际问题的能力。

通过实训，使学生能够熟练运用MATLAB等工具进行电力系统潮流计算，并能够根据计算结果对电力系统运行状态进行分析和评价。

二、实训内容1. 电力系统潮流计算的基本原理电力系统潮流计算是一种分析电力系统稳态运行状态的方法，其主要任务是确定电力系统中各节点的电压、电流和功率分布。

电力系统潮流计算的基本原理如下：（1）节点电压方程：根据节点电压和注入功率之间的关系，建立节点电压方程。

（2）支路功率方程：根据支路两端电压和电流之间的关系，建立支路功率方程。

（3）潮流计算方法：采用迭代方法求解节点电压方程和支路功率方程，得到电力系统中各节点的电压、电流和功率分布。

2. 电力系统潮流计算实训本次实训以MATLAB为工具，进行电力系统潮流计算。

实训步骤如下：（1）建立电力系统模型：根据实训要求，建立电力系统模型，包括节点、支路、变压器等。

（2）设置电力系统参数：根据电力系统模型，设置各节点的注入功率、支路参数、变压器参数等。

（3）进行潮流计算：运用MATLAB中的电力系统分析工具箱（Power System Toolbox）进行潮流计算。

（4）分析计算结果：对潮流计算结果进行分析，包括节点电压、电流、功率分布、网络损耗等。

三、实训结果与分析1. 潮流计算结果通过潮流计算，得到以下结果：（1）节点电压：各节点电压的幅值和相角。

（2）电流：各支路电流的幅值和相角。

（3）功率分布：各支路的有功功率和无功功率。

（4）网络损耗：电力系统中的网络损耗。

2. 结果分析（1）节点电压分析：分析各节点电压是否满足要求，是否存在过电压或欠电压现象。

（2）电流分析：分析各支路电流是否满足要求，是否存在过载现象。

（3）功率分布分析：分析电力系统中功率分布是否合理，是否存在不平衡现象。

高等电力系统分析潮流计算姓名：***学号：********第一部分 程序设计说明本设计采用牛顿-拉夫逊法实现电力系统的潮流计算。

相对于其它方法，选择牛顿-拉夫逊法，因为牛顿-拉夫逊法计算的结果精确度高，以导纳为基础，利用导纳矩阵的对称性、稀疏性及节电编号顺序优化的技巧，使该法的速度及收敛性加快，但该法内存的需要量也较大。

设计采用直角坐标系和matlab 语言来编程，全部程序在matlab6.5.1操作平台上编译并通过。

牛顿-拉夫逊法原理简述：1）选取方程根的初始值0x ，一般来说，0()0f x ≠2）对0x 进行修正，令100x x Δx =+，即010x x x ∆=-,将1()f x 在0x 点附近展开泰勒级数，取一阶近似 1000()()()0f x f x f x x '≈+∆≈,当'0()0f x ≠时有000()/()x f x f x '∆=- 3）综合1）2）有：1000()/()x x f x f x '=-4）若经k +1次修正得到了方程的解 1'()/()0,1,2,3,k k k k x x f x f x k +=-=注：1.若初始值充分接近于根，则N －R 法的收敛速度很快；2.由于方程的精确解的具体值事先不知道，在编程实施时，可以预先给定一个足够小的正数 ，以下式作为迭代终止的判定条件：1k k x x ε+-< 牛顿-拉夫逊法几何意义：图中()0x 为假设的初始值它和真值之间的差值 为：()0Δx ，然后求得：()1x ，其与真值之间的差值为：()1Δx 。

如此类推，求得()k x 逼近真值 *x 。

x本程序流程图：第二部分使用说明本程序使用matlab 6.5.1版本编译，使用时将本程序的m文件放入C:\MA TLAB6p5p1\work文件夹下运行即可。

首先运行ieee14.m文件，将ieee14节点数据存入到matlab缓存中，之后运行chaoliu.m文件，运行后结果自动输出到该文件夹下的result.txt文档中，打开可看到结果。

潮流计算实验报告潮流计算实验报告潮流计算是电力系统运行中的重要工具，用于分析电力系统中各节点的电压、功率等参数，以确保电力系统的稳定运行。

本次实验旨在通过潮流计算方法，对一个简化的电力系统进行分析，探讨电力系统的稳定性和可靠性。

1. 实验背景电力系统是一个复杂的网络，由发电厂、输电线路、变电站和用户组成。

在电力系统中，电流和电压的分布是非常重要的，因为它们直接影响到电力系统的稳定性和可靠性。

潮流计算是一种基于电力系统的拓扑结构和电气参数，通过求解节点电压和功率的方程组，来分析电力系统中各节点的电压、功率等参数的方法。

2. 实验目的本次实验的目的是通过潮流计算方法，对一个简化的电力系统进行分析，了解电力系统的稳定性和可靠性。

具体目标包括：- 分析电力系统中各节点的电压、功率等参数；- 研究电力系统中负荷变化对电压和功率的影响；- 探讨电力系统中的潮流分布情况。

3. 实验过程本次实验采用Matlab软件进行潮流计算。

首先，根据给定的电力系统拓扑结构和电气参数，建立电力系统的节点电压和功率方程组。

然后，通过求解该方程组，得到电力系统中各节点的电压和功率等参数。

最后，根据求解结果，分析电力系统中的潮流分布情况。

4. 实验结果通过潮流计算，得到了电力系统中各节点的电压和功率等参数。

根据实验结果，可以得出以下结论：- 在电力系统中，电压和功率的分布是不均匀的，不同节点的电压和功率存在差异；- 负荷变化会对电力系统中的电压和功率产生影响，负荷增加会导致电压下降，功率增加；- 电力系统中存在潮流集中的现象，即部分节点的潮流较大，而其他节点的潮流较小。

5. 实验分析通过对实验结果的分析，可以得出以下结论：- 电力系统中的电压和功率分布不均匀，这是由于电力系统中各节点的拓扑结构和电气参数的差异所导致的；- 负荷变化对电力系统的稳定性和可靠性具有重要影响，负荷增加会导致电力系统中的电压下降，功率增加，从而可能引发电力系统的故障；- 电力系统中的潮流集中现象可能会导致部分节点的负荷过载，从而影响电力系统的稳定运行。

潮流计算报告一、系统结构图：二、网络参数：1、支路参数：网络类型支路编号电压等级（kV）装机容量(MW)导线的技术参数1r（Ω）1x（Ω）1b（）环网1-222010013.6 125.5 67.85 1-3 8.321 130.5 52.24 3-5 10.2 128.8 74.99 2-3 8.5 105.4 28.36 1-4 7.579 129.6 51.45 4-5 13.84 125.31 2.78辐射网1-2————2 4——2-3 3 63-4 4 82-5 1 25-6 4 42、节点参数：节点类型节点编号发电功率（MW）负荷视在功率环网1 0 未知(平衡节点)2 100 0（PV节点）3 0 15+9.4i4 0 27+6i5 0 35.5+25.5i辐射网1 0 未知(平衡节点)2 0 4+2i3 0 6+3.2i4 0 3+1.44i5 0 4+3.2i6 0 2+1.1i三、潮流计算流程图:Un 2 1.1];FT=[%首端末端4 33 26 55 22 1];RX=[% R X4 83 64 41 22 4];NN=size(PQ,1); %节点数NB=size(FT,1); %支路数数V=PQ(:,1); %V初始电压相量maxd=1k=1while maxd>0.0001k=k+1;PQ2=PQ; %每一次迭代各节点的注入有功和无功相同PL=0.0;for i=1:NBkf=FT(i,1); %前推始节点号kt=FT(i,2); %前推终节点号x=(PQ2(kf,2)^2+PQ2(kf,3)^2)/V(kf)/V(kf);%计算沿线电流 /平方Alosss(i,1)=RX(i,1)*x; %计算线路有功损耗 /MWlosss(i,2)=RX(i,2)*x; %计算线路无功损耗/MWPQ1(i,1)=PQ2(kf,2)+RX(i,1)*x; %计算支路首端有功/MW RX(i,1)*RPQ1(i,2)=PQ2(kf,3)+RX(i,2)*x; %计算沿支路的无功/MW RX(i,2)*XPQ2(kt,2)= PQ2(kt,2)+PQ1(i,1); %用PQ1去修正支路末端节点的有功P 单位MWPQ2(kt,3)= PQ2(kt,3)+PQ1(i,2); %用PQ1去修正支路末端节点的有功Q 单位Mvarendangle(1)=0.0;for i=NB:-1:1kf=FT(i,2); %回代始节点号kt=FT(i,1); %回代终节点号dv1=(PQ1(i,1)*RX(i,1)+PQ1(i,2)*RX(i,2))/V(kf); %计算支路电压损耗的纵分量dv1dv2=(PQ1(i,1)*RX(i,2)-PQ1(i,2)*RX(i,1))/V(kf); %计算支路电压损耗的横分量dv2V2(kt)=sqrt((V(kf)-dv1)^2+dv2^2); %计算支路末端电压/kV angle(kt)=angle(kf)+atand(dv2/(V(kf)-dv1)); %计算支路endmaxd=abs(V2(2)-V(2));V2(1)=V(1);for i=3:1:NNif abs(V2(i)-V(i))>maxd;maxd=abs(V2(i)-V(i));endendfullloss(1,1)=0;%计算线路总损耗fullloss(1,2)=0;finalPQ=max(PQ1);for i=1:NBfullloss(1,1)=fullloss(1,1)+losss(i,1);fullloss(1,2)=fullloss(1,2)+losss(i,2);enddisp('辐射网迭代次数：')kdisp('辐射网系统电压差精度：')maxddisp('辐射网系统末端节点有功和无功：')finalPQ %潮流分布即支路首端潮流MVAdisp('辐射网系统总功率损耗：')fullloss %线路总损耗MVAdisp('辐射网系统各支路功率损耗：')losss %各支路损耗MVAdisp('辐射网系统各节点电压幅值：')V=V2 %节点电压模计算结果kVdisp('辐射网系统各节点电压相角：')angle %节点电压角度计算结果单位度endclcdisp('辐射网迭代次数：')kdisp('辐射网系统电压差精度：')maxddisp('辐射网系统末端节点有功和无功/MVA：')FinPQ=finalPQ(1,1)+finalPQ(1,2)*j %潮流分布即支路首端潮流MVA disp('辐射网系统总功率损耗/MVA：')Fulloss=fullloss (1,1)+fullloss(1,2)*j %线路总损耗MVA disp('辐射网系统各支路功率损耗/MVA：')for(a=1:5)LOSS=losss (a,1)+losss(a,2)*j %各支路损耗MVAenddisp('辐射网系统各节点电压幅值/KV：')V=V2 %节点电压模计算结果kVdisp('辐射网系统各节点电压相角：')angle %节点电压角度计算结果单位度n=5; %input('节点数');nl=6; %input('支路数');isb=1; %input('平衡母线节点号');pr=0.000001; %input('误差精度：pr=');B1=[1,2,13.6+125.5i,0.00006785i,1,0;1,3,8.321+130.5i,0.00005224i,1,0;3,5,10.2+128.8i,0.00007499i,1,0;2,3,8.5+105.4i,0.00002836i,1,0;1,4,7.579+129.6i,0.00005145i,1,0;4,5,13.84+125.31i,0.0000278i,1,0]; %input('由支路参数形成的矩阵');B2=[-FinPQ,0,Un,0,0,1;100,0,Un,Un,0,3;0,15+9.4i,Un,0,0,2;0,27+6i,Un,0,0,2;0,35.5+25.5i,Un,0,0,2]; %input('各节点参数形成的矩阵');Y=zeros(n);e=zeros(1,n);f=zeros(1,n);V=zeros(1,n);sida=zeros(1,n);S1= zeros(nl);%对各矩阵置零%－－－－－－－修改部分－－－－－－－－－－－－ym=1;SB=100;UB=Un; %定义视在功率和电压基值if ym~=0 %若不是标幺值YB=SB./UB./UB; %定义导纳标幺值BB1=B1;BB2=B2;for i=1:nlB1(i,3)=B1(i,3)*YB; %切换为阻抗标幺值B1(i,4)=B1(i,4)./YB; %切换为导纳标幺值enddisp('支路矩阵B1=');sparseB1=sparse(B1);disp(sparseB1) %输出标幺值稀疏矩阵B1disp('-----------------------------------------------------');for i=1:nB2(i,1)=B2(i,1)./SB; %切换为视在功率标幺值B2(i,2)=B2(i,2)./SB; %切换为视在功率标幺值B2(i,3)=B2(i,3)./UB; %切换为电压标幺值B2(i,4)=B2(i,4)./UB; %切换为电压标幺值B2(i,5)=B2(i,5)./SB; %切换为视在功率标幺值enddisp('节点矩阵B2=');sparseB2=sparse(B2);disp(sparseB2) %输出标幺值稀疏矩阵B2enddisp('-----------------------------------------------------');% % %---------------------------------------------------for i=1:nl %支路数if B1(i,6)==0 %左节点处于1侧p=B1(i,1);q=B1(i,2);elsep=B1(i,2);q=B1(i,1); %使左节点处于低压侧endY(p,q)=Y(p,q)-1./(B1(i,3)*B1(i,5)); %求解非对角元导纳Y(q,p)=Y(p,q); %对角元两侧对称Y(q,q)=Y(q,q)+1./(B1(i,3)*B1(i,5)^2)+B1(i,4)./2; %对角元K侧Y(p,p)=Y(p,p)+1./B1(i,3)+B1(i,4)./2; %对角元1侧end%求导纳矩阵disp('导纳矩阵 Y=');sparseY=sparse(Y);disp(sparseY) %输出导纳稀疏矩阵disp('-----------------------------------------------------');%----------------------------------------------------------G=real(Y);B=imag(Y); %分解出导纳阵的实部和虚部for i=1:ne(i)=real(B2(i,3)); %给定i节点初始电压的实部f(i)=imag(B2(i,3)); %给定i节点初始电压的虚部V(i)=B2(i,4); %PV节点电压给定模值endfor i=1:n %给定各节点注入功率S(i)=B2(i,1)-B2(i,2); %i节点注入功率SG-SLB(i,i)=B(i,i)+B2(i,5); %i节点无功补偿量end%=================================================================== P=real(S);Q=imag(S); %定义有功功率和无功功率ICT1=0;IT2=1;N0=2*n;N=N0+1;a=0; %定义迭代次数ICT1和不满足精度要求的节点个数IT2while IT2~=0 %仍有不满足精度要求的节点IT2=0;a=a+1; %IT2置零for i=1:nif i~=isb %非平衡节点C(i)=0;D(i)=0;for j1=1:nC(i)=C(i)+G(i,j1)*e(j1)-B(i,j1)*f(j1);%Σ(Gij*ej-Bij*fj)D(i)=D(i)+G(i,j1)*f(j1)+B(i,j1)*e(j1);%Σ(Gij*fj+Bij*ej)endP1=C(i)*e(i)+f(i)*D(i);%节点功率P计算eiΣ(Gij*ej-Bij*fj)+fi Σ(Gij*fj+Bij*ej)Q1=C(i)*f(i)-e(i)*D(i);%节点功率Q计算fiΣ(Gij*ej-Bij*fj)-ei Σ(Gij*fj+Bij*ej)%求P',Q'V2=e(i)^2+f(i)^2; %电压模平方%========= 以下针对非PV节点来求取功率差及Jacobi矩阵元素 =========if B2(i,6)~=3 %非PV节点DP=P(i)-P1; %节点有功功率差DQ=Q(i)-Q1; %节点无功功率差%=============== 以上为除平衡节点外其它节点的功率计算 =================%================= 求取Jacobi矩阵 ===================for j1=1:nif j1~=isb&j1~=i %非平衡节点&非对角元X1=-G(i,j1)*e(i)-B(i,j1)*f(i); %X1=N(i,j1)=dDP(i)/de(j1)X2=B(i,j1)*e(i)-G(i,j1)*f(i); %X2=H(i,j1)=dDP(i)/df(j1)X3=X2; %X2=H(i,j1)=dDP(i)/df(j1)=X3=M(i,j1)=dDQ(i)/de(j1)X4=-X1; %X1=N(i,j1)=dDP(i)/de(j1)=-X4=-L(i,j1)=-dDQ(i)/df(j1)p=2*i-1;q=2*j1-1;J(p,q)=X3;J(p,N)=DQ;m=p+1;%扩展列△QJ(m,q)=X1;J(m,N)=DP;q=q+1;%扩展列△PJ(p,q)=X4;J(m,q)=X2; %对Jacobi矩阵赋值elseif j1==i&j1~=isb %非平衡节点&对角元X1=-C(i)-G(i,i)*e(i)-B(i,i)*f(i);%X1=N(i,i)=dDP(i)/de(i)X2=-D(i)+B(i,i)*e(i)-G(i,i)*f(i);%X2=H(i,i)=dDP(i)/df(i)X3=D(i)+B(i,i)*e(i)-G(i,i)*f(i); %X3=M(i,i)=dDQ(i)/de(i)X4=-C(i)+G(i,i)*e(i)+B(i,i)*f(i);%X4=L(i,i)=dDQ(i)/df(i)p=2*i-1;q=2*j1-1;J(p,q)=X3;J(p,N)=DQ;%扩展列△Q m=p+1;J(m,q)=X1;q=q+1;J(p,q)=X4;J(m,N)=DP;%扩展列△PJ(m,q)=X2; %对Jacobi矩阵赋值endendelse%=============== 下面是针对PV节点来求取Jacobi矩阵的元素 ===========DP=P(i)-P1; % PV节点有功误差DV=V(i)^2-V2; % PV节点电压误差for j1=1:nif j1~=isb&j1~=i %非平衡节点&非对角元X1=-G(i,j1)*e(i)-B(i,j1)*f(i); %X1=N(i,j1)=dDP(i)/de(j1)X2=B(i,j1)*e(i)-G(i,j1)*f(i); %X2=H(i,j1)=dDP(i)/df(j1)X5=0;X6=0; %X5=R(i,j1)=X6=S(i,j1)=0p=2*i-1;q=2*j1-1;J(p,q)=X5;J(p,N)=DV;%扩展列△V m=p+1;J(m,q)=X1;J(m,N)=DP;q=q+1;J(p,q)=X6;%扩展列△PJ(m,q)=X2; %对Jacobi矩阵赋值elseif j1==i&j1~=isb %非平衡节点&对角元X1=-C(i)-G(i,i)*e(i)-B(i,i)*f(i);%X1=N(i,i)=dDP(i)/de(i)X2=-D(i)+B(i,i)*e(i)-G(i,i)*f(i);%X2=H(i,i)=dDP(i)/df(i)X5=-2*e(i); % X5=R(i,i)=-2e(i) X6=-2*f(i); % X6=F(i,i)=-2f(i) p=2*i-1;q=2*j1-1;J(p,q)=X5;J(p,N)=DV;%扩展列△V m=p+1;J(m,q)=X1;J(m,N)=DP;q=q+1;J(p,q)=X6;%扩展列△PJ(m,q)=X2; %对Jacobi矩阵赋值endendendendend%========= 以上为求雅可比矩阵的各个元素 =====================for k=3:N0 % N0=2*n （从第三行开始，第一、二行是平衡节点）k1=k+1;N1=N; % N=N0+1 即 N=2*n+1扩展列△P、△Qfor k2=k1:N1 % 扩展列△P、△QJ(k,k2)=J(k,k2)./J(k,k); % 非对角元规格化endJ(k,k)=1; % 对角元规格化if k~=3 % 不是第三行%========================================================== ==k4=k-1;for k3=3:k4 % 用k3行从第三行开始到当前行前的k4行消去for k2=k1:N1 % k3行后各行下三角元素J(k3,k2)=J(k3,k2)-J(k3,k)*J(k,k2);%消去运算endJ(k3,k)=0;endif k==N0break;end%==========================================for k3=k1:N0for k2=k1:N1J(k3,k2)=J(k3,k2)-J(k3,k)*J(k,k2);%消去运算endJ(k3,k)=0;endelsefor k3=k1:N0for k2=k1:N1J(k3,k2)=J(k3,k2)-J(k3,k)*J(k,k2);%消去运算endJ(k3,k)=0;endendend%====上面是用线性变换方式将Jacobi矩阵化成单位矩阵(利用线性代数求解电压实部与虚部)=====for k=3:2:N0-1L=(k+1)./2;e(L)=e(L)-J(k,N); %修改节点电压实部k1=k+1;f(L)=f(L)-J(k1,N); %修改节点电压虚部end%------修改节点电压-----------for k=3:N0DET=abs(J(k,N));if DET>=pr %电压偏差量是否满足要求IT2=IT2+1; %不满足要求的节点数加1endendICT2(a)=IT2;ICT1=ICT1+1;end%用高斯消去法解"w=-J*V"disp('迭代次数');disp(ICT1);disp('没有达到精度要求的个数');disp(ICT2);disp('-----------------------------------------------------'); for k=1:nV(k)=sqrt(e(k)^2+f(k)^2); %计算实际电压大小sida(k)=atan(f(k)./e(k))*180./pi;%计算实际电压相角E(k)=e(k)+f(k)*j; %计算实际电压相量end%=============== 计算各输出量 ===========================disp('各节点的实际电压标幺值E为(节点号从小到大排列)：');sparseE=sparse(E);disp(sparseE);EE=E*UB;disp('-----------------------------------------------------'); disp('各节点的实际电压EE为(节点号从小到大排列)：');disp(sparseEE);disp('-----------------------------------------------------'); disp('各节点的电压标幺值幅值V为(节点号从小到大排列)：');sparseV=sparse(V);disp(sparseV);disp('-----------------------------------------------------'); VV=V*UB;disp('各节点的电压幅值VV为(节点号从小到大排列)：');sparseVV=sparse(VV);disp(sparseVV);disp('-----------------------------------------------------'); disp('各节点的电压相角为(节点号从小到大排列)：');sparsesida=sparse(sida);disp(sparsesida)disp('-----------------------------------------------------'); for p=1:nC(p)=0;for q=1:nC(p)=C(p)+conj(Y(p,q))*conj(E(q));%计算电流的共轭endS(p)=E(p)*C(p);%计算节点的视在功率enddisp('各节点的功率标幺值S为(节点号从小到大排列)：');disp(sparseS);disp('-----------------------------------------------------');disp('各节点的功率实际值SS为(节点号从小到大排列)：');SS=S*SB;sparseSS=sparse(SS);disp(sparseSS);disp('-----------------------------------------------------');disp('各条支路的功率损耗S标幺值和实际值SS为(顺序支路参数矩阵顺序一致)：'); HDDS=0;for i=1:nlp=B1(i,1);q=B1(i,2);Si(p,q)=E(p)*(conj(E(p))*conj(B1(i,4)./2)+(E(p)-E(q))*(conj(E(p))-con j(E(q)))*conj(1./(B1(i,3))))+E(q)*(conj(E(q))*conj(B1(i,4)./2));ZF1=['S(',num2str(p),',',num2str(q),')=',num2str(Si(p,q))];disp(ZF1);SSi(p,q)=Si(p,q)*SB;%计算各条支路的消耗功率实际值SSiHDDS=HDDS+SSi(p,q);ZF=['SS(',num2str(p),',',num2str(q),')=',num2str(SSi(p,q))];disp(ZF);enddisp('环网总网损为；');ZH=['HDDS=',num2str(HDDS)];disp(ZH);%环网总网耗ZSS=HDDS+Fulloss;disp('总网损为：');ZSS五、额定电压不同时对系统参数的分析：（1）额定电压为240V：辐射网：环网：（2）额定电压为220V：辐射网：环网：（3）额定电压为200V：辐射网：环网：结果分析：240V时总损耗为0.8856KVA 220V时为0.95KVA 200V时为0.9828KVA电压等级越高，损耗越小。

１1． 手算过程已知：节点1：PQ 节点， s(1)= -0.5000-j0.3500 节点2：PV 节点， p(2)=0.4000 v(2)=1.0500 节点3：平衡节点，U(3)=1.0000∠0.0000 网络的连接图：0.0500+j0.2000 1 0.0500+j0.2000231）计算节点导纳矩阵由2000.00500.012j Z 71.418.112j y ;2000.00500.013j Z71.418.113j y ;导纳矩阵中的各元素：42.936.271.418.171.418.1131211j j j y y Y ;71.418.11212j y Y ; 71.418.11313j y Y; 21Y 71.418.11212j y Y ; 71.418.12122j y Y;002323j y Y;31Y 71.418.11313j y Y; 32Y 002323j y Y;71.418.13133j y Y;形成导纳矩阵BY ：71.418.10071.418.10071.418.171.418.171.418.171.418.142.936.2j j j j j j j j j Y B2）计算各PQ、PV 节点功率的不平衡量，及PV 节点电压的不平衡量：取:000.0000.1)0(1)0(1)0(1j jf e U000.0000.1)0(2)0(2)0(2j jf e U节点3是平衡节点，保持000.0000.1333j jf e U为定值。

nj j jij jij ijij jij i ieB fG f fB eG e P1)0()0()0()0()0()0()0(；２nj j jij jij ijij jij i ie B fG e f B eG f Q 1)0()0()0()0()0()0()0(；);(2)0(2)0(2)0(iiif e U)0.142.90.036.2(0.0)0.042.90.136.2(0.1)0(1P)0.171.40.018.1(0.0)0.071.40.118.1(0.1 )0.171.40.018.1(0.0)0.071.40.118.1(0.1 0.0 ；)0.142.90.036.2(0.1)0.042.90.136.2(0.0)0(1Q)0.171.40.018.1(0.1)0.071.40.118.1(0.0 )0.171.40.018.1(0.1)0.071.40.118.1(0.0 0.0 ；)0.171.40.018.1(0.0)0.071.40.118.1(0.1)0(2P)0.171.40.018.1(0.0)0.071.40.118.1(0.1 )0.00.00.00.0(0.0)0.10.00.10.0(0.1 0.0 ；101)(222)0(22)0(22)0(2f e U；于是：;)0()0(iiiP P P ;)0()0(iiiQQ Q);(2)0(2)0(22)0(iiiif e UU5.00.05.0)0(11)0(1P P P ;35.00.035.0)0(11)0(1QQ Q;4.00.04.0)0(22)0(2P P P ;1025.0)01(05.1)(2222)0(22)0(2222)0(2f e UU3）计算雅可比矩阵中各元素雅可比矩阵的各个元素分别为：３ji ij ji ij j i ij j i ij ji ij j i ij e U S f U R e Q L f Q J e P N f P H 22;;; 又： nj j jij jij i jij jij i ieB fG f fB eG e P1)0()0()0()0()0()0()0(； nj j jij jij ijij jij iieB fG e fB eG f Q 1)0()0()0()0()0()0()0(；);(2)0(2)0(2)0(iiif e U)0(1P )0(111)0(111)0(1)0(111)0(111)0(1e Bf G f f B e G e)0(212)0(212)0(1)0(212)0(212)0(1e B fG f f B e G e313313)0(1313313)0(1e Bf G f f B e G e ；)()()0(111)0(111)0(1)0(111)0(111)0(1)0(1e Bf Ge f B e G f Q)()()0(212)0(212)0(1)0(212)0(212)0(1e Bf G e f B e G f)()(313313)0(1313313)0(1e Bf G e f B e G f；)0(2P )0(121)0(121)0(2)0(121)0(121)0(2e Bf G f f B e G e)0(222)0(222)0(2)0(222)0(222)0(2eB fG f fBeG e323323)0(2323323)0(2e Bf G f f B e G e ；)(2)0(22)0(22)0(2f e U42.90.171.40.171.4313)0(212)0(1)0(1)0(11e B e Bf P H ； 36.20.118.10.118.10.136.222313)0(212)0(111)0(1)0(1)0(11 e G e G e G e P N 36.20.118.10.118.1313)0(212)0(1)0(1)0(11 e G e G f Q J４42.90.171.40.171.40.142.922313)0(212)0(111)0(1)0(1)0(11 e B e B e B e Q L 71.40.171.4)0(112)0(2)0(1)0(12 e B f P H ； 18.10.118.1)0(112)0(2)0(1)0(12 e G e P N ； 18.10.118.1)0(112)0(2)0(1)0(12 e G f Q J ；71.40.171.4)0(112)0(2)0(1)0(12 e B e Q L ； 71.40.171.4)0(221)0(1)0(2)0(21 e B f P H ； 11.40.111.4)0(221)0(1)0(2)0(21 e G e P N ； 0)0(12)0(2)0(21 f U R ； 0)0(12)0(2)0(21 e U S ； 71.40.10.00.171.4323)0(121)0(2)0(2)0(22 e B e B f P H ； 18.10.10.00.118.10.118.122323)0(121)0(222)0(2)0(2)0(22 e G e G e G e P N ；02)0(2)0(22)0(2)0(22 f f U R ； 0.20.122)0(2)0(22)0(2)0(22 e e U S ； 得到K=0时的雅可比矩阵：0.200018.171.418.171.471.418.142.936.218.171.436.242.9)0(J4）建立修正方程组：５)0(2)0(2)0(1)0(10.200011.4959.1011.4959.10959.1011.4918.2122.811.4959.1022.8918.210975.04.035.08.0e f e f 解得：04875.001828.00504.00176.0)0(2)0(2)0(1)0(1e f e f 因为 )0()0()1(iiie e e ； )0()0()1(iiif f f ；所以 9782.00218.00.1)0(1)0(1)1(1e e e ； 0158.00158.00)0(1)0(1)1(1f f f ；05125.105125.00.1)0(2)0(2)1(2e e e ；05085.005085.00)0(2)0(2)1(2f f f ；5）运用各节点电压的新值进行下一次迭代：即取: 0158.09782.0)1(1)1(1)1(1j jf e U05085.005125.1)1(2)1(2)1(2j jf e U节点3时平衡节点，保持000.0000.1333j jf e U为定值。

潮流计算研究报告一、潮流计算概述电力工业是国民经济的基础产业,为保证电力系统安全、稳定及可靠的运行,首先需计算电力系统网络潮流。

潮流计算指根据给定的电力系统运行条件及系统接线情况确定整个电力系统各部分的运行状态:各母线电压、各元件流过的功率及系统功率损耗等等。

在电力系统规划、设计及运行方式的研究中,都需要利用潮流计算来定量地分析比较供电方案或运行方式的合理性、可靠性及经济性,所以潮流计算是研究电力系统的一种很重要和很基础的计算。

在数学上潮流计算问题是一组多元非线性方程式求解问题,其解法离不开迭代。

二、潮流计算算法框图三、节点分类本次设计采用直角坐标牛顿拉夫逊法，用C语言编制潮流计算程序。

牛顿法拉夫逊：把非线性方程式的求解过程变成反复对相应的线性方程式的求解过程，通常称为逐次线性化过程。

节点分类：1）平衡节点已知节点的电压幅值和相角，求有功和无功，一般设在调频厂（一个）。

2）PQ节点已知节点的有功、无功，求电压幅值和相角，一般设在变电所母线，按给定频率发电的电厂母线（多个）。

3）PV节点已知节点的有功和电压幅值，求无功和电压相角，一般设在有无功补偿的变电所母线，无功可调的发电厂母线（少个）。

四、基本公式1、节点注入电流2、节点功率3、不平衡量4、雅可比矩阵（1）i ≠ j时（2）i=j 时5、线路功率及损耗五、IEEE30拓扑结构IEEE30节点结构六、算法输入原始数据1、支路参数（支路数L=41）始端末端回线数线路类型线路电阻线路电抗线路电纳(B/2)/ 变比2 1 1 0 0.0192 0.0575 0.0528 03 1 1 0 0.0452 0.1852 0.0408 04 2 1 0 0.057 0.1737 0.0368 04 3 1 0 0.0132 0.0379 0.0084 05 2 1 0 0.0472 0.1983 0.0418 06 2 1 0 0.0581 0.1763 0.0374 06 4 1 0 0.0119 0.0414 0.009 07 5 1 0 0.046 0.116 0.0204 07 6 1 0 0.0267 0.082 0.017 08 6 1 0 0.012 0.042 0.009 06 9 1 1 0 0.208 0 0.9786 10 1 1 0 0.556 0 0.96911 9 1 0 0 0.208 0 010 9 1 0 0 0.11 0 04 12 1 1 0 0.256 0 0.93213 12 1 0 0 0.14 0 014 12 1 0 0.1231 0.2559 0 015 12 1 0 0.0662 0.1304 0 016 12 1 0 0.0945 0.1987 0 015 14 1 0 0.221 0.1997 0 017 16 1 0 0.0524 0.1923 0 018 15 1 0 0.1073 0.2185 0 019 18 1 0 0.0639 0.1292 0 020 19 1 0 0.034 0.068 0 020 10 1 0 0.0936 0.209 0 017 10 1 0 0.0324 0.0845 0 021 10 1 0 0.0348 0.0749 0 022 10 1 0 0.0727 0.1499 0 022 21 1 0 0.0116 0.0236 0 023 15 1 0 0.1 0.202 0 024 22 1 0 0.115 0.179 0 024 23 1 0 0.132 0.27 0 025 24 1 0 0.1885 0.3292 0 026 25 1 0 0.2544 0.38 0 027 25 1 0 0.1093 0.2087 0 028 27 1 1 0 0.396 0 0.96829 27 1 0 0.2198 0.4153 0 030 27 1 0 0.3202 0.6027 0 030 29 1 0 0.2399 0.4533 0 028 8 1 0 0.0636 0.2 0.0428 028 6 1 0 0.0169 0.0599 0.013 02、节点参数（节点数N=30）编号节点类型电压实部电压虚部负荷有功负荷无功发电有功发电无功PV节点的V 并联电容1 1 1.05 0 0 0 0 0 1.05 02 3 1.045 0 0.217 0.127 0.8 0 1.045 03 2 1 0 0.024 0.012 0 0 1 04 2 1 0 0.076 0.016 0 0 1 05 3 1.01 0 0.942 0.190 0.5 0 1.01 06 2 1 0 0 0 0 0 1 07 2 1 0 0.228 0.109 0 0 1 08 3 1.01 0 0.30 0.30 0.2 0 1.01 09 2 1 0 0 0 0 0 1 010 2 1 0 0.058 0.02 0 0 1 0.1911 3 1.05 0 0 0 0.2 0 1.05 012 2 1 0 0.112 0.075 0 0 1 013 3 1.05 0 0 0 0.2 0 1.05 014 2 1 0 0.062 0.016 0 0 1 015 2 1 0 0.082 0.025 0 0 1 016 2 1 0 0.035 0.018 0 0 1 017 2 1 0 0.09 0.058 0 0 1 018 2 1 0 0.032 0.009 0 0 1 019 2 1 0 0.095 0.034 0 0 1 020 2 1 0 0.022 0.007 0 0 1 021 2 1 0 0.175 0.112 0 0 1 022 2 1 0 0 0 0 0 1 023 2 1 0 0.032 0.016 0 0 1 024 2 1 0 0.087 0.067 0 0 1 0.04325 2 1 0 0 0 0 0 1 026 2 1 0 0.035 0.023 0 0 1 027 2 1 0 0 0 0 0 1 028 2 1 0 0 0 0 0 1 029 2 1 0 0.024 0.009 0 0 1 0302 1 0 0.106 0.019 0 0 1 0七、潮流程序#include<iostream.h>#include<fstream.h>#include <iomanip.h> //使用setw函数#include<math.h>#include "stdlib.h"#include<stdio.h>#include "math.h"#include <iostream>#include <stdio.h>#include <tchar.h>#include <fstream>#include <cmath>#include <process.h>#include <math.h>#include <malloc.h>using namespace std;void main(){FILE *fp;fp=fopen("result.txt","w");ifstream fin;fin.open("node information.txt");int node_num;fin>>node_num;int n = node_num*(node_num-1);int Jocabi_rank=2*(node_num-1);double * * Jocabi=new double * [Jocabi_rank];int *II=new int[n];int *JJ=new int[n];double *WR=new double[n];double *WX=new double[n];double *WXC=new double[n];double *WNT=new double[n];for(int i=0;i<n;i++){II[i]=0;JJ[i]=0;WR[i]=0;WX[i]=0;WXC[i]=0;WNT[i]=0;}double *GF=new double[n];for(int GF_i=0;GF_i<=n;GF_i++)GF[GF_i]=0;double *BF=new double[n];for(int BF_i=0;BF_i<=n;BF_i++)BF[BF_i]=0;double * * GF1=new double * [node_num+1];for (int GF1_i=0;GF1_i<node_num;GF1_i++){GF1[GF1_i]=new double[node_num+1];for (int GF1_j=0;GF1_j<node_num;GF1_j++){GF1[GF1_i][GF1_j]=0;}} double * * BF1=new double * [node_num+1];for (int BF1_i=0;BF1_i<=node_num;BF1_i++) {BF1[BF1_i]=new double[node_num+1];for (int BF1_j=0;BF1_j<node_num;BF1_j++) {BF1[BF1_i][BF1_j]=0;}} double *GD=new double[node_num];for(int GD_i=0;GD_i<=node_num;GD_i++){GD[GD_i]=0;}double *BD=new double[node_num];for(int BD_i=0;BD_i<=node_num;BD_i++){BD[BD_i]=0;}double * BC=new double[node_num];for(int BC_i=0;BC_i<=node_num;BC_i++){BC[BC_i]=0;}for(i=0;i<n;i++)fin>>II[i]>>JJ[i]>>WR[i]>>WX[i]>>WXC[i]>>WNT[i];//节点导纳矩阵int p,q;double K;for(i=0;i<n;i++){p=0;q=0;K=0.0;if(WNT[i]==0){GF[i]=WR[i]/(WR[i]*WR[i]+WX[i]*WX[i]);BF[i]=(-WX[i])/(WR[i]*WR[i]+WX[i]*WX[i]);}if(WNT[i]>0){K=WNT[i];p=II[i];GF[i]=(WR[i]/(WR[i]*WR[i]+WX[i]*WX[i]))/K;BF[i]=((-WX[i])/(WR[i]*WR[i]+WX[i]*WX[i]))/K;GD[p-1]=GD[p-1]+((K-1)/K)*(WR[i]/(WR[i]*WR[i]+WX[i]*WX[i]));BD[p-1]=BD[p-1]+((K-1)/K)*(-WX[i])/(WR[i]*WR[i]+WX[i]*WX[i]);}if(WNT[i]<0){K=fabs(WNT[i]);q=JJ[i];GF[i]=(WR[i]/(WR[i]*WR[i]+WX[i]*WX[i]))/K;BF[i]=((-WX[i])/(WR[i]*WR[i]+WX[i]*WX[i]))/K;GD[q-1]=GD[q-1]+((1-K)/(K*K))*WR[i]/(WR[i]*WR[i]+WX[i]*WX[i]);BD[q-1]=BD[q-1]+((1-K)/(K*K))*(-WX[i])/(WR[i]*WR[i]+WX[i]*WX[i]);}}for(int I=1;I<=node_num;I++){BC[I-1]=0.0;for(int i=0;i<n;i++){int J=0;if(II[i]==I){if(WXC[i]<1000)BC[I-1]=BC[I-1]+WXC[i];J=JJ[i];GF1[I-1][J-1]=-GF[i];BF1[I-1][J-1]=-BF[i];GF1[I-1][I-1]=GF1[I-1][I-1]+GF[i];BF1[I-1][I-1]=BF1[I-1][I-1]+BF[i];}}GF1[I-1][I-1]=GF1[I-1][I-1]+GD[I-1];BF1[I-1][I-1]=BF1[I-1][I-1]+BD[I-1]+BC[I-1];} //输出节点导纳矩阵fprintf(fp,"节点导纳矩阵是： \n");for(int m=0;m<node_num;m++){for(int n=0;n<node_num;n++){fprintf(fp,"%9.6f",GF1[m][n]);fprintf(fp,"+j");fprintf(fp,"%9.6f",BF1[m][n]);fprintf(fp," ");}fprintf(fp,"\n");}fprintf(fp,"\n");fprintf(fp,"\n");fprintf(fp,"\n");//$$$$$$$$$$$$$$$$$输出节点导纳矩阵完毕$$$$$$$$$$$$$$$$$$$$$//$$$$$$$$$$$$$$$$$$$求节点初始差值$$$$$$$$$$$$$$$$$$$$$$$$$ double *wv=new double [node_num];double *we=new double [node_num];double *wf=new double [node_num];double *wp_g=new double [node_num];double *wq_g=new double [node_num];double *wp_l=new double [node_num];double *wq_l=new double [node_num];double *wn=new double [node_num];for(int p_i=0;p_i<node_num;p_i++){wv[p_i]=0;we[p_i]=0;wf[p_i]=0;wp_g[p_i]=0;wq_g[p_i]=0;wp_l[p_i]=0;wq_l[p_i]=0;wn[p_i]=0;}double * dp=new double [node_num];for (int dp_i=0;dp_i<node_num;dp_i++)dp[dp_i]=0;double * dq=new double [node_num];for (int dq_i=0;dq_i<node_num;dq_i++)dq[dq_i]=0;double * dvv=new double [node_num];for (int dvv_i=0;dvv_i<node_num;dvv_i++)dvv[dvv_i]=0;double * sm=new double [node_num];double * sn=new double [node_num];int n_m=0 ;ifstream ffin;ffin.open("node power.txt");for(int pi=0;pi<node_num;pi++){ffin>>wp_g[pi]>>wq_g[pi]>>wp_l[pi]>>wq_l[pi]>>we[pi]>>wf[pi]>> wn[pi];}for(int wv_i=0;wv_i<node_num;wv_i++){wv[wv_i]=we[wv_i];}double * w_p=new double [node_num];double * w_q=new double [node_num];for (int w_i=0;w_i<node_num;w_i++){w_p[w_i]=0;w_q[w_i]=0;}//开始迭代，次数为iterative_frequencyfor (intiterative_frequency=0;iterative_frequency<12;iterative_frequency++) {fprintf(fp,"第[");fprintf(fp,"%2d",iterative_frequency);fprintf(fp,"]次迭代结果如下：");fprintf(fp,"\n");n_m=0;for(int Jocabi_i=0;Jocabi_i<Jocabi_rank;Jocabi_i++){Jocabi[Jocabi_i]=new double[Jocabi_rank];for(int Jocabi_j=0;Jocabi_j<Jocabi_rank;Jocabi_j++)Jocabi[Jocabi_i][Jocabi_j]=0;}for(i=0;i<node_num;i++){sm[i]=0;sn[i]=0;}for(i=0;i<node_num;i++){if(wn[i]==1){for(int j=0;j<node_num;j++){sm[i]=sm[i]+(GF1[i][j]*we[j]-BF1[i][j]*wf[j]);sn[i]=sn[i]+(GF1[i][j]*wf[j]+BF1[i][j]*we[j]);}dp[i]=wp_l[i]-we[i]*sm[i]-wf[i]*sn[i];dq[i]=wq_l[i]-wf[i]*sm[i]+we[i]*sn[i];n_m++;}if(wn[i]==2){for(int j=0;j<node_num;j++){sm[i]=sm[i]+(GF1[i][j]*we[j]-BF1[i][j]*wf[j]);sn[i]=sn[i]+(GF1[i][j]*wf[j]+BF1[i][j]*we[j]);}dp[i]=wp_g[i]-we[i]*sm[i]-wf[i]*sn[i];dvv[i]=wv[i]*wv[i]-(we[i]*we[i]+wf[i]*wf[i]);w_p[i]=we[i]*sm[i]+wf[i]*sn[i];w_q[i]=wf[i]*sm[i]-we[i]*sn[i];fprintf(fp,"第[" );fprintf(fp,"%2d",i+1 );fprintf(fp, "]个节点是PV节点，且其节点功率为：");fprintf(fp,"%9.6f",w_p[i]);fprintf(fp,"+j" );fprintf(fp,"%9.6f",w_q[i]);fprintf(fp,"\n" );} if(wn[i]==0){for(int j=0;j<node_num;j++){sm[i]=sm[i]+(we[j]*GF1[i][j]-wf[j]*BF1[i][j]);sn[i]=sn[i]+(wf[j]*GF1[i][j]+we[j]*BF1[i][j]);}w_p[i]=we[i]*sm[i]+wf[i]*sn[i];;w_q[i]=wf[i]*sm[i]-we[i]*sn[i];fprintf(fp,"第[" );fprintf(fp,"%2d",i+1 );fprintf(fp, "]个节点是平衡节点，其节点功率为：");fprintf(fp,"%9.6f",w_p[i]);fprintf(fp,"+j" );fprintf(fp,"%9.6f",w_q[i]);fprintf(fp,"\n" );} //$$$$$$$$$$$$$$$$$$$$求Jocabi矩阵$$$$$$$$$$$$$$$$$$$$$for(int j=0;j<node_num;j++){if(j==i&&wn[i]==1){Jocabi[2*i][2*j]=-sm[i]-GF1[i][i]*we[i]-BF1[i][i]*wf[i]; Jocabi[2*i][2*j+1]=-sn[i]+BF1[i][i]*we[i]-GF1[i][i]*wf[i]; Jocabi[2*i+1][2*j]=sn[i]+BF1[i][i]*we[i]-GF1[i][i]*wf[i]; Jocabi[2*i+1][2*j+1]=-sm[i]+GF1[i][i]*we[i]+BF1[i][i]*wf[i];} if(j==i&&wn[i]==2){Jocabi[2*i][2*j]=-sm[i]-GF1[i][i]*we[i]-BF1[i][i]*wf[i]; Jocabi[2*i][2*j+1]=-sn[i]+BF1[i][i]*we[i]-GF1[i][i]*wf[i]; Jocabi[2*i+1][2*j]=(-2)*we[i];Jocabi[2*i+1][2*j+1]=(-2)*wf[i];} if(j!=i&&wn[i]==1){Jocabi[2*i][2*j]=(-1)*(GF1[i][j]*we[i]+BF1[i][j]*wf[i]);Jocabi[2*i][2*j+1]=BF1[i][j]*we[j]-GF1[i][j]*wf[i];Jocabi[2*i+1][2*j]=BF1[i][j]*we[j]-GF1[i][j]*wf[i];Jocabi[2*i+1][2*j+1]=GF1[i][j]*we[i]+BF1[i][j]*wf[i];} if(j!=i&&wn[i]==2){Jocabi[2*i][2*j]=(-1)*(GF1[i][j]*we[i]+BF1[i][j]*wf[i]);Jocabi[2*i][2*j+1]=BF1[i][j]*we[j]-GF1[i][j]*wf[i];Jocabi[2*i+1][2*j]=0;Jocabi[2*i+1][2*j+1]=0;}}} //$$$$$$$$$$$$$$$$$$$高斯法解方程$$$$$$$$$$$$$$$$$$$$$$$$$$$$$ double * Dalta_w=new double[Jocabi_rank];for(i=0;i<node_num;i++){if(wn[i]==1){Dalta_w[2*i]=dp[i];Dalta_w[2*i+1]=dq[i];}if(wn[i]==2){Dalta_w[2*i]=dp[i];Dalta_w[2*i+1]=dvv[i];}}double * M=new double[Jocabi_rank];double * X=new double[Jocabi_rank];for(i=0;i<Jocabi_rank;i++){X[i]=0;M[i]=0;}double t;int * js=new int [Jocabi_rank];for(i=0;i<Jocabi_rank;i++)js[i]=0;//交换Jocabi矩阵的行，使每列的对角线元素为所有行中最大的元素double * temp_swap_vector=new double[Jocabi_rank+1];for(inttemp_swap_vector_i=0;temp_swap_vector_i<Jocabi_rank;temp_swap_vector_ i++)temp_swap_vector[temp_swap_vector_i]=0;double temp_variable_for_compare=0;int temp_line=0;for(int diagonal_i=0;diagonal_i<Jocabi_rank;diagonal_i++){temp_variable_for_compare=Jocabi[diagonal_i][diagonal_i];for(intJocabi_line=diagonal_i;Jocabi_line<Jocabi_rank;Jocabi_line++) {if(temp_variable_for_compare<fabs(Jocabi[Jocabi_line][diagonal _i])){temp_variable_for_compare=fabs(Jocabi[Jocabi_line][diagonal_i] );temp_line=Jocabi_line;for(int Jocabi_j_j=0;Jocabi_j_j<Jocabi_rank;Jocabi_j_j++) {temp_swap_vector[Jocabi_j_j]=Jocabi[diagonal_i][Jocabi_j_j];Jocabi[diagonal_i][Jocabi_j_j]=Jocabi[temp_line][Jocabi_j_j];Jocabi[temp_line][Jocabi_j_j]=temp_swap_vector[Jocabi_j_j];}t=Dalta_w[diagonal_i];Dalta_w[diagonal_i]=Dalta_w[temp_line];Dalta_w[temp_line]=t;}}}//$$$$$$$$$$$$$$交换Jocabi矩阵的行完毕$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$ double * * temp=new double * [Jocabi_rank];for(i=0;i<Jocabi_rank;i++){temp[i]=new double[Jocabi_rank];for(int j=0;j<Jocabi_rank;j++)temp[i][j]=0.0;}for(int k=0;k<Jocabi_rank;k++){if(Jocabi[k][k]==0) cout<<"fail"<<endl;else{temp[k][k]=Jocabi[k][k];for(int j=0;j<Jocabi_rank;j++)Jocabi[k][j]=Jocabi[k][j]/temp[k][k];Dalta_w[k]=Dalta_w[k]/temp[k][k];for(int ii=k+1;ii<Jocabi_rank;ii++){M[ii]=0.0;M[ii]=Jocabi[ii][k];for(int jj=k;jj<Jocabi_rank;jj++)Jocabi[ii][jj]=Jocabi[ii][jj]-M[ii]*Jocabi[k][jj];Dalta_w[ii]=Dalta_w[ii]-M[ii]*Dalta_w[k];}}} X[Jocabi_rank-1]=Dalta_w[Jocabi_rank-1]/(-Jocabi[Jocabi_rank-1][J ocabi_rank-1]);for(i=Jocabi_rank-2;i>=0;i--){t=0;for(k=i+1;k<Jocabi_rank;k++){t=t+(-Jocabi[i][k])*X[k];}X[i]=(Dalta_w[i]-t)/(-Jocabi[i][i]);}for(i=0;i<node_num;i++){if(wn[i]==1){we[i]=we[i]+X[2*i];wf[i]=wf[i]+X[2*i+1];fprintf(fp,"第[");fprintf(fp,"%2d",i+1);fprintf(fp,"]个节点是PQ节点其节点电压实部修正量是：");fprintf(fp,"%9.6f",X[2*i]);fprintf(fp," 其节点电压虚部修正量是：");fprintf(fp,"%9.6f",X[2*i+1]);fprintf(fp,"\n");} if(wn[i]==2){we[i]=we[i]+X[2*i];wf[i]=wf[i]+X[2*i+1];fprintf(fp,"第[");fprintf(fp,"%2d",i+1);fprintf(fp,"]个节点是PV节点其节点电压实部修正量是：");fprintf(fp,"%9.6f",X[2*i]);fprintf(fp," 其节点电压虚部修正量是：");fprintf(fp,"%9.6f",X[2*i+1]);fprintf(fp,"\n");}} fprintf(fp,"\n");fprintf(fp,"\n");//$$$$$$$$$$$$$$$$判断是否收敛并求最后的差值$$$$$$$$$$$$$$$$$$$$$$ double ch=0;double * * s_p=new double * [node_num+1];for(int s_p_i=1;s_p_i<=node_num+1;s_p_i++){s_p[s_p_i]=new double[node_num+1];for(int s_p_j=1;s_p_j<=node_num+1;s_p_j++)s_p[s_p_i][s_p_j]=0;}double * * s_q=new double * [node_num+1];for(int s_q_i=1;s_q_i<=node_num+1;s_q_i++){s_q[s_q_i]=new double[node_num+1];for(int s_q_j=1;s_q_j<=node_num+1;s_q_j++)s_q[s_q_i][s_q_j]=0;}for(int ci=1;ci<=node_num-1;ci++){if((fabs(Dalta_w[ci]))>(fabs(ch))){ch=fabs(Dalta_w[ci]);}}fprintf(fp,"判断是否迭代的最大值是:");fprintf(fp,"%9.6f",ch);fprintf(fp,"\n");fprintf(fp,"\n");if(ch<1e-005){double *UU=new double [node_num];for(int k=0;k<node_num;k++)UU[k]=0.0;for(k=0;k<node_num;k++)UU[k]=we[k]*we[k]+wf[k]*wf[k];double *G_ground=new double [n];double *B_ground=new double [n];for(int i=0;i<n;i++){G_ground[i]=0;B_ground[i]=0;}cout<<"满足迭代要求，计算完成，迭代次数是"<<iterative_frequency<<endl;fprintf(fp,"||||||||||||||||||||||||||||||||||||||||||||||||||||| ||||||||\n");fprintf(fp,"\n");fprintf(fp,"满足迭代要求，计算完成，迭代次数是");fprintf(fp,"%2d",iterative_frequency);fprintf(fp,"\n");for(i=0;i<node_num;i++){fprintf(fp,"节点");fprintf(fp,"[");fprintf(fp,"%2d",i+1);fprintf(fp,"]的电压是：");fprintf(fp,"%9.6f",we[i]);if(wf[i]>0){fprintf(fp," + j");fprintf(fp,"%9.6f",wf[i]);}if(wf[i]<0){fprintf(fp," - j");fprintf(fp,"%9.6f",fabs(wf[i]));}fprintf(fp," 幅值是：");fprintf(fp,"%9.6f",sqrt(we[i]*we[i]+wf[i]*wf[i]));fprintf(fp," 相角是：");fprintf(fp,"%9.6f",atan(wf[i]/we[i])*180/3.1415926);fprintf(fp,"度");fprintf(fp,"\n");}fprintf(fp,"线路功率是:\n");for(int j=0;j<n;j++){double K=0.0;int p=0;int q=0;p=II[j];q=JJ[j];if(p==0&&q==0)break;GF[j]=WR[j]/(WR[j]*WR[j]+WX[j]*WX[j]);BF[j]=(-WX[j])/(WR[j]*WR[j]+WX[j]*WX[j]);if(WNT[j]<0){K=fabs(WNT[j]);G_ground[j]=((1-K)/(K*K))*GF[j];B_ground[j]=((1-K)/(K*K))*BF[j];}if(WNT[j]>0){K=WNT[j];G_ground[j]=((K-1)/K)*GF[j];B_ground[j]=((K-1)/K)*BF[j];}if(WXC[j]<1000)B_ground[j]=B_ground[j]+WXC[j];s_p[p][q]=UU[p-1]*G_ground[j]+UU[p-1]*GF1[p-1][q-1]-(we[p-1]*we[q -1]+wf[p-1]*wf[q-1])*GF1[p-1][q-1]+(we[p-1]*wf[q-1]-we[q-1]*wf[p-1])*BF1[p-1][q-1];s_q[p][q]=-UU[p-1]*B_ground[j]-UU[p-1]*BF1[p-1][q-1]+(we[p-1]*we[ q-1]+wf[q-1]*wf[q-1])*BF1[p-1][q-1]+(we[p-1]*wf[q-1]-we[q-1]*wf[p-1])*GF1[p-1][q-1];fprintf(fp,"S[");fprintf(fp,"%2d",p);fprintf(fp,"][");fprintf(fp,"%2d",q);fprintf(fp,"]=");fprintf(fp,"%9.6f",s_p[p][q]);if(s_q[p][q]>0){fprintf(fp," + j");fprintf(fp,"%9.6f",s_q[p][q]);}if(s_q[p][q]<0){fprintf(fp," - j");fprintf(fp,"%9.6f",fabs(s_q[p][q]));}fprintf(fp,"\n");}break;}}//迭代结束八、IEEE30节点的仿真结果1、节点电压编号电压实部电压虚部电压幅值电压相角节点1 1.05 0i 1.05 0度节点2 1.04445 -0.0337697i 1.045 -1.85186度节点3 1.01843 -0.067472i 1.02066 -3.79037度节点4 1.01033 -0.0798977i 1.01348 -4.52159度节点5 1.0035 -0.114413i 1.01 -6.50445度节点6 1.00662 -0.0943613i 1.01104 -5.35528度节点7 0.996459 -0.111039i 1.00263 -6.35844度节点8 1.00511 -0.0993071i 1.01 -5.64266度节点9 1.03035 -0.122151i 1.03756 -6.76104度节点10 1.02229 -0.156054i 1.03413 -8.67927度节点11 1.04666 -0.0837098i 1.05 -4.57268度节点12 1.03608 -0.141734i 1.04573 -7.78959度节点13 1.0436 -0.115738i 1.05 -6.32836度节点14 1.01898 -0.156444i 1.03092 -8.72848度节点15 1.01403 -0.157951i 1.02626 -8.85357度节点16 1.02183 -0.151553i 1.033 -8.43636度节点17 1.01658 -0.157803i 1.02876 -8.82354度节点18 1.00279 -0.167848i 1.01674 -9.50214度节点19 0.999803 -0.170757i 1.01428 -9.69206度节点20 1.00449 -0.16805i 1.01845 -9.49755度节点21 1.00872 -0.162656i 1.02175 -9.16004度节点22 1.00931 -0.162655i 1.02234 -9.15476度节点23 1.00254 -0.16504i 1.01604 -9.34827度节点24 0.996609 -0.169594i 1.01094 -9.65755度节点25 0.995082 -0.169371i 1.00939 -9.65966度节点26 0.976247 -0.173651i 0.991571 -10.0861度节点27 1.00354 -0.166036i 1.01718 -9.3945度节点28 1.00168 -0.102188i 1.00688 -5.82495度节点29 0.980068 -0.184114i 0.997212 -10.6395度节点30 0.96576 -0.197073i 0.985662 -11.5334度2、线路传输功率首端—末端首末功率末首功率2-1 -57.9109+(8.36395)i 58.5228+(-12.325)i3-1 -39.536+(-7.37948)i 40.2261+(5.83313)i4-2 -30.8909+(-9.48018)i 31.4524+(7.29204)i4-3 -36.9557+(-6.53076)i 37.136+(6.17948)i5-2 -44.4784+(-7.6178)i 45.4077+(7.10769)i6-2 -38.4904+(-7.58429)i 39.3508+(6.2414)i6-4 -34.7811+(4.04816)i 34.9241+(-4.02213)i 7-5 -0.260435+(-7.29197)i 0.278436+(5.2715)i7-6 -22.5396+(-3.60803)i 22.6765+(2.30528)i8-6 -11.9244+(0.486521)i 11.9413+(-1.34664)i 6-9 12.3726+(-12.7417)i -12.3726+(13.3835)i6-10 10.9034+(-3.88366)i -10.9034+(4.61235)i 11-9 20+(6.66081)i -20+(-5.82246)i10-9 -32.6509+(-2.67651)i 32.6509+(3.78043)i4-12 23.6005+(-12.0947)i -23.6005+(13.8474)i 13-12 20+(3.45425)i -20+(-2.93116)i14-12 -7.91606+(-2.10553)i 7.99377+(2.26709)i15-12 -18.28+(-5.90486)i 18.5119+(6.36176)i16-12 -7.55825+(-2.98863)i 7.61675+(3.11163)i15-14 -1.7094+(-0.499524)i 1.71605+(0.505537)i 17-16 -4.04947+(-1.1564)i 4.05825+(1.18863)i18-15 -6.09617+(-1.40631)i 6.13679+(1.48904)i19-18 -2.89082+(-0.495509)i 2.89617+(0.506313)i 20-19 6.6264+(2.93893)i -6.60918+(-2.90448)i 20-10 -8.82641+(-3.63893)i 8.90866+(3.82259)i17-10 -4.95054+(-4.64359)i 4.96464+(4.68038)i21-10 -16.1704+(-9.32613)i 16.2865+(9.57613)i22-10 -7.88783+(-4.19568)i 7.94335+(4.31016)i22-21 1.33022+(1.87505)i -1.32963+(-1.87386)i 23-15 -5.6167+(-2.34288)i 5.65258+(2.41535)i24-22 -6.50437+(-2.23775)i 6.55761+(2.32062)i24-23 -2.40853+(-0.726163)i 2.4167+(0.742882)i25-24 -0.212582+(-0.351348)i 0.212894+(0.351893)i 26-25 -3.5+(-2.29999)i 3.54539+(2.36778)i27-25 3.34908+(2.04752)i -3.3328+(-2.01643)i 28-27 16.1025+(-2.11682)i -16.1025+(3.14712)i 29-27 -6.10422+(-1.50686)i 6.1916+(1.67196)i30-27 -6.92977+(-1.35732)i 7.09411+(1.66665)i30-29 -3.67023+(-0.542645)i 3.70422+(0.60687)i28-8 -1.92156+(-3.12492)i 1.92445+(-1.21858)i28-6 -14.7132+(-3.43133)i 14.7506+(2.24037)i 3、发电机注入的功率编号功率实部功率虚部节点1 98.7489 -6.4919i 节点2 80 41.7051i 节点5 50 16.6537i 节点8 20 29.2679i 节点11 20 6.66081i 节点13 20 3.45425i。

摘要本文运用MATLAB软件进行潮流计算，对给定题目进行分析计算，再应用DDRTS软件，构建系统图进行仿真，最终得到合理的系统潮流。

潮流计算是电力系统最基本最常用的计算。

根据系统给定的运行条件，网络接线及元件参数，通过潮流计算可以确定各母线的电压幅值和相角，各元件流过的功率，整个系统的功率损耗。

潮流计算是实现电力系统安全经济发供电的必要手段和重要工作环节。

因此，潮流计算在电力系统的规划计算，生产运行，调度管理及科学计算中都有着广泛的应用。

首先，画出系统的等效电路图，在计算出各元件参数的基础上，应用牛顿—拉夫逊Newton-Raphson法以及MATLAB软件进行计算对给定系统图进行了四种不同负荷下的潮流计算，经过调节均得到符合电压限制及功率限制的潮流分布。

其次，轮流断开环网的三条支路，在新的系统结构下进行次潮流计算，结果亦均满足潮流分布要求。

牛顿—拉夫逊Newton-Raphson法具有较好的收敛性，上诉计算过程经过四到五次迭代后均能收敛。

最后，应用DDRTS软件，构建系统图，对给定负荷重新进行分析，潮流计算后的结果也能满足相应的参数要求。

关键词：牛顿—拉夫逊法MATLAB PSAT 潮流计算一、 题目原始资料1、系统图：两个发电厂分别通过变压器和输电线路与四个变电所相连。

2、发电厂资料：母线1和2为发电厂高压母线，发电厂一总装机容量为（ 400MW ），母线3为机压母线，机压母线上装机容量为（ 100MW ），最大负荷和最小负荷分别为50MW 和30MW ；发电厂二总装机容量为（200MW ）。

3、变电所资料：(一) 变电所1、2、3、4低压母线的电压等级分别为：10KV 35KV 10KV35KV(二) 变电所的负荷分别为：40MW 60MW 50MW 60MW (三) 每个变电所的功率因数均为cos φ=0.85；(四) 变电所2和变电所4分别配有两台容量为75MV A 的变压器，短路损耗变电所1 变电所2母线 电厂一电厂二414KW ，短路电压（%）=16.7；变电所1和变电所3分别配有两台容量为63MV A 的变压器，短路损耗为245KW ，短路电压（%）=10.5；4、输电线路资料：发电厂和变电所之间的输电线路的电压等级及长度标于图中，单位长度的电阻为Ω17.0，单位长度的电抗为Ω0.402，单位长度的电纳为S -610*2.78。