四川省成都市高中2010届高三一诊(数学理)word版

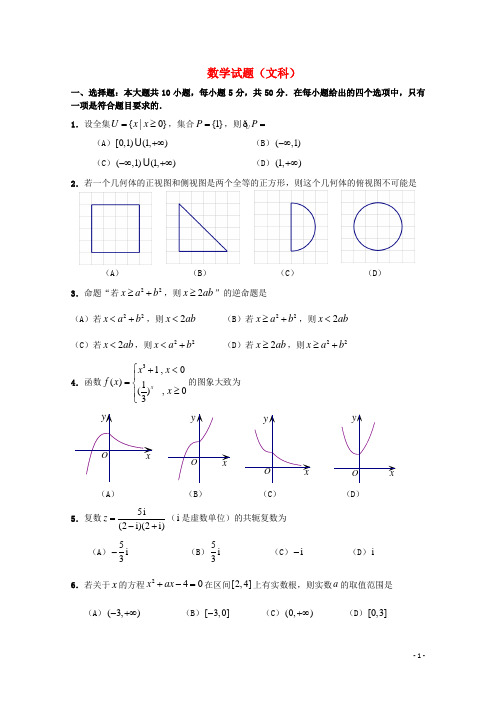
数学试题（文科）一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．设全集{|0}=≥U x x，集合{1}=P，则UP=ð（A）[0,1)(1,)+∞（B）(,1)-∞（C）(,1)(1,)-∞+∞（D）(1,)+∞2．若一个几何体的正视图和侧视图是两个全等的正方形，则这个几何体的俯视图不可能是（A）（B）（C）（D）3．命题“若22≥+x a b，则2≥x ab”的逆命题是（A）若22<+x a b，则2<x ab（B）若22≥+x a b，则2<x ab（C）若2<x ab，则22<+x a b（D）若2≥x ab，则22≥+x a b4．函数31,0()1(),03xx xf xx⎧+<⎪=⎨≥⎪⎩的图象大致为（A）（B）（C）（D）5．复数5i(2i)(2i)=-+z（i是虚数单位）的共轭复数为（A）5i3-（B）5i3（C）i-（D）i6．若关于x的方程240+-=x ax在区间[2,4]上有实数根，则实数a的取值范围是（A）(3,)-+∞（B）[3,0]-（C）(0,)+∞（D）[0,3]消费支出/元7．已知53cos()25+=πα，02-<<πα，则sin 2α的值是（A ）2425 （B ）1225 （C ）1225- （D ）2425-8．已知抛物线:C 28y x =，过点(2,0)P 的直线与抛物线交于A ，B 两点，O 为坐标原点，则OA OB ⋅的值为（A ）16- （B ）12- （C ）4 （D ）0 9．已知m ，n 是两条不同直线，α，β是两个不同的平面，且n ⊂β，则下列叙述正确的是（A ）若//m n ，m ⊂α，则//αβ （B ）若//αβ，m ⊂α，则//m n （C ）若//m n ，m α⊥，则αβ⊥ （D ）若//αβ，m n ⊥，则m α⊥10．如图，已知正方体1111ABCD A B C D -棱长为4，点H 在棱1AA 上，且11HA =．点E ，F 分别为棱11B C ，1C C 的中点，P 是侧面11BCC B 内一动点，且满足⊥PE PF .则当点P 运动时， 2HP 的最小值是 （A）7（B）27-（C）51-（D）14-二、填空题：本大题共5小题，每小题5分，共25分． 11．已知100名学生某月饮料消费支出情况的频率分布直方图如右图所示.则这100名学生中，该月饮料消费支出超过150元的人数是________．12．若非零向量a ，b 满足a b a b +=-，则a ，b 的夹角的大小为__________．ABCD1A 1B 1C 1D HPEF13．在∆ABC 中，内角,,A B C 的对边分别为,,a b c ，若2=c a ，4=b ，1cos 4=B ．则边c 的长度为__________．14．已知关于x 的不等式()(2)0---≤x a x a 的解集为A ，集合{|22}=-≤≤B x x ．若“x A ∈”是“x B ∈”的充分不必要条件，则实数a 的取值范围是__________． 15．已知函数21()()2f x x a =+的图象在点n P (,())n f n （*n ∈N ）处的切线n l 的斜率为n k ，直线n l 交x 轴，y 轴分别于点(,0)n n A x ，(0,)n n B y ，且11y =-．给出以下结论： ①1a =-；②记函数()=n g n x （*n ∈N ），则函数()g n 的单调性是先减后增，且最小值为1；③当*n ∈N 时，1ln(1)2n n n y k k++<+； ④当*n ∈N 时，记数列的前n 项和为n S ，则n S <． 其中，正确的结论有 （写出所有正确结论的序号）三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤． 16．（本小题满分12分）口袋中装有除编号外其余完全相同的5个小球，编号依次为1,2,3,4,5．现从中同时取出两个球，分别记录下其编号为,m n ． （Ⅰ）求“5+=m n ”的概率； （Ⅱ）求“5≥mn ”的概率．17．（本小题满分12分）如图，在多面体ECABD 中，EC ⊥平面ABC ，//DB EC ，ABC ∆为正三角形，F 为EA 的中点，2EC AC ==，1BD =．（Ⅰ）求证：DF //平面ABC ； （Ⅱ）求多面体ECABD 的体积． 18．（本小题满分12分）已知数列{}n a 的前n 项和为n S ，且122+=-n n S ；数列{}n b 满足11b =，12n n b b +=+．*n ∈N .（Ⅰ）求数列{}n a 和{}n b 的通项公式；（Ⅱ）记n n n c a b =，*n ∈N .求数列{}n c 的前n 项和n T ． 19．（本小题满分12分）某大型企业一天中不同时刻的用电量y （单位：万千瓦时）关于时间t （024t ≤≤，单位：小时）的函数()y f t =近似地满足()sin()(0,0,0)f t A t B A ωϕωϕπ=++>><<，下图是该企业一天中在0点至12点时间段用电量y 与时间t 的大致图象．（Ⅰ）根据图象，求A ，ω，ϕ，B 的值； （Ⅱ）若某日的供电量()g t （万千瓦时）与时间t （小时）近似满足函数关系式205.1)(+-=t t g （012t ≤≤）．当该日内供电量小于该企业的用电量时，企业就必须停产．请用二分法计算该企业当日停产的大致时刻（精确度0.1）. 参考数据:20．（本小题满分13分）已知椭圆Γ：12222=+by a x （0>>b a ）的右焦点为)0,22(，且过点．（Ⅰ）求椭圆Γ的标准方程；（Ⅱ）设直线:()l y x m m =+∈R 与椭圆Γ交于不同两点A 、B ，且AB =0(,2)P x 满足=PA PB ，求0x 的值．21．（本小题满分14分） 已知函数()ln 2mf x x x=+，()2g x x m =-，其中m ∈R ，e 2.71828=为自然对数的底数．（Ⅰ）当1m =时，求函数()f x 的极小值；（Ⅱ）对1[,1]e x ∀∈，是否存在1(,1)2m ∈，使得()()1>+f x g x 成立？若存在，求出m 的取值范围；若不存在，请说明理由；（Ⅲ）设()()()F x f x g x =，当1(,1)2m ∈时，若函数()F x 存在,,a b c 三个零点，且a b c <<，求证： 101ea b c <<<<<．数学（文科）参考答案及评分意见第Ⅰ卷（选择题，共50分）一、选择题：（本大题共10个小题，每小题5分，共50分）1．A ； 2．C ； 3．D ；4．A ；5．C ；6．B ；7．D ；8．B ；9．C ；10．B ．第Ⅱ卷（非选择题，共100分）二、填空题：（本大题共5个小题，每小题5分，共25分） 11．30 12．90︒ 13．4 14.[2,0]- 15．①②④ 三、解答题：（本大题共6个小题,共75分） 16．（本小题满分12分）解：同时取出两个球，得到的编号,m n 可能为： (1,2)，(1,3)，(1,4)，(1,5) (2,3)，(2,4)，(2,5) (3,4)，(3,5)(4,5)…………………………………………………………………………………6分 （Ⅰ）记“5+=m n ”为事件A ，则 21()105==P A ．……………………………………………………………………………3分（Ⅱ）记“5≥mn ”为事件B ，则 37()11010=-=P B ．…………………………………………………………………… 3分 17．（本小题满分12分）（Ⅰ）证明：作AC 的中点O ，连结BO ．在∆AEC 中，//=FO 12EC ，又据题意知，//=BD 12EC ． ∴//=FO BD ，∴四边形FOBD 为平行四边形． ∴//DF OB ，又⊄DF 面ABC ，⊂OB 平面ABC ．∴//DF 面ABC ．………………………6分（Ⅱ）据题意知，多面体ECABD 为四棱锥-A ECBD ． 过点A 作⊥AH BC 于H ．∵⊥EC 平面ABC ，⊂EC 平面ECBD ，∴平面⊥ECBD 平面ABC ．又⊥AH BC ，⊂AH 平面ABC ，平面ECBD 平面=ABC BC ， ∴⊥AH 面ECBD ．∴在四棱锥-A ECBD 中，底面为直角梯形ECBD，高=AH ．∴1(21)232-+⨯=⨯A ECBD V ∴多面体ECABD6分 18.（本小题满分12分） 解：（Ⅰ）∵122+=-n n S当2≥n 时，122-=-n n S-得，2=n n a （2≥n ）．∵当2≥n 时，11222--==nn n n a a ，且12=a ．∴数列{}n a 是以2为首项，公比为2的等比数列，∴数列{}n a 的通项公式为1222-=⋅=n n n a ．………………………………………4分 又由题意知，11b =，12n n b b +=+，即12+-=n n b b ∴数列{}n b 是首项为1，公差为2的等差数列，∴数列{}n b 的通项公式为1(1)221=+-⨯=-n b n n ．……………………………2分 （Ⅱ）由（Ⅰ）知，(21)2=-n n c n ……………………………………………………1分 ∴231123252(23)2(21)2-=⨯+⨯+⨯++-⋅+-⋅n n n T n n231121232(25)2(23)2(21)2-+=⨯+⨯++-⋅+-⋅+-⋅n n n n T n n n ④-④得2311222222222(21)2-+-=+⨯+⨯++⋅+⋅--⋅n n n n T n …………………1分23112(12222)(21)2-+-=++++--⋅n n n n T n∴12222(21)212+-⋅-=⨯--⋅-n n n T n …………………………………………………1分 ∴111224222+++-=⋅--⋅+n n n n T n 即1(32)24+-=-⋅-n n T n∴1(23)24+=-+n n T n∴数列{}n c 的前n 项和1(23)24+=-+n n T n ………………………………………3分19.（本小题满分12分） 解：（Ⅰ）由图知12T =，6πω=．………………………………………………………1分2125.15.22min max =-=-=y y A ，225.15.22min max =+=+=y y B ．……………2分 ∴0.5sin()26y x πϕ=++．又函数0.5sin()26y x πϕ=++过点(0,2.5)．代入，得22k πϕπ=+，又0ϕπ<<，∴2πϕ=．…………………………………2分综上，21=A ，6πω=，2πϕ=，21=B ． ………………………………………1分即2)26sin(21)(++=ππt t f ． （Ⅱ）令)()()(t g t f t h -=，设0)(0=t h ，则0t 为该企业的停产时间． 由0)11()11()11(<-=g f h ，0)12()12()12(>-=g f h ，则)12,11(0∈t ． 又0)5.11()5.11()5.11(<-=g f h ，则)12,5.11(0∈t ． 又0)75.11()75.11()75.11(>-=g f h ，则)75.11,5.11(0∈t ． 又0)625.11()625.11()625.11(<-=g f h ，则)75.11,625.11(0∈t ．又0)6875.11()6875.11()6875.11(>-=g f h ，则)6875.11,625.11(0∈t ．…4分……………………………………………1分 ∴应该在11．625时停产．……………………………………………………………1分 （也可直接由)625.11()625.11()625.11(<-=g f h ，0)6875.11()6875.11()6875.11(>-=g f h ，得出)6875.11,625.11(0∈t ；答案在11．625—11．6875之间都是正确的；若换算成时间应为11点37分到11点41分停产）20.（本小题满分13分）（Ⅰ）由已知得=a ，又=c ∴2224=-=b a c ．∴椭圆Γ的方程为141222=+y x ．…………………………………………………4分 （Ⅱ）由⎪⎩⎪⎨⎧=++=,1412,22y x m x y 得01236422=-++m mx x ① ………………………1分∵直线l 与椭圆Γ交于不同两点A 、B ，∴△0)123(163622>--=m m ， 得216<m ．设),(11y x A ，),(22y x B ，则1x ，2x 是方程①的两根，则2321mx x -=+， 2123124-⋅=m x x ．∴12=-=AB x又由AB =231294-+=m ，解之2m =±．……………………………3分 据题意知，点P 为线段AB 的中垂线与直线2=y 的交点． 设AB 的中点为),(00y x E ，则432210m x x x -=+=，400mm x y =+=，2m =时，31(,)22E -∴此时，线段AB 的中垂线方程为13()22y x -=-+，即1y x =--． 令2=y ，得03x =-．…………………………………………………………………2分2m =-时，31(,)22E -∴此时，线段AB 的中垂线方程为13()22y x +=--，即1y x =-+． 令2=y ，得01x =-．………………………………………………………………2分 综上所述，0x 的值为3-或1-． 21.（本小题满分14分）解：（Ⅰ）1m =时，1()ln ,02=+>f x x x x． ∴221121()22-'=-=x f x x x x……………………………………………………………………1分由()0'>f x ，解得12>x ；由()0'<f x ，解得102<<x ； ∴()f x 在1(0,)2上单调递减，1(,)2+∞上单调递增． (2)分∴=极小值)(x f 11()ln 11ln 222f =+=-．…………………………………………………… 2分（II ）令1()()()1ln 21,,12⎡⎤=--=+-+-∈⎢⎥⎣⎦m h x f x g x x x m x x e ，其中1(,1)2m ∈由题意，()0h x >对1,1x e ⎡⎤∈⎢⎥⎣⎦恒成立，∵2221221()1,,122-+-⎡⎤'=--=∈⎢⎥⎣⎦m x x m h x x x x x e ∵1(,1)2m ∈，∴在二次函数222=-+-y x x m 中，480∆=-<m ，∴2220-+-<x x m 对∈x R 恒成立∴()0'<h x 对1,1x e ⎡⎤∈⎢⎥⎣⎦恒成立， ∴()h x 在1,1e ⎡⎤⎢⎥⎣⎦上单减． ∴min 5()(1)ln11212022==+-+-=->m h x h m m ，即45>m ．故存在4(,1)5∈m 使()()f x g x >对1,1⎡⎤∀∈⎢⎥⎣⎦x e 恒成立．……………………………………4分 （III ）()(ln )(2),(0,)2mF x x x m x x=+-∈+∞，易知2x m =为函数()F x 的一个零点， ∵12>m ，∴21>m ，因此据题意知，函数()F x 的最大的零点1>c ， 下面讨论()ln 2mf x x x=+的零点情况，∵2212()22m x mf x x x x-'=-=． 易知函数()f x 在(0,)2m上单调递减，在(,)2m +∞上单调递增．由题知()f x 必有两个零点， ∴=极小值)(x f ()ln 1022=+<m m f ，解得20<<m e，∴122<<m e ，即(,2)2∈eme ．…………………………………………………………3分 ∴11(1)ln10,()ln 11102222=+=>=+=-<-=m m em emf f e e ．…………………1分 又10101010101()ln 10100224---=+=->->m m f e e e e e ．101()0,()0,(1)0f e f f e -∴><>．10101e a b c e -∴<<<<<<．101a b c e∴<<<<<，得证．……………………………………………………………1分。

四川省成都市新都区2010届高中毕业班诊断性考试(数学理)(考试时间150分钟满分150分)、选择题：(每小题有且只有一个正确选项，每小题5分，共60分)1 •定义集合运算：A B {z|z x y,x A,y B}，设A {1,2} , B {0,1}则集合A B的所有元素之和为A • 4B . 6 C.7 D . 82.已知函数y 、1 x 、、7的最大值为M，最小值为m,则m的值为M1 1 .2 .3A .-B .—C. D .4 2 2 2 3•设ABC的内角A、B、C所对的边长分别为a、b、c,且b2 c2 bc a2=0,则角A等于2 5A •B •C •D •6 3 3 64•若函数y g(x)的图像与函数y f(x)的图像关于直线y x对称，则函数y f (x 1)的反函数是A. y g(x 1) B.y g(x 1)C• y g(x) 1 D -y g(x) 15.在数列｛a n｝中，a1 3, a n 1 a n lg(1 ■1)，则a n =nA . 3+ lg nB . 3 (n 1)C . 3 n lg nD . 2+ n lg n 6•条件甲：“数列｛a n｝中，对任意的p、q N ,都有a p qa p a q条件乙：“数列｛a n｝是等差数列”则甲是乙的A .充分不必要条件B .必要不充分条件C .充要条件D .即不充分也不必要条件uuu LUUT7•空间四边形ABCD中，若AB ( 3,5,2) , CD ( 7, 1, 4)，点E、F分别是线段BC、AD的中点, uuu则EF等于A.(2, 3, 3)B.(-2, -3, -3)C .(-5, 2, -1)D .(5, 2,1)uuur 3 uuui 12 UJUT&已知::点B分AC 的定比为占D分BC的定比为—，则点B分AD的定比为59 9 1 1A .—B .—C .D .-7 7 4 49•若函数f(x)、g(x)分别是R 上的奇函数、偶函数，且满足 f(x) g(x) e x ，则有12 •定义在 R 上的函数 f(x)满足：f(x y) f (x)(y) 2xy,(x, y R)若 f(1)2，则 fA • 12B • 9C • 6D • 3二、填空题：(将正确答案直接填入题后的横线上，每小题5分，共20分)14 • ABC 中，已知三顶点的坐标是 A(0,0)、B(10,0)、C(5,12)，则 ABC 内心I 的坐标是 15 •设 A ｛x||3x b| 4｝，若 AI N ｛1,2,3｝，则 b 的取值范围为 __________ ;16 •等比例｛a n ｝中，若a 2 1，且a 3 0 ,则其前3项的和Q 的取值范围是 _______________三、解答题； (第17题10分，其它每题12分，共70 分)(1)将函数 g(x)化简成 g(x) Asin(wx ) B,( A 0,w0,(,])的形式;(2)求函数g(x)的值域。

郫县一中2010届高三第一次月考数 学（理工农医类）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分. 第Ⅰ卷1至2页，第Ⅱ卷3至8页，共150分.考试时间为120分.第Ⅰ卷（选择题共60分）注意事项：1.答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用钢笔和4B 或5B 铅笔写、涂写在答题卡上.2．每小题选出答案后，用4B 或5B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再涂选其它答案，不准答在试题单上. 3．考试结束后，将本试卷和答题卡一并交回. 4.参考公式：如果事件A 、B 互斥，那么P （A+B ）=P （A ）+P （B ） 如果事件A 、B 相互独立，那么P （A ·B ）=P （A ）·P （B ） 如果事件A 在一次试验中发生的概率是P ，那么n 次独立重复试验中恰好发生k 次的概率k n k k n n P P C k P --=)1()(一、 选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1、复数ii 2)1(-（其中i 是虚数单位）等于)(A 2-)(B 2)(C i 2-)(D i 22、与命题“若p 不正确，则q 不正确”的逆命题等价的命题是)(A 若q 不正确，则p 不正确 )(B 若p 正确，则q 正确 )(C 若p 正确，则q 不正确 )(D 若q 不正确，则p 正确3、若{}n a 为等差数列，43=a ，198=a ，则数列{}n a 的前10项的和为)(A 230)(B 140)(C115)(D 954、函数xx f 12)(-=的反函数为)(1x f -，若0)(1>-a f，则实数a 的取值范围是)(A )2,(-∞)(B ),2(+∞ )(C ),2()2,(+∞--∞)(D )2,2(-5、函数x x x f sin 3cos )(-=，]0,[π-∈x 的减区间是)(A ⎥⎦⎤⎢⎣⎡--32,ππ)(B ⎥⎦⎤⎢⎣⎡--3,32ππ )(C ⎥⎦⎤⎢⎣⎡-0,3π)(D ⎥⎦⎤⎢⎣⎡-0,6π 6、从5名学生中选出3人参加数学、物理、化学三科竞赛，每科1人．若学生甲不能参加物理竞赛，则不同的参赛方案共有)(A 24种 )(B 28种 )(C 48种 )(D 72种7、常数a 、b 满足b x x ax x =+++-→245lim22，则b a +的值为 )(A 23-)(B 21- )(C 23 )(D 21 8、平面向量a 与b 的夹角为60°，a ＝(2,0), | b |＝1，则 | a ＋2b |＝（A ）3 （B ）23 （C ）4 （D ）129、如图，直角三角形ABC 的边4,3==BC AC ，90=∠ACB ，三顶点在球O 上，若OC 与三角形ABC所在平面成30的角，则球O 的表面积为 )(A 950π)(B350π)(C 9100π)(D 3100π10设函数2()()f x g x x =+，曲线()y g x =在点(1,(1))g 处的切线方程为21y x =+，则曲线()y f x =在点(1,(1))f 处切线的斜率为A ．4B ．14-C ．2D ．12- 11、已知函数f (x )的定义域为[a ，b ]，函数f (x )的图象如右图所示， 则函数f (| x |)的图象是( )A ． B. C. D. 12．设函数()y f x =在（-∞，+∞）内有定义。

成都市2009届高中毕业班第一次诊断性检测数学（理）详解一、选择题1．函数f x x x ()sin cos =+的最小正周期是 A ．4πB ．2πC ．πD ．2π简解：选D。

考查和角公式（辅助角公式）与三角函数的周期性，4f x x x x ()sin cos )π=+=+。

2．设集合{|12,}A x x x =-<∈N ≤，集合{2,3}B =，则A B = A ．{1,2,3} B ．{0,1,2,3} C ．{2}D ．{1,0,1,2,3}-简解：选B 。

考查集合的概念与并集的概念，由0,1A A ∈-∉可得。

或由{0,1,2}A =得出。

3．某学校有教职工100人，其中教师80人，职员20人。

现从中选取10人组成一个考察团外出学习考察，则这10人中恰好有8名教师的不同选法的种数是A ．288020C CB ．288020A AC ．828020A CD ．828020C C 简解：选D 。

考查计数原理与排列组合的基本知识。

由于结果只与选出是哪8名教师和哪两名职员有关，与顺序无关，是组织问题。

分步计数，先选8名教师再选2名职员，共有828020C C 种选法。

4．已知等差数列{}n a 的前n 项和为(*)n S n ∈N ，且373,7S S =-=，那么数列{}n a 的公差d =A ．1B ．2C ．3D ．4 简解：选A 。

考查等差数列的基本知识（前n 项和公式与等差数列的性质）。

直接用前n 项和公式将条件转化为关于首项1a 与公差d 的方程求解，或者由等差数列的性质{}n S n 是公差为2d 的等差数列得：73732273S S d -==-得出结论。

或者由等差数列的性质得a ,a d =-=⇒=24111解题时不仅要熟练运用基本量转化解方程求解，更要善于运用性质整体处理。

5．“函数()f x 在点0x x =处有定义”是“函数()f x 在点0x x =处连续”的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．非充分非必要条件简解：选B 。

自贡市高2010级第一次诊断考试数学试题参考答案及评分标准一、选择题： 1－5.DABBC 6-10.ABCDD 11-12.AC 二、填空题 ：（本大题共4小题，每小题4分，共16分） （理）13. 120° ；14. 8 ；15. 427；16. 2 （文）13. 120° ；14. )1(12>-=x x y ；15. ① ④ ； 16.427三、解答题17、解：（Ⅰ）x x x x x f 2sin 232122cos 12sin 6cos 2cos 6sin)(-=-+-=ππ…（2分） ∴当231)()(4222max +=∈-=-=x f Z k k x k x 时即ππππ，其最小正周期为π。

…（4分） （Ⅱ）由23sin ,41sin 232141)2(=-=--=C C C f 解得即 ∵C 为锐角，∴3π=C ………（6分）由322sin 31cos ==B B 得 ………（8分）∴C B C B C B C B A cos cos sin sin )cos()](cos[cos -=+-=+-=π ＝6162213123322-=⨯-⨯………（12分）18、解：（Ⅰ）至少有一名女同学的概率1－61131036-=C C ＝65……（4分） 文（6分） （Ⅱ）甲被选中的概率为10331029=C C ， 则甲被选中且通过测试的概率0.3×0.7＝0.21 ……………(8分) 文（12分）（Ⅲ），，的可能取值为3,21,0ξ，==)0(ξP 30131034=C C , ==)1(ξP 1033102416=C C C ==)2(ξP 213101426=C C C , ==)3(ξP 6131036=C C …………（10分） ∴ξ的分布列为∴ 8.161321210313010=⨯+⨯+⨯+⨯=ξE ………（12分） 19、解：设A ),(11y x ，C ),(22y x由抛物线定义知｜AC ｜＝p x x ++21 ………（2分） 直线AC 的斜率存在且不为0，设为k ，则)2(px k y -= 联立 ⎪⎩⎪⎨⎧=-=pxy p x k y 2)2(2得 0)2(4422222=++-k p x k p x k ………（4分）由韦达定理有21x x +＝22)2(k k p +， ∴｜AC ｜＝p x x ++21＝22)1(2k k p +……（6分） 同理可得（用－k1代k ）｜BD ｜＝)1(22+k p ………（8分） ∴四边形ABCD 的面积222228)22(2)12(2||||21p p k k p BD AC S =+≥++==…（11分）当且仅当221kk =，即1±=k 时，2min 8p S = ……（12分）（理）21、（文）20、解：（Ⅰ）令)0()1()1(0,1f f f n m ===则∵1)0(,1)(00=∴<<>f x f x 时， ………（2分）……（文3分）令1)(1)(,1)()()0(,0,0>-=∴=-=>-=<=x f x f x f x f f x n x m 则 …（4分）（文6分）（Ⅱ）由（Ⅰ）知对任意的0)(,>∈x f R x任取1)(0,0,12122121<-<∴>-<x x f x x x x x x 则且、 ………（6分）（文9分） ∴0]1)()[()(])[()()(121111212<--=-+-=-x x f x f x f x x x f x f x f ∴R x f 在)(上是单调递减函数。

嘉定区2010学年高三年级第一次质量调研数学试卷(理)参考答案与评分标准一．填空题(本大题满分56分)本大题共有14题，考生必须在答题纸相应编号的空格内直接填写结果，每个空格填对得4分，否则一律得零分． 1．答案:1．因i a a ai i )1(1)1)(1(-++=-+是实数，所以=a 1． 2．答案:]2,0[．由022≥-x x ，得022≤-x x ，所以]2,0[∈x ． 3．答案:1．112+=a a ，314+=a a ，由已知得4122a a a =，即)3()1(1121+=+a a a ，解得11=a ． 4．答案:257-．由532sin =⎪⎭⎫ ⎝⎛+θπ，得53cos =θ，所以2571cos 22cos 2-=-=θθ．5．答案:2-．解法一:函数x x f -=)(的反函数为21)(x x f =-(0≤x )，由4)(1=-x f 得42=x ，因为0<x ，故2-=x ．解法二:由4)(1=-x f ，得2)4(-==f x ．6．答案:105arccos． 因为AB ∥11B A ，故1BAC ∠就是异面直线1AC 与11B A 所成的角，连结1BC ，在1ABC 中，1=AB ，511==BC AC ，所以10552121cos 11===∠AC ABBAC ． 7．答案:0．因)(x f 是定义在R 上的奇函数，所以0)0(=f ，在等式)()2(x f x f -=+中令2-=x ，得0)2(=-f ． 8．答案:2．9)21(x -展开式的第3项为288)2(2293=-=x C T ，解得23=x ，所以232132132lim 323232lim 111lim 22=-⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+++∞→∞→∞→nn nn n n x x x ．9．答案:1．三阶行列式xa x 1214532+中元素3的余子式为xa x x f 21)(+=，由0)(<x f 得022<-+ax x ，由题意得a b -=+-1，所以1=+b a ．10．答案:16．1=a ，满足3≤a ，于是4211==+b ；2=a ，满足3≤a ，8212==+b ；3=a ，满足3≤a ，则16213==+b ；4=a ，不满足3≤a ，则输出b ，16=b ．11．答案:21．满足条件的选法可分为三类:A 组2人，B 、C 组各1人，有121325C C C 种选法；B 组2人，A 、C 组各1人，有122315C C C 种选法；C 组2人，A 、B 组各1人，有221315C C C 种选法．所以A 、B 、C 三组的学生都有的概率21210105410221315122315121325==++=C C C C C C C C C C P ． 12．答案:65π．由题意，612cos 2>θ且212sin 2>θ，⎩⎨⎧==+22cos 34ab b a θ，⎪⎪⎩⎪⎪⎨⎧=⋅-=+21112sin 211a b a b θ，所以θθ2sin 22cos 32-=，32tan -=θ，因)2,(2ππθ∈，故352πθ=，65πθ=．13．答案:①③④．由y x y f x f ⋅=⋅)()(，得y x a y a y a x a x⋅=⋅⋅-⋅⋅⋅-])(2[])(2[，化简得)()()()(2y a x a a y a x a ⋅⋅⋅=⋅⋅⋅⋅，当0 =a 时，等式成立；当0 ≠a 时，有12=a，即1||=a，所以①、③、④都能使等式成立． 14．答案:4．11+<<t a t ，则t t a a <<-=112，t t a t a t a >+>-+=-+=1222123， t a t t a a <-+=-=1342，1452a a t a =-+=．所以}{n a 是以4为周期的周期数列．(第14题也可取满足条件的t 和1a 的特殊值求解)二．选择题(本大题满分20分)本大题共有4题，每题有且只有一个正确答案，考生必须在答题纸的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分． 15．C ．16．A ．17．D ．16．B ． 15．由5:4:3::=c b a 可得a ，b ，c 成等差数列；若a ，b ，c 成等差数列，则c a b +=2，由勾股定理，222c b a =+，得2222c c a a =⎪⎭⎫ ⎝⎛++，032522=-+c ac a ，解得53=c a ，令k a 3=(0>k )，则k c 5=，得k b 4=．所以5:4:3::=c b a ．16．①错．不在同一直线上的三点才能确定一个平面；②错．若圆锥的侧面展开图是一个圆面，则可得圆锥底面半径的长等于圆锥母线的长；③错．如果三棱锥的底面是等边三角形，一条侧棱垂直于底面且长度等于底面边长，则三个侧面都是等腰三角形；④错．若这两点是球的直径的两个端点，过这两点可作无数个大圆．17．作出函数xy 2=与2x y =，可发现两函数图像在第二象限有一个交点，在第一象限有两个交点(第一象限的两个交点是)4,2(和)16,4()．18．若取1x 、2x 为区间]4,2[的两个`端点，则8)()(21=x f x f ．若8>C ，取21=x ，4)(1=x f ，对任意]4,2[2∈x ，16)(2≤x f ，于是8)(4)()(221≤=x f x f x f ；若8<C ，取41=x ，16)(1=x f ，对任意]4,2[2∈x ，4)(2≥x f ，于是8)(16)()(221≥=x f x f x f ．所以8=C ．三．解答题(本大题满分74分)本大题共有5题，解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤． 19．(本题满分12分) 解:设半圆的半径为r ，在△ABC 中，090=∠ACB ，030=∠ABC ，3=BC ，连结OM ，则AB OM ⊥，……(2分) 设r OM =，则r OB 2=，…………(4分) 因为OB OC BC +=，所以r BC 3=，即33=r ．………………(6分)130tan 0=⋅=BC AC ．阴影部分绕直线BC 旋转一周所得旋转体为底面半径1=AC ，高3=BC 的圆锥中间挖掉一个半径33=r 的球．………………(8分) 所以，圆锥V V =球V -πππ27353334313132=⎪⎪⎭⎫ ⎝⎛⋅⋅-⋅⋅⋅=．…………(12分)20．(本题满分14分)本题共有2个小题，第1小题满分6分，第2小题满分8分．解:(1)若1=ω，则⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-=6cos ,1πx a ，⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-=6sin 2,2πx b ，由a ∥b 的充要条件知，存在非零实数λ，使得a b ⋅=λ，即⎪⎩⎪⎨⎧⎪⎭⎫ ⎝⎛-⋅=⎪⎭⎫ ⎝⎛-=6cos 6sin 22πλπλx x ， 所以⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-6cos 6sin ππx x ，16tan =⎪⎭⎫ ⎝⎛-πx ，…………(3分)(以下有两种解法:) 解法一:46πππ+=-k x ，Z k ∈，125ππ+=k x ，Z k ∈，32333333133164tan 125tan 125tan tan +=-+=-+=⎪⎭⎫ ⎝⎛+==⎪⎭⎫ ⎝⎛+=πππππk x ．…(6分)解法二:323313316tan 6tan 16tan 6tan 66tan tan +=-+=⎪⎭⎫ ⎝⎛--+⎪⎭⎫ ⎝⎛-=⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-=ππππππx x x x ． 所以321313tan +=-+=x ．…………(6分)(2)⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-+=6cos 6sin 226cos 6sin 22)(πωπωπωπωx x x x x f⎪⎭⎫ ⎝⎛-=32sin πωx ，…………(8分)因为)(x f 的最小正周期为π，所以πωπ=22，1=ω，所以⎪⎭⎫ ⎝⎛-=32sin )(πx x f ，…………(10分)当⎥⎦⎤⎢⎣⎡∈2,0πx 时，⎥⎦⎤⎢⎣⎡-∈-32,332πππx ，…………(12分) 所以函数)(x f 的值域为⎥⎦⎤⎢⎣⎡-1,23．…………(14分)21．(本题满分14分)本题共有2个小题，第1小题满分6分，第2小题满分8分．解:(1)由已知，当0=x 时，8)(=x C ，即85=k，所以40=k ，……(1分) 所以5340)(+=x x C ，…………(2分)又加装隔热层的费用为x x C 6)(1=．所以5380066534020)()(20)(1++=++⨯=+⋅=x x x x x C x C x f ，…………(5分) )(x f 定义域为]10,0[．…………(6分)(2)10380062103538003563538006538006)(-⨯≥-⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛++=++=x x x x x x x f70=，…………(10分)当且仅当⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+353800356x x ，18800352=⎪⎭⎫ ⎝⎛+x ，32035=+x ，即5=x 时取等号．…………(13分) 所以当隔热层加装厚度为5厘米时，总费用)(x f 最小．最小总费用为70万元．…(14分)22．(本题满分16分)本题共有3个小题，第1小题满分3分，第2小题满分7分，第3小题满分6分．解:(1)1=m 时，1)(2+=x x f ，因为01=a ，所以1)0()(12===f a f a ，2)(23==a f a ，5)(34==a f a ．…………(3分，每求对一项得1分)(2)m x x f +=2)(，则m a =2，m m a +=23，m m m m m m m a +++=++=2342242)(，…………(5分) 如果2a ，3a ，4a 成等比数列，则)2()(23422m m m m m m m +++=+，234523422m m m m m m m +++=++，0345=-+m m m ，…………(6分)因为02≠=m a ，所以012=-+m m ，251+-=m 或251--=m ．……(8分) 当251+-=m 时，数列的公比2511223+=+=+==m m m m a a q ．……(9分) 当251--=m ，251-=q ．…………(10分)(3)1)(2-=x x f ，),0[+∞∈x ，所以1)(1+=-x x f (1-≥x )，……(11分)11=b ，121+=+n n b b ，所以1221+=+n n b b ，而121=b ，所以{}2n b 是以1为首项，1为公比的等比数列，n b n =2，…………(13分)所以2)1(21+=+++=n n n S n ，…………(14分) 由2010>n S ，即20102)1(>+n n ，解得63≥n ，所以所求的最小正整数n 的值是63．…………(16分)23．(本题满分18分)本题共有3个小题，第1小题满分5分，第2小题满分6分，第3小题满分7分．23．解:(1)设点),(y x P 是函数)(x f 图像上任意一点，P 关于点A 对称的点为),(y x P '''，则12='+x x ，22='+y y ，于是x x -='2，y y -='4，…………(2分) 因为),(y x P '''在函数)(x g 的图像上，所以2|2|24-'-'⋅--='x x a ay ，……(3分) 即x x a a y --⋅--=-244||，x x a a y -⋅+=2||，所以xx a a x f -⋅+=2)(||(或x x aa x f 2)(||+=)．………………(5分)(2)令t a x=，因为1>a ，0>x ，所以1>t ，所以方程m x f =)(可化为m tt =+2，即关于t 的方程022=+-mt t 有大于1的相异两实数解．…………(8分)作2)(2+-=mt t t h ，则⎪⎪⎩⎪⎪⎨⎧>->>08120)1(2m m h ，…………(11分)解得322<<m ．所以m 的取值范围是)3,22(．…………(12分) (3)x x a ax g 2)(||+=，),2[∞+-∈x ．当0≥x 时，因为1>a ，所以1≥xa ，),3[3)(∞+∈=xa x g ，所以函数)(x g 不存在最大值．…………(13分)当02<≤-x 时，x xa a x g 12)(+=，令xt 2=，则t t t h x g 12)()(+==，⎪⎭⎫⎢⎣⎡∈1,12a t ， 当2212>a ，即421<<a 时，)(t h 在⎪⎭⎫⎢⎣⎡1,12a 上是增函数，存在最小值222a a +，与a有关，不符合题意．…………(15分) 当22102≤<a ，即42≥a 时，)(t h 在⎥⎦⎤⎢⎣⎡22,12a 上是减函数，在⎪⎪⎭⎫⎢⎣⎡1,22上是增函数，当22=t 即2log 21a x -=时，)(t h 取最小值22，与a 无关．…………(17分) 综上所述，a 的取值范围是),2[4∞+．…………(18分)。

四川省成都七中2010-2011学年高三“一诊”模拟考试英语试题本试卷分第一卷(选择题)和第二卷(非选择题)两部分。

第一卷1至l4页。

第二卷15至17页。

考试结束后，将第二卷和答题卡一并交回。

满分150分，考试时间120分钟。

第一卷注意事项：1. 答题前．考生在答题卡上务必用直径0．5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚。

请认真核准条形码上的准考证号、姓名和科目。

2. 每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后,再选涂其他答案标号，在试题卷上作答无效。

第一部分听力(共两节，满分30分)第一节(共5小题；每小题l 5分，满分7．5分)听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有l0秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1. How long is the library open on Saturday?A. 9 hours.B. 11 hours.C. 13 hours.2. Where is the man now?A. In WashingtonB. In New York.C. In Boston.3. What does the woman want to have?A. Ice water.B. Coffee.C. tea.4. Who was injured in the accident?A. No one.B. A baby.C. Three women.5. What kind of party might this be?A. wedding party.B. A birthday party.C. A farewell party.第二节(共15小题;每小题1 5分，满分22 .5分)听下面5段对话或独自。

每段对话或独自后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

成都市2O1O届高中毕业班第一次诊断性检测理科综合能力测试二、选择题 (本题共8小题。

在每小题中，有的只有一个选项正确，有的有多个选项正确，全部选对的得6分，选对但不全的得3分，有选错的得0分)14．一列简谐横波沿T轴传播，某时刻的波形如图所示。

关于该波的传播方向与质点以a、b、c、d、e的运动情况，下列叙述正确的是A．若波沿x轴正方向传播，则该时刻质点a的运动方向为x轴正方向B．若波沿x轴负方向传播，则该时刻质点c的运动方向为y轴负方向C．从该时刻起，若质点e比质点d先回到平衡位置，则波沿x轴正方向传播D．若波沿x轴正方向传播，则再经过半个周期，质点b将移动到质点d现在的位置15．在某地欢乐谷主题公园内有许多惊险刺激的游乐项目，双塔太空梭“天地双雄”就是其中之一(见右图)，双塔并立，一个塔的座椅由上而下做极速竖直降落运动。

另一个塔的座椅由下而上做高速竖直弹射运动。

有一位质量为50 kg的游客坐在高速弹射塔内的座椅上，若弹射塔的座椅在2 s内由静止开始匀加速冲到56 m高处，则在此过程中，游客对座椅的压力大小约为(g取10 m／s2)A．500 N B．1 400N C．1900 N D．750N16．一物体放在水平地面上，对物体施加一水平拉力F使之从静止开始运动，经过一段时间岛后撤去F，物体又运动了一段时间2t，刚好静止。

设物体在运动过程中受到的摩擦力大小恒为f，其速度一时间图象如图所示，那么以下说法正确的是A．在0~t和00~3t t两段时间内，加速度大小之比为3 ：1B．在0~t和00~3t t两段时间内，平均速度大小之比为2：lC．在0~t时间内，F的冲量与f的冲量大小之比为3：1D．F：f=3：117．如图所示，质量为m的小球被固定在竖直墙上的轻质水平弹簧系住，并用倾角为45°的光滑木板托住。

小球恰好处于静止状态，此后将撤去木板。

若弹簧的劲度系数为k，重力加速度为g，则以下说法正确的是A．图中小球处于静止状态时。