高考理科数学之高频考点解密14 空间几何体(解析版)

可编辑修改精选全文完整版第1讲空间几何体一、空间几何体1、空间几何体在我们周围存在着各种各样的物体，它们都占据着空间的一部分。

如果我们只考虑这些物体的形状和大小，而不考虑其他因素，那么由这些物体抽象出来的空间图形就叫做空间几何体。

2、多面体和旋转体多面体：由若干个平面多边形围成的几何体叫做多面体。

围成多面体的各个多边形叫做多面体的面；相邻两个面的公共边叫做多面体的棱；棱及棱的公共点叫做多面体的顶点。

旋转体：由一个平面图形绕它所在的平面内的一条定直线旋转所形成的封闭几何体，叫做旋转几何体。

这条定直线叫做旋转体的轴。

多面体旋转体圆台圆柱-圆锥圆柱+圆锥圆台+大圆锥-小圆锥二、柱、锥、台、球的结构特征1.棱柱定义图形表示分类性质有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体叫做棱柱。

两个互相平行的平面叫做棱柱的底面，其余各面叫做棱柱的侧面。

用平行的两底面多边形的字母表示棱柱,如：棱柱ABCDEF-A1B1C1D1E1F1。

棱柱的分类一(底面）：棱柱的底面可以是三角形、四边形、五边形、……我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱、……棱柱的分类二(根据侧棱及底面的关系）：斜棱柱: 侧棱不垂直于底面的棱柱.直棱柱: 侧棱垂直于底面的棱柱叫做直棱柱(1)上下底面平行,且是全等的多边形。

(2)侧棱相等且相互平行。

(3) 侧面是平行四边形。

正棱柱: 底面是正多边形的直棱柱叫做正棱柱三棱柱四棱柱五棱柱斜棱柱直棱柱正棱柱2.棱锥定义图形表示性质分类有一个面是多边形，其余各面是有一个公共顶点的三角形，由这些面所围成的几何体叫做棱锥。

用顶点及底面各顶点字母表示棱锥,如：棱锥Ｓ－ＡＢＣ侧面是三角形，底面是多边形。

按底面多边形的边数分类可分为三棱锥、四棱锥、五棱锥等等，其中三棱锥又叫四面体。

特殊的棱锥－正棱锥定义：如果一个棱锥的底面是正多边形，并且顶点在底面的射影是底面中心三棱锥四棱锥五棱锥直棱锥2.棱台定义图形表示分类性质用一个平行于棱锥底面的平面去截棱锥，底面和截面之间的部分叫做棱台。

空间几何体一：棱柱1，定义有两个面相互平行，其余各面都是四边形，并且每相邻两个四边形的公共边都相互平行，由这些面所围成的几何体叫做“棱柱”2，分类斜棱柱棱柱；正棱柱（侧棱垂直于底）其他棱柱面，且底面是正多边形）直棱柱（侧棱与底面垂直3，底面：两个可以重合的多边形4，侧面：平行四边形5，侧面积6，表面积7，体积二：棱锥1，“棱锥”定义有一个面是多边形，锥；2，分类“正棱锥”定义其余各面是有一个公共顶点的三角形，由这些面所围成的几何体叫做棱假如一个棱锥的底面是正多边形，棱锥；否就它是斜棱锥；3，底面4，侧面5，侧面积6，表面积7，体积并且顶点在底面的射影是底面的中心，这样的棱锥叫做正PCOBAD三：棱台1，“棱台”定义用一个平行于底面的平面去截棱锥，我们把截面与底面之间的部分称为棱台；2，分类“正棱台”定义由正棱锥截得的棱台叫做正棱台；3，底面4，侧面5，侧面积6，表面积7，体积留意：棱台常常补成棱锥讨论四：圆柱1，定义 以矩形的一边所在的直线为旋转轴， 2，底面 3，侧面 4，侧面积 5，表面积 6，体积其余各边旋转而形成的曲面所围成的几何体叫“圆柱”；五：圆锥1，定义 以直角三角形的一条直角边所在直线为旋转轴， “圆锥”；该直角边叫圆锥的轴； 2，底面 3，侧面 4，侧面积 5，表面积 6，体积其余两边旋转形成的面所围成的旋转体叫做六：圆台1，定义 用一个平行于圆锥底面的平面去截圆锥，底面与截面之间的部分叫做“圆台” 2，底面 3，侧面 4，侧面积 5，表面积 6，体积；七：空间几何体的体积与表面积 1，多面体的面积和体积公式名称 侧面积 (S 侧 ) 全面积 (S 全)体 积 (V)S 底 ·h=S 直截面 ·h 棱柱直截面周长 ×l棱 柱S 侧+2S 底S 底 ·h直棱柱 ch 棱锥 各侧面积之和棱 锥1 底 ·hS 3S 侧+S 12底正棱锥 ch ′ 棱台 各侧面面积之和1 棱 台上底 +S 下底 + h(S 3)侧+S 上底 +S 下底1 2S S 下S 下正棱台(c+c ′h )′表中 S 表示面积， c ′， c 分别表示上，下底面周长， h 表示高， h ′表示斜高， l 表示侧棱长；2，旋转体的面积和体积公式名称圆柱圆锥圆台球2πrl πrl π(r1+r2)lS 侧222 2πr(l+r ) πr(l +r ) π(r1+r 2)l+π(r 1+r 2)4πR S 全1 31343222322πr hπh(r 1+r1r 2+r 2)πR πr h( 即πr l)V表中l ，h 分别表示母线，高，r 表示圆柱，圆锥与球冠的底半径，r 1，r 2 分别表示圆台上，下底面半径，R表示半径；八：空间几何体的三视图与直观图1，正视图光线从几何体的前面对后面正投影，得到投影图；2，侧视图光线从几何体的左面对右面正投影，得到投影图；3，俯视图光线从几何体的左面对右面正投影，得到投影图；九，“斜二测”画法.正六面形的斜二测画法示意图xoy 901：在已知图形中取相互垂直的轴Ox，Oy，（即取）；o ' x ', o' y' ，取x ' o' y ' 45 (or135 ) ，它们确定的平2：画直观图时，把它画成对应的轴面表示水平平面；x 'o ' y ' 中画直观图时，已知图形中平行于数轴的线段保持平行性不变，平行于3：在坐标系x 轴（或在x 轴上）的线段保持长度不变，平行于y 轴（或在y 轴上）的线段长度减半；24结论：一般地，采纳斜二测法作出的直观图面积是原平面图形面积的倍.。

2014年高考一轮复习热点难点精讲精析：7.1空间几何体一、空间几何体的结构及其三视图和直观图（一）空间几何体的结构特征※相关链接※1、几种常见的多面体（1）正方体（2）长方体（3）直棱柱：指的是侧棱垂直于底面的棱柱，特别地当底面是正多边形时，这样的直棱柱叫正棱柱；（4）正棱锥：指的是底面是正多边形，且顶点在底面的射影是底面的中心的棱锥。

特别地，各条棱均相等的正三棱锥又叫正四面体；（5）平行六面体：指的是底面为平行四边形的四棱柱。

2、理解并掌握空间几何体的结构特征，对培养空间想象能力，进一步研究几何体中的线面位置关系或数量关系非常重要，每种几何体的定义都是非常严谨的，注意对比记忆。

※例题解析※〖例1〗平面内的一个四边形为平行四边形的充要条件有多个，如两组对边分别平行，类似地，写出空间中的一个四棱柱为平行六面体的两个充要条件：充要条件①充要条件②思路解析：利用类比推理中“线 面”再验证一下所给出的条件是否正确即可。

解答：平行六面体实质是把一个平行四边形按某一方向平移所形成的几何体，因此“平行四边形”与“平行六四体”有着性质上的“相似性”。

答案：两组相对侧面分别平行；一组相对侧面平行且全等；对角线交于一点且互相平行；底面是平行四边形（任选两个即可）。

〖例2〗一正方体表面沿着几条棱裁开放平得到如图的展开图，则在原正方体中（）A AB∥CDB AB∥EFC CD∥GHD AB∥GH解答：选C。

折回原正方体如图，则C与E重合，D与B重合。

显见CD∥GH（二）几何体的三视图※相差链接※1、几何体的三视图的排列规则：俯视图放在正视图的下面，长度与正视图一样，侧视图放在正视图右面，高度与正视图一样，宽度与俯视图一样，即“长对正，高平齐，宽相等”注意虚、实线的区别。

注：严格按排列规则放置三视图，并用虚线标出长、宽、高的关系，对准确把握几何体很有利。

2、应用：在解题的过程中，可以根据三视图的的及图中所涉及到的线段的长度，推断出原几何图形中的点、线、面之间的关系及图中一些线段的长度，这样我们就可以解出有关的问题。

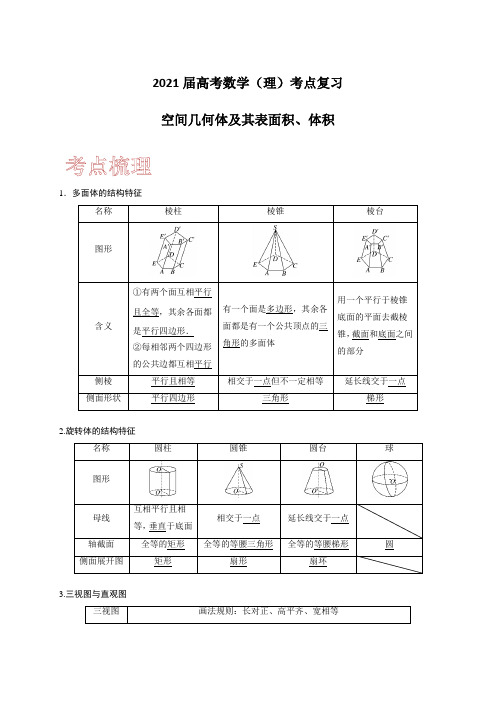
2021届高考数学（理）考点复习空间几何体及其表面积、体积1．多面体的结构特征名称棱柱棱锥棱台图形含义①有两个面互相平行且全等，其余各面都是平行四边形．②每相邻两个四边形的公共边都互相平行有一个面是多边形，其余各面都是有一个公共顶点的三角形的多面体用一个平行于棱锥底面的平面去截棱锥，截面和底面之间的部分侧棱平行且相等相交于一点但不一定相等延长线交于一点侧面形状平行四边形三角形梯形2.旋转体的结构特征名称圆柱圆锥圆台球图形母线互相平行且相等，垂直于底面相交于一点延长线交于一点轴截面全等的矩形全等的等腰三角形全等的等腰梯形圆侧面展开图矩形扇形扇环3.三视图与直观图三视图画法规则：长对正、高平齐、宽相等直观图斜二测画法：(1)原图形中x 轴、y 轴、z 轴两两垂直，直观图中x ′轴、y ′轴的夹角为45°或135°，z ′轴与x ′轴和y ′轴所在平面垂直．(2)原图形中平行于坐标轴的线段在直观图中仍平行于坐标轴，平行于x 轴和z 轴的线段在直观图中保持原长度不变，平行于y 轴的线段在直观图中长度为原来的一半.4.多面体的表面积、侧面积因为多面体的各个面都是平面，所以多面体的侧面积就是所有侧面的面积之和，表面积是侧面积与底面面积之和．5．圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱圆锥圆台侧面展开图侧面积公式S 圆柱侧＝2πrlS 圆锥侧＝πrlS 圆台侧＝π(r 1＋r 2)l6.柱、锥、台、球的表面积和体积名称几何体 表面积 体积 柱体(棱柱和圆柱) S 表面积＝S 侧＋2S 底 V ＝Sh 锥体(棱锥和圆锥) S 表面积＝S 侧＋S 底 V ＝13Sh台体(棱台和圆台)S 表面积＝S 侧＋S 上＋S 下V ＝13(S 上＋S 下＋S 上S 下)h球S ＝4πR 2V ＝43πR 3概念方法微思考1．如何求旋转体的表面积？提示 求旋转体的侧面积时需要将曲面展开为平面图形计算，而表面积是侧面积与底面积之和． 2．如何求不规则几何体的体积？提示 求不规则几何体的体积要注意分割与补形，将不规则的几何体通过分割或补形转化为规则的几何体求解．1．（2020•天津）若棱长为23的正方体的顶点都在同一球面上，则该球的表面积为( ) A ．12π B ．24πC ．36πD ．144π【答案】C【解析】由题意，正方体的对角线就是球的直径， 所以23236R =⨯=， 所以3R =，2436S R ππ==． 故选C ．2．（2020•新课标Ⅰ）埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥．以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为( )A 51- B 51-C 51+D 51+【答案】C【解析】设正四棱锥的高为h ，底面边长为a ，侧面三角形底边上的高为h '， 则依题意有：222212()2h ah a h h ⎧='⎪⎪⎨⎪='-⎪⎩，因此有222151()4()2()1022a h h h h ah a a a '''+'-='⇒--=⇒=51-+故选C ．3．（2020•新课标Ⅰ）已知A ，B ，C 为球O 的球面上的三个点，1O 为ABC ∆的外接圆．若1O 的面积为4π，1AB BC AC OO ===，则球O 的表面积为( )A ．64πB ．48πC ．36πD ．32π【答案】A【解析】由题意可知图形如图：1O 的面积为4π，可得12O A =，则 13sin 602AO AB =︒，13322AO AB =， 123AB BC AC OO ∴====，外接球的半径为：22114R AO OO =+=， 球O 的表面积：24464ππ⨯⨯=． 故选A ．4．（2019•新课标Ⅰ）已知三棱锥P ABC -的四个顶点在球O 的球面上，PA PB PC ==，ABC ∆是边长为2的正三角形，E ，F 分别是PA ，AB 的中点，90CEF ∠=︒，则球O 的体积为( ) A ．86π B ．46πC ．26πD ．6π【答案】D 【解析】如图，由PA PB PC ==，ABC ∆是边长为2的正三角形，可知三棱锥P ABC -为正三棱锥， 则顶点P 在底面的射影1O 为底面三角形的中心，连接1BO 并延长，交AC 于G ， 则AC BG ⊥，又1PO AC ⊥，11PO BG O =，可得AC ⊥平面PBG ，则PB AC ⊥，E ，F 分别是PA ，AB 的中点，//EF PB ∴，又90CEF ∠=︒，即EF CE ⊥，PB CE ∴⊥，得PB ⊥平面PAC ，∴正三棱锥P ABC -的三条侧棱两两互相垂直，把三棱锥补形为正方体，则正方体外接球即为三棱锥的外接球， 其直径为2222222221()2D PA PB PC PA PB PB PC PA PC ++=+++++ 22222211()(222)622AB BC AC =++=++=． 6，则球O 的体积为346(63ππ⨯=． 故选D ．5．（2018•新课标Ⅰ）已知圆柱的上、下底面的中心分别为1O ，2O ，过直线12O O 的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为( ) A ．122π B ．12π C ．82π D ．10π【答案】B【解析】设圆柱的底面直径为2R ，则高为2R ， 圆柱的上、下底面的中心分别为1O ，2O ，过直线12O O 的平面截该圆柱所得的截面是面积为8的正方形， 可得：248R =，解得2R ，则该圆柱的表面积为：2(2)2222212πππ⨯+⨯． 故选B ．6．（2018•新课标Ⅲ）设A ，B ，C ，D 是同一个半径为4的球的球面上四点，ABC ∆为等边三角形且面积为93D ABC -体积的最大值为( ) A ．123 B ．183 C ．243 D ．543【答案】B【解析】ABC ∆为等边三角形且面积为32393AB =6AB =， 球心为O ，三角形ABC 的外心为O '，显然D 在O O '的延长线与球的交点如图： 236233O C '==，224(23)2OO '-=，则三棱锥D ABC -高的最大值为：6，则三棱锥D ABC -体积的最大值为：313618334⨯⨯=．故选B ．7．（2017•全国）正三棱柱111ABC A B C -各棱长均为1，D 为1AA 的中点，则四面体1A BCD 的体积是( ) A ．3 B ．3 C ．3 D ．3 【答案】D 【解析】如图，111ABC A B C -为正三棱柱，∴底面ABC 为正三角形，侧面11BB C C 为正方形，1111111A BCD ABC A B C A BB C C D ABC V V V V ---=--131311313111123322=⨯⨯⨯-⨯⨯-⨯⨯⨯⨯=． 故选D ．8．（2017•新课标Ⅲ）已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为( ) A ．π B ．34πC ．2π D ．4π 【答案】B【解析】圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上， ∴该圆柱底面圆周半径22131()22r =-=，∴该圆柱的体积：233()124V Sh ππ==⨯⨯=． 故选B ．9．（2020•海南）已知正方体1111ABCD A B C D -的棱长为2，M 、N 分别为1BB 、AB 的中点，则三棱锥1A NMD -的体积为__________． 【答案】13【解析】如图，正方体1111ABCD A B C D -的棱长为2，M 、N 分别为1BB 、AB 的中点，∴111122ANM S ∆=⨯⨯=， ∴111112323A NMD D AMN V V --==⨯⨯=． 故答案为：13．10．（2020•浙江）已知圆锥的侧面积（单位：2)cm 为2π，且它的侧面展开图是一个半圆，则这个圆锥的底面半径（单位：)cm 是__________． 【答案】1cm【解析】圆锥侧面展开图是半圆，面积为22cm π，设圆锥的母线长为acm ，则2122a ππ⨯=，2a cm ∴=，∴侧面展开扇形的弧长为2cm π，设圆锥的底面半径OC rcm =，则22r ππ=，解得1r cm =． 故答案为：1cm ．11．（2020•江苏）如图，六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的．已知螺帽的底面正六边形边长为2cm ，高为2cm ，内孔半径为0.5cm ，则此六角螺帽毛坯的体积是__________．【答案】1232π-【解析】六棱柱的体积为：1622sin 6021232⨯⨯⨯⨯︒⨯=圆柱的体积为：2(0.5)22ππ⨯⨯=，所以此六角螺帽毛坯的体积是：3(123)2cm π，故答案为：1232π．12．（2020•新课标Ⅲ）已知圆锥的底面半径为1，母线长为3，则该圆锥内半径最大的球的体积为__________． 2 【解析】因为圆锥内半径最大的球应该为该圆锥的内切球，如图，圆锥母线3BS =，底面半径1BC =， 则其高2222SC BS BC =-=， 不妨设该内切球与母线BS 切于点D ， 令OD OC r ==，由SOD SBC ∆∆∽，则OD BCOS BS=， 即1322r=-，解得2r =， 3423V r ππ==，故答案为：2π．13．（2019•全国）已知平面α截球O 的球面所得圆的面积为π，O 到α的距离为3，则球O 的表面积为__________． 【答案】40π【解析】平面α截球O 的球面所得圆的面积为π，则圆的半径为1， 该平面与球心的距离3d =，∴球半径221310R =+ ∴球的表面积2440S R ππ==．故答案为：40π．14．（2019•江苏）如图，长方体1111ABCD A B C D -的体积是120，E 为1CC 的中点，则三棱锥E BCD -的体积是__________．【答案】10【解析】长方体1111ABCD A B C D -的体积是120，E 为1CC 的中点，∴11111120ABCD A B C D V AB BC DD -=⨯⨯=， ∴三棱锥E BCD -的体积：13E BCD BCD V S CE -∆=⨯⨯1132BC DC CE =⨯⨯⨯⨯ 1112AB BC DD =⨯⨯⨯ 10=．故答案为：10．15．（2019•新课标Ⅲ）学生到工厂劳动实践，利用3D 打印技术制作模型．如图，该模型为长方体1111ABCD A B C D -挖去四棱锥O EFGH -后所得的几何体，其中O 为长方体的中心，E ，F ，G ，H 分别为所在棱的中点，6AB BC cm ==，14.3AA cm D =打印所用原料密度为30.9/g cm ．不考虑打印损耗，制作该模型所需原料的质量为__________g ．【答案】118.8【解析】该模型为长方体1111ABCD A B C D -，挖去四棱锥O EFGH -后所得的几何体，其中O 为长方体的中心，E ，F ，G ，H ，分别为所在棱的中点，6AB BC cm ==，14AA cm =，∴该模型体积为：1111ABCD A B C D O EFGH V V ---11664(46432)332=⨯⨯-⨯⨯-⨯⨯⨯⨯314412132()cm =-=，3D 打印所用原料密度为30.9/g cm ，不考虑打印损耗，∴制作该模型所需原料的质量为：1320.9118.8()g ⨯=．故答案为：118.8．16．（2018•全国）已知三棱锥O ABC -的体积为1，1A 、1B 、1C 分别为OA 、OB 、OC 的中点，则三棱锥111O A B C -的体积为__________． 【答案】18【解析】如图，1A 、1B 、1C 分别为OA 、OB 、OC 的中点，∴△111A B C ABC ∆∽，则11114A B C ABC SS ∆=， 过O 作OG ⊥平面ABC ，交平面111A B C 于1G ，则112OG OG =．∴1111111111383A B C ABC O A B C V S OG S OG ∆-=⋅=⨯⋅三棱锥1188O ABC V -==．故答案为：18．17．（2018•天津）如图，已知正方体1111ABCD A B C D -的棱长为1，则四棱锥111A BB D D -的体积为__________．【答案】13【解析】由题意可知四棱锥111A BB D D -的底面是矩形，边长：1和2， 四棱锥的高：111222AC =． 则四棱锥111A BB D D -的体积为：1211233⨯⨯⨯=．故答案为：13．18．（2018•天津）已知正方体1111ABCD A B C D -的棱长为1，除面ABCD 外，该正方体其余各面的中心分别为点E ，F ，G ，H ，M （如图），则四棱锥M EFGH -的体积为__________．【答案】112【解析】正方体的棱长为1，M EFGH -的底面是正方形的边长为：2， 四棱锥是正四棱锥，棱锥的高为12， 四棱锥M EFGH -的体积：21211()32212⨯⨯=．故答案为：112．19．（2018•江苏）如图所示，正方体的棱长为2，以其所有面的中心为顶点的多面体的体积为__________．【答案】43【解析】正方体的棱长为22， 八面体看做两个正四棱锥，棱锥的高为1，多面体的中心为顶点的多面体的体积为：14222133⨯=．故答案为：43．20．（2018•上海）如图，在长方体1111ABCD A B C D -中，3AB =，4BC =，15AA =，O 是11A C 的中点，则三棱锥11A AOB -的体积为__________．【答案】5【解析】1111111111134553322A A OBC A OB A OB V V S CC --===⨯⨯⨯⨯⨯=．故答案为：5．21．（2017•天津）已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18，则这个球的体积为__________． 【答案】92π【解析】设正方体的棱长为a ， 这个正方体的表面积为18， 2618a ∴=，则23a =，即3a =一个正方体的所有顶点在一个球面上，∴正方体的体对角线等于球的直径，32a R =， 即32R =， 则球的体积3439()322V ππ==；故答案为：92π． 22．（2017•新课标Ⅰ）已知三棱锥S ABC -的所有顶点都在球O 的球面上，SC 是球O 的直径．若平面SCA ⊥平面SCB ，SA AC =，SB BC =，三棱锥S ABC -的体积为9，则球O 的表面积为__________． 【答案】36π【解析】三棱锥S ABC -的所有顶点都在球O 的球面上，SC 是球O 的直径，若平面SCA ⊥平面SCB ，SA AC =，SB BC =，三棱锥S ABC -的体积为9，可知三角形SBC 与三角形SAC 都是等腰直角三角形，设球的半径为r ， 可得112932r r r ⨯⨯⨯⨯=，解得3r =．球O 的表面积为：2436r ππ=． 故答案为：36π．23．（2017•新课标Ⅰ）如图，圆形纸片的圆心为O ，半径为5cm ，该纸片上的等边三角形ABC 的中心为O ．D 、E 、F 为圆O 上的点，DBC ∆，ECA ∆，FAB ∆分别是以BC ，CA ，AB 为底边的等腰三角形．沿虚线剪开后，分别以BC ，CA ，AB 为折痕折起DBC ∆，ECA ∆，FAB ∆，使得D 、E 、F 重合，得到三棱锥．当ABC ∆的边长变化时，所得三棱锥体积（单位：3)cm 的最大值为__________．【答案】3415cm【解析】解法一：由题意，连接OD ，交BC 于点G ，由题意得OD BC ⊥，3OG =， 即OG 的长度与BC 的长度成正比， 设OG x =，则23BC x =，5DG x =-，三棱锥的高222225102510h DG OG x x x x --+--， 2213(23)332ABC S x x ∆==，则24132510325103ABC V S h x x x ∆=⨯=--令45()2510f x x x =-，5(0,)2x ∈，34()10050f x x x '=-，令()0f x '，即4320x x -，解得2x ， 则()f x f （2）80=，3380415V cm ∴⨯=，∴体积最大值为3415cm ．故答案为：3415cm ．解法二：如图，设正三角形的边长为x ，则1333OG ==，35FG SG x ∴==， 2222333(5)()5(5)663SO h SG GO x x x ==----， ∴三棱锥的体积13ABC V S h ∆=451331535(5)533123x x x =--， 令453()5b x x =-，则3453()20b x x '=， 令()0b x '=，则43403x =，解得43x =∴3754854415()max V cm =-=． 故答案为：3415cm ．24．（2020•上海）已知四棱锥P ABCD -，底面ABCD 为正方形，边长为3，PD ⊥平面ABCD ． （1）若5PC =，求四棱锥P ABCD -的体积； （2）若直线AD 与BP 的夹角为60︒，求PD 的长．【解析】（1）PD ⊥平面ABCD ，PD DC ∴⊥．3CD =，5PC ∴=，4PD ∴=， 2134123P ABCD V -∴=⨯⨯=，所以四棱锥P ABCD -的体积为12． （2）ABCD 是正方形，PD ⊥平面ABCD ，BC PD ∴⊥，BC CD ⊥又PD CD D =BC ∴⊥平面PCD BC PC ∴⊥异面直线AD 与PB 所成角为60︒，//BC AD∴在Rt PBC ∆中，60PBC ∠=︒，3BC =故33PC =在Rt PDC ∆中，3CD = 32PD ∴=25．（2019•新课标Ⅱ）如图，长方体1111ABCD A B C D -的底面ABCD 是正方形，点E 在棱1AA 上，1BE EC ⊥．（1）证明：BE ⊥平面11EB C ；（2）若1AE A E =，3AB =，求四棱锥11E BB C C -的体积．【解析】（1）证明：由长方体1111ABCD A B C D -，可知 11B C ⊥平面11ABB A ，BE ⊂平面11ABB A ， 11B C BE ∴⊥，1BE EC ⊥，1111B C EC C =，BE ∴⊥平面11EB C ；（2）由（1）知190BEB ∠=︒，由题设可知Rt ABE Rt ∆≅△11A B E ， 1145AEB A EB ∴∠=∠=︒，3AE AB ∴==，126AA AE ==，在长方体1111ABCD A B C D -中，1//AA 平面11BB C C ，1E AA ∈，AB ⊥平面11BB C C ，E ∴到平面11BB C C 的距离3d AB ==，∴四棱锥11E BB C C -的体积1363183V =⨯⨯⨯=．26．（2017•新课标Ⅱ）如图，四棱锥P ABCD -中，侧面PAD 为等边三角形且垂直于底面ABCD ，12AB BC AD ==，90BAD ABC ∠=∠=︒． （1）证明：直线//BC 平面PAD ；（2）若PCD ∆面积为27，求四棱锥P ABCD -的体积．【解析】（1）四棱锥P ABCD -中，90BAD ABC ∠=∠=︒．//BC AD ∴，AD ⊂平面PAD ，BC ⊂/平面PAD ，∴直线//BC 平面PAD ；（2）解：四棱锥P ABCD -中，侧面PAD 为等边三角形且垂直于底面ABCD ，12AB BC AD ==，90BAD ABC ∠=∠=︒．设2AD x =，则AB BC x ==，2CD x =，O 是AD 的中点， 连接PO ，OC ，CD 的中点为：E ，连接OE ， 则2OE ，3PO x =，2272xPE PO OE +=PCD ∆面积为271272PE CD =即：1722722x x =2x =，23PO =则1111()(24)223433232P ABCD V BC AD AB PO -=⨯+⨯⨯=⨯⨯+⨯⨯1．（2020•沈河区校级模拟）在三棱锥A SBC -中，10AB =，4ASC BSC π∠=∠=，AC AS =，BC BS =，若该三棱锥的体积为15，则三棱锥S ABC -外接球的体积为( ) A ．π B ．43π C ．5π D ．3π【答案】B 【解析】如图，设SC 的中点为O ，AB 的中点为D ，连接OA 、OB 、OD ， 4ASC BSC π∠=∠=，AC AS =，BC BS =，90SAC SBC ∴∠=∠=︒，则OA OB OC OS ===，则O 为三棱锥三棱锥S ABC -外接球的球心，设半径为R ，又OD AB ⊥，且10AB 10AD DB ∴==252OD R =-．则211102522OAB S AB OD R ∆==- 又由SC OA ⊥，SC OB ⊥，且OAOB O =，可得SC ⊥平面OAB ，∴211151025232A SBC V R R -=-=，解得3R = ∴三棱锥S ABC -外接球的体积为34(3)433ππ=．故选B ．2．（2020•凉山州模拟）已知长方体1111ABCD A B C D -的体积12V =，2AB =，若四面体11A B CD -的外接球的表面积为S ，则S 的最小值为( ) A ．8π B ．9πC ．16πD ．32π【答案】C【解析】设BC x =，1BB y =，由于12V =，所以6xy =．根据长方体的对称性可知四面体11A B CD -的外接球的即为长方体的外接球，所以224x y r ++=，所以2224(4)(42)16S r x y xy ππππ==+++=（当且仅当6x y ==． 故选C ．3．（2020•迎泽区校级二模）已知三棱锥A BCD -中，2AB AC BC ===，2BD CD ==E 是BC 的中点，点A 在平面BCD 上的射影恰好为DE 的中点，则该三棱锥外接球的表面积为( ) A ．3011πB ．6011πC ．916π D ．2516π【答案】B【解析】由题意，BCD ∆为等腰直角三角形，E 是外接圆的圆心， 点A 在平面BCD 上的射影恰好为DE 的中点F ， 则1514BF =+=； 51144AF ∴=-； 设球心到平面BCD 是距离为h ，则221111()4h h +=+-， 11h ∴=41511111r =+=∴该三棱锥外接球的表面积为260411S R ππ==故选B ．4．（2020•南充模拟）在直角梯形ABCD 中，90ADC DAB ACB ∠=∠=∠=︒，ADC ∆与ABC ∆均为等腰直角三角形，且1AD =，若将直角梯形ABCD 沿AC 折叠成三棱锥D ABC -，则当三棱锥D ABC -的体积取得最大时其外接球的表面积为()A ．4πB ．6πC ．8πD ．10π【答案】A【解析】直角梯形ABCD 中，90ADC DAB ACB ∠=∠=∠=︒，ADC ∆与ABC ∆均为等腰直角三角形，且1AD =，所以2AB =，2BC =，2AC =，将直角梯形ABCD 沿AC 折叠成三棱锥D ABC -， 如图所示：即当平面ABC ⊥平面ADC 时，三棱锥D ABC -的体积取得最大值， 过E 作OE ⊥平面ACD 交AB 于O ，由于平面ABC ⊥平面ADC ， 所以EO AC ⊥，即O 为AB 的中点， 所以O 为ABC ∆的中心，即为三棱锥D ABC -的外接球的球心． 所以半径1r OA OB OC OD =====， 则2414S ππ=⋅=球． 故选A ．5．（2020•镜湖区校级模拟）已知三棱锥S ABC -中，SC ⊥平面ABC ，若2SC AB AC ===，120BAC ∠=︒，则其外接球O 的表面积为( )A ．20πB ．205πC ．16πD ．272π【答案】A【解析】如图所示：三棱锥S ABC -中，SC ⊥平面ABC ，若2SC AB AC ===，120BAC ∠=︒， 所以在ABC ∆中，利用余弦定理：22212cos 44222()122BC AB CA AB CA BAC =+-∠=+-⨯⨯⨯-=解得：23BC =，设ABC ∆的外接圆的半径为r ， 则2324r ==，解得2r =，设外接球的半径为R ，满足222215R =+=． 所以4520S ππ=⋅=球． 故选A ．6．（2020•南岗区校级模拟）已知三棱锥P ABC -的四个顶点都在球O 的球面上，若PA ⊥平面ABC ，2PA BC ==，1sin 3BAC ∠=，则球O 的表面积为( ) A 4010πB ．172π C ．80π D ．40π【答案】D【解析】如图所示：由于PA⊥平面ABC，2PA BC==，1 sin3BAC∠=，则ABC∆的外接圆的半径满足2261sin3BCRBAC===∠，解得3R=，三棱锥P ABC-的四个顶点都在球O的球面，设外接球的半径为r，所以22()102PAr R=+=，所以球O的表面积为24(10)40Sππ=⋅=球．故选D．7．（2020•全国四模）如图，在三棱锥A BCD-中，BD⊥平面ADC，1BD=，2AB=，3BC=，11AC=，则三棱锥A BCD-外接球的体积为()A．4πB．3πC．23πD．43π【答案】D【解析】由1BD=，2AB=，3BC=，11AC=BD⊥平面ADC，3AD∴22CD=，11AC AD CD⊥，三棱锥A BCD-，是长方体的一个角，外接球的直径是长方体的体对角线，所以三棱锥A BCD-22211(22)(3)32++所以外接球的体积34(3)433Vππ=⨯=．，故选D．8．（2020•碑林区校级模拟）已知正四棱锥P ABCD -中，2PA =，且所有的棱长相等，则该四棱锥的外接球的表面积为( ) A ．16π B ．12π C ．10π D ．8π【答案】D【解析】如图，设正四棱锥底面的中心为1O ，设外接球的球心为O ， 则O 在正四棱锥的高PO 上． 在直角三角形ABC 中，22AC =， 12AO =，则高1422PO =-=，则112OO PO R R =-=-，OA R =，在直角三角形1AO O 中，222(2)(2)R R =-+， 解得2R =，即O 与1O 重合，即正四棱锥外接球的球心是它的底面的中心1O ，且球半径2R =， 球的表面积248S R ππ==， 故选D ．9．（2020•黄州区校级三模）在三棱锥A BCD -中，ABC ∆和BCD ∆都是边长为2的正三角形，当三棱锥A BCD -的表面积最大时，其内切球的半径是( ) A ．226B ．23C 2D 6【答案】A【解析】在三棱锥A BCD -中，ABC ∆和BCD ∆都是边长为2的正三角形， 三棱锥A BCD -的表面积为S ，23234sin ABD ACD S S S ABD ∆∆=++=+∠故当AB BD ⊥时，表面积最大，为423+， 过A 作BC 的垂线，垂足为E ，连接ED ， 三棱锥A BCD -的体积为V ， 122223B AEDC AED V V V --=+==设内切球的半径为r ，因为13Sr V =，所以226r =-．故选A ．10．（2020•青羊区校级模拟）已知三棱锥A BCD -中，BAC ∆和BDC ∆是全等的等边三角形，边长为2，当三棱锥体积最大时，三棱锥的外接球表面积为( ) A ．4π B ．163π C ．203πD ．8π【答案】C【解析】如图，当平面BAC ⊥平面BDC 时，三棱锥体积最大， 取BC 中点E ，连接AE 、DE ，则AE BC ⊥，DE BC ⊥，因为平面BAC ⊥平面BDC ，所以可证得AE ⊥平面BCD ，DE ⊥平面ABC ， 取三角形BCD 的外心F ，作//FM AE ，则F 、M 、E 、A 四点共面， 取三角形ABC 的外心H ，过点H 作EF 的平行线交FM 于点O ， 因为EF 垂直平面ABC ，则HO 垂直平面ABC ， 于是点O 到A 、B 、C 、D 四点的距离相等， 所以点O 为三棱锥A BCD -外接球的球心． 连接OC ，可求得3OF HE =23CF所以2222145333R OC OF CF ==+=+=，所以外接球表面积为22043S R ππ==． 故选C ．11．（2020•青岛模拟）在三棱柱111ABC A B C -中，AB BC AC ==，侧棱1AA ⊥底面ABC ，若该三棱柱的所有顶点都在同一个球O 的表面上，且球O 的表面积的最小值为4π，则该三棱柱的侧面积为( ) A ．63B ．33C ．32 D ．3【答案】B【解析】设三棱柱两底面中心分别为12O O ，则12O O 的中点为球的球心， 设正三棱柱的底面边长AB a =，棱柱的高为h ，则13O A =，12hOO =， ∴球O 的半径2234a h r OA ==+ 222444234233Oa h h S r πππ⎛⎫∴==+⋅= ⎪⎝⎭球，球O 的表面积的最小值为4π， 3ah ∴=∴棱柱的侧面积为333S ah ==侧面积故选B ．12．（2020•运城模拟）已知长方体1111ABCD A B C D -的顶点A ，B ，C ，D 在球O 的表面上，顶点1A ，1B ，1C ，1D ，在过球心O 的一个平面上，若1AB =，3AD =，14AA =，则球O 的表面积为() A ．26π B ．29π C ．53π D ．74π【答案】D【解析】把两个这样的长方体叠放在一起，构成一个长宽高分别为1，3，8的长方体， 则球O 就是该长方体的外接球，所以球O 的半径满足222213874R =++=， 所以球O 的表面积2474S R ππ==， 故选D ．13．（2020•香坊区校级一模）《九章算术》是我国古代著名数学经典，其中对勾股定理的论述，比西方早一千多年，其中有这样一个问题：“今有圆材埋在壁中，不知大小；以锯锯之，深一寸，锯道长一尺，问径几何？”其意为：今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯该材料，锯口深1寸，锯道长1尺，问这块圆柱形木料的直径是多少？长为0.5丈的圆柱形木材部分镶嵌在墙体中，截面图如图所示（阴影部分为镶嵌在墙体内的部分）．已知弦1AB =尺，弓形高1CD =寸，估算该木材镶嵌墙内部分的体积约为( )（注：一丈10=尺100=寸， 3.14π≈，5sin 22.5)13︒≈A ．300立方寸B ．305.6立方寸C ．310立方寸D ．316.6立方寸【答案】D 【解析】如图，10AB =（寸)，则5AD =（寸)，1CD =（寸)，设圆O 的半径为x （寸)，则(1)OD x =-（寸)，在Rt ADO ∆中，由勾股定理可得：2225(1)x x +-=，解得：13x =（寸)． 5sin 13AD AOD AO ∴∠==，即22.5AOD ∠≈︒，则45AOB ∠=︒． 则弓形ACB 的面积211131012 6.3325242S π=⨯⨯-⨯⨯≈（平方寸）．则该木材镶嵌在墙中的体积约为 6.332550316.6V =⨯≈（立方寸）． 故选D ．14．（2020•内江三模）如图该几何体由半圆柱体与直三棱柱构成，半圆柱体底面直径4BC =，AB AC =，90BAC ∠=︒，D 为半圆弧的中点，若异面直线BD 和1AA 所成角的正切值为2，则该几何体的体积为( )A ．168π+B ．3216π+C ．328π+D ．1616π+【答案】A【解析】连1A D ，由题设知1A 、D 关于1B C 对称，以A 为坐标原点，分别以AC 、AB 、1AA 所在直线为x 、y 、z 轴建立如图所示的空间直角坐标系，设1AA h =，则(0A ，0，0)，(0B ，22，0)，1(0A ，0，)h ，(22D ，22，)h ，(22BD =，0，)h ，1(0AA =，0，)h ，异面直线BD 和1AA 所成角的正切值为22， ∴异面直线BD 和1AA 所成角的余弦值为63， ∴2121||63||||8BD AA h BD AA h h==+， 216h ∴=，得4h =，∴该几何体的体积221111()222242416822222BC V AB AC h h πππ=+=+=+． 故选A ．15．（2020•内江三模）如图该几何体由半圆柱体与直三棱柱构成，半圆柱体底面直径4BC =，AB AC =，90BAC ∠=︒，D 为半圆弧的中点，若异面直线BD 和1AB 所成角的余弦值为23，则该几何体的体积为( )A ．168π+B ．3216π+C ．328π+D ．1616π+【答案】A【解析】连1A D ，由题设知1A 、D 关于1B C 对称，以A 为坐标原点，分别以AC 、AB 、1AA 所在直线为x 、y 、z 轴建立如图所示的空间直角坐标系，设1AA h =，则(0A ，0，0)，(0B ，22，0)，1(0B ，22，)h ， (22D ，22，)h ，(22BD =，0，)h ，1(0AB =，22，)h ，异面直线BD 和1AB 所成角的的余弦值为23， ∴21221||23||||88BD AB BD AB h h ==++，222163h h ∴+=，解得4h =，∴该几何体的体积221111()222242416822222BC V AB AC h h πππ=+=+=+． 故选A ．16．（2020•市中区校级模拟）已知各顶点都在一个球面上的正四棱锥的高为3，体积为6，则这个球的半径为( ) A ．2 B 5 C 6 D ．3【答案】A【解析】正四棱锥P ABCD -的外接球的球心在它的高1PO 上，记为O ， PO AO R ==，13PO =，13OO R =-，在Rt △1AO O 中，223(3)R R =+-得2R =，∴球的半径为2．故选A ．17．（2020•雨花区校级模拟）如图，四边形ABCD 的面积为22，且90ABD BDC ∠=∠=︒，把BCD ∆绕BD 旋转，使点C 运动到P ，此时向量BA 与向量DP 的夹角为90︒．则四面体ABDP 外接球表面积的最小值为( )A ．823B ．62πC ．8πD ．10π【答案】C【解析】由题意，设2AB a =，2BD b =，2DC c =， 向量BA 与向量DP 的夹角为90︒． 则2cb bc +四面体ABDP 外接球为:R2222(2)(2)(2)(2)R a b c =++2222222211()()2()222R a b c a b b c ab bc ⇒=++=++++=，当且仅当22b a c ==时，取等号，故四面体ABDP 外接球表面积的最小值248S R ππ==． 故选C ．18．（2020•庐阳区校级模拟）中国古代第一部数学名著《九章算术》中，将一般多面体分为阳马，鳖臑，堑堵三种基本立体图形，其中四个面都为直角三角形的四面体称之为鳖臑，若三棱锥P ABC -为鳖臑，PA ⊥底面ABC ，AB BC ⊥，2PA BC ==7PC ，则此鳖臑的体积为() A ．3 B ．3 C ．23D ．23【答案】A【解析】三棱锥P ABC -为鳖臑，PA ⊥底面ABC ，AB BC ⊥， 2PA BC ==，7PC =，725AC ∴=-=，523AB =-=，∴此鳖臑的体积为：111332P ABC ABC V S PA AB BC PA -∆=⨯⨯=⨯⨯⨯⨯11332232=⨯⨯⨯⨯=． 故选A ．19．（2020•雨花区校级模拟）由棱长都为1的4个正四面体和1个正八面体，组合成一个正四面体，再将此正四面体削切、打磨成最大的球，则该球体积为( ) A 6B 6C 3D 646【答案】A【解析】把4个正四面体、12的正方体中，组成棱长为2的正四面体，转化为求其内切球体积．高为2232262(2)23-⨯⨯，12664r ==，334466()33V r ππ=⨯=⨯=，故选A ．20．（2020•吉林模拟）阿基米德立体是一种高度对称的半正多面体，并且都是可以从正多面体经过截角、截半、截边等操作构造而成．阿基米德立体的三个视图全都一样，如图是棱长为2的正方体经过截角得到的阿基米德立体的正视图，则该几何体的表面积为( )A ．623+B ．1223+C ．1243+D ．1643+【答案】C【解析】该几何体的直观图如图所示，是通过正方体各棱的中点，将八个角截去，形成的正14面体，其中有8个正三角形面，6个正方形面．正14面体的棱长为2，所以6个正方形面的面积之和为26(2)12⨯=，8个正三角形面的面积之和为218(2)sin 60432⨯⨯⨯︒=，所以几何体的表面积之和为1243+．故选C ．21．（2020•衡水模拟）已知圆锥的底面半径为2，高为4．一个圆柱的下底面在圆锥的底面上，上底面的圆周在圆锥的侧面上，当圆柱侧面积为4π时该圆柱的体积为( ) A ．π B ．2π C ．3π D ．4π【答案】B【解析】圆锥的轴截面如图所示， 设圆柱底面半径为r ，02r <<， 由题意可知△1AO D ∽△2AO C ， 则有12122AO AO O D O C==，12AO r ∴=，则圆柱的高42h r =-， 其侧面积22(42)4(2)4S r r r r πππ=-=-+=，解得1r =． 当1r =时，2h =，∴该圆柱的体积22V r h ππ==． 故选B ．22．（2020•原州区校级模拟）如图，正四面体ABCD ，E ，F ，P ，Q 分别是AB ，AD ，DC ，CB 的中点，AQ ，AP ，CE ，CF 的中点分别为L ，M ，K ，N ，四边形LMNK 的面积为1．则该正四面体体积是( )A ．4B ．2C ．163D ．23【答案】D【解析】设BD 的中点G ，连接AG ，CG ，则有BD AG ⊥，BD CG ⊥， 又AGCG G =，BD ∴⊥平面ACG ，则BD AC ⊥，又////BD PQ LM ，////LK EQ AC ，且1124LK EQ AC ==，1124LM PQ BD ==， ∴四边形LMNK 为正方形，设正四面体ABCD 的棱长为a ，则有14LM LK a ==，由四边形LMNK 的面积为1，得21116a =，即4a =． 设正四面体的高为AO ，则2246AO AC CO =-=， ∴正四面体的体积为111346162443323BCD V S AO ∆==⨯⨯⨯⨯⨯=． 故选D ．23．（2020•福州三模）若圆锥的内切球（球面与圆锥的侧面以及底面都相切）的半径为1，当该圆锥体积取最小值时，该圆锥体积与其内切球体积比为( ) A ．8:3 B ．6:1C ．3:1D ．2:1【答案】D【解析】设圆锥的高为h ，底面半径为r ， 则当圆锥体积最小时，如图，由~AOE ACF ∆∆可得：22(1)11h r --=22r h h =-∴圆锥的体积22148[(2)4]33(2)323h V r h h h h ππππ===-++--． 当且仅当22h -=，即4h =时取等号．∴该圆锥体积的最小值为83π． 内切球体积为43π． 该圆锥体积与其内切球体积比2:1． 故选D ．24．（2020•桃城区校级二模）在如图所示的空间几何体中，下面的长方体1111ABCD A B C D -的三条棱长4AB AD ==，12AA =，上面的四棱锥1111P A B C D -中11D E C E =，PE ⊥平面1111A B C D ，1PE =，则过五点A 、B 、C 、D 、P 的外接球的表面积为( )A ．3119πB ．31118πC ．3139πD ．31318π【答案】C【解析】问题转化为求四棱锥P ABCD -的外接球的表面积， 4913PC =+∴sin 13PCD ∠=所以PCD ∆外接圆的半径为13136213r =， 由于PE ⊥平面1111A B C D ，则PE ⊥平面ABCD ，PE ⊂平面PCD ， 所以平面PCD ⊥平面ABCD ， 所以222169313243636R r =+=+=， 所以231349S R ππ==球表面积．故选C ．25．（2020•梅河口市校级模拟）若正三棱柱的各个顶点均在同一个半径为1的球面上，且正三棱柱的侧面均为正方形，则该三棱柱的表面积为( ) A ．123(2)7+ B ．123(3)7+ C ．123(4)7+ D ．123(5)7+ 【答案】B【解析】根据题意，作出如下所示的图形，其中O 为球心，也为正三棱柱的中心，B 为上底面三角形的重心，设正三棱柱的侧棱长为x ，则其上下底面是边长为x 的等边三角形， 所以3AB ，12OB x =， 在Rt ABO ∆中，222AO AB BO =+，即22311()()2x x =+，解得2127x =． 所以该三棱柱的表面积21312332(327S x x x =+=． 故选B ．26．（2020•西安模拟）已知点A 、B 、C 在球心为O 的球面上，若5AB AC ==，6BC =，球心O 到截面ABC 的距离为1，则该球的表面积为__________． 【答案】68916π【解析】由5AB AC ==，6BC =，可知ABC ∆是等腰三角形，作BC 的高线h ，可得4h =，那么4sin 5B =； 由正弦定理：2sin ACr B=， 可得ABC ∆外接圆的半径258r =， 球心O 到平面ABC 的圆心1O 距离为1，得11O O =， 那么球的226898R r d =+=∴则该球的表面积2689416S R ππ==故答案为：68916π．27．（2020•启东市校级模拟）《九章算术》是我国数学史上堪与欧几里得《几何原本》相媲美的数学名著．其中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马；将四个面都为直角三角形的四面体称之为鳖臑．已知直三棱柱111A B C ABC -中，AB BC ⊥，3AB =，4BC =，153AA =，将直三棱柱沿一条棱和两个面的对角线分割为一个阳马和一个鳖臑，则鳖臑的体积与其外接球的体积之比为__________． 【答案】33:50π【解析】如图所示：，鳖臑为三棱锥111B AAC -，体积为11345310332⨯⨯⨯⨯=，因为鳖臑的四个面都为直角三角形，所以其外接球的球心为Rt △11AA C 的斜边的中点， 所以其外接球的半径为221115(53)522AC =⨯+=， 所以其外接球的体积为34500533ππ⨯=，所以鳖臑的体积与其外接球的体积之比为10333:505003ππ=， 故答案为：33:50π．28．（2020•红河州一模）已知圆台12O O 上底面圆1O 的半径为2，下底面圆2O 的半径为22，圆台的外接球的球心为O ，且球心在圆台的轴12O O 上，满足12||3||O O OO =，则圆台12O O 的外接球的表面积为__________． 【答案】34π【解析】设外接球的半径为R ，几何体的轴截面如图： 221||2O O R =-，222||(22)OO R =-，且12||3||O O OO =，得224972R R -=-， 解得2172R =，球O 的表面积为2434R ππ=． 故答案为：34π．29．（2020•龙潭区校级模拟）《九章算术》是中国古代张苍、耿寿昌所撰写的一部数学专著．是《算经十书》中最重要的一部，其中将有三条棱互相平行且有一个面为梯形的五面体称之为“羡除”，现有一个羡除如图所示，已知上底面ABCD 是高为2的等腰梯形，右侧面BCEF 是高为1的等腰梯形，下底面是梯形，前、后侧面均为三角形．8AD =，10BC =，6EF =，////AD BC EF ，且平面ABCD ⊥平面BCEF ，则该“羡除”的表面积为__________．【答案】267521++ 【解析】()18102182ABCD S =⨯+⨯=梯形，()1106182BCEF S =⨯+⨯=梯形， 在等腰梯形ABCD 中，8AD =，10BC =，梯形的高为2，221082()52AB -∴=+=， 同理可得：221061()52BF -=+=， 过F 作FM BC ⊥于M ，过M 作MN AD ⊥于N ，连接FN ，则有1FM =，2MN =，则2BM =，1AN =，BC FM ⊥，BC MN ⊥，FM M N M =，BC ∴⊥平面FMN ，BC FN ∴⊥，又//BC AD ，AD FN ∴⊥．平面ABCD ⊥平面BCEF ，90NMF ∴∠=︒，5FN ∴=，6AF =，()1865752ADEF S ∴=⨯+⨯=梯形， 在等腰ABF ∆中，B 到AF 的距离为26145()2-=， 1142162ABF S ∆∴=⨯⨯=， 由对称性可知21DCE ABF S S ∆∆==， ∴该“羡除”的表面积为：21211887526752122++++=++． 故答案为：267521++．。

收集整理：宋氏资料2016-1-12016 高考立体几何知识点总结一、空间几何体（一）空间几何体的类型1 多面体：由若干个平面多边形围成的几何体。

围成多面体的各个多边形叫做多面体的面，相邻两个面的公共边叫做多面体的棱，棱与棱的公共点叫做多面体的顶点。

2 旋转体：把一个平面图形绕它所在的平面内的一条定直线旋转形成了封闭几何体。

其中，这条直线称为旋转体的轴。

（二）几种空间几何体的结构特征1 、棱柱的结构特征1.1 棱柱的定义：有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体叫做棱柱。

1.2棱柱的分类图1-1 棱柱底面是四边形棱柱四棱柱底面是平行四边形侧棱垂直于底面底面是矩形底面是正方形平行六面体直平行六面体长方体棱长都相等正四棱柱正方体性质：Ⅰ、侧面都是平行四边形，且各侧棱互相平行且相等；Ⅱ、两底面是全等多边形且互相平行；Ⅲ、平行于底面的截面和底面全等；1.3棱柱的面积和体积公式S直棱柱侧（c 是底周长，h 是ch高）S 直棱柱表面= c·h+ 2S底V 棱柱= S 底·h2 、棱锥的结构特征2.1 棱锥的定义（1）棱锥：有一个面是多边形，其余各面是有一个公共顶点的三角形，由这些面所围成的几何体叫做棱锥。

（2）正棱锥：如果有一个棱锥的底面是正多边形，并且顶点在底面的投影是底面的中心，这样的棱锥叫做正棱锥。

2.2 正棱锥的结构特征Ⅰ、平行于底面的截面是与底面相似的正多边形，相似比等于顶点到截面的距离与顶点到1底面的距离之比；它们面积的比等于截得的棱锥的高与原棱锥的高的平方比；截得的棱锥的体积与原棱锥的体积的比等于截得的棱锥的高与原棱锥的高的立方比；Ⅱ、正棱锥的各侧棱相等，各侧面是全等的等腰三角形；正棱锥侧面积：1S正棱椎ch （c为底周长，h'为斜高）'2P体积：1V棱椎Sh（S为底面积，h 为高）3D CO H正四面体：A B2对于棱长为a正四面体的问题可将它补成一个边长为 a的正方体问题。

高三数学空间几何体试题答案及解析1.有一正方体,六个面上分别写有数字1、2、3、4、5、6,有3个人从不同的角度观察,结果如图所示.若记3的对面的数字为,4的对面的数字为,则 ( )A．3B．7C．8D．11【答案】C【解析】从图中可看出，与4相邻的是1、6、3、5，故与4相对的是2；与3相邻的是1、2、4、5，故与3相对的是6，所以.【考点】空间几何体.2.有一正方体,六个面上分别写有数字1、2、3、4、5、6,有3个人从不同的角度观察,结果如图所示.若记3的对面的数字为,4的对面的数字为,则 ( )A．3B．7C．8D．11【答案】C【解析】从图中可看出，与4相邻的是1、6、3、5，故与4相对的是2；与3相邻的是1、2、4、5，故与3相对的是6，所以.【考点】空间几何体.3.已知矩形的周长为36，矩形绕它的一条边旋转形成一个圆柱，则旋转形成的圆柱的侧面积的最大值为．【答案】81【解析】假设矩形的一边为（），则另一边为.以x长的变为轴旋转成的圆柱的侧面积为.所以当时，.【考点】1.旋转体的知识.2.函数的最值问题.4.已知四面体的外接球的球心在上，且平面，，若四面体的体积为，则该球的表面积为（）A．B．C．D．【答案】D【解析】如下图所示，由于四面体的外接球的球心在上，则为其外接球的一条直径，因此，设球的半径为，在中，，由勾股定理得，，由于为球上一点，则，且平面，所以，，所以球的表面积为，故选D.【考点】1.勾股定理；2.三角形的面积；3.三棱锥的体积；4.球的表面积5.如图所示,在正方体ABCD A1B1C1D1中,M,N分别是BC1,CD1的中点,则下列判断错误的是()A．MN与CC1垂直B．MN与AC垂直C．MN与BD平行D．MN与A1B1平行【答案】D【解析】由于C1D1与A1B1平行,MN与C1D1是异面直线,所以MN与A1B1是异面直线,故选项D错误.6.如图,正方形BCDE的边长为a,已知AB=BC,将直角△ABE沿BE边折起,A点在平面BCDE 上的射影为D点,则对翻折后的几何体有如下描述:(1)AB与DE所成角的正切值是.(2)三棱锥B-ACE的体积是a3.(3)AB∥CD.(4)平面EAB⊥平面ADE.其中正确的叙述有(写出所有正确结论的编号).【答案】(1)(2)(4)【解析】翻折后得到的直观图如图所示.AB与DE所成的角也就是AB与BC所成的角,即为∠ABC.因为AD⊥平面BCDE,所以平面ADC⊥平面BCDE. 又因为四边形BCDE为正方形,所以BC⊥CD.可得BC⊥平面ACD.所以BC⊥AC.因为BC=a,AB=BC=a,则AC== a.在Rt△ABC中,tan∠ABC==.故(1)正确;由AD==a,可得VB-ACE =VA-BCE=×a2·a=,故(2)正确;因为AB与CD异面,故(3)错;因为AD⊥平面BCDE,所以平面ADE⊥平面BCDE.又BE⊥ED,所以BE⊥平面ADE,故平面EAB⊥平面ADE,故(4)正确.7.如图所示的几何体ABCDFE中，△ABC，△DFE都是等边三角形，且所在平面平行，四边形BCED为正方形，且所在平面垂直于平面ABC．（Ⅰ）证明：平面ADE∥平面BCF；（Ⅱ）求二面角D－AE－F的正切值．【答案】（Ⅰ）利用线线平行，则面面平行证明，即可得证；（Ⅱ）.【解析】（Ⅰ）先证明四边形为平行四边形得，又，所以平面平面；（Ⅱ）建立空间直角坐标系，先求出平面的一个法向量，再求出平面的一个法向量，然后利用公式即可求出余弦值为，进而求出正切值.试题解析：（Ⅰ）取的中点，的中点，连接.则，又平面平面，所以平面，同理平面，所以又易得，所以四边形为平行四边形，所以，又，所以平面平面. （6分）（Ⅱ）建立如图所示的空间直角坐标系，设，则,,，，，.设平面的一个法向量是，则，令，得. （9分）设平面的一个法向量是，则令，得.所以，易知二面角为锐二面角，故其余弦值为，所以二面角的正切值为. （12分）【考点】1.平面与平面垂直的判定方法；2.二面角的求法.8.已知某四棱锥的三视图，如图。

空间几何体[考情分析] 几何体的结构特征是立体几何的基础，空间几何体的表面积与体积是高考题的重点与热点，多以小题的形式进行考查，属于中等难度． 考点一 表面积与体积 核心提炼1．旋转体的侧面积和表面积(1)S 圆柱侧＝2πrl ，S 圆柱表＝2πr (r ＋l )(r 为底面半径，l 为母线长)． (2)S 圆锥侧＝πrl ，S 圆锥表＝πr (r ＋l )(r 为底面半径，l 为母线长)． (3)S 球表＝4πR 2(R 为球的半径)． 2．空间几何体的体积公式 V 柱＝Sh (S 为底面面积，h 为高)； V 锥＝13Sh (S 为底面面积，h 为高)；V 球＝43πR 3(R 为球的半径)．例1 (1)已知圆锥的顶点为S ，母线SA ，SB 所成角的余弦值为78，SA 与圆锥底面所成角为45°.若△SAB 的面积为515，则该圆锥的侧面积为________． 答案 402π解析 因为母线SA 与圆锥底面所成的角为45°， 所以圆锥的轴截面为等腰直角三角形． 设底面圆的半径为r ，则母线长l ＝2r .在△SAB 中，cos ∠ASB ＝78，所以sin ∠ASB ＝158.因为△SAB 的面积为515，即12SA ·SB sin ∠ASB＝12×2r ×2r ×158＝515， 所以r 2＝40，故圆锥的侧面积为πrl ＝2πr 2＝402π.(2)如图，已知正三棱柱ABC －A 1B 1C 1的各棱长均为2，点D 在棱AA 1上，则三棱锥D －BB 1C 1的体积为________．答案 233解析 如图，取BC 的中点O ，连接AO .∵正三棱柱ABC －A 1B 1C 1的各棱长均为2， ∴AC ＝2，OC ＝1，则AO ＝ 3. ∵AA 1∥平面BCC 1B 1，∴点D 到平面BCC 1B 1的距离为 3. 又11BB C S＝12×2×2＝2， ∴11D BB C V ＝13×2×3＝233.易错提醒 (1)计算表面积时，有些面的面积没有计算到(或重复计算)． (2)一些不规则几何体的体积不会采用分割法或补形思想转化求解． (3)求几何体体积的最值时，不注意使用基本不等式或求导等确定最值．跟踪演练1 (1)已知圆柱的上、下底面的中心分别为O 1，O 2，过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为( ) A ．122π B ．12π C ．82π D ．10π答案 B解析 设圆柱的底面半径为r ，高为h ，由题意可知2r ＝h ＝22，∴圆柱的表面积S ＝2πr 2＋2πr ·h ＝4π＋8π＝12π.故选B.(2)如图，在Rt △ABC 中，AB ＝BC ＝1，D 和E 分别是边BC 和AC 上异于端点的点，DE ⊥BC ，将△CDE 沿DE 折起，使点C 到点P 的位置，得到四棱锥P －ABDE ，则四棱锥P －ABDE 的体积的最大值为________．答案327解析 设CD ＝DE ＝x (0<x <1)，则四边形ABDE 的面积S ＝12(1＋x )(1－x )＝12(1－x 2)，当平面PDE ⊥平面ABDE 时，四棱锥P －ABDE 的体积最大，此时PD ⊥平面ABDE ，且PD ＝CD ＝x ，故四棱锥P －ABDE 的体积V ＝13S ·PD ＝16(x －x 3)，则V ′＝16(1－3x 2)．当x ∈⎝⎛⎭⎫0，33时，V ′>0；当x ∈⎝⎛⎭⎫33，1时，V ′<0.∴当x ＝33时，V max ＝327. 考点二 多面体与球 核心提炼解决多面体与球问题的两种思路(1)利用构造长方体、正四面体等确定直径．(2)利用球心O 与截面圆的圆心O 1的连线垂直于截面圆的性质确定球心．例2 (1)已知三棱锥P －ABC 满足平面P AB ⊥平面ABC ，AC ⊥BC ，AB ＝4，∠APB ＝30°，则该三棱锥的外接球的表面积为__________． 答案 64π解析 因为AC ⊥BC ，所以△ABC 的外心为斜边AB 的中点，因为平面P AB ⊥平面ABC ，所以三棱锥P －ABC 的外接球球心在平面P AB 上， 即球心就是△P AB 的外心，根据正弦定理ABsin ∠APB ＝2R ，解得R ＝4，所以外接球的表面积为4πR 2＝64π.(2)(2020·全国Ⅲ)已知圆锥的底面半径为1，母线长为3，则该圆锥内半径最大的球的体积为________． 答案23π 解析 圆锥内半径最大的球即为圆锥的内切球，设其半径为r .作出圆锥的轴截面P AB ，如图所示，则△P AB 的内切圆为圆锥的内切球的大圆．在△P AB 中，P A ＝PB ＝3，D 为AB 的中点，AB ＝2，E 为切点，则PD ＝22，△PEO ∽△PDB ， 故PO PB ＝OE DB ，即22－r 3＝r 1，解得r ＝22， 故内切球的体积为43π⎝⎛⎭⎫223＝23π.规律方法 (1)长方体的外接球直径等于长方体的体对角线长．(2)三棱锥S －ABC 的外接球球心O 的确定方法：先找到△ABC 的外心O 1，然后找到过O 1的平面ABC 的垂线l ，在l 上找点O ，使OS ＝OA ，点O 即为三棱锥S －ABC 的外接球的球心． (3)多面体的内切球可利用等积法求半径．跟踪演练2 (1)已知A ，B 是球O 的球面上两点，∠AOB ＝90°，C 为该球面上的动点．若三棱锥O －ABC 体积的最大值为36，则球O 的表面积为( ) A ．36π B ．64π C ．144π D ．256π 答案 C解析 如图所示，设球O 的半径为R ，因为∠AOB ＝90°， 所以S △AOB ＝12R 2，因为V O －ABC ＝V C －AOB ， 而△AOB 的面积为定值，当点C 位于垂直于平面AOB 的直径端点时，三棱锥O －ABC 的体积最大， 此时V O －ABC ＝V C －AOB ＝13×12R 2×R ＝16R 3＝36，故R ＝6，则球O 的表面积为S ＝4πR 2＝144π.(2)中国古代数学经典《九章算术》系统地总结了战国、秦、汉时期的数学成就，书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的三棱锥称之为鳖臑，如图为一个阳马与一个鳖臑的组合体，已知P A ⊥平面ABCE ，四边形ABCD 为正方形，AD ＝5，ED ＝3，若鳖臑P －ADE 的外接球的体积为92π，则阳马P －ABCD 的外接球的表面积为________．答案 20π解析 ∵四边形ABCD 是正方形，∴AD ⊥CD ，即AD ⊥CE ，且AD ＝5，ED ＝3， ∴△ADE 的外接圆半径为r 1＝AE2＝AD 2＋ED 22＝2， 设鳖臑P －ADE 的外接球的半径为R 1， 则43πR 31＝92π，解得R 1＝322. ∵P A ⊥平面ADE ，∴R 1＝⎝⎛⎭⎫P A 22＋r 21， 可得P A 2＝R 21－r 21＝102，∴P A ＝10. 正方形ABCD 的外接圆直径为2r 2＝AC ＝2AD ＝10， ∴r 2＝102， ∵P A ⊥平面ABCD ，∴阳马P －ABCD 的外接球半径R 2＝⎝⎛⎭⎫P A 22＋r 22＝5， ∴阳马P －ABCD 的外接球的表面积为4πR 22＝20π. 专题强化练一、单项选择题1.水平放置的△ABC 的直观图如图，其中B ′O ′＝C ′O ′＝1，A ′O ′＝32，那么原△ABC 是一个( )A ．等边三角形B ．直角三角形C ．三边中只有两边相等的等腰三角形D ．三边互不相等的三角形 答案 A解析 AO ＝2A ′O ′＝2×32＝3，BC ＝B ′O ′＋C ′O ′＝1＋1＝2.在Rt △AOB 中，AB ＝12＋(3)2＝2，同理AC ＝2，所以原△ABC 是等边三角形．2．(2020·全国Ⅰ)埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥．以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为( )A.5－14 B.5－12 C.5＋14 D.5＋12答案 C解析 设正四棱锥的底面正方形的边长为a ，高为h ， 侧面三角形底边上的高(斜高)为h ′， 则由已知得h 2＝12ah ′.如图，设O 为正四棱锥S －ABCD 底面的中心，E 为BC 的中点，则在Rt △SOE 中，h ′2＝h 2＋⎝⎛⎭⎫a 22， ∴h ′2＝12ah ′＋14a 2，∴⎝⎛⎭⎫h ′a 2－12·h ′a －14＝0，解得h ′a ＝5＋14(负值舍去)．3．已知一个圆锥的侧面积是底面积的2倍，记该圆锥的内切球的表面积为S 1，外接球的表面积为S 2，则S 1S 2等于( )A.12B.13C.14D.18 答案 C 解析 如图，由已知圆锥侧面积是底面积的2倍，不妨设底面圆半径为r ，l 为底面圆周长，R 为母线长， 则12lR ＝2πr 2， 即12·2π·r ·R ＝2πr 2， 解得R ＝2r ，故∠ADC ＝30°，则△DEF 为等边三角形， 设B 为△DEF 的重心，过B 作BC ⊥DF ，则DB 为圆锥的外接球半径，BC 为圆锥的内切球半径，则BC BD ＝12，∴r 内r 外＝12，故S 1S 2＝14. 4．(2020·大连模拟)一件刚出土的珍贵文物要在博物馆大厅中央展出，如图，需要设计各面是玻璃平面的无底正四棱柱将其罩住，罩内充满保护文物的无色气体．已知文物近似于塔形，高1.8米，体积0.5立方米，其底部是直径为0.9米的圆形，要求文物底部与玻璃罩底边至少间隔0.3米，文物顶部与玻璃罩上底面至少间隔0.2米，气体每立方米1 000元，则气体的费用最少为( )A ．4 500元B ．4 000元C ．2 880元D ．2 380元 答案 B解析 因为文物底部是直径为0.9米的圆形，文物底部与玻璃罩底边至少间隔0.3米，所以由正方形与圆的位置关系可知，底面正方形的边长为0.9＋2×0.3＝1.5米，又文物高1.8米，文物顶部与玻璃罩上底面至少间隔0.2(米)，所以正四棱柱的高为1.8＋0.2＝2(米)，则正四棱柱的体积V ＝1.52×2＝4.5(立方米)．因为文物的体积为0.5立方米，所以罩内空气的体积为4.5－0.5＝4(立方米)，因为气体每立方米1 000元，所以气体的费用最少为4×1 000＝4 000(元)，故选B.5.如图所示，在正方体ABCD －A 1B 1C 1D 1中，动点E 在BB 1上，动点F 在A 1C 1上，O 为底面ABCD 的中心，若BE ＝x ，A 1F ＝y ，则三棱锥O －AEF 的体积( )A ．与x ，y 都有关B ．与x ，y 都无关C ．与x 有关，与y 无关D ．与y 有关，与x 无关 答案 B解析 由已知得V 三棱锥O －AEF ＝V 三棱锥E －OAF ＝13S △AOF ·h (h 为点E 到平面AOF 的距离)．连接OC ，因为BB 1∥平面ACC 1A 1，所以点E 到平面AOF 的距离为定值．又AO ∥A 1C 1，OA 为定值，点F 到直线AO 的距离也为定值，所以△AOF 的面积是定值，所以三棱锥O －AEF 的体积与x ，y 都无关．6．在梯形ABCD 中，∠ABC ＝π2，AD ∥BC ，BC ＝2AD ＝2AB ＝2.将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的体积为( ) A.2π3 B.4π3 C.5π3 D ．2π 答案 C解析 如图，过点C 作CE 垂直AD 所在直线于点E ，梯形ABCD 绕AD 所在直线旋转一周而形成的旋转体是由以线段AB 的长为底面圆半径，线段BC 为母线的圆柱挖去以线段CE 的长为底面圆半径，ED 为高的圆锥，该几何体的体积为V ＝V 圆柱－V 圆锥＝π·AB2·BC －13·π·CE 2·DE ＝π×12×2－13π×12×1＝5π3.7．(2020·全国Ⅰ)已知A ，B ，C 为球O 的球面上的三个点，⊙O 1为△ABC 的外接圆．若⊙O 1的面积为4π，AB ＝BC ＝AC ＝OO 1，则球O 的表面积为( ) A ．64π B ．48π C ．36π D ．32π 答案 A解析 如图，设圆O 1的半径为r ，球的半径为R ，正三角形ABC 的边长为a .由πr 2＝4π，得r ＝2， 则33a ＝2，a ＝23， OO 1＝a ＝2 3.在Rt △OO 1A 中，由勾股定理得R 2＝r 2＋OO 21＝22＋(23)2＝16，所以S 球＝4πR 2＝4π×16＝64π.8．(2020·武汉调研)已知直三棱柱ABC －A 1B 1C 1的6个顶点都在球O 的表面上，若AB ＝AC ＝1，AA 1＝23，∠BAC ＝2π3，则球O 的体积为( )A.32π3 B ．3π C.4π3 D ．8π 答案 A解析 设△ABC 外接圆圆心为O 1，半径为r ，连接O 1O ，如图，易得O 1O ⊥平面ABC ，∵AB ＝AC ＝1，AA 1＝23，∠BAC ＝2π3，∴2r ＝AB sin ∠ACB ＝112＝2，即O 1A ＝1，O 1O ＝12AA 1＝3，∴OA ＝O 1O 2＋O 1A 2＝3＋1＝2，∴球O 的体积V ＝43π·OA 3＝32π3.故选A.9.如图所示，某几何体由底面半径和高均为5的圆柱与半径为5的半球对接而成，在该封闭的几何体内部放入一个小圆柱体，且小圆柱体的上、下底面均与外层圆柱的底面平行，则小圆柱体积的最大值为( )A.2 000π9B.4 000π27C ．81πD ．128π答案 B解析 小圆柱的高分为上、下两部分，上部分的高同大圆柱的高相等，为5，下部分深入底部半球内．设小圆柱下部分的高为h (0<h <5)，底面半径为r (0<r <5)．由于r ，h 和球的半径构成直角三角形，即r 2＋h 2＝52，所以小圆柱的体积V ＝πr 2(h ＋5)＝π(25－h 2)(h ＋5)(0<h <5)，把V 看成是关于h 的函数，求导得V ′＝－π(3h －5)(h ＋5)．当0<h <53时，V ′>0，V 单调递增；当53<h <5时，V ′<0，V 单调递减．所以当h ＝53时，小圆柱的体积取得最大值．即V max ＝π⎝⎛⎭⎫25－259×⎝⎛⎭⎫53＋5＝4 000π27，故选B. 10．已知在三棱锥P －ABC 中，P A ，PB ，PC 两两垂直，且长度相等．若点P ，A ，B ，C 都在半径为1的球面上，则球心到平面ABC 的距离为( ) A.36 B.12 C.13 D.32答案 C解析 ∵在三棱锥P －ABC 中，P A ，PB ，PC 两两垂直，且长度相等， ∴此三棱锥的外接球即以P A ，PB ，PC 为三边的正方体的外接球O ， ∵球O 的半径为1，∴正方体的边长为233，即P A ＝PB ＝PC ＝233，球心到截面ABC 的距离即正方体中心到截面ABC 的距离，设P 到截面ABC 的距离为h ，则正三棱锥P －ABC 的体积V ＝13S △ABC ×h ＝13 S △P AB ×PC ＝13×12×⎝⎛⎭⎫2333， ∵△ABC 为边长为263的正三角形，S △ABC ＝233，∴h ＝23， ∴球心(即正方体中心)O 到截面ABC 的距离为13.二、多项选择题11．(2020·枣庄模拟)如图，透明塑料制成的长方体容器ABCD －A 1B 1C 1D 1内灌进一些水，固定容器一边AB 于地面上，再将容器倾斜，随着倾斜度的不同，有下面几个结论，其中正确的是( )A ．没有水的部分始终呈棱柱形B ．水面EFGH 所在四边形的面积为定值C ．随着容器倾斜度的不同，A 1C 1始终与水面所在平面平行D ．当容器倾斜如图③所示时，AE ·AH 为定值 答案 AD解析 由于AB 固定，所以在倾斜的过程中，始终有CD ∥HG ∥EF ∥AB ，且平面AEHD ∥平面BFGC ，故水的部分始终呈棱柱形(三棱柱或四棱柱)，且AB 为棱柱的一条侧棱，没有水的部分也始终呈棱柱形，故A 正确；因为水面EFGH 所在四边形，从图②，图③可以看出，EF ，GH 长度不变，而EH ，FG 的长度随倾斜度变化而变化，所以水面EFGH 所在四边形的面积是变化的，故B 错；假设A 1C 1与水面所在的平面始终平行，又A 1B 1与水面所在的平面始终平行，则长方体上底面A 1B 1C 1D 1与水面所在的平面始终平行，这就与倾斜时两个平面不平行矛盾，故C 错；水量不变时，棱柱AEH －BFG 的体积是定值，又该棱柱的高AB 不变，且V AEH －BFG ＝12·AE ·AH ·AB ，所以AE ·AH ＝2V AEH －BFG AB ，即AE ·AH 是定值，故D 正确．12. (2020·青岛检测)已知四棱台ABCD －A 1B 1C 1D 1的上、下底面均为正方形，其中AB ＝22，A 1B 1＝2，AA 1＝BB 1＝CC 1＝DD 1＝2，则下列叙述正确的是( )A ．该四棱台的高为 3B ．AA 1⊥CC 1C ．该四棱台的表面积为26D ．该四棱台外接球的表面积为16π 答案 AD解析 将四棱台补为如图所示的四棱锥P －ABCD ，并取E ，E 1分别为BC ，B 1C 1的中点，记四棱台上、下底面中心分别为O 1，O ，连接AC ，BD ，A 1C 1，B 1D 1，A 1O ，OE ，OP ，PE .由条件知A 1，B 1，C 1，D 1分别为四棱锥的侧棱P A ，PB ，PC ，PD 的中点，则P A ＝2AA 1＝4，OA ＝2，所以OO 1＝12PO ＝12P A 2－OA 2＝3，故该四棱台的高为3，故A 正确；由P A ＝PC＝4，AC ＝4，得△P AC 为正三角形，则AA 1与CC 1所成角为60°，故B 不正确；四棱台的斜高h ′＝12PE ＝12PO 2＋OE 2＝12×(23)2＋(2)2＝142，所以该四棱台的表面积为(22)2＋(2)2＋4×2＋222×142＝10＋67，故C 不正确；易知OA 1＝OB 1＝OC 1＝OD 1＝O 1A 21＋O 1O 2＝2＝OA ＝OB ＝OC ＝OD ，所以O 为四棱台外接球的球心，所以外接球的半径为2，外接球表面积为4π×22＝16π，故D 正确．三、填空题13．(2020·浙江)已知圆锥的侧面积(单位：cm 2)为2π，且它的侧面展开图是一个半圆，则这个圆锥的底面半径(单位：cm)是________． 答案 1解析 如图，设圆锥的母线长为l ，底面半径为r ，则圆锥的侧面积S 侧＝πrl ＝2π，即r·l＝2.由于侧面展开图为半圆，可知12πl2＝2π，可得l＝2，因此r＝1.14.在如图所示的斜截圆柱中，已知圆柱的底面直径为40 cm，母线长最短50 cm，最长80 cm，则斜截圆柱的侧面面积S＝________cm2.答案 2 600π解析将题图所示的相同的两个几何体对接为圆柱，则圆柱的侧面展开图为矩形．由题意得所求侧面展开图的面积S＝12×(π×40)×(50＋80)＝2 600π(cm2)．15．已知球O与棱长为4的正四面体的各棱相切，则球O的体积为________．答案82 3π解析将正四面体补成正方体，则正四面体的棱为正方体面上的对角线，因为正四面体的棱长为4，所以正方体的棱长为2 2.因为球O与正四面体的各棱都相切，所以球O为正方体的内切球，即球O的直径2R＝22，则球O的体积V＝43πR3＝823π.16．(2020·新高考全国Ⅰ)已知直四棱柱ABCD－A1B1C1D1的棱长均为2，∠BAD＝60°.以D1为球心，5为半径的球面与侧面BCC1B1的交线长为________．答案2π2解析如图，设B1C1的中点为E，球面与棱BB1，CC1的交点分别为P，Q，连接DB，D1B1，D1P，D1E，EP，EQ，由∠BAD ＝60°，AB ＝AD ，知△ABD 为等边三角形， ∴D 1B 1＝DB ＝2，∴△D 1B 1C 1为等边三角形， 则D 1E ＝3且D 1E ⊥平面BCC 1B 1，∴E 为球面截侧面BCC 1B 1所得截面圆的圆心， 设截面圆的半径为r ， 则r ＝R 2球－D 1E 2＝5－3＝ 2.又由题意可得EP ＝EQ ＝2，∴球面与侧面BCC 1B 1的交线为以E 为圆心的圆弧PQ . 又D 1P ＝5， ∴B 1P ＝D 1P 2－D 1B 21＝1， 同理C 1Q ＝1，∴P ，Q 分别为BB 1，CC 1的中点， ∴∠PEQ ＝π2，知PQ 的长为π2×2＝2π2，即交线长为2π2.。