回归分析实验课 实验8
- 格式:doc
- 大小:360.50 KB
- 文档页数:16



河北工业大学经济管理学院《计量经济学》课程上机指导书(2014年春季学期)班级:学号:姓名:2014年3月上机实习指导书1——EViews的基本使用一、实验目的1.认识计量经济学软件包EViews82.掌握EViews8的基本使用3.建立工作文件并将数据输入存盘二、实验要求熟悉E Views的基本使用三、实验数据四、实验内容(一)怎样启动EViews 8?安装软件后,开始==>程序==> Eviews 8==>Eviews 8。
或者,在桌面双击"EVIEWS"图标,或者双击Eviews8工作文件,进入EVIEWS,启动“EVIEWS”软件。
(二)怎样用EViews 8开始工作进入Eviews8 窗口以后,用户必须创建一个新的工作文件或者打开一个已经存在的工作文件,才能开始工作。
1、创建一个新的工作文件在主菜单上选择File,并点击其下的New,然后选择Workfile。
Eviews将弹出Workfile Creat 窗口。
要求用户输入工作文件的workfile structure type: 如果你的数据是非日期型的截面数据或时间间隔不一致的时间序列数据选unstructured/undated,然后在data specification的Observations 中输入观测值个数;如果你的数据是日期型的选dated——regular frequency,然后在data specification中选择数据的频度,如:年度,季度,月度,周等,最后输入开始日期和结束日期:如果数据是月度数据,则按下面的形式输入(从Jan. 1950 到 Dec. 1994): 1950:01 1994:12,如果数据是季度数据,则按下面的形式输入(从1st Q. 1950到3rd Q. of 1994):1950:1 1995:3,如果数据是年度数据,则按下面的形式输入(从1950 到 1994) 1950 1994,如果数据是按周的数据,则按下面的形式输入(从2001年1月第一周到2010年1月第四周): 2001 1 2010 4;如果你的数据是平衡的面板数据选balanced panel,然后在data specification中输入起始日期(同时间序列数据)及观测对象的个数(同截面数据)。
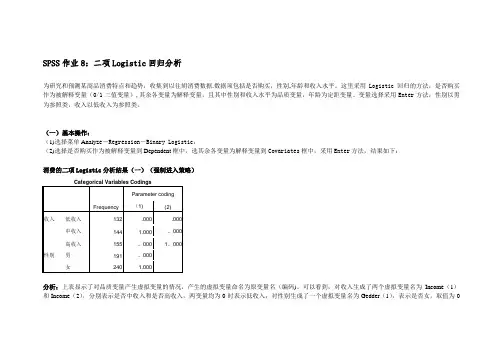
SPSS作业8:二项Logistic回归分析为研究和预测某商品消费特点和趋势,收集到以往胡消费数据.数据项包括是否购买,性别,年龄和收入水平。
这里采用Logistic回归的方法,是否购买作为被解释变量(0/1二值变量),其余各变量为解释变量,且其中性别和收入水平为品质变量,年龄为定距变量。
变量选择采用Enter方法,性别以男为参照类,收入以低收入为参照类。
(一)基本操作:(1)选择菜单Analyz e-Regression-Binary Logistic;(2)选择是否购买作为被解释变量到Dependent框中,选其余各变量为解释变量到Covariates框中,采用Enter方法,结果如下:消费的二项Logistic分析结果(一)(强制进入策略)Categorical Variables CodingsFrequency Parameter coding (1) (2)收入低收入132 .000 .000中收入144 1.000 。
000高收入155 。
000 1。
000性别男191 。
000女240 1.000分析:上表显示了对品质变量产生虚拟变量的情况,产生的虚拟变量命名为原变量名(编码)。
可以看到,对收入生成了两个虚拟变量名为Income(1)和Income(2),分别表示是否中收入和是否高收入,两变量均为0时表示低收入;对性别生成了一个虚拟变量名为Gedder(1),表示是否女,取值为0时表示为男。
消费的二项Logistic 分析结果(二)(强制进入策略)Block 0: Beginning BlockClassification Table a,bObserved Predicted是否购买 Percentage Correct不购买购买Step 0是否购买不购买 269 0 100。
购买162。
0 Overall Percentage62。
4a 。
Constant is included in the model 。


实验设计与分析第六版课程设计一、设计背景实验设计与分析是统计学和实验设计学科的重要基础课程,旨在培养学生对实验数据进行分析和解释的能力,以及提高他们在设计和执行实验时的技能。
本课程设计旨在通过设计一个实验来巩固和运用所学的理论知识和实践技能,同时提高学生的创新思维和解决问题的能力。
二、设计目标本课程设计的主要目标如下:1.确保学生掌握实验设计和数据分析的基本理论知识和实践技能;2.培养学生的实验设计和数据分析能力,提高他们的创新思维;3.培养学生的沟通、协作和问题解决能力,以便他们能够在多学科团队中发挥重要作用。
三、设计流程1.确定研究问题:为了研究某个现象或事物,首先需要明确研究的目的并确定研究问题。
考虑到本课程的性质,我们将选择一个具体的实验进行分析。
2.建立假设:假设是实验的重要组成部分,它们提供了关于可能的结果和因果关系的推测,并指导实验的设计和数据分析。
3.确定研究设计:根据研究问题和假设确定实验的设计。
在这个阶段,需要考虑下面的问题:实验设计类型、因子水平、处理次数、重复次数等。
4.收集实验数据:使用合适的方法收集实验数据。
要求使用至少两种数据收集方法,如问卷、实验记录、测试、观察等。
5.进行数据分析:对收集到的数据进行统计分析。
推荐使用至少两种数据分析方法,如t检验、方差分析、回归分析等。
6.结果展示和分析:根据实验的结果进行数据展示,解释和讨论。
将数据分析和统计结果清晰地展示出来,并结合假设和研究问题进行解释和讨论。
7.撰写实验报告:根据实验流程和结果撰写实验报告。
要求使用科学的语言和格式,报告中应包括实验设计、数据收集、分析和结果展示等重要信息。
四、评估标准为了确保本课程设计的顺利进行和学生的有效学习,我们将使用下面的几个标准来评估学生的成绩:1.实验报告的完成情况和质量;2.学生对实验设计和数据分析的理解和应用;3.学生对实验设计和数据分析中遇到问题的解决能力;4.学生对团队合作和沟通的表现。


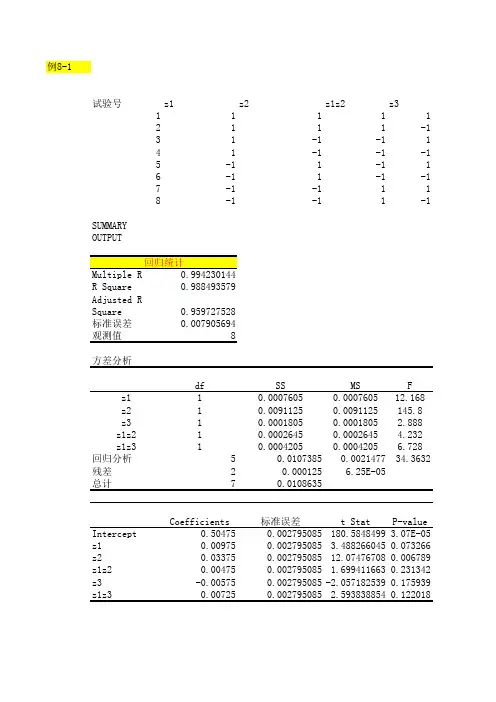

概率论与数理统计教程-魏宗舒-课后习题解答答案-7-8章概率论与数理统计教程-魏宗舒-课后习题解答答案-7-8章第七章假设检验7.1 设总体2(,)N ξµσ~,其中参数µ,2σ为未知,试指出下⾯统计假设中哪些是简单假设,哪些是复合假设:(1)0:0,1H µσ==;(2)0:0,1H µσ=>;(3)0:3,1H µσ<=;(4)0:03H µ<<;(5)0:0H µ=.解:(1)是简单假设,其余位复合假设 7.2 设1225,,,ξξξ取⾃正态总体(,9)N µ,其中参数µ未知,x 是⼦样均值,如对检验问题0010:,:H H µµµµ=≠取检验的拒绝域:12250{(,,,):||}c x x x x c µ=-≥,试决定常数c ,使检验的显著性⽔平为0.05解:因为(,9)N ξµ~,故9(,)25N ξµ~ 在0H 成⽴的条件下,00053(||)(||)53521()0.053cP c P c ξµξµ-≥=-≥??=-Φ=55()0.975,1.9633c cΦ==,所以c =1.176。
7.3 设⼦样1225,,,ξξξ取⾃正态总体2(,)N µσ,20σ已知,对假设检验0010:,:H H µµµµ=>,取临界域12n 0{(,,,):|}c x x x c ξ=>,(1)求此检验犯第⼀类错误概率为α时,犯第⼆类错误的概率β,并讨论它们之间的关系;(2)设0µ=0.05,20σ=0.004,α=0.05,n=9,求µ=0.65时不犯第⼆类错误的概率。
解:(1)在0H 成⽴的条件下,200(,)nN σξµ~,此时00000()P c P ξαξ=≥=10,由此式解出010c αµ-=+在1H 成⽴的条件下,20(,)nN σξµ~,此时101010()(P c P αξβξµ-=<=<=Φ=Φ=Φ由此可知,当α增加时,1αµ-减⼩,从⽽β减⼩;反之当α减少时,则β增加。

实验13 回归分析化工系 分0 毕啸天 2010011811【实验目的】1. 了解回归分析的基本原理,掌握MATLAB 实现的方法;2. 练习用回归分析解决实际问题。
【实验内容】题目一用切削机床加工时,为实时地调整机床需测定刀具的磨损程度,每隔一小时测量刀具的厚度得到以下的数据(见下表),建立刀具厚度对于切削时间的回归模型,对模型和回归系数进行检验,并预测7.5h 和15h 后刀具的厚度,用(30)和(31)式两种办法计算预测区间,解释计算结果。
1.1 模型分析此题是一个给出数据,确定回归并预测结果的基础题目。
可以首先作图观察二者的走势。
x1=0:10;y=[30.6 29.1 28.4 28.1 28.0 27.7 27.5 27.2 27.0 26.8 26.5]'; plot(x1,y,'*') xlabel('时间/h')ylabel('刀具厚度/cm')title('时间与刀具厚度的关系')时间/h刀具厚度/c m时间与刀具厚度散点图由上图可以看出,除了最初几个点偏离较大,刀具厚度y 与时间x 大致为线性关系。
因此确定回归模型为:xy 10ββ+=1.2 程序代码n=11;X=[ones(n,1),x1'];[b,bint,r,rint,s]=regress(y,X); rcoplot(r,rint)输出结果如下: b =29.545 -0.32909 bint =28.977 30.114 -0.4252 -0.23298 r =1.0545 -0.11636 -0.48727 -0.45818 -0.22909 -0.2 -0.070909 -0.041818 0.087273 0.21636 0.24545 rint =0.79381 1.3153 -1.046 0.81326 -1.3782 0.40364 -1.3873 0.47094 -1.2267 0.76848 -1.2067 0.80674 -1.0836 0.94177 -1.04 0.9564 -0.88264 1.0572 -0.70174 1.1345 -0.61524 1.1062 s =0.86957 60.002 2.8614e-005 0.19855回归结果整理成表格如下:不包含零点。
身高 0.75 0.85 0.95 1.08 1.12 1.16 1.35 1.51 1.55 1.6 1.63 1.67 1.71 1.78 1.85 体重 101215172022354148505154596675Matlab 实现:h=[0.75 0.85 0.95 1.08 1.12 1.16 1.35 1.51 1.55 1.6 1.63 1.67 1.71 1.78 1.85]; m=[10 12 15 17 20 22 35 41 48 50 51 54 59 66 75]; plot(x,y,'*')可令:adh m =,求系数可用p=polyfit(x,y,n), 其中h x m y ln ,ln ==,n=1,结果:p=[2.3,2.823]由此得d=16.8,a=2.3,即有经验公式:3..28.16h m =。
也直接利用Matlab 统计工具箱中的命令regress 求解,使用格式:[b,bint,r,rint,stats]=regress(y,x,alpha) alpha 为置信水平,r 为残差向量βˆx y -,stats 为回归模型的检验统计量,有3个值,第一个是回归方程的决定系数2R ,第二个是F 统计量值,第三个是与F 统计量对应的概率值p 。
上例可如下操作:y=log(m)';x=[ones(length(y),1),log(h)'];[b,bint,r,rint,stat]=regress(y,x)b =2.82282.3000 stat =1 1024 0.0000残差分析:rcoplot(r,rint)----------------------------------------------------------------------------------------------------------------------------------例2:施肥效果分析(1992建模赛题)磷肥施用量 0244973 98 147 196 245 294 342 土豆产量 33.46 32.47 36.06 37.96 41.04 40.09 41.26 42.17 40.36 42.73 磷肥施用量 0244973 98 147 196 245 294 342 土豆产量33.46 34.76 36.0637.9641.0440.0941.2642.1740.3642.73氮肥施用量 0244973 98 147 196 245 294 342 土豆产量33.46 34.76 36.0637.9641.0440.0941.2642.1740.3642.73对于磷肥-----土豆:可选择函数xbea y -+=1 或威布尔函数 0,≥-=-x Be A y cx对于氮肥-----土豆:可选择函数0,2210≥++=x x b x b b y2)模型的参数估计:可如下操作:x=[0 34 67 101 135 202 259 336 404 471]';y=[15.18 21.36 25.72 32.29 34.03 39.45 43.15 43.46 40.83 30.75]';X=[ones(length(y),1),x,x.^2];[b,bint,r,rint,stat]=regress(y,X)b =14.74160.1971-0.0003stat =0.9863 251.7971 0.0000 即20003.01971.07416.14x x y -+=拟合曲线图:3) 显著性检验: (仅以氮肥-----土豆模型为例说明)A):回归方程的显著性检验:检验的概率p=0,说明方程是高度显著的.B):回归系数的的显著性检验:对1β: 0:110=βH 检验统计量 =T 对2β: 0:220=βH检验统计量 =T -1004341.84343142都有 8945.1)7(05.0=>t T ,所以,均应拒绝原假设,认为系数)2,1(=i i β显著地不为0.4)残差诊断:标准化残差图如下12345678910标准化残差基本上均匀分布于-2至2之间,可以认为模型拟合是合理的.------------------------------------------------------------------------------------------------------------------------------ 案例:牙膏的销售量某牙膏制造企业要求销售部门根据市场调查,找出公司生产的牙膏销售量与销售价格、广告投入等之间的关系,从而预测出在不同价格和广告费用下的销售量。
《生物化学》实验指导(8个实验)生物化学实验指导吕杰编著新疆大学资源与环境科学学院生态学教研室内容介绍《生物化学实验指导》是新疆大学资源与环境科学学院《生物化学》课程组的教师在参考国内重点院校、科研院所的生物化学实验与实习教材的基础上,结合教师的教学经验汇编而成。
该实习指导围绕教学大纲设计了8个实验内容。
目目录实验一氨基酸纸层析4实验二DNS-CL法测定N末端氨基酸5实验三考马斯亮蓝法测定蛋白质的浓度7实验四酪蛋白的制备8实验五葡萄糖标准曲线的绘制10实验六酵母蔗糖酶的提取及活力测定12实验七酵母RNA的分离及组分鉴定14实验八维生素C的定量测定16 实验一一氨基酸纸层析一、实验目的1、通过氨基酸的纸层析分离,学习纸层析的基本原理和操作方法。
二、实验原理纸层析:是以滤纸作为支持物的分配层析法,是20世纪40年代发展起来的一种生化分离技术。
由于设备简单,操作方便,所需样品量少,分辨力较高等优点而广泛的用于物质的分离,并可进行定性和定量的分析。
缺点是展开时间较长。
分配层析法:是利用物质在两种或两种以上不同的混合溶剂中的分配系数不同,而达到分离的目的的一种实验方法。
在一定条件下,一种物质在某种溶剂系统中的分配系数是一个常数即=溶质在固定相的浓度/溶质在流动相的浓度。
溶剂系统:由有机溶剂和水组成,水和滤纸纤维素有较强的亲和力,因而其扩散作用降低形成固定相,有机溶剂和滤纸亲和力弱,所以在滤纸毛细管中自由流动,形成流动相,由于混合液中各种氨基酸的分配系数值不同,其在两相中的分配数量及移动速率(即迁移率Rf值)就不同,从而达到分离的目的。
三、实验材料、仪器和试剂:1、实验材料:标准氨基酸溶液2、仪器:层析缸,层析纸,毛细管,天平,吹风机等。
3、、试剂:(1)氨基酸标准溶液:0.1M丙氨酸和0.1M谷氨酸标准溶液。
(2)溶剂系统:正丁醇:甲酸:水=15:3:2(体积比)摇匀;(3)0.1%的茚三酮丙酮溶液;茚三酮15克,丙酮100毫升四、实验步骤:纸层析(1)取一长方形滤纸,在滤纸纵向对应的两边距边沿2cm处,用铅笔轻轻的各画两条平行线,一条作前沿标志,一条作点样线,在点线上每隔2cm画一个+作为点样位置,共5个点。
目录目录 (1)一、建立多元线性回归模型 (3)(一) 建立包括时间变量的三元线性回归模型; (3)1. 建立工作文件:CREATE A 78 94 (3)2. 输入统计资料:DATA Y L K (3)3. 生成时间变量t:GENR T=@TREND(77) (3)4. 建立回归模型:LS Y C T L K (3)(二) 建立剔除时间变量的二元线性回归模型; (4)(三) 建立非线性回归模型——C-D生产函数。
(5)二、比较、选择最佳模型 (8)(一) 回归系数的符号及数值是否合理; (8)(二) 模型的更改是否提高了拟合优度; (8)(三) 模型中各个解释变量是否显著; (8)(四) 残差分布情况 (8)实验三多元回归模型【实验目的】掌握建立多元回归模型和比较、筛选模型的方法。
【实验内容】建立我国国有独立核算工业企业生产函数。
根据生产函数理论,生产函数的基本形式为:()ε,tY=。
其中,L、K分别为生产过程中投入的劳动与资金,fL,K,时间变量t反映技术进步的影响。
表3-1列出了我国1978-1994年期间国有独立核算工业企业的有关统计资料;其中产出Y为工业总产值(可比价),L、K分别为年末职工人数和固定资产净值(可比价)。
资料来源:根据《中国统计年鉴-1995》和《中国工业经济年鉴-1995》计算整理【实验步骤】一、 建立多元线性回归模型(一) 建立包括时间变量的三元线性回归模型;在命令窗口依次键入以下命令即可:1. 建立工作文件: CREATE A 78 942. 输入统计资料: DATA Y L K3. 生成时间变量t : GENR T=@TREND(77)4. 建立回归模型: LS Y C T L K则生产函数的估计结果及有关信息如图3-1所示。
图3-1 我国国有独立核算工业企业生产函数的估计结果 因此,我国国有独立工业企业的生产函数为:K L t y 7764.06667.06789.7732.675ˆ+++-= (模型1)t =(-0.252) (0.672) (0.781) (7.433)9958.02=R 9948.02=R 551.1018=F 模型的计算结果表明,我国国有独立核算工业企业的劳动力边际产出为0.6667,资金的边际产出为0.7764,技术进步的影响使工业总产值平均每年递增77.68亿元。
苏教版科学第三单元《常见的力》3.1力与运动【教材分析】本课是新教材苏教版四年级《科学》上册第三单元《常见的力》的起始课,承接着上一单元的运动。
教学时,首先通过图片启发学生关于力的思考,然后提出探究问题:小车运动快慢与拉力大小是什么关系呢?明确探究的问题,接着通过实验搜集证据论证自己的假设,最后获得结论解决问题。
在此过程中,发展学生的实验设计能力、归纳概括能力和实证意识。
本案例的设计旨在使学生通过探究,初步理解物体运动与力之间的关系。
【学情分析】四年级学生已经掌握了一些实验方法,具备了一定的操作能力,对于力和物体运动之间的关系也具备了一些初步知识。
基于此,本案例教学可组织学生围绕力与小车快慢关系的问题自行设计控制变量的实验方案,教师帮助提供小车等相关实验材料,学生合作展开探究。
【教学目标】1通过观察生活现象,知道力可以使静止的物体运动起来,可以使运动的物体静止下来,可以改变物体运动的快慢与方向,懂得物体运动状态的改变离不开力,提升提出问题,思考问题,解决问题的能力。
2.通过实验,探究拉力大小与小车前进快慢的关系,懂得拉力越大,小车前进越快,拉力越小,小车前进越慢,掌握实验方法,提升合作探究的意识。
3.通过研究磁力能否改变钢珠的运动方向的实验,懂得力能够改变物体运动的方向,促进拓展迁移。
【教学重点】知道力可以改变物体的运动状态。
【教学难点】探究拉力大小与小车前进快慢的关系。
【教学方法】实验探究法、任务驱动法【教学准备】教师材料:PPT课件学生材料:小车、棉线、钩码、秒表、滑轮支架、钢珠、磁铁【课时安排】1课时【教学过程设计】一、导入新课1出示生活中有关运动和力的场景图片,如:运动中的自行车停下来、风车的转动、磁力小车拐弯、皮球弹起来、潜艇浮出水面等。
提出问题:图片中的运动与什么力有关?说说这些力改变了什么?(如,摩擦力使运动中的自行车减速直至停止)2.学生回答。
预设:风力,使静止的风车转动起来;磁力使小车拐弯;地面对皮球的弹力使皮球弹起;水对潜艇的浮力使潜艇浮出水面。
实验报告八实验课程:回归分析实验课专业:统计学年级:姓名:学号:指导教师:完成时间:得分:教师评语:学生收获与思考:实验八含定性变量的回归模型(4学时)一、实验目的1.掌握含定性变量的回归模型的建模步骤3.运用SAS计算含定性变量的各种回归模型的各参数估计及相关检验统计量二、实验理论与方法在实际问题的研究中,经常会遇到一些非数量型的变量。
如品质变量;性别;战争与和平。
我们把这些品质变量也称为定性变量,在建立回归模型的时候我们需要考虑到这些定性变量。
定性变量的回归模型分为自变量含定性变量的回归模型和因变量是定性变量的回归模型。
自变量含有定性变量的时候,我们一般引进虚拟变量,将这些定性变量数量化。
例如研究粮食产量问题,y为粮食产量,x为施肥量,另外考虑气候问题,分为正常年份和干旱年份两种情况,这个问题数量化方法就是引入一个0-1型变量D,令D i=1 表示正常年份,D i=0表示干旱年份,粮食产量的回归模型为:y i=β0+β1x i+β2D i+εi。
因变量是定性变量时,一般用logistic回归模型(分组数据的logistic回归模型,未分组数据的logistic回归模型,多类别的logistic回归模型),probit回归模型等。
三. 实验内容1.用DATA步建立一个永久SAS数据集,数据集名为xt103,数据见表21;对数据集xt103,建立y 对公司规模和公司类型的回归,并对所得到的模型进行解释。
2.研制一种新型玻璃,对其做耐冲实验。
用一个小球从不同的高度h对玻璃做自由落体撞击,玻璃破碎记为y=1,玻璃未破碎记y=0.数据见表22.是对表中数据建立玻璃耐冲性对高度h的logistic回归,并解释回归方程的含义。
3.某学校对本科毕业生的去向做了一个调查,分析影响毕业去向的相关因素,结果见表23.其中毕业去向“1”=工作,“2”=读研,“3”=出国留学。
性别“1”=男生,“0”=女生。
用多类别的Logisitic回归分析影响毕业去向的因素。
四.实验仪器计算机和SAS软件五.实验步骤和结果分析1.用DATA步建立一个永久SAS数据集,数据集名为xt103,数据见表21;对数据集xt103,建立y 对公司规模和公司类型的回归,并对所得到的模型进行解释。
R检验中R方为0.8951,可以认为回归拟合效果较好。
回归方程通过F检验,说明模型是显著成立的。
由参数估计表,可以看出,全部变量都是显著的,回归方程为:21^06.8102.087.33x x y +-=其中,x2是虚拟变量,当公司类型为“互助”时,x2为0,为“股份”时,x2为1。
由方程可知,x2为1,即股份制公司的保险革新措施速度y 会更大。
股份制公司采取保险革新措施的积极性比互助型公司高,股份制公司建立在共同承担风险上,更愿意革新。
公司规模越大,采取保险革新措施的倾向越大:大规模公司保险制度的更新对公司的影响程度比小规模公司大。
SAS 程序:data xt103;input y x1 x2 ;/*引入虚拟变量,将公司类型的互助设为0,股份设为1*/ cards ; 17 151 0 26 92 0 21 175 0 30 31 0 22 104 0 0 277 0 12 210 0 19 120 0 4 290 0 16 238 0 28 164 1 15 272 1 11 295 1 38 68 1 31 85 121 224 120 166 113 305 130 124 114 246 1;run;proc reg data=xt103;model y=x1 x2;run;2.研制一种新型玻璃,对其做耐冲实验。
用一个小球从不同的高度h对玻璃做自由落体撞击,玻璃破碎记为y=1,玻璃未破碎记y=0.数据见表22.是对表中数据建立玻璃耐冲性对高度h的logistic回归,并解释回归方程的含义。
模型信息:模型解出的是y=0的概率。
由三个检验中,统计量的P 值都小于0.05,可以认为模型是显著的。
由Wald 检验的显著性概率及其P 值,可以看出,h 变量对方程的影响是显著的。
由极大似然估计,各个参数系数也通过检验。
因此模型有效。
二元logit 模型为)98.759.14ex p(1)98.759.14ex p()0(h h y p -+-==模型意义为,小球掉落高度为h ,则玻璃未破碎的概率为p,而y=0表示玻璃未破碎。
也就是说,该种新型的玻璃,用小球对其撞击,当小球的掉落高度为h 时,玻璃未破碎的概率就是)98.759.14ex p(1)98.759.14ex p()0(h h y p -+-==,那么,玻璃会破碎的概率就为1-p(y=0),这也可以看成是一种比例,就是大量实验中,同个高度h ,玻璃会被击破的比例。
SAS程序:data wjz;input h y ;/*引入虚拟变量,将公司类型的互助设为0,股份设为1*/ cards;1.50 01.52 01.54 01.56 01.58 11.60 01.62 01.64 01.66 01.68 11.70 01.72 01.74 01.76 11.78 01.80 11.82 01.84 01.86 11.88 11.90 01.92 11.94 01.96 11.98 12.00 1;run;proc logistic data=wjz;model y=h;run;proc logistic data=wjz;class h;model y=h/link=glogit aggregate scale=none;run;3.某学校对本科毕业生的去向做了一个调查,分析影响毕业去向的相关因素,结果见表23.其中毕业去向“1”=工作,“2”=读研,“3”=出国留学。
性别“1”=男生,“0”=女生。
用多类别的Logisitic 回归分析影响毕业去向的因素。
专业课x1英语x2性别x3月生活费x4毕业去向y两个统计量的P值均大于0.05,说明模型拟合的较好。
检验全局零假设: BETA=0 无效假设检验结果(似然比,评分)的结果P值均小于0.01,具有显著统计学意义。
三个变量中,有两个是不显著的变量,x3,x2,剔除x3:两个统计量的P值均大于0.05,说明模型拟合的较好。
检验全局零假设: BETA=0 无效假设检验结果(似然比,评分,wald)的结果P值均小于0.01,具有显著统计学意义。
三个变量都是显著的。
以x4=“1”,即参加工作,为参照。
由模型可以看出:)0101.0122.0012.08.011-ex p()004.0038.017.0116.19-ex p(1)004.0038.017.0116.19-ex p()2(421421421x x x x x x x x x y p ++-++++++++==)0101.0122.0012.08.011-ex p()004.0038.017.0116.19-ex p(1)0101.0122.0012.08.011-ex p()3(421421421x x x x x x x x x y p ++-+++++++-==从参数估计表中,与参加工作的同学相比,读研的(y=2)的同学相比,读研的同学其专业课成绩更好(x1的P 值=0.003),而外语成绩(x2的p 值=0.356)和经济状况(x4的P 值=0.184)没有显著差异;出国留学的(y=3)学生其专业课成绩和参加工作的没有显著差异,外语成绩和经济状况则更好。
Sas 程序:data a;input x1 x2 x3 x4 y; cards ; 95 65.0 1 600 2 63 62.00 850 182 53.0 0 700 260 88.0 0 850 372 65.0 1 750 185 85.0 0 1000 3 95 95.0 0 1200 2 92 92.0 1 950 263 63.0 0 850 178 75.0 1 900 190 78.0 0 500 182 83.0 1 750 280 65.0 1 850 383 75.0 0 600 260 90.0 0 650 375 90.0 1 800 263 83.0 1 700 185 75.0 0 750 273 86.0 0 950 286 66.0 1 1500 3 93 63.0 0 1300 2 73 72.0 0 850 186 60.0 1 950 276 63.0 0 1100 1 96 86.0 0 750 271 75.0 1 1000 1 63 72.0 1 850 260 88.0 0 650 167 95.0 1 500 186 93.0 0 550 163 76.0 0 650 186 86.0 0 750 276 85.0 1 650 182 92.0 1 950 373 60.0 0 800 182 85.0 1 750 275 75.0 0 750 172 63.0 1 650 181 88.0 0 850 392 96.0 1 950 2;run;proc print;run;proc logistic;class x3;model y(ref='3')=x1 x2 x3 x4/link=glogit aggregate scale=none ;run;proc logistic;class x3;model y(ref='3')=x1 x2 x4/link=glogit aggregate scale=none ;run;proc logistic;class x3;model y(ref='1')=x1 x2 x4/link=glogit aggregate scale=none ;run;六.收获与思考七. 思考题当自变量是定性变量的时候,我们需要引进虚拟变量进行数量化,当定性变量有n个水平的时候,我们该引进多少的虚拟变量,否则会怎样?不妨试试在sas中试试会出现什么问题。
答:当定性变量有n个水平时应该引进n-1个虚拟变量。
否则最后一个虚拟变量无法用最小二乘估计计算出来。
例:X1-X3为虚拟变量。
Data a;input x1 x2 x3 x y@@;cards;1 0 0 1.26 75 1 0 0 1.35 77 1 0 0 1.40 78 1 0 0 1.58 820 1 0 1.71 65 0 1 0 1.76 66 0 1 0 1.80 68 0 1 0 1.85 700 0 1 1.22 68 0 0 1 1.35 69 0 0 1 1.46 70 0 0 1 1.44 72;proc reg data=a;model y=x1-x3 x;run;X3没有参数估计结果。