求自变量之间的相关系数矩阵

PL S回归在消除多重共线性中的作用王惠文 朱韵华(北京航空航天大学管理学院,北京,100083)摘 要本文详细阐述了解释变量的多重共线性在回归建模与分析中的危害作用,并指出目前常用的几种消除多重线性影响的方法,以及它们的不足之处。

本文结合实证研究指出:利用一种新的建模思路 PLS回归,可以更好地消除多重共线性对建模准确性与可靠性所带来的影响。

关键词:多重共线性 PLS回归一、引 言在多元回归的建模与分析中,解释变量之间存在高度相关性的现象十分普遍。

在这种情况下,要很好地解释模型中某个自变量对因变量的效应,是非常困难的。

然而,在从事建模工作过程中,为了更完备地描述系统,尽可能不遗漏一些举足轻重的系统特征,分析人员往往倾向于尽可能周到地选取有关指标,在这样构成的多变量系统中必然经常出现变量多重相关的现象。

事实上,许多社会、经济及技术指标都有同步增长的趋势,因此,在多元回归建模实施过程中,变量多重相关的现象是很难避免的。

二、多重共线性在回归建模中的危害作用1.危害性讨论多重共线性的现象是由Fr isch.A.K在其著名论著 完全回归体系的统计合流分析 中首次提出的,用数学语言来描述,它是指变量之间存在着线性关系。

在多重共线性现象存在的情况下,对多元回归分析会产生如下影响:(1)如果变量之间存在完全的多重共线性,那么将无法估计变量的回归系数。

而由于各个自变量的回归系数无法估计,所以也就无法估计各个自变量单独对因变量的影响,自然也就无法判断自变量对因变量的效应,即使自变量之间不存在完全的多重共线性,但是当自变量有较高度的相关关系时,一个自变量的回归系数,在模型中只反映这个自变量对因变量边际的或部分的效应,因而所得到的回归模型是不准确的。

(2)回归系数的估计方差为无穷大。

例如在一个简单的多元回归中,自变量X1和X2之间收稿日期:1996年2月9日*本文系国家自然科学基金资助项目存在共线现象:如x i2=kx i1+v i其中v i是个随机变量,且满足v i~N(0, 2),这时,回归系数是可以估计的,但是回归系数的估计方差将随着自变量之间的共线程度的不断增强而逐渐增大。

两个连续变量之间的相关关系两个连续变量之间的相关关系，即指两个随机变量之间的相关性。

它是衡量两个连续变量之间相互依赖程度的重要指标。

在数据分析、统计学以及机器学习等领域，相关性分析是一项基础而重要的任务。

一、计算相关性系数在统计学中，通常通过相关系数来衡量两个连续变量之间的相关关系。

相关系数通常是在-1到1之间取值，其中-1表示完全的负相关关系，即两个变量之间有完全相反的关系；1则表示完全的正相关关系，即两个变量之间具有完全相同的变化趋势；而0则表示两个变量之间没有线性关系。

计算相关系数的方法有多种，其中比较常用的是皮尔逊相关系数和斯皮尔曼等级相关系数。

皮尔逊相关系数适用于连续型变量，并且假设变量服从正态分布。

斯皮尔曼等级相关系数则适用于序数型数据以及不满足正态分布的变量。

在这里以皮尔逊相关系数为例进行说明。

二、使用Python计算相关性系数在Python中，统计分析库numpy和pandas都提供了计算相关性系数的函数。

numpy提供的pearsonr函数可以计算两个变量之间的皮尔逊相关系数以及相关性显著性；而pandas提供的corr函数可以计算两个DataFrame对象中所有列的相关系数矩阵。

下面通过一个例子来说明如何使用Python计算相关系数。

```pythonimport numpy as npimport pandas as pd# 构造样本数据x = np.array([1, 2, 3, 4, 5])y = np.array([2, 4, 6, 8, 10])# 计算皮尔逊相关系数correlation, p_value = np.corrcoef(x, y)[0][1],scipy.stats.pearsonr(x, y)[0]print(f"皮尔逊相关系数: {correlation:.4f} (p-value:{p_value:.4f})")# 构造DataFrame对象df = pd.DataFrame({'x': [1, 2, 3, 4, 5], 'y': [2, 4, 6, 8, 10]})# 计算相关系数矩阵corr_matrix = df.corr()print(f"相关系数矩阵: \n{corr_matrix}")```以上代码首先构造了两个变量x和y，分别表示1到5的整数和2到10的偶数。

第八章 相关与回归分析一、填空题8.1.1 客观现象之间的数量联系可以归纳为两种不同的类型，一种是 ，另一种是 。

8.1.2 回归分析中对相互联系的两个或多个变量区分为 和 。

8.1.3 是指变量之间存在的严格确定的依存关系。

8.1.4 变量之间客观存在的非严格确定的依存关系，称为 。

8.1.5 按 的多少不同，相关关系可分为单相关、复相关和偏相关。

8.1.6 两个现象的相关，即一个变量对另一个变量的相关关系，称为 。

8.1.7 在某一现象与多个现象相关的场合，当假定其他变量不变时，其中两个变量的相关关系称为 。

8.1.8 按变量之间相关关系的 不同，可分为完全相关、不完全相关和不相关。

8.1.9 按相关关系的 不同可分为线性相关和非线性相关。

8.1.10 线性相关中按 可分为正相关和负相关。

8.1.11 研究一个变量与另一个变量或另一组变量之间相关方向和相关密切程度的统计分析方法，称为 。

8.1.12 当一个现象的数量由小变大，另一个现象的数量也相应由小变大，这种相关称为 。

8.1.13 当一个现象的数量由小变大，而另一个现象的数量相反地由大变小，这种相关称为 。

8.1.14 当两种现象之间的相关只是表面存在，实质上并没有内在的联系时，称之为 。

8.1.15根据相关关系的具体形态，选择一个合适的数学模型来近似地表达变量间平均变化关系的统计分析方法，称为 。

8.1.16 反映变量之间相关关系及关系密切程度的统计分析指标是 。

8.1.17 就是寻找参数01ββ和的估计值01ββ和，使因变量实际值与估计值的残差平方和达到最小。

8.1.18 正如标准差可以说明平均数代表性大小一样， 则可以说明回归线代表性的大小。

8.1.19 回归分析中的显著性检验包括两方面的内容，一是对 的显著性检验；二是对 的显著性检验。

8.1.20 对各回归系数的显著性检验，通常采用 ；对整个回归方程的显著性检验，通常采用 。

自变量之间的相关性分析方法介绍自变量之间的相关性分析方法介绍引言：在统计学和数据分析中，相关性分析是一种用于确定自变量之间关系的常用方法。

通过分析自变量之间的相关性，我们可以了解它们之间的连接和依赖关系，从而更好地理解数据和推断有关结果的潜在因素。

在这篇文章中，我将介绍一些常用的相关性分析方法，帮助您更好地理解自变量之间的关联性。

1. 皮尔逊相关系数：皮尔逊相关系数是最常用的用于测量两个连续变量之间线性关系强度的指标。

它的取值范围从-1到1，其中-1表示完全负相关，1表示完全正相关，0表示无相关性。

通过计算变量之间的协方差和标准差，可以得到皮尔逊相关系数。

2. 斯皮尔曼相关系数：如果数据之间的关系不是线性的，而是通过其他方式相关，斯皮尔曼相关系数就是一种更合适的选择。

它通过对变量的排序而不是数值本身的差异进行计算，因此适用于有序和非有序的数据。

它的取值范围也是-1到1，与皮尔逊相关系数类似。

3. 判定系数：判定系数也被称为R方值，用于衡量一个自变量对因变量变异的解释程度。

它的取值范围从0到1，越接近1表示自变量对因变量变异的解释越好。

通过计算总体变异和回归模型残差的变异，可以得到判定系数。

4. 点双相关系数：点双相关系数是用于测量多个变量之间关系的指标。

它度量特定自变量与因变量之间的线性关系，并控制其他自变量的影响。

通过与多元回归模型相结合，可以得到点双相关系数。

结论：在进行相关性分析时，我们可以使用多种方法来评估自变量之间的关系。

皮尔逊相关系数适用于线性关系的连续变量，而斯皮尔曼相关系数适用于非线性关系和有序的变量。

判定系数和点双相关系数可以衡量自变量对因变量变异的解释程度和多个变量之间的关系。

理解不同的相关性分析方法可以帮助我们更全面地理解自变量之间的连接和依赖关系，为我们的数据分析提供更深入的见解。

个人观点和理解：在进行相关性分析时，选择适当的方法非常重要。

不同的方法适用于不同类型的数据和变量之间的关系。

多元回归分析论文引言多元回归分析是一种利用多个自变量与因变量之间关系的统计方法。

它是统计学中重要的工具之一，在许多研究领域都有广泛的应用。

本论文将通过介绍多元回归分析的原理以及应用案例，探讨其在实践中的作用，并提出相关的方法和建议。

方法数据收集在进行多元回归分析之前，首先需要收集相关的数据。

这些数据应该包括自变量和因变量的观测值。

数十个样本的规模是多元回归分析的常见要求之一。

此外，在进行数据收集时，还需要注意数据的质量和准确性，以确保多元回归分析的可靠性。

模型设定在进行多元回归分析时，需要确定一个适当的回归模型。

回归模型是通过自变量对因变量进行预测的数学模型。

在确定回归模型时，可以使用领域知识、经验和统计指标等来指导模型设定的过程。

参数估计参数估计是多元回归分析中的关键步骤之一。

它通过最小化预测值与观测值之间的误差，来确定自变量与因变量之间的关系。

常用的参数估计方法有最小二乘法、最大似然法等。

模型诊断在进行参数估计之后，需要对模型进行诊断，以评估模型的拟合度和有效性。

常用的模型诊断方法包括检验残差的正态性、检验自变量之间的共线性等。

解释结果在完成参数估计和模型诊断之后，需要解释多元回归分析的结果。

这涉及到解释每个自变量的系数和拟合优度指标等。

通过解释结果，可以获取对因变量的预测和解释性的认识。

应用案例以某学校的学生成绩预测为例，假设因变量为学生成绩，自变量为学生的学习时间、就餐次数和睡眠时间。

收集到了100个样本的数据。

通过上述方法进行多元回归分析。

数据收集在数据收集阶段，通过学校的学生管理系统，获取了学生的学习时间、就餐次数和睡眠时间的观测值。

模型设定根据领域知识和经验，我们假设学生的学生成绩与学习时间、就餐次数和睡眠时间存在一定的关系。

因此，我们可以设定模型为：成绩= β0 + β1 * 学习时间+ β2 * 就餐次数+ β3 * 睡眠时间+ ε。

参数估计通过最小二乘法，我们可以估计回归模型的参数。

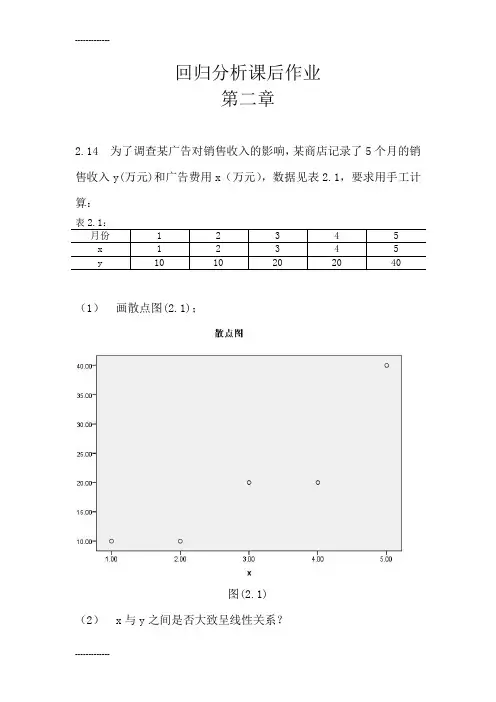
回归分析课后作业第二章2.14 为了调查某广告对销售收入的影响，某商店记录了5个月的销售收入y(万元)和广告费用x（万元），数据见表2.1，要求用手工计算：（1）画散点图(2.1)；图(2.1)（2） x与y之间是否大致呈线性关系？从（1）中看出x 与y 没有线性关系。

（3） 用最小二乘估计求出回归方程；令回归方程为x y ∧∧-=10ββ,则可知道()()∑∑==∧--=512511i ii iixxy x xβ，代入数据易得71=∧β，110-=-=∧∧x y ββ，从而得到回归方程为x y 71+-=。

（4） 求回归标准误差∧σ；我们知道回归标准差0553.6)(2112=--=∑=∧∧ni i i y y n σ。

（5） 给出∧∧10ββ和置信度为%95的区间估计；因为我们知道()⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-+∑∧22200)(1,~σββx x x n N i ，可以算出3333.40var 0=⎪⎭⎫ ⎝⎛∧β，所以我们知道∧0β置信度为%95的区间估计为（∧0β-⎪⎭⎫ ⎝⎛∧02/var βαt ，∧0β-⎪⎭⎫ ⎝⎛∧02/var βαt ），所以∧0β的得到区间为]211.19,211.21[-（注意这里的2σ估计时用其有偏估计值）。

同理我们知道()⎪⎪⎭⎫ ⎝⎛-∑∧2211,~x x N i σββ，可以算出667.3var 1=⎪⎭⎫ ⎝⎛∧β，所以可得∧1β置信度为%95的区间估计为()()⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-∧∧∧∧12/112/1var 3,var 3ββββααt t ，所以可得到∧1β的区间估计为]094.13,906.0[。

（6） 计算x 与y 的决定系数。

因为()8167.022212122==-⎪⎭⎫ ⎝⎛-==∑∑==∧yyxxxy ni ini i LL L yyy y SSTSSRr 。

（7） 对回归方程作方差分析；（8） 做回归系数1β显著性的检验；我们用t 检验做回归系数1β的显著性。

毕业论文题目多元回归分析中的变量选取——SPSS的应用多元回归分析中的变量选取——SPSS的应用摘要本文不仅对于复杂的统计计算通过常用的计算机应用软件SPSS来实现，同时通过对两组数据的实证分析，来研究统计学中多元回归分析中的变量选取，让大家对统计中的多元回归数据的选取和操作方法有更深层次的了解。

一组数据是对于淘宝交易额的未来发展趋势的研究，一组数据时对于我国财政收入的研究。

本文通过两个实证从不同程度上对数据选取的研究运用通俗的语言和浅显的描述将SPSS在多元回归分析中的统计分析方法呈现在大家面前，让大家对多元回归分析以及SPSS软件都可以有更深一步的了解。

通过SPSS软件对数据进行分析，对数据进行处理的方法进行总结，找出SPSS对于数据处理和分析的优缺点，最后得在对变量的选取和软件的操作提出建议。

关键词：统计学 SPSS 变量的选取多元回归分析AbstractIn this paper, not only for complex statistical calculations done by the commonly used computer application software of SPSS, through the empirical analysis of the two groups of data at the same time, to study the statistics of the variables in the multivariate regression analysis, let everybody to select multiple regression in statistical data and operation methods have a deeper understanding. Is a set of data for the future development trend of taobao transactions of research, a set of data for the research of our country's financial income. In this paper, through two empirical to select data from different extent research using a common language and plain the SPSS statistical analysis method in multiple regression analysis of present in front of everyone, let everyone to multiple regression analysis and SPSS software can have a deeper understanding. Through the SPSS software to analyze data, and summarizes method of data processing, find out the advantages and disadvantages of SPSS for data processing and analysis, finally had to put forward the proposal to the operation of the selection of variables and software.Keywords: Statistical SPSS The selection of variables multiple regression analysis目录摘要 (1)英文摘要 (1)引言 (3)第一章回归分析 (3)1.1自变量的选择 (4)1.2国内外研究现状 (5)第二章案例分析一：淘宝交易额的研究 (6)2.1数据的来源及变量的选取 (6)2.2相关分析 (7)2.2.1散点图 (7)2.2.2计算相关系数 (8)2.3回归分析 (11)2.4小结 (13)第三章案例分析二：财政收入的研究 (14)3.1数据的来源及变量的选取 (14)3.2相关分析 (15)3.2.1散点图 (15)3.2.2计算相关系数 (17)3.3回归分析 (19)3.4逐步回归 (21)3.5小结 (24)第四章总结及建议 (25)参考文献 (26)引言统计学是一门提供数据信息的收集、处理、归纳和分析的理论与方法的科学。

1、简述多元统计分析中协差阵检验的步骤 第一，提出待检验的假设H0和H1； 第二，给出检验的统计量及其服从的分布；第三，给定检验水平，查统计量的分布表，确定相应的临界值，从而得到否定域； 第四，根据样本观测值计算出统计量的值，看是否落入否定域中，以便对待判假设做出决策（拒绝或接受）。

协差阵的检验检验0=ΣΣ0p H =ΣI ： /2/21exp 2np n e tr n λ⎧⎫⎛⎫=-⎨⎬ ⎪⎩⎭⎝⎭S S00p H =≠ΣΣI ： /2/2**1exp 2np n e tr n λ⎧⎫⎛⎫=-⎨⎬ ⎪⎩⎭⎝⎭S S检验12k ===ΣΣΣ012k H ===ΣΣΣ：统计量/2/2/2/211i i kkn n pn np k iii i nnλ===∏∏SS2. 针对一个总体均值向量的检验而言，在协差阵已知和未知的两种情形下，如何分别构造的统计量？3. 作多元线性回归分析时，自变量与因变量之间的影响关系一定是线性形式的吗？多元线性回归分析中的线性关系是指什么变量之间存在线性关系？ 答：作多元线性回归分析时，自变量与因变量之间的影响关系不一定是线性形式。

当自变量与因变量是非线性关系时可以通过某种变量代换，将其变为线性关系，然后再做回归分析。

多元线性回归分析的线性关系指的是随机变量间的关系，因变量y 与回归系数βi 间存在线性关系。

多元线性回归的条件是：（1）各自变量间不存在多重共线性； （2）各自变量与残差独立；（3）各残差间相互独立并服从正态分布； （4）Y 与每一自变量X 有线性关系。

4.回归分析的基本思想与步骤 基本思想：所谓回归分析，是在掌握大量观察数据的基础上，利用数理统计方法建立因变量与自变量之间的回归关系函数表达式（称回归方程式）。

回归分析中，当研究的因果关系只涉及因变量和一个自变量时，叫做一元回归分析；当研究的因果关系涉及因变量和两个或两个以上自变量时，叫做多元回归分析。

此外，回归分析中，又依据描述自变量与因变量之间因果关系的函数表达式是线性的还是非线性的，分为线性回归分析和非线性回归分析。

我国居民消费现状的统计分析我国居民消费现状的统计分析专业：经济学姓名：000 学号：00000000⼀、我国城镇居民现状近年来,我国宏观经济形势发⽣了重⼤变化,经济发展速度加快,居民收⼊稳定增加,在国家连续出台住房、教育、医疗等各项改⾰措施和实施“刺激消费、扩⼤内需、拉动经济增长”经济政策的影响下,全国居民的消费⽀出也强劲增长,消费结构发⽣了显著变化,消费结构不合理现象得到了⼀定程度的改善。

本⽂通过相关数据分析总结出了我国城镇居民消费呈现富裕型、娱乐教育⽂化服务类消费攀升的趋势特点。

⼆、我国居民消费结构的横向分析第⼀,⾷品消费⽀出⽐重随收⼊增加呈现出明显的下降趋势,这与恩格尔定律的表述⼀致。

但最低收⼊户与最⾼收⼊恩格尔系数相差太过悬殊,城镇最低收⼊户刚刚解决了温饱问题,⽽最⾼收⼊户的⽣活⽔平按照恩格尔系数的评价标准早已达到了富裕型,甚⾄接近最富裕型。

第⼆,⾐着消费⽀出⽐重随收⼊增加缓慢上升,到⾼收⼊户⼜有所下降,但各收⼊组⽀出⽐重相差不⼤。

⾐着⽀出⽐重没有更多的递增且最⾼收⼊户的⽀出⽐重有所下降,这些都符合恩格尔定律关于⾐着消费的引申。

随着收⼊的增加,⾐着⽀出⽐重呈现先上升后下降的⾛势。

事实上,在当前的价格⽔平和服装业的发展⽔平下,城镇居民的穿着是有⼀定限度的,⽽且居民对⾐着的需求也不是⽆限膨胀的,即使收⼊⽔平继续提⾼,也不需要将更⼤的⽐例⽤于购买服饰⽤品了。

第三,家庭设备⽤品及服务、交通通讯、娱乐教育⽂化服务和杂项商品与服务的⽀出⽐重呈逐组上升趋势,说明居民的⽣活⽔平随收⼊的增加⽽不断提⾼和改善。

第四,医疗保健⽀出⽐重随收⼊⽔平提⾼呈现⼀种两端⾼、中间低的⾛势。

这是因为医疗保健⽀出作为⽣活必须⽀出,不论居民⽣活⽔平⾼低,都要将⼀定⽐例的收⼊⽤于维持⾃⾝健康,⽽且由于医疗制度改⾰,加重了个⼈负担的同时,也减⼩了旧制度可能造成的不同⾏业、不同体制下居民医疗保健⽀出的差别,因⽽不同收⼊等级的居民在医疗保健⽀出⽐重上差别不⼤。