高三数学函数练习题教师版

高三数学函数试题答案及解析1.对于函数，若存在非零常数，使得当取定义域内的每一个值时，都有，则称为准偶函数.下列函数中是准偶函数的是（）A．B．C．D．【答案】D.【解析】∵，∴的函数图像关于直线对称，A：函数图像不关于某直线对称，B：函数图像关于轴，即直线对称，C：函数图像不关于某直线对称，D：函数图像关于直线，对称，符合题意，故选D.【考点】1.新定义问题；2.常见函数图像的对称性.2.具有性质：＝－f(x)的函数，我们称为满足“倒负”变换的函数，下列函数：①y＝x－；②y＝x＋；③y＝，其中满足“倒负”变换的函数是________(填序号)．【答案】①③【解析】对于①，f(x)＝x－，f＝－x＝－f(x)，满足；对于②，f＝＋x＝f(x)，不满足；对于③，f＝即f＝故f＝－f(x)，满足．综上可知，满足“倒负”变换的函数是①③.3.如果函数在上的最大值和最小值分别为、，那么.根据这一结论求出的取值范围（）.A．B．C．D．【答案】B【解析】函数在区间上最大值为1，最小值为，即，所以，，即取值范围为，选B.【考点】新定义概念与函数的最值.4.类比“两角和与差的正弦公式”的形式，对于给定的两个函数：S(x)＝a x－a－x，C(x)＝a x＋a－x，其中a>0，且a≠1，下面正确的运算公式是()①S(x＋y)＝S(x)C(y)＋C(x)S(y)；②S(x－y)＝S(x)C(y)－C(x)S(y)；③2S(x＋y)＝S(x)C(y)＋C(x)S(y)；④2S(x－y)＝S(x)C(y)－C(x)S(y)．A．①②B．③④C．①④D．②③【答案】B【解析】经验证易知①②错误．依题意，注意到2S(x＋y)＝2(a x＋y－a－x－y)，又S(x)C(y)＋C(x)S(y)＝2(a x＋y－a－x－y)，因此有2S(x＋y)＝S(x)C(y)＋C(x)S(y)；同理有2S(x－y)＝S(x)C(y)－C(x)S(y)，综上所述，选B.5.已知函数.若，则的取值范围是( )A．B．C．D．【答案】D【解析】依题意可得或解得.【考点】1.分段函数的应用.2.二次不等式的解法.3.分类的数学思想.6.若函数满足，当x∈[0，1]时，，若在区间(-1，1]上，有两个零点，则实数m的取值范围是A．0<m≤B．0<m<C．<m≤l D．<m<1【答案】A【解析】有两个零点，即曲线有两个交点.令，则，所以.在同一坐标系中，画出的图象（如图所示）：直线过定点，所以，满足即选.【考点】分段函数，函数的图象，函数的零点.7.已知函数满足：对定义域内的任意，都有，则函数可以是（）A．B．C．D．【答案】C【解析】由可知，对A，，不满足；对B，，不满足；对C，，满足；故选C. 或解，由得，表示的是上凸函数，只有C选项满足.【考点】1.函数性质的应用.8.若直角坐标平面内的亮点P，Q满足条件： P，Q都在函数y=f(x)的图像上， P，Q关于原点对称，则称点对[P,Q]是函数y=f(x)的一对“友好点对”(点对[P,Q]与[Q,P]看作同一对“友好点对”)。

专题3.3函数的奇偶性与周期性练基础1．（2021·海南海口市·高三其他模拟）已知函数()(0)f x kx b k =+≠，则“(0)0f =”是“函数()f x 为奇函数”的（）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】C 【解析】化简“(0)0f =”和“函数()f x 为奇函数”，再利用充分必要条件的定义判断得解.【详解】(0)0f =，所以0b =，函数()f x 为奇函数，所以()()0f x kx b f x kx b -=-+=-=--=，所以0b =.所以“(0)0f =”是“函数()f x 为奇函数”的充分必要条件.故选：C2．（2021·福建高三三模）若函数()y f x =的大致图象如图所示，则()f x 的解析式可能是（）A ．()1xf x x =-B ．()1x f x x=-C ．()21x f x x =-D ．()21x f x x =-【答案】C 【解析】利用排除法，取特殊值分析判断即可得答案解：由图可知，当(0,1)x ∈时，()0f x <，取12x =，则对于B ，112(101212f ==>-，所以排除B ，对于D ，1122()012314f ==>-，所以排除D ，当0x >时，对于A ，()1111x f x x x ==+--，此函数是由1y x =向右平移1个单位，再向上平移1个单位，所以1x >时，()1f x >恒成立，而图中，当1x >时，()f x 可以小于1，所以排除A,故选：C3．（2021·广东高三其他模拟）下列函数中，既是奇函数又在区间()0,1上单调递增的是（）A．y =B ．1y x x=+C ．xx y ee =-﹣D ．2log y x=【答案】C 【解析】利用函数奇偶性的定义和函数的解析式判断.【详解】A.函数y =的定义域是[0,)+∞，所以函数是非奇非偶函数，故错误；B.1y x x=+在()0,1上单调递减，故错误；C.因为()()()xx x x f x ee e ef x --=---=-=﹣，所以函数是奇函数，且在()0,1上单调递增，正确；D.因为()()22log =log f x x x f x -=-=，所以函数是偶函数，故错误；故选：C ．4．（2021·湖南高三月考）定义函数1,()1,x D x x ⎧=⎨-⎩为有理数，为无理数，则下列命题中正确的是（）A ．()D x 不是周期函数B ．()D x 是奇函数C ．()yD x =的图象存在对称轴D ．()D x 是周期函数，且有最小正周期【答案】C 【解析】当m 为有理数时恒有()()D x m D x +=，所以()D x 是周期函数，且无最小正周期，又因为无论x 是有理数还是无理数总有()()D x D x -=，所以函数()D x 为偶函数，图象关于y 轴对称．当m 为有理数时，()1,1,x D x m x ⎧+=⎨-⎩为有理数为无理数，()()D x m D x ∴+=，∴任何一个有理数m 都是()D x 的周期，()D x ∴是周期函数，且无最小正周期，∴选项A ，D 错误，若x 为有理数，则x -也为有理数，()()D x D x ∴=-，若x 为无理数，则x -也为无理数，()()D x D x ∴=-，综上，总有()()D x D x -=，∴函数()D x 为偶函数，图象关于y 轴对称，∴选项B 错误，选项C 正确，故选：C5．【多选题】（2021·淮北市树人高级中学高一期末）对于定义在R 上的函数()f x ，下列说法正确的是（）A ．若()f x 是奇函数，则()1f x -的图像关于点()1,0对称B ．若对x ∈R ，有()()11f x f x =+-，则()f x 的图像关于直线1x =对称C ．若函数()1f x +的图像关于直线1x =-对称，则()f x 为偶函数D ．若()()112f x f x ++-=，则()f x 的图像关于点()1,1对称【答案】ACD 【解析】四个选项都是对函数性质的应用，在给出的四个选项中灵活的把变量x 加以代换，再结合函数的对称性、周期性和奇偶性就可以得到正确答案.【详解】对A ，()f x 是奇函数，故图象关于原点对称，将()f x 的图象向右平移1个单位得()1f x -的图象，故()1f x -的图象关于点（1，0）对称，正确；对B ，若对x ∈R ，有()()11f x f x =+-，得()()2f x f x +=，所以()f x 是一个周期为2的周期函数，不能说明其图象关于直线1x =对称，错误.；对C ，若函数()1f x +的图象关于直线1x =-对称，则()f x 的图象关于y 轴对称，故为偶函数，正确；对D ，由()()112f x f x ++-=得()()()()112,202f f f f +=+=，()()()()312,422,f f f f +-=+-= ，()f x 的图象关于（1，1）对称，正确.故选：ACD.6．【多选题】（2020·江苏南通市·金沙中学高一期中）已知偶函数()f x 在区间[)0,+∞上是增函数,则满足1(21)()3f x f -<的x 的取值是（）A ．0B ．12C ．712D ．1【答案】BC 【解析】根据偶函数和单调性求得不等式的解，然后判断各选项．．【详解】由题意1213x -<，解得1233x <<，只有BC 满足．故选：BC ．7．【多选题】（2021·广东高三二模）函数()f x 的定义域为R ，且()1f x -与()1f x +都为奇函数，则下列说法正确的是（）A ．()f x 是周期为2的周期函数B ．()f x 是周期为4的周期函数C ．()2f x +为奇函数D ．()3f x +为奇函数【答案】BD 【解析】AB 选项，利用周期函数的定义判断；CD 选项，利用周期性结合()1f x -，()1f x +为奇函数判断.【详解】因为函数()f x 的定义域为R ，且()1f x -与()1f x +都为奇函数，所以()()11f x f x --=--，()()11f x f x -+=-+，所以()()2f x f x =---，()()2f x f x =--+，所以()()22f x f x --=-+，即()()4f x f x +=，故B 正确A 错误；因为()()()3341f x f x f x +=+-=-，且()1f x -为奇函数，所以()3f x +为奇函数，故D 正确；因为()2f x +与()1f x +相差1，不是最小周期的整数倍，且()1f x +为奇函数，所以()2f x +不为奇函数，故C 错误.故选：BD.8．（2021·吉林高三二模（文））写出一个符合“对x R ∀∈，()()0f x f x +-=”的函数()f x =___________.【答案】3x （答案不唯一）【解析】分析可知函数()f x 的定义域为R ，且该函数为奇函数，由此可得结果.【详解】由题意可知，函数()f x 的定义域为R ，且该函数为奇函数，可取()3f x x =.故答案为：3x （答案不唯一）.9．（2021·全国高三二模（理））已知()y f x =为R 上的奇函数，且其图象关于点()2,0对称，若()11f =，则()2021f =__________．【答案】1【解析】根据函数的对称性及奇函数性质求得函数周期为4，从而()2021(1)1f f ==.【详解】函数关于点()2,0对称，则()(4)f x f x =--，又()y f x =为R 上的奇函数，则()(4)(4)f x f x f x =--=-，因此函数的周期为4，因此()2021(1)1f f ==.故答案为：1.10．（2021·上海高三二模）已知函数()f x 的定义域为R ，函数()g x 是奇函数，且()()2x g x f x =+，若(1)1f =-，则(1)f -=___________．【答案】32-【解析】通过计算(1)(1)g g +-可得．【详解】因为()g x 是奇函数，所以(1)(1)0g g +-=，即1(1)2(1)02f f ++-+=，所以53(1)122f -=-=-．故答案为：32-．练提升1．（2021·安徽高三三模（文））若把定义域为R 的函数()f x 的图象沿x 轴左右平移后，可以得到关于原点对称的图象，也可以得到关于y 轴对称的图象，则关于函数()f x 的性质叙述一定正确的是（）A ．()()0f x f x -+=B ．()()11f x f x -=-C ．()f x 是周期函数D ．()f x 存在单调递增区间【答案】C 【解析】通过举例说明选项ABD 错误；对于选项C 可以证明判断得解.【详解】定义域为R 的函数()f x 的图象沿x 轴左右平移后，可以得到关于原点对称的图象，也可以得到关于y 轴对称的图象，∴()f x 的图象既有对称中心又有对称轴，但()f x 不一定具有奇偶性，例如()sin 3f x x π⎛⎫=+⎪⎝⎭，由()()0f x f x -+=，则()f x 为奇函数，故选项A 错误；由()()11f x f x -=-，可得函数()f x 图象关于0x =对称，故选项B 错误；由()0f x =时，()f x 不存在单调递增区间，故选项D 错误；由已知设()f x 图象的一条对称抽为直线x a =，一个对称中心为(),0b ，且a b ¹，∴()()2f a x f x +=-，()()2f x f b x -=-+，∴()()22f a x f b x +=-+，∴()()()2222f a x b f b x b f x +-=-+-=-，∴()()()()442222f x a b f b x b f x a b f x +-=-+-=-+-=，∴()f x 的一个周期()4T a b =-，故选项C 正确.故选：C2．（2021·天津高三二模）已知函数()f x 在R 上是减函数，且满足()()f x f x -=-，若31log 10a f ⎛⎫=- ⎪⎝⎭，()3log 9.1b f =，()0.82c f =，则a ，b ，c 的大小关系为（）A ．a b c >>B ．c b a >>C ．b a c >>D ．c a b>>【答案】B 【解析】根据对数运算性质和对数函数单调性可得331log log 9.1210->>，根据指数函数单调性可知0.822<；利用()f x 为减函数可知()()0.8331log log 9.1210f f f ⎛⎫-<< ⎪⎝⎭，结合()f x 为奇函数可得大小关系.【详解】33331log log 10log 9.1log 9210-=>>= ，0.822<即：0.8331log log 9.1210->>又()f x 是定义在R 上的减函数()()0.8331log log 9.1210f f f ⎛⎫∴-<< ⎪⎝⎭又()f x 为奇函数3311log log 1010f f⎛⎫⎛⎫∴-=- ⎪ ⎪⎝⎭⎝⎭()()0.8331log log 9.1210f f f ⎛⎫∴-<< ⎪⎝⎭，即：c b a >>.故选：B.3.（2021·陕西高三三模（理））已知函数f (x )为R 上的奇函数，且()(2)f x f x -=+，当[0,1]x ∈时，()22x xaf x =+，则f (101)+f (105)的值为（）A ．3B ．2C ．1D ．0【答案】A 【解析】根据函数为奇函数可求得函数的解析式，再由()(2)f x f x -=+求得函数f (x )是周期为4的周期函数，由此可计算得选项．【详解】解：根据题意，函数f (x )为R 上的奇函数，则f (0)=0，又由x ∈[0，1]时，()22xx a f x =+，则有f (0)=1+a =0，解可得：a =﹣1，则有1()22xxf x =-，又由f (﹣x )=f (2+x )，即f (x +2)=﹣f (x )，则有f (x +4)=﹣f (x +2)=f (x )，即函数f (x )是周期为4的周期函数，则1313(101)(1)2,(105)(1)22222f f f f ==-===-=，故有f (101)+f (105)=3，故选：A ．4．（2021·上海高三二模）若()f x 是R 上的奇函数，且()f x 在[0,)+∞上单调递增，则下列结论：①|()|y f x =是偶函数；②对任意的x ∈R 都有()|()|0f x f x -+=；③()()y f x f x =-在(,0]-∞上单调递增；④反函数1()y fx -=存在且在(,0]-∞上单调递增．其中正确结论的个数为（）A ．1B ．2C ．3D ．4【答案】C 【解析】根据奇函数定义以及单调性性质，及反函数性质逐一进行判断选择.【详解】对于①，由()f x 是R 上的奇函数，得()()f x f x -=-，∴|()||()||()|-=-=f x f x f x ，所以|()|y f x =是偶函数，故①正确；对于②，由()f x 是R 上的奇函数，得()()0f x f x -+=，而()|()|f x f x =不一定成立，所以对任意的x ∈R ，不一定有()|()|0f x f x -+=，故②错误；对于③，因为()f x 是R 上的奇函数，且()f x 在[0,)+∞上单调递增，所以()f x 在(,0]-∞上单调递增，且()(0)0f x f £=，因此2()()[()]y f x f x f x =-=-，利用复合函数的单调性，知()()y f x f x =-在(,0]-∞上单调递增，故③正确.对于④，由已知得()f x 是R 上的单调递增函数，利用函数存在反函数的充要条件是，函数的定义域与值域是一一映射，且函数与其反函数在相应区间内单调性一致，故反函数1()y f x -=存在且在(,0]-∞上单调递增，故④正确；故选：C5．【多选题】（2021·全国高三专题练习）已知函数()f x 是偶函数，(1)f x +是奇函数，并且当[]1,2x ∈，()1|2|f x x =--，则下列选项正确的是（）A ．()f x 在(3,2)--上为减函数B ．()f x 在(3,2)--上()0f x <C ．()f x 在(3,2)--上为增函数D ．()f x 在(3,2)--上()0f x >【答案】CD 【解析】根据题意，分析可得(4)()f x f x +=，结合函数的解析式可得当(3,2)x ∈--时函数的解析式，据此分析可得答案．【详解】解：根据题意，函数(1)f x +为奇函数，则有(1)(1)f x f x +=--+，即(2)()f x f x +=--，又由()f x 为偶函数，则()()f x f x -=，则有(2)()f x f x +=-，即有(4)()f x f x +=，当[1x ∈，2]时，()1|2|1f x x x =--=-，若(3,2)x ∈--，则4(1,2)x +∈，则(4)(4)13f x x x +=+-=+，则当(3,2)x ∈--时，有()3f x x =+，则()f x 为增函数且()(3)0f x f >-=；故()f x 在(3,2)--上为增函数，且()0f x >；故选：CD ．6．【多选题】（2021·全国高三专题练习）若函数()f x 对任意x ∈R 都有()()0f x f x +-=成立，m R ∈，则下列的点一定在函数()y f x =图象上的是（）A ．(0,0)B ．(,())m f m --C ．(,())m f m --D ．(,())m f m -【答案】ABC 【解析】根据任意x ∈R 满足()()0f x f x +-=，得到()f x 是奇函数判断.【详解】因为任意x ∈R 满足()()0f x f x +-=，所以()f x 是奇函数，又x ∈R ，所以令0x =，则(0)(0)f f -=-，得(0)0f =，所以点(0,0)，且点(,())m f m --与(,())m f m --也一定在()y f x =的图象上，故选：ABC ．7．【多选题】（2021·浙江高一期末）已知函数()y f x =是定义在[1,1]-上的奇函数，当0x >时，()(1)f x x x =-，则下列说法正确的是（）A ．函数()y f x =有2个零点B ．当0x <时，()(1)f x x x =-+C ．不等式()0f x <的解集是(0,1)D ．12,[1,1]x x ∀∈-，都有()()1212f x f x -≤【答案】BCD 【解析】根据函数奇偶性定义和零点定义对选项一一判断即可．【详解】对A ，当0x >时，由()(1)0f x x x =-=得1x =，又因为()y f x =是定义在[1,1]-上的奇函数，所以()()()00,110f f f =-=-=，故函数()y f x =有3个零点，则A 错；对B ，设0x <，则0x ->，则()()()()11f x f x x x x x =--=----=-+⎡⎤⎣⎦，则B 对；对C ，当01x <≤时，由()(1)0f x x x =-<，得01x <<；当10x -≤≤时，由()(1)0f x x x =-+<，得x 无解；则C 对；对D ，12,[1,1]x x ∀∈-，都有()()()()12max min 1111122442f x f x f x f x f f ⎛⎫⎛⎫⎛⎫-≤-=--=--= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，则D 对．故选：BCD ．8．【多选题】（2021·苏州市第五中学校高一月考）高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的称号.设x ∈R ，用[]x 表示不超过x 的最大整数，[]y x =也被称为“高斯函数”，例如：[ 3.5]4-=-，[2.1]2=.已知函数()[1]f x x x =+-，下列说法中正确的是（）A ．()f x 是周期函数B ．()f x 的值域是[0,1]C ．()f x 在(0,1)上是减函数D ．x ∀∈R ，[()]0f x =【答案】AC 【解析】根据[]x 定义将函数()f x 写成分段函数的形式，再画出函数的图象，根据图象判断函数的性质.【详解】由题意可知[]1,210,1011,012,12x x x x x --≤<-⎧⎪-≤<⎪⎪+=≤<⎨⎪≤<⎪⎪⎩，()[]1,21,1011,012,12x x x x f x x x x x x x ---≤<-⎧⎪--≤<⎪⎪∴=+-=-≤<⎨⎪-≤<⎪⎪⎩，可画出函数图像，如图：可得到函数()f x 是周期为1的函数，且值域为(]0,1，在()0,1上单调递减，故选项AC 正确，B 错误；对于D ，取1x =-()11f -=，则()11f -=⎡⎤⎣⎦，故D 错误.故选：AC ．9．【多选题】（2021·湖南高三月考）函数()f x 满足以下条件：①()f x 的定义域是R ，且其图象是一条连续不断的曲线；②()f x 是偶函数；③()f x 在()0,∞+上不是单调函数；④()f x 恰有2个零点.则函数()f x 的解析式可以是（）A ．2()2f x x x =-B ．()ln 1f x x =-C ．2()1f x x x =-++D ．()2xf x e =-【答案】CD 【解析】利用函数图象变换画出选项A ，B ，C ，D 对应的函数图象，逐一分析即可求解.【详解】解：显然题设选项的四个函数均为偶函数，但()ln 1f x x =-的定义域为{}0x x R ≠≠，所以选项B 错误；函数2()2f x x x =-的定义域是R ，在(),1-∞-，()0,1单调递减，在()1,0-，()1,+∞单调递增，但()()()2020f f f -===有3个零点，选项A 错误；函数2()1f x x x =-++的定义域是R ，当()0,x ∈+∞时，2()1f x x x =-++的图象对称轴为12x =，其图象是开口向下的抛物线，故()f x 在1,2⎛⎫-∞- ⎪⎝⎭，10,2⎛⎫ ⎪⎝⎭单调递增，在1,02⎛⎫- ⎪⎝⎭，1,2⎛⎫+∞ ⎪⎝⎭单调递减，由图得()f x 恰有2个零点，选项C 正确；函数()2xf x e =-的定义域是R ，在(),ln 2-∞-，()0,ln 2单调递减，在()ln 2,0-，()ln 2,+∞单调递增，且()()ln 2ln 20f f -==有2个零点，选项D 正确.故选：CD.10．（2021·黑龙江大庆市·高三二模（理））定义在R 上的函数()f x 满足()2()f x f x +=，当[]1,1x ∈-时，2()f x x =，则函数()f x 的图象与()3x g x =的图象的交点个数为___________.【答案】7由题设可知()f x 的周期为2，结合已知区间的解析式及()3x g x =，可得两函数图象，即知图象交点个数.【详解】由题意知：()f x 的周期为2，当[1,1]x ∈-时，2()f x x =，∴()f x 、()g x 的图象如下：即()f x 与()g x 共有7个交点，故答案为：7.【点睛】结论点睛：()()f m x f x +=有()f x 的周期为||m .练真题1.（2020·天津高考真题）函数241xy x =+的图象大致为（）A．B．C．D．【解析】【分析】由题意首先确定函数的奇偶性，然后考查函数在特殊点的函数值排除错误选项即可确定函数的图象.【详解】由函数的解析式可得：()()241xf x f x x --==-+，则函数()f x 为奇函数，其图象关于坐标原点对称，选项CD 错误；当1x =时，42011y ==>+，选项B 错误.故选：A.2.（2020·全国高考真题（理））设函数()ln |21|ln |21|f x x x =+--，则f (x )（）A．是偶函数，且在1(,)2+∞单调递增B．是奇函数，且在11(,22-单调递减C．是偶函数，且在1(,)2-∞-单调递增D．是奇函数，且在1(,2-∞-单调递减【答案】D 【解析】由()ln 21ln 21f x x x =+--得()f x 定义域为12x x ⎧⎫≠±⎨⎬⎩⎭，关于坐标原点对称，又()()ln 12ln 21ln 21ln 21f x x x x x f x -=----=--+=-，()f x ∴为定义域上的奇函数，可排除AC；当11,22x ⎛⎫∈-⎪⎝⎭时，()()()ln 21ln 12f x x x =+--，()ln 21y x =+Q 在11,22⎛⎫- ⎪⎝⎭上单调递增，()ln 12y x =-在11,22⎛⎫- ⎪⎝⎭上单调递减，()f x ∴在11,22⎛⎫- ⎪⎝⎭上单调递增，排除B；当1,2x ⎛⎫∈-∞-⎪⎝⎭时，()()()212ln 21ln 12ln ln 12121x f x x x x x +⎛⎫=----==+ ⎪--⎝⎭，2121x μ=+- 在1,2⎛⎫-∞- ⎪⎝⎭上单调递减，()ln f μμ=在定义域内单调递增，根据复合函数单调性可知：()f x 在1,2⎛⎫-∞- ⎪⎝⎭上单调递减，D 正确.故选：D.3．（2020·海南省高考真题）若定义在R 的奇函数f (x )在(,0)-∞单调递减，且f (2)=0，则满足(10)xf x -≥的x 的取值范围是（）A．[)1,1][3,-+∞ B．3,1][,[01]-- C．[1,0][1,)-⋃+∞D．[1,0][1,3]-⋃【答案】D 【解析】因为定义在R 上的奇函数()f x 在(,0)-∞上单调递减，且(2)0f =，所以()f x 在(0,)+∞上也是单调递减，且(2)0f -=，(0)0f =，所以当(,2)(0,2)x ∈-∞-⋃时，()0f x >，当(2,0)(2,)x ∈-+∞ 时，()0f x <，所以由(10)xf x -≥可得：021012x x x <⎧⎨-≤-≤-≥⎩或或001212x x x >⎧⎨≤-≤-≤-⎩或或0x =解得10x -≤≤或13x ≤≤，所以满足(10)xf x -≥的x 的取值范围是[1,0][1,3]-⋃，故选：D.4.（2018年理全国卷II）已知op 是定义域为(−∞,+ ∞)的奇函数，满足o1−p =o1+p ．若o1)=2，则o1)+o2)+o3)+⋯+o50)=()A.−50B.0C.2D.50【答案】C 【解析】因为op 是定义域为(−∞,+ ∞)的奇函数，且o1−p =o1+p ，所以o1+p =−o −1)∴o3+p =−o +1)=o −1)∴=4,因此o1)+o2)+o3)+⋯+o50)=12[o1)+o2)+o3)+o4)]+o1)+o2)，因为o3)=−o1)，o4)=−o2)，所以o1)+o2)+o3)+o4)=0，∵o2)=o −2)=−o2)∴o2)=0，从而o1)+o2)+o3)+⋯+o50)=o1)=2，选C.5.（2019·全国高考真题（文））设()f x 是定义域为R 的偶函数，且在()0,∞+单调递减，则（）A．233231log 224f f f --⎛⎫⎛⎫⎛⎫>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭B．233231log 224f f f --⎛⎫⎛⎫⎛⎫>> ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭C．23332122log 4f f f --⎛⎫⎛⎫⎛⎫>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭D．23323122log 4f f f --⎛⎫⎛⎫⎛⎫>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭【答案】C 【解析】()f x 是R 的偶函数，()331log log 44f f ⎛⎫∴= ⎪⎝⎭．223303322333log 4log 31,1222log 422---->==>>∴>> ，又()f x 在(0，+∞)单调递减，∴()23323log 422f f f --⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭，23323122log 4f f f --⎛⎫⎛⎫⎛⎫∴>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，故选C．6.（2019·全国高考真题（理））已知()f x 是奇函数，且当0x <时，()e ax f x =-.若(ln 2)8f =，则a =__________.【答案】-3【解析】因为()f x 是奇函数，且当0x >时0x ->，()()ax f x f x e -=--=．又因为ln 2(0,1)∈，(ln 2)8f =，所以ln 28a e-=，两边取以e 为底的对数得ln 23ln 2a -=，所以3a -=，即3a =-．。

第02讲 利用导数研究函数的单调性 ---练1．（2017·某某高考真题（文））若函数()e xf x (e=2.71828,是自然对数的底数)在()f x 的定义域上单调递增,则称函数()f x 具有M 性质,下列函数中具有M 性质的是（ ） A ．()2xf x -= B ．()2f x x = C ．()-3xf x = D ．【答案】A【解析】对于A,令,,则()g x 在R 上单调递增,故()f x 具有M 性质,故选A. 2.（2019·某某高考模拟（文））函数的导函数满足在上恒成立，且，则下列判断一定正确的是（ ） A ．B ．C ．D ．【答案】A 【解析】令函数F （x ），则F ′（x ），∵f ′（x ）＞f （x ），∴F ′（x ）＞0， 故函数F （x ）是定义在R 上的增函数， ∴F （1）＞F （0），即 ，故有f （1）＞ef （0）；又， ∴，故选：A.3.（2018·某某镇海中学高三期中）已知函数，则函数的图象为（ ）A． B．C． D．【答案】D【解析】=，当x＜0时，=．令g（x）=2x3﹣1+ln（﹣x），由，得，当x∈（﹣∞，）时，g′（x）＞0，当x∈（，0）时，g′（x）＜0．所以g（x）有极大值为=．又x2＞0，所以f′（x）的极大值小于0．所以函数f（x）在（﹣∞，0）上为减函数．当x＞0时，=．令h（x）=2x3﹣1+lnx，．所以h（x）在（0，+∞）上为增函数，而h（1）=1＞0，h（）=﹣．又x2＞0，所以函数f′（x）在（0，+∞）上有一个零点，则原函数有一个极值点．综上函数f （x ）的图象为D 中的形状． 故选：D ．4.（2018·某某高考模拟）已知数列的前项和为，则下列选项正确的是（ ）A ．B ．C ．D ．【答案】B 【解析】构造函数，所以在上递增，，可得，令，，，化为，，即，故选B.5.（2019·某某高考模拟）设函数()f x 是定义在(),0-∞上的可导函数，其导函数为()'f x ，且有，则不等式的解集为（ ）A ．()2020,0-B ．C ．()2016,0-D ．【答案】B 【解析】由， 0x （＜），得： 即令，则当0x ＜ 时，得'0F x （）＜，即上是减函数，即不等式等价为F x （） 在0-∞（，）是减函数， ∴由F 得，，即2020.x -＜故选B ．6. （2019·某某省实验高三月考（理））已知函数，则的小关系是（ ）A ．B ．C ．D ．【答案】B 【解析】 函数为偶函数，，，当时，，函数在上递增，，即，故选：．7. （2019·高考模拟（文））已知函数的单调递减区间为)2,0(，单调递增区间为(2,)+∞，那么=a ____．【答案】4. 【解析】依题意可知x ＝2是函数f （x ）的极小值点， 又，所以，'(2)14af =-＝0， 解得：a ＝4,经检验成立 故答案为：48.（2019·某某高考模拟（文））若定义域为R 的函数()f x 满足，则不等式的解集为______（结果用区间表示）．【答案】(0,)e 【解析】 令，则，因为，所以()0g x '>，所以，函数()g x 为(,)-∞+∞上的增函数， 由，得：，即，因为函数()g x 为(,)-∞+∞上的增函数， 所以ln 1x <．所以不等式的解集是(0,)e ． 故答案为(0,)e ．9．（2019·某某高考模拟（文））已知定义在R 上的函数()f x 的导函数为'()f x ，满足，且(2)f x +为偶函数，(4)2f =，则不等式()2x f x e <的解集为______.【答案】(0,)+∞ 【解析】 ∵为偶函数，∴的图象关于0x =对称，∴()y f x =的图像关于2x =对称，∴.又(4)2f =，∴(0)2f =.设，则.又∵，∴，∴'()0g x <，∴()y g x =在R 上单调递减.∵()2xf x e <，∴()2x f x e<，即()2g x <.又∵，∴()(0)g x g <，∴0x >.10．（2019·某某某某实验中学高考模拟（文））已知定义在上的偶函数()f x 的导函数为()f x '，对定义域内的任意x ，都有成立，则使得成立的x的取值X 围为_____．【答案】【解析】由()f x 是偶函数， 所以当0x >时，由得，设，则，即当0x >时，函数()g x 为减函数， 由得，即，因为()f x 是偶函数， 所以()g x 也是偶函数， 则，等价为，即2x，得2x >或2x <-，即x 的取值X 围是， 故答案为：．1. （2017·某某高考模拟）已知函数（a R ∈），下列选项中不可能是函数()f x 图象的是（ ）A ．B ．C ．D ．【答案】D【解析】∵（a R ∈）∴当0a =时，，易得()f x 在(),1-∞-上为减函数，在()1,-+∞上为增函数，故A 可能；当14a ≥时， 0∆≤， ()0f x '≥， ()f x 为增函数，故B 可能； 当0a <时， 0∆>， ()f x '有两个不相等且互为异号的实数根， ()f x 先递减再递增然后再递减，故C 可能； 当104a <<时， 0∆>， ()f x '有两个不相等的负实数根， ()f x 先递增再递减然后再递增，故D 错误. 故选D2．（2019·某某高考模拟（文））若函数在(0,)+∞上单调递增，则实数a 的取值X围是_____.【答案】1,8⎡⎫+∞⎪⎢⎣⎭【解析】，由题意得，'()0f x ≥在()0,∞+上恒成立， 即在()0,∞+上恒成立，因为的最大值为18， 所以a 的取值X 围是1[,)8+∞， 故答案是：1[,)8+∞.3．（2019·某某高考模拟（文））已知曲线1xe y x a=+在1x =处的切线l 与直线230x y +=垂直，则实数a 的值为______.【答案】25e 【解析】直线230x y +=的斜率为2-3,可得曲线在1x =处的切线为32，，当1x =，'32y =，可得312e a -+=，可得25a e =， 故答案：25a e =. 4．（2019·某某高三期末）已知函数在开区间()1,0-上单调递减，则22a b +的取值X 围是_____.【答案】9)5∞⎡+⎢⎣，【解析】由题意，在()1,0-恒成立.只需要即可，整理得，作出其对应的平面区域如图所示；所以把22a b +视为平面区域内的点与原点距离的平方， 由点到直线的距离公式可得，所以22a b +的最小值为95， 则22a b +的取值X 围是9)5∞⎡+⎢⎣，. 故答案为9)5∞⎡+⎢⎣，5.（2018·某某余姚中学高考模拟）已知函数．（1）当时，试求曲线在点处的切线；（2）试讨论函数的单调区间．【答案】（1）；（2）见解析【解析】（Ⅰ）当时，函数定义域为，切线为（Ⅱ）当时，函数定义域为，在上单调递增当时，恒成立，函数定义域为，又在单调递增，单调递减，单调递增当时，函数定义域为，在单调递增，单调递减，单调递增当时，设的两个根为且，由韦达定理易知两根均为正根，且，所以函数的定义域为，又对称轴，且，在单调递增，单调递减，单调递增6．（2018届某某市第八中学高考适应性（八））已知函数.（1）当时，讨论的导函数的单调性；（2）当时，，求的取值X围.【答案】(1) 当时，，的单调递减区间为；当时，，的单调递增区间为.(2).【解析】 （1）当时，，，当时，，的单调递减区间为；当时，，的单调递增区间为.（2），（i ）当时，，所以在上单调递增，.（ii ）当时，，由，得， ①当时，，所以时，，在上单调递增，又由，所以，即在上单调递增，所以有.②当时，，当时，，在上单调递减，又由，所以，所以在上单调递减，所以有，故此时不满足，综上，.1．（2017·某某高考真题）函数的图像如图所示，则函数()y f x =的图像可能是（ ）A． B．C． D．【答案】Dx 位于增区间内，因此选D．【解析】原函数先减再增，再减再增，且02．（2018·全国高考真题（理））函数的图像大致为 ( ) A．B．C．D．【答案】B【解析】为奇函数，舍去A,舍去D;，所以舍去C ；因此选B.3．（2019·高考真题（理））设函数f （x ）=e x +a e −x （a 为常数）．若f （x ）为奇函数，则a =________；若f （x ）是R 上的增函数，则a 的取值X 围是___________．【答案】-1; (],0-∞.【解析】若函数为奇函数,则， 对任意的x 恒成立.若函数是R 上的增函数,则恒成立,. 即实数a 的取值X 围是(],0-∞ 4．（2017·某某高考真题）已知函数，其中e 是自然数对数的底数，若，则实数a 的取值X 围是_________。

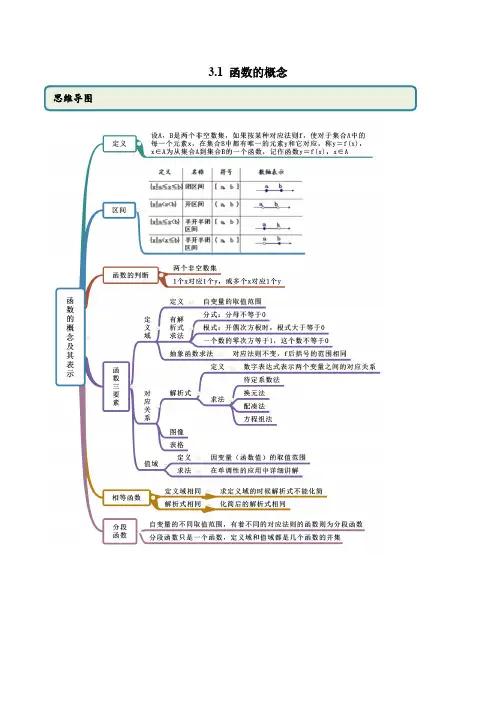
1§02 函数的概念一．填空题 1．函数()y f x =的图象与直线x ＝2的公共点共有 个。

0或12. 在函数①x y sin 1= ，② x x y ln =，③y ＝xe x ，④x x y sin =中，与函数31xy =定义域相同的函数为 ．④3．已知函数()f x 的定义域为()1,0-,则函数()21f x -的定义域为．1(0,)24．函数()f x =的定义域为 ． 5．若函数)22log 21y ax ax =++的定义域为R ，则a 的取值范围是 ．[)0,1 6．已知函数f (2x ）的定义域是［-1，1］，则f (log 2x )的定义域为 ．［2，4］7．若函数f (x )=log a (x +1)(a ＞0，a ≠1)的定义域和值域都是［0，1］，则a 等于 ．2 8．若a b c <<,则函数()()()()()()()f x x a x b x b x c x c x a =--+--+--的两个零点分别位于区间 内．(),a b 和(),b c9. 如果函数f (x )=ax -1的定义域为[－21，+)∞，那么实数a 的取值是 ．-2 10.若一系列函数的解析式相同值域相同但是定义域不同，则称这些函数为“孪生函数”。

那么函数解析式为y =2x 2+1,值域为{1,5}的孪生函数共有 个．3二．解答题11. 判断下列各组中的两个函数是否是同一函数？为什么？（1）3)5)(3(1+-+=x x x y ；52-=x y 解：不是同一函数，定义域不同 （2）111-⋅+=x x y ；)1)(1(2-+=x x y 解：不是同一函数，定义域不同 （3）21)52()(-=x x f ，52)(2-=x x f 解：不是同一函数，定义域、对应法则都不同（4） f (n )=2n -1,g (n )=2n +1,(n ∈Z ). 解：不是同一函数，对应法则不同（5）||)(2x x x f =， ⎩⎨⎧-∞∈-+∞∈=)0,(,),0(,)(t t t t t g 解：是同一函数12．求下列函数的定义域： （1）1lg4x y x -=-； （2）()2lg 4y x x=- 解：（1）()1,4；（2）((()0,2223,224⎤⎡-++⎦⎣ 。

2022学年高三上（编号：1-25）三角函数小题汇编（教师版）一、选择题1：（2023届如皋市高三上期初调研解析第1题）1：（2022⋅全国⋅模拟题）声音是由物体振动产生的声波，我们听到的声音中包含着正弦函数．若某声音对应的函数近似为()1sin sin 22f x x x =+，则下列叙述正确的是（ ）A ．2x π=为()f x 的对称轴 B ．3,02π⎛⎫⎪⎝⎭为()f x 的对称中心C ．()f x 在区间[]0,10上有3个零点D ．()f x 在区间57,33ππ⎡⎤⎢⎥⎣⎦上单调递增方法提供与解析：（嘉兴陈超群）知识点：含sin x 函数的单调性问题、求正弦（型）函数的对称轴、对称中心、二倍角正弦公式、正弦（型）函数零点、利用导数研究函数的零点问题（或方程的根）分析：本题考查三角函数的图像与性质，利用导数研究函数单调性，属较难题．利用诱导公式，计算可知22f x f x ππ⎛⎫⎛⎫+≠- ⎪ ⎪⎝⎭⎝⎭，3322f x f x ππ⎛⎫⎛⎫+≠- ⎪ ⎪⎝⎭⎝⎭即可判定选项A 、B ，求出()f x 的零点即可判定选项C ；利用导数求出函数()f x 的增区间，即可判定选项D ． 解析：因为()11sin sin 2cos sin 22222f x x x x x πππ⎛⎫⎛⎫+=+++=- ⎪ ⎪⎝⎭⎝⎭，()11sin sin 2cos sin 22222f x x x x x πππ⎛⎫⎛⎫-=-+-=+ ⎪ ⎪⎝⎭⎝⎭，所以22f x f x ππ⎛⎫⎛⎫+≠- ⎪ ⎪⎝⎭⎝⎭． 所以2x π=不是()f x 的对称轴，故A 错误； 因为()3311sin sin 32cos sin 22222f x x x x x πππ⎛⎫⎛⎫+=+++=--⎪ ⎪⎝⎭⎝⎭， ()3311sin sin 32cos sin 22222f x x x x x πππ⎛⎫⎛⎫-=-+-=-+ ⎪ ⎪⎝⎭⎝⎭，所以3322f x f x ππ⎛⎫⎛⎫+≠- ⎪ ⎪⎝⎭⎝⎭． 所以3,02π⎛⎫⎪⎝⎭不是()f x 的对称中心，故B 错误；因为()()1sin sin 2sin sin cos sin 1cos 2f x x x x x x x x =+=+=+，令()0f x =，则sin 0x =或cos 1x =-，所以,x k k Z π=∈或,x k k Z ππ=+∈．因为[]0,10x ∈，所以0,,2,3x πππ=． 所以()0f x =有四个零点，故C 错误；()()()2'cos cos 22cos cos 1cos 12cos 1f x x x x x x x =+=+-=+-．令()'0f x >，解得1cos 2x >，解得22,33k x k k Z ππππ-+<<+∈．所以()f x 在57,33ππ⎡⎤⎢⎥⎣⎦上是单调递增函数，故选D2：（2023届麓山国际实验学校高三上入学考解析第6题） 2：关于函数()sin sin f x x x =+有下述四个结论：①()f x 是偶函数②()f x 在区间,2ππ⎫⎛ ⎪⎝⎭单调递增③()f x 的最大值为2；④()f x 在[],ππ-有4个零点。

专题10 求函数的单调区间【热点聚焦与扩展】从高考来看，对导数的应用的考查主要从以下几个角度进行：(1)考查导数的几何意义，往往与解析几何、微积分相联系．(2)利用导数求函数的单调区间，判断单调性；已知单调性，求参数．(3)利用导数求函数的最值(极值)，解决生活中的优化问题．(4)证明不等式、研究函数的零点等.（5）考查数形结合思想的应用．单调性是函数的一个重要性质，对函数作图起到决定性的作用，而导数是分析函数单调区间的一个便利工具.高考对单调性的考查有小题，但多出现在大题中，涉及单调性应用的题目较多.1、函数的单调性：在内可导函数，在任意子区间内都不恒等于0.在上为增函数． 在上为减函数．2、导数与单调区间的联系（1）函数在可导，那么在上单调递增.此结论可以这样理解：对于递增的函数，其图像有三种类型： ，无论是哪种图形，其上面任意一点的切线斜率均大于零.等号成立的情况：一是单调区间分界点导数有可能为零，例如：的单调递增区间为，而，另一种是位于单调区间内但导数值等于零的点，典型的一个例子为在处的导数为0，但是位于单调区间内.（2）函数在可导，则在上单调递减（3）前面我们发现了函数的单调性可以决定其导数的符号，那么由的符号能否推出在的单调性呢？如果不是常值函数，那么便可由导数的符号对应推出函数的单调性.（这也是求函数单调区间的理论基础） 3、利用导数求函数单调区间的步骤 （1）确定函数的定义域（2）求出的导函数（3）令（或），求出的解集，即为的单调增（或减）区间(,)a b ()f x '()f x (,)a b '()0()f x f x ≥⇔(,)a b '()0()f x f x ≤⇔(,)a b ()f x (),a b ()f x (),a b ()',()0x a b f x ⇒∀∈≥，()2f x x =[)0+∞，()'00f =()3f x x =0x =()0,0()f x (),a b ()f x (),a b ()',()0x a b f x ⇒∀∈≤，()',()x a b f x ∀∈，()f x (),a b ()f x ()f x '()f x '()0f x >0<x ()f x（4）列出表格4、求单调区间的一些技巧（1）强调先求定义域，一方面定义域对单调区间有限制作用（单调区间为定义域的子集）.另一方面通过定义域对取值的限制，对解不等式有时会起到简化的作用，方便单调区间的求解 （2）在求单调区间时优先处理恒正恒负的因式，以简化不等式（3）一般可令，这样解出的解集就是单调增区间（方便记忆），若不存在常值函数部分，那么求减区间只需要取增区间在定义域上的补集即可(简化求解的步骤）（4）若的解集为定义域，那么说明是定义域上的增函数，若的解集为，那么说明没有一个点切线斜率大于零，那么是定义域上的减函数（5）导数只是求单调区间的一个有力工具，并不是唯一方法，以前学过的一些单调性判断方法也依然好用，例如：增+增→增，减+减→减，增→减，复合函数单调性同增异减等.如果能够通过结论直接判断，那么就无需用导数来判定. 5、求单调区间的一些注意事项（1）单调区间可以用开区间来进行表示，如果用闭区间那么必须保证边界值在定义域内.例如函数的单调减区间为，若写成就出错了（0不在定义域内）. （2）如果增（或减）区间有多个，那么在书写时用逗号隔开，一定不要用并集的符号.有些同学觉得不等式的解集是多个部分时用“”连接，那么区间也一样，这个观点是错误的.并集是指将两个集合的元素合并到一起成为一个集合，用在单调区间上会出现问题.依然以为例，如果写成，那么就意味着从合并在一起的集合中任取两个变量，满足单调减的条件.由性质可知，如果在两个区间里各取一个，是不满足单调减的性质的.【经典例题】例1. 【2020年高考全国Ⅱ卷理数9】设函数()ln 21ln 21f x x x =+--，则()f x（ ）A ．是偶函数，且在1,2⎛⎫+∞⎪⎝⎭单调递增 B ．是奇函数，且在11,22⎛⎫-⎪⎝⎭单调递减 C ．是偶函数，且在1,2⎛⎫-∞-⎪⎝⎭单调递增 D ．是奇函数，且在1,2⎛⎫-∞-⎪⎝⎭单调递减 x '()0f x >()f x '()0f x >()f x '()0f x >∅()f x ()1-⨯1y x=()()0,,,0+∞-∞[)0,+∞1y x=()()0,,0+∞-∞1y x=()()0,,,0+∞-∞【答案】D【思路导引】根据奇偶性的定义可判断出()f x 为奇函数，排除AC ；当11,22x ⎛⎫∈-⎪⎝⎭时，利用函数单调性的性质可判断出()f x 单调递增，排除B ；当1,2x ⎛⎫∈-∞- ⎪⎝⎭时，利用复合函数单调性可判断出()f x 单调递减，从而得到结果． 【解析】由()ln 21ln 21f x x x =+--得()f x 定义域为12x x ⎧⎫≠±⎨⎬⎩⎭，关于坐标原点对称，又()()ln 12ln 21ln 21ln 21f x x x x x f x -=----=--+=-，()f x ∴为定义域上的奇函数，可排除AC ；当11,22x ⎛⎫∈-⎪⎝⎭时，()()()ln 21ln 12f x x x =+--， ()ln 21y x =+在11,22⎛⎫- ⎪⎝⎭上单调递增，()ln 12y x =-在11,22⎛⎫- ⎪⎝⎭上单调递减，()f x ∴在11,22⎛⎫- ⎪⎝⎭上单调递增，排除B ；当1,2x ⎛⎫∈-∞- ⎪⎝⎭时，()()()212ln 21ln 12ln ln 12121x f x x x x x +⎛⎫=----==+ ⎪--⎝⎭， 2121x μ=+-在1,2⎛⎫-∞- ⎪⎝⎭上单调递减，()ln f μμ=在定义域内单调递增，根据复合函数单调性可知：()f x 在1,2⎛⎫-∞-⎪⎝⎭上单调递减，D 正确．故选D ． 【专家解读】本题的特点是注重函数性质的综合应用，本题考查了函数的奇偶性、单调性，考查数学运算、逻辑推理等学科素养．解题关键是正确理解函数奇偶性、单调性的含义． 例2.【2020年高考全国Ⅰ卷文数20】已知函数()()e 2xf x a x =-+．（1）当1a =时，讨论()f x 的单调性；【答案】（1）减区间为(,0)-∞，增区间为(0,)+∞；（2）1(,)e+∞．【思路导引】（1）将1a =代入函数解析式，对函数求导，分别令导数大于零和小于零，求得函数的单调增区间和减区间；（2）若()f x 有两个零点，即(2)0xe a x -+=有两个解，将其转化为2xea x =+有两个解，令()(2)2xe h x x x =≠-+，求导研究函数图像的走向，从而求得结果．【解析】（1）当1a =时，()(2)xf x e x =-+，'()1xf x e =-， 令'()0f x <，解得0x <，令'()0f x >，解得0x >， ∴()f x 的减区间为(,0)-∞，增区间为(0,)+∞．【专家解读】本题的特点是灵活运用导数研究函数的性质，本题考查了导数与函数的单调性，考查导数与函数的零点，考查数形结合思想，考查数学运算、直观想象、数学建模等学科素养．解题关键是结合函数的图像研究问题．例3.【2020年高考全国Ⅰ卷理数21】已知函数()2e xf x ax x =+-．（1）当1a =时，讨论()f x 的单调性；【答案】（1）当(),0x ∈-∞时，()()'0,f x f x <单调递减，当()0,x ∈+∞时，()()'0,f x f x >单调递增; 【思路导引】(1)由题意首先对函数二次求导，然后确定导函数的符号，最后确定原函数的单调性即可； (2)首先讨论0x =的情况，然后分离参数，构造新函数，结合导函数研究构造所得的函数的最大值即可确定实数a 的取值范围．【解析】(1)当1a =时，()2x x x e f x =+-，()'21x f x e x =+-，由于()''20x f x e =+>，故()'f x 单调递增，注意到()'00f =，故：当(),0x ∈-∞时，()()'0,f x f x <单调递减； 当()0,x ∈+∞时，()()'0,f x f x >单调递增．【专家解读】本题的特点是注重导数的灵活运用，本题考查了导数与函数的单调性、极值（最值），考查数形结合、分类讨论思想，考查数学运算、直观想象、逻辑推理等学科素养．解题关键是正确构造新函数，结合导函数研究构造所得的函数．【考向总结】导数是研究函数的单调性、极值(最值)最有效的工具，而函数是高中数学中重要的知识点，对导数的应用的考查主要从以下几个角度进行：(1)考查导数的几何意义，往往与解析几何、微积分相联系； (2)利用导数求函数的单调区间，判断单调性；已知单调性，求参数； (3)利用导数求函数的最值(极值)，解决生活中的优化问题； (4)考查数形结合思想的应用．例4.【2020年高考全国Ⅱ卷文数21】已知函数()2ln 1f x x =+．（1）设0a >，讨论函数()()()f x f a g x x a-=-的单调性．【答案】（1）对函数()g x 求导，把导函数()g x '的分子构成一个新函数()m x ，再求导得到()m x '，根据()m x '的正负，判断()m x 的单调性，进而确定()g x '的正负性，最后求出函数()g x 的单调性． 【解析】（1）2ln 1(2ln 1)2(ln ln )()(0x a x a g x x x a x a+---==>--且)x a ≠，因此22(ln ln )()()x a x x x a g x x x a --+'=-，设()2(ln ln )m x x a x x x a =--+，则有()2(ln ln )m x a x '=-，当x a >时，ln ln x a >，∴()0m x '<，()m x 单调递减，因此有()()0m x m a <=，即()0g x '<，∴()g x 单调递减；当0x a <<时，ln ln x a <，∴()0m x '>，()m x 单调递增，因此有()()0m x m a <=，即()0g x '<，∴()g x 单调递减，∴函数()g x 在区间(0,)a 和(,)a +∞上单调递减，没有递增区间．【专家解读】本题的特点是注重导数的灵活运用，本题考查了导数与函数单调性，考查不等式恒成立的参数取值范围问题，考查转化与化归思想，考查数学运算、逻辑推理、数学建模等学科素养．解题关键是应用参数分离法解决不等式恒成立的参数取值范围问题．例5.【2020年高考全国Ⅱ卷理数21】已知函数()2sin sin 2f x x x =．（1）讨论()f x 在区间()0,π的单调性；【答案】（1）当0,3x π⎛⎫∈ ⎪⎝⎭时，()()'0,f x f x >单调递增，当2,33x ππ⎛⎫∈ ⎪⎝⎭时，()()'0,f x f x <单调递减，当2,3x ππ⎛⎫∈⎪⎝⎭时，()()'0,f x f x >单调递增． 【思路导引】(1)首先求得导函数的解析式，然后由导函数的零点确定其在各个区间上的符号，最后确定原函数的单调性即可；【解析】(1)由函数的解析式可得：()32sin cos f x x x =，则：()()224'23sin cos sin f x x x x =-()2222sin 3cos sin x x x =- ()222sin 4cos 1x x =-()()22sin 2cos 12cos 1x x x =+-，()'0f x =在()0,x π∈上的根为：122,33x x ππ==， 当0,3x π⎛⎫∈ ⎪⎝⎭时，()()'0,f x f x >单调递增； 当2,33x ππ⎛⎫∈⎪⎝⎭时，()()'0,f x f x <单调递减； 当2,3x ππ⎛⎫∈ ⎪⎝⎭时，()()'0,f x f x >单调递增． 【专家解读】本题的特点是注重导数的灵活运用，本题考查了导数与函数的单调性，考查应用导数证明不等式，考查数学运算、逻辑推理、数学建模等学科素养．解题关键是应用三角函数的有界性进行合理放缩证明不等式．例6.【2020年高考全国Ⅲ卷文数20】已知函数()32f x x kx k =-+．（1）讨论()f x 的单调性： 【答案】（1）详见解析；【思路导引】（1）'2()3f x x k =-，对k 分0k ≤和0k >两种情况讨论即可； 【解析】（1）由题，'2()3f x x k =-，当0k ≤时，'()0f x ≥恒成立，∴()f x 在(,)-∞+∞上单调递增；当0k >时，令'()0f x =，得x ='()0f x <，得x <<令'()0f x >，得x <x >()f x在(上单调递减，在(,-∞，)+∞上单调递增．【专家解读】本题的特点是注重导数的灵活运用，本题考查了导数与函数的单调性，考查导数与函数的零点，考查数形结合及分类讨论思想，考查数学运算、逻辑推理、直观想象等学科素养． 例7. （2019·天津高三期中（理））已知函数，. （Ⅰ）若 ，求的值；（Ⅰ）讨论函数的单调性. 【答案】(Ⅰ)a=3；(Ⅰ)答案见解析. 【解析】(Ⅰ)由题意可得：，故，Ⅰ. (Ⅰ)Ⅰ函数，其中a >1， Ⅰf (x )的定义域为(0,+∞)，， 令f ′(x )=0,得x 1=1,x 2=a −1. Ⅰ若a −1=1,即a =2时,，故f (x )在(0,+∞)单调递增.Ⅰ若0<a −1<1，即1<a <2时， 由f ′(x )<0得，a −1<x <1； 由f ′(x )>0得，0<x <a −1，或x >1.故f (x )在(a −1,1)单调递减,在(0,a −1),(1,+∞)单调递增. Ⅰ若a −1>1，即a >2时，由f ′(x )<0得,1<x <a −1;由f ′(x )>0得，0<x <1，或x >a −1. 故f (x )在(1,a −1)单调递减,在(0,1),(a −1,+∞)单调递增. 综上可得,当a =2时,f (x )在(0,+∞)单调递增；当1<a <2时,f (x )在(a −1,1)单调递减,在(0,a −1),(1,+∞)单调递增； 当a >2时,f (x )在(1,a −1)单调递减,在(0,1),(a −1,+∞)单调递增.()()211ln 2f x x ax a x =-+-1a >'(2)0f =a ()f x ()1a f x x a x '-=-+()122=02a f a -=-+'3a =()()211ln 2f x x ax a x =-+-()()()()()11111'x x a x x a a f x x a x x x⎡⎤----+--⎣⎦=-+==()()21'0x f x x-=≥例8.（2019·北京高考模拟（理））已知函数 ．（Ⅰ）当时，求曲线在点处的切线方程； （Ⅰ）当时，（Ⅰ）求的单调区间；（Ⅰ）若在区间内单调递减，求的取值范围． 【答案】（Ⅰ）；（Ⅰ）（Ⅰ）递增区间为，单调递减区间为和，（Ⅰ）【解析】（Ⅰ）当时，， 所以所以曲线在点 处的切线方程为 即； （Ⅰ）时，（Ⅰ）函数，定义域为 ，所以，令 ，得 Ⅰ时，在 和， ；在， ．Ⅰ所以的单调递增区间为 和，单调递减区间为；Ⅰ当 时，在， ；在和 ， ．()2kxe f x x=()k R ∈0k =()y f x =()()1,1f --0k ≠()f x ()f x ()0,1k 230x y -+=2,0k ⎛⎫⎪⎝⎭2,k ⎛⎫-∞ ⎪⎝⎭()0,∞+()(],00,2-∞0k ≠()221f x x x -==()3322f x x x -'=-=-()12f '-=()11f -=()y f x =()()1,1f --()()()111y f f x --=---⎡⎤⎣⎦230x y -+=0k ≠()2kxe f x x={}0x x ≠()()224422kxkx kx e kxx ke x e x f x xx -⋅-⋅'==()0f x '=2x k=0k >(),0-∞2,k ⎛⎫+∞⎪⎝⎭()0f x '>20,k ⎛⎫ ⎪⎝⎭()0f x '<()f x (),0-∞2,k ⎛⎫+∞⎪⎝⎭20,k ⎛⎫ ⎪⎝⎭k 0<2,0k ⎛⎫⎪⎝⎭()0f x '>2,k ⎛⎫-∞ ⎪⎝⎭()0,∞+()0f x '<所以 的单调递增区间为，单调递减区间为和；（Ⅰ）由 在区间 内单调递减，Ⅰ时，，有，所以 ； Ⅰ当时，在 递减，符合题意 综上的取值范围是【精选精练】1．（2020·安徽肥东·高三三模）已知a 为实数，3()32=++f x ax x ，若'(1)3-=-f ，则函数()f x 的单调递增区间为（ ） A．( B．22⎛- ⎝⎭C．(D．2⎛ ⎝⎭【答案】B【解析】()332f x ax x =++，则()2'33,f x ax =+又()'13f -=-，则()1333f a '-=+=-，解得a=-2,()263,f x x '=-+解()0,f x '>得x <<则函数()f x的单调递增区间为,⎛ ⎝⎭故选B. 2．（2020·浙江柯桥·高三三模）已知函数()f x 与()'f x 的图象如图所示，则函数()()x f x g x e=（其中e 为自然对数的底数）的单调递减区间为（ ）()f x 2,0k ⎛⎫ ⎪⎝⎭2,k ⎛⎫-∞ ⎪⎝⎭()0,∞+()f x ()0,10k >()20,10,k ⎛⎫⊆ ⎪⎝⎭21k≥02k <≤k 0<()f x ()0,∞+k ()(],00,2-∞A ．()4,1,,43⎛⎫-∞ ⎪⎝⎭B ．()()0,1,4,+∞C ．40,3⎛⎫ ⎪⎝⎭D ．(0,4)【答案】B【解析】结合图象：()01x ∈，和()4x ∈+∞，时，()()f x f x '<，即()()0f x f x -<′， 而()()()0xf x f xg x e -=<′′，故()g x 在()0,1，()4,+∞递减，故选B ．3．（2020·四川宜宾·高三三模）定义在[]22-,上的函数()f x 与其导函数()f x '的图象如图所示，设O 为坐标原点，A 、B 、C 、D 四点的横坐标依次为12-、16-、1、43，则函数()x f x y e=的单调递减区间是（ ）A ．14,63⎛⎫-⎪⎝⎭ B ．1,12⎛⎫-⎪⎝⎭C ．11,26--⎛⎫⎪⎝⎭ D ．()1,2【答案】B【解析】若虚线部分为函数()y f x =的图象，则该函数只有一个极值点，但其导函数图象（实线）与x 轴有三个交点，不合乎题意；若实线部分为函数()y f x =的图象，则该函数有两个极值点，则其导函数图象（虚线）与x 轴恰好也只有两个交点，合乎题意. 对函数()xf x y e=求导得()()xf x f x y e'='-，由0y '<得()()f x f x '<，由图象可知，满足不等式()()f x f x '<的x 的取值范围是1,12⎛⎫-⎪⎝⎭， 因此，函数()xf x y e =的单调递减区间为1,12⎛⎫-⎪⎝⎭.故选：B. 4．（2020·湖南高三三模）若函数()()122f x x x =≠- ，则f (x ) A ．在(-2Ⅰ+∞ ),内单调递增 B ．在(-2Ⅰ+∞)内单调递减C ．在(2Ⅰ+∞)内单调递增D ．在(2Ⅰ+∞)内单调递减【答案】D【解析】由()12f x x =-可得()()21'2f x x =-- 因为2x <或2x >时Ⅰ()()21'02f x x =-<-Ⅰ()()122f x x x ∴=≠-在(),2-∞和()2,+∞内是减函数，故选D. 5．（2020·江苏崇川·南通一中高三三模）如果函数y ＝f(x)在区间I 上是增函数，且函数()f x y x=在区间I 上是减函数，那么称函数y ＝f(x)是区间I 上的“缓增函数”，区间I 叫做“缓增区间”．若函数213()22f x x x =-+是区间I 上的“缓增函数”，则“缓增区间”I 为( )A ．[1，＋∞)B ．[0C ．[0，1]D ．[1]【答案】D【解析】因为函数213()22f x x x =-+的对称轴为x ＝1， 所以函数y ＝f(x)在区间[1，＋∞)上是增函数， 又当x≥1时，()13122f x x x x=-+，令13()122g x x x =-+(x ≥1)，则222133'()222x g x x x-=-=， 由g′(x)≤0得1x ≤≤即函数()13122f x x x x=-+在区间上单调递减， 故“缓增区间”I为，故选D.6．（2020·聊城一中高三三模）若直线y ex b =+是曲线ln y x =的一条切线，则函数()3ln f x b x x x=---的单调递增区间是（ ） A ．()0,3 B ．()1,3-C ．()3,+∞D ．(),1-∞-和()3,+∞【答案】A【解析】设切点为()00,ln x x ，则可得过该点的切线方程为：001ln 1y x x x =+-，又知切线为：y ex b =+， 故得：01x e =，1ln 12b e ⎛⎫=-=- ⎪⎝⎭，则： ()33ln 2ln f x b x x x x x x=---=--， ()2231f x x x=-+'，令0f x ，解得：2230x x --<，即()1,3x ∈- 又该函数定义域为：0,，故单调增区间为()0,3.故选：A.7．（2020·全国高三三模）函数()1xx f x xe e +=-的单调递增区间是____________.【答案】()1,e -+∞【解析】因为函数()1xx f x xe e+=-，则()()11xxx x f x e e ee x x e ++'=--+=，令()0f x '>，可得1x e >-，所以单调递增区间是()1,e -+∞. 故答案为：()1,e -+∞8．（2020·天津市滨海新区塘沽第一中学高三三模）函数3()ln 4f x x =-的单调递减区间是_________【答案】90,4⎛⎤ ⎥⎝⎦或90,4⎛⎫ ⎪⎝⎭【解析】33'()44f x x x -=-=，由3'()04f x x =<，又0x >得904x <<． Ⅰ减区间为9(0,)4，答9(0,]4也对． 故答案为9(0,)4或9(0,]4．9．（2020·贵州毕节·高三三模）已知函数()()()()21ln 10xf x x f x f e '=-+-，则()f x 的单调递减区间为______. 【答案】(]1,0-【解析】由题意，1x >-，()()()()()00021ln 0100f f f e f '=-+-=-，所以(0)0f =，故()()()21ln 1f x x f x '=-+，()()2111f f x x ''=-+， 所以()()211111f f ''=-+，解得()112f '=，故()1111xf x x x '=-=++， 0f x，即01xx +≤，解得，10x -<≤，故()f x 的单调递减区间为1,0.故答案为：1,010．（2020·五华·云南师大附中高三三模）函数()2sin cos 2[,0]f x x x x π=-∈-，的单调增区间为_____________. 【答案】5,62ππ⎛⎫-- ⎪⎝⎭和,06π⎛⎤- ⎥⎝⎦【解析】因为()2sin cos 2f x x x =-，所以()2cos 2sin 22cos (12sin )f x x x x x '=+=+.令()0f x '>，则cos 012sin 00x x x π>⎧⎪+>⎨⎪-⎩，或cos 012sin 00x x x π<⎧⎪+<⎨⎪-⎩，所以06x π-<或562x ππ-<<-，所以函数()2sin cos 2,[,0]f x x x x π=-∈-的单调增区间为5,62ππ⎛⎫-- ⎪⎝⎭和,06π⎛⎤- ⎥⎝⎦故答案为5,62ππ⎛⎫-- ⎪⎝⎭和,06π⎛⎤- ⎥⎝⎦． 11．（2020·四川省绵阳江油中学高三三模）已知函数()()2102xf x axe ax ax a =--≠. （1）求函数()f x 的单调区间；（2）当0a <时，函数()f x 在(),0-∞上的最小值为()g a ，若不等式()()ln g a ta a ≥--有解，求实数t 的取值范围．【答案】（1）答案见解析；（2）12,2e ⎡⎫-+∞⎪⎢⎣⎭【解析】（1）由()212xf x axe ax ax =--， 得()()()()()'1111xxf x a x e x a x e ⎡⎤=+-+=+-⎣⎦，Ⅰ当0a >时，令()0f x '>，得()()110xx e +->，所以1010xx e +>⎧⎨->⎩，或1010x x e +<⎧⎨-<⎩，即11x x e >-⎧⎨>⎩或11x x e <-⎧⎨<⎩， 解得0x >或1x <-．令()0f x '<，得()()110xx e +-<，所以1010xx e +>⎧⎨-<⎩或1010x x e +<⎧⎨->⎩，即11x x e >-⎧⎨<⎩或11x x e <-⎧⎨>⎩， 解得10x -<<或x ∈∅．所以函数()f x 的单调递增区间为(),1-∞-，()0,+∞；单调递减区间为()1,0-．Ⅰ当0a <时，令()0f x '>，得()()110xx e +-<，由Ⅰ可知10x -<<；令()0f x '<，得()()110xx e +->，由Ⅰ可知1x <-或0x >．所以函数()f x 的单调递增区间为()1,0-；单调递减区间为(),1-∞-，()0,+∞． 综上可得，当0a >时，()f x 的单调递增区间为(),1-∞-，()0,+∞；单调递减区间为()1,0-． 当0a <时，()f x 的单调递增区间为()1,0-；单调递减区间为(),1-∞-，()0,+∞．（2）由（1）可知若0a <，则当(),0x ∈-∞时，函数()f x 在(),1-∞-上单调递减，在()1,0-上单调递增，所以()()1111122g a f ae a a a e -⎛⎫=-=--+=- ⎪⎝⎭， 所以不等式()()ln g a ta a ≥--有解等价于()11ln 2a ta a e ⎛⎫-≥--⎪⎝⎭有解， 即()ln 112a t e a-≥-+有解(0)a <， 设()()ln (0)x x x xϕ-=<，则()()21ln 'x x xϕ--=，所以当(),x e ∈-∞-时，()'0x ϕ<，()x ϕ单调递减， 当(),0x e ∈-时，()'0x ϕ>，()x ϕ单调递增， 所以()x ϕ的极小值也是最小值，且最小值为()()ln 1e e e eϕ-==--， 从而1111222t e e e≥--=-， 所以实数t 的取值范围为12,2e ⎡⎫-+∞⎪⎢⎣⎭． 12．（2020·湖南高三三模）已知函数2()(2)ln f x ax a x x =+--.(1)讨论()f x 的单调性；(2)若()f x 有两个零点，求a 的取值范围. 【答案】(1)见解析；(2) ()0,1 【解析】（1）()()()()()1211'220ax x f x ax a x x x-+=+--=>若0a ≤，()'0f x <，()f x 在()0,+∞上单调递减； 若0a >，当10,x a ⎛⎫∈ ⎪⎝⎭时，()'0f x <，即()f x 在10,a ⎛⎫⎪⎝⎭上单调递减，当1,x a ⎛⎫∈+∞⎪⎝⎭时，()'0f x >，即()f x 在1,a ⎛⎫+∞ ⎪⎝⎭上单调递增. （2）若0a ≤，()f x 在()0,+∞上单调递减，()f x 至多一个零点，不符合题意. 若0a >，由（1）可知，()f x 的最小值为11ln 1f a a a ⎛⎫=-+ ⎪⎝⎭令()1ln 1h a a a =-+，()211'0h a a a=+>，所以()h a 在()0,+∞上单调递增， 又()10h =，当()0h a ≥时，[)1,a ∈+∞，()f x 至多一个零点，不符合题意， 当()0h a <时，()0,1a ∈ 又因为21210a a f e e e e ⎛⎫⎛⎫=++-> ⎪ ⎪⎝⎭⎝⎭，结合单调性可知()f x 在11,e a ⎛⎫ ⎪⎝⎭有一个零点 令()ln g x x x =-，()11'1x g x x x-=-=，当()0,1x ∈时，()g x 单调递减，当()1,x ∈+∞时，()g x 单调递增，()g x 的最小值为()110g =>，所以ln x x > 当3ax a->时， ()()()222ln 2f x ax a x x ax a x x =+-->+-- ()()2330ax a x x ax a =+-=+->结合单调性可知()f x 在3,a a -⎛⎫+∞⎪⎝⎭有一个零点 综上所述，若()f x 有两个零点，a 的范围是()0,1。

第四节 指数与指数函数A 组 三年高考真题（2016～2014年）1.(2016·新课标全国Ⅲ，7)已知a ＝243，b ＝323，c ＝2513，则( )A.b <a <cB.a <b <cC.b <c <aD.c <a <b2．(2015·某某，7)已知定义在R 上的函数f (x )＝2|x －m |－1(m 为实数)为偶函数，记a ＝f (log 0.53)，b ＝f (log 25)，c ＝f (2m )，则a ，b ，c 的大小关系为( )A ．a ＜b ＜cB ．c ＜a ＜bC ．a ＜c ＜bD ．c ＜b ＜a3.(2015·某某，3)设a ＝0.60.6，b ＝0.61.5，c ＝1.50.6，则a ，b ，c 的大小关系是( ) A ．a ＜b ＜c B ．a ＜c ＜b C ．b ＜a ＜cD ．b ＜c ＜a4.(2015·某某，8)某食品的保鲜时间y (单位：小时)与储藏温度x (单位：℃)满足函数关系y ＝e kx ＋b (e ＝2.718…为自然对数的底数，k ，b 为常数)．若该食品在0 ℃的保鲜时间是192小时，在22 ℃的保鲜时间是48小时，则该食品在33 ℃的保鲜时间是( ) A ．16小时 B ．20小时 C ．24小时D ．28小时5.(2014·某某，5)已知实数x ，y 满足a x＜a y(0＜a ＜1)，则下列关系式恒成立的是( ) A ．x 3＞y 3B ．sin x ＞sin yC ．ln(x 2＋1)＞ln(y 2＋1)D.1x 2＋1＞1y 2＋16.(2014·某某，7)下列函数中，满足“f (x ＋y )＝f (x )f (y )”的单调递增函数是( ) A ．f (x )＝x 3B ．f (x )＝3xC ．f (x )＝x 12D ．f (x )＝⎝ ⎛⎭⎪⎫12x7.(2015·，10)2－3，123，log 25三个数中最大的数是________．B 组 两年模拟精选(2016～2015年)1.(2016·某某某某调研)已知a ＝20.2，b ＝0.40.2，c ＝0.40.6，则( ) A.a ＞b ＞cB.a ＞c ＞bC.c ＞a ＞bD.b ＞c ＞a2.(2016·某某质量监测)指数函数y ＝⎝ ⎛⎭⎪⎫b a x与二次函数y ＝ax 2＋2bx (a ∈R ，b ∈R )在同一坐标系中的图象可能是( )3.(2016·某某市统考)若∀x ∈⎝ ⎛⎭⎪⎫0，12，均有9x＜log a x (a ＞0且a ≠1)，则实数a 的取值X围是( ) A.[132-，1)B.(0，132-]C.( 132，3) D.(1，132)4.(2015·某某市期末)设f (x )为定义在R 上的奇函数，当x ≥0时，f (x )＝2x＋2x ＋m (m 为常数)，则f (－1)＝( ) A.3 B.1 C.－1D.－35.(2015·某某聊城模拟)化简416x 8y 4(x ＜0，y ＜0)的结果为( ) A.2x 2y B.2xy C.4x 2yD.－2x 2y6.(2015·某某江门、某某模拟)已知函数f (x )＝⎩⎪⎨⎪⎧x 2＋12a －2，x ≤1，a x －a ，x ＞1， 若f (x )在(0，＋∞)上单调递增，则实数a 的取值X 围为________.7.(2015·某某某某一模)(1)设f (x )＝⎩⎪⎨⎪⎧f （x ＋2） （x <4），⎝ ⎛⎭⎪⎫12x （x ≥4），求f (1＋log 23)的值；(2)已知g (x )＝ln[(m 2－1)x 2－(1－m )x ＋1]的定义域为R ，某某数m 的取值X 围. 8.(2015·某某聊城一模)设k ∈R ，函数f (x )＝⎩⎪⎨⎪⎧1x ，x ＞0，e x ，x ≤0，F (x )＝f (x )＋kx ，x ∈R .(1)k ＝1时，求F (x )的值域； (2)试讨论函数F (x )的单调性.答案精析A 组 三年高考真题（2016～2014年）1.解析 a ＝243＝316，b ＝323＝39，c ＝2513＝325，所以b <a <c .答案 A2.解析 由函数f (x )＝2|x －m |－1为偶函数，得m ＝0，所以f (x )＝2|x |－1，当x ＞0时，f (x )为增函数，log 0.53＝－log 23， ∴log 25＞|－log 23|＞0，∴b ＝f (log 25)＞a ＝f (log 0.53)＞c ＝f (2m )＝f (0)，故选B. 答案 B3.解析 根据指数函数y ＝0.6x 在R 上单调递减可得0.61.5＜0.60.6＜0.60＝1， 根据指数函数y ＝1.5x在R 上单调递增可得1.50.6＞1.50＝1， ∴b ＜a ＜c . 答案 C4.解析 由题意知⎩⎪⎨⎪⎧192＝e b，48＝e22k ＋b，∴e 22k ＝48192＝14，∴e 11k＝12， ∴x ＝33时，y ＝e33k ＋b＝(e 11k )3·e b＝⎝ ⎛⎭⎪⎫123×192＝24.答案 C5.解析 根据指数函数的性质得x ＞y ，此时，x 2，y 2的大小不确定，故选项C 、D 中的不等式不恒成立；根据三角函数的性质知选项B 中的不等式不恒成立； 根据不等式的性质知选项A 中的不等式恒成立． 答案 A6.解析 根据和的函数值等于函数值的积的特征，其典型代表函数为指数函数，又所求函数为单调递增函数，故选B. 答案 B7.解析 2－3＝18<1，又因为23<22<5，所以log223<log222<log 25，即3<log 25. 所以最大值为log 25. 答案 log 25B 组 两年模拟精选(2016～2015年)1.解析 由0.2＜0.6，0.4＜1，并结合指数函数的图象可知0.40.2＞0.40.6，即b ＞c . 因为a ＝20.2＞1，b ＝0.40.2＜1，所以a ＞b . 综上a ＞b ＞c ，选A. 答案 A2.解析 A 项中二次函数的对称轴－1<－ba <0，与指数函数的底数b a>1矛盾，A 项错误； B 项中二次函数的对称轴0<－b a <1，与指数函数的底数0<b a<1矛盾，B 项错误； C 项中二次函数的对称轴－b a <－1，与指数函数的底数b a>1相符合，C 项正确； D 项中二次函数的对称轴－b a<－1，与指数函数的底数0<b a<1矛盾，D 项错误，故选C. 答案 C3.解析 由题意可得：⎩⎪⎨⎪⎧0＜a ＜1，log a 12≥912，解得a ∈[132-，1).答案 A4.解析 ∵f (x )是R 上的奇函数，∴f (0)＝20＋m ＝0，m ＝－1，∴f (－1)＝－f (1)＝－(21＋2－1)＝－3，故选D. 答案 D 5.解析 416x 8y 4＝424·（x 2）4y 4＝2x 2|y |＝－2x 2y .故选D.答案 D6.解析 若f (x )在(0，＋∞)上单调递增，需满足⎩⎪⎨⎪⎧a ＞1，1＋a 2－2≤0，即1＜a ≤2.答案 (1，2]7.解 (1)因为1＋log 23<1＋log 24＝3，所以f (1＋log 23)＝f (3＋log 23)＝⎝ ⎛⎭⎪⎫123＋log 23＝⎝ ⎛⎭⎪⎫123×⎝ ⎛⎭⎪⎫12log 23＝18×2log 213＝18×13＝124.(2)由题设得(m 2－1)x 2－(1－m )x ＋1>0(*)在x ∈R 时恒成立， 若m 2－1＝0⇒m ＝±1，当m ＝1时，(*)为1>0恒成立；当m ＝－1时，(*)为－2x ＋1>0不恒成立， ∴m ＝1；若m 2－1≠0，则⎩⎪⎨⎪⎧m 2－1>0，Δ＝[－（1－m ）]2－4（m 2－1）<0⇒⎩⎪⎨⎪⎧m <－1或m >1，m <－53或m >1⇒m <－53或m >1.综上，实数m 的取值X 围是⎝ ⎛⎭⎪⎫－∞，－53∪(1，＋∞). 8.解 (1)k ＝1时，F (x )＝f (x )＋x ＝⎩⎪⎨⎪⎧1x ＋x ，x ＞0，e x ＋x ，x ≤0.可以证明F (x )在(0，1)上递减，在(1，＋∞)和(－∞，0]上递增， 又f (0)＝1，f (1)＝2，所以F (x )的值域为(－∞，1]∪[2，＋∞). (2)F (x )＝f (x )＋kx ＝⎩⎪⎨⎪⎧1x ＋kx ，x ＞0，e x ＋kx ，x ≤0.若k ＝0，则F (x )在(0，＋∞)上递减，在(－∞，0)上递增；若k ＞0，则F (x )在⎝⎛⎦⎥⎤0，1k 上递减，在⎫+∞⎪⎭上递增，在(－∞，0)上递增； 若k ＜0，则F (x )在(0，＋∞)上递减. 当x ≤0时，F ′(x )＝e x＋k ， 若F ′(x )＞0，则x ＞ln(－k )； 若F ′(x )＜0，则x ＜ln(－k ).若k ≤－1，－k ≥1，则F (x )在(－∞，0]上递减，若－1＜k ＜0，0＜－k ＜1，则F (x )在(－∞，ln(－k ))上递减，在(ln(－k )，0)上递增.。

高三理科数学基础知识晚测试题：函数的值域与最值一、选择题1.下列函数中，值域是（0，+∞）的函数是A ．151+=-xy B ．xy 21-=C ．1)21(-=x y D ．x y -=1)31( 2.函数y=3-222x x +-的值域是（） A.（-∞,2）B.［1，2］C.［1，3］D.［2，+∞）3.设a ＞1,函数f(x)＝log a x 在区间［a,2a ］上的最大值与最小值之差为21,则a 等于() A.2B.2C.22 D.4 4.已知函数31++-=x x y 的最大值为M,最小值为m,则Mm的值为() A.41B.21C.22D.23 5.已知32()26f x x x a =-+（a 是常数），在[]2,2-上有最大值3，那么在[]2,2-上的最小值是A ．5-B ．11-C ．29-D ．37-6.已知函数322+-=x x y 在区间[0，m]上有最大值3，最小值2，则m 的取值范围是A 、[1，+∞）B 、[0，2]C 、（-∞，2]D 、[1，2]7.已知f(x)是奇函数,且当x ＜0时,f(x)＝x 2+3x+2.若当x ∈［1,3］时,n ≤f(x)≤m 恒成立,则m-n 的最小值为() A.49B.2C.43D.418.把长为12cm 的细铁丝截成两段,各自围成一个正三角形,那么这两个正三角形面积之和的最小值是() A.233cm 2B.4cm 2C.23cm 2D.32cm 2二、填空题9.函数f(x)=log 2(32-x 2)的定义域为A ，值域为B ，则A ∩B=_____________.10．函数122x y -=-，(],2x ∈-∞的值域为 ．11.若函数y ＝x 2+(a+2)x+3,x ∈［a,b ］的图象关于直线x ＝1对称,则b ＝___________.12.不等式(a-2)x 2+2(a-2)x-4＜0对一切x ∈R 恒成立,则a 的取值范围是__________.13.已知函数f(x)＝2+log 3x,x ∈［1,9］,则函数y ＝［f(x)］2+f(x 2)的值域为___________.14.函数y=x x 37-在［21，3］上的最小值是________________. 15.函数y=⎪⎩⎪⎨⎧>+-≤<+≤+)1(5),10(3),0(32x x x x x x 的值域为________________.高三理科数学基础知识晚测试题答题卡二、填空题9. 10. 11. 12.13. 14. 15.高三理科数学基础知识晚测试题参考答案二、填空题-20，11.612.-2＜a≤213.［6,13］14.215.（-∞,4］9.［-42，5］10.(]。

3.1 函数的概念考点一 区间的表示【例1】(2019·全国高一)一般区间的表示设,a b ∈R ，且a b <，规定如下:【答案】[],a b (),a b [),a b (],a b 【解析】(1).若{|}x a x b ≤≤,写成区间形式为[],a b(2).若{|}x a x b <<,写成区间形式为(),a b (3).若{|}x a x b ≤<,写成区间形式为[),a b (4).若{|}x a x b <≤,写成区间形式为(],a b故答案为: (1). [],a b (2). (),a b (3). [),a b (4). (],a b【举一反三】1．(2019·全国高一课时练习)已知区间()41,21p p -+，则p 的取值范围为______． 【答案】(),1-∞【解析】由题意，区间()41,21p p -+，则满足4121p p -<+，解得1p <，即p 的取值范围为(),1-∞．故答案为(),1-∞．2．(2019·全国高一课时练习)用区间表示下列集合：(1){}1x x ≥=______；(2)201x x x ⎧⎫-≥=⎨⎬+⎩⎭______；(3){}128x x x =≤≤=或______．【答案】[)1,+∞ ()[),12,-∞-+∞ {}[]12,8【解析】(1)根据集合与区间的改写，可得{}[)11,x x ≥=+∞．(2)由20{11x xx x x ⎧⎫-≥=<-⎨⎬+⎩⎭或()[)2}=,12,x ≥-∞-⋃+∞．(3)由{|1x x =或{}[]28}=128x ≤≤⋃，． 3．(2019·全国高一课时练习)用区间表示下列集合：{}1x x >-=______；{}25x x <≤=______； {}3x x ≤-=______；{}24x x ≤≤=______.【答案】()1,-+∞ (]2,5 (],3-∞- []2,4【解析】集合{}1x x >-表示大于1-的所有实数，可用开区间表示为()1,-+∞；集合{}25x x <≤表示大于2且小于或等于5的所有实数，可用左开右闭区间表示为(]2,5；集合{}3x x ≤-表示小于或等于3-的所有实数，可用左开右闭区间表示为(],3-∞-；集合{}24x x ≤≤表示大于或等于2且小于或等于4的所有实数，可用闭区间表示为[]2,4.考点二 函数的判断【例2-1】(2020·浙江高一开学考试)下列各曲线中，不能表示y 是x 的函数的是( )A ．B ．C ．D ．【答案】C【解析】函数的定义：设在一个变化过程中有两个变量x 与y ，对于x 的每一个确定的值，y 都有唯一的值与其对应，那么就说y 是x 的函数，x 是自变量．如图，C 选项中，在x 允许的取值范围内取x ＝x 0，此时函数y 与之对应的有2个值，y ＝y 1，y ＝y 2，不符合函数的定义.其它三个选项都符合函数的定义.故选：C ．【例2-2】(2019·浙江湖州.高一期中)下列对应关系是从集合A 到集合B 的函数的是( ) A ．A R =，{}0B x x =>，f ：x y x →=B ．A R =，{}0B x x =>，f ：ln x y x →=C ．A Z =，B N =，f ：x y →=D ．A Z =，B N =，f ：2x y x →= 【答案】D【解析】A.A R =，{}0B x x =>，f ：x y x →=不是函数关系，∵当x ＝0时，|0|＝0，|x |＞0不成立，∴不是函数关系；B. A R =，{}0B x x =>，f ：ln x y x →=的定义域是()0,∞+，不是R ，当0x ≤时，ln y x =无意义，∴不是函数关系；C. A Z =，B N =，f ：x y →=[)0,+∞，不是Z ，当x 是负整数时，y =∴不是函数关系；D. A Z =，B N =，f ：2x y x →=是函数关系.故选：D 【举一反三】1．(2020·上海高一课时练习)如图所示，表示函数图像的是( )A ．B ．C ．D ．【答案】B【解析】根据函数的定义知，一个x 有唯一的y 对应，由图象可看出，只有选项B 的图象满足这一点．故选：B ．2．(2020·上海高一课时练习)下列各图中能作为函数图像的是( )．A ．①②B ．①③C ．②④D ．③④【答案】A【解析】对①②，对于定义域内的任意一个x ，都有唯一的y 值与x 对应，则①②正确； 对③，在[]0,1x ∈内，此时一个x 有两个y 值与x 对应，则③错误； 对④，在[]1,0x ∈-内，此时一个x 有两个y 值与x 对应，则④错误； 故选：A3．(2020·全国高一课时练习)判断下列对应是否为函数： (1)x →y ＝x ，x ∈{x |0≤x ≤6}，y ∈{y |0≤y ≤3}； (2)x →y ＝16x ，x ∈{x |0≤x ≤6}，y ∈{y |0≤y ≤3}； (3)x →y ＝3x ＋1，x ∈R ，y ∈R . 【答案】(1)不是；(2)是；(3)是【解析】(1)根据函数概念知，当4x =时，在{}|03y y ≤≤没有值与x 对应，所以不是函数；(2)根据函数概念，当{}06|x x x ∈≤≤时，{}1|016x x x ∈≤≤，所以对于每一个x 值，都有唯一的y 值与之对应，所以是函数；(3)根据函数概念，对于每一个x 值，都有唯一的y 值与之对应，所以是函数；考点三 定义域【例3-1】(2020·上海高一开学考试)函数()12f x x =-的定义域为( ) A ．[)0,2B ．()2,+∞C ．()1,22,2⎡⎫⋃+∞⎪⎢⎣⎭D ．()(),22,-∞+∞【答案】C 【解析】由21020x x -≥⎧⎨-≠⎩，解得x ≥12且x ≠2．∴函数()12f x x =-的定义域为()1,22,2⎡⎫⋃+∞⎪⎢⎣⎭．故选：C ． 【例3-2】(2020·全国高一)已知(1)f x +的定义域为(2,4)， (1)求()f x 的定义域； (2)求(2)f x 的定义域 【答案】(1)(3，5)；(2)35,22⎛⎫ ⎪⎝⎭. 【解析】(1))1(f x +的定义域为(2,4)，24x ∴<<，则315x <+<，即()f x 的定义域为(3,5)；(2)()f x 的定义域为(3,5)；∴由325x <<得3522x <<，即(2)f x 的定义域为35,22⎛⎫ ⎪⎝⎭．【举一反三】1．(2019·浙江高一期中)函数1()f x x=的定义域是( ) A ．R B ．[1,)-+∞C ．(,0)(0,)-∞+∞ D ．[1,0)(0,)-+∞【答案】D【解析】由题意可得：10x +≥，且0x ≠，得到1x ≥-，且0x ≠，故选：D 2．(2019·内蒙古集宁一中高三月考)函数y =的定义域为( )A ．()3,1-B ．[]1,3C ．[]3,1-D ．[]0,1【答案】A【解析】由2032x x --> ，可得31x -<< ， 所以函数y =的定义域为(3,1)- .故选A .3．(2020·浙江高一课时练习)已知函数f(x)的定义域为(－1，0)，则函数f(2x ＋1)的定义域为________． 【答案】1(1,)2--【解析】由－1<2x ＋1<0，得－1<x<－12，所以函数f(2x ＋1)的定义域为1(1,)2--4．(2020·呼和浩特开来中学高二期末(文))设()f x 的定义域为[]0,2，则函数()2f x 的定义域是___________.【答案】⎡⎣【解析】∵函数()y f x =的定义域为[]0,2， ∴函数()2y f x =满足[]20,2x ∈，解不等式202x ≤≤x ≤≤，即函数()2y f x =的定义域是⎡⎣，故选A5．(2020·全国高一)已知函数()f x 的定义域为[1,2]-，求()()()g x f x f x =+-的定义域 . 【答案】[1,1]-【解析】由题意，函数()f x 的定义域为[1,2]-，则函数()()()g x f x f x =+-满足1212x x -≤≤⎧⎨-≤-≤⎩，解得1221x x -≤≤⎧⎨-≤≤⎩，即11x -≤≤，即函数()g x 的定义域为[1,1]-.6(2020·全国高一)已知函数()f x 的定义域为[1，4]，求12f x ⎛⎫+⎪⎝⎭的定义域 . 【答案】(,1]-∞-∪1,2⎡⎫+∞⎪⎢⎣⎭.【解析】由1124x ≤+≤，得112x -≤≤，即110x -≤<或102x<≤， 解得x ≤ 1-，或12x ≥.∴函数的定义域为(-∞，1-]∪[12，+∞). 考点四 解析式【例4】(2020·全国高一课时练习)根据下列条件，求f (x )的解析式. (1)f (x )是一次函数，且满足3f (x ＋1)－f (x )＝2x ＋9； (2)f (x ＋1)＝x 2＋4x ＋1； (3)12()(0)f f x x x x ⎛⎫+=≠⎪⎝⎭. 【答案】(1)f (x )＝x ＋3；(2)f (x )＝x 2＋2x －2；(3)2()(0)33xf x x x =-≠ 【解析】(1)解由题意，设f (x )＝ax ＋b (a ≠0)∵3f (x ＋1)－f (x )＝2x ＋9∴3a (x ＋1)＋3b －ax －b ＝2x ＋9， 即2ax ＋3a ＋2b ＝2x ＋9，由恒等式性质，得22329a ab =⎧⎨+=⎩∴a ＝1，b ＝3∴所求函数解析式为f (x )＝x ＋3.(2)设x ＋1＝t ，则x ＝t －1f (t )＝(t －1)2＋4(t －1)＋1 即f (t )＝t 2＋2t －2.∴所求函数解析式为f (x )＝x 2＋2x －2. (3)解1()2f x f x x ⎛⎫+= ⎪⎝⎭，将原式中的x 与1x 互换，得112()f f x x x ⎛⎫+= ⎪⎝⎭.于是得关于f (x )的方程组()()12112f x f x x f f x x x ⎧⎛⎫+=⎪⎪⎪⎝⎭⎨⎛⎫⎪+= ⎪⎪⎝⎭⎩解得2()(0)33xf x x x =-≠.【举一反三】1．(2020·全国高一课时练习)根据下列条件，求f (x )的解析式. (1)f (f (x ))＝2x －1，其中f (x )为一次函数； (2)f (2x ＋1)＝6x ＋5； (3)f (x )＋2f (－x )＝x 2＋2x .【答案】(1)()1f x +()1f x =+(2)f (x )＝3x ＋2；(3)21()23f x x x =-.【解析】(1)由题意，设f (x )＝ax ＋b (a ≠0)，则f (f (x ))＝af (x )＋b ＝a (ax ＋b )＋b ＝a 2x ＋ab ＋b ＝2x －1由恒等式性质，得221a ab b ⎧=⎨+=-⎩1a b ⎧=⎪∴⎨=-⎪⎩1a b ⎧=⎪⎨=+⎪⎩∴所求函数解析式为()1f x =+()1f x =+(2)设2x ＋1＝t ，则12t x -=1()65322t f t t -∴=⋅+=+ ∴f (x )＝3x ＋2.(3)将x 换成－x ，得f (－x )＋2f (x )＝x 2－2x ，∴联立以上两式消去f (－x )，得3f (x )＝x 2－6x ，21()23f x x x ∴=- 2．(2020·全国高一)(1)已知函数()f x 是一次函数，若()48f f x x =+⎡⎤⎣⎦，求()f x 的解析式； (2)已知()f x 是二次函数，且满足()01f =，()()12f x f x x +-=，求()f x 的解析式． 【答案】(1)()823f x x =+或()28f x x =--；(2)()21f x x x =-+． 【解析】(1)设()()0f x ax b a =+≠，则()()()()2f f x f ax b a ax b b a x ab b =+=++=++⎡⎤⎣⎦，又()48f f x x =+⎡⎤⎣⎦，所以，248a ab b ⎧=⎨+=⎩，解得283a b =⎧⎪⎨=⎪⎩或28a b =-⎧⎨=-⎩， 因此，()823f x x =+或()28f x x =--； (2)()()20f x ax bx c a =++≠，则()01f c ==，()()12f x f x x +-=，即()()()2211112a x b x ax bx x ++++-++=，即()22ax a b x ++=，所以220a a b =⎧⎨+=⎩，解得11a b =⎧⎨=-⎩. 因此，()21f x x x =-+.3．(2019·山西高一月考)(1)已知()22112x f x x++=，求()f x 的解析式； (2)已知()132g x g x x ⎛⎫-=+⎪⎝⎭，求()g x 的解析式． 【答案】(1)()()()222511x x f x x x -+=≠-；(2)()3188x g x x=--- 【解析】(1)由题意得：()12f x +定义域为{}0x x ≠设()121t x t =+≠，则12t x -= ()()()2222112521112t t t f t t t t -⎛⎫+ ⎪-+⎝⎭∴==≠--⎛⎫ ⎪⎝⎭()()()222511x x f x x x -+∴=≠-(2)由()132g x g x x ⎛⎫-=+⎪⎝⎭…①得：()1132g g x x x ⎛⎫-=+ ⎪⎝⎭…② ①②联立消去1g x ⎛⎫⎪⎝⎭得：()3188x g x x =--- 考点五 函数值【例5】(2020·浙江高一课时练习)若函数()()221120x f x x x--=≠，那么12f ⎛⎫= ⎪⎝⎭( ) A ．1 B ．3C ．15D ．30【答案】C【解析】由于()()221120x f x x x --=≠，当14x =时，11116151216f -⎛⎫== ⎪⎝⎭，故选C.【举一反三】1．(2020·浙江杭州 高二期末)已知()2231f x x x =-+，则()1f =( )A ．15B ．21C ．3D ．0【答案】D【解析】根据()f x 的解析式，有()21213112310f =⨯-⨯+=-+=.故选：D2．(2020·上海高一课时练习)已知22()1x f x x=+，则111(1)(2)(3)(4)234f f f f f f f ⎛⎫⎛⎫⎛⎫++++++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭_________． 【答案】72【解析】22()1xf x x =+，222211()()1111x x f x f x x x∴+=+=++，()22111211f =+= 所以111(1)(2)(3)(4)234f f f f f f f ⎛⎫⎛⎫⎛⎫++++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭111(1)(2)(3)(4)234f f f f f f f ⎡⎤⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫=++++++ ⎪ ⎪ ⎪⎢⎥⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎣⎦1711122=+++=故答案为：723．(2020·全国高一课时练习)若函数f (x )＝221x x+，g (x )()()2f g 的值为____________. 【答案】23【解析】()()()()2222231g f g f ====+.故答案为：234．(2018·浙江下城.杭州高级中学高一期中)若函数()2212f x x x +=-，则()3f =______________． 【答案】-1【解析】当213x +=时1x =,故()3f =()2211121f ⨯+=-=-.故答案为：1-考点六 相等函数【例6】(2019·内蒙古集宁一中高三月考)下列四组函数中,表示同一函数的是( ) A．(),()f x x g x ==B．2(),()f x x g x ==C ．21(),()11x f x g x x x -==+-D．()()f x g x ==【答案】A【解析】对于A :()||f x x =，()||g x x == ，两个函数的定义域和对应关系都相同,表示同一函数；对于B :()f x 的定义域为R,()g x 的定义域为[0,)+∞,两个函数的定义域不同,不是同一函数;对于C .()1(1)f x x x =+≠的定义域为{|1}x x ≠,()1g x x =+的定义域为R ,两个函数的定义域不同,不是同一函数;对于D .()f x 的定义域为{|1}x x ≥,()g x 的定义域为{|1x x ≤-或1}x ≥,两个函数的定义域不同,不是同一函数. 故选A .【举一反三】1．(2020·全国高一课时练习)下列各组函数中，表示同一个函数的是__________(填序号).(1)y ＝x －1和y ＝211x x -+；(2)y ＝x 0和y ＝1；(3)f (x )＝x 2和g (x )＝(x ＋1)2；(4)f (x )＝2x和g (x )＝()2x.【答案】(4)【解析】(1)1y x =-的定义域为R ；211x y x -=+的定义域为{|1}x x ≠-，定义域不同，故不是同一个函数；(2)0y x =的定义域为{|0}x x ≠；1y =的定义域为R ，定义域不同，故不是同一个函数；(3)两个函数的对应关系不同，故不是同一个函数；(4)因为两个函数的定义域均为()0,+∞，且()()1f x g x ==，故两函数是同一个函数. 故答案为：(4)2．(2020·全国高一课时练习)下列函数2y =；2x y x=；=y ；y =y x =是同一函数的是________.【答案】=y【解析】2y =定义域是[0,)+∞，所以与函数y x =不是同一函数；2x y x=定义域是(,0][0,)-∞+∞，所以与函数y x =不是同一函数；==y x ，所以与函数y x =是同一函数；y x =，所以与函数y x =不是同一函数.故答案为：=y 3．(2020·全国高一课时练习)下列对应或关系式中是A 到B 的函数的序号为________. ①，∈∈A R B R ，221x y +=；②A ＝{1，2，3，4}，B ＝{0，1}，对应关系如图：③，==A R B R ，1:2→=-f x y x ；④，==A Z B Z ，:→=f x y 【答案】②【解析】①，∈∈A R B R ，221x y +=，存在x 对应两个y 的情况，所以不是A 到B 的函数；②符合函数的定义，是A 到B 的函数； ③，==A R B R ，1:2→=-f x y x ，对于集合A 中的2x =没有对应y ，所以不是A 到B 的函数； ④，==A Z B Z，:→=f x y A 中的{|0,}x x x z ≤∈没有对应y ，所以不是A 到B 的函数.故答案为：②考点七 分段函数【例7-1】(2020·上海高一开学考试)已知函数2,01,()2,12,1,2,2x x f x x x ⎧⎪≤≤⎪=<<⎨⎪⎪≥⎩，则3[()]2f f f ⎧⎫⎨⎬⎩⎭的值为( )A ．1B ．2C ．3-D ．12【答案】A【解析】由题意得,3()=22f ,1(2)=2f ,1()=2=1122f ⨯,所以3[()]=[(2)]=()=1212f f f f f f ⎧⎫⎨⎬⎩⎭,故选：A.【例7-2】(2020·全国高一课时练习)设函数若f(a)＝4，则实数a ＝( )A ．－4或－2B ．－4或2C ．－2或4D ．－2或2【答案】B【解析】当0a ≤时，()4f a a =-=，解得4a =-；当0a >时，24()f a a ==，解得2a =±，因为0a >，所以2a =，综上，4a =-或2，故答案选B 【举一反三】1．(2020·全国高一课时练习)设()1,01,01,0x x f x x x +>⎧⎪==⎨⎪-<⎩，则()()0f f 等于( )A ．1B ．0C ．2D ．-1【答案】C【解析】1,0()1,01,0x x f x x x +>⎧⎪==⎨⎪-<⎩∴ (0)1f =,((0))(1)112f f f ==+=.故选: C .2．(2020·全国高一课时练习)已知函数y ＝21,02,0x x x x ⎧+≤⎨->⎩，则使函数值为5的x 的值是( )A ．2-或2B ．2或52-C ．2-D ．2或2-或52-【答案】C【解析】当0x ≤时，令5y =，得215x +=，解得2x =-； 当0x >时，令5y =，得25x -=，解得52x =-，不合乎题意，舍去.综上所述，2x =-.故选：C.3．(2020·全国高一课时练习)已知2,11()1,11,1x x f x x x ⎧-≤≤⎪=>⎨⎪<-⎩(1)画出f (x )的图象；(2)若1()4f x =，求x 的值； (3)若1()4f x ≥，求x 的取值范围.【答案】(1)作图见解析；(2)12x =±；(3)11,,22⎛⎤⎡⎫-∞-⋃+∞ ⎪⎥⎢⎝⎦⎣⎭【解析】(1)函数2yx 的对称轴0x =，当0x =时，0y =；当1x =-时，1y =；当1x =时，1y =，则f (x )的图象如图所示.(2)1()4f x=等价于21114xx-≤≤⎧⎪⎨=⎪⎩①或1114x>⎧⎪⎨=⎪⎩②或1114x<-⎧⎪⎨=⎪⎩③解①得12x=±，②③的解集都为∅∴当1()4f x=时，12x=±.(3)由于1124f⎛⎫±=⎪⎝⎭，结合此函数图象可知,使1()4f x≥的x的取值范围是11,,22⎛⎤⎡⎫-∞-⋃+∞⎪⎥⎢⎝⎦⎣⎭。

2013届高三数学复习讲义函数应用题1. 如图，一块曲线部分是抛物线形的钢板，其底边长为2，高为1，将此钢板切割成 等腰梯形的形状，记x CD 2=，梯形面积为S ． 则S 的最大值是 ．1. 2732.2.省环保研究所对市中心每天环境放射性污染情况进行调查研究后，发现一天中环境综合放射性污染指数()f x 与时刻x （时）的关系为()[]222,0,2413x f x a a x x =-++∈+，其中a 是与气象有关的参数，且1[0,]2a ∈，若用每天()f x 的最大值为当天的综合放射性污染指数，并记作()M a ．（1）令21xt x =+，[]0,24x ∈，求t 的取值范围； （2）省政府规定，每天的综合放射性污染指数不得超过2，试问目前市中心的综合放射性污染指数是否超标？2.（1）当0x =时，t ＝0；当024x <≤时，12x x+≥（当1x =时取等号）， ∴2110,112x t x x x ⎛⎤==∈ ⎥+⎝⎦+， 即t 的取值范围是10,2⎡⎤⎢⎥⎣⎦．（2）当10,2a ⎡⎤∈⎢⎥⎣⎦时，记()223g t t a a =-++则()23,0321,32t a t a g t t a a t ⎧-++≤≤⎪⎪=⎨⎪++<≤⎪⎩∵()g t 在[]0,a 上单调递减，在1,2a ⎛⎤⎥⎝⎦上单调递增，且()()2171103,,0232624g a g a g g a ⎛⎫⎛⎫⎛⎫=+=+-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭．故()()1171,0,02464211113,0,34242g a a a M a a a g a ⎧⎛⎫⎧≤≤+≤≤ ⎪⎪⎪⎪⎪⎝⎭==⎨⎨⎪⎪+<≤<≤⎪⎪⎩⎩. ∴当且仅当49a ≤时，()2M a ≤.故当409a ≤≤时不超标，当4192a <≤时超标．3.在某次水下考古活动中,需要潜水员潜入水深为30米的水底进行作业.其用氧量包含3个方面:①下潜时,平均速度为v (米/单位时间),单位时间内用氧量为2cv (c 为正常数);②在水底作业需5个单位时间,每个单位时间用氧量为0.4;③返回水面时,平均速度为2v(米/单位时间), 单位时间用氧量为0.2.记该潜水员在此次考古活动中,总用氧量为y . (1)将y 表示为v 的函数;(2)设0<v ≤5,试确定下潜速度v ,使总的用氧量最少. 3.4. 如图，在C 城周边已有两条公路12,l l 在点O 处交汇，现规划在公路12,l l 上分别选择A ，B 两处为交汇点（异于点O ）直接修建一条公路通过C 城，已知OC＝km ，075AOB ∠=，045AOC ∠=，设,OA xkm OB ykm ==.（１） 求ｙ关于ｘ的函数关系式并指出它的定义域；（２） 试确定点A 、B 的位置，使ABC ∆的面积最小.l 2l 1O CBA4．⑴因为AOC △的面积与BOC △的面积之和等于AOB △的面积，所以11145sin 75222x y xy +=，即12y +=，所以2)y x =>． ⑵AOB △的面积1sin 752S xy ===22x x -=424)2x x -++-81)=+．当且仅当4x =时取等号，此时y = 故4km OA =，OB =时，△OAB面积的最小值为21)km ．5.如图，2013年春节，摄影爱好者S 在某公园A 处，发现正前方B 处有一立柱，测得立柱顶端O 的仰角和立柱底部B 的俯角均为30︒，已知S米处理）(1) 求摄影者到立柱的水平距离和立柱的高度；(2) 立柱的顶端有一长2米的彩杆MN 绕中点O 在S 与立柱所在的平面内旋转．摄影者有一视角范围为60︒的镜头，在彩杆转动的任意时刻，摄影者是否都可以将彩杆全部摄入画面？说明理由．5． 如图,不妨将摄影者眼部设为S 点,做SC 垂直OB 于C ,,60,30=∠=∠ASB CSB 又,3=SA 故在SAB Rt ∆中,可求得BA =3,即摄影者到立柱的水平距离为3米.由SC =3，,30=∠CSO 在SCO Rt ∆中,可求得,3=OC又,3==SA BC 故,32=OB 即立柱高为32米.(2)连结SM ,SN , 在△SON 和△SOM 中分别用余弦定理,13221)32(13221)32(222222⋅⋅-+-=⋅⋅-+a b 2622=+∴b a211311221122cos 22222>=+≥=-+=∠b a ab ab b a MSN60<∠∴MSN 故摄影者可以将彩杆全部摄入画面.6.现有一张长为80cm ，宽为60cm 的长方形铁皮ABCD ，准备用它做成一只无盖长方体铁皮盒，要求材料利用率为100%，不考虑焊接处损失。

高三数学总复习20 三角函数两角和差公式一．考纲要求：1.掌握和、差的正弦、余弦、正切公式；2.能正确运用三角公式，进行简单三角函数式的化简、求值和证明二．典型例题：例1.cos 43cos77sin 43cos167o o o o +的值为＿＿例2.已知βα,⎪⎭⎫ ⎝⎛∈ππ,43，sin(βα+)=－,53 sin ,13124=⎪⎭⎫ ⎝⎛-πβ则cos ⎪⎭⎫ ⎝⎛+4πα=______ 例3.若βαβααβα且.54sin )cos(cos )sin(=---是第三象限角，则ββ2cos 22sin -的值 等于例4.已知0,1413)cos(,71cos 且=β-α=α<β<α<2π, (Ⅰ)求α2tan 的值. （Ⅱ）求β.例5.已知3123,cos(),sin(),24135ππβααβαβ<<<-=+=-求sin 2.α三．基础训练（A 组）1.若α为锐角，且1sin 63πα⎛⎫-= ⎪⎝⎭,则cos α= ( ).A 16.B 16.C 14.D 14 2.已知πβπα<<<<20,又53sin =α,54)cos(-=+βα,则=βsin ( ) A.0 B.0或2524 C.2524 D. 0或2524- 3．若)4tan(.21)4tan(.43)tan(παπββα+=-=+那么的值为 （ ） A ．1110 B ．112 C ．52 D ．2 4．已知3(,),sin ,25παπα∈=则tan()4πα+等于 （ ） （A ）17 （B ）7 （C ）17- （D ）7- 5.要使m m x x --=-464cos 3sin 有意义,则m 的取值X 围是( ) A.]37,(-∞ B.[)+∞,1 C.[-1,37] D.(]⎪⎭⎫⎢⎣⎡+∞-∞-,371, 6.βα,均为锐角,且21sin sin -=-βα,21cos cos =-βα,则=-)tan(βα( ) A.37 B 37- C.37± D.773- 7.三角形ABC 中,若54sin =A ,cosB=1312,则cosC=( ) A.6556 B.6516- C. 6556或6516- D. 6533- 8.函数)3x (cos cosx y π++=的最大值是9.求函数x x x x y cos sin cos sin 22+++=的最大值和最小值四．巩固提高（B 组）10.已知4320παπβ<<<<,53)4cos(=-απ,135)43sin(=+βπ,求)sin(βα+11.已知21)tan(=-βα,71tan -=β,且),0(,πβα∈,试求βα-2的值。

一、选择题：1．（山东省济南市2013年1月高三上学期期末文5）在ABC ∆中，若ab b c a 3222=+-，则C=A. 30° B . 45°C. 60°D. 120°2．（山东省济南市2013年1月高三上学期期末文8）把函数sin y x =的图象上所有的点向左平行移动6π个单位长度，再把所得图象上所有点的横坐标缩短到原来的12倍（纵坐标不变），得到的图象所表示的函数解析式是 A ．sin 23y x π⎛⎫=-⎪⎝⎭ B ．sin 26x y π⎛⎫=+ ⎪⎝⎭C ．sin(2)6y x π=-D ．sin(2)6y x π=+3. (山东省烟台市2013届高三上学期期末文3)已知1sin()23πα+=，则cos(2)πα+的值为 A.79-B.79C.29D.23-4. (山东省烟台市2013届高三上学期期末文9)函数()sin()f x A x ωϕ=+其中（02A πϕ><，）的图象如图所示，为了得到()sin 2g x x =的图象，则只需将()f x 的图象A.向右平移6π个长度单位 B.向右平移3π个长度单位 C.向左平移6π个长度单位D.向左平衡3π个长度单位5．(山东省潍坊市2013年1月高三上学期期末考试A 卷文2)已知,54cos ,23,-=⎪⎭⎫⎝⎛∈αππα则)4tan(απ-等于（A ）7（B ）71（C ）71-（D ）7-6．(山东省潍坊市2013年1月高三上学期期末考试A 卷文4)要得到函数)23sin(-=x y 的图象，只要将函数x y 3sin =的图象（A ）向左平移2个单位 （B ）向右平移2个单位 （C ）向左平移32个单位（D ）向右平移32个单位 【答案】D【解析】因为2sin(32)sin 3()3y x x =-=-，所以只需将函数x y 3sin =的图象向右平移32个单位，即可得到)23sin(-=x y 的图象，选D.7. （山东省泰安市2013届高三上学期期末文4）设向量()()cos ,1,2,sin a b αα=-=，若a b ⊥，则tan 4πα⎛⎫- ⎪⎝⎭等于 A.13-B.13C.3-D.38. （山东省泰安市2013届高三上学期期末文7）函数212sin 4y x π⎛⎫=-- ⎪⎝⎭是 A.最小正周期为π的偶函数 B.最小正周期为π的奇函数 C.最小正周期为2π的偶函数D.最小正周期为2π的奇函数9. （山东省泰安市2013届高三上学期期末文12）函数()()sin f x A x ωϕ=+（其中0,2A πϕ><）的图象如图所示，为了得到()sin 2g x x =的图象，则只需将()f x 的图象A.向右平移6π个长度单位 B.向右平移12π个长度单位 C.向左平移6π个长度单位D.向左平移12π个长度单位【答案】A【解析】由图象可知1A =，741234T πππ=-=，即周期2T ππω==，所以2ω=，所以函数为()()sin 2f x x ϕ=+。

高三数学函数专题训练题（附详解）第1卷（选择题）一、单选题1. 已知定义在R 上的可导函数f(x)的导函数为f(x)，满足f '(x) < f(x)，且f(-x) = f(2+x)，f(2)=1，则不等式f(x)< e x 的解集为（ ） A.（-∞，2） B.（2，+∞） C.（1，+∞） D.（0，+∞）2. 函数y=sinx+2|sinx|，x ∈[0，2x]的图像与直线y=k 有且仅有两个不同的交点，则k 的取值范围为（ ）A. k ∈ [0，3]B. k ∈ [1，3]C. k ∈（1，3）D. k ∈（0，3） 3. 已知sina 1+cosa= 2，则 tana =（ ）A. - 43B. - 34C. 43D. 24. 定义在R 上的奇函数f(x)满足f(x+4) = f(x)，当x ∈(0，2)时，f(x)=3x -1，则f(2022)+f(2023)=（ ）A. -2023B. -1C. 1D. 32022 5. 设a=log 20.3，b=0.2，c=（12）0.2，则a,b,c 三者的大小关系为（ ） A. a<b<c B. c<a<b C. b<c<a D. a<c<b6. 设函数f(x)(x ∈R)的导函数为f '(x)，满足f '(x)>f(x)，则当a>0时，f(a)与e a f(0)的大小关系为（ ）A. f(a)>e a f(0)B. f(a)<e a f(0)C. f(a)=e a f(0)D. 不能确定7. 已知f(x)=2x2x +1+ax+cos2x ，若f (π3)=2，则f(-π3)等于（ ）A. -2B. -1C. 0D. 18. 已知函数f(x)=√3sin(ωx+φ)(ω>0,-π2<φ<π2)，A （13，0）为f(x)图像的对称中心，B 、C 是该图像上相邻的最高点和最低点，且|BC|=4，则下列结论正确的是（ ） A. 函数f(x)的对称轴方程为x=43+4k(k ∈Z)B. 若函数f(x )在区间(0，m)内有5个零点，则在此区间内f(x )有且只有2个极小值点C. 函数f(x )在区间(0，2)上单调递增D. f(x -π3)的图象关于y 轴对称9. 已知函数f(x)={|x|x+4√x 36−x，−4<x<2，2≤x<6,若方程f(x)+αx 2=0有5个不等实根，则实数α的取值范围是（ ）A. (-∞，- √24) ∪ {- 13}B. [- 13，- 14] C. [13，√24] D. ( √24，+∞)∪ { 13} 10. 已知F 1，F 2分别为双曲线x 2-y 23=1的左、右焦点，直线l 过点F 2，且与双曲线右支交于A ，B 两点，O 为坐标原点，△AF 1F 2、△BF 1F 2的内切圆的圆心分别为O 1，O 2，则△OO 1O 2面积的取值范围是（ ） A. (1，2√33) B. [1，2√33)C. [1，2√33] D. (1，2√33] 11. 设定义在R 上的函数f(x)与g(x)的导函数分别为f '(x)和g'(x)，若g(x)-f(3-x)=2，f '(x)=g'(x-1)，且g(x+2)为奇函数，g(1)=1。

2013年新课标数学40个考点总动员 考点04 函数的定义域和值域、解析式和分段函数（教师版）热点一 函数的定义域和值域1.（2012年高考（江西理））下列函数中,与函数定义域相同的函数为 （ ） A ．y=1sin xB ．y=1nxxC ．y=xe xD ．sin xx2.（2012年高考（山东文））函数1()ln(1)f x x =+ （ ）A ．[2,0)(0,2]-B ．(1,0)(0,2]-C ．[2,2]-D ．(1,2]-【答案】B【解析】要使函数)(x f 有意义只需⎩⎨⎧≥-≠+040)1ln(2x x ,即⎩⎨⎧≤≤-≠->220,1x x x ,解得21≤<-x ,且0≠x .答案应选B.3.（2012年高考（上海春））函数224log ([2,4])log y x x x=+∈的最大值是______. 【答案】5【解析】22log ,24,1log 2,1 2.t x x x t =≤≤∴≤≤∴≤≤ 令因对号函数4y t t=+在区间[1,2]上单调递减，故当1t =时函数取得最大值为5.4.（2012年高考（江苏））函数x x f 6log 21)(-=的定义域为____.5.（2012年高考（四川文））函数()f x =的定义域是____________.(用区间表示)【答案】(21-，∞)【解析】由12>0x -,得1(-)2x ∈∞，.6.（2012年高考（广东文））(函数)函数y =的定义域为__________.热点二 函数的解析式7.（2012年高考（安徽理））下列函数中,不满足(2)2()f x f x =的是 （ ）A ．()f x x =B ．()f x x x =-C ．()f x x =+1D ．()f x x =-【解析】C【解析】()f x kx =与()f x k x =均满足:(2)2()f x f x =得:,,A B D 满足条件 ，故C 不满足.8.（2012年高考（上海理））已知2)(x x f y +=是奇函数,且1)1(=f .若2)()(+=x f x g , 则=-)1(g _______ .热点三 分段函数9.（2012年高考（江西理））若函数21(1)()lg (1)x x f x x x ⎧+≤=⎨>⎩，则((10))f f =（ ）A.lg101B.2C.1D.0 【答案】B【解析】本题考查分段函数的求值.因为101>，所以()10lg101f ==.所以2((10))(1)112f f f ==+=.10.（2012年高考（福建理））设函数1,()0,D x ⎧⎪=⎨⎪⎩x x 为有理数为无理数,则下列结论错误的是（ ）A ．()D x 的值域为{}0,1B ．()D x 是偶函数C ．()D x 不是周期函数D ．()D x 不是单调函数11.（2012年高考（陕西文））设函数发0,()1(),0,2x x f x x ìï³ïï=íï<ïïïî,则((4))f f -=_____【考点剖析】一．明确要求1．主要考查函数的定义域、值域、解析式的求法． 2．考查分段函数的简单应用．3．由于函数的基础性强，渗透面广，所以会与其他知识结合考查． 二．命题方向三．规律总结 一个方法求复合函数y ＝f (t )，t ＝q (x )的定义域的方法：①若y ＝f (t )的定义域为(a ，b )，则解不等式得a ＜q (x )＜b 即可求出y ＝f (q (x ))的定义域；②若y ＝f (g (x ))的定义域为(a ，b )，则求出g (x )的值域即为f (t )的定义域． 两个防范(1)解决函数问题，必须优先考虑函数的定义域． (2)用换元法解题时，应注意换元前后的等价性．【基础练习】1.(教材习题改编)设函数f (x )＝⎩⎨⎧x ，x ≥0，－x ，x ＜0，若f (a )＋ f (－1)＝2，则a ＝( )A ．－3B ．±3C ．－1D ．±1【答案】C【解析】若a ≥0，则a ＋1＝2，得a ＝1；若a <0，则－a ＋1＝2，得a ＝－1.2.(教材习题改编)函数f (x )＝x －4|x |－5的定义域为________．【答案】{x |x ≥4且x ≠5}【解析】由⎩⎪⎨⎪⎧x －4≥0，|x |－5≠0∴x ≥4且x ≠5.3.(教材习题改编)若x 有意义，则函数y ＝x 2＋3x －5的值域是________．4.(教材习题改编)若f (x )＝x 2＋bx ＋c ，且f (1)＝0，f (3)＝0，则f (－1)＝________. 【答案】8【解析】由已知得⎩⎪⎨⎪⎧1＋b ＋c ＝0，9＋3b ＋c ＝0，得⎩⎪⎨⎪⎧b ＝－4，c ＝3.∴f (x )＝x 2－4x ＋3.∴f (－1)＝(－1)2－4×(－1)＋3＝8.5. (人教A 版教材习题改编)函数f (x )＝log 2(3x＋1)的值域为( )． A ．(0，＋∞) B ．[0，＋∞) C ．(1，＋∞) D ．[1，＋∞)【答案】A【解析】 ∵3x＋1＞1，∴f (x )＝log 2(3x＋1)＞log 21＝0.6．（经典习题）函数y ＝f (x )的图象如图所示．那么，f (x )的定义域是________；值域是________；其中只与x 的一个值对应的y 值的范围是________．【名校模拟】 一．扎实基础1. （2012海淀区高三年级第二学期期末练习文）函数21,12y x x =-+-?的值域是（A ）(3,0]- （B ） (3,1]- （C ）[0,1] （D ）[1,5) 【答案】B【解析】212,(4,0],(3,1].xx y -?\-?\?2. (唐山市2011—2012学年度高三年级第一次模拟考试文)函数2l o g (12y x =+的定义域为(A ) (-1, 2) (B ) (0, 2] (C ) (0, 2) (D ) (-1, 2]3.(湖北省八校2012届高三第一次联考理)函数3()33x f x =-的值域为 （ ） A ．(,1)-∞-B ．(1,0)(0,)-+∞C ．(1,)-+∞D ．(,1)(0,)-∞-+∞4. (浙江省2012届重点中学协作体高三第二学期高考仿真试题理)设3,10,()[(5),10,x x f x f f x x -≥⎧=⎨+<⎩则(6)f 的值为A ．5B ．6C ．7D ．8【答案】C【解析】()()()()(6)11813107f f f f f f f =====⎡⎤⎡⎤⎣⎦⎣⎦．5. (长春市实验中学2012届高三模拟考试（文）)若函数⎩⎨⎧≥<<-=)2()20(ln 1)(2x x x x x f ，且2)(=x f ，则x 的值为e A . 2.B 1.-e C 1.-e D 或2【答案】C【解析】本题考查函数的定义和对分段函数的解析式的理解。

高三数学函数专题练习函数图象与性质1、 二次函数),1()0()(),2()2()(f f a f x f x f x f <≤-=+且满足则实数a 的取值范围是（ ）2、 A ．a ≥0B ．a ≤0C ．0≤a ≤4D ．a ≤0或a ≥43、已知函数f 1(x)=x, f 2(x)=121-⎪⎭⎫⎝⎛X ,f 3(x)=4-x,函数g(x)取f 1(x)、f 2(x)、f 3(x)中的最小值，则函数g(x)的最大值是（ ）4、 A. 2 B. 1C.21D. 不存 5、 已知函数f(x)＝log 2(x 2－ax ＋3a)在区间[2，＋∞]上递增，则实数a 的取值范围是（ ） 6、 A.(－∞，4) B.(－4，4) C.(－∞，－4)∪[2，＋∞] D.[－4，2]7、 若函数y =f (x ) (x ∈R )满足f (x +2)=f (x )，且x ∈(－1,1]时，f (x )=|x |．则函数y =f (x )的图象与函数y =log 4|x |的图象的交点的个数为（ ）8、 A ．3 B ．4 C ．6 D ．85..已知函数y=f(x) (R x ∈)满足)1()1(-=+x f x f 且[]2x f(x ) 1,1=-∈时x ，则y=f(x)与y=x 2log 的图象的交点个数为（ ）A. 1B. 2C. 3D. 4 6.已知函数()y f x =的图象与函数21xy -=-的图象关于直线y x =对称，则(3)f 的值为（ ）A ．1B ．1-C ．2D ．2- 7.设0<a <1，实数x ,y 满足x +y a log =0，则y 关于x 的函数的图象大致形状是（ ）A B C D 8.将函数y=3x m+的图像按向量a =(-1,0)平移后，得到y=f(x)的图像C 1，若曲线C 1关于原点对称，那么实数m 的值为（ ） （A ）1（B ）－1（C ）0（D ）－39．(2005年高考·湖北卷·理4文4)函数|1|||ln --=x ey x 的图象大致是（ ）10．(2005年高考·浙江卷·文9)函数y ＝ax 2＋1的图象与直线y ＝x 相切，则a ＝( )A ．18B ．41 C ．21 D ．111．(2005年高考·天津卷·理10)若函数)1,0( )(log )(3≠>-=a a ax x x f a 在区间)0,21(-内单调递增，则a 的取值范围是( )（ B ）A ．)1,41[B ． )1,43[C ．),49(+∞D ．)49,1(12．(2005年高考·天津卷·文10)设f (x )是定义在R 上以6为周期的函数，f (x )在(0,3)内单调递增，且y =f (x )的图象关于直线x=3对称，则下面正确的结论是( )A ． f (1.5)<f (3.5)<f (6.5)B ． f (3.5)<f (1.5)<f (6.5)C ． f (6.5)<f (3.5)<f (1.5)D ． f (3.5)<f (6.5)<f (1.5)13．(2005年高考·全国卷Ⅰ·理7)设0>b ，二次函数122-++=a bx ax y 的图象下列之一：则a 的值为( )A ．1B ．－1函数的解析式与反函数1. 如果45)1(2+-=+x x x f ，那么f(x)是（ ） 2. A.x 2－7x+10B.x 2－7x －10C.x 2+7x －10D.x 2－4x+63. 已知2 x (x>0)() e (x=0)0 (x<0)f x ⎧⎪=⎨⎪⎩则()()()-2f f f 的值是（ ）4. A.0 B.e C.e2D.43．(2005年高考·浙江卷·理3)设f (x )＝2|1|2,||1,1, ||11x x x x--≤⎧⎪⎨>⎪+⎩，则f [f (21)]＝ ( )A ．21B ．413C ．－95D ． 25414．(2005年高考·浙江卷·文4)设f (x )＝|x －1|－|x |，则f [f (21)]＝( )A ．－21B ．0C ．21D ． 15.若函数f(x)的图像经过点（0，1），则函数f(x+4)的反函数的图像必经过点（ ） A.（－1，－4） B.（4，－1）C.（－4，－1）D.（1，－4）6、已知函数y ＝f(x)的反函数f －1(x)＝2x ＋1，则f(1)等于( )A.－1B.0C. 1D.4 7．(2005年高考·辽宁卷5)函数1ln(2++=x x y 的反函数是( )A ．2xx ee y -+=B ．2xx e e y -+-=C ．2xx e e y --=D ．2xx e e y ---=8．(2005年高考·江苏卷2)函数)(321R x y x∈+=-的反函数的解析表达式为 ( )A ．32log 2-=x y B ． 23log 2-=x yC ．23log 2xy -=D ． xy -=32log 29．(2005年高考·湖南卷·理14文14)设函数f (x )的图象关于点（1，2）对称，且存在反函数f －1(x )，f (4)＝0，则f －1(4)＝10.已知函数()y f x =的图象与函数21xy -=-的图象关于直线y x =对称，则(3)f 的值为( ）A ．1B ．1-C ．2D ．2- 9．(2005年高考·广东卷9)在同一平面直角坐标系中，函数)(x f y =和)(x g y =的图象关于直线x y =对称. 现将)(x g y =的图象沿x 轴向左平移2个单位，再沿y 轴向上平移1个单位，所得的图象是由两条线段组成的折线（如图2所示），则函数)(x f 的表达式为（ ）A ．⎪⎩⎪⎨⎧≤<+≤≤-+=20,2201,22)(x x x x x fB ．⎪⎩⎪⎨⎧≤<-≤≤--=20,2201,22)(x x x x x fC ．⎪⎩⎪⎨⎧≤<+≤≤-=42,1221,22)(x x x x x fD ．⎪⎩⎪⎨⎧≤<-≤≤-=42,3221,62)(x x x x x f导数部分1.函数f (x )＝x 2－2 ln x 的单调递减区间是 ( )A ．(0，1]B ．(－∞，－1] 、(0，1]C ．[－1，1]D ．[1，+∞]2.曲线2)(3-+=x x x f 在P 点处的切线平行直线14-=x y ，则P 点坐标为（ ） A ．（1，0）B ．（2，8）C ．（2，8）和（－1，4）D ．（1，0）和（－1，－4）3.已知32()26f x x x a =-+（a 是常数），在[]2,2-上有最大值3，那么在[]2,2-上的最小值是（ ） A ．－5B ．－11C ．－29D ．－374.点P 的曲线323+-=x x y 上移动，在点P 处的切线的倾斜角为α，则α的取值范围是（ ）A ．]2,0[πB ．),43[)2,0[πππC ．),43[ππD ．]43,2(ππ不等式部分1．(2005年高考·重庆卷·文5)不等式组⎩⎨⎧>-<-1)1(log ,2|2|22x x 的解集为 ( C )A ．)3,0(B ．)2,3(C ．)4,3(D ．)4,2(2．(2005年高考·全国卷Ⅰ·理8文8)设10<<a ，函数)22(log )(2--=xx a a a x f ，则使x x f 的0)(<取值范围是（ B ）A ．)0,(-∞B ．),0(+∞C ．)3log ,(a -∞D ．),3(log +∞a3.f(x)=42++-ax x 在区间(]1,∞-上递增，则不等式0log)32(2<+-x x a的解集是)23,1()21.0(⋃ 。

高三数学函数专题训练题题1：设函数$f(x)=e^x+ax^2+bx+c$，已知点$A(0,\ln2)$是$f(x)$的极小值点，且$f(x)$在$x=1$处取得极大值。

求函数$f(x)$的解析式。

解：由题意，点$A(0,\ln2)$是$f(x)$的极小值点，即$f'(0)=0$且$f''(0)>0$。

首先求导，得到$f'(x)=e^x+2ax+b$，再求二次导数得到$f''(x)=e^x+2a$。

代入$x=0$得到$f'(0)=1+b=0$，解得$b=-1$。

代入$x=0$得到$f''(0)=1+2a>0$，解得$a>-\frac{1}{2}$。

再代入$x=1$得到$f'(1)=e+2a-1=0$，代入$a>-\frac{1}{2}$，解得$a=\frac{1}{2}-\frac{e}{2}$。

所以，$f(x)=e^x+(\frac{1}{2}-\frac{e}{2})x^2-x+1$。

题2：设函数$f(x)=x^3+ax^2+bx+c$，已知曲线$y=f(x)$与直线$y=2x+1$有两个相交点，其中一个为$A(2,5)$。

求函数$f(x)$的解析式。

解：由题意，曲线$y=f(x)$与直线$y=2x+1$有两个相交点，即方程$f(x)=2x+1$有两个根。

代入$A(2,5)$，得到$5=2(2)+1=5$，所以$A(2,5)$是曲线$y=f(x)$的一个点。

根据韦达定理，设另一个相交点为$B(x_0,y_0)$，那么$(x-2)(x_0-2)<0$。

展开得到$x_0-2+x-2<0$，即$x_0+x<4$。

由于$x_0$和$x$分别是$f(x)$和$2x+1$的根，根据根的性质，$x_0+x=-\frac{a}{1}$，即$a=-x_0-x$。

所以，函数$f(x)=x^3+(-x_0-x)x^2+bx+c$。

《三角函数的图像与性质》专题一、相关知识点1．用五点法作正弦函数和余弦函数的简图正弦函数y ＝sin x ，x ∈[0,2π]图像五个关键点：(0,0)，⎝⎛⎭⎫π2，1，(π，0)，⎝⎛⎭⎫3π2，－1，(2π，0)． 余弦函数y ＝cos x ，x ∈[0,2π]图像五个关键点：(0,1)，⎝⎛⎭⎫π2，0，(π，－1)，⎝⎛⎭⎫3π2，0，(2π，1)． 2．正弦函数、余弦函数、正切函数的图像与性质(1)正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是半个周期，相邻的对称中心与对称轴之间的距离是14个周期．(2)正切曲线相邻两对称中心之间的距离是半个周期． 4．奇偶性相关结论(1)若f (x )＝A sin(ωx ＋φ)(A ，ω≠0)，则①f (x )为偶函数的充要条件是φ＝π2＋k π(k ∈Z)；②f (x )为奇函数的充要条件是φ＝k π(k ∈Z)．(2)若f (x )＝A cos(ωx ＋φ)(A ＞0，ω＞0)，则①f (x )为奇函数的充要条件：φ＝k π＋π2，k ∈Z ；②f (x )为偶函数的充要条件：φ＝k π，k ∈Z.题型一 三角函数的定义域1．函数y ＝log 2(sin x )的定义域为________．解析：根据题意知sin x >0，得x ∈(2k π，2k π＋π)(k ∈Z)． 2．函数y ＝2sin x －3的定义域为( )A ．⎣⎡⎦⎤π3，2π3B ．⎣⎡⎦⎤2k π＋π3，2k π＋2π3(k ∈Z) C ．⎝⎛⎭⎫2k π＋π3，2k π＋2π3(k ∈Z) D ．⎣⎡⎦⎤k π＋π3，k π＋2π3(k ∈Z) 解析：由2sin x －3≥0得sin x ≥32，∴π3＋2k π≤x ≤23π＋2k π(k ∈Z)，故选B ． 3．y ＝2sin x －2的定义域为________________________． 解析：要使函数式有意义，需2sin x －2≥0，即sin x ≥22，借助正弦函数的图象(图略)，可得π4＋2k π≤x ≤3π4＋2k π，k ∈Z ，所以该函数的定义域是⎣⎡⎦⎤π4＋2k π，3π4＋2k π(k ∈Z)． 4．函数y ＝tan 2x 的定义域是( )A ．⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠k π＋π4，k ∈Z B ．⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠k π2＋π8，k ∈Z C ．⎩⎨⎧⎭⎬⎫x ⎪⎪ x ≠k π＋π8，k ∈Z D ．⎩⎨⎧⎭⎬⎫x ⎪⎪ x ≠k π2＋π4，k ∈Z 解析：D ，由2x ≠k π＋π2，k ∈Z ，得x ≠k π2＋π4，k ∈Z ，∴y ＝tan 2x 的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠k π2＋π4，k ∈Z .] 5．x ∈[0,2π]，y ＝tan x ＋－cos x 的定义域为( )A.⎣⎡⎭⎫0，π2B.⎝⎛⎦⎤π2，πC.⎣⎡⎭⎫π，3π2D.⎝⎛⎦⎤3π2，2π解析：法一：由题意，⎩⎪⎨⎪⎧tan x ≥0，－cos x ≥0，x ∈[0，2π]，所以函数的定义域为⎣⎡⎭⎫π，3π2.故选C. 法二：x ＝π时，函数有意义，排除A 、D ；x ＝54π时，函数有意义，排除B.故选C.题型二 三角函数的值域(最值)三角函数值域的不同求法(1)利用sin x 和cos x 的值域直接求(2)把所给的三角函数式变换成y ＝A sin(ωx ＋φ)的形式求值域 (3)把sin x 或cos x 看作一个整体，转换成二次函数求值域 (4)利用sin x ±cos x 和sin x cos x 的关系转换成二次函数求值域1．函数f (x )＝4－2cos 13x 的最小值是________，取得最小值时，x 的取值集合为________．解析：f (x )min ＝4－2＝2，此时，13x ＝2k π(k ∈Z)，x ＝6k π(k ∈Z)，所以x 的取值集合为{x |x ＝6k π，k ∈Z}．] 2．函数f (x )＝2cos x ＋sin x 的最大值为________． 解析：f (x )＝2cos x ＋sin x ＝5⎝⎛⎭⎫255cos x ＋55sin x ＝5sin(x ＋α)(其中tan α＝2)，故函数f (x )＝2cos x ＋sin x 的最大值为 5. 3．已知函数f (x )＝2cos 2x －sin 2x ＋2，则( )A ．f (x )的最小正周期为π，最大值为3B ．f (x )的最小正周期为π，最大值为4C ．f (x )的最小正周期为2π，最大值为3D ．f (x )的最小正周期为2π，最大值为4解析：∵f (x )＝2cos 2x －sin 2x ＋2＝1＋cos 2x －1－cos 2x 2＋2＝32cos 2x ＋52，∴f (x )的最小正周期为π，最大值为4.故选B.4．函数f (x )＝3sin ⎝⎛⎭⎫2x －π6在区间⎣⎡⎦⎤0，π2上的值域为( ) A ．⎣⎡⎦⎤－32，32 B ．⎣⎡⎦⎤－32，3 C ．⎣⎡⎦⎤－332，332 D ．⎣⎡⎦⎤－332，3 解析：因为x ∈⎣⎡⎦⎤0，π2，以2x －π6∈⎣⎡⎦⎤－π6，5π6，所以sin ⎝⎛⎭⎫2x －π6∈⎣⎡⎦⎤－12，1，所以3sin ⎝⎛⎭⎫2x －π6∈⎣⎡⎦⎤－32，3，所以函数f (x )在区间⎣⎡⎦⎤0，π2上的值域是⎣⎡⎦⎤－32，3，故选B ． 5．函数y ＝2cos ⎝⎛⎭⎫2x ＋π3，x ∈⎝⎛⎭⎫－π6，π6的值域为________． 解析：∵－π6<x <π6，∴0<2x ＋π3<2π3，∴－12<cos ⎝⎛⎭⎫2x ＋π3<1，∴－1<2cos ⎝⎛⎭⎫2x ＋π3<2. ∴函数y ＝2cos ⎝⎛⎭⎫2x ＋π3，x ∈⎝⎛⎭⎫－π6，π6的值域为(－1,2)． 6．函数y ＝2sin ⎝⎛⎭⎫πx 6－π3(0≤x ≤9)的最大值与最小值之和为( )A ．2－3B ．0C ．－1D ．－1－ 3解析：因为0≤x ≤9，所以－π3≤πx 6－π3≤7π6，所以sin ⎝⎛⎭⎫πx 6－π3∈⎣⎡⎦⎤－32，1. 所以y ∈[－3，2]，所以y max ＋y min ＝2－ 3.7．已知f (x )＝sin 2x －3cos 2x ，若对任意实数x ∈⎝⎛⎦⎤0，π4，都有|f (x )|<m ，则实数m 的取值范围是________．解析：因为f (x )＝sin 2x －3cos 2x ＝2sin ⎝⎛⎭⎫2x －π3，x ∈⎝⎛⎦⎤0，π4，所以⎝⎛⎭⎫2x －π3∈⎝⎛⎦⎤－π3，π6， 所以2sin ⎝⎛⎭⎫2x －π3∈(－3，1]，所以|f (x )|＝|2sin ⎝⎛⎪⎪2x －π3）<3，所以m ≥ 3. 8．函数f (x )＝sin 2x ＋3cos x －34⎝⎛⎭⎫x ∈⎣⎡⎦⎤0，π2的最大值是________． 解析：依题意，f (x )＝sin 2x ＋3cos x －34＝－cos 2x ＋3cos x ＋14＝－⎝⎛⎭⎫cos x －322＋1，因为x ∈⎣⎡⎦⎤0，π2，所以cos x ∈[0,1]，因此当cos x ＝32时，f (x )max ＝1. 9．函数f (x )＝cos 2x ＋6cos π2－x 的最大值为解析：∵f (x )＝cos 2x ＋6cos ⎝⎛⎭⎫π2－x ＝cos 2x ＋6sin x ＝1－2sin 2x ＋6sin x ＝－2⎝⎛⎭⎫sin x －322＋112， 又sin x ∈[－1,1]，∴当sin x ＝1时，f (x )取得最大值5. 10．函数y ＝sin x ＋cos x ＋sin x cos x 的值域为_______解析：设t ＝sin x ＋cos x ，则sin x cos x ＝t 2－12(－2≤t ≤2)，y ＝t ＋12t 2－12＝12(t ＋1)2－1，当t ＝2时，y 取最大值为2＋12，当t ＝－1时，y 取最小值为－1.所以函数值域为⎣⎡⎦⎤－1，12＋2.]11．函数y ＝sin x －cos x ＋sin x cos x ，x ∈[0，π]的值域为________．解析：设t ＝sin x －cos x ，则t 2＝sin 2x ＋cos 2x －2sin x cos x ， 即sin x cos x ＝1－t 22，且－1≤t ≤ 2. ∴y ＝－t 22＋t ＋12＝－12(t －1)2＋1.当t ＝1时，y max ＝1；当t ＝－1时，y min ＝－1. ∴函数的值域为[－1,1]． 12．函数y ＝tan ⎝⎛⎭⎫π2－x ⎝⎛⎭⎫x ∈⎣⎡⎦⎤－π4，π4，且x ≠0的值域为________．解析：∵－π4≤x ≤π4且x ≠0，∴π4≤π2－x ≤3π4且π2－x ≠π2.由函数y ＝tan x 的单调性，可得y ＝tan ⎝⎛⎭⎫π2－x 的值域为(－∞，－1]∪[1，＋∞)．题型三 三角函数的单调性类型一 求三角函数的单调区间 1．f (x )＝|tan x |；解析：观察图象可知，y ＝|tan x |的单调递增区间是⎣⎡⎭⎫k π，k π＋π2，k ∈Z ，单调递减区间是( k π－π2，k π ]，k ∈Z.2．y ＝|cos x |的一个单调递增区间是( )A.⎣⎡⎦⎤－π2，π2 B ．[0，π] C.⎣⎡⎦⎤π，3π2 D.⎣⎡⎦⎤3π2，2π 解析：选D ，将y ＝cos x 的图象位于x 轴下方的部分关于x 轴对称向上翻折，x 轴上方(或x 轴上)的图象不变，即得y ＝|cos x |的图象(如图)．故选D.3．函数f (x )＝tan ⎝⎛⎭⎫2x －π3的递增区间是________． 解析：由－π2＋k π＜2x －π3＜π2＋k π(k ∈Z)，得k π2－π12＜x ＜k π2＋5π12(k ∈Z)．故函数的递增区间为⎝⎛⎭⎫k π2－π12，k π2＋5π12.4．已知函数f (x )＝2sin ⎝⎛⎭⎫π4－2x ，则函数f (x )的单调递减区间为( ) A.⎣⎡⎦⎤3π8＋2k π，7π8＋2k π(k ∈Z) B.⎣⎡⎦⎤－π8＋2k π，3π8＋2k π(k ∈Z) C.⎣⎡⎦⎤3π8＋k π，7π8＋k π(k ∈Z) D.⎣⎡⎦⎤－π8＋k π，3π8＋k π(k ∈Z) 解析： f (x )＝2sin ⎝⎛⎭⎫π4－2x ＝－2sin ( 2x －π4 )，令－π2＋2k π≤2x －π4≤π2＋2k π(k ∈Z)，故－π4＋2k π≤2x ≤3π4＋2k π(k ∈Z)，解得f (x )的单调递减区间为⎣⎡⎦⎤－π8＋k π，3π8＋k π(k ∈Z)．故选D. 5．函数f (x )＝sin ⎝⎛⎭⎫－2x ＋π3的减区间为________． 解析：f (x )＝sin ⎝⎛⎭⎫－2x ＋π3＝－sin ⎝⎛⎭⎫2x －π3，函数f (x )的减区间就是函数y ＝sin ⎝⎛⎭⎫2x －π3的增区间．由2k π－π2≤2x －π3≤2k π＋π2，k ∈Z ，得k π－π12≤x ≤k π＋5π12，k ∈Z.故所给函数的减区间为⎣⎡⎦⎤k π－π12，k π＋5π12，k ∈Z. 6．函数y ＝cos ⎝⎛⎭⎫π4－2x 的单调递减区间为________．解析：由y ＝cos ⎝⎛⎭⎫π4－2x ＝cos ⎝⎛⎭⎫2x －π4，得2k π≤2x －π4≤2k π＋π(k ∈Z)， 解得k π＋π8≤x ≤k π＋5π8(k ∈Z)，所以函数的单调递减区间为⎣⎡⎦⎤k π＋π8，k π＋5π8(k ∈Z)． 7．函数 f (x )＝cos ⎝⎛⎭⎫2x －π6在x ∈⎣⎡⎦⎤－π2，π2上的单调性递增区间为 ； 递减区间为解析：当2k π－π≤2x －π6≤2k π(k ∈Z)，即k π－5π12≤x ≤k π＋π12，k ∈Z 时，函数f (x )是增函数；当2k π≤2x －π6≤2k π＋π(k ∈Z)，即k π＋π12≤x ≤k π＋7π12，k ∈Z 时，函数f (x )是减函数．因此函数f (x )在⎣⎡⎦⎤－π2，π2上的单调递增区间是[ －5π12，π12]， 单调递减区间为⎣⎡⎦⎤－π2，－5π12，⎣⎡⎦⎤π12，π2. 8．函数y ＝sin ⎝⎛⎭⎫12x ＋π3，x ∈[－2π，2π]的递增区间是( )A ．⎣⎡⎦⎤－2π，－5π3 B ．⎣⎡⎦⎤－2π，－5π3和⎣⎡⎦⎤π3，2π C ．⎣⎡⎦⎤－5π3，π3 D ．⎣⎡⎦⎤π3，2π解析：令z ＝12x ＋π3，函数y ＝sin z 的递增区间为⎣⎡⎦⎤2k π－π2，2k π＋π2(k ∈Z)，由2k π－π2≤12x ＋π3≤2k π＋π2得4k π－5π3≤x ≤4k π＋π3，而x ∈[－2π，2π]，故其递增区间是⎣⎡⎦⎤－5π3，π3，故选C ． 9．已知函数f (x )＝4sin ⎝⎛⎭⎫2x －π3，x ∈[－π，0]，则f (x )的单调递增区间是________． 解析：由－π2＋2k π≤2x －π3≤π2＋2k π(k ∈Z)，得－π12＋k π≤x ≤5π12＋k π(k ∈Z)，又因为x ∈[－π，0]，所以f (x )的增区间为⎣⎡⎦⎤－π，－7π12和⎣⎡⎦⎤－π12，0. 10．若锐角φ满足sin φ－cos φ＝22，则函数f (x )＝sin 2(x ＋φ)的单调递增区间为( ) A.⎣⎡⎦⎤2k π－5π12，2k π＋π12(k ∈Z) B.⎣⎡⎦⎤k π－5π12，k π＋π12(k ∈Z) C.⎣⎡⎦⎤2k π＋π12，2k π＋7π12(k ∈Z) D.⎣⎡⎦⎤k π＋π12，k π＋7π12(k ∈Z) 解析：选B ，因为sin φ－cos φ＝22，所以2sin ⎝⎛⎭⎫φ－π4＝22⇒φ－π4＝π6⇒φ＝5π12.因为f (x )＝sin 2(x ＋φ)＝1－cos (2x ＋2φ)2＝1－cos ⎝⎛⎭⎫2x ＋5π62，所以由2x ＋5π6∈[2k π，2k π＋π](k ∈Z)得f (x )的单调递增区间为⎣⎡⎦⎤k π－5π12，k π＋π12(k ∈Z). 11．比较大小：sin ⎝⎛⎭⎫－π18________sin ⎝⎛⎭⎫－π10. 解析：因为y ＝sin x 在⎣⎡⎦⎤－π2，0上为增函数且－π18＞－π10>－π2，故sin ⎝⎛⎭⎫－π18＞sin ⎝⎛⎭⎫－π10. 12．已知f (x )＝2sin ⎝⎛⎭⎫2x ＋π4. (1)求f (x )的单调递增区间；(2)当x ∈⎣⎡⎦⎤π4，3π4时，求函数f (x )的最大值和最小值． 解析：(1)令2k π－π2≤2x ＋π4≤2k π＋π2，k ∈Z ，则k π－3π8≤x ≤k π＋π8，k ∈Z.故f (x )的单调递增区间为⎣⎡⎦⎤k π－3π8，k π＋π8，k ∈Z. (2)当x ∈⎣⎡⎦⎤π4，3π4时，3π4≤2x ＋π4≤7π4，所以－1≤sin ⎝⎛⎭⎫2x ＋π4≤22，所以－2≤f (x )≤1，所以当x ∈⎣⎡⎦⎤π4，3π4时，函数f (x )的最大值为1，最小值为－ 2.13．已知函数f (x )＝sin ⎝⎛⎭⎫2x －π6.讨论函数f (x )在区间⎣⎡⎦⎤－π12，π2上的单调性并求出其值域．解析：令－π2≤2x －π6≤π2，则－π6≤x ≤π3.令π2≤2x －π6≤32π，则π3≤x ≤5π6.因为－π12≤x ≤π2，所以f (x )＝sin ⎝⎛⎭⎫2x －π6在区间⎣⎡⎦⎤－π12，π3上单调递增， 在区间⎣⎡⎦⎤π3，π2上单调递减．当x ＝π3时，f (x )取得最大值为1. 因为f ⎝⎛⎭⎫－π12＝－32<f ⎝⎛⎭⎫π2＝12，所以当x ＝－π12时，f (x )min ＝－32. 所以f (x )的值域为⎣⎡⎦⎤－32，1. 类型二 已知单调性求参数值或范围 已知单调区间求参数范围的3种方法 1．函数f (x )＝sin ωx (ω>0)在区间⎣⎦⎤0，π3上单调递增，在区间⎣⎡⎦⎤π3，π2上单调递减，则ω等于 解析：因为f (x )＝sin ωx (ω>0)过原点，所以当0≤ωx ≤π2，即0≤x ≤π2ω时，y ＝sin ωx 是增函数；当π2≤ωx ≤3π2，即π2ω≤x ≤3π2ω时，y ＝sin ωx 是减函数．由f (x )＝sin ωx (ω>0)在⎣⎡⎦⎤0，π3上单调递增，在⎣⎡⎦⎤π3，π2上单调递减知，π2ω＝π3，所以ω＝32. 2．若f (x )＝cos 2x ＋a cos ( π2＋x )在区间⎝⎛⎭⎫π6，π2上是增函数，则实数a 的取值范围为________． 解析：f (x )＝1－2sin 2x －a sin x ，令sin x ＝t ，t ∈⎝⎛⎭⎫12，1，则g (t )＝－2t 2－at ＋1，t ∈⎝⎛⎭⎫12，1， 因为f (x )在⎝⎛⎭⎫π6，π2上单调递增，所以－a4≥1，即a ≤－4. 3．已知ω＞0，函数f (x )＝sin ⎝⎛⎭⎫ωx ＋π4的一个递减区间为⎣⎡⎦⎤π8，5π8，则ω＝________. 解析：由π8≤x ≤5π8得π8ω＋π4≤ωx ＋π4≤5π8ω＋π4.又函数f (x )的递减区间为⎣⎡⎦⎤2k π＋π2，2k π＋32π(k ∈Z)，则⎩⎨⎧π8ω＋π4＝2k π＋π2，58πω＋π4＝2k π＋32π，k ∈Z ，即⎩⎪⎨⎪⎧ω＝16k ＋2ω＝165k ＋2，解得ω＝2. 4．若函数f (x )＝sin ⎝⎛⎭⎫ωx ＋π4在⎝⎛⎭⎫π2，π上是减函数，则ω的取值范围是 ． 解析：由π2＜x ＜π，得π2ω＋π4＜ωx ＋π4＜πω＋π4，由题意，知⎝⎛⎭⎫π2ω＋π4，πω＋π4⊆⎣⎡⎦⎤2k π＋π2，2k π＋3π2，k ∈Z ， ∴⎩⎨⎧π2ω＋π4≥2k π＋π2，k ∈Zπω＋π4≤2k π＋3π2，k ∈Z ，∴4k ＋12≤ω≤2k ＋54，k ∈Z ，当k ＝0时，12≤ω≤54.5．已知函数f (x )＝sin ⎝⎛⎭⎫ωx －π3(ω＞0)，若函数f (x )在区间⎝⎛⎭⎫π，3π2上为减函数，则实数ω的取值范围是________．解析：由π＜x ＜3π2得πω－π3＜ωx －π3＜3π2ω－π3，由题意知⎝⎛⎭⎫πω－π3，3π2ω－π3⊆⎣⎡⎦⎤2k π＋π2，2k π＋3π2(k ∈Z)． ∴⎩⎨⎧πω－π3≥2k π＋π2，k ∈Z3π2ω－π3≤2k π＋3π2，k ∈Z ，解得⎩⎨⎧ω≥2k ＋56，k ∈Zω≤43k ＋119，k ∈Z，当k ＝0时，56≤ω≤119.6．已知函数f (x )＝sin ⎝⎛⎭⎫ωx ＋π4(ω>0)，f ⎝⎛⎭⎫π6＝f ⎝⎛⎭⎫π3，且f (x )在⎝⎛⎭⎫π2，π上单调递减，则ω＝________. 解析：由f ⎝⎛⎭⎫π6＝f ⎝⎛⎭⎫π3，可知函数f (x )的图象关于直线x ＝π4对称，∴π4ω＋π4＝π2＋k π，k ∈Z ，∴ω＝1＋4k ，k ∈Z ，又f (x )在⎝⎛⎭⎫π2，π上单调递减，∴T 2≥π－π2＝π2，T ≥π，∴2πω≥π，∴ω≤2，又ω＝1＋4k ，k ∈Z ，∴当k ＝0时，ω＝1.7．若函数f (x )＝2sin ωx (0<ω<1)在区间⎣⎡⎦⎤0，π3上的最大值为1，则ω＝________. 解析：因为0<ω<1,0≤x ≤π3，所以0≤ωx <π3，所以f (x )在区间⎣⎡⎦⎤0，π3上单调递增，则 f (x )max ＝f ⎝⎛⎭⎫π3＝2sin ωπ3＝1，即sin ωπ3＝12.又0≤ωx <π3，所以ωπ3＝π6，解得ω＝12. 8．若函数f (x )＝cos x －sin x 在[0，a ]是减函数，则a 的最大值是________．解析：f (x )＝cos x －sin x ＝2cos ⎝⎛⎭⎫x ＋π4，当x ∈[0，a ]时，π4≤x ＋π4≤a ＋π4， 由题意知a ＋π4≤π，即a ≤3π4，故所求a 的最大值为3π4.题型四 三角函数的周期性三角函数周期的求解方法1．已知函数f (x )＝cos ⎝⎭⎫ωx ＋π4(ω>0)的最小正周期为π，则ω＝________. 解析：22．函数f (x )＝cos ⎝⎛⎭⎫πx ＋π3的最小正周期为________ 解析：T ＝2ππ＝2．3．函数f (x )＝sin ⎝⎛⎭⎫2x ＋π3的最小正周期为________ 解析：函数f (x )＝sin ⎝⎛⎭⎫2x ＋π3的最小正周期T ＝2π2＝π. 4．函数 ＋ 的最小正周期为______.解析：函数,所以，最小正周期，5．在函数：①y ＝cos|2x |，②y ＝|cos x |，③y ＝cos2x ＋π6，④y ＝tan ⎝⎛⎭⎫2x －π4中，最小正周期为π的所有函数为( )A ．②④B ．①③④C ．①②③D ．①③解析：①y ＝cos|2x |＝cos 2x ，T ＝π. ②由图像知，函数的周期T ＝π. ③T ＝π. ④T ＝π2.综上可知，最小正周期为π的所有函数为①②③，故选C ．6．函数f (x )＝tan x 1＋tan 2x的最小正周期为________ 解析：由已知得f (x )＝tan x 1＋tan 2x ＝sin x cos x 1＋⎝⎛⎭⎫sin x cos x 2＝sin xcos x cos 2x ＋sin 2x cos 2x＝sin x ·cos x ＝12sin 2x ，所以f (x )的最小正周期为T ＝2π2＝π. 题型五 三角函数的奇偶性与三角函数奇偶性相关的结论：三角函数中，判断奇偶性的前提是定义域关于原点对称，奇函数一般可化为y ＝A sin ωx 或y ＝A tan ωx 的形式，而偶函数一般可化为y ＝A cos ωx ＋b 的形式．常见的结论有：(1)若y ＝A sin(ωx ＋φ)为偶函数，则有φ＝k π＋π2(k ∈Z)；若为奇函数，则有φ＝k π(k ∈Z)． (2)若y ＝A cos(ωx ＋φ)为偶函数，则有φ＝k π(k ∈Z)；若为奇函数，则有φ＝k π＋π2(k ∈Z)． (3)若y ＝A tan(ωx ＋φ)为奇函数，则有φ＝k π(k ∈Z)．1．函数y ＝1－2sin 2( x －3π4)是( ) A ．最小正周期为π的奇函数 B ．最小正周期为π的偶函数C ．最小正周期为π2的奇函数D ．最小正周期为π2的偶函数 解析：y ＝1－2sin 2⎝⎛⎭⎫x －3π4＝cos ⎝⎛⎭⎫2x －3π2＝cos ⎝⎛⎭⎫3π2－2x ＝－sin 2x ， 故函数y 是最小正周期为π的奇函数，故选A.2．若函数 是偶函数，则 等于______解析：由题 ，又()0,ϕπ∈，故 =3．若函数 是偶函数，则 ________．解析：函数为偶函数，则当 时函数取得最值，即： .4．若 是定义在 上的偶函数，其中 ，则 _____ 解析：根据题意可知若f （x ）是定义在R 上的偶函数，即 的对称轴为x=0则有 ，又因为 ，所以可解得5．将函数 向右平移 个单位，得到一个偶函数的图象，则 最小值为__ 解析：将函数 的图象向右平移 个单位长度，所得图象对应的函数解析式为 ，因为函数 为偶函数， ，当 时， 的最小值 ，故答案为 .6．若函数f (x )＝sin x ＋φ3(φ∈[0,2π])是偶函数，则φ＝________. 解析：由已知f (x )＝sin x ＋φ3是偶函数，可得φ3＝k π＋π2，即φ＝3k π＋3π2(k ∈Z)，又φ∈[0,2π]，所以φ＝3π2. 7．函数f (x )＝3sin ⎝⎛⎭⎫2x －π3＋φ，φ∈(0，π)满足f (|x |)＝f (x )，则φ的值为( ) A.π6 B.π3 C.5π6 D.2π3解析：因为f (|x |)＝f (x )，所以函数f (x )＝3sin ⎝⎛⎭⎫2x －π3＋φ是偶函数， 所以－π3＋φ＝k π＋π2，k ∈Z ，所以φ＝k π＋5π6，k ∈Z ，又因为φ∈(0，π)，所以φ＝5π6. 题型五 三角函数的对称性(1) 求形如y ＝A sin(ωx ＋φ)或y ＝A cos(ωx ＋φ)函数的图象对称轴或对称中心时，都是把“ωx ＋φ”看作一个整体，然后根据三角函数图象的对称轴或对称中心列方程进行求解．(2) 在判断对称轴或对称中心时，用以下结论可快速解题：设y ＝f (x )＝A sin(ωx ＋φ)，g (x )＝A cos(ωx ＋φ)，x ＝x 0是对称轴方程⇔f (x 0)＝±A ，g (x 0)＝±A ；(x 0,0)是对称中心⇔f (x 0)＝0，g (x 0)＝0.(3)函数y ＝A sin(ωx ＋φ)的对称轴为x ＝k πω－φω＋π2ω，对称中心为⎝⎛⎭⎫k πω－φω，0；函数y ＝A cos(ωx ＋φ)的对称轴为x ＝k πω－φω，对称中心为⎝⎛⎭⎫k πω－φω＋π2ω，0；函数y ＝A tan(ωx ＋φ)的对称中心为⎝⎛⎭⎫k π2ω－φω，0.上述k ∈Z1．列函数的最小正周期为π且图像关于直线x ＝π3对称的是( ) A ．y ＝2sin ⎝⎛⎭⎫2x ＋π3 B ．y ＝2sin ⎝⎛⎭⎫2x －π6C ．y ＝2sin ⎝⎛⎭⎫x 2＋π3D ．y ＝2sin ⎝⎛⎭⎫2x －π3 解析：根据函数的最小正周期为π知，排除C ，又当x ＝π3时，2x ＋π3＝π，2x －π6＝π2，2x －π3＝π3，故选B ． 2．函数y ＝sin ⎝⎛⎭⎫x －π4的图象的一个对称中心是( ) A ．(－π，0) B.⎝⎛⎭⎫－3π4，0 C.⎝⎛⎭⎫3π2，0 D.⎝⎛⎭⎫π2，0 解析：令x －π4＝k π，k ∈Z ，得函数图象的对称中心为⎝⎛⎭⎫π4＋k π，0，k ∈Z.当k ＝－1时， y ＝sin ⎝⎛⎭⎫x －π4的图象的一个对称中心为⎝⎛⎭⎫－3π4，0.故选B. 3．函数f (x )＝sin ⎝⎛⎭⎫2x －π6－cos 2x 的图象的一条对称轴的方程可以是( ) A ．x ＝－π6 B ．x ＝11π12 C ．x ＝－2π3 D ．x ＝7π12解析：f (x )＝sin ⎝⎛⎭⎫2x －π6－cos 2x ＝32sin 2x －32cos 2x ＝3sin ⎝⎛⎭⎫2x －π3.令2x －π3＝π2＋k π(k ∈Z)，可得x ＝512π＋k 2π(k ∈Z)．令k ＝1可得函数图象的一条对称轴的方程是x ＝1112π. 3．已知函数y ＝sin(2x ＋φ)( －π2<φ<π2 )的图象关于直线x ＝π3对称，则φ的值为 解析：由题意得f ⎝⎛⎭⎫π3＝sin ⎝⎛⎭⎫2π3＋φ＝±1，∴2π3＋φ＝k π＋π2，k ∈Z ， ∴φ＝k π－π6，k ∈Z.∵φ∈⎝⎛⎭⎫－π2，π2，∴φ＝－π6. 4．函数f (x )＝2sin(ωx ＋φ)(ω>0)对任意x 都有f ( π6＋x )＝f ⎝⎛⎭⎫π6－x ，则f ⎝⎛⎭⎫π6的值为( ) A ．2或0 B ．－2或2 C ．0 D ．－2或0解析：选B ，因为函数f (x )＝2sin(ωx ＋φ)对任意x 都有f ⎝⎛⎭⎫π6＋x ＝f ⎝⎛⎭⎫π6－x ，所以该函数图象关于直线x ＝π6对称，因为在对称轴处对应的函数值为最大值或最小值. 5．函数f (x )＝sin x －cos x 的图像( )A ．关于直线x ＝π4对称B ．关于直线x ＝－π4对称 C ．关于直线x ＝π2对称 D ．关于直线x ＝－π2对称解析：f (x )＝sin x －cos x ＝2sin ⎝⎛⎭⎫x －π4，又f ⎝⎛⎭⎫－π4＝2sin ⎝⎛⎭⎫－π2＝－2，故选B. 6．如果函数y ＝3cos(2x ＋φ)的图像关于点⎝⎛⎭⎫4π3，0中心对称，那么|φ|的最小值为( )A ．π6B ．π4C ．π3D ．π2解析：由题意得3cos ⎝⎛⎭⎫2×4π3＋φ＝3cos ⎝⎛⎭⎫2π3＋φ＋2π＝3cos ⎝⎛⎭⎫2π3＋φ＝0， ∴2π3＋φ＝k π＋π2，k ∈Z ，∴φ＝k π－π6，k ∈Z ，取k ＝0，得|φ|的最小值为π6. 7．函数f (x )＝sin ⎝⎛⎭⎫2x ＋π3－13在区间(0，π)内的所有零点之和为( ) A.π6 B.π3 C.7π6 D.4π3解析：选C ，函数零点即y ＝sin ⎝⎛⎭⎫2x ＋π3与y ＝13图象交点的横坐标，在区间(0，π)内，y ＝sin ⎝⎛⎭⎫2x ＋π3与y ＝13的图象有两个交点，由2x ＋π3＝k π＋π2，得x ＝π12＋k π2，k ∈Z ，取k ＝1，得x ＝7π12，可知两个交点关于直线x ＝7π12对称，故两个零点的和为7π12×2＝7π6. 8．已知函数y ＝sin(2x ＋φ)在x ＝π6处取得最大值，则函数y ＝cos(2x ＋φ)的图象( ) A ．关于点⎝⎛⎭⎫π6，0对称B ．关于点⎝⎛⎭⎫π3，0对称C ．关于直线x ＝π6对称D ．关于直线x ＝π3对称 解析：选A ，由题意可得π3＋φ＝π2＋2k π，k ∈Z ，即φ＝π6＋2k π，k ∈Z ，所以y ＝cos(2x ＋φ)＝cos ⎝⎛⎭⎫2x ＋π6＋2k π＝cos ⎝⎛⎭⎫2x ＋π6，k ∈Z.当x ＝π6时，cos ⎝⎛⎭⎫2×π6＋π6＝cos π2＝0，所以函数y ＝cos ()2x ＋φ的图象关于点⎝⎛⎭⎫π6，0对称，不关于直线x ＝π6对称，故A 正确，C 错误；当x ＝π3时，cos ⎝⎛⎭⎫2×π3＋π6＝cos 56π＝－32，所以函数y ＝cos(2x ＋φ)的图象不关于点⎝⎛⎭⎫π3，0对称，B 错误，也不关于直线x ＝π3对称，D 错误．故选A. 9．(理科)已知函数f (x )＝2sin ⎝⎛⎭⎫ωx ＋π3的图象的一个对称中心为⎝⎛⎭⎫π3，0，其中ω为常数，且ω∈(1,3)．若对任意的实数x ，总有f (x 1)≤f (x )≤f (x 2)，则|x 1－x 2|的最小值是( )A ．1 B.π2C ．2D ．π 解析：选B ，∵函数f (x )＝2sin ⎝⎛⎭⎫ωx ＋π3的图象的一个对称中心为⎝⎛⎭⎫π3，0，∴π3ω＋π3＝k π，k ∈Z ，∴ω＝3k －1，k ∈Z ，由ω∈(1,3)，得ω＝2.由题意得|x 1－x 2|的最小值为函数的半个周期，即T 2＝πω＝π2. 10．(理科)设函数f (x )＝3sin ωx ＋cos ωx (ω>0)，其图象的一条对称轴在区间⎝⎛⎭⎫π6，π3内，且f (x )的最小正周期大于π，则ω的取值范围为( )A.⎝⎛⎭⎫12，1 B ．(0,2) C ．(1,2) D ．[1,2)解析：选C ，由题意f (x )＝3sin ωx ＋cos ωx ＝2sin ⎝⎛⎭⎫ωx ＋π6(ω>0)．令ωx ＋π6＝π2＋k π，k ∈Z ，得x ＝π3ω＋k πω，k ∈Z.∵函数图象的一条对称轴在区间⎝⎛⎭⎫π6，π3内，∴π6<π3ω＋k πω<π3，k ∈Z ，∴3k ＋1<ω<6k ＋2，k ∈Z.又∵f (x )的最小正周期大于π，∴2πω>π，解得0<ω<2.∴ω的取值范围为(1,2)． 题型六 三角函数的性质综合运用1．下列函数中，周期为π，且在⎣⎡⎦⎤π4，π2上单调递增的奇函数是( )A ．y ＝sin ⎝⎛⎭⎫2x ＋3π2 B ．y ＝cos ⎝⎛⎭⎫2x －π2 C ．y ＝cos ⎝⎛⎭⎫2x ＋π2 D ．y ＝sin ⎝⎛⎭⎫π2－x解析：选C ，y ＝sin ⎝⎛⎭⎫2x ＋3π2＝－cos 2x 为偶函数，排除A ；y ＝cos ⎝⎛⎭⎫2x －π2＝sin 2x 在⎣⎡⎦⎤π4，π2上为减函数，排除B ；y ＝cos ⎝⎛⎭⎫2x ＋π2＝－sin 2x 为奇函数，在⎣⎡⎦⎤π4，π2上单调递增，且周期为π，符合题意；y ＝sin ⎝⎛⎭⎫π2－x ＝cos x 为偶函数，排除D.2．下列四个函数中，以π为最小正周期，且在区间⎝⎛⎭⎫π2，π上为减函数的是( )A ．y ＝sin 2xB ．y ＝2|cos x |C ．y ＝cos x 2D ．y ＝tan(－x ) 解析：选D ，A 选项，函数在⎝⎛⎭⎫π2，3π4上单调递减，在⎝⎛⎭⎫3π4，π上单调递增，故排除A ；B 选项，函数在⎝⎛⎭⎫π2，π上单调递增，故排除B ；C 选项，函数的周期是4π，故排除C.3．设函数f (x )＝cos ⎝⎛⎭⎫x ＋π3，则下列结论错误的是( ) A ．f (x )的一个周期为－2π B ．y ＝f (x )的图像关于直线x ＝8π3对称 C ．f (x ＋π)的一个零点为x ＝π6D ．f (x )在⎝⎛⎭⎫π2，π单调递减 解析：D ，A 项，因为f (x )＝cos ⎝⎛⎭⎫x ＋π3的周期为2k π(k ∈Z)，所以f (x )的一个周期为－2π，A 项正确．B 项，因为f (x )＝cos ⎝⎛⎭⎫x ＋π3图像的对称轴为直线x ＝k π－π3(k ∈Z)，所以y ＝f (x )的图像关于直线x ＝8π3对称，B 项正确． C 项，f (x ＋π)＝cos ⎝⎛⎭⎫x ＋4π3.令x ＋4π3＝k π＋π2(k ∈Z)，得x ＝k π－56π，当k ＝1时，x ＝π6，所以f (x ＋π)的一个零点为x ＝π6，C 项正确． D 项，因为f (x )＝cos ⎝⎛⎭⎫x ＋π3的递减区间为2k π－π3，2k π＋2π3(k ∈Z)，递增区间为2k π＋2π3，2k π＋5π3(k ∈Z)，所以⎝⎛⎭⎫π2，2π3是减区间，⎣⎡⎭⎫2π3，π是增区间，D 项错误．故选D ． 4．将函数f (x )＝sin ⎝⎛⎭⎫2x ＋π3的图象向右平移π6个单位长度，得到函数g (x )的图象，则下列说法不正确的是( )A ．g (x )的最小正周期为πB ．g ⎝⎛⎭⎫π6＝32C ．x ＝π6是g (x )图象的一条对称轴 D ．g (x )为奇函数 解析：选C ，由题意得g (x )＝sin ⎣⎡⎦⎤2⎝⎛⎭⎫x －π6＋π3＝sin 2x ，所以周期为π，g ⎝⎛⎭⎫π6＝sin π3＝32，直线x ＝π6不是g (x )图象的一条对称轴，g (x )为奇函数，故选C. 5．定义在R 上的函数f (x )既是偶函数又是周期函数，若f (x )的最小正周期是π，且当x ∈⎣⎡⎦⎤0，π2时，f (x )＝sin x ，则f ⎝⎛⎭⎫5π3的值为( )A ．－12 B.12 C.716 D.32解析：选D ，∵f (x )的最小正周期是π，∴f ⎝⎛⎭⎫5π3＝f ⎝⎛⎭⎫5π3－2π＝f ⎝⎛⎭⎫－π3，∵函数f (x )是偶函数，∴f ⎝⎛⎭⎫5π3＝f ⎝⎛⎭⎫－π3＝f ⎝⎛⎭⎫π3＝sin π3＝32. 6．已知f (x )＝2sin ⎝⎛⎭⎫2x ＋π4. (1)求函数f (x )图像的对称轴方程；(2)求f (x )的递增区间；(3)当x ∈⎣⎡⎦⎤π4，3π4时，求函数f (x )的最大值和最小值．解析：(1)f (x )＝2sin ⎝⎛⎭⎫2x ＋π4，令2x ＋π4＝k π＋π2，k ∈Z ，则x ＝k π2＋π8，k ∈Z. 所以函数f (x )图像的对称轴方程是x ＝k π2＋π8，k ∈Z. (2)令2k π－π2≤2x ＋π4≤2k π＋π2，k ∈Z ，则k π－3π8≤x ≤k π＋π8，k ∈Z. 故f (x )的递增区间为⎣⎡⎦⎤k π－3π8，k π＋π8，k ∈Z. (3)当x ∈⎣⎡⎦⎤π4，3π4时，3π4≤2x ＋π4≤7π4， 所以－1≤sin ⎝⎛⎭⎫2x ＋π4≤22，所以－2≤f (x )≤1，所以当x ∈⎣⎡⎦⎤π4，3π4时，函数f (x )的最大值为1，最小值为－ 2.7．已知函数f (x )＝2cos 2⎝⎛⎭⎫x －π6＋2sin ⎝⎛⎭⎫x －π4sin ⎝⎛⎭⎫x ＋π4. (1)求函数f (x )的最小正周期和图象的对称中心；(2)求f (x )在区间⎣⎡⎦⎤0，π2上的最大值和最小值． 解析：(1)∵f (x )＝2cos 2⎝⎛⎭⎫x －π6＋2sin ( x －π4)·sin ⎝⎛⎭⎫x ＋π4 ＝cos ⎝⎛⎭⎫2x －π3＋1＋2sin ⎝⎛⎭⎫x －π4sin ⎝⎛⎭⎫x ＋π2－π4＝cos ⎝⎛⎭⎫2x －π3＋2sin ⎝⎛⎭⎫x －π4cos ⎝⎛⎭⎫x －π4＋1 ＝12cos 2x ＋32sin 2x ＋sin ⎝⎛⎭⎫2x －π2＋1＝32sin 2x －12cos 2x ＋1＝sin ⎝⎛⎭⎫2x －π6＋1， ∴f (x )的最小正周期为2π2＝π，图象的对称中心为⎝⎛⎭⎫π12＋k π2，1，k ∈Z. (2)x ∈⎣⎡⎦⎤0，π2时，2x －π6∈⎣⎡⎦⎤－π6，5π6， 当2x －π6＝π2，即x ＝π3时，函数有最大值2； 当2x －π6＝－π6，即x ＝0时，函数有最小值12.8．已知函数f (x )＝a ( 2cos 2x 2＋sin x )＋b . (1)若a ＝－1，求函数f (x )的单调递增区间；(2)当x ∈[0，π]时，函数f (x )的值域是[5,8]，求a ，b 的值．解析：已知函数f (x )＝a (1＋cos x ＋sin x )＋b ＝2a sin ⎝⎛⎭⎫x ＋π4＋a ＋b . (1)当a ＝－1时，f (x )＝－2sin ⎝⎛⎭⎫x ＋π4＋b －1， 由2k π＋π2≤x ＋π4≤2k π＋3π2(k ∈Z)，得2k π＋π4≤x ≤2k π＋5π4(k ∈Z)， ∴f (x )的单调递增区间为[ 2k π＋π4，2k π＋5π4](k ∈Z)． (2)∵0≤x ≤π，∴π4≤x ＋π4≤5π4，∴－22≤sin ⎝⎛⎭⎫x ＋π4≤1，依题意知a ≠0. ①当a >0时，得⎩⎪⎨⎪⎧ 2a ＋a ＋b ＝8，b ＝5，∴a ＝32－3，b ＝5. ②当a <0时，得⎩⎪⎨⎪⎧b ＝8，2a ＋a ＋b ＝5，∴a ＝3－32，b ＝8. 综上所述，a ＝32－3，b ＝5或a ＝3－32，b ＝8.9．已知函数f (x )＝cos ⎝⎛⎭⎫2x －π3＋sin 2x －cos 2x ＋ 2. (1)求函数f (x )的最小正周期和单调递增区间；(2)若存在x ∈⎣⎡⎦⎤π12，π3满足[f (x )]2－22f (x )－m ＞0，求实数m 的取值范围． 解析：(1)∵f (x )＝12cos 2x ＋32sin 2x ＋sin 2x －cos 2x ＋ 2 ＝12cos 2x ＋32sin 2x －cos 2x ＋2＝sin ⎝⎛⎭⎫2x －π6＋2， ∴函数f (x )的最小正周期T ＝π.∵由2k π－π2≤2x －π6≤2k π＋π2(k ∈Z)，得k π－π6≤x ≤k π＋π3(k ∈Z)， ∴单调递增区间为⎣⎡⎦⎤k π－π6，k π＋π3(k ∈Z)． (2)当x ∈⎣⎡⎦⎤π12，π3时，可得2x －π6∈⎣⎡⎦⎤0，π2，解得f (x )＝sin ⎝⎛⎭⎫2x －π6＋2∈[2，2＋1] ⇒F (x )＝[f (x )]2－22f (x )＝[f (x )－2]2－2∈[－2，－1]．存在x ∈⎣⎡⎦⎤π12，π3，满足F (x )－m ＞0的实数m 的取值范围为(－∞，－1)．。

函数与导数班级 姓名 成绩一．填空题1.函数12+=+x a y （1,0≠>a a ）恒过定点2.函数y =的定义域为 3.223y x x =+-,[]1,2-∈x 的值域是4.已知函数2(1)4f x x x -=-，函数()f x 的解析式为5.函数y =的单调增区间是6.不等式2212()4x x x +-≤的解集为 7.若0()ln 0xe x g x x x ⎧≤=⎨>⎩，则1(())2g g = 8.曲线2ln 3++=x x y 在点P 0处的切线方程为014=--y x ，则点P 0的坐标是9.设)(x f 为定义在R 上的奇函数，当0≥x 时，b x x f x ++=22)((b 为常数)，则=-)1(f10.若函数h (x )＝2x －k x ＋k 3在(2，＋∞)上是增函数，则实数k 的取值范围是________ 11.函数错误！未找到引用源。

在定义域R 内可导，若错误！未找到引用源。

，且当错误！未找到引用源。

时，错误！未找到引用源。

，设错误！未找到引用源。

则c b a ,,的大小关系是 （用“<”连结） 12.函数2x +2x-3,x 0x)=-2+ln x,x>0f ⎧≤⎨⎩（的零点个数为 13.定义在R 上的函数)(x f 满足)(x f = ⎩⎨⎧>---≤-0),2()1(0),1(log 2x x f x f x x ，则)2009(f 的值为 14.已知()x xe x f =，()()a x x g ++-=21，若∈∃21,x x R ，使得()()12x g x f ≤成立，则实数a 的取值范围是____________．15已知a 为正实数，函数22()f x ax a x c =-+的图象与x 轴交于,A B 两点,与y 轴交于C 点.且△ABC 为直角三角形.则线段AB 的最小值为二．解答题16.已知函数2()1x f x x =+ （1）证明：该函数是奇函数； （2）证明：该函数在区间上(],1-∞-是减函数．17.已知函数c bx ax x x f +++=23)(，曲线)(x f y =在点1=x 处的切线为l ：013=+-y x ，若32=x 时，)(x f y =有极值．(1)求c b a ,,的值；(2)求)(x f y =在[]1,3-上的最大值和最小值．18.已知函数)(ln )(R a ax x x f ∈-=．(1)求函数)(x f y =的单调区间；(2)当0>a 时，求函数)(x f 在[1,2]上的最小值19.设函数x x xe e x x f -+=221)(. (1)求)(x f 的单调区间；(2)若当[]2,2-∈x 时，不等式m x f >)(恒成立，求实数m 的取值范围．20．已知函数R a ax x x f ∈-+=,1cos )(2．（1）求证：函数)(x f 是偶函数；（2）当1=a 时，求函数)(x f 在[]ππ,-上的最大值及最小值；（3）若对于任意的实数x 恒有0)(≥x f ，求实数a 的取值范围．21.某水产养殖场的休闲垂钓水域如图所示，水域由以AB 为直径的半圆和以AB 为斜边的等腰直角三角形ABD 组成，其中,AD DB 和圆弧AEFB 为水域岸边， O 为半圆圆心，200AB =m .为方便客人垂钓，决定架设两座木桥,DE DF ，,E F 点在岸边上，且2(0)4EOA FOB παα∠=∠=<<.据估测，岸边,,,AD DB AE BF 上单位长度（m ）内垂钓的人数均为k （k 为常数），桥,DE DF 上和岸边圆弧EF 上单位长度（m ）内垂钓的人数均为2k .水域垂钓总人数记为y .（1）求y 关于α的函数表达式；（2）估测当α取何值时，垂钓总人数最多？（第21题图） D。

专题03 函数的单调性和最值【高考地位】函数的单调性是函数的一个重要性质，几乎是每年必考的内容，例如判断和证明单调性、求单调区间、利用单调性比较大小、求值域、最值或解不等式． 【方法点评】方法一 定义法使用情景：一般函数类型解题模板：第一步 取值定大小：设任意12,x x D ∈，且12x x <； 第二步 作差：12()()f x f x -；第三步 变形（合并同类项、通分、分解因式、配方等）； 第四步 定符号； 第五步 得出结论.例1 已知函数(),f x ax b =+且()12f =，()2 1.f = (1)求()1f m +的值；(2)判断函数()f x 的单调性,并用定义证明. 【答案】（1）2m -+；（2）证明见解析.所以函数()f x 在R 上单调递减.【点评】本题主要考查待定系数法求函数解析式以及函数的单调性，属于中档题.利用定义法判断函数的单调性的一般步骤是：（1）在已知区间上任取21x x >；（2）作差()()21f x f x -分解因式；（3）判断()()21f x f x -的符号，()()210f x f x ->可得()f x 在已知区间上是增函数，()()210f x f x -<可例2 判断并证明：21()1f x x=+在(,0)-∞上的单调性． 【答案】()f x 在(,0)-∞上单调递增，证明见解析.考点：用定义法证明单调性．【变式演练1】已知()f x 是定义在R 上的奇函数，且当0x <时，21()f x x x=+. （1）求()f x 的表达式；（2）判断并证明函数()f x 在区间(0,)+∞上的单调性.【答案】（1）2210()0,01,0x x f x x x x x ⎧+<⎪⎪==⎨⎪⎪-+>⎩；（2）函数()f x 在区间(0,)+∞上是减函数，证明见解析.【解析】试题分析：（1）由()f x 是奇函数，令0x =得，(0)0f =，当0x >时，0x -<，得出21()()f x f x x x=--=-+，即可得出函数()f x 的表达式；（2）利用函数单调性的定义，即可证明函数的单调性.试题解析：（1）∵()f x 是奇函数，∴对定义域R 内任意的x ，都有()()f x f x -=-.……1分 令0x =得，(0)(0)f f =-，即(0)0f =又当0x >时，0x -<，此时2211()()[()()]f x f x x x x x=--=--+=-+- 综合可得：2210()0,01,0x x f x x x x x ⎧+<⎪⎪==⎨⎪⎪-+>⎩考点：函数的解析式与函数的单调性的定义.例3 定义在[1,1]-上的奇函数()f x ，对任意,0m n ≠时，恒有()()0f m f n m n+>+.（1）比较1()2f 与1()3f 大小；（2）判断()f x 在[1,1]-上的单调性，并用定义证明；（3）若810a x -+>对满足不等式11()(2)024f x f x -+-<的任意x 恒成立，求a 的取值X 围. 【答案】（1）11()()23f f >；（2）函数()f x 在[1,1]-上为单调递增函数，证明见解析；（3）4a >. 【解析】试题分析：（1）利用作差法，即可比较1()2f 与1()3f 大小；（2）利用单调性定义证明步骤，即可得出结论；考点：函数奇偶性与单调性的综合问题. 【变式演练2】已知函数2()1ax b f x x +=+是定义在()1,1-上的奇函数，且12()25f =． （1）求()f x 的解析式；（2）用定义证明()f x 在(1,1)-上是增函数； （3）解不等式(1)()0f t f t -+<． 【答案】（1）1)(2+=x x x f ；（2）证明见解析；（3）210<<t . 【解析】试题分析：（1）根据条件建立方程关系即可求出函数)(x f 的解析式；（2）利用定义证明)(x f 在(1,1)-上是增函数；（3）根据函数奇偶性和单调性之间的关系即可解不等式(1)()0f t f t -+<.试题解析：（1）(0)0,12(),25f f =⎧⎪⎨=⎪⎩即1a =，0b =,1)(2+=x xx f （2）设1x ∀，2(1,1)x ∈-且12x x <，则12122212()()11x x f x f x x x -=-++1221122212()()(1)(1)x x x x x x x x -+-=++21122212()(1)(1)(1)x x x x x x --=++， ∵210x x ->，1210x x -<，2110x +>，2210x +>，∴12()()0f x f x -<，即12()()f x f x <，∴()f x 在(1,1)-上是增函数．（3）依题意得，(1)()f t f t -<-，则111,11,1,t t t t -<-<⎧⎪-<-<⎨⎪-<-⎩∴102t <<．考点：1.函数奇偶性的应用；2.利用定义法证明函数的单调性.方法二 导数法使用情景：较复杂的函数类型解题模板：第一步 求函数()f x 的定义域； 第二步 求导()f x '；第三步 在定义域X 围内解不等式()0f x '>或()0f x '<； 第四步 得出函数()f x 的增减区间.例4 已知函数32()39f x x x x a =-+++．求()f x 的单调递减区间； 【答案】(,1)-∞-，(3,)+∞【变式演练3】已知函数（）在上为增函数，则的取值X 围是（ ）A. B. C. D.【答案】A 【解析】由题函数为增函数，则在上恒成立，则，设则令得到，可知函数在上单调递增，在上单调递减，则， 即的取值X 围是，选A方法三 复合函数分析法使用情景：简单的复合函数类型 解题模板：第一步 先求函数的定义域；第二步 分解复合函数，分别判断内外层函数的单调性； 第三步 根据同增异减，确定原函数的增减区间.例5 求函数20.7log (32)y x x =-+的单调区间；【答案】在(,1)-∞上单调递增，在(2,)+∞上单调递减.【点评】函数的问题，必须注意定义域优先的原则，所以利用导函数求函数的单调区间也必须先考虑函数的定义域.【变式演练4】已知定义在R 上的函数)(x f y =是偶函数，且0≥x 时，)22ln()(2+-=x x x f . （1）当0<x 时，求)(x f 解析式； （2）写出)(x f 的单调递增区间.【答案】（1）)22ln()(2++=x x x f ；（2）)0,1(-，),1(+∞. 【解析】试题分析：(1)利用奇偶性，0<x 时，0>-x ，()2()ln(22)f x f x x x =-=++；（2）0<x 时，222x x ++对称轴是1x =-，开口向上，左减右增，根据复合函数单调性可知，增区间为)0,1(-；同理，当0x ≥，222x x -+的对称轴是1x =，开偶向上，左减右增，根据复合函数单调性可知，增区间为(1,)+∞.复合函数单调性利用同增异减来解决. 试题解析：（1）0<x 时，0>-x ，∴)22ln()(2++=-x x x f ， ∵)(x f y =是偶函数，∴)()(x f x f =-，0<x 时，)22ln()(2++=x x x f .（2）由（1）知0<x 时，)22ln()(2++=x x x f ，函数的单调增区间)0,1(-，0≥x 时，)22ln()(2+-=x x x f ，根据复合函数的单调性可得函数的单调增区间),1(+∞，所以函数的单调增区间为)0,1(-，),1(+∞. 考点：待定系数，导数与单调区间．方法四 图像法使用情景：图像比较容易画出的函数类型 解题模板：第一步 通过题目条件画出函数图像； 第二步 从图像中读出函数的单调区间. 例6 求函数2()||f x x x =-+的单调区间。