圆心角圆周角的经典练习

圆心角圆周角练习题圆心角和圆周角是圆内角的一种特殊形式，它们在几何学中具有重要的地位。

本文将介绍关于圆心角和圆周角的一些练习题，帮助读者加深对这一概念的理解。

一、选择题1. 在同一个圆中，圆心角和对应的圆周角的关系是：A. 圆心角大于对应的圆周角B. 圆心角等于对应的圆周角C. 圆心角小于对应的圆周角2. 已知在同一个圆中，圆心角的度数为56°，则对应的圆周角的度数为：A. 56°B. 112°C. 224°3. 在圆O中，∠ACB是圆心角，则它所对应的圆周角的度数为：A. 30°B. 60°C. 120°4. 若∠ACD是圆O中的圆心角，且其度数为72°，则弧AB所对应的圆周角的度数为：A. 72°B. 144°C. 288°5. 在同一个圆中，圆心角和对应的弧所对应的圆周角之间的关系是：A. 圆心角小于对应的圆周角B. 圆心角等于对应的圆周角C. 圆心角大于对应的圆周角二、填空题1. 在同一圆中，一条弧的度数等于其所对应的圆周角的度数，则这条弧所对应的圆心角的度数为________。

2. 在圆O中，已知∠ACB是圆心角，则它所对应的圆周角的度数为________。

3. 在同一个圆中，圆心角的度数等于所对应的弧所对应的圆周角的度数，则该弧所对应的圆周角的度数为________。

三、解答题1. 在同一个圆中，圆心角和对应的圆周角的关系是什么？为什么？2. 已知在同一个圆中，圆心角的度数为60°，则对应的圆周角的度数是多少？并通过计算或推理进行解答。

3. 在圆O中，∠ACB是圆心角，则它所对应的圆周角的度数是多少？并通过计算或推理进行解答。

4. 若∠ACD是圆O中的圆心角，且其度数为90°，则弧AB所对应的圆周角的度数是多少？并通过计算或推理进行解答。

总结：本文通过选择题、填空题和解答题的形式，对圆心角和圆周角的概念进行了练习和探讨。

1《圆》练习题（垂径定理, 弧、弦、圆心角, 圆周角）一、选择题1.已知在⊙O 中, 弦AB 的长为8厘米, 圆心O 到AB 的距离为3厘米, 则⊙O 的半径是（ ）A. 3厘米B. 4厘米C. 5厘米D. 8厘米2.半径等于12的圆中, 垂直平分半径的弦长为（ ）A. B. C. D.3.如图1, 在⊙O 中, ∠ABC=50°, 则∠AOC 等于（ ）A. 50°B. 80°C. 90°D. 100°4.如图2, AB 是⊙O 的直径, ∠ABC=30°, 则∠BAC =（ ）A. 90°B. 60°C. 45°D. 30°5.如图3, △ABC 内接于⊙O, 连结OA.OB, 若∠ABO ＝25°, 则∠C 的度数为（ ）．A. 55°B. 60°C. 65°D. 70°6.如图4, 四边形ABCD 内接于⊙O, 若它的一个外角∠DCE=70°, 则∠BOD=( )A. 35°B.70°C. 110°D.140°7、如图5, △ABC 内接于⊙O, AD ⊥BC 于点D, AD=2cm, AB=4cm, AC=3cm, 则⊙O 的直径是（ ）A. 2cmB. 4cmC. 6cmD. 8cm8、如图6, BD 是⊙O 的直径, 圆周角∠A = 30(, 则∠CBD 的度数是（ ）A. 30(B. 45(C. 60(D. 80(9、如图7, AB 为⊙O 的直径, C ．D 是⊙O 上的两点, ∠BAC=30º, AD=CD, 则∠DAC 的度数是（ ）A. 30ºB. 60ºC. 45ºD. 75º10、圆内接四边形ABCD 中, ∠A ∶∠B ∶∠C ∶∠D 可以是（ ）A. 1∶2∶3∶4B. 1∶3∶2∶4C. 4∶2∶3∶1D. 4∶2∶1∶3AB O C图1 图2 O 30D B C A O D CBA 图3 图4图6图7图52二、填空题11.如图8, ∠A 是⊙O 的圆周角, ∠A=40°, 则∠OBC 的度数为_______.12.如图9, AB 是⊙O 的直径, 点D 在⊙O 上∠AOD=130°, BC ∥OD 交⊙O 于C, 则∠A= .13、如图10, ⊙O 的直径AB=8cm, C 为⊙O 上的一点, ∠BAC=300, 则BC= .14、如图，量角器外沿上有A 、B 两点，它们的读数分别是70°、40°，则∠1的度数为 .三、解答题: 15、.如图, AB 、CD 是⊙O 的两条弦, 延长AB 、CD 交于点P, 连结AD 、BC 交于点E ． , , 求 的度数．16.如图所示, AB 是⊙O 的一条弦, OD ⊥AB , 垂足为C, 交⊙O 于点D , 点E 在⊙O 上。

圆的相关知识第一部分姓名：一、圆的定义:（1）在同一平面内，所有到定点的距离等于定长的点组成的图形叫做圆。

这个定点叫做圆的圆心。

图形一周的长度，就是圆的周长。

（2）线段绕一固定不动的端点旋转一周时另一个端点所形成的封闭曲线叫做圆，固定不动的端点叫做圆心，线段的长叫做半径。

（3）综合看成：圆可以看成是所有到定点O的距离等于定长r 的点组成的图形．二、点与圆的位置：关系有三种（点到圆心的距离与圆的半径的数量比较）：（1）点在圆外，这个点到圆心的距离大于半径；（2）点在圆上，这个点到圆心的距离等于半径；（3）点在圆内，这个点到圆心的距离小于半径.。

二、相关概念：（1）弧：圆上任意两点间的部分叫做圆弧，简称弧。

弧用符号“⌒”表示以A，B为端点的弧记作“”，读作“圆弧AB”或“弧AB”。

（2）优弧：大于半圆的弧（多用三个字母表示）；（3）劣弧：小于半圆的弧（多用两个字母表示）（4）半圆（弧）：圆的任意一条直径的两个端点分圆成两条弧，每一条弧都叫做半圆。

（5）弦：连接圆上任意两点之间的线段叫做弦；（6）弦心距：圆心到弦的距离。

（7）圆心角：顶点在圆心，两边为半径所组成的图形；（8）圆周角：顶点在圆上，两边为弦组成的图形。

（9）同心圆：圆心相同，半径不等的两个圆叫做同心圆。

（10）等圆：能够重合的两个圆（即半径相等的两个圆）叫做等圆。

（11）等弧：在同圆或等圆中能够完全重合的两条弧叫做等弧三、圆心角定理：（1）圆心角的度数等于它所对弧的度数；（2）在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等，所对的弦心距相等，所对的圆周角相等。

（3）简单地说：知一则知四。

即同圆或等圆中，两个圆心角、两条弧、两条弦、两条弦心距、两个圆周角中，有一组量相等，它们所对应的其余各组量也相等．四、圆周角定理：（1）同弧或等弧所对的圆周角相等。

（2）圆周角等于同弧所对圆心角的度数的一半。

（3）半圆（直径）所对的圆周角是直角，反之90°的圆周角所对的弧是半圆，所对的弦是直径。

圆周角定理专题练习1.在圆周角定理中，已知∠CBO=45°，∠CAO=15°，求∠AOB的度数。

答案：B.60°。

2.在平面直角坐标系中，已知⊙A经过原点O，并且分别与x轴、y轴交于B、C两点，已知B（8，），C（，6），求⊙A的半径。

答案：C.5.3.在圆周角定理中，已知点A,B,C在⊙O上，且∠A=50°，求∠BOC的度数。

答案：A.130°。

4.已知⊙O是△ABD的外接圆，AB是⊙O的直径，CD是⊙O的弦，∠ABD=58°，求∠BCD的度数。

答案：A.116°。

5.已知圆心角∠BOC=78°，求圆周角∠BAC的度数。

答案：A.156°。

6.在圆周角定理中，已知OA，OB是⊙O的两条半径，且OA⊥OB，点C在⊙O上，求∠XXX的度数。

答案：D.20°。

7.在圆周角定理中，已知AB是半圆的直径，点D是AC 的中点，∠ABC=50°，求∠DAB的度数。

答案：XXX°。

8.在圆周角定理中，已知A、B、C三点在⊙O上，且∠AOB=80°，求∠XXX的度数。

答案：D.40°。

9.已知AB是⊙O的直径，弦CD交AB于点E，且AE=CD=8，∠BAC=12∠BOD，求⊙O的半径。

答案：B.5.10.在圆周角定理中，已知DC是⊙O直径，XXX⊥CD于F，连接BC，DB，判断下列结论错误的是：答案：B.AF=XXX。

11.在圆周角定理中，已知点A，B，C，D为⊙O上的四个点，AC平分∠BAD，AC交BD于点E，CE=4，CD=6，求AE的长。

答案：B.5.12.在圆周角定理中，已知点A、B、C在⊙O上，且∠C=30°，求∠AOB的度数。

答案：XXX°。

13.在圆周角定理中，已知⊙O中∠BAC=∠CDA=20°，求∠ABO的度数。

答案：B.70°。

圆---圆心角、圆周角1. 如图，已知AB是⊙O的直径，C.D是上的三等分点，∠AOE＝60°，则∠COE是( )A.40°B.60°C.80°D.120°2.如图，已知在⊙O中，点C为的中点，∠A＝40°，则∠BOC等于( )A.40°B.50°C.70°D.80°3. 下面四个图中的角，是圆心角的是( )4. 下列说法正确的是( )A.相等的圆心角所对的弦相等B.相等的圆心角所对的弧相等C.等弧所对的弦相等D.度数相等的弧的长度相等5. 如图，在⊙O中，弦AB.CD相交于点E，且AB＝CD，连接AD.BC，则下列给出的结论中，正确的有( )①②AD＝BC ③∠CBD＝∠ADB ④∠A＝∠C ⑤AE＝CEA.5个B.4个C.3个D.2个6. 如图，在⊙O中，AC∥OB，∠BAO＝25°，则∠BOC的度数为( )A.25°B.50°C.60°D.80°7. 如图，已知经过原点的⊙P与x、y轴分别交于A.B两点，点C是劣弧OB上一点，则∠ACB＝( )A.80°B.90°C.100°D.无法确定8. 圆内接四边形ABCD中，已知∠A＝70°，则∠C＝( )A.20°B.30°C.70°D.110°9. 如图，四边形ABCD为⊙O的内接四边形，已知∠BOD＝100°，则∠BCD的度数为( )A.50°B.80°C.100°D.130°10. 顶点在圆心，两边与圆相交的角叫做_________.在同圆或等圆中，相等的圆心角所对的弧_____，所对的弦也______；在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角______，所对的弦_________；在同圆或等圆中，如果两条弦相等，那么它们所对的圆心角_____，所对的弦_______-.11. 顶点在_________，两边都和圆_______的角叫圆周角.一条弧所对的圆周角等于它所对的圆心角的_______.在__________(或相等的圆)中，同弧或等弧所对的圆周角_______；反之，相等的圆周角所对的弧_________.12. 半圆(或直径)所对的圆周角是_______；90°的圆周角所对的弦是________.13.如果一个多边形的所有顶点都在同一个圆上，这个多边形叫做__________，这个圆叫做___________；圆内接四边形对角_________-.14. 已知圆O的半径为5cm，弦AB的长为5cm，则弦AB所对的圆心角∠AOB＝__________.15. 如图，已知AB为⊙O的直径，点D为半圆周上的一点，且所对圆心角的度数是所对圆心角度数的两倍，则圆心角∠BOD的度数为_____.16. 下列四个图中，∠x是圆周角的是________.17. 如图，AB.CD是⊙O的两条互相垂直的弦，圆心角∠AOC＝130°，AD.CB的延长线相交于P，则∠P＝_______-.18. 如图所示，A.B.C.D是⊙O上顺次四点.若∠AOC＝160°，则∠D＝_______________ ，∠B＝____________.19. 如图，已知A.B.C.D是⊙O上四点，若AC＝BD，求证：AB＝CD.20. 如图，在△AOB中，AO＝AB，以点O为圆心，OB为半径的圆交AB于D，交AO于点E，AD＝BO.试说明，并求∠A的度数.21. 如图，A.B.C在圆上，弦AE平分∠BAC交BC于D.求证：BE2＝ED·EA.22. 如图所示，AB是⊙O的直径，AB＝8cm，∠ADE＝60°，DC平分∠ADE，求AC.BC的长.23. 如图，△ABC内接于⊙O，过C作CD∥AB与⊙O相交于D点，E是上一点，且满足AD＝DE，连接BD 与AE相交于点F.求证：△ADF∽△ABC.24. 如图，四边形ABCD内接于⊙O，点E在对角线AC上，EC＝BC＝DC.(1)若∠CBD＝39°，求∠BAD的度数；(2)求证：∠1＝∠2.25. 如图，已知△ABC是等边三角形，⊙O经过点A.B.C，点P是BC上任一点.(1)图中与∠PBC相等的角为________；(2)试猜想三条线段PA.PB.PC之间的数量关系，并证明.26. 如图，以△ABC的一边AB为直径的半圆与其它两边AC.BC的交点分别为D.E，且.(1)试判断△ABC的形状，并说明理由；(2)已知半圆的半径为5，BC＝12，求sin∠ABD的值.参考答案：1—9 CBDCA BBDD10. 圆心角相等相等相等相等相等相等11. 圆上相交一半同一圆相等相等12. 90°直径13. 圆的内接多边形多边形的外接圆互补14. 60°15. 60°16. ③17. 40°18. 80° 100°19.20. 解：设∠A ＝x°.∵AD ＝BO ，又OB ＝OD ，∴OD ＝AD ，∴∠AOD ＝∠A ＝x°，∴∠ABO ＝∠ODB ＝∠AOD ＋∠A ＝2x°.∵AO ＝AB ，∴∠AOB ＝∠ABO ＝2x°.从而∠BOD ＝2x°－x°＝x°，即∠BOD ＝∠AOD ，∴由三角形的内角和为180°，有2x°＋2x°＋x°＝180°，x°＝36°，即∠A ＝36°.21. 证明：∵AE 平分∠BAC ，∴∠EAB ＝∠EAC ，又∵∠EBC ＝∠EAC ，∴∠EBC ＝∠EAB ，又∵∠E 公用，∴△EBD ∽△EAB ，∴EB EA ＝ED EB，∴EB2＝EA·ED. 22. 解：∵∠ADE ＝60°，DC 平分∠ADE ，∴∠ADC ＝12∠ADE ＝30°＝∠ABC.又∵AB 为⊙O 的直径，∴∠ACB ＝90°，∴AC ＝12AB ＝4cm.BC ＝AB2－AC2＝82－42＝43(cm). 23. 证明：∵AB ∥CD ，∴∠BAC ＝∠ACD ，∵AD ＝DE ，∴∠DAE ＝∠AED ，∴∠DAE ＝∠AED ＝∠ACD ＝∠BAC ，∵∠ADF ＝∠ACB ，∠DAE ＝∠BAC ，∴△ADF ∽△ABC.24. (1)解：∵BC ＝DC ，∴∠CBD ＝∠CDB ＝39°，∵∠BAC ＝∠CDB ＝39°，∠CAD ＝∠CBD ＝39°，∴∠BAD ＝∠BAC ＋∠CAD ＝39°＋39°＝78°；(2)证明：∵EC ＝BC ，∴∠CEB ＝∠CBE ，而∠CEB ＝∠2＋∠BAE ，∠CBE ＝∠1＋∠CBD ，∴∠2＋∠BAE ＝∠1＋∠CBD ，∵∠BAE ＝∠CBD ，∴∠1＝∠2.25. 解：(1)∠PAC ；(2)PA ＝PB ＋PC.在AP 上截取PD ＝PC ，连接CD 可证△PCD 是等边三角形，△ACD ≌△BCP.26. 解：(1)△ABC 为等边三角形.理由如下：连接AE ，如图，∵，∴∠DAE ＝∠BAE ，即AE 平分∠BAC ，∵AB 为直径，∴∠AEB ＝90°，∴AE ⊥BC ，∴△ABC 为等腰三角形；(2)∵△ABC 为等腰三角形，AE ⊥BC ，∴BE ＝CE ＝12BC ＝12×12＝6，在Rt △ABE 中，∵AB ＝10，BE ＝6，∴AE ＝102－62＝8，∵AB 为直径，∴∠ADB ＝90°，∴12AE·BC＝12BD·AC，∴BD ＝8×1210＝485，在Rt △ABD 中，∵AB ＝10，BD ＝485，∴AD ＝AB2－BD2＝145，∴sin ∠ABD ＝AD AB ＝14510＝725.。

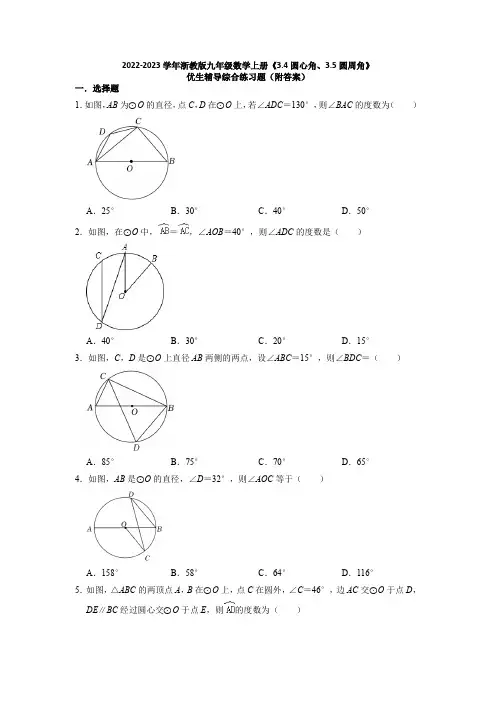
2022-2023学年浙教版九年级数学上册《3.4圆心角、3.5圆周角》优生辅导综合练习题（附答案）一．选择题1．如图，AB为⊙O的直径，点C，D在⊙O上，若∠ADC＝130°，则∠BAC的度数为（）A．25°B．30°C．40°D．50°2．如图，在⊙O中，＝，∠AOB＝40°，则∠ADC的度数是（）A．40°B．30°C．20°D．15°3．如图，C，D是⊙O上直径AB两侧的两点，设∠ABC＝15°，则∠BDC＝（）A．85°B．75°C．70°D．65°4．如图，AB是⊙O的直径，∠D＝32°，则∠AOC等于（）A．158°B．58°C．64°D．116°5．如图，△ABC的两顶点A，B在⊙O上，点C在圆外，∠C＝46°，边AC交⊙O于点D，DE∥BC经过圆心交⊙O于点E，则的度数为（）A．44°B．80°C．88°D．92°6．一副学生三角板放在一个圈里恰好如图所示，顶点D在圆圈外，其他几个顶点都在圆圈上，圆圈和AD交于点E，已知AC＝8cm，则这个圆圈上的弦CE长是（）A．6cm B．6cm C．4cm D．cm 二．填空题7．如图，AB为⊙O的直径，点C、D在⊙O上．若∠ACD＝50°，则∠BAD的大小为°．8．如图所示，在△ABC中，AB＝AC，以AB为直径作半圆O，交BC于点D，交AC于点E．若∠BAC＝44°，BD＝2，则弧AE的度数是，DC的长为．9．如图，在△ABC中，∠ACB＝90°，∠A＝30°，AB＝4，以点B为圆心，BC长为半径画弧，交边AB于点D，则CD的长为．10．在半径为r的圆中，长度为r的弦所对的圆周角的度数是．11．如图，在⊙O中，∠BAC＝15°，∠ADC＝20°，则∠ABO的度数为．12．如图，A，B，C，D都是⊙O上的点，OA⊥BC，垂足为E，若∠OBC＝20°，则∠ADC 等于度．13．如图，矩形ABCD中，AB＝6，以点D为圆心，CD长为半径的圆弧与以BC为直径的半圆O相交于点E，若的度数为60°，则直径BC长为．14．如图，边长为2的正方形ABCD的顶点A、B在一个半径为2的圆上，顶点C、D在该圆内．将正方形ABCD绕点A逆时针旋转，当点D第一次落在圆上时，点C旋转到C′，则∠C′AB＝°．15．如图，OA、OB是⊙O的半径且OA＝OB＝1，AB＝，在⊙O上一点C，使BC＝，则∠BAC的度数为．三．解答题16．如图，在下列4×4（边长为1）的网格中，已知△ABC的三个顶点A，B，C在格点上，请分别按不同要求在网格中描出一个格点D，并写出点D的坐标．（1）将△ABC绕点C顺时针旋转90°，画出旋转后所得的三角形，点A旋转后落点为D；（2）经过A，B，C三点有一条抛物线，请找到点D，使点D也落在这条抛物线上；（3）经过A，B，C三点有一个圆，请找到一个横坐标为2的点D，使点D也落在这个圆上，①点D的坐标为；②点D的坐标为；③点D的坐标为．17．如图，在⊙O中，B，C是的三等分点，弦AC，BD相交于点E．（1）求证：AC＝BD；（2）连接CD，若∠BDC＝25°，求∠BEC的度数．18．如图，AB是⊙O的直径，弦CD⊥AB于点M，连接CO，CB．（1）若AM＝2，BM＝8，求CD的长度；（2）若CO平分∠DCB，求证：CD＝CB．19．如图所示，已知AB为⊙O的直径，CD是弦，且AB⊥CD于点E，连接AC、OC、BC．（1）求证：∠ACO＝∠BCD；（2）若EB＝8，CD＝24，求⊙O的直径．20．如图，AB是⊙O的直径，点C，E都在⊙O上，OC⊥AB，＝2，DE∥AB交OC 于点D，延长OC至点F，使FC＝OC，连接EF．（1）求证：CD＝OD．（2）若⊙O的直径是4，求EF的长．21．如图，AD为⊙O的直径，∠BAD＝∠CAD，连接BC．点E在⊙O上，AB＝BE，求证：（1）BC平分∠ACE；（2）AB∥CE．22．如图，AB是⊙O的直径，C是弧BD的中点，CE⊥AB，垂足为E，BD交CE于点F．（1）求证：CF＝BF；（2）若AD＝6，⊙O的半径为5，求BC的长．23．如图，AB为⊙O的直径，C，D为⊙O上不同于A，B的两点，且OC平分∠ACD，延长AC与DB交于点E，过点C作CF⊥OC交DE于点F．（1）求证：∠A＝∠E．（2）若BF＝5，，求⊙O的半径．24．如图，Rt△ABC中，AC＝CB，点E，F分别是AC，BC上的点，△CEF的外接圆交AB 于点Q，D．（1）如图1，若点D为AB的中点，求证：∠DEF＝∠B；（2）在（1）问的条件下：①如图2，连接CD，交EF于H，AC＝4，若△EHD为等腰三角形，求CF的长度．②如图2，△AED与△ECF的面积之比是3：4，且ED＝3，求△CED与△ECF的面积之比（直接写出答案）．（3）如图3，连接CQ，CD，若AE+BF＝EF，求证：∠QCD＝45°．参考答案一．选择题1．解：∵四边形ABCD是圆内接四边形，∴∠ADC+∠B＝180°，∵∠ADC＝130°，∴∠B＝180°﹣130°＝50°，∵AB是⊙O的直径，∴∠ACB＝90°，∴∠BAC＝90°﹣∠B＝40°．故选：C．2．解：连接CO，如图：∵在⊙O中，＝，∴∠AOC＝∠AOB，∵∠AOB＝40°，∴∠AOC＝40°，∴∠ADC＝∠AOC＝20°，故选：C．3．解：∵AB是⊙O的直径，∴∠ACB＝90°，∵∠ABC＝15°，∴∠CAB＝75°，∴∠BDC＝∠CAB＝75°，故选：B．4．解：∵∠D＝32°，∴∠BOC＝2∠D＝64°，∴∠AOC＝180°﹣64°＝116°．故选：D．5．解：∵DE||BC，∴∠C＝∠ADE＝46°，∴的度数是92°，∴的度数为180°﹣92°＝88°．故选：C．6．解：作AH⊥CE于H，如图，∠ACB＝90°，∠ABC＝∠BAC＝45°，∠BAD＝30°，∴∠BCE＝∠BAD＝30°，∴∠ACE＝60°，在Rt△ACH中，CH＝AC＝×8＝4cm，∴AH＝CH＝4cm，∵∠AEC＝∠ABC＝45°，∴AH＝HE＝4cm，∴CE＝CH+HE＝（4+4）cm．故选：C．二．填空题7．解：连接BD，∵BD是直径，∴∠ADB＝90°，∵∠ABD和∠ACD所对的弧都是，∴∠ABD＝∠ACD＝50°，∴∠BAD＝90°﹣∠ABD＝90°﹣50°＝40°，故答案为：40．8．解：连接OE，AD，∵OA＝OE，∠BAC＝44°，∴∠BAC＝∠OEA＝44°，∴∠AOE＝92°，∴弧AE的度数是92°，∵AB为半圆O的直径，∴∠ADB＝90°，∵AB＝AC，∴AD是△ABC的中线，∴BD＝CD，∵BD＝2，∴CD＝2．故答案为：92°，2．9．解：连接CD，∵∠ACB＝90°，∠A＝30°，AB＝4，∴∠B＝60°，BC＝AB＝2，∵以点B为圆心，BC长为半径画弧，交边AB于点D，∴△BCD是等边三角形，∴CD＝BC＝2，故答案为：2．10．解：如图，作OD⊥AB，垂足为D，则由垂径定理知，点D是AB的中点，∴AD＝AB＝r，∴∠AOD＝45°，∴∠AOB＝2∠AOD＝90°，∴∠ACB＝∠AOB＝45°，∵A、C、B、E四点共圆，∴∠ACB+∠AEB＝180°，∴∠AEB＝135°，故答案为：45°或135°．11．解：连接AO，CO，则∠AOC＝2∠ADC，∠BOC＝2∠BAC，∴∠AOB＝∠BOC+∠AOC＝2∠BAC+2∠ADC＝2×15°+2×20°＝70°，∵OA＝OB，∴∠ABO＝（180°﹣∠AOB）＝55°，故答案为：55°．12．解：∵OA⊥BC，∴∠OEB＝90°，∵∠OBC＝20°，∴∠AOB＝90°﹣∠OBC＝70°，∴的度数是70°，∵OA⊥BC，OA过圆心O，∴＝，∴的度数是70°，∴圆周角∠ADC＝＝35°，故答案为：35．13．解：如图，连接BE，EC．∵BC是直径，∴∠BEC＝90°，∵的度数＝60°，∴∠BCE＝×60°＝30°，∵四边形ABCD是矩形，∴AB＝CD＝6，∠DCB＝90°，∴∠DCE＝90°﹣30°＝60°，∵DE＝DC，∴△DEC是等边三角形，∴EC＝CD＝6，∴BC＝4．故答案为：．14．解：如图，分别连接OA、OB、OD′、OC、OC′；∵OA＝OB＝AB，∴△OAB是等边三角形，∴∠OAB＝60°；同理可得△OAD′为等边三角形，∴∠OAD′＝60°，∴∠D′AB＝60°+60°＝120°；∵AC′为正方形AB′C′D′的对角线，∴∠D′AC′＝45°，∴∠C′AB＝∠D′AB﹣∠D′AC′＝120°﹣45°＝75°．故答案为75．15．解：如图，作OH⊥BC于H．连接AC．∵OH⊥BC，∴BH＝CH＝，∴∠OBH＝30°，∵OA＝OB＝1，AB＝，∴AB2＝OA2+OB2，∴∠AOB＝90°，∴∠ACB＝∠AOB＝45°，∵∠ABC＝∠ABO+∠OBC＝45°+30°＝75°，∴∠BAC＝180°﹣75°﹣45°＝60°，作点C关于直线OB的对称点C′，连接AC′，BC′，CC′，∵∠OBC＝∠OBC′＝30°，∴∠CBC′＝60°，∵BC＝BC′，∴△BCC′是等边三角形，∴∠BCC′＝60°，∴∠BAC′＝180°﹣60°＝120°，故答案为60°或120°．三．解答题16．解：（1）如图，点B的对应点为B′，点A的对应点为点D（4，2）；故①答案为：（4，2）；（2）抛物线的对称轴在BC的中垂线上，则点D、A关于函数对称轴对称，故点D（3，2），故②的答案为：（3，2）；（3）AB中垂线的表达式为：y＝x，BC的中垂线为：x＝，则圆心O为：（，），设点D（2，m），则OD＝OB，（）2+（）2＝（2﹣）2+（m﹣）2，解得：m＝0或3（舍去0），故点D（2，3）；故③的答案为（2，3）．17．（1）证明：∵B，C是的三等分点，∴＝＝，∴+＝+，∴＝，∴AC＝BD；（2）解：如图，连接CD，AD，∵∠BDC＝25°，＝＝，∴∠CAD＝∠BDA＝∠BDC＝25°，∵∠AED+∠CAD+∠BDA＝180°，∴∠AED＝180°﹣∠CAD﹣∠BDA＝130°，∴∠BEC＝∠AED＝130°．18．解：（1）∵AB是⊙O的直径，弦CD⊥AB，∴CM＝DM，∵AM＝2，BM＝8，∴AB＝10，∴OA＝OC＝5，在Rt△OCM中，OM2+CM2＝OC2，∴CM＝＝4，∴CD＝8；（2）过点O作ON⊥BC，垂足为N，∵CO平分∠DCB，∴OM＝ON，∴CB＝CD．19．（1）证明：∵AB⊥CD，∴，∴∠A＝∠BCD，∵OA＝OC，∴∠A＝∠ACO，∴∠ACO＝∠BCD；（2）解：设⊙O的半径为r，则OC＝r，OE＝OA﹣BE＝r﹣8，∵AB⊥CD，∴CE＝DE＝CD＝×24＝12，在Rt△OCE中，122+（r﹣8）2＝r2，解得r＝13，∴⊙O的直径＝2r＝26．20．（1）证明：连接OE、CE，如图，∵OC⊥AB，∴∠AOC＝90°，∵＝2，∴∠COE＝2∠AOE，∴∠COE＝60°，而OE＝OC，∴△OCE为等边三角形，∵DE∥AB，OC⊥AB，∴DE⊥OC，∴CD＝OD；（2）解：∵⊙O的直径是4，∴OE＝OC＝CF＝2，CD＝OD＝1，在Rt△ODE中，DE＝＝，在Rt△EFD中，EF＝＝＝2．21．证明：（1）∵AB＝BE，∴，∴∠ACB＝∠BCE，∴BC平分∠ACE；（2）连接OC、OB，∵OA、OB、OC是⊙O半径，∴OA＝OB＝OC，∴∠OAB＝∠OBA，∠OAC＝∠OCA，∵∠BAD＝∠CAD，∴∠ABO＝∠ACO，∵OB＝OC，∴∠OBC＝∠OCB，∴∠OBA+∠OBC＝∠OCA+∠OCB，∴∠ABC＝∠ACB，∴AB＝AC，∵AB＝BE，∴AC＝BE，∴，∴∠ABC＝∠ECB，∴AB∥CE．22．（1）证明：连接AC，如图1所示：∵C是弧BD的中点，∴∠DBC＝∠BAC，在ABC中，∠ACB＝90°，CE⊥AB，∴∠BCE+∠ECA＝∠BAC+∠ECA＝90°，∴∠BCE＝∠BAC，又C是弧BD的中点，∴∠DBC＝∠CDB，∴∠BCE＝∠DBC，∴CF＝BF．（2）解：连接OC交BD于G，如图2所示：∵AB是O的直径，AB＝2OC＝10，∴∠ADB＝90°，∴BD＝＝＝8，∵C是弧BD的中点，∴OC⊥BD，DG＝BG＝BD＝4，∵OA＝OB，∴OG是△ABD的中位线，∴OG＝AD＝3，∴CG＝OC﹣OG＝5﹣3＝2，在Rt△BCG中，由勾股定理得：BC＝＝＝2．23．（1）证明：由题意∠ACO＝∠A＝∠D．∵OC平分∠ACD，∴∠ACO＝∠OCD，∴∠OCD＝∠D．∴OC∥DE，∴∠E＝∠ACO，∴∠E＝∠A．（2）解：∵，∴设BD＝3x，OB＝4x，由（1）得∠E＝∠A＝∠CDE，OC∥DE．∵CF⊥OC，∴CF⊥DE，∴EF＝DF＝3x+5．∴BE＝3x+10，∵∠E＝∠A，∴AB＝BE，即3x+10＝8x，解得x＝2∴半径OB＝4x＝8．24．（1）证明：连接CD．在Rt△ABC中，∵AC＝CB，∴∠A＝∠B＝45°，∵CD＝DB，∴∠DCB＝∠B＝45°，∵∠DEF＝∠DCB，∴∠DEF＝∠B．（2）解：①如图2﹣1中，当EH＝HD，可证四边形CFDE是正方形CF＝2．如图2﹣2中，当EH＝ED时，∠EDH＝∠EHD＝67.5°，∵∠EDF＝∠CDB＝90°，∴∠EDH＝∠BDF＝67.5°，∴∠BFD＝180°﹣45°﹣67.5°＝67.5°，∴∠BDF＝∠BFD，∴BD＝BF，∵AC＝BC＝4，∠ACB＝90°，∴AB＝＝4，∴BD＝BF＝2，∴CF＝4﹣2．如图2﹣3中，当DA＝FH时，点E于A重合，点H与C重合，CF＝0．综上所述，满足条件的CF的值为0或2或4﹣2．②如图2﹣4中，作DM⊥AC于M，DN⊥BC于N，连接DF．∵CA＝CB，AD＝DB，∠ACB＝90°，∴CD⊥AB，∠ACD＝∠BCD＝45°，CD＝DA＝DB∴DE＝DF，∵∠ADC＝∠EDF＝90°，∴∠ADE＝∠CDF，∴△ADE≌△CDF（SAS），∴AE＝CF，S△ADE＝S△CDF，∵DC平分∠ACB，DM⊥AC，DN⊥BC，∴DM＝DN，可得四边形DMCN是正方形，∴DM＝CM＝CN＝DN，∵＝＝＝＝，∴可以假设DN＝3k，EC＝4k，则AC＝BC＝6k，AE＝CF＝2k，∴＝＝．（3）证明：连接OD，OQ，作ER⊥AB，OH⊥AB，FK⊥AB．∵ER∥OH∥FK，EO＝OF，∴RH＝HK∴OH＝（ER+FK），∵ER＝AE，FK＝FB，∴OH＝（AE+BF）＝EF＝OE＝OQ，∴∠OQD＝∠ODQ＝45°，∴∠QOD＝90°，∴∠QCD＝45°．。

圆周角和圆心角的关系一、基础概念 (1)圆心角：顶点在圆心的角叫圆心角. 圆心角的性质：圆心角的度数等于它所对的弧的度数. (2)圆周角：顶点在圆上，两边都和圆相交的角叫做圆周角.1、下图中是圆心角的有 . 下图中是圆周角的有 .①Image ②Image ③Image④ Image ⑤Image ⑥Image圆周角的性质： ①圆周角等于它所对的弧所对的圆心角的一半. ②同弧或等弧所对的圆周角相等；在同圆或等圆中，相等的圆周角所对的弧相等. ③90°的圆周角所对的弦为直径；半圆或直径所对的圆周角为直角. ④如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形. ⑤圆内接四边形的对角互补；外角等于它的内对角.2、如图，∠A是⊙O的圆周角，且∠A＝35°,则∠OBC=_____.3、如图，若∠A＝40°,则∠B=_____.4、如图，若∠A＝∠B，则弧CD_____弧EF。

5、如图，AB是圆O的直径，∠B＝30°，则∠A＝_____.6、如图，A,B,C,D四点在圆O上，且∠A＝40°，则∠C＝_____.ImageImageImageImageImage(2) (3) (4) (5)(6)二、课堂练习7.如图,已知圆心角∠BOC=100°,则圆周角∠BAC的度数是( )A.50°B.100°C.130°D.200°8.如图,等边三角形ABC的三个顶点都在⊙O上,点D是弧AC上任一点(不与A、C重合),则∠ADC的度数是________.ImageImageImage9.已知∠BAD=100°,则∠BOC=_______.10.如图,A、B、C为⊙O上三点，若∠OAB=46°,则∠ACB=_______度.11.如图,AB是⊙O的直径, 弧BC=弧BD,∠A=25°,则∠BOD的度数为________.12.如图,AB是半圆O的直径,AC=AD,OC=2,∠CAB= 30 °, 则点O 到CD 的距离OE=______.ImageImageImage( 10) (11) (12)三、能力提升13、如图，点、、是上的三点，.（1）求证：平分.（2）过点作于点，交于点. 若，求OA,OE,PE的长．14、（2009年广州市）如图，在⊙O中，∠ACB=∠BDC=60°，AC=，（1）求∠BAC的度数； （2）求⊙O的半径15.如图所示，已知AB为⊙O的直径，CD是弦，且AB CD于点E．连接AC、OC、BC．（1）求证：ACO=BCD．EDBAOC（2）若EB=，CD=，求⊙O的直径．。

松滋市实验中学九年级培优辅差《圆周角》训练题命题人：胡海洋题号一、选择题二、填空题三、简答题总分得分一、选择题1、如图，内接于,若，则的大小为（)A．B． C．D．（第1题） (第2题) （第3题) （第4题）（第5题）2、如图，AB是的直径，点C、D在上,，则（）A．70° B．60° C．50° D．40°3、如图，是的外接圆，已知，则的大小为（）A．40° B．30° C．45°D．50°4、如图，已知A、B、C、D、E均在⊙O上，且AC为⊙O的直径,则∠A+∠B+∠C= （）A．180°B．90°C．45°D．30°5、如图，四边形ABCD内接于⊙O,BC是直径，AD＝DC，∠ADB＝20º,则∠ACB，∠DBC分别为（ )A．15º与30º B．20º与35º C．20º与40º D．30º与35º6、. 如右图,A、B、C、D为⊙O的四等分点,若动点P从点C出发,沿C→D→O→C路线作匀速运动，设运动时间为t,∠APB的度数为y,则y与t之间函数关系的大致图象是A B CD二、填空题7、如图，在⊙O中，∠AOB＝46º，则∠ACB＝º．8、如图，过D、A、C三点的圆的圆心为E，过B、E、F三点的圆的圆心为D，如果∠A=63 º,那么∠B= º．（第7题) （第8题）（第9题） (第10题） (第11题）9、如图，AB是⊙0的直径，弦AC长为4a,弦BC长为5a，∠ACB的平分线交⊙0于点D,则CD的长为。

10、如图, ⊙P过O、、，半径PB⊥PA，双曲线恰好经过B点，则k的值是____________．11、如图，以原点O为圆心的圆交x轴于点A、B两点,交y轴的正半轴于点C，D为第一象限内⊙O上的一点，若∠DAB = 20°，则∠OCD = _____________．12、如图，已知AB是⊙O的直径，BC是弦,∠ABC=30°，过圆心O作OD⊥BC交BC于点D，连接DC，则∠DCB= 。

第5卷 圆心角、圆周角专题一、选择题1．如图，AC 是⊙O 的直径，点B 、D 在⊙O 上，那么图中（不再添辅助线）等于21∠BOC 的角有（ ） （A ）1个（B ）2个（C ）3个（D ）4个（第1题图）（第2题图）（第3题图）2．如图，A ，B ，C ，D 是⊙O 上的四个点，B 是AC 的中点，M 是半径OD 上任意一点．若∠BDC ＝40°，则∠AMB 的度数不可能是（ ） （A ）45°（B ）60°（C ）75°（D ）85°3．如图，在扇形OAB 中，∠AOB ＝110°，将扇形OAB 沿过点B 的直线折叠，点O 恰好落在AB 上的点D 处，折痕交OA 于点C ，则AD 的度数为（ ）（A ）40°（B ）50° （C ）60° （D ）70°4．如图，⊙O 中，AB 、AC 是弦，O 在∠BAC 的内部，∠ABO ＝α，∠ACO ＝β，∠BOC ＝θ，则下列关系式中，正确的是（ ） （A ）θ＝α+β（B ）θ＝2α+2β （C ）θ+α+β＝180° （D ）θ+α+β＝360°5．如图，E ，B ，A ，F 四点共线，点D 是正三角形ABC 的边AC 的中点，点P 是直线AB 上异于A ，B 的一个动点，且满足∠CPD ＝30°，则（ ）（A ）点P 一定在射线BE 上 （B ）点P 可以在射线AF 上，也可以在线段AB 上（C ）点P 一定在线段AB 上 （D ）点P 可以在射线BE 上，也可以在线段（第4题图）（第5题图）（（（6．如图，AB 是⊙O 的直径，点C 是半径OA 的中点，过点C 作DE ⊥AB ，交⊙O 于D ，E 两点，过点D 作直径DF ，连结AF ，则∠DF A ＝ ．7．如图，已知⊙O 的半径是R ．C ，D 是直径AB 同侧圆周上的两点，AC 的度数为96°，BD 的度数为36°，动点P 在AB 上，则PC +PD 的最小值为 ． 8．已知，AB 是⊙O 直径，半径OC ⊥AB ，点D 在⊙O 上，且点D 与点C 在直径AB 的两侧，连结CD ，BD ．若∠OCD ＝22°，则∠ABD 的度数是 ．9．如图，AB 是⊙O 的直径，AB ＝AC ，BC 交⊙O 于点D ，AC 交⊙O 于点E ，∠BAC ＝45°，给出下列五个结论：①∠EBC ＝22.5°；②BD ＝DC ；③AE ＝2EC ；④劣弧AE 是劣弧DE 的2倍；⑤AE ＝BC ．其中正确结论的序号是 ．10．如图，已知EF 是⊙O 的直径，把∠A 为60°的直角三角板ABC 的一条直角边BC 放在直线EF 上，斜边AB 与⊙O 交于点P ，点B 与点O 重合；将三角形ABC 沿OE 方向平移，使得点B 与点E 重合为止．设∠POF ＝x °，则x 的取值范围是 ． 11．如图，已知AB 为⊙O 的直径，点C 为半圆上的四等分点，在直径AB 所在的直线上找一点P ，连接CP 交⊙O 于点Q （异于点P ），使PQ ＝OQ ，则∠CPO ＝ ． 12．如图，⊙O 的半径是2，直线l 与⊙O 相交于A 、B 两点，M 、N 是⊙O 上的两个动点，且在直线l 的异侧，若∠AMB ＝45°，则四边形MANB 面积的最大值是 ．（第6题图）（第7题图）（第9题图）（第10题图）（第11题图）（第12题图）（（13．如图，AB 为⊙O 的直径，弦CD ⊥AB 于E ，∠CDB ＝15°，OE ＝32． （1）求⊙O 的半径；（2）将△OBD 绕O 点旋转，使弦BD 的一个端点与弦AC 的一个端点重合，则弦BD与弦AC 的夹角为 ．14．已知：如图，在⊙O 中，AB ＝2AC ，AD ⊥OC 于D ．求证：AB ＝2AD ．15．已知：如图，已知AB 是⊙O 的直径，D 是⊙O 上一点，弦DE ⊥AB 于C ，弦EF 交线段CB 于G ． 求证：BD 平分∠FDG ．（第13题图）（第15题图） （第14题图） （（16．如图，△ABC 内接于⊙O ，∠BAC ＝60°，点D 是BC 的中点．BC ，AB 边上的高AE ，CF 相交于点H ．试证明： （1）∠F AH ＝∠CAO ； （2）四边形AHDO 是菱形．17.已知：AB 、AC 是⊙O 的两条弦，AB ＝AC ，BG ⊥AC 于点G ，∠ABG 的平分线交AC 点D 交⊙O 于点E ，连接AE 、BC ．（1）如图①，求∠EBC 的度数；（2）如图②，F 为BG 上一点，连接DF ，当∠BAC ＝2∠FDG 时，求证：DC ＝BF ； （3）如图③，在（2）的条件下，当BE 为⊙O 的直径时，经过点G 的弦MN 交AB 于点H ，若MH ＝GN ，△BDF 的面积为4，求线段AE 的长．（第16题图）（第17题图③）（第17题图②）（第17题图①）（九上第5卷 圆心角、圆周角专题参考答案一．选择题 1．C提示∵OA ＝OB ，∴∠OAB ＝∠OBA ，由圆周角定理知，∠BAC ＝∠CDB ＝21∠BOC ， 故∠OBA ＝∠BAC ＝∠CDB ＝21∠BOC . 2．D提示∵B 是AC 的中点，∴∠AOB ＝2∠BDC ＝80°， 又∵M 是OD 上一点，∴∠AMB ≤∠AOB ＝80°． 则不符合条件的只有85°． 3．B提示：连结OD ，如图，∵扇形OAB 沿过点B 的直线折叠，点O 恰好落在AB 上的点D 处，折痕交OA 于点C ，∴BC 垂直平分OD ， ∴BD ＝BO ， ∵OB ＝OD ，∴△OBD 为等边三角形， ∴∠DOB ＝60°，∴∠AOD ＝∠AOB －∠DOB ＝110°－60°＝50°， ∴AD 的度数为为50°. 4．B提示：过A 作⊙O 的直径，交⊙O 于D ；△OAB 中，OA ＝OB ，则∠BOD ＝∠OBA +∠OAB ＝2α； 同理可得：∠COD ＝∠OCA +∠OAC ＝2β； ∵∠BOC ＝∠BOD +∠COD ，∴θ＝2α+2β. 5．C提示：连接BD 、PC 、PD ，如图，∵△ABC 等边三角形， ∴∠CBD ＝30°，又∠CPD ＝30°，∴∠CBD ＝∠CPD ， ∴B 、C 、D 、P 四点共圆，又∠BDC ＝90°，∴点P 在以BC 为直径的圆上，∴点P 一定在线段AB 上． 二．填空题 6.30°（第3题图）（第4题图）（第5题图）（（（7.R 3提示：将C 点对称，连接DC ’，根据题意以及垂径定理，得弧C ’D 的度数是120°， 则∠C ’OD ＝120°．作OE ⊥C ’D 于E ， 则∠DOE ＝60°，则DE ＝R 23，C ’D ＝R 3．8．23°或67°①当点D 在直线OC 左侧时，如图所示． 连接OD ，则∠1＝∠2＝22°， ∴∠COD ＝180°－∠1－∠2＝136°，∴∠AOD ＝∠COD －∠AOC ＝136°－90°＝46°， ∴∠ABD ＝21∠AOD ＝23°； ②当点D 在直线OC 右侧时，如图所示． 连接OD ，则∠1＝∠2＝22°； 并延长CO ，则∠3＝∠1+∠2＝44°． ∴∠AOD ＝90°+∠3＝90°+44°＝134°， ∴∠ABD ＝21∠AOD ＝67°． 9.①②④．提示：连接AD ，AB 是⊙O 的直径，则∠AEB ＝∠ADB ＝90°，∵AB ＝AC ，∠BAC ＝45°，∴∠ABE ＝45°， ∠C ＝∠ABC ＝67.5°，AD 平分∠BAC ， ∴AE ＝BE ，∠EBC ＝90°－67.5°＝22.5°， DB ＝CD ，故②正确，∵∠ABE ＝45°，∠EBC ＝22.5°，故①正确， ∵AE ＝BE ，∴AE ＝BE ，又AD 平分∠BAC ， 所以，即劣弧AE 是劣弧DE 的2倍，④正确．∵∠EBC ＝22.5°，BE ⊥CE ，∴BE ＞2EC ，∴AE ＞2EC ，故③错误． ∵∠BEC ＝90°，∴BC ＞BE ，又∵AE ＝BE ，∴BC ＞AE ，故⑤错误． 10.30≤x ≤60．提示：当O 、B 重合时，∠POF 的度数最小，此时∠POF ＝∠PBF ＝30°； 当B 、E 重合时，∠POF 的度数最大，∠POF ＝2∠PBF ＝60°；（第7题图）（第8题图①）（第8题图②）（第9题图）（（故x 的取值范围是30≤x ≤60． 11. 15°或30°或45°或105°．提示：当P 在直线AB 延长线上时，如图所示： 连接OC ， 设∠CPO ＝x °， ∵PQ ＝OQ ，∴∠QOP ＝∠CPO ＝x °， ∴∠CQO ＝2x °， ∵OQ ＝OC ，∴∠OCQ ＝∠CQO ＝2x °， ∵点C 为半圆上的四等分点，∴∠AOC ＝45°或∠AOC ＝90°（此时点C 亦为半圆的二等分点）， ∴x +2x ＝45或x +2x ＝90， ∴x ＝15或x ＝30，∴∠CPO ＝15°或∠CPO ＝30°，当P 在直线BA 延长线上，PC 是切线时，点C 与点Q 重合，此时∠CPO ＝45°． 同理可得，当P 在线段AB 上时，∠CPO ＝105°． 12.24提示：过点O 作OC ⊥AB 于C ，交⊙O 于D 、E 两点，连结OA 、OB 、DA 、DB 、EA 、EB ，∵∠AMB ＝45°，∴∠AOB ＝2∠AMB ＝90°，∴△OAB 为等腰直角三角形， ∴AB ＝2OA ＝22，∵S 四边形MANB ＝S △MAB +S △NAB ，∴当M 点到AB 的距离最大，△MAB 的面积最大；当N 点到AB 的距离最大时，△NAB 的面积最大，此时，MN 过圆心是直径.此时四边形MANB 面积的最大值＝21AB （CM +CN ）＝21AB •MN ＝21×22×4＝42． 三．解答题13．（1）∵AB 为⊙O 的直径，弦CD ⊥AB 于E ，∴弧BC ＝弧BD ，∴∠BDC ＝21∠BOD ， 而∠CDB ＝15°，∴∠BOD ＝2×15°＝30°，在Rt △ODE 中，∠DOE ＝30°，OE ＝23，∴OE ＝3DE ，OD ＝2DE ，∴DE ＝332＝2;∴OD ＝4，即⊙O 的半径为4；（第11题图）（2）有4种情况：如图：（第13题图①）（第13题图②）（第13题图③）①如图①所示：∵OA ＝OB ，∠AOB ＝30°， ∴∠OAB ＝∠OBA ＝75°， ∵CD ⊥AB ，AB 是直径， ∴弧BC ＝弧BD ， ∴∠CAB ＝21∠BOD ＝15°， ∴∠CAB ＝∠BAO +∠CAB ＝15°+75°＝90°； ②如图②所示，∠CAD ＝75°－15°＝60°； ③如图③所示：∠ACB ＝90°； ④如图④所示：∠ACB ＝60°； 故答案为：60°或90°． 14.证明：延长AD 交⊙O 于E ， ∵OC ⊥AD ，∴AE =2AC ，AE ＝2AD ， ∵AB =2AC ，∴AE =AB ，，∴AB ＝AE ，∴AB ＝2AD ．15.证明：连接BD 、BE ，如图所示： ∵AB 为直径，DE ⊥AB ， ∴AB 垂直平分DE ， ∴BD ＝BE ，CD ＝CE ， ∴△BDG ≌△BEG （SSS ）， ∴∠BDG ＝∠BEG ， ∵∠BDF ＝∠BEF ， ∴∠BDG ＝∠BDF ， 即：BD 平分∠FDG ．（第14题图）（第13题图④）（第14题图）（第15题图） （（ （（（ （16.证明：（1）连接AD ，∵点D 是BC 的中点， ∴∠BAD ＝∠CAD ，OD ⊥BC ， ∵AE ⊥BC ， ∴AE ∥OD ， ∴∠DAH ＝∠ODA ， ∵OA ＝OD ， ∴∠DAO ＝∠ODA ，∴∠BAD －∠DAH ＝∠CAD －∠DAO ， ∴∠F AH ＝∠CAO ；（2）过点O 作OM ⊥AC 于M ，∴AC ＝2AM ， ∵CF ⊥AB ，∠BAC ＝60°，∴AC ＝2AF ，∴AF ＝AM ， 在△AFH 与△AMO 中，∵∠F AH ＝∠CAO ，AF ＝AM ，∠AFH ＝∠AMO ， ∴△AFH ≌△AMO ，∴AH ＝OA ， ∵OA ＝OD ，∴AH 平行且等于OD ．∴四边形AHDO 是平行四边形（一组对边平行且相等的四边形是平行四边形）， 又∵OA ＝OD ，∴平行四边形AHDO 是菱形（邻边相等的平行四边形是菱形） 17.解：（1）设∠GBC ＝α， ∵BG ⊥AC ， ∴∠BGC ＝90°， ∴∠C ＝90°－α， ∵AB ＝AC ，∴∠ABC ＝∠C ＝90°－α，∴∠BAC ＝180°－（∠ABC +∠C ）＝180°－（90°－α+90°－α）＝2α， ∴∠ABG ＝90°－2α， ∵BE 平分∠ABG ， ∴∠DBG ＝45°－α，∴∠EBC ＝∠DBG +∠GBC ＝45°－α+α＝45°； （2）延长DF 交BC 于点P ，如图① 由（1）∠BAC ＝2α＝2∠GBC（第16题图）（∵∠BAC ＝2∠FDG ，∴∠FDG ＝∠GBC ， ∵∠BFP ＝∠DFG ，∴∠BPF ＝∠DGF ＝90°， ∴∠BDF ＝∠DBC ＝45°，∴DP ＝BP ， ∴△DPC ≌△BPF （ASA ）， ∴DC ＝BF ；（3）∵当BE 为⊙O 的直径， ∴∠BAE ＝90°＝∠AGB ∵∠EAC ＝∠EBC ＝45°， ∴∠BAC ＝∠ABG ＝45°， ∵BE 平分∠ABG ，∴∠ABE ＝∠DBG ＝∠CBG ＝22.5°， ∴∠BDG ＝∠BCG ＝67.5°， ∴BD ＝BC ，∴设DG ＝CG ＝a ， ∴BF ＝CD ＝2a ，S △BDF ＝21BF •DG ＝21×2a •a ＝4， ∴a ＝2，BF ＝CD ＝4过点O 作OK ⊥MN 于点K ，连接OH 、OG ，∴MK ＝NK ， ∵MH ＝GN ，∴HK ＝GK ，∴OH ＝OG ，连接OA 、OC ，延长GO 交AB 于T ，过O 作OQ ⊥AC 于Q （图②）， ∵BC=BC ，∴∠BOC ＝2∠BAC ＝90°， ∵G 为CD 的中点，∴OG ＝21CD ＝2， ∵AG ＝BG ，AO ＝BO ，∴TG ⊥AB ，AT ＝BT ， ∴∠AGT ＝45°，∴OQ ＝2， ∵AB ＝AC ＝2BT ＝2CQ ，BO ＝CO ， ∴Rt △BOT ≌Rt △COQ （HL ）， ∴OT ＝OQ ＝2，∵Rt △OTH ≌Rt △OQG （HL ）， ∴TH ＝QG ，∴AH ＝CG ＝2，∵AT ＝BT ，EO ＝BO ，∴AE ＝2TO ＝22．（第17题图②）（第17题图①）（（。

完整版)圆心角圆周角练习题知识点三：弧、弦、圆心角与圆周角1.定义圆心角为顶点在圆心的角。

2.在同圆或等圆中，弧、弦、圆心角之间的关系：两个圆心角相等，圆心角所对的弧相等（无论是优弧还是劣弧），圆心角所对的弦相等。

3.一个角是圆周角必须满足两个条件：（1）角的顶点在圆上；（2）角的两边都与圆有除顶点外的交点。

4.同一条弧所对的圆周角有两个。

5.圆周角定理：圆周角等于圆心角的一半。

6.圆周角定理的推论：（1）同弦或等弦所对的圆周角相等；（2）半圆或直径所对的圆周角相等；（3）90°的圆周角所对的弦是直径。

需要注意的是，“同弦或等弦”改为“同弧或等弧”结论就不一定成立了，因为一条弦所对的圆周角有两类，它们是相等或互补关系。

7.圆内接四边形定义为所有顶点都在圆上的多边形，圆心即为这个圆内接四边形的交点。

圆内接四边形的对角线相互垂直，且交点为对角线的中点。

夯实基础1.如果两个圆心角相等，则它们所对的弧相等，选项B正确。

2.不正确的语句为③，因为圆不一定是轴对称图形，只有圆上的任何一条直径所在直线才是它的对称轴。

3.错误的说法是D，相等圆心角所对的弦不一定相等。

4.根据圆心角的性质，∠A=2∠B，所以∠A=140°。

5.∠BAC与∠BCD互补，∠BCD与∠CBD相等，所以与∠BAC相等的角有2个，即∠CBD和∠ABD。

6.因为∠CAB为30°，所以∠ABC为60°，由正弦定理可得BC=5√3.7.根据圆周角定理，∠ACB=40°。

8.设∠A=3x，∠B=4x，∠C=6x，则∠D=360°-3x-4x-6x=120°。

9.∠DCE=∠A。

1、如图，AB是⊙O的直径，C，D是BE上的三等分点，∠AOE=60°，求证∠COE=80°。

证明：由三等分点的性质可知，BC=CD=DE，又∠AOE=60°，所以∠AOC=120°。

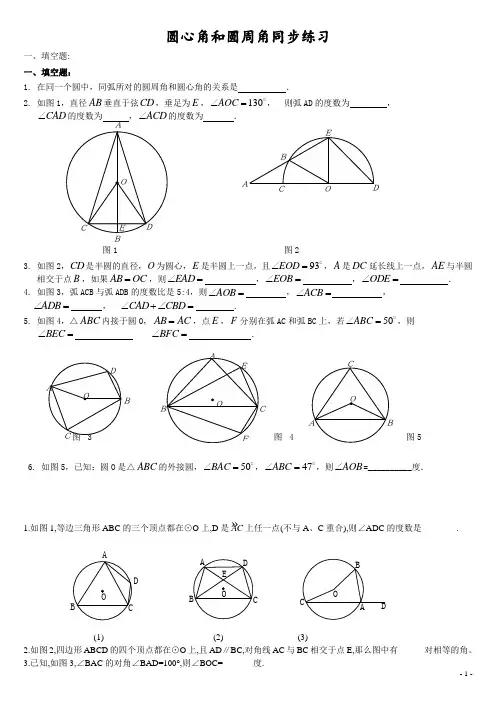
圆心角和圆周角同步练习一、填空题: 一、填空题：1. 在同一个圆中，同弧所对的圆周角和圆心角的关系是．2. 如图1，直径AB 垂直于弦CD ，垂足为E ，130AOC ∠=o， 则弧AD 的度数为 ，CAD ∠的度数为 ，ACD ∠的度数为 ．图1 图23. 如图2，CD 是半圆的直径，O 为圆心，E 是半圆上一点，且93EOD ∠=o，A 是DC 延长线上一点，AE 与半圆相交于点B ，如果AB OC =，则EAD ∠= ，EOB ∠=，ODE ∠=．4. 如图3，弧ACB 与弧ADB 的度数比是5:4，则AOB ∠= ，ACB ∠=，ADB ∠= ， CAD CBD ∠+∠= ．5. 如图4，△ABC 内接于圆O ，AB AC =，点E ，F 分别在弧AC 和弧BC 上，若50ABC ∠=o，则BEC ∠= BFC ∠=．图图56. 如图5，已知：圆O 是△ABC 的外接圆，50BAC ∠=o，47ABC ∠=o，则AOB ∠=__________度．1.如图1,等边三角形ABC 的三个顶点都在⊙O 上,D 是»AC 上任一点(不与A 、C 重合),则∠ADC 的度数是________.DDCBAO(1) (2) (3)2.如图2,四边形ABCD 的四个顶点都在⊙O 上,且AD ∥BC,对角线AC 与BC 相交于点E,那么图中有______对相等的角。

3.已知,如图3,∠BAC 的对角∠BAD=100°,则∠BOC=_______度.Ａ4.如图4,A 、B 、C 为⊙O 上三点，若∠OAB=46°,则∠ACB=_______度.BAA(4) (5) (6)5.如图5,AB 是⊙O 的直径, »»BC BD =,∠A=25°,则∠BOD 的度数为________.6.如图6,AB 是半圆O 的直径,AC=AD,OC=2,∠CAB= 30 °, 则点O 到CD 的距离OE=______.二、选择题:7.如图7,已知圆心角∠BOC=100°,则圆周角∠BAC 的度数是( ) A.50° B.100° C.130° D.200°DDCBA(7) (8) (9) (10)8.如图8,A 、B 、C 、D 四个点在同一个圆上,四边形ABCD 的对角线把四个内角分成的八个角中,相等的角有( ) A.2对 B.3对 C.4对 D.5对9.如图9,D 是»AC 的中点,则图中与∠ABD 相等的角的个数是( ) A.4个 B.3个 C.2个 D.1个10.如图10,∠AOB=100°,则∠A+∠B 等于( )A.100°B.80°C.50°D.40°11.在半径为R 的圆中有一条长度为R 的弦,则该弦所对的圆周角的度数是( ) A.30° B.30°或150° C.60° D.60°或120°12.如图,A 、B 、C 三点都在⊙O 上,点D 是AB 延长线上一点,∠AOC=140°, ∠CBD 的度数是( ) A.40° B.50° C.70° D.110°三、解答题:13.如图,⊙O 的直径AB=8cm,∠CBD=30°,求弦DC 的长.BA14.如图,A 、B 、C 、D 四点都在⊙O 上,AD 是⊙O 的直径,且AD=6cm,若∠ABC= ∠CAD,求弦AC 的长.15.如图,在⊙O 中,AB 是直径,CD 是弦,AB ⊥CD.(1)P 是¼CAD上一点(不与C 、D 重合),试判断∠CPD 与∠COB 的大小关系, 并说明理由. (2)点P′在劣弧CD 上(不与C 、D 重合时),∠CP′D 与∠COB 有什么数量关系?请证明你的结论.16.在足球比赛场上,甲、乙两名队员互相配合向对方球门MN 进攻.当甲带球部到A 点时,乙随后冲到B 点,如图所示,此时甲是自己直接射门好,还是迅速将球回传给乙,让乙射门好呢?为什么?(不考虑其他因素)答案：1.120°2.3 13.160°4.44°5.50°7.A 8.C 9.B 10.C 11.B 12.C 13.连接OC 、OD,则OC=OD=4cm,∠COD=60°,故△COD 是等边三角形,从而CD= 4cm. 14.连接DC,则∠ADC=∠ABC=∠CAD,故AC=CD.∵AD 是直径,∴∠ACD=90°, ∴AC 2+CD 2=AD 2,即2AC 2=36,AC 2. 15.(1)相等.理由如下:连接OD,∵AB ⊥CD,AB 是直径,∴»»BCBD ,∴∠COB= ∠DOB. ∵∠COD=2∠P,∴∠COB=∠P,即∠COB=∠CPD.(2)∠CP′D+∠COB=180°.理由如下:连接P′P,则∠P′CD=∠P′PD,∠P′PC=∠P′DC.∴∠P′CD+∠P′DC=∠P′PD+∠P′PC=∠CPD.∴∠CP′D=180°-(∠P′CD+∠P′DC)=180°-∠CPD=180°-∠COB,从而∠CP′D+∠COB=180°.16.迅速回传乙,让乙射门较好,在不考虑其他因素的情况下, 如果两个点到球门的距离相差不大,要确定较好的射门位置,关键看这两个点各自对球门MN的张角的大小,当张角越大时,射中的机会就越大,如图所示,则∠A<MCN=∠B,即∠B>∠A, 从而B处对MN的张角较大,在B处射门射中的机会大些.。

随堂练习 1. 如图，在⊙O 中，∠BOC=50°，求∠BAC 的大小解：在⊙O 中，∠BOC=50°1 1 BAC BOC2 20 0 50 252. 如图，哪个角与∠BAC 相等，你还能找到那些相等的角？解：∠BAC=∠BDCA D ∠ADB=∠ACB∠CAD=∠CBDC ∠ABD=∠ACDB习题1. 如图，OA、OB、OC 都是⊙O 的直径，∠AOB=2 ∠BOC，∠ACB 与∠BAC 的大小有什么关系，为什么？解：∠BAC= 2 ∠ACB，理由:1Q 1 AOB2 O 1C2 12BOC2A B又∵∠AOB=2 ∠BOC1 11 AOB2 BOC BOC 2 22 2即∠BAC= 2∠ACB2. 如图，A、B、C、D 是⊙O 上的四点，且∠BCD=100°，求∠BOD 与∠BAD的大小 A解：∵∠BCD=100°O∴优弧所对的圆心角∠BOD=2∠BCD=200°∴劣弧所对的圆心角∠BOD=36O°-200°=160°B D1 BAD BOD2o80C3. 为什么电影院的作为排列呈弧形，说一说这设计的合理性.答：有些电影院的坐位排列呈圆弧形，这样设计的理由是尽量保证同排的观众视角相等.4. 船在航行过程中，船长通过测定角数来确定是否遇到暗礁，如图，A、B 表示灯塔，暗礁分布在经过A、B 两点的一个圆形区域内，优弧AB 上任一点 C 都是有触礁危险的临界点，∠ACB就是“危险角”，当船位于安全区域时，∠α与“危险角”有怎样的大小关系？解：当船位于安全区域时，即船位于暗礁区域外（即⊙O 外），与两个灯塔的夹角∠α小于“危险角”.。

圆心角与圆周角练习题一、选择题（每题3分，共30分）1. 在同圆或等圆中，如果圆心角相等，那么对应的圆周角：A. 相等B. 不相等C. 无法确定D. 可能相等2. 已知圆的半径为5，圆心角为30°，求圆周角的度数：A. 15°B. 30°C. 45°D. 60°3. 在圆中，圆心角的度数是圆周角度数的：A. 2倍B. 1/2倍C. 1/4倍D. 4倍4. 如果一个圆周角的度数是60°，那么它所对的圆心角是：A. 120°B. 60°C. 30°D. 180°5. 在同圆或等圆中，圆心角和圆周角的关系是：A. 相等B. 互补C. 互余D. 没有固定关系6. 已知圆的半径为10，圆心角为45°，求圆周角的度数：A. 22.5°B. 45°C. 90°D. 无法确定7. 圆心角和圆周角的关系可以用以下哪个公式表示：A. 圆心角= 2 × 圆周角B. 圆周角= 2 × 圆心角C. 圆心角 = 圆周角D. 圆周角 = 圆心角 / 28. 如果一个圆周角的度数是90°，那么它所对的圆心角是：A. 45°B. 90°C. 180°D. 270°9. 在圆中，圆心角和圆周角的度数之和：A. 总是等于180°B. 总是等于360°C. 总是小于360°D. 总是大于360°10. 已知圆的半径为8，圆心角为60°，求圆周角的度数：A. 30°B. 60°C. 90°D. 120°二、填空题（每题2分，共20分）11. 在同圆或等圆中，如果圆心角是圆周角度数的2倍，那么圆周角的度数是圆心角的________倍。

12. 圆心角的度数是圆周角度数的________倍。

（完整版）圆心角圆周角练习题知识点三：弧、弦、圆心角与圆周角1、圆心角定义：顶点在的角叫做圆心角2. 在同圆或等圆中，弧、弦、圆心角之间的关系：两个圆心角相等?圆心角所对的弧(都是优弧或都是劣弧)相等?圆心角所对的弦相等3、一个角是圆周角必须满足两个条件：（1）角的顶点在________;(2)角的两边都是与圆有除顶点外的交点。

4. 同一条弧所对的圆周角有__________个5.圆周角定理：1=2圆周角圆心角6.圆周角定理推论：（1）同弧或等弧所对的圆周角相等（2）半圆或直径所对的圆周角相等（3）90°的圆周角所对的弦是直径。

注意：“同弧或等弧”改为“同弦或等弦”结论就不一定成立了，因为一条弦所对的圆周角有两类，它们是相等或互补关系。

7. 圆内接四边形：定义：如果一个多边形的所有顶点都在圆上，这个多边形叫做，这个圆叫做。

性质：圆内接四边形的对角夯实基础1．如果两个圆心角相等，那么（）A ．这两个圆心角所对的弦相等;B ．这两个圆心角所对的弧相等C ．这两个圆心角所对的弦的弦心距相等;D ．以上说法都不对2.下列语句中不正确的有（）①相等的圆心角所对的弧相等②平分弦的直径垂直于弦③圆是轴对称图形，任何一条直径所在直线都是它的对称轴④长度相等的两条弧是等弧A.3个B.2个C.1个D.以上都不对3. 在同圆或等圆中，下列说法错误的是（）A ．相等弦所对的弧相等B ．相等弦所对的圆心角相等C ．相等圆心角所对的弧相等D ．相等圆心角所对的弦相等4、如图，在⊙O 中，??AB AC ，∠B =70°，则∠A 等于．5、如图，在⊙O 中，若C 是?BD的中点，则图中与∠BAC 相等的角有（） A.1个 B.2 个 C.3个 D.4个6、如图，若AB 是⊙O 的直径，AB=10cm ，∠CAB=30°，则BC= cm ．7、如图，已知OA ，OB 均为⊙O 上一点，若∠AOB=80°，则∠ACB=（）A．80°B．70°C．60°D．40°8、圆内接四边形ABCD，∠A，∠B，∠C的度数之比为3：4：6，则∠D的度数为（）A．60 B．80 C．100 D．1209、已知如图，四边形ABCD内接于⊙O，若∠A＝60°，则∠DCE ＝.题型一：利用圆心角圆周角定理求角度1、如图，AB是⊙O的直径，C，D是BE上的三等分点，∠AOE=60°，则∠COE是（）A．40° B. 60° C. 80° D. 120 °2、如图，AB是⊙O的直径，BC⌒=BD⌒ ,∠A=25°，则∠BOD= .3、已知圆O的半径为5,弦AB的长为5,则弦AB所对的圆心角∠AOB= .4、在⊙O中，弦AB所对的劣弧为圆周的41，圆的半径等于12，则圆心角∠AOB＝；弦AB的长为.5、如图，AB是⊙O的直径，点C在⊙O上，若∠A=40 o，则∠B 的度数为（）A．80 oB．60 oC．50 oD．40 o6、如图，在△ABC中，AB为⊙O的直径，∠B=60°，∠BOD=100°，则∠C的度数为（）OEDCBAODCBAA．50°B．60°C．70°D．80°7、如图，AB、CD是⊙O的两条弦，连接AD、BC，若∠BAD=60°，则∠BCD的度数为（）A.40°B.50°C.60°D.70°8、如图，点A、B、C在⊙O上，∠AOC=60°，则∠ABC的度数是．9、如图，点A、B、C、D在⊙O上，OB⊥AC，若∠BOC=56°，则∠ADB=度．10、如图，⊙O的弦CD与直径AB相交，若∠BAD＝50°，则∠ACD＝..11、如图，AB是⊙O的直径，点C是圆上一点，∠BAC=70°，则∠OCB=．12、如图，在Rt △ABC 中，∠C=90°，∠A=26°，以点C 为圆心，BC 为半径的圆分别交AB 、AC 于点D 、点E ，则弧BD 的度数为（）A ．26°B ．64°C ．52°D ．128°题型二：利用圆心角圆周角的性质定理求线段1、在⊙O 中，圆心角∠AOB =90°,点O 到弦AB 的距离为4,则⊙O 的直径的长为( )A.4B.82C.24D.162、如图，⊙O 是△ABC 的外接圆，∠B=60°，OP ⊥AC 于点P ，，则⊙O 的半径为（）A ．B ．C ．8D ．123、如图，△ABC 内接于⊙O ，∠BAC=120°，AB=AC ，BD 为⊙O 的直径，AD=6，则DC= ．题型三：利用弧、弦、圆心角、圆周角之间的关系证明弧相等，线段相等，角度相等1、如图，在⊙O 中,AB =AC ,∠ACB=60°，求证∠AOB ＝∠BOC ＝∠AOC .333B2．如图，在⊙O 中，C 、D 是直径AB 上两点，且AC=BD ，MC ⊥AB ，ND ⊥AB ，M 、N?在⊙O 上．（1）求证：?AM =?BN ；（2）若C 、D 分别为OA 、OB 中点，则?AM MN NB ==成立吗？3、如图，以⊙O 的直径BC 为一边作等边△ABC,AB 、AC 交⊙O 于D 、E,求证：BD=DE=EC4、如图，⊙O 的直径AB 为10cm ，弦AC 为6cm ，∠ACB 的平分线交⊙O 于D ，求BC ，AD ，BD 的长.5、如图，AB 是⊙O 的直径，C 是?BD的中点，CE ⊥AB 于 E ，BD 交CE 于点F ．（1）求证：CF ﹦BF ；（2）若CD ﹦6， AC ﹦8，则⊙O 的半径为，CE 的长是．BA作业1、如图，AB 是⊙O 的直径，==，∠COD=34°，则∠AEO 的度数是（）A ．51°B ．56°C ．68°D ．78°2、圆中有两条等弦AB=AE ，夹角∠A=88°，延长AE 到C ，使EC=BE ，连接BC ，如图．则∠ABC 的度数是（）A ．90°B ．80°C ．69°D ．65°3. 如图所示⊙O 中，已知∠BAC=∠CDA=20°，则∠ABO 的度数为．B4. 如图，A，P，B，C是半径为8的⊙O上的四点，且满足∠BAC=∠APC=60°，（1）求证：△ABC是等边三角形；（2）求圆心O到BC的距离OD．5、如图，⊙O是△ABC的外接圆，AB是⊙O的直径，D为⊙O 上一点，OD⊥AC，垂足为E，连接BD（1）求证：BD平分∠ABC；（2）当∠ODB=30°时，求证：BC=OD．。

圆周角和圆心角的关系—巩固练习（基础）一、选择题1．（2016•张家界）如图，AB是⊙O的直径，BC是⊙O的弦．若∠OBC=60°，则∠BAC 的度数是（）A．75°B．60°C．45° D．30°2.如图所示，∠1，∠2，∠3的大小关系是（）．A．∠1>∠2>∠3 B．∠3>∠1>∠2 C．∠2>∠1>∠3 D．∠3>∠2>∠13．如图，AC是⊙O的直径，弦AB∥CD，若∠BAC=32°，则∠AOD等于( )．A．64°B．48°C．32°D．76°4．如图，弦AB，CD相交于E点，若∠BAC=27°，∠BEC=64°，则∠AOD等于( )．A．37°B．74°C．54°D．64°（第3题图）（第4题图）（第5题图）5．如图，四边形ABCD内接于⊙O，若∠BOD=138°，则它的一个外角∠DCE等于( )．A．69°B．42°C．48°D．38°6．（2015•酒泉）△ABC为⊙O的内接三角形，若∠AOC=160°，则∠ABC的度数是（）A．80°B．160°C．100°D．80°或100°二、填空题7.在同圆或等圆中，两个圆心角及它们所对的两条弧、两条弦中如果有一组量相等，那么_ _________．8. （2016•嘉定区一模）在⊙O中，已知=2，那么线段AB与2AC的大小关系是．（从“＜”或“=”或“＞”中选择）9．如图，AB 是⊙O的直径，弦CD⊥AB于H ，BD∥OC，则∠B的度数是 .10．如图，△ABC内接于⊙O，AB＝BC，∠BAC＝30°，AD为⊙O的直径，AD＝2，则BD ＝ .11．如图，已知⊙O的直径MN＝10，正方形ABCD四个顶点分别在半径OM、OP和⊙O上，且∠POM＝45°，则AB＝ .（第11题图）（第12题图）ODA BC（第10题图）12．如图，已知A、B、C、D、E均在⊙O上，且AC为直径，则∠A+∠B+∠C=________度．三、解答题13. 如图所示，AB，AC是⊙O的弦，AD⊥BC于D，交⊙O于F，AE为⊙O的直径，试问两弦BE与CF的大小有何关系，说明理由．14．（2015•嵊州市一模）如图，AB是半圆O的直径，C、D是半圆O上的两点，且OD∥BC，OD与AC交于点E．（1）若∠D=70°，求∠CAD的度数；（2）若AC=8，DE=2，求AB的长．15．如图，⊙O中，直径AB=15cm，有一条长为9cm的动弦CD在上滑动(点C与A，点D与B不重合)，CF⊥CD交AB于F，DE⊥CD交AB于E．(1)求证：AE=BF；(2)在动弦CD滑动的过程中，四边形CDEF的面积是否为定值?若是定值，请给出证明并求这个定值；若不是，请说明理由．【答案与解析】一、选择题1.【答案】D【解析】∵AB 是⊙O 的直径，∴∠ACB=90°，又∵∠OBC=60°，∴∠BAC=180°﹣∠ACB ﹣∠ABC=30°．故选D ．2.【答案】D ；【解析】圆内角大于圆周角大于圆外角.3.【答案】A ；【解析】∵弦AB ∥CD ，∠BAC=32°，∴∠C=∠A=32°，∠AOD=2∠C=64°.4.【答案】B ；【解析】 ∠ACD=64°-27°=37°，∠AOD=2∠ACD=74°.5.【答案】A ；【解析】 ∠BAD=∠BOD=69°，由圆内接四边形的外角等于它的内对角得∠DCE=∠BAD=69°.6.【答案】D ；【解析】如图，∵∠AOC=160°，∴∠ABC=∠AOC=×160°=80°，∵∠ABC+∠AB′C=180°，∴∠AB′C=180°﹣∠ABC=180°﹣80°=100°． 12∴∠ABC的度数是：80°或100°．故选D．二、填空题7．【答案】它们所对应的其余各组量也分别相等；8.【答案】＜【解析】如图，∵=2，∴=，∴AC=BC，在△ABC中，AC+BC＞AB，∴AB＜2AC，故答案为：＜．9．【答案】60°；10．；11．【答案】；【解析】如图，设AB＝x，在Rt⊿AOD 中:x²+（2x）²＝5²，x＝, 即AB的长＝.第11题 第12题12．【答案】90° ； 【解析】如图，连结AB 、BC ，则∠CAD + ∠EBD +•∠ACE=∠CBD +∠EBD +•∠ABE=∠ABC=90°.三、解答题13.【答案与解析】BE=CF ．理由：∵AE 为⊙O 的直径，AD ⊥BC ，∴∠ABE=90°=∠ADC ，又∠AEB=∠ACB ，∴∠BAE=∠CAF ，∴．∴BE=CF ．14.【答案与解析】BE CF解：（1）∵OA=OD，∠D=70°，∴∠OAD=∠D=70°，∴∠AOD=180°﹣∠OAD﹣∠D=40°，∵AB是半圆O的直径，∴∠C=90°，∵OD∥BC，∴∠AEO=∠C=90°，即OD⊥AC，∴=，∴∠CAD=∠AOD=20°；（2）∵AC=8，OE⊥AC，∴AE=AC=4，设OA=x，则OE=OD﹣DE=x﹣2，∵在Rt△OAE中，OE2+AE2=OA2，∴（x﹣2）2+42=x2，解得：x=5，∴OA=5，∴AB=2OA=10．15.【答案与解析】(1)如图，作OH ⊥CD 于H ，利用梯形中位线易证OF=OE ，OA=OB ， 所以AF=BE ，AF+EF=BE+EF ，即AE=BF ．(2)四边形CDEF 的面积是定值. 连结OC ，则， ＝54(cm 2)．11()2O 6922S CF DE CD H CD =+⋅=⋅⋅⋅=⨯。

垂径定理圆心角圆周角练习1.如图．⊙O中OA⊥BC，∠CDA=25o，则∠AOB的度数为_______．2.如图．AB为⊙O的直径，点C、D在⊙O上，∠BAC=50o．则∠ADC=_______．第1题第2题第3题3.如图，点A、B、C都在⊙O上，连结AB、BC、AC、OA、OB，且∠BAO=25°，则∠ACB的大小为___________.第4题第5题4.已知：如图，四边形ABCD是⊙O的内接四边形，∠BOD=140°，则∠DCE=.5、如图，AB是⊙O的直径，C,D,E都是⊙O上的点，则∠1＋∠2=.6、⊙O中，若弦AB长22cm，弦心距为2cm，则此弦所对的圆周角等于．7、已知AB是⊙O的直径，AC,AD是弦，且AB=2,AC=2，AD=1，则圆周角∠CAD的度数是()A.45°或60°B.60°C.105°D.15°或105°8、如图，AB是⊙的直径，弦CD垂直平分OB，则∠BDC=（）A.20°B.30°C.40°D.50°9、如图，点A、B、C为圆O上的三个点，∠AOB=的度数．13∠BOC,∠BAC=45°，求∠ACB 10、如图，AD是∆ABC的高，AE是∆ABC的外接圆的直径．试说明狐B E CF。

DF11、如图，AB,AC是⊙O的两条弦，且AB=AC．延长CA到点D．使AD=AC，连结DB并延长,交⊙O于点E．求证：CE是⊙O的直径．12、已知：如图，AB为⊙O的直径，AB=AC，B C交⊙O于点D，AC交⊙O于点E，∠BAC=45°．（1）求∠EBC的度数；（2）求证：BD=CD．△13．如图所示，ABC为圆内接三角形，A B＞AC，∠A的平分线AD交圆于D，作D E⊥AB于E，D F⊥AC于F，求证：BE=CFAEB CFD△14．如图所示，在ABC中，∠BAC与∠ABC的平分线AE、BE相交于点E，延长AE交△ABC的外接圆于D点，连接BD、CD、CE，且∠BDA=60°（1）求证△BDE是等边三角形；（2）若∠BDC=120°，猜想BDCE是怎样的四边形，并证明你的猜想。