辽宁省葫芦岛市五校协作体2014-2015学年高一下学期期中数学试卷
- 格式:doc
- 大小:646.00 KB
- 文档页数:20

2012---2013学年度上学期省五校协作体高一期中考试英语试题第一部分:第一节:单项填空(共15小题;每小题1.分,共15分)从每题所给的A、B、C、D四个选项中,选出可以填入空白处的最佳选项,并在答题卡上将该项涂黑。
21.—Why do you suggest the West Lake?—I believe __beauty of nature there will make __excellent impression upon you.A.the; the B.the; / C.a; an D.the; an22. Hurry up! The train _____ .You know it _____ at 10:30a.m.A leaves; leavesB is leaving; leavesC leaves; is leavingD is leaving; leaving23. The new castle being built for fun will be _____ the present one。
A three times more than size ofB as three times big asC bigger three times thanD three times as big as24. It is the second time that I ____ in Shanghai. What great changes! It’s years since I ____ herelast time.A went; had leftB had been; leftC have; had leftD have been; left25. Internet shopping will really _____ when people believe that it is safe.A. take offB. take upC. get offD. get up26. China recently control its waters near the HuangYan Island to prevent Chinese fishing boatsfrom ____in the South China SeaA. attackingB. having attackedC. being attackedD. having been attacked27 Was it at the school gate, if I may ask, _______ you met your friends from your hometown?A. whereB. thatC. whichD. ones28 .The Great Wall travels______ deep valleys, _____ deserts and______ mountains.A. over; across; throughB. through; across; overC. across; over; throughD. through; across; across29. Among the competitors, there are three little girls, is Mary.A.the smallest of whom B.the smaller of whomC.the smallest of them D.the smallest one30. As we all know, typing is a ___job to a__ heart.A tired ,tired B. tired ,tiring C.tiring,tired D. tiring,tiring31 The people living in these apartments have free ___to the swimming pool.A timeB entranceC chargeD access32. _____ I do feel pity, I can’t really do ver y much to help them out of the difficulty.A. As long asB. AsC. whileD. Even33. The plan he _____ at the meeting is under consideration now and the result will be____ soon.A. put up with; put upB. came up with; come upC. put forward; put upD. came up with; come out34–--Do you have enough to _____ all your daily expenses?----Oh, yes, enough and to spare.A spendB affordC fillD cover35. -----What a fine day! Shall we go picnicking?------_____________,b ut we need to be home before six o’clock for the football match. .A. Have a nice time.B. Pardon meC. That’s greatD. You are right第二节完形填空(共20小题;每小题1.5分,满分30分)阅读下面短文,从短文后各题所给的从四个选项中(A、B、C和D),选出可以填人空白处的最佳选项,并在答题卡上将该项涂黑。
辽宁省五校协作体2014-2015学年高二上学期期中考试数学文试题一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1. 命题“任意x R ∈,都有012>++x x ”的否定为( )A .对任意x R ∈,都有012≤++x xB .不存在x R ∈,都有012≤++x xC .存在x R ∈,使得012>++x xD .存在x R ∈,使得012≤++x x2. 某高级中学有高一、二、三三个年级的学生共1600名,其中高三学生400名,如果通过分层抽样的方法从全体高中学生中抽取一个容量为80人的样本,则应从高三年级学生中抽取的人数是( )A .40B .30C .20D .10 3. 原命题:“设a 、b 、c R ∈,若22ac bc >则a b >”和它的逆命题、否命题、逆否命题这四个命题中,真命题共有 ( ) A .1个 B .2个 C .3个 D . 0个 4. 执行下边的程序框图,若0.8p =,则输出的n =( )A .5B .2C .3D .45. 若动点),(y x M 到点)0,4(F 的距离等于它到直线04=+x 距离,则M 点的轨迹方程是 ( )A .04=+xB .04=-xC .28y x =D .216y x =6.函数3()1f x x ax =-+在区间),2[+∞内是增函数,则实数a 的取值范围是( ) A. 12a ≤ B. 12a < C. 12a ≥ D. 12a >7. 与椭圆 2216x y +=共焦点,且渐近线为2y x =±的双曲线方程是 ( )A .2214y x -= B .2214x y -= C .2214x y -= D .2214y x -= 8. 已知a R ∈,则“22a a >”是“2a >”的 ( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件9.已知21,F F 是椭圆191622=+y x 的两焦点,过点2F 的直线交椭圆于点,A B , 若5AB =,则12||||AF BF -=( )A.3B.8C.13D.1610.过抛物线x y 42=的焦点作直线交抛物线于),(),,(2211y x B y x A 两点,如果21x x +=6,那么AB =( )A. 10B. 9C. 8D. 611. 已知点F 是双曲线)0,0(12222>>=-b a by a x 的左焦点,点E 是该双曲线的右顶点,过F 且垂直于x 轴的直线与双曲线交于B A ,两点,若ABE ∆是锐角三角形,则该双曲线的离心率e 的取值范围是 ( )A .),1(+∞B .)2,1(C .)21,1(+D .)21,2(+12. 已知动点()P x y ,在椭圆22:12516x y C +=上,F 为椭圆C 的右焦点,若点M 满足||1MF =u u u r 且0MP MF ⋅=u u u r u u u r,则||PM u u u u r 的最小值为( )A .3B .3C .512 D . 1二.填空题:本大题共4小题,每小题5分13. 设抛物线的顶点在原点,准线方程为2x =,则抛物线方程为__________.14. 设变量y x ,满足约束条件⎪⎩⎪⎨⎧≤-≥+≥+-03005x y x y x ,则目标函数x y z -=2的最小值为________.15. 已知命题:p “0],2,1[2≥-∈∀a x x ”,命题:q “022,2=-++∈∃a ax x R x 使”,若命题“q p ∧”是真命题,则实数a 的取值范围是__________________ .16. 与圆()221:31C x y ++=,圆()222:39C x y -+=同时外切的动圆圆心的 轨迹方程是__________________________.三.解答题:解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分10分)设命题p 实数x 满足0)3)((<--a x a x ,其中0a >, 命题:q 实数x 满足023≤--x x . (1)若1,a =且q p ∨为假,求实数x 的取值范围; (2)若p 是q 的必要不充分条件,求实数a 的取值范围.18.(本小题满分12分)在ABC ∆中,角C B A ,,所对边分别为a 、b 、c ,ABC ∆的外接圆半径且满足bca B C -=2cos cos .(1)求角B 的大小;(2)求ABC ∆的面积的最大值.19.(本小题满分12分)已知数列{}n a 的前n 项和n n S n 22-=.(1)求数列{}n a 的通项公式n a ; (2)令3nn na b =,求数列{}n b 的前n 项和n T .20.(本小题满分12分)已知函数)(ln )(R a x a x x f ∈-=(1)当2=a 时,求曲线)(x f y =在点))1(,1(f A 处的切线方程; (2)讨论函数)(x f 的单调性与极值.21.(本小题满分12分)椭圆)0(1:2222>>=+b a by a x C 的离心率为12,其右焦点到点)1,3(-P的距离为17.(1)求椭圆C 的标准方程;(2)若直线:l y kx m =+与椭圆C 相交于A ,B 两点(A B ,不是左右顶点),且以AB 为直径的圆过椭圆C 的左顶点.求证直线l 过定点,并求出该定点的坐标.22.(本小题满分12分)设()ln af x x x x=+,32()3g x x x =--. (1)当]2,0[∈x 时,求)(x g 的最大值和最小值;(2)如果对任意的1,[,2]2s t ∈,都有()()f s g t ≥成立,求实数a 的取值范围.2014——2015学年度上学期省五校协作体高二期中考试数学(文科)参考答案一、选择题二、填空题13、x y 82-= 14、—9 15、}12|{=-≤a a a 或 16、()22108y x x -=< 三、解答题17、解:(1)由0)3)((<--a x a x ,0>a 得a x a 3<<当1=a 时,31<<x ,即p 为真时,实数x 的取值范围是31<<x …… 1分 由023≤--x x ,得32≤<x ,即q 为真时,实数x 的取值范围是32≤<x ……3分若q p ∨为假,则p 假,q 假,所以⎩⎨⎧>≤≥≤3231x x x x 或或,…………… 4分所以实数x 的取值范围是:31>≤x x 或.…………… 5分 (2)Θp 是q 的必要不充分条件,q p p q /,⇒⇒∴设集合}3|{},32|{a x a x B x x A <<=≤<=,则B A ≠⊂…………… 6分⎪⎩⎪⎨⎧>≤>∴3320a a a ,…………… 8分解得,21≤<a因此,实数a 的取值范围是21≤<a .…………… 10分18、解:(1)[方法一]:由正弦定理得:BCA B C sin sin sin 2cos cos -=B AC B C B cos sin 2sin cos cos sin =+∴B AC B cos sin 2)sin(=+∴B A A cos sin 2sin =∴ 21cos 0sin =∴≠B A Θ…………… 4分 30ππ=∴<<B B Θ……………6分[方法二]:由余弦定理得:b ca b c a ac ab c b a -=-+⋅-+222222222ac b c a =-+∴222212222=-+∴ac b c a 21cos =∴B ………… 4分 30ππ=∴<<B B Θ ………… 6分(2)[方法一]:B ac ac B ac c a b cos 22cos 2222-≥-+=Θ………… 8分921229cos 222=⨯-=-≤∴Bb ac ………… 10分.43923921sin 21=⨯⨯≤=∴∆B ac S ABC ………… 12分 [方法二]:C B A R B ac S ABC sin sin sin )2(21sin 212⋅⋅⋅⋅==∆433)62sin(233)32sin(sin 33+-=-=ππA A A ……… 8分ππππ67626320<-<-∴<<A A Θ1)62sin(21≤-<-∴πA ……… 10分.439,31)62sin(max ===-∴∆ABC S A A 时即当ππ……… 12分 19、解:(1)当1=n 时,12111-=-==S a ………… 2分当2≥n 时,32)]1(2)1[(2221-=-----=-=-n n n n n S S a n n n (4)分又31211-⨯=-=a 也符合上式,………… 5分 因此,32-=n a n ………… 6分(2)nn n b 332-=n n n n n T 31)32(31)52(313311311132⨯-+⨯-++⨯+⨯+⨯-=-Λ……………. ③143231)32(31)52(31331131131+⨯-+⨯-++⨯+⨯+⨯-=n n n n n T Λ……… ④③-④得13231)32()313131(23132+⨯--++++-=n n n n T Λ…………………… 9分整理得 n n nT 3-=…………………… 12分20、解:(1)2a =时,()2ln f x x x =-,2()1f x x'=-, ∴(1)1k f '==-, (2)分又(1)1f =,故切线方程为:11(1)y x -=--即2y x =-+.…… 4分 (2)函数()f x 的定义域为(0,)+∞,xax x a x f -=-='1)( …… 6分 ① 当0a ≤时,()f x 在(0,)+∞上单调递增,无极值;…… 9分 ② 当0a >时,()f x 在(0,)a 上单调递减,在(,)a +∞上单调递增,()ln f f a a a a ==-极小, 无极大值. …… 12分21、解 (1)由题12c e a ==;①右焦点)0,(c 到点)1,3(-P 的距离为171)3(22=++c . ② 由①②可解得222431a b c ===,,. ………2分∴所求椭圆C 的方程为22+143x y = ………4分 (2)设1122(,),(,)A x y B x y ,由22143y kx m x y =+⎧⎪⎨+=⎪⎩得 222(34)84(3)0k x mkx m +++-=,22226416(34)(3)0m k k m ∆=-+->,22340k m +->.212122284(3),.3434mk m x x x x k k-+=-⋅=++ ………6分 22221212121223(4)()()().34m k y y kx m kx m k x x mk x x m k -⋅=+⋅+=+++=+Q 以AB 为直径的圆过椭圆的左顶点)0,2(-D ,因此0=⋅即0)2)(2(2121=+++y y x x ,展开得04)(2212121=++++y y x x x x043)4(34431643)3(4222222=+-+++-+-k k m k mk k m0416722=+-k mk m ………9分解得 k m 2=或72k m =,且满足22340k m +->………10分 当k m 2=时,)2(:+=x k y l ,直线过定点)0,2(-,与已知矛盾;………11分当72k m =时,)72(:+=x k y l ,直线过定点)0,72(-. 综上可知,直线l 过定点,定点坐标为)0,72(-.………12分22、解:(1) 对于函数32()3g x x x =--, ]2,0[∈x22'()323()3g x x x x x =-=-,令0)(='x g ,得0=x 或32=x ………2分 当x 变化时,)(),(x g x g '变化情况如下表:由上表可知: min max 285()(),()(2)1327g x g g x g ==-==,………6分 (2)由(1)知,在区间1[,2]2上,()g x 的最大值为(2)1g =.因此,原问题等价于当1[,2]2x ∈时,()ln 1af x x x x=+≥恒成立 等价于2ln a x x x ≥-恒成立,记2()ln h x x x x =-,'()12ln h x x x x =--, '(1)0h =………8分记()12ln m x x x x =--,'()32ln m x x =--,由于1[,2]2x ∈,'()32ln 0m x x =--<, 所以()'()12ln m x h x x x x ==--在1[,2]2上递减,当1[,1)2x ∈时,'()0h x >,(1,2]x ∈时,'()0h x <,即函数2()ln h x x x x =-在区间1[,1)2上递增,在区间(1,2]上递减,所以max ()(1)1h x h ==,………10分 所以1a ≥. L L L L 12分。

辽宁省沈阳市五校协作体2024-2025学年高一上学期期中联考数学试题学校:___________姓名:___________班级:___________考号:___________A.1B.2C.3D.08.已知集合{}U=,若A,B是U的两个非空子集,记满足“A中元素的最小值大1,2,3,4于B中元素的最大值”为集合对(,)A B,则所有集合对(,)A B的个数为()A.16B.17C.18D.19C.若()35++=则()f x xx xf x为R上的“弱增函数”D.若()()a= 24f x x a x a=+-+在区间(]0,2上是“弱增函数”,则4故()f x 不是奇函数也不是偶函数,故①、②错误;结合其周期性可得()f x 的值域为{}0,1,故③正确;令010x -+=可得1x =,令110x -+=可得2x =,又()10f =,()21f =,故函数()g x 有两个不同的零点1,2,故④正确.故选:B.8.B【分析】根据题意,分类讨论A 中元素的最小值为1,2,3,4时的情况,即可得到答案.【详解】当A 中元素的最小值为1时,不符合题意.当A 中元素的最小值为2时,集合A 为:{}{}{}{}2,2,3,2,4,2,3,4,集合{}1B =,集合对(,)A B 的个数为4,当A 中元素的最小值为3时,集合A 为:{}{}3,3,4,集合B 为{}{}{}1,2,1,2,集合对(,)A B 的个数为6,当A 中元素的最小值为4时,集合A 为:{}4,集合B 为{}{}{}{}{}{}{}1,2,3,1,2,1,3,2,3,1,2,3,集合对(,)A B 的个数为7,综上:所有集合对(,)A B 的个数为46717++=.故选:B 9.AB【分析】结合指数函数的单调性解得a b £,然后由不等式性质逐项分析各选项即可;【详解】由31a b -£,即033a b -£,所以0a b -£,则a b £,故A 正确,则()()()00002f f f +=+-,于是()02f =,令2,2-==y x ,则()()()()022222f f f f =-=+--,又()23f -=,则()21f =;(2)()f x 是R 上的单调递减函数.证明:任取,R,m n m n Î<,则()()()()()()()()()22f m f n f m n n f n f m n f n f n f m n -=-+-=-+--=--,由于当0x <时,()2f x >,易知0m n -<,则()2f m n ->,故()()f m f n >,可得()f x 是R 上的单调递减函数.(3)不等式可化为()()()2212222f x f t t m t t f --éù-£+-++-ëû,也即()()22122f x f t t m t t --éù£+-++ëû,令1a t t -=+于是][3,3,5,7x m "Î-"Îéùëû,都有()()22f x f a ma £-恒成立,由于()f x 为R 上的单减函数,则][3,3,5,7x m "Î-"Îéùëû,都有22x a ma ³-恒成立,可知0t=或1t³时,每一个t 要使原方程有3个不等实根,①(*)式一根为零,另一根在。

2014——2015学年度上学期省五校协作体高一期中考试英语试题注意事项:1.本试卷分第卷和第卷两部分。
答卷前,考试务必将自己的姓名、准考证号填写在答题卡上。
2.作答时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和卡题卡一并交回。
第二部分阅读理解(共两节,满分40分)第一节(共15小题;每小题2分,满分30分)阅读下列短文,从每题所给的四个选项(A, B, C和D)中.选出最佳选项,并在答题卡上将该项涂黑。
ASometimes two very different individuals (个体)become the best friends. For example,, who could have thought that a spider would become friends with a pig? But in American writer E.B.White’ novel Charlotte’s Web, this is exactly what happensWibur the pig grows up in a barn(谷仓) and makes many friends, including a spider called Charlotte. One day a sheep tells Wibur that he will finally be served up as dinner. But Charlotte decides to save her friend. To help Wibur,Charlotte writes words like “terrific”, “radiant”and “humble”on her web to praise Wibur. This makes the farmer believe that is too important to kill.Wibur is saved, but Charlotte is so tired that she dies.The book was first published in 1952. In over 60 years Charlotte has become one of the most famous spiders of all time. She teaches us about love and promise. “She is very, very loving under that crusty(暴躁),that ugly look,”Peter Neumeyer, writer of The Annotated Charlott’s Web The book’s success drew the attention of Hollywood filmmakers , however, they wanted a happier ending. White was strongly against this idea and as a result the film, like the book, ends with Charlotte’s death.Jen Doll, reporter with The Atlantic, believe that “death is a part of life”. She says this is one of the main messages of the book.As Charlotte tells Wibur, “You have been my friend. That in itself is a wonderful thing. I wove(纺织)my webs for you because I like you. After all, what’s a life, anyway? We’re born, we live a little while and then we die. A spider’s life can’t help being something of a mess(杂乱), with all this trapping and eating flies. By helping you, perhaps I was trying to lift up my life a little. God knows anyone’s life can stand a little of that.”21.Which of the following about the story is TRUE?A.It’s a good example of how differences make us differentB.It encourages children to love their family and friendsC.The farmer kills Wibur as dinnerD.Charlotte is loving and helpful although she is ugly22.What is the disagreement about Charlotte’s Web between Hollywood filmmaker and White?A.How Charlotte makes friends with WiburB.How to make Charlotte lovelyC.Whether Charrlotte should dieD.Whether Wibur should be killed23.In the last paragraph, Charlotte’s main message is that _________A.life could be boring and troublesomeB.friendship is more important than lifeC.dying for a good cause is worthwhile(值得的)D.life is like a webBElizabeth and I are 18 now, and about to graduate. I think about our elementary school friendship, but some memories have blurred(模糊). What happened that day in the fifth grade when Beth suddenly stopped speaking to me? D oes she know that I’ve been thinking about her for seven years? If only we could go back, and discover what ended our relationship.I have to speak with Beth. I see her sometimes, and find out school is “fine”. It’s not the same. It nvever will be. Someone says that she’s Liz now. what happened to Beth?I can’t call her. Should I write? What if she doesn’t answer me? How will I know what she’s thinking?Yes, I’ll write her a letter. These things are easier to express in writing. “Dear Be-,” no, “Dea r Li-” no, “Dear Elizabeth,” I begin. The words flow freely, as seven-year-old memories are reborn. I ask her all the questions that have been left unanswered in my mind, and pray she will answer. I seal my thoughts in the perfect white envelope, and imagine Beth looking into the mailbox. Will she know why I’m writing? Maybe she once thought of writing the same letter.As the mailman takes my envelope from me forever, I wonder if I’ve made the right decision. Do I have the right to force myself into Bet h’s life again? Am I simply part of the past? I have taken the first stop. Beth has control of the situation now.One day has passed. Are my words lying on the bottom of the post office floor.Two days are gone. I’m lost in thought and don’t even he ar the phone ring.“Hello? It’s Elizabeth”24.What can we learn about Beth?A. She had a quarrel with the author in the fifth gradeB. She moved to another school in the fifth gradeC. She is now called Liz instead of BethD. She hasn’t seen the auth or for seven years25.Why does the author decide to write a letter instead of calling?A. She is sure that Beth will not answerB. She’s afraid that they’ll quarrel on the phoneC. She doesn’t know Beth’s telephone numberD. It is easier to express her feelings in writing26.What does the underlined sentence mean in the fifth paragraph?A .It’s up to Beth to decide what to do nextB .Beth is to be blamed for the ending of their friendshipC. Beth is in the same situation as the author isD .The author is completely in the hands of Beth now27.What might happen at the end of the story?A. Beth answers her letter two day laterB. The letter doesn’t reach Beth at allC. They make up their friendshipD. Beth refuses to make peace with herCThere are thousands of products of all colors and shapes in a supermarket, making you believe that they are worth a try. How? Packaging is the silent but persuading salesman.There on the shelves, each bottle, can ,box, and jar has been carefully designed and measured to speak to the inner self of the consumer, because he/she is buying not only a product but also his/her belief in life. Scientists have studied consumer behavior recently and found that the look of the package has a great effect on the “quality” of the product and on how well it sells, because “consumers generally cannot tell between a product and its package. Many products are packages and many packages are products.”, as Louis Cheskin, the first social scientist studying consumers’ feelings for packaging, noticed.Colors are one of the best tools in packaging. Studies of eye movement have shown that colours draw human attention quickly. Take V8 for example. For many years, the bright red color of tomatoes and carrots on the thin bottle makes you feel that is it very good for your body. And the word“green” today can keep food prices going up.Shapes are another attraction. Circles often suggest happiness and peacefulness, because these shapes are pleasing to both the eye an d the heart. That’s why the round yellow M signs of McDonald’s are inviting to both young and old.This new consumer response to the colors and shapes of packages reminds producers and sellers that people by to satisfy both body and soul.28.According to the passage, _____ seems to be able to persuade a consumer to buy the product.A.the pleasing color of the packageB. he special taste of the productC. the strange shape of the packageD. the belief in the product29.If a package or a product is round in shape, it can ____________.A. bring excitement to the consumersB. attract the consumers’ attentionC. catch the eye movement of the consumersD produce a happy and peaceful feeling30.“And the word green today can keep food prices going up ” This sentence suggests thatconsumers today are _________.A. starting to notice the importance of new foodB. enjoying the beauty of nature more than beforeC. beginning to like green vegetablesD. paying more attention to their health31.It can be inferred from the passage that V8 is a kind of ________.A vegetable dish B. healthy juice C. iced drink D red vegetableDTayka Hotel de SalWhere:Tahua,BoliviaHow much:About $95 a nightWhy it’s cool:You’ve stayed at hotels made of brick or wood,but salt?That’s something few can claim.Tayka Hotel de Sal is made totally of salt—including the beds (though you’ll sleep on regular mattresses(床垫) and blankets).The hotel sits on the Salar de Uyuni,a prehistoric dried-up lake which is the world’s biggest salt flat.Builders use the salt from the 4,633-square-mile flat to make the bricks,and glue them together with a paste (糊) of wet salt that hardens when it dries.When rain starts to dissolve the hotel,the owners just mix up more salt paste to strengthen the bricks.Green Magic Nature ResortWhere:Vythiri,IndiaHow much:About $240 a nightWhy it’s cool:Taking a pulley(滑轮)-operated lift 86 feet to your treetop room is just the start of your adventure.As you look out of your open window—there is no glass!—you watch monkeys and birds in the rain forest canopy(罩篷).Later you might test your fear of heights by crossing the handmade rope bridge to the main part of the hotel,or just sit on your bamboo bed and read.You don’t even have to come down for breakfast—the hotel will send it up on the pulley-drawn “elevator”.Dog Bark Park Inn B&BWhere:Cottonwood,IdahoHow much:$92 a nightWhy it’s cool:This doghouse isn’t just for the family pet.Sweet_Willy is a 30-foot-tall dog with guest rooms in his belly.Climb the wooden stairs beside his hind leg to enter the door in his side.Youcan relax in the main bedroom,go up a few steps of the loft(阁楼) in Willy’s head,or hang out inside his nose.Although you have a full private bathroom in your quarters,there is also a toilet in the 12-foot-tall fire hydrant(消防栓) outside.Gamirasu Cave HotelWhere:Ayvali,TurkeyHow much:Between $130 and $475 a nightWhy it’s cool:This is caveman cool!Experience what it was like 5,000 years ago,when people lived in these mountain caves formed by volcanic ash.But your stay will be much more modern.Bathrooms and electricity provide what you expect from a modern hotel,and the white volcanic ash,called tufa,keeps the rooms cool,’t worry—there is heat in winter.)32.What do we know about Tayka Hotel de Sal?A.It is located on a prehistoric lake.B.It should be protected against the rain.C.Everything in the hotel is made of salt.D.You have to cross a rope bridge to the hotel.33.What is the similarity of the four hotels?A.Being expensive.B.Being comfortable.C.Being natural.D.Being unique.34.What does the underlined words “Sweet Willy” refer to?A.The name of the hotel.B.The name of the hotel owner.C.The building of Dog Bark Park Inn B&B.D.The name of a pet dog of the hotel owner.35.Which of the hotels makes you have a feeling of living in the far past?A.Tayka Hotel de Sal.B.Green Magic Nature Resort.C.Dog Bark Park Inn B&B.D.Gamirasu Cave Hotel.第二节(共5小题;每小题2分, 满分10分)根据短文内容,从短文后的选项中选出能填入空白处的最佳选项,并在答题卡上将该项涂黑。

2021-2022学年辽宁省沈阳市五校协作体高一下学期期中数学试题一、单选题1.()sin 600tan240-︒+︒=( )A .BC .12D .12-【答案】B【分析】根据已知条件,利用诱导公式化简即可求解. 【详解】解:()()()sin 600tan 240sin 2360120tan 18060-︒+︒=-⨯+︒+︒︒+︒sin120tan 60=︒+︒=+=, 故选:B.2.已知平面向量,a b ,满足()25a a b ⋅-=,且2,3a b ==,则向量a 与向量b 的夹角余弦值为( ) A .1 B .-1 C .12D .-12【答案】C【分析】利用平面向量的数量积运算性质即可得出.【详解】平面向量,a b ,满足()25a a b ⋅-=,且2,3a b ==, ∴252cos ,a a b a b =-<>,解得25221cos ,232a b -⨯<>==-⨯.故选:C【点睛】本题考查了平面向量的数量积和夹角公式,属于基础题.3.在ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,2a =,c =,30A =︒,则角C 为( ) A .60° B .60°或120° C .45° D .45°或135°【答案】B【分析】利用正弦定理进行转化求解即可.【详解】解:由正弦定理得sin sin a c A C =得212=sin C =c a >,C A ∴>,得60C =︒或120︒, 故选:B .【点睛】本题主要考查解三角形的应用,利用正弦定理进行求解是解决本题的关键.比较基础.4.要得到函数()cos 23f x x π⎛⎫=+ ⎪⎝⎭的图象,只需将函数()sin 23g x x π⎛⎫=+ ⎪⎝⎭的图象( )A .向左平移2π个单位长度 B .向右平移2π个单位长度 C .向左平移4π个单位长度D .向右平移4π个单位长度【答案】C【分析】先将函数()f x 的化为正弦型函数,在将函数()f x 的解析式表示为()()sin 23f x x πϕ⎡⎤=++⎢⎥⎣⎦,并结合ϕ的符号与绝对值确定平移的方向与长度.【详解】由诱导公式可得()cos 2sin 2sin 232343f x x x x πππππ⎡⎤⎛⎫⎛⎫⎛⎫=+=++=++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,因此,只需在将函数()sin 23g x x π⎛⎫=+ ⎪⎝⎭的图象向左平移4π个单位长度,即可得到函数()cos 23f x x π⎛⎫=+ ⎪⎝⎭的图象,故选C .【点睛】在考查两个三角函数平移的过程中,需注意以下两个问题; ①两个函数的名称一定要一致;②左右平移法则中的“左加右减”指的是在自变量x 上变化了多少.5.已知1sin()33πα-=,则sin(2)6πα-=A .79B .79-C .79±D .29-【答案】B【分析】由题意,利用诱导公式和二倍角的余弦函数公式,即可计算得到答案.【详解】因为1sin()cos[()]cos()32363ππππααα-=--=+=,∴217sin(2)cos[(2)]cos[2()]2cos ()1216266699πππππαααα-=--=+=+-=⨯-=-,故选B .【点睛】本题主要考查了三角函数的化简求值问题,其中熟记三角函数的诱导公式和二倍角的余弦公式的合理运用是解答的关键,着重考查了计算能力和转化思想,属于基础题.6.已知)1tan10sin100cos100,cos 44cos 78cos 46cos12,1tan10M N P -︒=︒-︒=︒︒+︒︒=+︒,()()11tan 221tan 232Q =+︒+︒,那么M ,N ,P ,Q 之间的大小顺序是( ) A .M N P Q <<< B .P Q M N <<< C .N M Q Р<<< D .Q P N M <<<【答案】B【分析】由辅助角公式可得()10045451M =︒-︒=︒>︒=,逆用两角和的正弦公式可得()4412N M =︒+︒=︒>︒=,逆用两角差的正切公式可得()tan 4510tan35tan 451P =︒-︒=︒<︒=,利用两角和正切公式的变形可得()11tan 22tan 23tan 22tan 2312Q =+︒+︒+︒︒=,从而即可求解. 【详解】解:()sin100cos100sin100cos10010045M =︒-︒=︒-︒=︒-︒⎭55451=︒>︒=,))cos44cos78cos46cos12cos44sin12sin 44cos12N =︒︒+︒︒=︒︒+︒︒ ()4412M =︒+︒=︒>︒=, ()1tan10tan 45tan10tan 4510tan 35tan 4511tan101tan 45tan10P -︒︒-︒===︒-︒=︒<︒=+︒+︒︒,又()tan 22tan tan 11232223tan 22tan 23︒+︒-+︒=︒︒=︒,即tan 22tan 23tan 22tan 231︒+︒+︒︒=,所以()()()111tan 221tan 231tan 22tan 23tan 22tan 23122Q =+︒+︒=+︒+︒+︒︒=, 所以N M Q P >>>, 故选:B.7.若关于x 的方程22sin 210x x m +-=在0,2x π⎡⎤∈⎢⎥⎣⎦有两个不等实根,则实数m的取值范围是( )A .(B .[]0,2C .[)1,2D .⎡⎣【答案】C【分析】先化简三角函数为2sin 26y x m π⎛⎫=-++ ⎪⎝⎭,再由x 的范围,得到函数2sin 26y x π⎛⎫=-+ ⎪⎝⎭的值域,由此得到m 的取值范围.【详解】22sin 3sin 21cos 23sin 22sin 2=06x x m x x m x m π⎛⎫-+-=--+=-++ ⎪⎝⎭,方程22sin 3sin 210x x m -+-=在0,2x π⎡⎤∈⎢⎥⎣⎦有两个不等实根,即2sin 26y x π⎛⎫=+ ⎪⎝⎭与y m =的图象有两个交点,因为0,2x π⎡⎤∈⎢⎥⎣⎦,所以72,666x πππ⎡⎤+∈⎢⎥⎣⎦,所以[]2sin 21,26y x π⎛⎫=+∈- ⎪⎝⎭,要使方程22sin 3sin 210x x m -+-=在0,2x π⎡⎤∈⎢⎥⎣⎦有两个不等实根,如下图,即则12m ≤<.故选:C.8.将函数()cos 23f x x π⎛⎫=- ⎪⎝⎭的图象向左平移02πϕϕ⎛⎫<< ⎪⎝⎭个单位长度得到函数()g x 的图象,若1x ,2x 使得()()121f x g x =-,且12x x -的最小值为6π,则ϕ=( ). A .12πB .6πC .4π D .3π 【答案】D【分析】由三角函数平移变换可得()g x ,可确定()()1211f x g x ⎧=⎪⎨=-⎪⎩或()()1211f xg x ⎧=-⎪⎨=⎪⎩;在()()1211f xg x ⎧=⎪⎨=-⎪⎩时,可求得12,x x 的取值,由12min 6x x π-=可构造方程求得ϕ的值. 【详解】()()cos 223g x f x x πϕϕ⎛⎫=+=+- ⎪⎝⎭,()[]1,1f x ∈-,()[]1,1g x ∈-,∴若1x ,2x 使得()()121f x g x =-,则()()1211f x g x ⎧=⎪⎨=-⎪⎩或()()1211f x g x ⎧=-⎪⎨=⎪⎩,不妨设()11f x =,()21g x =-,则()111223x k k Z ππ-=∈,()2222223x k k Z πϕππ+-=+∈,解得:()1116x k k Z ππ=+∈,()22223x k k Z πϕπ=-+∈, ()()121212,2x x k k k k Z πϕπ∴-=-++-∈,12min 6x x π-=,即()()1212min,26k k k k Z ππϕπ-++-=∈,又02πϕ<<,∴当120k k -=时,226πππϕϕ-+=-=,解得:3πϕ=.故选:D.【点睛】关键点点睛:本题考查三角函数知识的综合应用,解题关键是能够通过函数值域确定12,x x 分别对应()(),f x g x 的最大值和最小值点,从而利用整体对应的方式构造方程确定12x x -的值. 二、多选题9.函数()sin()f x A x ωϕ=+(A ,ω,ϕ是常数,0A >,0>ω)的部分图象如图所示,下列结论正确的是( )A .(0)3f =B .在区间,02π⎡⎤-⎢⎥⎣⎦上单调递增C .()f x 的图象关于5(,0)6π中心对称 D .将()f x 的图象向左平移12π个单位,所得到的函数是偶函数【答案】ACD【分析】根据函数()f x 的部分图象求出函数解析式,然后根据正弦型函数的图象与性质,对各选项逐一分析即可得答案.【详解】解:由图可知2A =,33273441264T ππππω⎛⎫==--= ⎪⎝⎭,解得2ω=, 由五点作图法可得206πϕ⎛⎫⨯-+= ⎪⎝⎭,即3πϕ=,所以()2sin(2)3f x x π=+,对A :(0)2sin33f π==A 正确;对B :因为,02x ⎡⎤∈-⎢⎥⎣⎦π,所以22,333x πππ⎡⎤+∈-⎢⎥⎣⎦,而2sin y x =在2,32ππ⎡⎤--⎢⎥⎣⎦上单调递减,在,23上单调递增,所以()2sin(2)3f x x π=+在5,212ππ⎡⎤--⎢⎥⎣⎦上单调递减,在5,012π⎡⎤-⎢⎥⎣⎦上单调递增,故选项B 错误; 对C :因为55()2sin(2)0663f πππ=⨯+=,所以()f x 的图象关于5(,0)6π中心对称,故选项C 正确;对D :将()f x 的图象向左平移12π个单位,所得到的函数是2sin 22sin 22cos 21()232x x g x x πππ⎡⎤⎛⎫⎛⎫=++=+= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,又()()cos 2cos2()g x x x g x -=-==,所以()g x 为偶函数,故选项D 正确.故选:ACD.10.给出下列命题,其中正确的命题是( ) A .α∀∈R ,sin cos 1αα+>-; B .0α∃∈R ,003sin cos 2αα+=;C .α∀∈R ,1sin cos 2αα≤; D .0α∃∈R ,003sin cos 4αα=【答案】CD【解析】求出sin cos αα+、sin cos αα的值域后可得正确的选项.【详解】因为sin cos 2sin 2,24πααα⎛⎫⎡⎤+=+∈- ⎪⎣⎦⎝⎭,故A ,B 错误. 因为111sin cos sin 2,222ααα⎡⎤=∈-⎢⎥⎣⎦,故CD 正确.故选:CD.【点睛】本题考查二倍角的正弦、辅助角公式,注意利用三角变换公式把三角函数式整合成正弦型函数(或余弦型函数)的形式,从而可利用复合函数的方法来研究它们的性质,本题属于基础题.11.如图,在矩形ABCD 中,22AB AD ==,E 为边AB 的中点,若P 为折线段DEC 上的动点,则AP BP ⋅的可能取值为( )A .1-B .2-C .3-D .12-【答案】AD【分析】建立平面直角坐标系,利用坐标法求出数量积,再根据二次函数的性质求出AP BP ⋅的取值范围,即可得解;【详解】解:以D 为坐标原点,DC 所在直线为x 轴,DA 所在直线为y 轴,建立如图所示平面直角坐标系:则()0,1A ,()2,1B ,()2,0C ,()1,1E , 当P 在DE 上时,设(),P a a ,(01)a , 则(),1AP a a =-,()2,1BP a a =--,所以222(2)(1)2412(1)1AP BP a a a a a a ⋅=-+-=-+=--,因为01a ,所以[]22(1)11,1a --∈-,即[]1,1AP BP ⋅∈-.当P 在EC 上时,设(),2P a a -,(12)a , 则(),1AP a a =-,()2,1BP a a =--,所以222(2)(1)2412(1)1AP BP a a a a a a ⋅=-+-=-+=--,因为12a ,所以[]22(1)11,1a --∈-,即[]1,1AP BP ⋅∈-. 故选:AD12.已知ABC 的内角A ,B ,C 所对边的长分别为a ,b ,c ,已知O 为ABC 的外心,8,5b c ==,ABC 的面积S 满足()224,3b c a S AO AB AC λμ+-==+,则下列结论正确的是()A.S=B.AO=C.392AO BC⋅=D.71120λμ+=【答案】ACD【分析】cos1A A-=,利用两角差的正弦公式可得1sin()62Aπ-=,根据A为三角形的内角可得3Aπ=.再根据三角形的面积公式可求出三角形面积,知A正确;利用余弦定理求出a,再根据正弦定理可求出73 ||3 AO=知B不正确;根据O为三角形的外心可求出AO AB⋅和AO AC⋅,由此可求出AO BC AO AC AO AB ⋅=⋅-⋅392=,知C正确;将=AO AB ACλμ+两边分别同时乘以AB和AC,得到两个方程,解方程组可得2151124λμ⎧=⎪⎪⎨⎪=⎪⎩,知D正确.【详解】由22()b c a+-=得22212sin2b c a bc bc A+-+=,得22212b c aAbc+--,得cos1AA=-cos1A A-=,得1sin()62Aπ-=,因为0Aπ<<,所以5666Aπππ-<-<,所以66Aππ-=,所以3Aπ=,所以11sin8522S bc A==⨯⨯=A正确;由余弦定理得22212cos6425285492a b c bc A=+-=+-⨯⨯⨯=,所以7a=,所以2||sinaAOA==,所以73||3AO=B不正确;因为=AO AB ACλμ+,所以AO AB⋅||||cosAO AB OAB=⋅⋅∠1||2||||||ABAB AOAO=⋅⋅221125||222AB c===,||||cosAO AC AO AC OAC⋅=⋅∠1||2|||||ACAO ACAO=⋅⋅2211||3222AC b===,所以()AO BC AO AC AB AO AC AO AB⋅=⋅-=⋅-⋅25393222=-=,故C正确;又AO AB AB AB AB ACλμ⋅=⋅+⋅,所以251258522λμ=+⨯⨯,即2525202λμ+=,AO AC AB AC AC AC λμ⋅=⋅+⋅,所以13258642λμ=⨯⨯+,所以206432λμ+=,联立2525202206432λμλμ⎧+=⎪⎨⎪+=⎩,解得2151124λμ⎧=⎪⎪⎨⎪=⎪⎩,所以211711524120λμ+=+=,故D 正确.故选:ACD 三、填空题13.若1sin cos ,05αααπ+=<<,则sin 2cos2αα+=___________. 【答案】3125-【分析】将1sin cos 5αα+=两边同时平方可得242sin cos 025αα=-<,进而可得sin 0,cos 0αα><,7sin cos 5αα-==,联立方程可得43sin ,cos 55αα==-,从而根据二倍角公式即可求解.【详解】解:因为1sin cos 5αα+=①,所以两边同时平方得221sin 2sin cos cos 25αααα++=,即242sin cos 025αα=-<,因为0απ<<,所以2απ<<π, 所以sin 0,cos 0αα><,所以7sin cos 5αα-==②, 联立①②可得43sin ,cos 55αα==-,所以2231sin 2cos 22sin cos cos sin 25αααααα+=+-=-, 故答案为:3125-. 14.在函数tan 3y x π⎛⎫=- ⎪⎝⎭的图像对称中心中,与原点O 最近的为点M ,定点()1,1P ,则OP 在OM 上投影的数量是___________. 【答案】1-【分析】由正切函数的性质可得函数tan 3y x π⎛⎫=- ⎪⎝⎭的图像对称中心为,0,23k k Z ππ⎛⎫+∈ ⎪⎝⎭,进而可得,06M π⎛⎫- ⎪⎝⎭,从而利用向量数量积的几何意义即可求解OP 在OM上投影的数量为cos ,OM OM OMOP OP OP ⋅=.【详解】解:由题意,令,32k x k Z ππ-=∈,可得,23k x k Z ππ=+∈, 所以函数tan 3y x π⎛⎫=- ⎪⎝⎭的图像对称中心为,0,23k k Z ππ⎛⎫+∈⎪⎝⎭, 所以与原点O 最近的为点,06M π⎛⎫- ⎪⎝⎭,所以,06OM π⎝=⎛⎫- ⎪⎭,()1,1OP =,所以OP 在OM 上投影的数量为1016cos ,16OP OP OP OP OP OM OM OM OMP O O Mππ-⨯+⨯⋅⋅=⋅===-,故答案为:1-.15.设ABC ∆的内角A ∠、B 、C ∠的对边分别为a 、b 、c ,且满足3cos cos 5a B b A c -=.则tan tan AB=______. 【答案】4【详解】解法1 有题设及余弦定理得2222223225c a b b c a a b c ca bc +-+-⋅-⋅= 22235a b c ⇒-=.故222222tan sin cos 2tan sin cos 2c a b a A A B ca b c a B B A b bc +-⋅⋅==+-⋅⋅2222224c a b c b a +-==+-. 解法2 如图4,过点C 作CD AB ⊥,垂足为D .则cos a B DB =,cos b A AD =.由题设得35DB AD c -=.又DB DA c +=,联立解得15AD c =,45DB c =.故tan 4tan CDA DB AD CD B AD DB===.解法3 由射影定理得cos cos a B b A c +=. 又3cos cos 5a Bb Ac -=,与上式联立解得4cos 5a B c =,1cos 5b A c =.故tan sin cos cos 4tan sin cos cos A A B a B B B A b A⋅===⋅. 16.若函数()()24sin sin cos 21024x f x x x ωπωωω⎛⎫=++->⎪⎝⎭在,33ππ⎡⎤-⎢⎥⎣⎦内有且仅有一个最大值点,则ω的取值范围是___________. 【答案】90,2⎛⎫⎪⎝⎭【分析】根据降幂公式及二倍角余弦公式化简函数解析式为()2sin (0)f x x ωω=>,从而利用正弦型函数的图象与性质即可求解. 【详解】解:函数21cos 2()4sin sin cos 214sin cos 21242x x f x x x x x πωωπωωωω⎛⎫-+ ⎪⎛⎫⎝⎭=++-=+- ⎪⎝⎭ 221sin 4sin cos 212sin 2sin 12sin 12sin (0)2xx x x x x x ωωωωωωωω+=+-=++--=>,因为()f x 在,33ππ⎡⎤-⎢⎥⎣⎦内有且仅有一个最大值,且33ππ-=,0>ω,所以343T π>,即3243ππω⨯>,解得902ω<<, 所以ω的取值范围是90,2⎛⎫⎪⎝⎭,故答案为:90,2⎛⎫⎪⎝⎭.四、解答题17.已知()()tan ,1,1,2a b θ=-=-,其中θ为锐角,若a b +与a b -夹角为90°, (1)求()()3sin sin 23sin 2sin 2ππθθπθπθ⎛⎫-++ ⎪⎝⎭⎛⎫--+ ⎪⎝⎭的值(2)求1cos 2sin 2cos 2θθθ-+的值【答案】(1)17(2)8【分析】(1)依题意可得()()0a b a b +⋅-=,即可得到a b =,从而求出tan θ,再利用诱导公式将式子化简,最后利用同角三角函数的基本关系将弦化切,代入计算可得; (2)利用二倍角公式及同角三角函数的基本关系计算可得;【详解】(1)解:因为a b +与a b -夹角为90︒,所以()()0a b a b +⋅-=,即220a b -=,即220a b -=,即a b =,又()tan ,1a θ=-,()1,2b =-,即()()2222tan 112θ+-=+-,所以tan 2θ=±,又θ为锐角,所以tan 2θ=, 所以()()3sin sin 23sin 2sin 2ππθθπθπθ⎛⎫-++ ⎪⎝⎭⎛⎫--+ ⎪⎝⎭sin cos 3cos 2sin θθθθ-=+tan 121132tan 3227θθ--===++⨯(2)解:1cos 2sin 2cos 2θθθ-+()222112sin 2sin cos cos sin θθθθθ--=+-2222sin 2sin cos cos sin θθθθθ=+- 222tan 2tan 1tan θθθ=+- 222282212⨯==⨯+- 18.在①222cos sin sin sin cos C B C B A +=+②22cos b a C c =+这两个条件中任选一个,补充在下面的问题中并作答.在ABC 中,角A 、B 、C 所对的边分别是a 、b 、c ,___________. (1)求角A ﹔(2)若10a =,ABC 的面积为ABC 的周长. 【答案】(1)3π(2)24【分析】(1)如选择①,根据平方关系得到222sin sin sin sin sin B C A B C +-=,再由正弦定理将角化边,最后由余弦定理计算可得.选择②,由正弦定理将边化角,再利用诱导公式、和差公式即可得出.(2)由已知利用三角形的面积公式可求bc 的值,进而根据余弦定理可求b c +的值,进而可求ABC 的周长.【详解】(1)解:若选择①,由222cos sin sin sin cos C B C B A +=+, 得2221sin sin sin sin 1sin C B C B A -+=+-, 即222sin sin sin sin sin B C A B C +-=,由正弦定理得222b c a bc +-=, 由余弦定理得2221cos 22b c a A bc +-==,又(0,)A π∈, 所以3A π=.若选择②,因为22cos b a C c =+,由正弦定理可得2sin 2sin cos sin B A C C =+, 又A B C π++=,所以sin sin()B A C =+,则2sin()2(sin cos cos sin )2sin cos sin A C A C A C A C C +=+=+, 所以2cos sin sin A C C =. 由于(0,)C π∈,sin 0C ≠, 所以1cos 2A =,(0,)A π∈, 故3A π=.(2)因为3A π=,10a =,ABC 的面积为11sin 22bc A bc =⨯, 所以32bc =,由余弦定理2222cos a b c bc A =+-,可得2222100()3()332b c bc b c bc b c =+-=+-=+-⨯, 解得14b c +=,所以ABC 的周长101424a b c ++=+=.19.函数()2cos sin 3f x x x π=+⎫⎪⎭⎛⎝(1)求函数()f x 的单调增区间;(2)若锐角ABC 的三个角为A ,B ,C ,其中12B f ⎛⎫= ⎪⎝⎭,求()f A 的取值范围.【答案】(1)5,,1212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦(2)⎛⎫⎪ ⎪⎝⎭【分析】(1)利用两角和的正弦公式及降幂公式化简函数解析式为()sin 23f x x π⎛⎫=+ ⎪⎝⎭,解不等式222,232k x k k Z πππππ-≤+≤+∈即可得答案;(2)由12B f ⎛⎫= ⎪⎝⎭,可得6B π=,进而由ABC 为锐角三角形,可得32A ππ<<,从而利用正弦型函数的图象与性质即可求解()f A 的取值范围. 【详解】(1)解:函数()31332cos sin 2cos sin cos 32222f x x x x x x π⎛⎫=+-=+ ⎛⎫ ⎪⎝-⎪ ⎪⎝⎭⎭13sin 2cos 2sin 2223x x x π⎛⎫=+=+ ⎪⎝⎭, 由222,232k x k k Z πππππ-≤+≤+∈,可得5,1212k x k k Z ππππ-≤≤+∈, 所以函数()f x 的单调增区间为5,,1212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦; (2)解:因为12B f ⎛⎫= ⎪⎝⎭,即sin 13B π⎛⎫+= ⎪⎝⎭,因为ABC 为锐角三角形,所以02B π<<,所以5336B πππ<+<, 所以32B ππ+=,即6B π=,因为025062A C A πππ⎧<<⎪⎪⎨⎪<=-<⎪⎩,所以32A ππ<<,所以4233A πππ<+<所以3sin 2023A π⎛⎫-<+< ⎪⎝⎭, 所以()sin 23f A A π⎛⎫=+ ⎪⎝⎭的取值范围为3,02⎛⎫- ⎪ ⎪⎝⎭. 20.如图,在ABC 中,已知1,2,60.CA CB ACB ==∠=(1)求B ;(2)已知点D 是AB 上一点,满足,AD AB λ=点E 是边CB 上一点,满足BE BC λ=,是否存在非零实数λ,使得AE CD ⊥?若存在,求出λ的值;若不存在,请说明理由. 【答案】(1)30; (2)存在,23λ=. 【分析】(1)根据给定条件,结合向量数量积求出||AB ,再求出夹角B 作答. (2)假定存在满足条件的实数λ,利用向量的线性运算、数量积运算求解作答.【详解】(1)在ABC 中,AB CB CA =-,·21cos601CB CA =⨯⨯︒=, 则()222222221213AB CB CACB CA CB CA =-=+-⋅=+-⨯=,显然有222||||4||AB AC BC +==,于是得90BAC ∠=,9030B ACB =-∠=, 所以30B =.(2)假设存在非零实数λ,使得AE CD ⊥,由AD AB λ=,得()AD CB CA λ=-, 则()()1CD CA AD CA CB CA CB CA λλλ=+=+-=+-,又BE BC λ=,则()()()1AE AB BE CB CA CB CB CA λλ=+=-+-=--, 于是得()()2221(1)1AE CD CB CB CA CB CA CA λλλλλ⋅=--⋅+-⋅--()()2241(1)1320λλλλλλλ=--+---=-+=,而0λ≠,解得23λ=, 所以存在非零实数23λ=,使得AE CD ⊥. 21.某公园为了吸引更多的游客,准备进一步美化环境.如图,准备在道路AB 的一侧进行绿化,线段AB 长为4百米,C ,D 都设计在以AB 为直径的半圆上.设COB θ∠=.(1)现要在四边形ABCD 内种满郁金香,若3COD π∠=,则当θ为何值时,郁金香种植面积最大;(2)为了方便游客散步,现要铺设一条栈道,栈道由线段BC ,CD 和DA 组成,若BC =CD ,则当θ为何值时,栈道的总长l 最长,并求l 的最大值(单位:百米). 【答案】(1)当3πθ=时,郁金香种植面积最大;(1)当3πθ=为时,栈道的总长l 最长,l 的最大值为6百米.【分析】(1)求出利用三角形的面积公式可得四边形ABCD 关于θ的函数,利用三角函数的恒等变换可以得到“一角一函”的形式,然后根据角的范围利用正弦函数的性质可求得面积最大值;(2)利用余弦定理求得,BC DA 关于θ的三角函数,相加可求出l 关于θ的三角函数表达式,利用二倍角公式和换元思想转化为二次函数的最值,进而求解.【详解】解:(1)∵线段AB 长为4百米,所以圆的半径为2百米,即2OA OB OC OD ====, 当3COD π∠=时,由三角形的面积公式得:ABCD BOCCODDOAS S SS=++2221112sin 2sin 2sin 22323⎛⎫=⨯+⨯+⨯-- ⎪⎝⎭πθππθ6⎛⎫=+ ⎪⎝⎭θπ,203θπ∴<<,则5666ππθπ<+<,sin 16πθ⎛⎫∴+≤ ⎪⎝⎭,当62ππθ+=,即3πθ=时取等号,∴当3πθ=时,6⎛⎫+ ⎪⎝⎭πθ ∴当3πθ=时,郁金香种植面积最大;(2)由余弦定理得:4sin 2BC ==θ,4cos DA θ,8sin4cos 022l ⎛⎫∴=+<< ⎪⎝⎭θπθθ, 令sin2t θ=,∵024θπ<<,∴0t <<()2228sin412sin 2284121862l t t t ⎛⎫∴=+- ⎪⎝⎭=+-⎛⎫=--+ ⎪⎝⎭θθ,12t ∴=,即3πθ=时,l 的最大值为6. 故当3πθ=为时,栈道的总长l 最长,l 的最大值为6百米.22.已知向量()()3cos ,cos ,sin ,c s (o )a x x b x x R ωωωωω=-=∈,若函数()12f x a b =⋅+的最小正周期为π,且在06,π⎡⎤⎢⎥⎣⎦上单调递增. (1)求()f x 的解析式;(2)若关于x 的不等式22cos 22cos 2501212a fx x f x x a ππ⎡⎤⎡⎤⎛⎫⎛⎫++-+--≥ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦在,84ππ⎛⎤ ⎥⎝⎦上恒成立,求实数a 的取值范围.【答案】(1)()sin 26f x x π⎛⎫=- ⎪⎝⎭(2),⎛-∞ ⎝⎦【分析】(1)根据向量数量积的坐标运算及降幂公式和辅助角公式可得()sin 26f x x πω⎛⎫=- ⎪⎝⎭,由()f x 的最小正周期为π,可得1ω=±,又()f x 在06,π⎡⎤⎢⎥⎣⎦上单调递增,从而即可求解;(2)令sin 2cos 224t x x x π⎛⎫=-=- ⎪⎝⎭,(]0,1t ∈,则原不等式在,84x ππ⎛⎤∈ ⎥⎝⎦上恒成立,可化为()222250a t t a ---≥在(]0,1t ∈上恒成立,即2221t a t -≤+在(]0,1t ∈上恒成立,利用均值不等式求出(]20,2211,ty t t -=+∈的最小值即可得答案. 【详解】(1)解:因为向量()()3cos ,cos ,sin ,c s (o )a x x b x x R ωωωωω=-=∈,所以()2111cos 21cos cos 22222x f x a b x x x x ωωωωω+=⋅+=-+=-+12cos 2sin 226x x x πωωω⎛⎫-=- ⎪⎝⎭, 因为2|2|T ππω==,所以1ω=±, 当1ω=时,()sin 26f x x π⎛⎫=- ⎪⎝⎭, 此时()f x 在06,π⎡⎤⎢⎥⎣⎦上单调递增, 符合题意,当1ω=-时,()sin 2sin 266f x x x ππ⎛⎫⎛⎫=--=-+ ⎪ ⎪⎝⎭⎝⎭,此时()f x 在06,π⎡⎤⎢⎥⎣⎦上单调递减,不符合题意,综上,()sin 26f x x π⎛⎫=- ⎪⎝⎭;(2)解:由(1)可知sin 212f x x π⎛⎫+= ⎪⎝⎭,因为222(sin 2cos 2)sin 22sin 2cos 2cos 212sin 2cos 2x x x x x x x x +=++=+,222(sin 2cos 2)sin 22sin 2cos 2cos 212sin 2cos 2x x x x x x x x -=-+=-,所以222(sin 2cos 2)12sin 2cos 211(sin 2cos 2)2(sin 2cos 2)x x x x x x x x ⎡⎤+=+=+--=--⎣⎦,令sin 2cos 224t x x x π⎛⎫=-=- ⎪⎝⎭,因为,84x ππ⎛⎤∈ ⎥⎝⎦,所以(]0,1t ∈,所以不等式22cos 22cos 2501212a fx x f x x a ππ⎡⎤⎡⎤⎛⎫⎛⎫++-+--≥ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦在,84x ππ⎛⎤∈ ⎥⎝⎦上恒成立,可化为()222250a t t a ---≥在(]0,1t ∈上恒成立,即2221ta t -≤+在(]0,1t ∈上恒成立, 令(]20,2211,ty t t -=+∈,则221221212t y t t t -==-⋅≥-=++t =所以a ≤所以实数a 的取值范围为,⎛-∞ ⎝⎦.。

辽宁省五校协作体(沈阳七中,育才,丹东,锦州等)2023-2024学年九年级上学期期末数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题A ....2.关于x 一元二次方程2024x -+有一个根是1x =,则的值是()A .2022.2022-20232023-3.下列性质中,菱形不具有的性质是(A .对角线相等.四条边相等.对角线互相垂直.对角线互相平分4.如图,任意掷一枚质地均匀的骰子,朝上的点数大于4的可能性是()A .12.1314165.如图,在Rt △中,90C ∠=︒,10AB =的值为(A .35B .4534436.如图,已知AB CD EF ∥∥,AC 3,7BD =的值为()A .737.在平面直角坐标系中,ABC 缩小为原来的A .()3,2-C .()2,3-8.已知关于x 的一元二次方程是()A .2m ≥-9.如图,已知D A .AD AEBD CE =C .AD DEAB BC=10.抛物线2y ax bx =++其部分图像如图所示,给出以下判断:①0abc >;②42a b c -+其中正确的个数有()A .2个B .12.木箱里装有仅颜色不同的下颜色后再放回,经过多次的重复实验,发现摸到红球的频率稳定在木箱中蓝球有13.小丽身高1.5米,经太阳光照射,在地面的影长为地面的影长为20米,那么旗杆高为14.如图,矩形ABCDD,对角线CA的延长线经过原点k=.15.如图,已知等边ABC,AC逆时针方向排列),BC和ED的延长线相交于到达点F时停止,点Q在线段AC连接EQ,EP,PQ,当5 EQ PQ=Y是菱形;(1)求证:ABCD(2)延长BC至点E,连接OE交CD于点19.“天宫课堂”第一课,神舟十三号乘组航天员翟志刚、王亚平、叶光富在中国空间站进行太空授课,神奇的太空实验堪称宇宙级精彩!兴趣,组织全校1200名学生进行了“航天知识竞赛的竞赛成绩(满分100分,每名学生的成绩记为组:7080≤<;Dxx≤<;C组:8090并得到如下不完整的频数分布表、频数直方图和扇形统计图.根据图中信息,解答下列问题:分组频数x≤<aA:6070x≤<18B:7080C:8090≤<24x(1)b 的值为________.(2)请补全频数直方图并计算扇形统计图中表示(3)若规定学生竞赛成绩80x ≥为优秀,请估算全校竞赛成绩达到优秀的学生人数.(4)竞赛结束后,某班从本班获得优秀的甲、乙、丙、丁四名同学中随机抽取两名宜讲航天知识.请用列表或画树状图的方法求恰好抽到甲、乙两名同学的概率.20.如图,一次函数()1110y k x b k =+≠的图象分别与函数()2220k y k x=≠相交于点()8,4C --,(4,8D (1)求一次函数和反比例函数的表达式;(2)当x 为何值时,10y <;(3)当x 为何值时,12y y >,请直接写出x 的取值范围.21.锦州古塔,也叫锦州辽塔,建于辽道宗清宁三年(舍利子而建.在一次数学综合实践活动中,李老师布置了一个任务:请根据所学知识设计一种方案,测量锦州古塔的高.(1)【实践探究】某小组通过思考,绘制了如图2所示的测量示意图,即在水平地面上的点C 处测得塔顶端A 的仰角为α,点C 到点B 的距离BC a =米,请写出解答过程(结果用α和a 表示).分析:把AC 沿A ∠的角平分线翻折,因为AB AC >,所以点即AC AC '=,据以上操作,易证明ACD AC D '≌ ,所以AC D B '∠>∠,所以C B ∠>∠.感悟与应用:(1)如图(a ),在ABC 中,90ACB ∠=︒,30B ∠=︒BD 之间的数量关系,并说明理由;(2)如图(b ),在四边形ABCD 中,AC 平分BAD ∠,AC 求AB 的长.【拓展提高】(3)如图(c ),在四边形ABDF 若5CD =,26AC =,AE =23.根据以下素材,探索完成任务素材1如图a,电缆在空中架设时挂起的电缆下垂都可以近似的看成抛物线的形状.如图b,在一个斜坡平距离间隔75米架设两个塔柱每个塔柱固定电缆的位置离地面高度为26.75米(26.75AB CD==按如图b建立坐标系(平方向上),可得抛物线表达式:20.0050.2y x x=-+在同一水平线上,经测量,45OG=米,斜坡BD1:8.素材2若电缆下垂的安全高度是米,即电缆距离坡面铅直高度的最小值不小于米时,符合安全要求,否则存在安全隐患.(说明:直线EF⊥轴分别交直线BD和抛物线于点E、F.点E距离坡面的铅直高度为EF的长)任务1确定电缆形状求点D的坐标及直线BD的函数表达式.任务判断电缆安全上述这种电缆的架设是否符合安全要求?请说明理由.。
2013-2014学年辽宁省五校协作体联考高三(上)期中数学试卷(理科)2013-2014学年辽宁省五校协作体联考高三(上)期中数学试卷(理科)一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)已知一元二次不等式f(x)≤0的解集为,则f(e x)>0的解集为()2.(5分)(2012•重庆)=()D.3.(5分)(2013•安徽)设△ABC的内角A,B,C所对边的长分别为a,b,c,若b+c=2a,3sinA=5sinB,则角C=.C D.4.(5分)已知函数f(x)是R上的增函数,A(0,﹣1),B(3,1)是其图象上的两点,那么|f(x+1)|<1的解5.(5分)棱长均为3三棱锥S﹣ABC,若空间一点P满足(x+y+z=1)则的最小值为().C D6.(5分)(2014•泰安一模)如图,矩形OABC内的阴影部分是由曲线f(x)=sinx(x∈(0,π))及直线x=a(a∈(0,π))与x轴围成,向矩形OABC内随机投掷一点,若落在阴影部分的概率为,则a的值是().C D.7.(5分)已知=ad﹣bc,则++…+=()8.(5分)(2014•市中区二模)已知z=2x+y,x,y满足,且z的最大值是最小值的4倍,则m的值是().C D.9.(5分)已知点A、B、C三点不共线,且有,则有()||||||||| ||||| ||||10.(5分)规定[x]表示不超过x的最大整数,f(x)=,若方程f(x)=ax+1有且),﹣),﹣)﹣,﹣x.12.(5分)(2011•江西模拟)已知可导函数f(x)的导函数为g(x),且满足:①;②f(2﹣x)﹣f二、填空题:本大题共4小题,每小题5分.13.(5分)某几何体的三视图如图所示,主视图和左视图是长为3,宽为2的矩形,俯视图是边长为2的正方形,则该几何体的体积为_________.14.(5分)数列{a n}中,a2=2,a n,a n+1是方程的两个根,则数列{b n}的前n项和S n=_________.15.(5分)(2011•宁波模拟)点(a,b)为第一象限内的点,且在圆(x+1)+(y+1)=8上,ab的最大值为_________.16.(5分)(2012•鹰潭模拟)已知三棱锥A﹣BOC,OA、OB、OC两两垂直且长度均为6,长为2的线段MN的一个端点M在棱OA上运动,另一个端点N在△BCO内运动(含边界),则MN的中点P的轨迹与三棱锥的面所围成的几何体的体积为_________、三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.(10分)(2008•四川)求函数y=7﹣4sinxcosx+4cos2x﹣4cos4x的最大值与最小值.18.(12分)四棱锥P﹣ABCD中,侧面PAD⊥底面ABCD,底面ABCD是边长为2的正方形,又PA=PD,∠APD=60°,E、G分别是BC、PE的中点.(1)求证:AD⊥PE;(2)求二面角E﹣AD﹣G的正切值.19.(12分)在数列{a n}中,a1=1,a n+1=(1+)a n+.(1)设b n=,求数列{b n}的通项公式;(2)求数列{a n}的前n项和S n.20.(12分)设△ABC的内角A,B,C所对的边长分别为a,b,c,且.(1)求tanAcotB的值;(2)求tan(A﹣B)的最大值.21.(12分)定义在R上的函数f(x)=ax3+bx2+cx+3同时满足以下条件:①f(x)在(0,1)上是减函数,在(1,+∞)上是增函数;②f′(x)是偶函数;③f(x)在x=0处的切线与直线y=x+2垂直.(Ⅰ)求函数y=f(x)的解析式;(Ⅱ)设g(x)=lnx﹣,若存在x∈[1,e],使g(x)<f′(x),求实数m的取值范围.22.(12分)(2014•郑州模拟)已知函数f(x)=ln2(1+x)+2ln(1+x)﹣2x.(Ⅰ)证明函数f(x)在区间(0,1)上单调递减;(Ⅱ)若不等式≤e2对任意的n∈N*都成立,(其中e是自然对数的底数),求实数a的最大值.2013-2014学年辽宁省五校协作体联考高三(上)期中数学试卷(理科)参考答案与试题解析一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)已知一元二次不等式f(x)≤0的解集为,则f(e x)>0的解集为(){x|<,然后由的解集为{x|要保证2.(5分)(2012•重庆)=()D..3.(5分)(2013•安徽)设△ABC的内角A,B,C所对边的长分别为a,b,c,若b+c=2a,3sinA=5sinB,则角C=.C D.c=cosC==C=,4.(5分)已知函数f(x)是R上的增函数,A(0,﹣1),B(3,1)是其图象上的两点,那么|f(x+1)|<1的解5.(5分)棱长均为3三棱锥S﹣ABC,若空间一点P满足(x+y+z=1)则的最小值为().C D满足满足为垂足时,∴∴.中,=6.(5分)(2014•泰安一模)如图,矩形OABC内的阴影部分是由曲线f(x)=sinx(x∈(0,π))及直线x=a(a∈(0,π))与x轴围成,向矩形OABC内随机投掷一点,若落在阴影部分的概率为,则a的值是().C D.×7.(5分)已知=ad﹣bc,则++…+=()解:∵∴8.(5分)(2014•市中区二模)已知z=2x+y,x,y满足,且z的最大值是最小值的4倍,则m的值是().C D.表示的平面区域,9.(5分)已知点A、B、C三点不共线,且有,则有()||||||||| ||||| ||||,是最大边.由,利用正弦定理可化为三点不共线,且有∴,化为∵∴10.(5分)规定[x]表示不超过x的最大整数,f(x)=,若方程f(x)=ax+1有且),﹣),﹣)﹣,﹣由图象可知,当直线介于两红色线之间时,符合题意,而它们的斜率分别为,[,x.12.(5分)(2011•江西模拟)已知可导函数f(x)的导函数为g(x),且满足:①;②f(2﹣x)﹣f和利用积商符号法则判断函数∵二、填空题:本大题共4小题,每小题5分.13.(5分)某几何体的三视图如图所示,主视图和左视图是长为3,宽为2的矩形,俯视图是边长为2的正方形,则该几何体的体积为8.××14.(5分)数列{a n}中,a2=2,a n,a n+1是方程的两个根,则数列{b n}的前n项和S n=.的两个根,∵=)((故答案为:15.(5分)(2011•宁波模拟)点(a,b)为第一象限内的点,且在圆(x+1)2+(y+1)2=8上,ab的最大值为1.2ab+416.(5分)(2012•鹰潭模拟)已知三棱锥A﹣BOC,OA、OB、OC两两垂直且长度均为6,长为2的线段MN的一个端点M在棱OA上运动,另一个端点N在△BCO内运动(含边界),则MN的中点P的轨迹与三棱锥的面所围成的几何体的体积为或36﹣、或该三棱锥减去此球体的故答案为:.三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.(10分)(2008•四川)求函数y=7﹣4sinxcosx+4cos2x﹣4cos4x的最大值与最小值.18.(12分)四棱锥P﹣ABCD中,侧面PAD⊥底面ABCD,底面ABCD是边长为2的正方形,又PA=PD,∠APD=60°,E、G分别是BC、PE的中点.(1)求证:AD⊥PE;(2)求二面角E﹣AD﹣G的正切值.OP=,,∴∴,∴∴的一个法向量为=,的正切值为19.(12分)在数列{a n}中,a1=1,a n+1=(1+)a n+.(1)设b n=,求数列{b n}的通项公式;(2)求数列{a n}的前n项和S n.+,即+++ +++,且,++,+++++=1++++++++﹣=2﹣,.20.(12分)设△ABC的内角A,B,C所对的边长分别为a,b,c,且.(1)求tanAcotB的值;(2)求tan(A﹣B)的最大值.)求出中,由正弦定理及当且仅当时,)的最大值为21.(12分)定义在R上的函数f(x)=ax3+bx2+cx+3同时满足以下条件:①f(x)在(0,1)上是减函数,在(1,+∞)上是增函数;②f′(x)是偶函数;③f(x)在x=0处的切线与直线y=x+2垂直.(Ⅰ)求函数y=f(x)的解析式;(Ⅱ)设g(x)=lnx﹣,若存在x∈[1,e],使g(x)<f′(x),求实数m的取值范围.,即22.(12分)(2014•郑州模拟)已知函数f(x)=ln2(1+x)+2ln(1+x)﹣2x.(Ⅰ)证明函数f(x)在区间(0,1)上单调递减;(Ⅱ)若不等式≤e2对任意的n∈N*都成立,(其中e是自然对数的底数),求实数a的最大值.≤转化为最小值即可.()不等式等价于不等式,∴的最大值为参与本试卷答题和审题的老师有:qiss;sllwyn;wyz123;孙佑中;吕静;刘长柏;ywg2058;lincy;wfy814;394782;zlzhan;zwx097;翔宇老师;minqi5;wodeqing(排名不分先后)菁优网2014年10月29日。
第1页 共10页 ◎ 第2页 共10页绝密★启用前2014-2015学年度期中卷高一数学考试范围:必修一;考试时间:120分钟;命题人: 注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明一、选择题(题型注释)1.已知集合{}1,2,3M =,{}2,3,4N =,则 ( ) A .M N ⊆ B .N M ⊆ C .{}1,4MN = D .{}2,3M N =【答案】D【解析】解:因为根据已知 的集合,可以判定集合间的关系,以及集合的运算,那么显然选项D 成立。
2.设集合}1,0,1{-=M ,},{2a a N =,则使M∩N=N 成立的a 的值是( ) A .1 B .0 C .-1 D .1或-1 【答案】C 【解析】试题分析:由于集合中的元素互不相同,所以20,1a a a a ≠⇒≠≠.又因为M∩N=N ,所以1a =-. 考点:集合的特征及集合的基本运算. 3.设,则( )A .﹣2<x <﹣1B .﹣3<x <﹣2C .﹣1<x <0D .0<x <1 【答案】A【解析】因为y=3x在R 上单调递增,又,故﹣2<x <﹣1故选A4.若0.90.48 1.54,8,0.5a b c -===则( )A .c b a >> B. a c b >> C.b a c >> D.b c a >> 【答案】D【解析】0.9 1.80.48 1.44 1.5 1.542,82.(0.5)2.-===函数2x y =是增函数,1.8 1.5 1.44,>>所以.a c b >>故选D5.函数()f x =的定义域是 A. {x ︱34x >} B. {01x x <≤} C. {1x x ≥} D. {x ︱314x <≤} 【答案】D 【解析】略6.设函数))((R x x f ∈为奇函数,),2()()2(,21)1(f x f xf f +=+=则=)5(f ()A.0B .1C .25D .5【答案】C【解析】令x=-1可得(1)(1)(2)(1)(2),(2)2(1)1,f f f f f f f =-+=-+∴==13(3)(1)(2)122f f f ∴=+=+=,35(5)(3)(2)122f f f =+=+=.7.某同学家门前有一笔直公路直通长城,星期天,他骑自行车匀速前往旅游,他先前进了a km ,觉得有点累,就休息了一段时间,想想路途遥远,有些泄气,就沿原路返回骑了b km(b <a ), 当他记起诗句“不到长城非好汉”,便调转车头继续前进. 则该同学离起点的距离s 与时间t 的函数关系的图象大致为 ( )【答案】C【解析】分析:本题根据运动变化的规律即可选出答案.依据该同学出门后一系列的动作,匀速前往对应的图象是上升的直线,匀速返回对应的图象是下降的直线,等等,从而选出答案. 解答:解:根据他先前进了akm ,得图象是一段上升的直线,DCBA第3页 共10页 ◎ 第4页 共10页由觉得有点累,就休息了一段时间,得图象是一段平行于t 轴的直线,由想想路途遥远,有些泄气,就沿原路返回骑了bkm (b <a ),得图象是一段下降的直线, 由记起诗句“不到长城非好汉”,便调转车头继续前进,得图象是一段上升的直线, 综合,得图象是C , 故选C .点评:本小题主要考查函数的图象、运动变化的规律等基础知识,考查数形结合思想.属于基础题. 8.函数的单调增区间为( )A .B .(3,+∞)C .D .(﹣∞,2)【答案】D【解析】由题意知,x 2﹣5x+6>0∴函数定义域为(﹣∞,2)∪(3,+∞),排除A 、C , 根据复合函数的单调性知的单调增区间为(﹣∞,2),故选D9.若函数()1(0,1)1x mf x a a a =+>≠-是奇函数,则m 为 A.1- B.2 C.1 D.2-【答案】B 【解析】 试题分析:111111x a(),()()xxxm m mf x f x aaa --=+=+-=-+--- 由于函数是奇函数,()(),f x fx ∴-=-即x a (1)1(1)2111x x x x m m m a a a a -+=-+∴=--- 所以2m =,故选:B.考点:函数的奇偶性10. 下列每组中两个函数是同一函数的组数共有( ) (1)2()1f x x =+和2()1f v v =+(2) y =和y =(3) y=x 和321x xy x +=+ (4) y=和y(A) 1组 (B) 2组 (C) 3组 (D) 4组 【答案】C【解析】根据同意哈函数的定义可知选项A 中定义域和对应关系相同,成立,选项B 中,定义域相同,对应关系相同,选项C 中,相同,选项D 中,定义域不同,故是同一函数的 组数有3组,故选C 11.已知1a >,函数x y a =与log ()a y x =-的图像可能是( )【答案】B【解析】试题分析:因为根据1a >,可知指数函数递增函数,排除C ,D 选项,同时在选项A,B 中,由于对数函数log ()a y x =-的图像与log a y x =的图像关于y 轴堆成,那么可知.排除A.正确的选项为B.考点:本题主要是考查同底的指数函数与对数函数图像之间的关系的运用。
辽宁省县级重点高中协作体2024-2025学年高二上学期期中考试数学试卷一、单选题1.已知直线:210l x y +-=,则l 不经过()A .第一象限B .第二象限C .第三象限D .第四象限2.已知直线:230l x y +-=与圆22:2450M x y ax y +--+=相离,则实数a 的取值范围为()A .3,12⎛⎫-- ⎪⎝⎭B .()2,1--C .()1,2D .31,2⎛⎫ ⎪⎝⎭3.记椭圆22:163x y C m m +=+-的离心率为e,若e ⎫∈⎪⎪⎝⎭,则实数m 的取值范围为()A .()3,4B .()3,6C .()4,5D .()4,64.已知四边形ABCD 为空间四边形,点E 满足2DE DC =- ,F 为BE 的中点,且12AF AB AC AD λμ=++ ,则λμ-的值为()A .52-B .12-C .14D .1185.已知双曲线C :()222210,0x y a b a b-=>>的左、右焦点分别为1F ,2F ,点P 为C 在第一象限上的一点.若12PF F 为直角三角形,12122PF PF F F +=,则C 的离心率为()A .32BC .2D .526.已知圆M 的半径为1r ,圆N 的半径为2r ,且210r r >>,12MN r r >+,点P 为圆M 上的动点,过点P 作圆N 的切线,切点分别为A 、B .若APB ∠的最小值为60o ,最大值为120 ,则21r r 的值为()AB .2C.32D.1+7.某飞船返回舱顺利到达地球后,为了及时将航天员安全救出,地面指挥中心在返回舱预计到达区域安排了三个救援中心(记为A 、B 、C ),A 在B 的正东方向,相距6km ;C 在B 的北偏西30o 方向,相距4km ;P 为航天员的着陆点.某一时刻,A 接收到P 的求救信号,由于B 、C 两地比A 距P 远,4s 后B 、C 两个救援中心才同时接收到这一信号.已知该信号的传播速度为1km /s ,则在A 处测得P 的方向角为()A .北偏东30oB .北偏东60oC .北偏西30oD .北偏西60o8.如图,在正方体1111ABCD A B C D -中,2AB =,P ,Q 分别是棱BC 和11C D 上的两个动点,且PQ =,则PQ 的中点M 到1CC 的距离为()A .12B C .1D 二、多选题9.方程()2210Ax By AB +=≠表示的曲线可以为()A .直线B .圆C .椭圆D .双曲线10.如图,在正四棱台1111ABCD A B C D -中,111224BC BB B C ===,则()A .11B B D D⊥B .1//BB 平面1ACD C .侧棱与底面所成的角为60oD .点1B 到平面1ACD 的距离为211.已知椭圆C :()222210+=>>x y a b a b的左、右焦点分别为1F ,2F ,O 为坐标原点,直线l :y x =与C 相交于A ,B 两点,点2F 关于l 的对称点为M ,线段2F M 与1AF 交于点N ,四边形12AF BF 的周长为,AB 4=,则()A .C 的方程为22142x y +=B .12MF F △的面积为3C .2ON AF ∥D .C 上的点到l 距离的最大值为2三、填空题12.已知直线1l :()110m x my --+=,2l :()2120mx m y ++-=,若12l l ⊥,则m 的值为.13.已知双曲线()2222:10,0x y C a b a b-=>>的左、右焦点分别为()1,0F c -、()2,0F c ,O 为坐标原点,P 为C 右支上的一点,点M 是线段OP 上靠近点O 的三等分点,线段1PF 交y 轴于点50,4Q ⎛⎫ ⎪⎝⎭,且2F 、M 、Q 三点共线,12PF F 的周长为15,则12sin F PF ∠的值为.14.已知正方体1111ABCD A B C D -的棱长为2,点P 为底面ABCD 内的动点(不含边界),1D P =11PA PC +的最小值为四、解答题15.已知圆1C 与x 轴相切,圆心在直线20x y -=上,且被直线340x y -=截得的弦长为圆222:440C x y x y m ++++=.(1)求1C 的方程;(2)若1C 与2C 外切,求实数m 的值.16.《九章算术》是我国古代的一部数学经典著作,在其中一篇《商功》中有如下描述:“斜解立方,得两堑堵”,堑堵是底面为直角三角形的直三棱柱.如图,在堑堵111ABC A B C -中,AB BC ⊥,1AB BC ==,12CC =,P 为棱AC 的中点,Q 为棱11A C 的中点.(1)证明:平面1//PBC 平面1AB Q ;(2)求平面1AQB 与平面ABC 夹角的正弦值.17.已知椭圆C :()222210+=>>x y a b a b的左、右焦点分别为1F ,2F ,M 为C 的上顶点,N 为C的右顶点,MN =,12MF F △为直角三角形.(1)求C 的方程;(2)若直线l :1y kx =-交C 于A ,B 两点,求MAB △面积的最大值.18.如图1,在ABC V 中,,D E 分别为,AB AC 的中点,O 为DE的中点,AB AC ==4BC =.将ADE V 沿DE 折起到1A DE △的位置,使得平面1A DE ⊥平面BCED ,如图2.(1)求证:1AO BD ⊥.(2)线段1AC 上是否存在点F ,使得直线DF 和BC11A F A C的值;若不存在,说明理由.19.已知圆A :()2239x y ++=,圆B :()2231x y -+=,动圆P 与圆A ,圆B 均外切,线段PA 与圆A 交于点M ,线段PB 与圆B 交于点N .(1)求动圆P 的圆心P 的轨迹方程;(2)证明:PM PN =;(3)过B 的直线l 与点P 的轨迹交于E ,F 两点,O 为坐标原点,试判断OEF 的形状,并说明理由.。
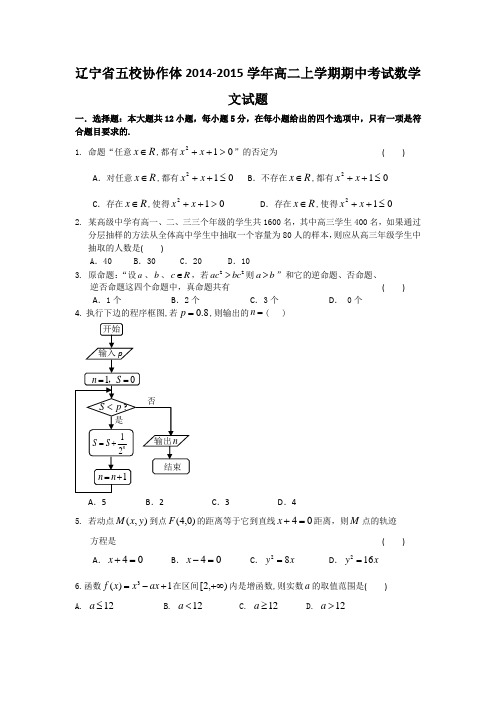
辽宁省葫芦岛市五校协作体2014-2015学年高一下学期期中数学试卷一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知点P(﹣3,4)在角α的终边上,则的值为()A.﹣B.C.D.﹣12.(5分)已知向量=(2,1),=(x,﹣2),若∥,则+等于()A.(﹣2,﹣1)B.(2,1)C.(3,﹣1)D.(﹣3,1)3.(5分)下列四个函数中,以π为最小周期,且在区间()上为减函数的是()A.y=sin2x B.y=2|cosx| C.y=cos D.y=tan(﹣x)4.(5分)若sinαtanα<0,且<0,则角α是()A.第一象限B.第二象限C.第三象限D.第四象限5.(5分)已知α为锐角,且有,tan(π+α)+6sin(π+β)﹣1=0,则sinα的值是()A.B.C.D.6.(5分)设向量满足:,则等于()A.B.1C.D.27.(5分)记a=sin(cos2015°),b=sin(sin2015°),c=cos(sin2015°),d=cos(cos2015°),则a、b、c、d中最大的是()A.a B.b C.c D.d8.(5分)给出下列命题:①函数y=cos是奇函数;②存在实数α,使得sin α+cos α=;③若α、β是第一象限角且α<β,则tan α<tan β;④x=是函数y=sin的一条对称轴方程;⑤函数y=sin的图象关于点成中心对称图形.其中正确的序号为()A.①③B.②④C.①④D.④⑤9.(5分)已知函数f(x)=2sin(ωx+φ)(ω>0,﹣π<φ<π)图象的一部分(如图所示),则ω与φ的值分别为()A.,﹣B.1,﹣C.,﹣D.,﹣10.(5分)函数y=tan(x﹣)(0<x<4)的图象如图所示,A为图象与x轴的交点,过点A的直线l与函数的图象交于B、C两点,则(+)•等于()A.﹣8 B.﹣4 C.4D.811.(5分)为了得到函数y=sin2x+cos2x的图象,只需把函数y=sin2x﹣cos2x的图象()A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度12.(5分)如图,BC是单位圆(即半径为1的圆)圆A的一条直径,F是线段AB上的一点,且,若DE是圆A中绕圆心A运动的一条直径,则的值是()A.B.C.D.不确定二、填空题:本大题共4小题,每小题5分,共20分,将答案填在答题纸上.13.(5分)已知关于x的方程2sin2x﹣sin2x+m﹣1=0在x∈(,π)上有两个不同的实数根,则m的取值范围是.14.(5分)计算:=.15.(5分)使不等式sin2x+acosx+a2≥1+cosx对一切x∈R恒成立的负数a的取值范围是.16.(5分)已知θ∈(,π),+=2,则sin(2θ+)=.三、解答题:本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤. 17.(10分)已知0<α<π,tanα=﹣2.(1)求sin(α+)的值;(2)求的值;(3)2sin2α﹣sinαcosα+cos2α18.(12分)已知A(3,0),B(0,3),C(cosα,sinα);(1)若•=﹣1,求sin(α+)的值;(2)O为坐标原点,若|﹣|=,且α∈(0,π),求与的夹角.19.(12分)已知函数f(x)=sin2xsinφ+cos2xcosφ﹣sin(+φ)(0<φ<π),其图象过点(,).(Ⅰ)求φ的值;(Ⅱ)将函数y=f(x)的图象上各点的横坐标缩短到原来的,纵坐标不变,得到函数y=g (x)的图象,求函数g(x)在上的最大值和最小值.20.(12分)已知两个不共线的向量,的夹角为θ,且||=3,||=1,x为正实数.(1)若+2与﹣4垂直,求tanθ;(2)若θ=,求|x﹣|的最小值及对应的x值,并指出向量与x﹣的位置关系.21.(12分)已知函数(1)求函数f(x)的最小正周期和最大值;(2)求函数f(x)单调递增区间.22.(12分)已知向量=(1,1),向量与向量的夹角为,且•=﹣1(1)求向量;(2)若向量与向量=(1,0)的夹角为,而向量,其中,试求|+|的取值范围.辽宁省葫芦岛市五校协作体2014-2015学年高一下学期期中数学试卷参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知点P(﹣3,4)在角α的终边上,则的值为()A.﹣B.C.D.﹣1考点:同角三角函数基本关系的运用.专题:三角函数的求值.分析:根据P坐标,利用任意角的三角函数定义求出tanα的值,原式分子分母除以cosα,利用同角三角函数间基本关系化简,把tanα的值代入计算即可求出值.解答:解:∵点P(﹣3,4)在角α的终边上,∴tanα=﹣,则原式===,故选:B.点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.2.(5分)已知向量=(2,1),=(x,﹣2),若∥,则+等于()A.(﹣2,﹣1)B.(2,1)C.(3,﹣1)D.(﹣3,1)考点:平面向量共线(平行)的坐标表示;平面向量的坐标运算.专题:计算题.分析:根据题意,由向量平行的判断方法,可得2x﹣2=0,解可得x的值,即可得的坐标,由向量加法的坐标运算方法,可得答案.解答:解:根据题意,向量=(2,1),=(x,﹣2),若∥,则有1•x=2•(﹣2),即x=﹣4,即=(﹣4,﹣2),则+=(﹣2,﹣1),故选A.点评:本题考查向量平行的判断,解题的关键是熟练掌握平面向量共线(平行)的坐标表示,以及进行正确的运算.3.(5分)下列四个函数中,以π为最小周期,且在区间()上为减函数的是()A.y=sin2x B.y=2|cosx| C.y=cos D.y=tan(﹣x)考点:函数的周期性;函数单调性的判断与证明.专题:计算题.分析:y=sin2x的最小正周期是π,在区间()上先减后增;y=2|cosx|最小周期是π,在区间()上为增函数;y=cos的最小正周期是4π,在区间()上为减函数;y=tan(﹣x)的最小正周期是π,在区间()上为减函数.解答:解:在A中,y=sin2x的最小正周期是π,在区间()上先减后增;在B中,y=2|cosx|的最小周期是π,在区间()上为增函数;在C中,y=cos的最小正周期是4π,在区间()上为减函数;在D中,y=tan(﹣x)的最小正周期是π,在区间()上为减函数.故选D.点评:本题考查三角函数的单调性和周期性的灵活应用,是基础题.解题时要认真审题,注意合理地进行等价转化.4.(5分)若sinαtanα<0,且<0,则角α是()A.第一象限B.第二象限C.第三象限D.第四象限考点:三角函数值的符号.专题:三角函数的求值.分析:直接由α的正弦和正切异号且余弦和正切异号得答案.解答:解:∵sinαtanα<0,可知α是第二或第三象限角,又<0,可知α是第三或第四象限角.∴角α是第三象限角.故选:C.点评:本题考查了三角函数的象限符号,是基础题.5.(5分)已知α为锐角,且有,tan(π+α)+6sin(π+β)﹣1=0,则sinα的值是()A.B.C.D.考点:三角函数的化简求值.专题:计算题.分析:先根据诱导公式进行化简整理,然后求出tanα,最后根据同角三角函数关系求出sinα即可.解答:解:∵,tan(π+α)+6sin(π+β)﹣1=0∴﹣2tanα+3sinβ+5=0…①tanα﹣6si nβ﹣1=0…②①×2+②得tanα=3∵α为锐角,∴sinα=故选C.点评:本题主要考查了三角函数的化简求值,同时考查了诱导公式和同角三角函数关系,属于基础题.6.(5分)设向量满足:,则等于()A.B.1C.D.2考点:平面向量数量积的性质及其运算律;向量的模.专题:计算题.分析:把平方,再把条件代入即可求出的值.解答:解:∵,∴,故选B.点评:本题主要考查两个向量的数量积的定义,求向量的模的方法,属于基础题.7.(5分)记a=sin(cos2015°),b=sin(sin2015°),c=cos(sin2015°),d=cos(cos2015°),则a、b、c、d中最大的是()A.a B.b C.c D.d考点:运用诱导公式化简求值;三角函数线.专题:三角函数的求值.分析:结合诱导公式进行化简a,b,c,d,借助于三角函数的单调性进行比较大小即可.解答:解:a=sin(cos2015°)=sin(cos215°)=sin(﹣cos35°),b=sin(sin2015°)=sin(sin215°)=sin(﹣sin35°),c=cos(sin2015°)=cos(sin215°)=cos(﹣sin35°)=cos(sin35°),d=cos(cos2015°)=cos(cos215°)=cos(﹣cos35°)=cos(cos35°),∵sin35°<cos35°,∴0>﹣sin35°>﹣cos35°>﹣1,即0>sin(﹣sin35°)>sin(﹣cos35°)>﹣1∵0<sin35°<cos35°<1,∴cos(sin35°)>cos(cos35°)>0,∴sin(﹣cos35°)<sin(﹣sin35°)<cos(cos35°)<cos(sin35°),即a<b<d<c,则c为最大的.故选:C.点评:此题考查了运用诱导公式化简求值,以及三角函数的单调性及其应用,熟练掌握诱导公式是解本题的关键.8.(5分)给出下列命题:①函数y=cos是奇函数;②存在实数α,使得sin α+cos α=;③若α、β是第一象限角且α<β,则tan α<tan β;④x=是函数y=s in的一条对称轴方程;⑤函数y=sin的图象关于点成中心对称图形.其中正确的序号为()A.①③B.②④C.①④D.④⑤考点:余弦函数的对称性;正弦函数的定义域和值域;正弦函数的对称性.分析:①根据诱导公式化简,即可得到y=cos是奇函数,从而正确;②求出sinα+cosα的最大值,发现最大值<,从而可得到不存在实数α,使得sinα+cosα=;③找两个特殊角α、β,满足α<β,比如45°<30°+360°,但是tan45°>tan(30°+360°)不满足要求,故不对;④把x=代入得到y=sin(2x+)=sin=﹣1,x=是函数y=sin(2x+)的一条对称轴;⑤把x=代入得到y=sin=sin=1,故点不是函数y=sin的对称中心.解答:解:①函数y=cos=﹣sin是奇函数;②由sinα+cosα=sin()的最大值为,因为<,所以不存在实数α,使得sinα+cosα=;③α,β是第一象限角且α<β.例如:45°<30°+360°,但tan45°>tan(30°+360°),即tanα<tanβ不成立;④把x=代入y=sin(2x+)=sin=﹣1,所以x=是函数y=sin(2x+)的一条对称轴;⑤把x=代入函数y=sin=sin=1,所以点不是函数y=sin的对称中心.综上所述,只有①④正确.故选C.点评:本题主要考查诱导公式的应用、正弦函数的基本性质﹣﹣最值、对称性.三角函数的内容比较琐碎,要记忆的比较多,平时要注意公式的记忆和基础知识的积累.9.(5分)已知函数f(x)=2sin(ωx+φ)(ω>0,﹣π<φ<π)图象的一部分(如图所示),则ω与φ的值分别为()A.,﹣B.1,﹣C.,﹣D.,﹣考点:由y=Asin(ωx+φ)的部分图象确定其解析式.专题:三角函数的图像与性质.分析:由f(0)=﹣1,﹣π<φ<π,可求得φ=﹣或φ=﹣;利用T=>,且T<,可求得ω∈(,);分φ=﹣与φ=﹣讨论,即可求得答案.解答:解:∵f(0)=2sinφ=﹣1,∴sinφ=﹣,又﹣π<φ<π,∴φ=﹣或φ=﹣;由图知,T=>,且T=×<,∴<ω<;又ω+φ=π,∴当φ=﹣时,ω+φ=π,解得ω=∉(,),舍去;当φ=﹣时,由ω﹣=π,得ω=∈(,).∴ω与φ的值分别为:,﹣.故选:A.点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查识图与运算求解、等价转化思想与分类讨论思想的综合应用,属于中档题.10.(5分)函数y=tan(x﹣)(0<x<4)的图象如图所示,A为图象与x轴的交点,过点A的直线l与函数的图象交于B、C两点,则(+)•等于()A.﹣8 B.﹣4 C.4D.8考点:平面向量数量积的运算.专题:平面向量及应用.分析:令tan(x﹣)=0,0<x<4,可得x=2.设B(x1,y1),C(x2,y2).由于函数y=tan(x﹣)(0<x<4)关于点(2,0)中心对称,可得x1+x2=4.利用数量积运算性质即可得出.解答:解:令tan(x﹣)=0,∵0<x<4,∴﹣<,∴=0,解得x=2.设直线l的方程为:y=k(x﹣2),B(x1,y1),C(x2,y2).由于函数y=tan(x﹣)(0<x<4)关于点(2,0)中心对称,∴x1+x2=4.∴(+)•=(x1+x2,y1+y2)•(2,0)=2(x1+x2)=8.故选:D.点评:本题考查了向量数量积运算性质、正切函数的图象与性质,考查了推理能力与计算能力,属于中档题.11.(5分)为了得到函数y=sin2x+cos2x的图象,只需把函数y=sin2x﹣cos2x的图象()A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度考点:函数y=Asin(ωx+φ)的图象变换.专题:三角函数的图像与性质.分析:利用两角和与差的正弦函数化简两个函数的表达式为同名函数,然后利用左加右减的原则确定平移的方向与单位.解答:解:分别把两个函数解析式简化为y=sin2x+cos2x=sin(2x+).函数y=sin2x﹣cos2x═sin(2x﹣),又y=sin=sin(2x+),可知只需把函数y=sin2x﹣cos2x的图象向左平移个长度单位,得到函数y=sin2x+cos2x的图象.故选:A.点评:本题是中档题,考查两角和与差的正弦函数的化简,三角函数的图象的变换,注意化简同名函数与x的系数为“1”是解题的关键.12.(5分)如图,BC是单位圆(即半径为1的圆)圆A的一条直径,F是线段AB上的一点,且,若DE是圆A中绕圆心A运动的一条直径,则的值是()A.B.C.D.不确定考点:平面向量数量积的运算.专题:计算题.分析:利用向量的运算法则将分别用表示,利用向量的运算律求出数量积的值.解答:解:=故选B点评:求向量的数量积,一般应该先将各个未知的向量利用已知向量线性表示,再利用向量的运算律展开,转化为已知向量的数量积求出值.二、填空题:本大题共4小题,每小题5分,共20分,将答案填在答题纸上.13.(5分)已知关于x的方程2sin2x﹣sin2x+m﹣1=0在x∈(,π)上有两个不同的实数根,则m的取值范围是(﹣2,﹣1).考点:函数的零点.专题:函数的性质及应用.分析:利用三角函数的倍角公式,将方程进行化简,利用三角函数的图象和性质,确定条件关系,进行求解即可.解答:解:∵2sin2x﹣sin2x+m﹣1=0,∴1﹣cos2x﹣sin2x+m﹣1=0即cos2x+sin2x﹣m=0,∴2sin(2x)=m,即sin(2x)=,∵x∈(,π),∴2x∈(),由三角函数图象可知,要使方程有两个不同的实数根,则,即﹣2<m<﹣1,∴m的取值范围是(﹣2,﹣1).故答案为:(﹣2,﹣1).点评:本题主要考查函数零点的判断,利用三角函数的倍角公式,将三角函数进行化简,利用三角函数图象和性质去解决问题.14.(5分)计算:=.考点:两角和与差的正切函数.专题:计算题;三角函数的求值.分析:逆用两角和的正切tan20°+tan40°=tan(1﹣tan20°•tan40°),代入所求关系式即可.解答:解:∵tan20°+tan40°=tan(1﹣tan20°•tan40°),∴====﹣.故答案为:﹣.点评:本题考查两角和与差的正切函数,逆用两角和的正切是解决问题的关键,考查分析转化与运算能力,属于中档题.15.(5分)使不等式sin2x+acosx+a2≥1+cosx对一切x∈R恒成立的负数a的取值范围是a≤﹣2.考点:其他不等式的解法.专题:计算题;换元法.分析:利用公式1=cos2x+sin2x,进行代换,可得cos2x+(1﹣a)cosx﹣a2≤0,然后利用换元法和二次函数的性质列出性质进行求解.解答:解:1﹣cos2x+acosx+a2≥1+cosx⇒cos2x+(1﹣a)cosx﹣a2≤0,令t=cosx,∵x∈R,∴t∈,t2+(1﹣a)t﹣a2≤0,∴.故答案为a≤﹣2.点评:此题考查函数的恒成立问题,是一道中档题,利用不等式的性质进行求解.16.(5分)已知θ∈(,π),+=2,则sin(2θ+)=.考点:两角和与差的正弦函数;同角三角函数基本关系的运用.专题:三角函数的求值.分析:由已知条件易得sin2θ,结合角的范围和同角三角函数基本关系可得cos2θ,由两角和的正弦公式可得.解答:解:∵+=2,∴=2,∴sinθ+cosθ=2sinθcosθ,平方可得8(sinθcosθ)2﹣2sinθcosθ﹣1=0解得sinθcosθ=,或∵θ∈(,π),∴sinθcosθ<0,∴sin2θ=2sinθcosθ=,∴sinθ+cosθ=﹣,∴(sinθ﹣cosθ)2=1﹣2sinθcosθ=∴sinθ﹣cosθ=,∴(sinθ﹣cosθ)(sinθ+cosθ)=﹣=sin2θ﹣cos2θ=﹣cos2θ∴cos2θ=﹣,∴sin(2θ+)=sin2θ+cos2θ=﹣+=;故答案为:点评:本题考查两角和与差的三角函数运算,涉及一元二次方程的解法和同角三角函数的基本关系,属中档题.三、解答题:本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤. 17.(10分)已知0<α<π,tanα=﹣2.(1)求sin(α+)的值;(2)求的值;(3)2sin2α﹣sinαcosα+cos2α考点:同角三角函数间的基本关系;诱导公式的作用.专题:计算题.分析:(1)由已知中0<α<π,tanα=﹣2,根据同角三角函数关系,我们可以求出sinα,cosα的值,代入两角和的正弦公式,即可求出sin(α+)的值;(2)利用诱导公式,我们可以将原式化为用α的三角函数表示的形式,弦化切后,tanα=﹣2,即可得到答案.(3)根据sin2α+cos2α=1,我们可以将2sin2α﹣sinαcosα+cos2α化为齐次分式,弦化切后,代入tanα=﹣2,即可得到答案.解答:解:因为0<α<π,tanα=﹣2,所以sinα=,cosα=(1)sin(α+)=sinαcos+cosαsin=+()×=(2)原式===﹣1(3)原式===点评:本题考查的知识点是同角三角函数间的基本关系,诱导公式,两角和的正弦公式,其中(2)(3)中齐次分式弦化切是三角函数给值求值中最常用的方法.18.(12分)已知A(3,0),B(0,3),C(cosα,sinα);(1)若•=﹣1,求sin(α+)的值;(2)O为坐标原点,若|﹣|=,且α∈(0,π),求与的夹角.考点:平面向量数量积的运算;数量积表示两个向量的夹角;运用诱导公式化简求值.专题:计算题.分析:(1)根据已知中A,B,C三点的坐标,我们易求出向量,的坐标,根据=﹣1,我们易得到一个三角方程,解方程即可得到sin()的值.(2)根据向量减法的三角形法则,我们易将=转化为||=,结合(1)中结论,易构造出关于α的三角方程,解方程即可求解.解答:解:(1)∵A(3,0),B(0,3),C(cosα,sinα);∴=(cosα﹣3,sinα);=(cosα,sinα﹣3);∴=cos2α+sin2α﹣3(sinα+cosα)=1﹣3(sinα+cosα)=1﹣3sin()=﹣1∴sin()=(2)∵=||=||===∴cosα=﹣又∵α∈(0,π)∴α=点评:本题考查的知识点是平面向量的数量积运算,同角三角函数关系,辅助角公式,三角函数给值求角,其中根据平面向量数量积运算公式,将问题转化为三角函数问题是解答问题的关键.19.(12分)已知函数f(x)=sin2xsinφ+cos2xcosφ﹣sin(+φ)(0<φ<π),其图象过点(,).(Ⅰ)求φ的值;(Ⅱ)将函数y=f(x)的图象上各点的横坐标缩短到原来的,纵坐标不变,得到函数y=g (x)的图象,求函数g(x)在上的最大值和最小值.考点:y=Asin(ωx+φ)中参数的物理意义;三角函数的最值.专题:三角函数的图像与性质.分析:(I)由已知中函数f(x)=sin2xsinφ+cos2xcosφ﹣sin(+φ)(0<φ<π),其图象过点(,).我们将(,)代入函数的解析式,结合φ的取值范围,我们易示出φ的值.(II)由(1)的结论,我们可以求出y=f(x),结合函数图象的伸缩变换,我们可以得到函数y=g(x)的解析式,进而根据正弦型函数最值的求法,不难求出函数的最大值与最小值.解答:解:(I)∵函数f(x)=sin2xsinφ+cos2xcosφ﹣sin(+φ)(0<φ<π),又因为其图象过点(,).∴φ﹣解得:φ=(II)由(1)得φ=,∴f(x)=sin2xsinφ+cos2xcosφ﹣sin(+φ)=∴∵x∈∴4x+∈∴当4x+=时,g(x)取最大值;当4x+=时,g(x)取最小值﹣.点评:本题考查三角函数的诱导公式即二倍角等基本公式的灵活应用、图象变换及三角函数的最值问题、分析问题与解决问题的能力.已知函数图象求函数y=Asin(ωx+φ)(A>0,ω>0)的解析式时,常用的解题方法是待定系数法,由图中的最大值或最小值确定A,由周期确定ω,由适合解析式的点的坐标来确定φ,但由图象求得的y=Asin(ωx+φ)(A>0,ω>0)的解析式一般不唯一,只有限定φ的取值范围,才能得出唯一解,否则φ的值不确定,解析式也就不唯一.20.(12分)已知两个不共线的向量,的夹角为θ,且||=3,||=1,x为正实数.(1)若+2与﹣4垂直,求tanθ;(2)若θ=,求|x﹣|的最小值及对应的x值,并指出向量与x﹣的位置关系.考点:平面向量数量积的运算.专题:平面向量及应用.分析:(1)由(+2)⊥(﹣4),可得(+2)•(﹣4)=0.展开可得cosθ=,又θ∈(0,π),利用sinθ=,tanθ=即可得出.(2)利用数量积运算性质可得|x﹣|=,故当x=时,|x﹣|取得最小值,计算•(x﹣)即可得出.解答:解:(1)∵(+2)⊥(﹣4),∴(+2)•(﹣4)=0.∴2﹣2•﹣82=0,得32﹣2×3×1×cosθ﹣8×12=0,得cosθ=,又θ∈(0,π),故θ∈(0,),因此,sinθ==,∴tanθ==.(2)|x﹣|===,故当x=时,|x﹣|取得最小值,此时,•(x﹣)=x2﹣•=×9﹣3×1×cos=0,故向量与x﹣垂直.点评:本题考查了向量垂直与数量积的关系、数量积运算性质、二次函数的单调性,考查了推理能力与计算能力,属于中档题.21.(12分)已知函数(1)求函数f(x)的最小正周期和最大值;(2)求函数f(x)单调递增区间.考点:三角函数中的恒等变换应用;三角函数的周期性及其求法;复合三角函数的单调性.专题:计算题;三角函数的图像与性质.分析:(1)利用两角和与差的余弦公式展开,结合二倍角公式和辅助角公式进行化简,可得f(x)=,再利用三角函数的周期公式即可求出函数f(x)的最小正周期,再根据余弦函数的值域即可求得函数f(x)的最大值.(2)根据余弦函数的单调区间的结论,解关于x的不等式并将所得不等式变成区间,即可求出函数f(x)单调递增区间.解答:解:(1)∵…(1分)=…(2分)==…(4分)==…(6分)∴函数f(x)的最小正周期为T==π,…(7分)当=2kπ(k∈Z)时,即x=﹣+kπ(k∈Z)时,函数f(x)的最大值为…(8分)(2)设…(10分)解之可得:…(11分)∴函数f(x)的单调递增区间为…(12分)点评:本题给出三角函数表达式,求函数的最小正周期和单调减区间,着重考查了三角恒等变换和三角函数的图象与性质等知识点,属于中档题.22.(12分)已知向量=(1,1),向量与向量的夹角为,且•=﹣1(1)求向量;(2)若向量与向量=(1,0)的夹角为,而向量,其中,试求|+|的取值范围.考点:余弦函数的定义域和值域;向量的模;平面向量数量积的运算;三角函数的化简求值.专题:计算题.分析:(1)利用向量的数量积公式将已知条件转化为的坐标满足的方程,解方程求出的坐标.(2)利用向量垂直的充要条件求出的坐标,进一步求出的坐标,利用向量模的坐标公式表示出的模为含一个角的余弦函数,求出整体角的范围,利用三角函数的有界性求出的模的范围.解答:解:(1)令,则由=﹣1得a+b=﹣1①由向量与向量的夹角为,得a2+b2=1②由①②解得或∴=(﹣1,0)或=(0,﹣1),(2)由向量与向量的夹角为,得=(0,﹣1),∴,∴=1+∵0<x<,∴,∴,∴,∴|.点评:本题考查向量的数量积公式、向量垂直的充要条件、向量模的坐标公式及求三角函数在闭区间上的值域问题,属于中档题.。