最新5.3.1平行线的性质同步练习题

描述：初一数学下册(人教版)知识点总结含同步练习题及答案第五章 相交线与平行线 5.3 平行线的性质一、学习任务1. 能够熟练的运用平行线的性质定理和判定定理解题．2. 发展空间观念、逻辑推理能力和有条理的表达能力．二、知识清单平行线的性质三、知识讲解1.平行线的性质平行线性质① 两条平行线被第三条直线所截，同位角相等；② 两条平行线被第三条直线所截，内错角相等；③ 两条平行线被第三条直线所截，同旁内角互补．平行线间的拐点问题① 已知 ，如图，当点 处于以下位置时， 与 ， 的关系是：② 已知 ，如图，当存在 个 点时， 的值．③ 已知 ，如图，当存在 个 点时，， 与 的关系．AB ∥CD E ∠E ∠B ∠D AB ∥CD n E ∠B +∠D +∠+∠+∠+⋯+∠E 1E 2E 3E n AB ∥CD n E ∠B ∠D ∠+∠+∠+⋯+∠E 1E 2E 3E n例题：四、课后作业（查看更多本章节同步练习题，请到快乐学）AB ∥CD如图所示，已知直线 ，，则 _______．解：．AB ∥CD ∠1=50∘∠2=50∘答案：1. 如图，直线 ，直线 与 ， 相交，，则 ．A ．B ．C ．D ．Ba ∥bc a b ∠1=65∘∠2=()115∘65∘35∘25∘答案：2. 一辆汽车在公路上行驶，两次拐弯后，仍在原来的方向上平行行驶，那么两个拐弯的角度可能为 A ．先向左转 ，再向左转 B ．先向左转 ，再向右转 C ．先向左转 ，再向右转 D ．先向左转 ，再向左转 B()130∘50∘50∘50∘50∘40∘50∘40∘答案：3. 如图，，直线 分别交 、 于点 、 ，若 ，则 的度数为 ．A ．B ．C ．D ．DAB ∥CD BC AB CD B C ∠1=50∘∠2()40∘50∘120∘130∘4. 如图，直线 ，， 交直线 于点，，则 的度数是 a ∥b AC ⊥AB AC b C ∠1=60∘∠2()高考不提分，赔付1万元，关注快乐学了解详情。

人教版七年级数学下册《5.3 平行线的性质》同步练习-附答案学校:___________班级：___________姓名：___________考号：___________一、选择题1．下列角的平分线中，互相垂直的是（）A．平行线的同旁内角的平分线B．平行线的同位角的平分线C．平行线的内错角的平分线D．对顶角的平分线2．如图，已知∠1=70°，CD∥BE，则∠B的度数为（）A．70°B．100°C．110°D．120°3．下列命题中，是真命题的是（）A．在同一平面内，垂直于同一条直线的两条直线平行B．三角形一个外角大于它的任何一个内角C．两条直线被第三条直线所截，同旁内角互补D．过一点有且只有一条直线与已知直线平行4．将一直角三角板与两边平行的纸条如图所示放置，若∠1=55°，则∠2的度数为（）A．135°B．130°C．45°D．35°5．如图∠1=30°，∠B=60°，AB⊥AC则下列说法正确的是（）A．AB//CD B．AC⊥CD C．∠D=60°D．AD//BC 6．如图，直线l1//l2，则∠α为（）A．150°B．140°C．130°D．120°7．如图，下列结论中不正确的是（）A．若AD∥BC，则∠1=∠B B．若∠1=∠2，则AD∥BCC．若∠2=∠C，则AE∥CD D．若AE∥CD，则∠1+∠3=180°8．如图AB//EF，∠ABD=13∠ABC，∠EFD=13∠EFC若∠BCF=120°，则∠D的度数为（）A．60°B．80°C．90°D．100°二、填空题9．命题“如果x2=9，那么x=3”是命题(填“真”或“假”).10．如图，AB∥CD，∠C=55°，则∠1的度数是.11．把命题“对顶角相等”改写成“如果……，那么……”的形式为．12．如图AB∥CD，∠A=24°，∠C=55°则∠E=°．13．如图，将直角三角板ABC与直尺贴在一起，使三角板ABC的直角顶点C（∠ACB=90°）在直尺的一边上，若∠1=65°，则∠2的度数等于.14．如图，点E在DF上，点B在AC上∠1=∠2，∠C=∠D若∠A=45°，试求∠F的度数．15．如图，△ABC中，点D，E分别在AB，AC上，F，G在BC上，EF与DG交于点O，∠B=∠3若∠1+∠2= 180°，∠C=60°．（1）判断线段DE和BC的位置关系，并说明理由；（2）求∠DEC的度数．16．如图∠BCD=∠BFE，∠1+∠2=180°．（1）求证：AD∥CE；（2）若DA⊥AB，∠1−∠2=80°求∠BEF的度数．1．A2．C3．A4．D5．D6．D7．A8．B9．假10．125°11．如果两个角是对顶角，那么这两个角相等12．3113．25°14．解：∵∠1=∠2，∠2=∠ANC∴∠1=∠ANC∴DB//EC∴∠ABD=∠C∵∠C=∠D∴∠D=∠ABD∴DF//AC∴∠A=∠F=45°∴∠F的度数为45°．15．（1）解：DE与BC平行，理由如下：∵∠1+∠2=180°∴BD∥EF∴∠B=∠OFC∵∠3=∠B∴∠OFC=∠3∴DE∥BC；（2）解：∵DE∥BC∴∠DEC+∠C=180°又∵∠C=60°∴∠DEC=180°−∠C=180°−60°=120°．16．（1）证明：∵∠BCD=∠BFE∴CD∥EF∴∠2=∠DCE∵∠1+∠2=180°∴∠1+∠DCE=180°∴AD∥CE；（2）解：∵∠1+∠2=180°，∠1−∠2=80°∴∠2=50°∵AD∥CE，DA⊥AB∴∠CEB=∠DAB=90°∴∠BEF=90°−∠2=40°。

5.3.1 平行线的性质班级:___________ 姓名:___________ 得分:___________一、填空题(每小题6分，共30分)1.如图，已知a∥b，∠1＝55°，则∠2的度数是( )A.35°B.45°C.55°D.125°第1题图第2题图第3题图2.如图，将三角形的直角顶点放在直尺的一边上，若∠1＝65°，则∠2的度数为()A.10°B.15°C.2021D.25°3.如图，已知AB∥CD，直线EF分别交AB、CD于点E、F，EG平分∠BEF，若∠1＝50°，则∠2的度数是( )A.70°B.65°C.60°D.50°4.如图，若AB//CD，∠BEF＝70°，则∠ABE＋∠EFC＋∠FCD的度数是( )A.215°B.250°C.32021D.无法知道第4题图第5题图5.如图，AF∥CD，BC平分∠ACD，BD平分∠EBF，且BC⊥BD下列结论:①BC平分∠ABE；②AC∥BE；③∠BCD＋∠D＝90°；④∠DBF＝2∠ABC.其中正确的个数为( )A.1个B.2个C.3个D.4个二、填空题(每小题6分，共30分)6.如图，已知∠1＝∠2，∠3＝73°，则∠4的度数为.CBA D第6题图第7题图第8题图7.如图，点D、E分别在AB、BC上，DE∥AC，AF∥BC，∠1＝70°，则∠2＝.8.如图,AD∥BC,∠D＝100°,CA平分∠BCD,则∠DAC＝_______9.如图，BC⊥AE，垂足为C，过C作CD∥AB.若∠ECD＝48°，则∠B＝.第9题图第10题图10.如图，直线a∥b，AB⊥BC，如果∠1＝60°，那么∠2＝.三、解答题(每小题2021共40分)11.如图，AB∥CD,直线EF交AB、CD于点G、H.如果GM平分∠BGF,HN平分∠CHE，那么，GM与HN平行吗？为什么？12.如图，已知EF∥AD，∠1＝∠2，∠BAC＝70°，求∠AGD的度数.3.B【解析】∵AB∥CD，∴∠1＋∠BEF＝180°，∵∠1＝50°，∴∠BEF＝130°，∵EG平分∠BEF，∴∠BEG＝∠BEF＝65°，∴∠2＝∠BEG＝65°.故选:B.4.B【解析】分别过点E、F作EG∥AB，HF∥CD，再根据平行线的性质即可得出结论.解:分别过点E、F作EG∥AB，HF∥CD，则AB∥EG∥HF∥CD，∵AB∥EG，∴∠ABE＝∠BEG，又∵EG∥HF，∴∠EFH＝∠GEF，∴∠ABE＋∠EFH＝∠BEG＋∠GEF＝∠BEF＝70°，∵∠HFC＋∠FCD＝180°，∠EFH＋∠HFC＝∠EFC，∴∠ABE＋∠EFC＋∠FCD＝180°＋70°＝250°.故选B.5.C【解析】根据平行线的性质、角平分线的定义、余角的定义作答.解:①∵BC⊥BD，∴∠DBE＋∠CBE＝90°，∠ABC＋∠DBF＝90°，又∵BD平分∠EBF，∴∠DBE＝∠DBF，∴∠ABC＝∠CBE，即BC平分∠ABE，正确；②由AB∥CE，BC平分∠ABE、∠ACE易证∠ACB＝∠CBE，∴AC∥BE正确；③∵BC⊥AD，∴∠BCD＋∠D＝90°正确；④无法证明∠DBF＝60°，故错误.故选C.6.107°【解析】根据已知一对同位角相等，利用同位角相等两直线平行得到a与b平行，利用两直线平行同旁内角互补得到一对角互补，再利用对顶角相等即可确定出∠4的度数.解:∵∠1＝∠2，∴a∥b，∴∠5＋∠3＝180°，∵∠4＝∠5，∠3＝73°，∴∠4＋∠3＝180°，则∠4＝107°.故答案为:107°7.70°【解析】根据两直线平行，同位角相等可得∠C＝∠1，再根据两直线平行，内错角相等可得∠2＝∠C.解:∵DE∥AC，∴∠C＝∠1＝70°，∵AF∥BC，∴∠2＝∠C＝70°.故答案为:70°.8.400【解析】由AD∥BC,∠D＝100°，根据两直线平行，同旁内角互补，可以得到∠DCB＝80°，再由CA平分∠BCD，得到∠BCA＝40°，从而由两直线平行，内错角相等，可得∠DAC＝40°.9.42°【解析】先根据两直线平行，同位角相等求出∠A，再根据直角三角形两锐角互余即可求出.解:∵CD∥AB，∠ECD＝48°，∴∠A＝∠ECD＝48°，∵BC⊥AE，∴∠B＝90°－∠A＝42°.10.30°【解析】∵AB⊥BC，∴∠1＋∠3＝∠ABC＝90°，∴∠3＝∠ABC－∠1＝90°－60°＝30°，∵a//b，∴∠2＝∠3＝30°.11.GM∥HN【解析】首先根据平行线的性质可得∠BGF＝∠CHE,再根据角平分线的性质可以证明∠NHG＝∠MGH,然后根据内错角相等，两直线平行得证结果.答:GM∥HN理由如下:∵AB∥CD∴∠BGF＝∠GHC又∵GM平分∠BGF∴∠HGM＝12∠BGF又∵HN平分∠CHG。

5.3 平行线的性质(三)◆典型例题【例1】下列语句是不是命题.(1)画∠AOB的角平分线;(2)平面上有几个点；(3)两点之间，线段最短;(4)若a≠b，则|a|≠|b|.【解析】(1)是操作性的语句；(2)是问句；(3)、(4)是判定语句.【答案】(1)、(2)不是命题；(3)、(4)是命题.【例2】指出下列命题的题论、结论:(1)如果两条直线相交，那么它们只有一个交点.(2)两条直线被第三条直线所截，如果同旁内角互补，即这两条直线平行.(3)两条平行平行线被第三条直线所截，内错角相等.(4)若∠1=∠2，∠2=∠3，则∠1=∠3.【解析】每个命题都是由题设、结论两部分组成，题设是知事项，结论是由已知事项推出的事项，命题常写成“如果…，那么…”的形式，具有这种形式的命题中，用“如果”开始的部分是题设，用“那么”开始的部分是结论.【答案】(1)题设:两条直线相交；结论:它们只有—个交点；(2)题设:两条直线被第三条直线所截，同旁内角互补；结论:这两条直线平行.(3)因为这个命题可以改写成：“如果两条平行线被第三条直线所截，那么内错角相等”；也可以简写成“如果两直线平行，那么内错角相等”，所以可以简单说成，题设:两直线平行，结论:内错角相等.(4)题设:∠1=∠2，∠2=∠3，结论:∠1=∠3.◆课前热身1.每个命题都由____________和____________两部分组成.2.命题“对顶角相等”的题设是____________,结论________________________.◆课上作业3.命题“同位角相等”改写成“如果…，那么…”的形式是____________________________.4.请用“如果…，那么…”的形式写一个命题______________5.一个命题，如果题设成立，结论一定成立，这样的命题是_____________命题；如果题设成立，结论不成立或不一定成立，这样的命题叫_______命题(填“真”、“假”).6.以下四个命题：①一个锐角与一个钝角的和为180°；②若m不是正数，则m一定小于零；③若ab＞0，则a＞0，b＞0；④如果一个数能被2整除，那么这个数一定能被4整除.真命题有_______个.◆课下作业一、填空题7.下列语句∶①对顶角相等；②OA是∠BOC的平分线；③相等的角都是直角；④线段AB.其中不是命题的是____________________________________________.8.“垂线段最短”的题设是_____________________，结论是____________________.9.命题“a、b是有理数，若a＞b，则a2＞b2”，若结论保持不变，怎样改变条件，命题才是真命题.请你写出一种改法：_______________________________________________10.对于同一平面的三条直线a、b、c，给出以下五个结论:①a∥b;②b∥c;③a⊥b;④a∥c;⑤a⊥c以其中两个为题设，一个为结论，组成一个正确的命题______________________.二、选择题11.唐伯虎点秋香的故事家喻户晓了，现在来玩个游戏：“唐伯虎点秋香”【规则】下面有四个人，其中一个人是秋香，请你通过下面提示辨别出谁是秋香.友情提示:这四个人分别是∶春香、夏香、秋香、冬香【所给人物】A、B、C、D①A不是秋香，也不是夏香；②B不是冬香，也不是春香；③如果A不是冬香，那么C不是春香；④D既不是夏香，也不是春香；⑤C不是春香，也不是冬香若上面的命题都是真命题，问谁是秋香?A.AB.BC.CD.D12.下列命题正确的是( )A.两直线与第三条直线相交，同位角相等;B.两直线与第三条直线相交，内错角相等C.两直线平行，内错角相等;D.两直线平行，同旁内角相等三、解答题13.阅读以下两小题后作出相应的解答:(1)“同位角相等，两直线平行”，“两直线平行，同位角相等”，这两个命题的题设和结论在命题中的位置恰好对凋，我们把其中一命题叫做另一个命题的逆命题，请你写出命题“角平分线上的点到角两边的距离相等的逆命题，并指出逆命题的题设和结论；(2)根据以下语句作出图形，并写出该命题的文字叙述.已知:过直线AB上一点O任作射线OC，OM、ON分别平分∠AOC、∠BOC，则OM⊥ON.14.如图5-122，给出下列论断:(1)AB∥DC；(2)AD∥BC；(3)∠A+∠B=180°；(4)∠B+∠C=180°，以其中一个作为题设，一个作为结论，写出一个真命题.想一想，若连接BD，你能自已写出一个真命题吗?试写出—个真命题并写出推理过程.图5-122参考答案◆课下作业一、填空题7.下列语句∶①对顶角相等；②OA是∠BOC的平分线；③相等的角都是直角；④线段AB.其中不是命题的是____________________________________________.答案：④8.“垂线段最短”的题设是_____________________，结论是____________________.答案：连接直线外一点与直线上一点的所有线段中；垂线段最短9.命题“a、b是有理数，若a＞b，则a2＞b2”，若结论保持不变，怎样改变条件，命题才是真命题.请你写出一种改法：_______________________________________________答案：答案不唯一，如：a＞b＞0，|a|＞|b|等10.对于同一平面的三条直线a、b、c，给出以下五个结论:①a∥b;②b∥c;③a⊥b;④a∥c;⑤a⊥c以其中两个为题设，一个为结论，组成一个正确的命题______________________.答案：下列答案任选其一：①若a∥b，b∥c则a∥c②若a∥b，a∥c则b∥c；③若a∥c，b∥c，则a∥b④若a⊥b，a⊥c，则b∥c⑤若a⊥c,b∥c，则a⊥b;⑥若a⊥b，b∥c，则a⊥c二、选择题11.唐伯虎点秋香的故事家喻户晓了，现在来玩个游戏：“唐伯虎点秋香”【规则】下面有四个人，其中一个人是秋香，请你通过下面提示辨别出谁是秋香.友情提示:这四个人分别是∶春香、夏香、秋香、冬香【所给人物】A、B、C、D①A不是秋香，也不是夏香；②B不是冬香，也不是春香；③如果A不是冬香，那么C不是春香；④D既不是夏香，也不是春香；⑤C不是春香，也不是冬香若上面的命题都是真命题，问谁是秋香?A.AB.BC.CD.D答案：D12.下列命题正确的是( )A.两直线与第三条直线相交，同位角相等;B.两直线与第三条直线相交，内错角相等C.两直线平行，内错角相等;D.两直线平行，同旁内角相等答案：C三、解答题13.阅读以下两小题后作出相应的解答:(1)“同位角相等，两直线平行”，“两直线平行，同位角相等”，这两个命题的题设和结论在命题中的位置恰好对凋，我们把其中一命题叫做另一个命题的逆命题，请你写出命题“角平分线上的点到角两边的距离相等的逆命题，并指出逆命题的题设和结论；(2)根据以下语句作出图形，并写出该命题的文字叙述.已知:过直线AB上一点O任作射线OC，OM、ON分别平分∠AOC、∠BOC，则OM⊥ON.答案：(1)到角两边距离相等的点在这个角的平分线上；题设是到角两边距离相等的点，结论是该点在这个角的平分线上(2)图略；邻补角的平分线互相垂直14.如图5-122，给出下列论断:图5-122(2)AB∥DC；(2)AD∥BC；(3)∠A+∠B=180°；(4)∠B+∠C=180°，以其中一个作为题设，一个作为结论，写出一个真命题.想一想，若连接BD，你能自已写出一个真命题吗?试写出—个真命题并写出推理过程.答案：(1)(4)、(2)(3)、(4)(1)、(3)(2)中任选一个；AD∥BC则∠ADB=∠CBD或∠ADB=∠CBD则AD∥BC.略。

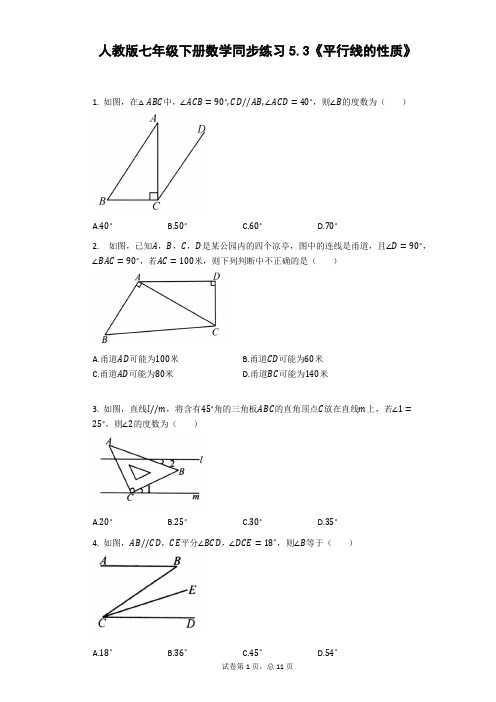
人教版七年级下册数学同步练习5.3《平行线的性质》1. 如图，在△ABC中，∠ACB=90∘,CD//AB,∠ACD=40∘，则∠B的度数为（）A.40∘B.50∘C.60∘D.70∘2. 如图，已知A，B，C，D是某公园内的四个凉亭，图中的连线是甬道，且∠D=90∘，∠BAC=90∘，若AC=100米，则下列判断中不正确的是（）A.甬道AD可能为100米B.甬道CD可能为60米C.甬道AD可能为80米D.甬道BC可能为140米3. 如图，直线l//m，将含有45∘角的三角板ABC的直角顶点C放在直线m上，若∠1=25∘，则∠2的度数为（）A.20∘B.25∘C.30∘D.35∘4. 如图，AB//CD，CE平分∠BCD，∠DCE=18∘，则∠B等于（）A.18∘B.36∘C.45∘D.54∘5. 将一直角三角尺与两边平行的硬纸条如图所示放置，下列结论（1）∠1=∠2；（2）∠3=∠4；（3）∠2+∠4=90∘；（4）∠4+∠5=180∘．其中错误的个数是（）A.0B.1C.2D.36. 如图，下列说法错误的是（）A.若a//b，b//c，则a//cB.若∠1=∠2，则a//cC.若∠3=∠2，则b//cD.若∠3+∠5=180∘，则a//c7. 下列命题中，正确的是（）互为相反数 B.3和−3互为绝对值A.3和−13C.绝对值为2020的数是−2020D.−3的绝对值是38. 下列命题中的真命题是( )A.锐角大于它的余角B.锐角大于它的补角C.钝角大于它的补角D.锐角与钝角之和等于平角9. 甲、乙、丙、丁四个小朋友在院里玩球，忽听“砰”的一声，球击中了李大爷家的窗户．李大爷跑出来查看，发现一块窗户玻璃被打裂了．李大爷问：“是谁闯的祸？”甲说：“是乙不小心闯的祸．”乙说：“是丙闯的祸．”丙说：“乙说的不是实话．”丁说：“反正不是我闯的祸．”如果这四个小朋友中只有一个人说了实话，请你帮李大爷判断一下，究竟是谁闯的祸（）A.甲B.乙C.丙D.丁10. 下列句子中，属于命题的是()A.直线AB和CD垂直吗B.作线段AB的垂直平分线C.同位角相等，两直线平行D.画∠11. 如图，AD//BC，BD平分∠ABC，且∠A=110∘，则∠D=________．12. 如图，已知AB//CD，BF平分∠ABE，DF平分∠CDE,∠BED=115∘，则∠BFD=________．13. 把命题“邻补角互补”改写成“如果…，那么…”的形式________．14. 下列说法：①两条不相交的直线叫平行线；②两条不相交的线段，在同一平面内必平行；③经过直线外一点有且只有一条直线与这条直线平行；④若直线a//b，a//c，那么b//c．其中错误的是________．（填序号）15. 如图，AD是△ABC的角平分线，ED//AB，FD//AC，问DA是否是∠EDF的平分线？为什么？16. 如图，在三角形ABC中，DE//BC，且CD是∠ACB的角平分线，那么∠EDC与∠ECD 有什么关系？并说明理由．17. 如图，直线AB//CD，BC平分∠ABD,∠1=65∘．求∠2的度数．18. 如图，已知AB//CD．试探索：∠A,∠C与∠AEC之间的关系；∠B,∠D与∠BFD之间的关系．参考答案人教版七年级下册数学同步练习5.3《平行线的性质》一、选择题1.【答案】B【解答】解：因为∠ACB=90∘，∠ACD=40∘，所以∠BCD=130∘.因为CD//AB，所以∠B=180∘−130∘=50∘.故选B.2.【答案】A【解答】解：由∠D=90∘,∠BAC=90∘，若AC=100米，得AD<AC，CD<AC，BC>AC，故A不符合题意；故选A.3.【答案】A【解答】解：过点B作BD//m，如图：则∠CBD=∠1=25∘，∵ ∠ABC=45∘，∵ ∠ABD=∠ABC−∠CBD=20∘，∵ l//m,BD//m，∵ BD//l，∵ ∠2=∠ABD=20∘，故选A.4.【答案】B【解答】解：∵ CE平分∠BCD,∠DCE=18∘，∵ ∠BCD=2∠DCE=2×18∘=36∘，∵ AB//CD，∵ ∠B=∠BCD=36∘，故选B．5.【答案】A【解答】解：∵ 纸条的两边平行，∵ （1）∠1=∠2（同位角）；（2）∠3=∠4（内错角）；（4）∠4+∠5=180∘（同旁内角）均正确；又∵ 直角三角板与纸条下线相交的角为90∘，∵ （3）∠2+∠4=90∘，正确．故选：A．6.【答案】C【解答】解：A．若a//b,b//c，则a//c，利用了平行公理，正确；B．若∠1=∠2，则a//c，利用了内错角相等，两直线平行，正确；C．∠3=∠2，不能判断b//c，错误；D．若∠3+∠5=180∘，则a//c，利用同旁内角互补，两直线平行，正确．故选：C．7.【答案】D【解答】A、∵ 3和−3互为相反数，∵ 选项A不符合题意；B、∵ 3和−3的绝对值为3，∵ 选项B不符合题意；C、∵ 绝对值为2020的数是−2020和2020，∵ 选项C不符合题意；D、∵ −3的绝对值是3，∵ 选项D符合题意；8.【答案】C【解答】解：A，锐角大于它的余角，不一定成立，故本选项错误；B，锐角小于它的补角，故本选项错误；C，钝角大于它的补角，本选项正确；D，锐角与钝角之和等于平角，不一定成立，故本选项错误．故选C．9.【答案】D【解答】解：本题可分三种情况进行讨论：①若甲真，则乙假，丙真，丁真；这种情况下，三人说了实话，显然与条件不符；②若甲假，乙真，则丙假，丁真；这种情况下，两人说了实话，显然与条件不符；③若甲假，乙假，则丙真，丁假；这种情况下，只有丙说了实话，符合题目给出的条件．由于丁说了假话，因此闯祸的人一定是丁．故选D．10.【答案】C【解答】A、直线AB和CD垂直吗？这是疑问句，不是命题，所以A选项错误；B、作线段AB的垂直平分线，这是描叙性语言，不是命题，所以B选项错误；C．同位角相等，两直线平行是命题，所以C选项正确；D、画∠AOB=45∘，这是描叙性语言，不是命题，所以D选项错误．故选C二、填空题11.【答案】35∘【解答】解：因为AD//BC，∠A=110∘，所以∠ABC=70∘.因为BD平分∠ABC，所以∠ABD=∠DBC=35∘.又AD//BC，所以∠D=∠DBC=35∘.故答案为：35∘.12.【答案】57.5∘【解答】解：如图，过E作EG//AB，过F作FH//AB，∵ AB//CD，∵ EG//CD，FH//CD，∵ ∠ABE=∠GEB,∠CDE=∠GED，∵ ∠BED=∠ABE+∠CDE=115∘，又∵ BF平分∠ABE，DF平分∠CDE，∵ ∠ABF=12∠ABE,∠CDF=12∠CDE，∵ ∠ABF+∠CDF=12(∠ABE+∠CDE)=57.5∘，∵ AB//FH//CD，∵ ∠ABF=∠BFH,∠CDF=∠DFH，∵ ∠BFD=∠BFH+∠DFH=∠ABF+∠CDF=57.5∘，故答案为：57.5∘.13.【答案】如果两个角是邻补角，那么它们互补．【解答】解：表示为：如果两个角是邻补角，那么它们互补．14.【答案】①②【解答】解：①在同一平面内，两条不相交的直线叫平行线；故错误；②两条不相交的线段，在同一平面内不一定平行；故错误；③经过直线外一点有且只有一条直线与这条直线平行；故正确；④若直线a//b,a//c,那么b//c，故正确；其中错误的是①②，故答案为：①②．三、解答题15.【答案】解：是．∵ AD是△ABC的角平分线，∵ ∠CAD=∠BAD．∵ ED//AB,FD//AC，∵ ∠EDA=∠BAD，∠FDA=∠CAD．∵ ∠EDA=∠FDA，∵ DA是∠EDF的平分线．【解答】解：是．∵ AD是△ABC的角平分线，∵ ∠CAD=∠BAD．∵ ED//AB,FD//AC，∵ ∠EDA=∠BAD，∠FDA=∠CAD．∵ ∠EDA=∠FDA，∵ DA是∠EDF的平分线．16.【答案】解：∠EDC=∠ECD，理由如下：∵ CD是∠ACB的平分线，∵ ∠ECD=∠BCD，∵ DE//BC，∵ ∠EDC=∠BCD，∵ ∠EDC=∠ECD.17.【答案】解：50∘【解答】解：因为AB//CD，所以∠ABC=∠1=65∘,∠ABD+∠BDC=180∘，因为BC平分∠ABD，所以∠ABD=2∠ABC=130∘，所以∠BDC=180∘−∠ABD=50∘，所以∠2=∠BDC=50∘.18.【答案】解：∠A+∠C=∠AEC解：∠B+∠D+∠BFD=360∘【解答】解：（1）如图，过点E作EG//AB，则：∠A=∠AEG，AB//CD，∵ CD//EG，∵ ∠C=∠CEG，∵ ∠A+∠C=∠AEG+∠CEG，即：∵ ∠A+∠C=∠AEC.（2）过点F作FH//AB，则：∠B+∠BFH=180∘，∵ AB//CD，∵ CD//FH，∵ ∠DFH+∠D=180∘，∵ ∠B+∠BFH+∠DFH+∠D=180∘+180∘，即：∠B+∠BFD+∠D=360∘.试卷第11页，总11页。

.《平行线的性质》练习题1．如图，a∥b，a、b被c所截，得到∠1=∠2的依据是（）A．两直线平行，同位角相等 B．两直线平行，内错角相等C．同位角相等，两直线平行 D．内错角相等，两直线平行2．如图，AB∥CD，那么（）A．∠1=∠4 B．∠1=∠3 C．∠2=∠3 D．∠1=∠53．如图，在平行四边形ABCD中，下列各式不一定正确的是（）A．∠1+∠2=180° B．∠2+∠3=180° C．∠3+∠4=180° D．∠2+∠4=180°4．如图，AD∥BC，∠B=30°，DB平分∠ADE，则∠DEC的度数为（）A．30° B．60° C．90° D．120°6. 下列说法中，错误的是（）A.在同一平面内，直线a∥b，若c与a相交，则b与c也相交B.直线a与b相交，c与a相交，则b∥cC.直线a∥b，b∥c,则a∥cD.直线AB与CD平行，则AB上所有点都在CD同侧7．下列语句中不是命题的有（）（1）两点之间，直线最短；（2）不许大声讲话；（3）连接A、B两点；（4）花儿在春天开放． A．1个 B．2个 C．3个 D．4个8．下列命题中，正确的是（）A．在同一平面内，垂直于同一条直线的两条直线平行； B．相等的角是对顶角；C．两条直线被第三条直线所截，同位角相等； D．和为180°的两个角叫做邻补角。

9. 下列说法中，正确的个数是（）①两条不相交的直线是平行线；②过一点有且只有一条直线与已知直线平行；③同一平面内的三条直线，它们的交点个数可能是0或1或2或3；④在同一平面内，和第三条直线都不相交的两条直线平行；⑤过两条相交直线外一点A，能作一直线m与这两条直线都平行；⑥在同一平面内不相交的两条射线必平行。

A．1个 B．2个C．3个 D．4个10．如图，已知AB∥CD，直线L分别交AB、CD•于点E、F，EG平分∠BEF，若∠EFG=40°，则∠EGF的度数是（）A．60° B．70° C．80° D．90°11. 已知：如图，AB∥DE，∠E=65°，则∠B+∠C•的度数是（）A．135° B．115° C．65° D．35°12．同一平面内有四条直线a、b、c、d，若a∥b，a⊥c，b⊥d，则直线c、d的位置关系为（）A．互相垂直 B．互相平行 C．相交 D．无法确定13．如图，AB∥EF，BC∥DE，则∠E+∠B的度数为________．14. 如图所示：EF在同一平面内，直线l1与l2满足下列条件，写出其对应的位置关系：（1）l1与l2没有公共点，则l1与l 2 ；（2）l1与l2有且只有一个公共点，则l1与l2；（3）l1与l2有两个公共点，则l1与l 2 。

5.3.1平行线的性质(1)班级 _______ 姓名____________ 座号_____主要内容:平行线的性质一、课堂练习：1.如图，完成下列各题的说理过程，括号内填写说理根据：①若DE//BC,则可得出Z1二___ ,根据 _____________________________ ;②若AB//EF.则可得出,1二 _______ ,根据 ___________________________ :③若____ // _____ ,则可得1BZ5+Z4+ZO180°,根据 __________________________________ •2.如图，直线a//b, Zl = 54e,那么Z2、Z3、Z4各是多少度?3.如图，在四边形ABCD中，如果AD//BC, ZA二60°,求ZB的度数，不用度量的方法，能否求得ZD的度数？门c二、课后作业：4•如图所示,(1) 若DE//BC,则可得到：① Zl= ______ ,根据 __________________________________ ；② Z2二 _____ ,根据；③ Z4+ ______ =180°,根据 _______________________________(2) 若EF//AB,则可得到：① _________ Zl= ____________ ；②ZB 二 ________ ； ③Z2+____________ =180°.5. 如图，平行线AB 、CD 被直线AE 所截.⑴从Zl = 110\则可知道Z2二 ______ 度，根据 _________________________________________(2)从Z1 = 110°，则可知道Z3二 ___ 度，根据 _________________________________⑶从Zl = 110\则可知道Z4二 _______ 度,根据 ____________________________ .6. 如下图所示,一条公路两次转弯后，和原来的方向相同，如果第一次拐的角是36',第二 次拐的角是 _____ 度,根据 ____________________________7. 如图，要在公路的两侧铺设平行管道，如果公路一侧铺设的角度为120：那么力了使管道对接，另一侧应以 ____ 角度铺设，根据8. 如图,用式子表示下列句子(阅读⑴，完成⑵(3))C第6题 第7题 第8题⑴因为Z1和ZB相等，根据“同位角相等，两直线平行”，所以DE和BC平行;9.如图，已知d〃"c・、d是截线，若Z1二80°, Z5二70°.求Z2、Z3、Z4各是多少度?为什么？三、新课预习：10.如图，"60°, Z2=60°, Z3=85°求Z4 的度数.b参考答案一、课堂练习：1.如图，完成下列各题的说理过程，括号内填写说理根据：①若DE//BC,则可得出Z1=Z B ,根据两直线平行，同位角相等；②若AB//EF.则可得出,1二Z_5_,根据两直线平行，内错角相等；③若DE〃BC ,则可得出Z5+Z4+ZO180°,根据两直线平行，同旁内角耳补•2.如图，直线a//b t Zl = 54e,那么Z2、Z3、Z4各是多少度?解:I Z1 = 54°・・・Z2 = Z1 = 54°'：a// b・•・ Z2 + Z3 = 180°・•・ Z3 = 180°-Z2 = 180°一54° = 126°9： a// b・•・ Z4 = Z2 = 54°3.如图，在四边形ABCD屮，如果AD//BC. ZA=60\求ZB的度数，不用度量的方法，能否求得ZD的度数？解:*：AD//BC:.ZA+Z3二180°又・・・ZA= 60°・・・ZB二120°不用度量的方法,仅根据平行线的性质，不能求得ZD的度数二、课后作业：4.如图所示，(1)若DE//BC,则可得到：①Z1 ,根据两直线平行，同位角相等②Z2二Z5 、根据两直线平行，内错角相等；③Z4+ ZB 二180",根据两直线平行，同旁内角互补⑵若EF//AB,则可得到：①Zl= Z2 ；②ZB= Z5 ；③ Z2+ Z4 二180°.5.如图，平行线AB、CD被直线AE所截.⑴从Zl=110\则可知道Z2二110 度, 根据两右线平行，内错角相等；(2)从Zl = 110\则可知道Z3二110度, 根据两直线平行，同位角相等；(3)从Z1二110°,则可知道Z4二70 度,根据两直线平行,同旁内角互补•6.如下图所示,一条公路两次转弯后，和原来的方向相同，如果第一次拐的角是36。