初中数学直角三角形模型总结——完整全面版2018.5.28

三角形全等模型巩固三角形全等--------角平分线模型（角平分线做两边垂直、作与角平分线垂直的线段、截长补短、作平行线）图1 （角平分线做两边垂直）图2（作与角平分线垂直的线段）图3 截长补短图4截长补短图5作平行线得到等腰三角形（△OEF为等腰三角形）1、 如图，D 、E 、F 分别是△ABC 的三边上的点，CE=BF ，且△DCE 的面积与△DBF 的面积相等，求证：AD 平分∠BAC 。

2、如图9所示，在△ABC 中，BC 边的垂直平分线DF 交△BAC 的外角平分线AD 于点D ，F为垂足，DE ⊥AB 于E ，并且AB>AC 。

求证：BE －AC=AE 。

B C AD E FF E DC BA图93、AD 是ABC ∆的角平分线，BE AD ⊥交AD 的延长线于E ，EF AC ∥交AB 于F ．求证：AF FB =．4、如图所示，已知ABC ∆中，AD 平分BAC ∠，E 、F 分别在BD 、AD 上．DE CD =，EF AC =． 求证：EF ∥AB （角平分线模型+倍长中线模型）DE C FB AFAC D E B5、已知：在△ABC 中，B ∠的平分线和外角ACM ∠的平分线相交于,,D DF BC 交AC 于,,E AB F 交于求证：EF BF CE -=三角形全等———垂直模型图1 直角都在腰内图2 直角都在腰内结论：△ABD全等三角形AOADO=DB-CO结论：△ABE全等△BCD，EC=AB-DC 图3直角都在腰内图4 两直角在腰外图5 两直角在腰外结论：△BDC全等△ACO，AO+BD=DO模型特点：含有等腰直角三角形，三个直角，垂直模型又分为腰在内，腰在外的情况如图1和图2，三个直角在两等边内侧，AB=AC。

A点过Y轴，两端点作Y轴垂线。

得到△AOC全等△ABD。

如图3，三个直角在两等边内侧，等腰的两个端点，其中一个端点作第三条边的垂线，另外一条边作直角边的垂线。

初中三角形模型总结三角形是初中数学中的基础知识之一，它是由三条边和三个内角组成的平面图形。

在初中阶段，我们学习了三角形的性质、分类和计算方法。

下面我将对初中三角形模型进行总结。

一、三角形的定义和性质三角形是由三条边和三个内角组成的平面图形。

根据三角形的边长关系，我们可以将三角形分为等边三角形、等腰三角形和普通三角形。

等边三角形的三条边长度相等，等腰三角形的两条边长度相等，而普通三角形的三条边长度都不相等。

三角形的内角和为180度。

我们可以利用这个性质来计算三角形的内角。

例如，如果我们已知一个三角形的两个内角的度数，我们可以通过180度减去这两个角的度数，得到第三个角的度数。

二、三角形的分类根据三角形的内角关系，我们还可以将三角形分为锐角三角形、直角三角形和钝角三角形。

锐角三角形的三个内角都小于90度，直角三角形有一个内角等于90度，而钝角三角形有一个内角大于90度。

根据三角形的边长关系，我们可以将三角形分为等边三角形、等腰三角形和普通三角形。

等边三角形的三条边长度相等，等腰三角形的两条边长度相等，而普通三角形的三条边长度都不相等。

三、三角形的计算方法在初中阶段，我们学习了一些计算三角形的方法。

其中，计算三角形的周长和面积是最常见的。

计算三角形的周长，我们只需要将三条边的长度相加即可。

例如，如果一个三角形的三条边的长度分别为a、b、c，那么它的周长就是a+b+c。

计算三角形的面积，我们可以使用海伦公式或底边乘以高的方法。

海伦公式适用于已知三边长度的情况，它的公式为：面积= √(s(s-a)(s-b)(s-c))，其中s为三边长度的半周长。

底边乘以高的方法适用于已知底边和高的情况，它的公式为：面积= 1/2 × 底边长度× 高。

四、三角形模型的应用三角形模型在几何学和实际生活中有着广泛的应用。

在几何学中，我们可以利用三角形模型来研究形状、角度和距离等问题。

在实际生活中，三角形模型也被广泛应用于建筑、地理测量和机械工程等领域。

解直角三角形一、锐角三角函数 （一）、锐角三角函数定义在直角三角形ABC 中，∠C=900，设BC=a ，CA=b ，AB=c ，锐角A 的四个三角函数是：(1)正弦定义：在直角三角形中ABC ，锐角A 的对边与斜边的比叫做角A 的正弦，记作sinA ，即sinA=ca,（2）余弦的定义：在直角三角行ABC ，锐角A 的邻边与斜边的比叫做角A 的余弦，记作cosA ，即cosA=cb ,（3）正切的定义：在直角三角形ABC 中，锐角A 的对边与邻边的比叫做角A 的正切，记作tanA ，即tanA=ba ，(4)锐角A 的邻边与对边的比叫做∠A 的余切,记作cotA 即 锐角A 的正弦、余弦，正切、余切都叫做角A 的锐角三角函数。

这种对锐角三角函数的定义方法，有两个前提条件： （1）锐角∠A 必须在直角三角形中，且∠C=900；（2）在直角三角形ABC 中，每条边均用所对角的相应的小写字母表示。

否则，不存在上述关系注意:锐角三角函数的定义应明确(1)c a，c b，b a，ab四个比值的大小同△ABC 的三边的大小无关，只与锐角的大小有关，即当锐角A 取固定值时，它的四个三角函数也是固定的；（2）sinA 不是sinA 的乘积，它是一个比值，是三角函数记号，是一个整体，其他三个三角函数记号也是一样；（3）利用三角函数定义可推导出三角函数的性质，如同角三角函数关系，互余两角的三角函数关系、特殊角的三角函数值等； （二）、同角三角函数的关系（1）平方关系：122sin =∂+COS α (2)倒数关系：tan ａcota=1 (3)商数关系：∂∂=∂∂∂=sin cos cot ,cos sin tan 注意：（1）这些关系式都是恒等式，正反均可运用，同事还要注意它们的变形公式。

(2)()∂∂sin sin 22是的简写，读作“∂sin 的平方”，不能将∂∂22sin 写成sin 前者是a 的正弦值的平方，后者无意义；（3）这里应充分理解“同角”二字，上述关系式成立的前提是所涉及的角必须相同，如1cot tan ,1223030cossin22=•=∂+∂ ，而1cossin 22=+∂β就不一定成立。

初中数学三角形的模型-概述说明以及解释1.引言1.1 概述三角形作为数学中的重要概念，在初中阶段是数学学习的基础之一。

它不仅具有一定的几何形态，而且具有丰富的性质和应用。

通过研究三角形的模型，我们可以更加深入地了解三角形的特点和变化规律，提高数学学习的效果。

本文将从三个方面对初中数学中的三角形模型进行探讨。

首先，我们将介绍三角形的定义和性质。

通过学习三角形的构成要素和相关性质，我们可以更好地理解三角形的基本特征，为后续的模型应用打下坚实的基础。

其次，我们将对三角形进行分类。

根据边长和角度大小，三角形可以分为等边三角形、等腰三角形、直角三角形等多种类型。

通过对这些特殊类型三角形的研究，我们可以进一步认识三角形的特殊性质，深化对三角形模型的理解。

最后，我们将介绍三角形模型在实际生活中的应用。

三角形的应用广泛涉及建筑、工程、航空、计算机图像等多个领域。

通过具体的案例分析，我们可以发现三角形模型在解决实际问题时的重要性和实用性。

总之，初中数学中的三角形模型是数学学习中不可或缺的一部分。

通过深入学习和研究三角形的定义、分类以及应用，我们可以更好地理解和掌握数学知识，提高数学解决问题的能力。

此外，对于培养我们的逻辑思维和推理能力也有重要意义。

展望未来，随着科学技术的不断发展，三角形模型在数学和其他领域的应用将更加广泛。

因此，加强对三角形模型的研究和应用，对于我们的学术发展和创新能力的培养具有重要意义。

1.2 文章结构文章结构：本文总共分为三个部分，包括引言、正文和结论。

在引言部分，首先对文章的主题进行了概述，简要介绍了初中数学中三角形的模型。

接着通过说明文章结构，给读者明确了文章的框架和内容。

然后明确了本文的目的，即探讨三角形模型在数学学习中的应用和重要性。

最后进行总结，概括了本文所包含的内容和主要观点。

正文部分则进一步展开了对三角形的定义和性质的讨论，介绍了三角形的分类方法，并详细描述了三角形的模型应用。

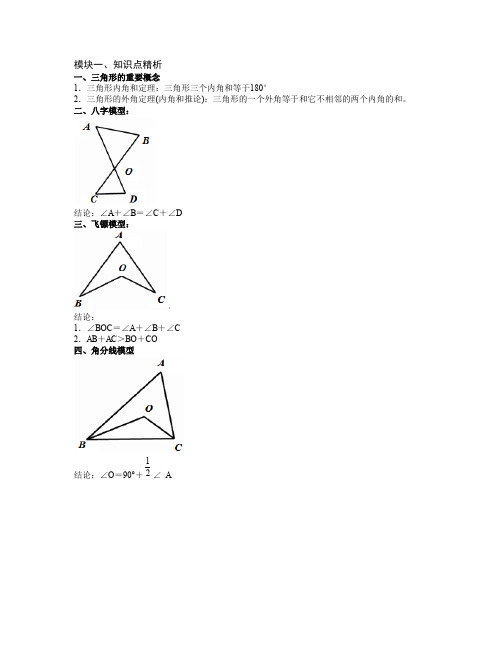
模块一、知识点精析
一、三角形的重要概念
1．三角形内角和定理：三角形三个内角和等于180°
2．三角形的外角定理(内角和推论)：三角形的一个外角等于和它不相邻的两个内角的和。

二、八字模型：
结论：∠A＋∠B＝∠C＋∠D
三、飞镖模型：
结论：
1．∠BOC＝∠A＋∠B＋∠C
2．AB＋AC＞BO＋CO
四、角分线模型
结论：∠O＝90°＋1
2∠A
模块二、重点题型精练
题型一、八字模型应用
【例1】求五角星的五个角之和。

【例2】将例1中的∠E切掉，得到一个如图所示的“六角星”，求这六个角之和。

【例3】已知BE、CD为△ABC高线，且∠ACB＝35°，∠BCD＝10.5°，则∠ABE＝°。

题型二、飞镖模型应用
【例4】如下图，求∠A＋∠B＋∠C＋∠D＝。

【例5】如图，设∠CGE＝α，则∠A＋∠B＋∠C＋∠D＋∠E＋∠F ＝______。

题型三、角分线模型应用
【例6】如图，BD、CD分别是△ABC的两个外角∠CBE、∠BCF•的平分线，若∠D＝70°，则∠A＝_____。

模块三：杯赛题精讲：
【例7】如图，△ABC中，∠A＝80°，A1B平分∠ABC，A1C平分∠ACE，A2B平分∠A1BE，A2C 平分∠A1CE…。

则∠A1＝，∠A2011＝。

初二数学三角形全等经常使用几何模型及构造方式大全把握它轻松弄定全等题！全等是初中数学中超级重要的内容，一样会在压轴题中进行考察，而把握几何模型能够为考试节省很多时刻，这次整理了经常使用的各大模型，必然要认真把握~全等变换类型：（一）平移全等：平行等线段（平行四边形）（二）对称全等模型：角平分线或垂直或半角1：角平分线模型；2：对称半角模型；（三）旋转全等模型：相邻等线段绕公共极点旋转1. 旋转半角模型2. 自旋转模型3. 共旋转模型4. 中点旋转如图，在△ABC的边上取两点D、E，且BD=CE，求证：AB+AC>AD+AE分析：将△ACE平移使EC与BD重合。

B\D，上方交点，左右两个三角形，两边和大于第三边！1：角平分线模型：说明：以角平分线为轴在角两边进行截长补短或作边的垂线，形成对称全等。

两边进行边或角的等量代换，产生联系。

垂直也能够做为轴进行对称全等。

2：对称半角模型说明：上图依次是45°、30°、45+ 22.5°、对称（翻折）15°+30°直角三角形对称（翻折）30+60+90直角三角形对称（翻折）翻折成正方形或等腰直角三角形、等边三角形、对称全等。

1. 半角：有一个角含1/2角及相邻线段2. 自旋转：有一对相邻等线段，需要构造旋转全等3. 共旋转：有两对相邻等线段，直接寻觅旋转全等（共极点）4. 中点旋转：倍长中点相关线段转换成旋转全等问题（专题七）一、旋转半角模型说明：旋转半角的特点是相邻等线段所成角含一个二分之一角，通过旋转将另外两个和为二分之一的角拼接在一路，成对称全等。

二、自旋转模型构造方式：遇60度旋60度，造等边三角形遇90度旋90度，造等腰直角遇等腰旋极点，造旋转全等遇中点旋180度，造中心对称3、共旋转模型说明：旋转中所成的全等三角形，第三边所成的角是一个常常考察的内容。

通过“8”字模型能够证明。

（接上------共旋转模型）模型变形说明：模型变形要紧是两个正多边形或等腰三角形的夹角的转变，另外是等腰直角三角形与正方形混用。

直角三角形的性质和定理知识点总结直角三角形是指其中一个角度为90度的三角形。

在数学中，直角三角形是研究三角函数和几何概念的基本形式之一。

本文将对直角三角形的性质和定理进行总结，并探讨其在几何学中的应用。

一、性质1. 直角三角形的性质直角三角形的两条直角边分别称为两条腿，而与直角相对的边称为斜边。

直角三角形的性质包括以下几点：- 直角三角形的两条腿相互垂直。

- 直角三角形的斜边是两条腿长度的平方和的平方根。

- 直角三角形的两条腿的平方和等于斜边的平方。

- 直角三角形的两条腿的长度可以通过勾股定理计算。

2. 直角三角形的角度关系直角三角形中，直角角度为90度，其余两个角度之和为90度。

- 如果已知直角三角形中两个角的度数，可以求得第三个角的度数。

- 利用三角函数，可以求出直角三角形中各个角的正弦、余弦和正切值。

二、定理1. 勾股定理勾股定理是直角三角形中最为著名的定理之一，描述了直角三角形的边长关系：在直角三角形中，设两直角边长分别为a和b，斜边长为c，那么有a² + b² = c²。

2. 肯定定理和否定定理肯定定理和否定定理也是直角三角形的两个重要定理。

- 肯定定理：如果一个三角形的两条边的平方和等于第三条边的平方，那么这个三角形一定是直角三角形。

- 否定定理：如果一个三角形不是直角三角形，那么它的两条边的平方和一定不等于第三条边的平方。

三、应用直角三角形的性质和定理在几何学中有广泛的应用，例如：1. 测量未知边长：在已知一个角度和一个边长的情况下，可以利用三角函数和勾股定理求解未知边长。

2. 判断角度关系：通过已知两个边长求解角度大小，进而判断三角形的类型。

3. 解决实际问题：直角三角形的应用不仅局限于数学领域，还包括工程学、物理学等实际问题的解决。

总结：本文对直角三角形的性质和定理进行了总结，并探讨了其在几何学中的应用。

直角三角形作为最基础的三角形之一，它的性质和定理为我们理解和运用三角函数提供了重要基础。

人教版八年级数学全等三角形的常见模型总结(精选.)人教版八年级数学全等三角形常见模型总结要点梳理：全等三角形的判定与性质：一般三角形：边角边（SAS）、判角边角（ASA）、定角角边（AAS）、边边边（SSS）。

直角三角形：斜边、直角边定理（HL）。

性质：对应边相等，对应角相等（其他对应元素也相等，如对应边上的垂高相等）。

备判定：三角形全等必须有一组对应边相等。

注类型一：角平分线模型应用1.角平分性质模型：利用角平分线的性质。

例题解析：例1：如图1，在△ABC中，∠C=90°，AD平分∠CAB，BC=6cm，BD=4cm，那么点D到直线AB的距离是多少？答案】作DE⊥XXX于点E，DE=3cm。

例2：如图2，已知，∠1=∠2，∠3=∠4，求证：AP平分∠BAC。

答案】如图2，由角平分线的性质可知，PM=PN，PN=PQ，故PM=PQ，又因为PA是角BAC的平分线，所以XXX平分∠BAC。

类型二：角平分线模型应用2.角平分线，分两边，对称全等（截长补短构造全等）。

例题解析：例1：在△ABC中，∠BAC=60°，∠C=40°，AP平分∠XXX于P，BQ平分∠XXX于Q，求证：AB+BP=BQ+AQ。

答案】如图1，过O作OD∥BC交AB于D，∠ADO=∠ABC=180°－60°－40°=80°，又∵∠AQO=∠C+∠QBC=80°，∴∠ADO=∠AQO，又∵∠DAO=∠QAO，OA=AO，∴△ADO≌△AQO，∴OD=OQ，AD=AQ，又因为OD∥BP，所以∠PBO=∠DOB，又∠PBO=∠DBO，∴∠DBO=∠DOB，∴BD=OD，又∵∠XXX∠C+∠PAC=70°，∠BOP=∠OBA+∠BAO=70°，∴∠BOP=∠BPO，∴BP=OB，∴AB+BP=AD+DB+BP=AQ+OQ+BO=AQ+BQ。

如图，将△ADE逆时针旋转60°，使△ADE≌△ABC，从而得到△MDE≌△MAC，因为M为BD的中点，所以ME=MC，因此△EMC为等腰三角形，且∠MDE=∠MAC=30°，所以△EMC为等腰直角三角形。

初中数学直角三角形判定知识点结构初中数学直角三角形判定知识点结构直角三角形中有两个重要的知识点，一个是射影定理、一个是勾股定理。

直角三角形判定直角三角形的判定方法：判定1：有一个角为90°的三角形是直角三角形。

判定2：若a的平方+b的平方=c的平方，则以a、b、c为边的三角形是以c 为斜边的直角三角形(勾股定理的逆定理)。

判定3：若一个三角形30°内角所对的边是某一边的一半，那么这个三角形是以这条长边为斜边的直角三角形。

判定4：两个锐角互余的三角形是直角三角形。

判定5：证明直角三角形全等时可以利用HL ，两个三角形的斜边长对应相等，以及一个直角边对应相等，则两直角三角形全等。

[定理：斜边和一条直角对应相等的两个直角三角形全等。

简称为HL]判定6：若两直线相交且它们的斜率之积互为负倒数，则这两直线垂直。

判定7：在一个三角形中若它一边上的中线等于这条中线所在边的一半，那么这个三角形为直角三角形。

直角三角形判定知识常常运用在现实生活中，比如做房子时就要用到。

初中数学知识点总结：平面直角坐标系下面是对平面直角坐标系的内容学习，希望同学们很好的掌握下面的内容。

平面直角坐标系平面直角坐标系：在平面内画两条互相垂直、原点重合的数轴，组成平面直角坐标系。

水平的数轴称为x轴或横轴，竖直的数轴称为y轴或纵轴，两坐标轴的交点为平面直角坐标系的原点。

平面直角坐标系的要素：①在同一平面②两条数轴③互相垂直④原点重合三个规定：①正方向的规定横轴取向右为正方向，纵轴取向上为正方向②单位长度的规定；一般情况，横轴、纵轴单位长度相同；实际有时也可不同，但同一数轴上必须相同。

③象限的规定：右上为第一象限、左上为第二象限、左下为第三象限、右下为第四象限。

相信上面对平面直角坐标系知识的讲解学习，同学们已经能很好的掌握了吧，希望同学们都能考试成功。

初中数学知识点：平面直角坐标系的构成对于平面直角坐标系的构成内容，下面我们一起来学习哦。