当前位置：文档之家 › 高中数学 解三角形 课件

高中数学 解三角形 课件

  • 格式：doc
  • 大小：927.50 KB
  • 文档页数：11

下载文档原格式

  / 11

合集下载

高中数学第一章解三角形第1节正弦定理和余弦定理第1课时正弦定理课件新人教A版必修53

高中数学第一章解三角形第1节正弦定理和余弦定理第1课时正弦定理课件新人教A版必修53

45°＝
23，
∴C＝60°或 C＝120°.
当 C＝60°时，B＝75°，
b＝cssiinnCB＝ s6isnin607°5°＝ 3＋1； 当 C＝120°时，B＝15°， b＝cssiinnCB＝ s6insi1n2105°°＝ 3－1. ∴b＝ 3＋1，B＝75°，C＝60°或 b＝ 3 －1，B＝15°，C＝120°.
代入已知式子得
cos ksin
AA＝kcsoisn
BB＝kcsoisn
CC.
∴csoins
AA＝csoins
BB＝csoins
C C.
∴tan A＝tan B＝tan C.
又∵A、B、C∈(0，π)，
∴A＝B＝C.∴△ABC 为等边三角形．
法二：化边为角
由正弦定理得sina A＝sinb B＝sinc C.
提示：sina A＝sinb B＝sinc C
2．归纳总结，核心必记 (1)正弦定理 在一个三角形中，各边和它所对角的正弦的
比相等，即 (2)解三角形
一般地，把三角形的三个角 A，B，C 和它 们的对边 a，b，c 叫做三角形的元素．已知 三角形的几个元素求其他元素的过程叫做 解三角形．
[问题思考] (1)在△ABC 中 sin A＝sin B，则 A＝B 成立 吗？ (2)在△ABC 中，sin A∶sin B∶sin C＝a∶b∶c 成立吗？ (3)在△ABC 中，若 A>B，是否有 sin A>sin B？ 反之，是否成立？
—————————[课堂归纳·感悟提升]————————— 1．本节课的重点是正弦定理的应用，难点是正
弦定理的推导．
2．本节课要牢记正弦定理及其常见变形：
(1)sina A＝sinb B＝sinc C＝2R(其中 R 为△ABC 外

高中数学解三角形PPT课件

高中数学解三角形PPT课件
6.俯角和仰角的概念：在视线与水平线所成的角中,视线在水 平线上 方的角叫仰角,视线在水平线下方的角叫俯角.如图中OD、 OE是视线，是仰角， 是俯角.
22
7.关于三角形面积问题
23
用同样高度的两个测角仪AB和CD同时望见气球E在它们的正西方 向的上空，分别测得气球的仰角是α和β,已知B、D间的距离为a，测 角仪的高度是b，求气球的高度.
6
7
考点2: 三角形中的三角变换
8
9
10
考点3 与三角形的面积相关的题
11
题型2:已知面积求线段长或角
12
13
2020/1/15
14
C
15
16
17
18
19
20
解三角形应用举例
1.已知两角和一边（如A、B、C），由A+B+C = π求C，由正弦定理 求a、b
2.已知两边和夹角（如a、b、c），应用余弦定理求c边；再应用正弦定 理先求较短边所对的角，然后利用A+B+C = π，求另一角．
3.已知两边和其中一边的对角（如a、b、A），应用正弦定理 求B，由A+B+C = π求C，再由正弦定理或余弦定理求c边，要 注意解可能有多种情况．
4.已知三边a、b、c，应用余弦定理求A、B，再由A+B+C = π， 求角C．
21
5.方向角一般是指以观测者的位置为中心，将正北或正南方向作 为起始方向旋转到目 标的方向线所成的角（一般指锐角），通常表达成.正北或正南， 北偏东××度， 北偏西××度，南偏东××度，南偏西××度.
第四章 解三角形
正弦定理和余弦定理 内角和定理：
1
面积公式: 3．正弦定理：在一个三角形中,各边和它的所对角的正弦的比相等.

2024高中数学解三角形ppt课件

2024高中数学解三角形ppt课件

目录•三角形基本概念与性质•正弦定理及其应用•余弦定理及其应用•三角形面积公式及其应用•解三角形综合应用举例三角形基本概念与性质三角形的分类按边可分为不等边三角形、等腰三角形；按角可分为锐角三角形、直角三角形、钝角三角形。

三角形的定义由不在同一直线上的三条线段首尾顺次连接所组成的封闭图形。

三角形的定义与分类三角形内角和定理01三角形内角和定理三角形的三个内角之和等于180°。

02证明方法通过平行线的性质或者撕拼法等方法进行证明。

三角形外角性质三角形外角的定义三角形的一个外角等于与它不相邻的两个内角的和。

三角形外角的性质三角形的外角大于任何一个与它不相邻的内角。

三角形边与角关系01正弦定理在任意三角形中，各边和它所对角的正弦值的比相等且等于外接圆的直径。

02余弦定理在任意三角形中，任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。

03三角形的面积公式S=1/2absinC，其中a、b为两边长，C为两边夹角。

正弦定理及其应用正弦定理的推导与证明推导过程通过三角形的外接圆和正弦函数的定义，推导出正弦定理的表达式。

证明方法利用三角形的面积公式和正弦函数的性质，证明正弦定理的正确性。

利用正弦定理求解三角形已知两边及夹角求第三边通过正弦定理计算出已知两边夹角对应的第三边的长度。

已知两角及夹边求其他元素利用正弦定理和三角形内角和定理，求出三角形的其他元素。

解决三角形中的角度问题通过正弦定理计算出三角形中的未知角度。

解决三角形中的边长问题利用正弦定理求出三角形中的未知边长。

解决力学问题在力学中，正弦定理可用于解决涉及三角形的问题，如力的合成与分解等。

解决光学问题在光学中，正弦定理可用于解决涉及光的反射和折射等问题。

余弦定理及其应用余弦定理的推导与证明向量法推导余弦定理通过向量的数量积和模长关系，推导余弦定理的表达式。

几何法证明余弦定理利用三角形的面积公式和正弦定理，结合相似三角形的性质，证明余弦定理。

高中数学第二章解三角形2.1.1正弦定理课件北师大版必修5

高中数学第二章解三角形2.1.1正弦定理课件北师大版必修5

中,
sin
=

sin
=

.
sin
【做一做1】
在△ABC 中,若 3a=2bsin A,则角 B 等于
.
解析:根据已知条件及正弦定理可知 3sin A=2sin Bsin A⇔
3
π
2π
3=2sin B⇔sin B= 2 ,所以角 B 为3 或 3 .
π
2π
答案:3 或 3
知识拓展1.正弦定理的证明
Bcos A,又 sin B≠0,则 sin A= 3cos A,即 tan A= 3,又△ABC 为锐角三
π
角形,所以 A= .
3
答案:(1)7∶5∶3 (2)A
探究一
探究二
探究三
探究二
探究四
思维辨析
利用正弦定理解三角形
【例2】 在△ABC中,
(1)若A=45°,B=30°,a=2,求b,c与C.
(2)若B=30°,b=5, c=5 3 ,求A,C与a.
分析:先根据三角形中解的个数的判断方法得出解的情况,再求
出各元素的值.
解:(1)由三角形内角和定理得,
C=180°-(A+B)=180°-(45°+30°)=105°.
sin
由正弦定理得,b=
sin
1
=
sin 105°=sin(60°+45°)=
(5)在△ABC中,若 cos = 1 + cos2 ,则△ABC为等腰三角形或直
角三角形. (
)
答案:(1)
(2)
(3)× (4)× (5)
探究一
探究二
探究一
探究三
探究四
思维辨析

《高中数学课件-解三角形》

《高中数学课件-解三角形》

如何利用三角函数求解三角形边长？
1
余弦定理
2
可以用已知角度的余弦值、已知角度、
另一条边，计算第三边。
3
正弦定理
可以用已知角度的正弦值、已知角度、 另一条边，计算第三边。
正切定理
可以用已知角度的正切值、已知角度、 另一条边，计算第三边。
如何应用海伦公式求解三角形面积？
公式
海伦公式：$\sqrt{s(s-a)(sb)(s-c)}$
如何解三角形在平面几何中的 应用？
可以用来计算各种图形的面积、周长、角度大小等，是很多数学问题的基础 和工具。
如何应用三角函数求解解决实 际问题？
可以用来求解各种实际问题，如测量高度、距离、角度大小、速度等。
含义
s是半周长，a、b、c是三 角形的三条边长。
优点不需要知道高或者角度，来自适用面较广。如何应用正弦定理、余弦定理判定三角 形形状？
正弦定理
三角形是锐角；两个边长和对应角度的正弦值 成正比。
余弦定理
三角形是直角、钝角；其中直角三角形满足勾 股定理；余角大小决定了所求角度，等于对应 锐角角度的补角。
如何利用三角函数公式求解各种角度和 边长？
1
正弦函数公式
${\sin x} = \frac{\text{对边}}{\text{斜
余弦函数公式
2
边}}$
${\cos x} = \frac{\text{邻边}}{\text{斜
边}}$
3
正切函数公式
${\tan x} = \frac{\text{对边}}{\text{邻 边}}$
如何求解等腰三角形的各个角 度和边长？
可以直接应用角度和及等腰三角形的性质求解。
如何求解等边三角形的各个角度和边长？

高中数学第一章解三角形1.1.1正弦定理课件新人教A版必修5

高中数学第一章解三角形1.1.1正弦定理课件新人教A版必修5
第一章 解三角形
1.1 正弦定理和余弦定理
1.1.1 正弦定理
课标阐释 1.掌握正弦定理及 其变形. 2.了解正弦定理的 证明方法. 3.能运用正弦定理 解决相关问题.
思维脉络
正弦定理 正弦定理的变形 正弦定理 正弦定理的应用 解三角形
判断三角形的形状
一二三
一、正弦定理
【问题思考】 1.已知△ABC,设其三个内角分别为 A,B,C,角 A,B,C 所对的边分
答案(1)4 (2)45°
一二三
二、正弦定理的变形 【问题思考】 1.正弦定理揭示了三角形中边与角的数量关系,那么根据正弦定理, 怎样由边转化为角?怎样由角转化为边?
提示通过对正弦定理 ������
sin������
=
������ sin������
=
si���n��� ������=2R
进行不同的变形,可以实
以 ������
sin������
=
������ sin������
=
si���n��� ������成立.
(2)成立,不妨设 C=90°,则 sin A=������������,sin B=������������,sin C=1=������������,所以
������ sin������
=
现由边到角、由角到边的转化.
2.填空: 正弦定理的变形(R 为△ABC 外接圆的半径) (1)a=2Rsin A,b=2Rsin B,c=2Rsin C;
(2)sin A=2������������,sin B=2������������,sin C=2������������;
(3)a∶b∶c=sin A∶sin B∶sin C.

高中数学第二章解三角形2.1.2余弦定理课件北师大版必修5


1
2
3
4
5
1.在△ABC 中,已知 a=5,b=4,C=120°,则 c 的长为(
A. 41
C. 41或 61
)
B. 61
D. 21
1
解析: 因为 c2=a2+b2-2abcos C,所以 c2=52+42-2×5×4× - 2 =61,即
c= 61.
答案:B
1
2
3
4
5
2.在△ABC中,若bcos A=acos B,则△ABC是(
角A,B,C的对边,且b2,c2是关于x的一元二次方程x2-(a2+bc)x+m=0的
两根.
(1)求角A的大小;
(2)若 a= 3 ,设B=θ,△ABC的周长为y,求y=f(θ)的最大值.
分析:(1)利用余弦定理求出角A;(2)先利用正弦定理将△ABC的周
长y表示成关于θ的函数,再结合三角函数的性质进行求解.
探究一
探究二
探究三
思维辨析
解:(1)在△ABC中,依题意有b2+c2=a2+bc,即b2+c2-a2=bc,
所以 cos
2
+2 -2
A=
2
1
2
= ,
π
3
又因为 A∈(0,π),所以 A= .
π
3
(2)由 a= 3,A= ,及正弦定理得

sin
=
所以 b=2sin B=2sin θ,c=2sin C=2sin
1 .2
余弦定理
学 习 目 标
1.掌握余弦定理及其证明.
2.会用余弦定理解决两类解三角形问题.
3.能综合应用正弦定理与余弦定理解决三角形

“高中数学选修4-解三角形课件”


探讨海龙公式的应用
学习使用海龙公式解决特殊情况下的三角形问题。
1 海龙公式
s =(a +b +c) / 2
解决一个三角形不唯一的情况的方法
探讨当一个三角形不唯一时，如何确定其特殊属性和解决问题的方法。
1
等腰三角形
了解等腰三角形的特点和解决方法。
直角三角形
2
讲解如何确定直角三角形以及解题
技巧。
3
其他特殊情况
余弦定理公式
c²= a²+ b ² - 2ab *co sC
应用技巧
学习使用余弦定理解决复杂 问题的技巧。
实例演示
通过例题演示如何使用余弦 定理求解。
使用正切定理求解的方法
详细讲解如何运用正切定理解决三角形问题。
1
解决步骤
2
说明使用正切定理求解的步骤。
3
正切定理公式
a/b = tanA
实战演练
通过实例演示如何应用正切定理。
正弦函数
绘制正弦函数的图像和周期 特性。
余弦函数
绘制余弦函数的图像和周期 特性。
正切函数
绘制正切函数的图像和周期 特性。
使用三角函数解决三角形问题
演示如何应用三角函数解决各种实际三角形问题。
1 角度问题
通过角度信息和三角函数求 解缺失的边长。
2 边长问题
通过边长和三角函数求解未 知的角度。
3 应用实例
介绍其他特殊情况下的处理方式。
三角函数的概念和基本性质
详细介绍三角函数的概念、定义和基本性质。
正弦函数
解释正弦函数的定义和性质。
余弦函数
介绍余弦函数的特点和性质。
正切函数
讨论正切函数的定义和特性。

解直角三角形ppt课件

经济学中的复利计算
在经济学中，经常需要进行复利计算。虽然复利计算本身与解直角三角形没有直接关系， 但是可以通过构造类似直角三角形的数学模型并求解，得到复利计算的精确结果。
06
解直角三角形的拓展与延伸
斜三角形的解法探讨
斜三角形的定义与性质
斜三角形是指一个三角形中不包含直角的情况。其性质包 括三角形的内角和为180度，以及三边关系等。
工程问题中的解直角三角形
土木工程中的坡度计算
在土木工程中，经常需要计算坡度，即斜坡的倾斜程度。 通过构造直角三角形并求解，可以得到精确的坡度值。
机械工程中的力学分析
在机械工程中，经常需要对物体进行力学分析。通过构造 直角三角形并利用三角函数求解，可以得到物体受到的力 的大小和方向。
电气工程中的相位差计算
在电气工程中，经常需要计算两个交流信号之间的相位差 。通过构造直角三角形并求解，可以得到精确的相位差值 。
其他实际问题中的解直角三角形
航海问题中的航向和航程计算
在航海问题中，经常需要计算航向和航程。通过构造直角三角形并求解，可以得到精确的 航向和航程值。
物理学中的矢量合成与分解
在物理学中，经常需要对矢量进行合成与分解。通过构造直角三角形并利用三角函数求解 ，可以得到合成或分解后的矢量的大小和方向。
在直角三角形中，已知任意两边长，可以利用勾股定理求出 第三边长。
已知角度和一边求另一边
在直角三角形中，已知一个锐角和一条边长，可以利用三角 函数和勾股定理求出另一条边长。
勾股定理在实际问题中的应用
测量问题
在测量问题中，可以利用 勾股定理解决距离、高度 等测量问题。
工程问题
在工程问题中，可以利用 勾股定理解决角度、长度 等计算问题。

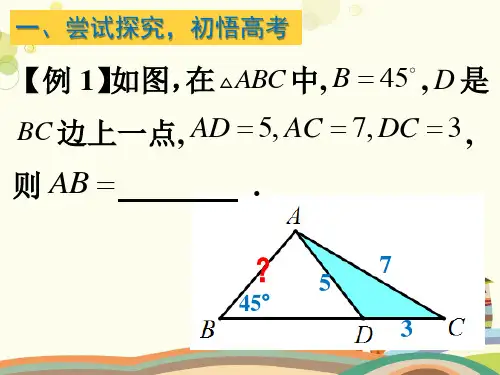
解三角形完整版课件


1 2
c.
（1）求角 B 的大小；
B
3
.
（3）若 b 3 ，求△ABC 面积的最大值．
深度探究
四、横向拓展，发散思维
【例 2】在△ABC 中,内角 A、B、C 的对边分别为 a,b,c ，
且
b
cos C
a
1 2
c.
（1）求角 B 的大小；
B
3
.
（4）若 b 3 ，求△ABC 周长的最大值．
c.
（1）求角 B 的大小；
二、边角转化，学会分析
【例 2】在△ABC 中，内角 A、B、C 的对边分别为 a、b、
c，且 bcosC a 1 c.
2
（1）求角 B 的大小；
【解析一】(角化边)由余弦定理，有 b
a2
b2 c2 2ab
a
1 c. 2
化简得 a2 c2 b2 ac.
a2 c2 b2 1
2
sin B cosC sin B C 1 sinC
2
sin B cosC cos B sinC 1 sinC. 2
即 cos BsinC 1 sinC ，又 C 0, ，所以 sinC 0,1 ，
2
于是 cos B 1 . 又因为 B 0, ，所以 B .
2
3
三、纵向引申、深度感知
一、尝试探究，初悟高考
【例 1】如图，在 ABC 中, B 45 , D 是
BC 边上一点, AD 5, AC 7, DC 3,
则 AB
.
？5 7
45°
3
一、尝试探究，初悟高考
【例 1】如图，在 ABC 中, B 45 ,D 是 BC 边上一点, AD 5, AC 7, DC 3,则 AB
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

解三角形亲爱的同学，太阳每天都是新的，你是否每天都在努力。

（数学5必修）第一章：解三角形[基础训练A 组]一、选择题1．在△ABC 中，若0030,6,90===B a C ，则b c -等于（ ）A ．1B ．1-C ．32D ．32-2．若A 为△ABC 的内角，则下列函数中一定取正值的是（ ） A ．A sin B ．A cos C ．A tan D ．Atan 1 3．在△ABC 中，角,A B 均为锐角，且,sin cos B A >则△ABC 的形状是（ ） A ．直角三角形 B ．锐角三角形 C ．钝角三角形 D ．等腰三角形4．等腰三角形一腰上的高是3，这条高与底边的夹角为060，则底边长为（ ）A ．2B ．23 C ．3 D ．32 5．在△ABC 中，若B a b sin 2=，则A 等于（ ）A ．006030或B ．006045或C ．0060120或D ．0015030或6．边长为5,7,8的三角形的最大角与最小角的和是（ ）A ．090B ．0120C ．0135D ．0150二、填空题1．在Rt △ABC 中，090C =，则B A sin sin 的最大值是_______________。

2．在△ABC 中，若=++=A c bc b a 则,222_________。

3．在△ABC 中，若====a C B b 则,135,30,200_________。

4．在△ABC 中，若sin A ∶sin B ∶sin C =7∶8∶13，则C =_____________。

5．在△ABC 中，,26-=AB 030C =，则AC BC +的最大值是________。

三、解答题1． 在△ABC 中，若,cos cos cos C c B b A a =+则△ABC 的形状是什么？2．在△ABC 中，求证：)cos cos (aA bB c a b b a -=-3．在锐角△ABC 中，求证：C B A C B A cos cos cos sin sin sin ++>++。

4．在△ABC 中，设,3,2π=-=+C A b c a 求B sin 的值。

（数学5必修）第一章：解三角形[综合训练B 一、选择题1．在△ABC 中，A ．1:2:3 B 2．在△ABC A ．大于零 B 3．在△ABC A ．A b sin 2 B 4．在△ABC A ．直角三角形 5．在△ABC A ．090 B ．6．在△ABC A ．51- B ．-7．在△ABC A ．直角三角形 二、填空题1．若在△ABC 2．若,A B 3．在△ABC 4．在△ABC 中，若,12,10,9===c b a 则△ABC 的形状是_________。

5．在△ABC 中，若=+===A c b a 则226,2,3_________。

6．在锐角△ABC 中，若2,3a b ==，则边长c 的取值范围是_________。

三、解答题1． 在△ABC 中，0120,,ABC A c b a S =>==，求c b ,。

2． 在锐角△ABC 中，求证：1tan tan tan >⋅⋅C B A 。

3． 在△ABC 中，求证：2cos 2cos 2cos4sin sin sin C B A C B A =++。

4． 在△ABC 中，若0120=+B A ，则求证：1=+++ca b c b a 。

5．在△ABC[提高训练C 一、选择题1．A 为△ABC A ．)2,2( B 2．在△ABC A ．2cos 2B A + 3．在△ABC A ．12 B ．221 4．在△ABC 中，∠A ．sin cos A A >5．在△ABC A ．090 B ．6．在△ABC 2tan b B A ．直角三角形 B ．等腰或直角三角形 C ．不能确定 D ．等腰三角形二、填空题1．在△ABC 中，若,sin sin B A >则A 一定大于B ，对吗？填_________（对或错）2．在△ABC 中，若,1cos cos cos 222=++C B A 则△ABC 的形状是______________。

3．在△ABC 中，∠C 是钝角，设,cos cos ,sin sin ,sin B A z B A y C x +=+==则z y x ,,的大小关系是___________________________。

4．在△ABC 中，若b c a 2=+，则=+-+C A C A C A sin sin 31cos cos cos cos ______。

5．在△ABC 中，若,tan lg tan lg tan lg 2C A B +=则B 的取值范围是_______________。

6．在△ABC 中，若ac b =2，则B B C A 2cos cos )cos(++-的值是_________。

三、解答题1．在△ABC 中，若)sin()()sin()(2222B A b a B A b a +-=-+，请判断三角形的形状。

2． 如果△ABC 内接于半径为R 的圆，且,sin )2()sin (sin 222B b a C A R -=-求△ABC 的面积的最大值。

3． 已知△ABC4． 在△ABC ,,A B C 的大小与边,,a b c（数学5必修）第一章 [基础训练A 组]一、选择题1.C 00tan 30,tan 302b b a c b c b a=====-=2.A 0,sin 0A A π<<> 3.C cos sin()sin ,,22A A B A B ππ=->-都是锐角，则,,222A B A B C πππ->+<> 4.D 作出图形 5.D 012sin ,sin 2sin sin ,sin ,302b a B B A B A A ====或01506.B 1.12 2.01203.6-4. 1205. 4 1. 所以△ABC 是直角三角形。

2. 证明：将ac b c a B 2cos 222-+=，bca cb A 2cos 222-+=代入右边 得右边2222222222()222a c b b c a a b c abc abc ab+-+--=-= 22a b a b ab b a-==-=左边， ∴)cos cos (aA bB c a b b a -=-3．证明：∵△ABC 是锐角三角形，∴,2A B π+>即022A B ππ>>-> ∴sin sin()2A B π>-，即sin cos A B >；同理sin cos B C >；sin cos C A >∴C B A C B A cos cos cos sin sin sin ++>++4.解：∵2,a c b +=∴sin sin 2sin A C B +=，即2sin cos 4sin cos 2222A C A CB B +-=，∴1sin cos 2224B A C -==，而0,22B π<<∴cos 24B =，∴sin 2sin cos 2B B B ===391.CA 2.A A3.D4.D5.B (a b6.C 2c7.D 所以A B =或2A B += 二、填空题1.3392 211sin 4,13,222ABC S bc A c c a a ∆==⨯==== sin sin sin sin a b c a A B C A ++===++2.> ,22A B A B ππ+>>-，即sin()2tan tan()2cos()2B A B B πππ->-=- cos 1sin tan B B B ==，1tan ,tan tan 1tan A A B B>> 3. 2 sin sin tan tan cos cos B C B C B C+=+ sin cos cos sin sin()2sin 1cos cos sin sin 2B C B C B C A B C A A +++=== 4. 锐角三角形5. 060 cos A =6． 三、解答题1.解：12ABC S ∆=22a b =+所以,1=b 2. 证明：∵△ ∴sin A ∴sin A ∴tan A 3. 证明：∵sin2sin 2222=2sin (cos cos )222A B A B A B +-+=+2cos 2cos cos 222C A B =⋅ 4cos cos cos 222A B C = ∴2cos 2cos 2cos 4sin sin sin C B A C B A =++4．证明：要证1=+++ca b c b a ，只要证2221a ac b bc ab bc ac c +++=+++， 即222a b c ab +-=而∵0120,A B +=∴060C =2222220cos ,2cos 602a b c C a b c ab ab ab+-=+-== ∴原式成立。

5．证明：∵223cos cos 222C A b a c += ∴1cos 1cos 3sin sin sin C A B A C ++⋅+⋅= ABC S =cos B = B << 二、填空题1. 对 ,sin sin B A >则22a b a b A B R R >⇒>⇒> 2. 直角三角形 21(1cos 21cos 2)cos ()1,2A B A B +++++= 21(cos 2cos 2)cos ()0,2A B A B +++= 2cos()cos()cos ()0A B A B A B +-++=cos cos cos 0A B C =3. z y x << ,,sin cos ,sin cos ,22A B A B A B B A y z ππ+<<-<<< ,sin sin sin ,,c a b C A B x y x y z <+<+<<<4．1 sin sin 2sin ,2sin cos 4sin cos 2222A C A C A C A C A CB +-+++== cos 2cos ,cos cos 3sin sin 222222A C A C A C A C -+== 则221sin sin 4sin sin 322A C A C = 1cos cos cos cos sin sin A C A C A C +-+5. 3[π6．1 1.2. 解：2sin sin 2sin sin )sin ,R A A R C C b B ⋅-⋅=-222sin sin )sin ,,a A c C b B a c b -=--=-2222220,cos ,4522a b c a b c C C ab +-+-====2222,2sin ,2,sin c R c R C a b R C===+-= 222222,R a b ab ab +=+≥≤21sin 244S ab C ab ==≤2max 212R S +=另法：1sin 2sin 2sin 244S ab C R A R B ===⨯22sin 2sin sin sin 4R A R B A B =⨯⨯=21[cos()cos()]2A B A B =⨯⨯--+21[cos()22A B =⨯⨯-+≤3. 解：a 4. 解：( 得tan tan ⎧⎪⎨⎪⎩ 当0075,45A C ==时，1),8bc a ==== 当0045,75A C ==时，1),8sin b c a A==== ∴当00075,60,45A B C ===时，8,1),a b c ===当00045,60,75A B C ===时，8,1)a b c ===。