等差数列常考题型归纳总结很全面
- 格式:doc
- 大小:1.66 MB
- 文档页数:10

根据等差数列知识点总结及题型归纳
等差数列是数学中常见的数列,也是初中数学中的基础概念之一。
以下是关于等差数列的知识点总结及题型归纳。
等差数列的定义
等差数列是指一个数列中的每个数与它的前一个数的差值都相等的数列。
通常用字母 a 表示首项,d 表示公差,数列的通项公式为 an = a + (n-1)d。
等差数列的性质
1. 首项与末项之和等于中间项之和的两倍(也即数列的平均值):a + an = 2 * (a + (n-1)d)。
2. 求和公式:等差数列前 n 项和 Sn = (n/2) * (2a + (n-1)d)。
3. 最后一项的值可以通过首项、末项和公差求得:an = a + (n-1)d。
4. 任意一项的值可以通过首项、公差和项数求得:ak = a + (k-1)d。
等差数列的题型归纳
1. 求等差数列的第 n 项的值。
2. 求等差数列的前 n 项和。
3. 求等差数列中缺失的项或差值。
4. 求等差数列中满足一定条件的项数。
5. 求等差数列中满足一定条件的和。
示例题目
1. 已知等差数列的首项 a = 3,公差 d = 2,求第 5 项的值和前5 项的和。
2. 一个等差数列的首项 a = 1,公差 d = 3,已知数列中缺失了第 4 项,求第 4 项的值。
3. 已知等差数列的首项 a = 2,公差 d = 5,求该等差数列中满足大于 20 的项数。
以上是对于等差数列的知识点总结及题型归纳,希望对你有所帮助。
如有需要,可以参考相应的解题方法和公式。

等差数列的19种经典题型
等差数列是指一个数列中,从第二项起,每一项与它的前一项之差都相等的数列。
以下是一些常见的等差数列题型:
1. 求等差数列的通项公式;
2. 已知等差数列的首项和公差,求第n项的值;
3. 求等差数列前n项的和;
4. 求等差数列中有多少项满足某个条件;
5. 求等差数列的前n项和与后n项和的关系;
6. 求等差数列的和等于某个数的情况下,确定首项和项数;
7. 求等差数列的和等于另一个等差数列的情况下,确定首项、项数及公差;
8. 求等差数列中的两个数之和等于某个数的情况下,确定这两个数的位置;
9. 求等差数列中的两个数之积等于某个数的情况下,确定这两个数的位置;
10. 求等差数列中的两个数之差等于某个数的情况下,确定这两个数的位置;
11. 求等差数列中的两个数之商等于某个数的情况下,确定这两个数的位置;
12. 求等差数列中的两个项之和等于某个数的情况下,确定这两个项的位置;
13. 求等差数列中的两个项的积等于某个数的情况下,确定
这两个项的位置;
14. 求等差数列中的两个项的差等于某个数的情况下,确定这两个项的位置;
15. 求等差数列中的一个项与它前面的项和后面的项的和的比值;
16. 求等差数列中任意两项之间的差的绝对值;
17. 求等差数列的平均值;
18. 已知等差数列的前n项和及项数,求公差;
19. 已知等差数列的前n项和及公差,求项数。
以上是一些经典的等差数列题型,通过掌握这些题型的解题方法和技巧,可以更好地解决与等差数列相关的问题。

数列一、等差数列题型一、等差数列定义:一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫等差数列,这个常数叫做等差数列的公差,公差通常用字母d 表示。
用递推公式表示为1(2)n n a a d n --=≥或1(1)n n a a d n +-=≥。
例:等差数列12-=n a n ,=--1n n a a 题型二、等差数列的通项公式:1(1)n a a n d =+-;说明:等差数列(通常可称为A P 数列)的单调性:d 0>为递增数列,0d =为常数列,0d < 为递减数列。
例:1.已知等差数列{}n a 中,12497116a a a a ,则,==+等于( ) A .15 B .30 C .31 D .642.{}n a 是首项11a =,公差3d =的等差数列,如果2005n a =,则序号n 等于 (A )667 (B )668 (C )669 (D )6703.等差数列12,12+-=-=n b n a n n ,则n a 为 n b 为 (填“递增数列”或“递减数列”)题型三、等差中项的概念:定义:如果a ,A ,b 成等差数列,那么A 叫做a 与b 的等差中项。
其中2a bA += a ,A ,b 成等差数列⇔2a bA +=即:212+++=n n n a a a (m n m n n a a a +-+=2) 例:1.设{}n a 是公差为正数的等差数列,若12315a a a ++=,12380a a a =,则111213a a a ++= ( )A .120B .105C .90D .752.设数列{}n a 是单调递增的等差数列,前三项的和为12,前三项的积为48,则它的首项是( ) A .1 B.2 C.4 D.8题型四、等差数列的性质:(1)在等差数列{}n a 中,从第2项起,每一项是它相邻二项的等差中项; (2)在等差数列{}n a 中,相隔等距离的项组成的数列是等差数列; (3)在等差数列{}n a 中,对任意m ,n N +∈,()n m a a n m d =+-,n ma a d n m-=-()m n ≠;(4)在等差数列{}n a 中,若m ,n ,p ,q N +∈且m n p q +=+,则m n p q a a a a +=+; 题型五、等差数列的前n 和的求和公式:11()(1)22n n n a a n n S na d +-==+n da )(2n 2112-+=。


等差数列知识点及考点试题解析一.等差数列的定义如果一个数列从第2项起,每一项与它的前一项的差都等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差,通常用字母d表示.二.等差中项如果三个数a,A,b组成等差数列,那么A叫做a与b的等差中项,由等差数列的定义知2A =a+b.①a,A,b是等差数列的充要条件是2A=a+b.②数列{an}是等差数列⇔2an=an-1+an+1(n≥2).③若{an}为等差数列,且k+l=m+n(k,l,m,n∈N*),则ak+al=am+an.三.等差数列的通项公式首项为a1,公差为d的等差数列{an}的通项公式为an=a1+(n-1)d;an=am+(n-m)d(n,m ∈N*)四.等差数列的前n项和公式1.设等差数列{an}的首项为a1,公差为d,其前n项和Sn=n(a1+an)2或Sn=na1+n(n-1)d.22.等差数列的前n项和公式与函数的关系Sn=dn2n⇌数列{an}是等差数列⇔Sn=2An2+Bn(A,B为常数).3.等差数列的前n项和的最值在等差数列{an}中,若a1>0,d<0≥0,+1≤0的项数m 使得Sn 取得最大值Sm ;若a1<0,d>0≤0,+1≥0的项数m 使得Sn 取得最小值Sm .一.等差数列运算问题的通性方法1.等差数列运算的一般求法是设出首项a1和公差d ,然后由通项公式或前n 项和公式转化为方程(组)求解.2.等差数列的通项公式及前n 项和公式,共涉及五个量a1,an ,d ,n ,Sn ,知其中三个就能求另外两个。
二.等差数列的判定与证明的常用方法1.定义法:an +1-an =d(d 是常数,n ∈N*)或an -an -1=d(d 是常数,n ∈N*,n≥2)⇔{an}为等差数列.2.等差中项法:2an +1=an +an +2(n ∈N*)⇔{an}为等差数列.3.通项公式法:an =an +b(a ,b 是常数,n ∈N*)⇔{an}为等差数列.4.前n 项和公式法:Sn =an2,b 为常数)⇔{an}为等差数列.三.在等差数列{an}中前n项和性质1.Sm ,S2m -Sm ,S3m -S2m ,…,构成等差数列;2.S2n =n(a1+a2n)=…=n(an +an +1);3.S2n -1=(2n -1)an .n n n n 2n 1n 2n 1n 2n-12m 1m2n 1n(S T a b n S (2n 1)a S a 1S =(2)T (2m 1)b T b -----==-−−→特例n 4.数列项数为奇数2n-1时、分别是等差数列、的前项和)()(2n-1)a 5.若项数为偶数2n ,则S2n =n(a1+a2n)=n(an +an +1);S 偶-S 奇=nd ;S 奇S 偶=anan +1.6.若项数为奇数2n-1,则S2n-1=(2n-1)an;S奇-S偶=an;S奇S偶=nn-1.四.求等差数列前n项和Sn及最值1,二次函数法:用求二次函数最值的方法(配方法)求其前n项和的最值,但要注意n∈N*.2.图象法:利用二次函数图象的对称性来确定n的值,使Sn取得最值.3.项的符号法(邻项变号法):①当a1>0,d<0≥0,+1≤0的项数m使得Sn取得最大值为Sm;②当a1<0,d>0≤0,+1≥0的项数m使得Sn取得最小值为Sm.数列的单调性当d>0时,{an}是递增数列;当d<0时,{an}是递减数列;当d=0时,{an}是常数列.考点等差数列基本量的计算【例1-1】(2023·河南洛阳·模拟预测)已知等差数列{}na的前n项和为nS,131,18a S==,则6S=()A.54B.71C.80D.81【答案】D【解析】设等差数列{}n a的公差为d ,因为131,18a S ==,可得1333318a d d +=+=,解得5d =,所以166********S a d =+=+⨯=.故选:D.【例1-2】(2023·河北·统考模拟预测)已知等差数列{}n a 的前n 项和是376,1,3n S a S a ==,则3S =()A .1B .1-C .3D .3-【答案】D【解析】由已知设等差数列的公差为d ,则3121a a d =+=,117673(5)2a d a d ⨯+=+,解得13a =-,2d =,所以31333S a d =+=-.故选:D.【例1-3】(2023·全国·统考高考真题)记n S 为等差数列{}n a的前n 项和.若264810,45a a a a +==,则5S =()A .25B .22C .20D .15【答案】C【解析】方法一:设等差数列{}n a的公差为d ,首项为1a ,依题意可得,2611510a a a d a d +=+++=,即135a d +=,又()()48113745a a a d a d =++=,解得:11,2d a ==,所以515455210202S a d ⨯=+⨯=⨯+=.故选:C.方法二:264210a a a +==,4845a a =,所以45a =,89a =,从而84184a a d -==-,于是34514a a d =-=-=,所以53520S a ==.故选:C.【一隅三反】1.(2023·四川雅安·统考三模)已知数列{}n a 的前n 项和为n S .若()*111,2N n n n a S S a n +==++∈,则5S =()A .16B .25C .29D .32【答案】B【解析】由12n n n S S a +=++可得12n n a a +=+,即12n n a a +-=,故数列{}n a是以11a =为首项,2为公差的等差数列,所以5154=52252S a ⨯+⨯=,故选:B2.(2023春·广东佛山)(多选)若{}n a为等差数列,211a =,55a =,则下列说法正确的是()A .152n a n=-B .-11是数列{}n a中的项C .数列{}n a 的前n 项和212n S n n =-+D .数列{}n a的前7项和最大【答案】ABD【解析】2111a a d =+=,5145a a d =+=,解得113a =,2d =-,对选项A :()()1312152n a n n=+-⨯-=-,正确;对选项B :取15211n a n =-=-,13n =,正确;对选项C :()21132142n n n S n n n -=-⨯=-+,错误;对选项D :152n a n =-,710a =>,810a =-<,故数列{}n a的前7项和最大,正确.故选:ABD3.(2023·全国·高三专题练习)(多选)已知等差数列{}n a为递减数列,且31a =,2434a a =,则下列结论中正确的有()A .数列{}n a的公差为12-B .1522n a n =-+C .数列{}1n a a 是公差为1-的等差数列D .1741a a a +=-【答案】ABC【解析】由题意知,2432 2.a a a +==又2434a a =,故24,a a 可看出方程23204x x -+=的两根,∵数列{}n a为递减数列,412a ∴=,232a =.∴公差42122a a d -==-,故A 正确;又122a a d =-=,11521222n a n n ∴=+-⨯-=-+()(),故B 正确;由上可知12n n a a a =,则当2n ≥时,()111222212n n n n a a a a --⎛⎫-=-=⨯-=- ⎪⎝⎭,当1n =时,214a =,∴数列{}1n a a 是首项为4,公差为1-的等差数列,故C 正确;由C 选项知:15n a a n =-,故17572a a =-=-,∵451222a =-=,174135722a a a ∴+=-+=-,故D 错误.故选:ABC4.(2023·河北唐山·唐山市第十中学校考模拟预测)(多选)已知数列{}n a的前n 项和为n S ,若数列{}n a和均为等差数列,且518a=,则()A .16a =B .830a =C .560S =D .798S =【答案】BD【解析】数列{}n a为等差数列,设其首项为1a ,公差为d ,则18(5)185n n d dn d a =+-=+-,5(184)(3692182)n n nS d dn d dn d +-=+-+=-,由数列为等差数列,可得则7215d -=两边平方整理得,28160d d -+=,解之得4d =,则42n a n =-,22n S n =,选项A :1422a =-=.判断错误;选项B :848230a =⨯-=.判断正确;选项C :252550S =⨯=.判断错误;选项D :272798S =⨯=.判断正确.故选:BD考点等差数列的判定与证明【例2-1】(2023·全国·高三专题练习)已知数列{}n a满足1111,22n n a a a +=-=--.证明:11n a ⎧⎫⎨⎬+⎩⎭是等差数列,并求出数11n a ⎧⎫⎨+⎩⎭的通项公式.【答案】证明见解析,111n n a =++【解析】因为112n n a a +=--,所以1111122n n n n a a a a +++=+=--+,则12111111n n n n a a a a ++==++++,即111111n n a a +-=++,又112a =-,则1121112n a ==+-,所以11n a ⎧⎫⎨+⎩⎭是首项为2,公差为1的等差数列,所以()121111n n n a =+-⨯=++.【例2-2】(2023·北京)已知数列{}n a满足()1144,41n n a a n a -==->,记12n n b a =-.求证:数列{}n b 是等差数列.【答案】证明见解析【解析】(定义法)111111422242n n n n n nb b a a a a ++-=-=------()121222nn a a -==-,所以数列{}n b 是首项为11122a =-,公差为12的等差数列.(等差中项法)12n n b a =-,()1111422242n n n n na b a a a ++===----,()1214412224242n nn n n n n a a a b a a a +++--==--⎛⎫-- ⎪⎝⎭,所以()21112202222n n n n n n n n a a b b b a a a ++-+-=+-⨯=---,所以()*212N n n n b b b n +++=∈,所以数列{}n b 是首项为11122a =-,公差为12的等差数列.【一隅三反】1.(2023·安徽)若数列{}n a为等差数列,则下列说法中错误的是()A .数列12a ,22a ,32a ,…,2n a …为等差数列B .数列2a ,4a ,6a ,…,2n a ,…为等差数列C .数列{}1n n a a +为等差数列D .数列{}1n n a a ++为等差数列【答案】C【解析】A 选项:因为{}n a为等差数列,所以设1n n a a d --=(d 为常数),又()112222n n n n a a a a d---=-=,所以数列{}2n a 也为等差数列,故A 正确;B 选项:2222n n a a d --=,所以数列{}2n a 为等差数列,故B 正确;C 选项:112n n n n n a a a a da +--={}1n n a a +不是等差数列,故C 错;D 选项:()112n n n n a a a a d+-+-+=,所以数列{}1n n a a ++为等差数列,故D 正确.故选:C.2.(2023·云南)已知等差数列{}n a的前n 项和为n S ,若6812,72,a S ==(1)求数列{}n a的通项公式.(2)证明:数列n S n ⎧⎫⎨⎬⎩⎭为等差数列.【答案】(1)2n a n =(2)证明见解析【解析】(1)设等差数列{}n a 的公差为d ,由题意得11512878722a d a d +=⎧⎪⎨⨯+=⎪⎩,解得122a d =⎧⎨=⎩,有22(1)2n a n n=+-=,所以等差数列{}n a 的通项公式为2n a n =;(2)由(1)知(22)(1)2n nS n n n =+=+,1n S n n =+,所以1(1)1(1)11n n S S n n n n +-=++-+=+,又121S =,故数列n S n ⎧⎫⎨⎬⎩⎭是以2为首项,1为公差的等差数列.3.(2023·广东)已知数列{n a }满足112,12nn n a a a a +==+.(1)求证:数列1n a ⎧⎫⎨⎬⎩⎭是等差数列;(2)求数列{n a }的通项公式.【答案】(1)证明见解析(2)243n a n =-【解析】(1)证明:数列{n a }满足112,12nn n a a a a +==+.两边取倒数可得:1112n n a a +=+,即1112n n a a +-=,∴数列{1n a }是等差数列,首项为1112=a ,公差为2;(2)由(1)可得:()11432122n n n a -=+-=,解得243n a n =-.。

等差数列的性质总结1.等差数列的定义:(d 为常数)();d a a n n =--12≥n 2.等差数列通项公式:, 首项:,公差:d ,末项:*11(1)()n a a n d dn a d n N =+-=+-∈1a n a 推广: . 从而;d m n a a m n )(-+=mn a a d mn --=3.等差中项(1)如果,,成等差数列,那么叫做与的等差中项.即:或a A b A a b 2ba A +=b a A +=2(2)等差中项:数列是等差数列{}n a )2(211-≥+=⇔+n a a a n n n 212+++=⇔n n n a a a 4.等差数列的前n 项和公式:1()2n n n a a S +=1(1)2n n na d -=+特别地,当项数为奇数时,是项数为2n+1的等差数列的中间项21n +1n a +5.等差数列的判定方法(1) 定义法:若或(常数) 是等差数列. d a a n n =--1d a a n n =-+1*∈N n ⇔{}n a (2) 等差中项:数列是等差数列. {}n a )2(211-≥+=⇔+n a a a n n n 212+++=⇔n n n a a a (3) 数列是等差数列(其中是常数)。
{}n a ⇔b kn a n +=b k ,(4) 数列是等差数列,(其中A 、B 是常数)。
{}n a ⇔2n S An Bn =+6.等差数列的证明方法定义法:若或(常数) 是等差数列.d a a n n =--1d a a n n =-+1*∈N n ⇔{}n a 7.提醒:等差数列的通项公式及前n 项和公式中,涉及到5个元素:,其中n a n S n n S a n d a 及、、、1称作为基本元素。
只要已知这5个元素中的任意3个,便可求出其余2个,即知3求2.d a 、18. 等差数列的性质:(1)当公差时,0d ≠等差数列的通项公式是关于的一次函数,且斜率为公差;11(1)n a a n d dn a d =+-=+-n d 前和是关于的二次函数且常数项为0.n 211(1)(222n n n d dS na d n a n -=+=+-n (2)若公差,则为递增等差数列,若公差,则为递减等差数列,若公差,则为常数列。

等差数列知识清单1、等差数列定义:一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫等差数列,这个常数叫做等差数列的公差,这个常数叫做等差数列的公差,公差通常用字母公差通常用字母d 表示。
用递推公式表示为1(2)n n a a d n --=³或1(1)n n a a d n+-=³。
根据定义,当我们看到形如:d a a n n =--1、da a n n =--212、d aa n n=--1d a a n n =--111、211-++=n n na a a 、d S S n n =--1时,应能从中得到相应的等差数列。
的等差数列。
等差数列的判定方法1. 定义法:若d aa n n=--1或da an n =-+1(常数*ÎN n )Û {}n a 是等差数列.是等差数列.2.2.等差中项:数列等差中项:数列{}n a 是等差数列)2(211-³+=Û+n a a a n n n 212+++=Ûn n n a a a . 3.3.数列数列{}n a 是等差数列Ûbkn a n+=(其中b k ,是常数)。
是常数)。
4.4.数列数列{}n a 是等差数列Û2n S An Bn =+,(其中(其中A A 、B 是常数)。
是常数)。
等差数列的证明方法定义法:若d aa n n=--1或d a ann =-+1(常数*ÎN n )Û {}n a 是等差数列.例1.设S n 是数列{a n }的前n 项和,且S n =n 2,则{a n }是(是( )A.等比数列,但不是等差数列等比数列,但不是等差数列B.等差数列,但不是等比数列等差数列,但不是等比数列C.等差数列,而且也是等比数列等差数列,而且也是等比数列D.既非等比数列又非等差数列既非等比数列又非等差数列 答案:B ;解法一:a n =îíì³-==Þîíì³-=-)2( 12)1( 1)2( )1( 11n n n a n S S n S n n n ∴a n =2n -1(n ∈N ) 又a n +1-a n =2为常数,12121-+=+n n a a n n ≠常数≠常数 ∴{a n }是等差数列,但不是等比数列. 2.等差数列通项公式:*11(1)()n a a n d dn a d n N =+-=+-Î ,, 首项首项首项::1a ,公差,公差:d :d :d,末项,末项,末项::n a=1,=1得=2,=1+×2,项起开始为正数,则公差的取值范围是______ ______ ______ ;;11<11<=19(a 119)==120=ac(C )8 8 ((D )10 【答案】A 【解析】由角标性质得1952a a a +=,所以5a =5.=5.2.在等差数列{a n }中,a 2+a 6=3π2,则sin(2a 4-π3)=( ) A.32 B.12 C .-32 D .-12 答案 D 解析 ∵a 2+a 6=3π2,∴2a 4=3π2,∴sin(2a 4-π3)=sin(3π2-π3)=-cos π3=-12,选D. 1. (2009北京东城高三第一学期期末检测,理9)已知{a n }为等差数列,若a 1+a 5+a 9=π,则cos(a 2+a 8)的值为________________.答案:21-2。

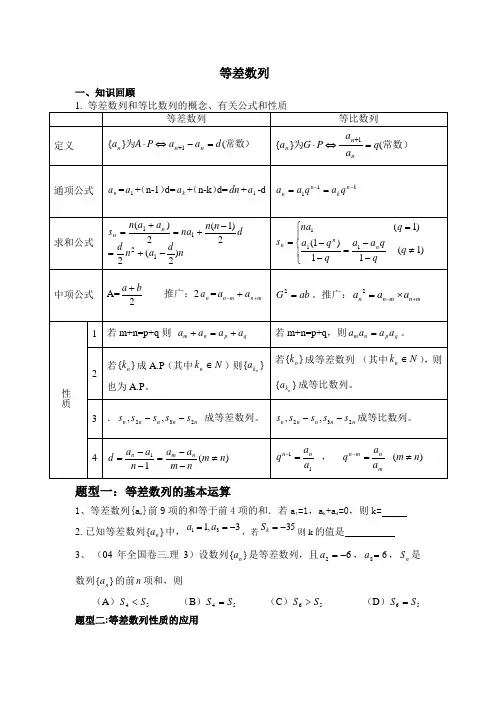
等差数列一、知识回顾题型一:等差数列的基本运算1、等差数列{a n }前9项的和等于前4项的和.若a 1=1,a k +a 4=0,则k= 2. 已知等差数列}{n a 中,3,131-==a a ,若35-=k S 则k 的值是3、 (04年全国卷三.理3)设数列}{n a 是等差数列,且62-=a ,68=a ,n S 是数列}{n a 的前n 项和,则(A )54S S < (B )54S S = (C )56S S > (D )56S S = 题型二:等差数列性质的应用4、在等差数列}{n a 中,=+++=+864273,37a a a a a a 则5若两个等差数列{}n a 、{}n b 的前n 项和分别为n A 、n B ,且满足5524-+=n n B A nn,则135135b b a a ++=6、nS 为等差数列{}n a 的前n 项和,1,442==a S S 则=5a7、在等差数列{a n }中,前四项之和为20,最后四项之和为60,前n 项之和是100,则项数n 为8、等差数列{a n }的前n 项和为S n ,若S n =30,S 2n =100,则S 3n =( )题型三:等差数列的判定9、已知数列{a n }的前n 项和S n =25n-2n 2.(1)求证:{a n }是等差数列.(2)求数列{|a n |}的前n 项和T n .10、等差数列{a n }的前n 项和为S n ,且满足21),2(0.211=≥=+-a n S S a n n n ,求证:数列⎭⎬⎫⎩⎨⎧n S1是等差数列11、已知数列{}n a 中,),2(12,5311*-∈≥-==N n n a a a n n ,数列{}n b 满足11-=n n a b (1)求证:数列{}n b 为等差数列 (2)求数列{}n a 中的最大项和最小项总结:. 判断和证明数列是等差(等比)数列常有三种方法:(1)定义法:对于n ≥2的任意自然数,验证1--n n a a =d 为同一常数。

10.1等差数列知识梳理.等差数列1.等差数列的有关概念(1)定义:如果一个数列从第2项起,每一项与它的前一项的差都等于同一个常数,那么这个数列就叫做等差数列.这个常数叫做等差数列的公差,符号表示为a n +1-a n =d (n ∈N *,d 为常数).(2)①通项公式:a n =a 1+(n -1)d =nd +(a 1-d )⇒当d ≠0时,a n 是关于n 的一次函数.②通项公式的推广:a n =a m +(n -m )d (n ,m ∈N *).(3)等差中项:数列a ,A ,b 成等差数列的充要条件是A =a +b2,其中A 叫做a ,b 的等差中项.①若m +n =2p ,则2a p =a m +a n (m ,n ,p ∈N *).②当m +n =p +q 时,a m +a n =a p +a q (m ,n ,p ,q ∈N *).(4)前n 项和公式:S n =n (a 1+a n )2――→a n =a 1+(n -1)dS n =na 1+n (n -1)2d =d 2n 2+a 1-d2n ⇒当d ≠0时,S n 是关于n 的二次函数,且没有常数项.2.常用结论:已知{a n }为等差数列,d 为公差,S n 为该数列的前n 项和.(1)S n ,S 2n -S n ,S 3n -S 2n ,…也成等差数列,公差为n 2d .(2)若{a n }是等差数列,则S nn 也成等差数列,其首项与{a n }首项相同,公差是{a n }公差的12.(3)若项数为偶数2n ,则S 2n =n (a 1+a 2n )=n (a n +a n +1);S 偶-S 奇=nd ;S 奇S 偶=a na n +1.若项数为奇数2n -1,则S 2n -1=(2n -1)a n ;S 奇-S 偶=a n ;S 奇S 偶=nn -1.题型一.等差数列的基本量1.已知等差数列{a n}满足a3+a4=12,3a2=a5,则a6=11.【解答】解:设等差数列{a n}的公差为d,∵a3+a4=12,3a2=a5,∴2a1+5d=12,3(a1+d)=a1+4d,联立解得a1=1,d=2,∴a6=a1+5d=11故答案为:112.(2018•新课标Ⅰ)记S n为等差数列{a n}的前n项和.若3S3=S2+S4,a1=2,则a5=()A.﹣12B.﹣10C.10D.12【解答】解:∵S n为等差数列{a n}的前n项和,3S3=S2+S4,a1=2,∴3×(31+3×22p=a1+a1+d+4a1+4×32d,把a1=2,代入得d=﹣3∴a5=2+4×(﹣3)=﹣10.故选:B.3.(2017•新课标Ⅰ)记S n为等差数列{a n}的前n项和.若a4+a5=24,S6=48,则{a n}的公差为()A.1B.2C.4D.8【解答】解:∵S n为等差数列{a n}的前n项和,a4+a5=24,S6=48,∴1+3+1+4=2461+6×52=48,解得a1=﹣2,d=4,∴{a n}的公差为4.故选:C.题型二.等差数列的基本性质1.在等差数列{a n}中,已知a5+a10=12,则3a7+a9等于()A.30B.24C.18D.12【解答】解:∵等差数列{a n}中,a5+a10=12,∴2a1+13d=12,∴3a7+a9=4a1+26d=2(2a1+13d)=24.故选:B.2.在等差数列{a n}中,若a4+a6+a8+a10+a12=120,则a9−1311的值为()A.17B.16C.15D.14【解答】解:由a4+a6+a8+a10+a12=(a4+a12)+(a6+a10)+a8=5a8=120,解得a8=24.a9−1311=a1+8d−1+103=23a1+143d=23(a1+7d)=23a8=16故选:B.3.设等差数列{a n}的前n项和为S n,若a3=10,S4=36,则公差d为2.【解答】解:∵a3=10,S4=36,∴a1+2d=10,4a1+4×32d=36,解得d=2.故答案为:2.题型三.等差数列的函数性质1.下面是关于公差d>0的等差数列{a n}的四个命题:(1)数列{a n}是递增数列;(2)数列{na n}是递增数列;(3)数列{}是递减数列;(4)数列{a n+3nd}是递增数列.其中的真命题的个数为()A.0B.1C.2D.3【解答】解:设等差数列的首项为a1,公差d>0,则a n=a1+(n﹣1)d=dn+a1﹣d,∴数列{a n}是递增数列,故(1)正确;B=B2+(1−p,当n<K12时,数列{na n}不是递增数列,故(2)错误;=+1−,当a1﹣d≤0时,数列{}不是递减数列,故(3)错误;a n+3nd=4nd+a1﹣d,数列{a n+3nd}是递增数列,故(4)正确.∴真命题个数有2个.故选:C.2.已知数列{a n}的前n项和S n=n2(n∈N*),则{a n}的通项公式为()A.a n=2n B.a n=2n﹣1C.a n=3n﹣2D.=1,=12,≥2【解答】解:∵S n=n2,∴当n=1时,a1=S1=1.当n≥2时,a n=S n﹣S n﹣1=n2﹣(n﹣1)2=2n﹣1,而当n=1时也满足,∴a n=2n﹣1.故选:B.3.在数列{a n}中,若a n=5n﹣16,则此数列前n项和的最小值为()A.﹣11B.﹣17C.﹣18D.3【解答】解:令a n=5n﹣16≤0,解得n≤3+15.则此数列前n项和的最小值为S3=3×(−11+15−16)2=−18.故选:C.题型四.等差数列的前n项和经典结论1.设等差数列{a n}的前n项和为S n,若S3=9,S9=72,则S6=()A.27B.33C.36D.45【解答】解:∵等差数列{a n}的前n项和为S n,若S3=9,S9=72,∴S3,S6﹣S3,S9﹣S6成等差数列,故2(S6﹣S3)=S3+S9﹣S6,即2(S6﹣9)=9+72﹣S6,求得S6=33,故选:B.2.等差数列{a n}中,S n是其前n项和,1=−11,1010−88=2,则S11=()A.﹣11B.11C.10D.﹣10【解答】解:=B1+oK1)2,得=1+(K1)2,由1010−88=2,得1+10−12−(1+8−12)=2,d=2,1111=1+(11−1)2=−11+5×2=−1,∴S11=﹣11,故选:A.3.若两个等差数列{a n}和{b n}的前n项和分别是S n和T n,已知=2r1,则77等于()A.1321B.214C.1327D.827【解答】解:∵=2r1,∴77=2727=132(1+13)132(1+13)=1313=132×13+1=1327,故选:C.题型五.等差数列的最值问题1.已知等差数列{a n}中,S n是它的前n项和,若S16>0,S17<0,则当S n最大时,n的值为()A.8B.9C.10D.16【解答】解:∵等差数列{a n}中,S16>0且S17<0∴a8+a9>0,a9<0,∴a8>0,∴数列的前8项和最大故选:A.2.在等差数列{a n}中,已知a1=20,前n项和为S n,且S10=S15,求当n为何值时,S n取得最大值,并求出它的最大值.【解答】解:∵等差数列{a n}中S10=S15,∴S15﹣S10=a11+a12+a13+a14+a15=5a13=0,∴a13=0,∴数列的前12项为正数,第13项为0,从第14项开始为负值,∴当n=12或13时,S n取得最大值,又公差d=13−113−1=−53,∴S12=12×20+12×112(−53)=130∴S n的最大值为1303.(2014·江西)在等差数列{a n}中,a1=7,公差为d,前n项和为S n,当且仅当n=8时S n取得最大值,则d的取值范围为(﹣1,−78).【解答】解:∵S n=7n+oK1)2,当且仅当n=8时S n取得最大值,∴7<8 9<8,即49+21<56+2863+36<56+28,解得:>−1<−78,综上:d的取值范围为(﹣1,−78).题型六.证明等差数列1.已知数列{a n}满足1=35,=2−1K1(≥2,∈∗),数列{b n}满足=1−1(∈∗).(1)求证数列{b n}是等差数列;(2)求数列{a n}中的最大项和最小项.【解答】解:(1)由1=35,=2−1K1(≥2,∈∗),得a n+1=2−1(n∈N•)b n+1﹣b n=1r1−1−1−1=12−1−1−1−1=1…(4分)又b1=−52,所以{b n}是以−52为首项,1为公差的等差数列…(6分)(2)因为b n=b1+(n﹣1)=n−72,所以a n=1+1=22K7+1.…(9分)1≤n≤3时数列{a n}单调递减且a n<1,n≥4时数列{a n}单调递减且a n>1所以数列{a n}的最大项为a4=3,最小项为a3=﹣1.…(14分)2.已知数列{a n}中,a2=1,前n项和为S n,且S n=o−1)2.(1)求a1;(2)证明数列{a n}为等差数列,并写出其通项公式;【解答】解:(1)令n=1,则a1=S1=1(1−1)2=0(2)由=o−1)2,即=B2,①得r1=(r1)r12.②②﹣①,得(n﹣1)a n+1=na n.③于是,na n+2=(n+1)a n+1.④③+④,得na n+2+na n=2na n+1,即a n+2+a n=2a n+1又a1=0,a2=1,a2﹣a1=1,所以,数列{a n}是以0为首项,1为公差的等差数列.所以,a n=n﹣1课后作业.等差数列1.设等差数列{a n}的前n项和为S n,若S9=72,则a1+a5+a9=()A.36B.24C.16D.8【解答】解:由等差数列的求和公式可得,S9=92(a1+a9)=72,∴a1+a9=16,由等差数列的性质可知,a1+a9=2a5,∴a5=8,∴a1+a5+a9=24.故选:B.2.设等差数列{a n}的前n项和为S n,S8=4a3,a7=﹣2,则a10=()A.﹣8B.﹣6C.﹣4D.﹣2【解答】解:等差数列{a n}中,前n项和为S n,且S8=4a3,a7=﹣2,则81+28=41+81+6=−2,解得a1=10,d=﹣2,∴a10=a1+9d=﹣8.故选:A.3.已知等差数列{a n}的前n项和为S n,且a1>0,2a5+a11=0,则下列说法错误的为()A.a8<0B.当且仅当n=7时,S n取得最大值C.S4=S9D.满足S n>0的n的最大值为12【解答】解:∵2a5+a11=0,∴2a1+8d+a1+10d=0,∴a1=﹣6d,∵a1>0,∴d<0,∴{a n}为递减数列,∴a n=a1+(n﹣1)d=﹣6d+(n﹣1)d=(n﹣7)d,由a n≥0,(n﹣7)d≥0,解得n≤7,∴数列前6项大于0,第7项等于0,从第8项都小于0,∴a8<0,当n=6或7时,S n取得最大值,故A正确,B错误;∵S4=4a1+6d=﹣24d+6d=﹣18d,S9=9a1+36d=﹣28d+36d=﹣18d,∴S4=S9,故C正确;∴S n=na1+oK1)2=2(n2﹣13n)>0,解得0<n<13,∴满足S n>0的n的最大值为12,故D正确.故选:B.4.若等差数列{a n}满足a7+a8+a9>0,a7+a10<0,则当n=8时,{a n}的前n项和最大;当S n>0时n的最大值为15.【解答】解:∵a7+a8+a9=3a8>0,a7+a10=a8+a9<0,∴a8>0,a9<0,∴n=8时,{a n}的前n项和最大;∵S15=15(1+15)2=15a8>0,S16=16(1+16)2=8(a8+a9)<0,∴当S n>0时n的最大值为15.故答案为:8;15.5.在数列{a n}中,a2=8,a5=2,且2a n+1﹣a n+2=a n(n∈N*),则|a1|+|a2|+…+|a10|的值是()A.210B.10C.50D.90【解答】解:∵2a n+1﹣a n+2=a n(n∈N*),即2a n+1=a n+2+a n(n∈N*),∴数列{a n}是等差数列,设公差为d,则a1+d=8,a1+4d=2,联立解得a1=10,d=﹣2,∴a n=10﹣2(n﹣1)=12﹣2n.令a n≥0,解得n≤6.S n=o10+12−2p2=11n﹣n2.∴|a1|+|a2|+…+|a10|=a1+a2+…+a6﹣a7﹣…﹣a10=2S6﹣S10=2(11×6﹣62)﹣(11×10﹣102)=50.故选:C.6.已知在正整数数列{a n}中,前n项和S n满足:S n=18(a n+2)2.(1)求数列{a n}的通项公式;(2)若b n=12a n﹣30,求数列{b n}的前n项和的最小值.【解答】解:(1)∵S n=18(a n+2)2,∴当n=1时,1=18(1+2)2,化为(1−2)2=0,解得a1=2.当n≥2时,a n=S n﹣S n﹣1=18(a n+2)2−18(K1+2)2,化为(a n﹣a n﹣1﹣4)(a n+a n﹣1)=0,∵∀n∈N*,a n>0,∴a n﹣a n﹣1=4.∴数列{a n}是等差数列,首项为2,公差为4,∴a n=2+4(n﹣1)=4n﹣2.(2)b n=12a n﹣30=12(4−2)−30=2n﹣31.由b n≤0,解得≤312,因此前15项的和最小.又数列{b n}是等差数列,∴数列{b n}的前15项和T15=15(−29+2×15−31)2=−225.∴数列{b n}的前n项和的最小值为﹣225.。

等差数列知识点归纳总结等差数列是数学中常见的一种数列形式,具有重要的应用价值。
本文将针对等差数列的定义、通项公式、求和公式以及应用进行归纳总结。
一、等差数列的定义等差数列是指数列中后一项与前一项之差始终相等的一种特殊数列。
用常数d表示公差,那么等差数列可以表示为:a₁, a₁+d, a₁+2d,a₁+3d, ...二、等差数列的通项公式等差数列通项公式是指通过已知的首项和公差,计算数列中第n项的公式。
假设首项为a₁,公差为d,则等差数列的通项公式为:an =a₁ + (n-1)d三、等差数列的求和公式等差数列求和公式是指通过已知的首项、末项和项数,计算数列所有项之和的公式。
假设首项为a₁,末项为an,项数为n,则等差数列的求和公式为:Sn = (n/2)(a₁+an)四、等差数列的性质1. 等差数列的任意三项成一等差数列。
2. 等差数列的任意两项之和与中间项的和相等。
3. 等差数列的任意相邻两项之和相等。
4. 等差数列的对称性:数列中的相等距离的项之和相等。
五、等差数列的应用等差数列广泛应用于数学、物理、经济等领域,以下是一些常见的应用场景:1. 金融贷款:假设每月还款金额等差递增,可利用等差数列求得贷款总额和还款期限。
2. 平均速度问题:假设行程中速度等差减小,可利用等差数列求得平均速度。
3. 等差数列的和与平均数关系:等差数列的和即为等差数列所有项的平均数乘以项数。
4. 数列排序问题:对于给定的一组数据,若满足等差关系,可通过等差数列的求和公式快速求得该数列的和。
六、等差数列的扩展1. 差数列:每一项与其后一项之差构成的数列。
2. 等差中项:等差数列中,若某项的前后两项之和为定值,该项称为等差数列的中项。
总结:本文对等差数列的定义、通项公式、求和公式进行了详细介绍,并归纳了其性质和应用场景。
了解等差数列的相关知识,对于解决实际问题及培养数学思维能力都具有重要的帮助。
希望读者通过本文的阅读,对等差数列有更深入的理解。
等差数列及其前n 项和考点与题型归纳一、基础知识1.等差数列的有关概念(1)定义:如果一个数列从第2项起,每一项与它的前一项的差都等于同一个常数,那么这个数列就叫做等差数列.这个常数叫做等差数列的公差,符号表示为a n +1-a n =d (n ∈N *,d 为常数).(2)等差中项:数列a ,A ,b 成等差数列的充要条件是A =a +b 2,其中A 叫做a ,b 的等差中项.在一个等差数列中,从第2项起,每一项有穷等差数列的末项除外都是它的前一项与后一项的等差中项.2.等差数列的有关公式 (1)通项公式:a n =a 1+(n -1)d . (2)前n 项和公式:S n =na 1+n (n -1)2d =n (a 1+a n )2. 3.等差数列的通项公式及前n 项和公式与函数的关系(1)a n =a 1+(n -1)d 可化为a n =dn +a 1-d 的形式.当d ≠0时,a n 是关于n 的一次函数;当d >0时,数列为递增数列;当d <0时,数列为递减数列.(2)数列{a n }是等差数列,且公差不为0⇔S n =An 2+Bn (A ,B 为常数).二、常用结论已知{a n }为等差数列,d 为公差,S n 为该数列的前n 项和. (1)通项公式的推广:a n =a m +(n -m )d (n ,m ∈N *).(2)在等差数列{a n }中,当m +n =p +q 时,a m +a n =a p +a q (m ,n ,p ,q ∈N *).特别地,若m +n =2p ,则2a p =a m +a n (m ,n ,p ∈N *).(3)a k ,a k +m ,a k +2m ,…仍是等差数列,公差为md (k ,m ∈N *). (4)S n ,S 2n -S n ,S 3n -S 2n ,…也成等差数列,公差为n 2d . (5)若{a n },{b n }是等差数列,则{pa n +qb n }也是等差数列.(6)若{a n }是等差数列,则⎩⎨⎧⎭⎬⎫S n n 也成等差数列,其首项与{a n }首项相同,公差是{a n }公差的12. (7)若项数为偶数2n ,则S 2n =n (a 1+a 2n )=n (a n +a n +1);S 偶-S 奇=nd ;S 奇S 偶=a na n +1.(8)若项数为奇数2n -1,则S 2n -1=(2n -1)a n ;S 奇-S 偶=a n ;S 奇S 偶=nn -1.(9)在等差数列{a n }中,若a 1>0,d <0,则满足⎩⎪⎨⎪⎧a m ≥0,a m +1≤0的项数m 使得S n 取得最大值S m ;若a 1<0,d >0,则满足⎩⎪⎨⎪⎧a m ≤0,a m +1≥0的项数m 使得S n 取得最小值S m .考点一 等差数列的基本运算[典例] (1)(2018·全国卷Ⅰ)记S n 为等差数列{a n }的前n 项和,若3S 3=S 2+S 4,a 1=2,则a 5=( )A .-12B .-10C .10D .12(2)已知等差数列{a n }的前n 项和为S n ,若a 2=4,S 4=22,a n =28,则n =( ) A .3 B .7 C .9D .10[解析] (1)设等差数列{a n }的公差为d ,由3S 3=S 2+S 4,得3(3a 1+3d )=2a 1+d +4a 1+6d ,即3a 1+2d =0.将a 1=2代入上式,解得d =-3,故a 5=a 1+(5-1)d =2+4×(-3)= -10.(2)因为S 4=a 1+a 2+a 3+a 4=4a 2+2d =22,d =(22-4a 2)2=3,a 1=a 2-d =4-3=1,a n=a 1+(n -1)d =1+3(n -1)=3n -2,由3n -2=28,解得n =10.[答案] (1)B (2)D[解题技法] 等差数列的基本运算的解题策略(1)等差数列的通项公式及前n 项和公式共涉及五个量a 1,a n ,d ,n ,S n ,知其中三个就能求另外两个,体现了方程思想.(2)数列的通项公式和前n 项和公式在解题中起到变量代换的作用,而a 1和d 是等差数列的两个基本量,用它们表示已知量和未知量是常用方法.[提醒] 在求解数列基本量运算中,要注意公式使用时的准确性与合理性,更要注意运算的准确性.在遇到一些较复杂的方程组时,要注意整体代换思想的运用,使运算更加便捷.[题组训练]1.(2019·开封高三定位考试)已知等差数列{a n }的前n 项和为S n ,且a 1+a 5=10,S 4=16,则数列{a n }的公差为( )A .1B .2C .3D .4解析:选B 设等差数列{a n }的公差为d ,则由题意,得⎩⎪⎨⎪⎧a 1+a 1+4d =10,4a 1+4×32×d =16,解得⎩⎪⎨⎪⎧a 1=1,d =2,故选B. 2.已知等差数列{a n }的前n 项和为S n ,且a 3·a 5=12,a 2=0.若a 1>0,则S 20=( ) A .420 B .340 C .-420D .-340解析:选D 设数列{a n }的公差为d ,则a 3=a 2+d =d ,a 5=a 2+3d =3d ,由a 3·a 5=12得d =±2,由a 1>0,a 2=0,可知d <0,所以d =-2,所以a 1=2,故S 20=20×2+20×192×(-2)=-340,选D.3.在等差数列{a n }中,已知a 5+a 10=12,则3a 7+a 9=( ) A .12 B .18 C .24D .30解析:选C 设等差数列{a n }的首项为a 1,公差为d , 因为a 5+a 10=12, 所以2a 1+13d =12,所以3a 7+a 9=3(a 1+6d )+a 1+8d =4a 1+26d =2(2a 1+13d )=2×12=24.考点二 等差数列的判定与证明[典例] 已知数列{a n }的前n 项和为S n 且满足a n +2S n ·S n -1=0(n ≥2),a 1=12.(1)求证:⎩⎨⎧⎭⎬⎫1S n 是等差数列.(2)求a n 的表达式.[解] (1)证明:因为a n =S n -S n -1(n ≥2),又a n =-2S n ·S n -1,所以S n -1-S n =2S n ·S n -1,S n ≠0. 因此1S n -1S n -1=2(n ≥2).故由等差数列的定义知⎩⎨⎧⎭⎬⎫1S n 是以1S 1=1a 1=2为首项,2为公差的等差数列.(2)由(1)知1S n =1S 1+(n -1)d =2+(n -1)×2=2n ,即S n =12n.由于当n ≥2时,有a n =-2S n ·S n -1=-12n (n -1),又因为a 1=12,不适合上式.所以a n=⎩⎪⎨⎪⎧12,n =1,-12n (n -1),n ≥2.[题组训练]1.(2019·陕西质检)已知数列{a n }的前n 项和S n =an 2+bn (a ,b ∈R )且a 2=3,a 6=11,则S 7等于( )A .13B .49C .35D .63解析:选B 由S n=an 2+bn (a ,b ∈R )可知数列{an }是等差数列,所以S 7=7(a 1+a 7)2=7(a 2+a 6)2=49. 2.已知数列{a n }中,a 1=2,a n =2-1a n -1(n ≥2,n ∈N *),设b n =1a n -1(n ∈N *).求证:数列{b n }是等差数列.证明:∵a n =2-1a n -1(n ≥2),∴a n +1=2-1a n .∴b n +1-b n =1a n +1-1-1a n -1=12-1a n-1-1a n -1=a n -1a n -1=1,∴{b n }是首项为b 1=12-1=1,公差为1的等差数列.考点三 等差数列的性质及应用考法(一) 等差数列项的性质[典例] (1)已知在等差数列{a n }中,a 5+a 6=4,则log 2(2a 1·2a 2·…·2a 10)=( ) A .10 B .20 C .40D .2+log 25(2)(2019·福建模拟)设S n ,T n 分别是等差数列{a n },{b n }的前n 项和,若a 5=2b 5,则S 9T 9=( )A .2B .3C .4D .6[解析] (1)因为2a 1·2a 2·…·2a 10=2a 1+a 2+…+a 10=25(a 5+a 6)=25×4, 所以log 2(2a 1·2a 2·…·2a 10)=log 225×4=20.选B.(2)由a 5=2b 5,得a 5b 5=2,所以S 9T 9=9(a 1+a 9)29(b 1+b 9)2=a 5b 5=2,故选A.[答案] (1)B (2)A考法(二) 等差数列前n 项和的性质[典例] 设等差数列{a n }的前n 项和为S n ,若S 3=9,S 6=36,则a 7+a 8+a 9等于( ) A .63 B .45 C .36D .27[解析] 由{a n }是等差数列, 得S 3,S 6-S 3,S 9-S 6为等差数列, 即2(S 6-S 3)=S 3+(S 9-S 6), 得到S 9-S 6=2S 6-3S 3=45,故选B. [答案] B考法(三) 等差数列前n 项和的最值[典例] 在等差数列{a n }中,a 1=29,S 10=S 20,则数列{a n }的前n 项和S n 的最大值为( )A .S 15B .S 16C .S 15或S 16D .S 17[解析] ∵a 1=29,S 10=S 20,∴10a 1+10×92d =20a 1+20×192d ,解得d =-2,∴S n =29n +n (n -1)2×(-2)=-n 2+30n =-(n -15)2+225.∴当n =15时,S n 取得最大值. [答案] A[解题技法]1.应用等差数列的性质解题的2个注意点(1)如果{a n }为等差数列,m +n =p +q ,则a m +a n =a p +a q (m ,n ,p ,q ∈N *).因此,若出现a m -n ,a m ,a m +n 等项时,可以利用此性质将已知条件转化为与a m (或其他项)有关的条件;若求a m 项,可由a m =12(a m -n +a m +n )转化为求a m -n ,a m +n 或a m +n +a m -n 的值.(2)要注意等差数列通项公式及前n 项和公式的灵活应用,如a n =a m +(n -m )d ,d =a n -a m n -m,S 2n -1=(2n -1)a n ,S n =n (a 1+a n )2=n (a 2+a n -1)2(n ,m ∈N *)等.2.求等差数列前n 项和S n 最值的2种方法(1)函数法:利用等差数列前n 项和的函数表达式S n =an 2+bn ,通过配方或借助图象求二次函数最值的方法求解.(2)邻项变号法:①当a 1>0,d <0时,满足⎩⎪⎨⎪⎧ a m ≥0,a m +1≤0的项数m 使得S n 取得最大值为S m ;②当a 1<0,d >0时,满足⎩⎪⎨⎪⎧a m ≤0,a m +1≥0的项数m 使得S n 取得最小值为S m .[题组训练]1.在等差数列{a n }中,若a 3=-5,a 5=-9,则a 7=( )A .-12B .-13C .12D .13解析:选B 法一:设公差为d ,则2d =a 5-a 3=-9+5=-4,则d =-2,故a 7=a 3+4d =-5+4×(-2)=-13,选B.法二:由等差数列的性质得a 7=2a 5-a 3=2×(-9)-(-5)=-13,选B.2.设等差数列{a n }的前n 项和为S n ,且a 1>0,a 3+a 10>0,a 6a 7<0,则满足S n >0的最大自然数n 的值为( )A .6B .7C .12D .13解析:选C 因为a 1>0,a 6a 7<0,所以a 6>0,a 7<0,等差数列的公差小于零,又a 3+a 10=a 1+a 12>0,a 1+a 13=2a 7<0,所以S 12>0,S 13<0,所以满足S n >0的最大自然数n 的值为12.3.设等差数列{a n }的前n 项和为S n ,已知前6项和为36,最后6项的和为180,S n =324(n >6),则数列{a n }的项数为________.解析:由题意知a 1+a 2+…+a 6=36,① a n +a n -1+a n -2+…+a n -5=180,②①+②得(a 1+a n )+(a 2+a n -1)+…+(a 6+a n -5)=6(a 1+a n )=216, ∴a 1+a n =36,又S n =n (a 1+a n )2=324,∴18n =324,∴n =18. 答案:18[课时跟踪检测]A 级1.在数列{a n }中,a 1=2,a n +1=a n +2,S n 为{a n }的前n 项和,则S 10等于( ) A .90 B .100 C .110D .130解析:选C 由递推公式可知该数列是公差为2的等差数列,S 10=10×2+10×92×2=110.故选C.2.(2018·北京东城区二模)已知等差数列{a n }的前n 项和为S n ,a 3=3,a 5=5,则S 7的值是( )A .30B .29C .28D .27解析:选C 由题意,设等差数列的公差为d ,则d =a 5-a 35-3=1,故a 4=a 3+d =4,所以S 7=7(a 1+a 7)2=7×2a 42=7×4=28.故选C.3.(2019·山西五校联考)在数列{a n }中,a n =28-5n ,S n 为数列{a n }的前n 项和,当S n 最大时,n =( )A .2B .3C .5D .6解析:选C ∵a n =28-5n ,∴数列{a n }为递减数列. 令a n =28-5n ≥0,则n ≤285,又n ∈N *,∴n ≤5.∵S n 为数列{a n }的前n 项和,∴当n =5时,S n 最大.故选C.4.(2019·广东中山一中统测)设数列{a n }的前n 项和为S n ,且a n =-2n +1,则数列⎩⎨⎧⎭⎬⎫S n n 的前11项和为( )A .-45B .-50C .-55D .-66解析:选D ∵a n =-2n +1,∴数列{a n }是以-1为首项,-2为公差的等差数列, ∴S n =n [-1+(-2n +1)]2=-n 2,∴S n n =-n 2n =-n ,∴数列⎩⎨⎧⎭⎬⎫S n n 是以-1为首项,-1为公差的等差数列,∴数列⎩⎨⎧⎭⎬⎫S n n 的前11项和为11×(-1)+11×102×(-1)=-66,故选D.5.(2018·南昌模拟)已知等差数列{a n }的前n 项和为S n ,且S 5=50,S 10=200,则a 10+a 11的值为( )A .20B .40C .60D .80解析:选D 设等差数列{a n }的公差为d ,由已知得⎩⎨⎧S 5=5a 1+5×42d =50,S 10=10a 1+10×92d =200,即⎩⎪⎨⎪⎧a 1+2d =10,a 1+92d =20,解得⎩⎪⎨⎪⎧a 1=2,d =4. ∴a 10+a 11=2a 1+19d =80.故选D.6.(2019·广州高中综合测试)等差数列{a n }的各项均不为零,其前n 项和为S n .若a 2n +1=a n +2+a n ,则S 2n +1=( )A .4n +2B .4nC .2n +1D .2n解析:选A 因为{a n }为等差数列,所以a n +2+a n =2a n +1,又a 2n +1=a n +2+a n ,所以a 2n +1=2a n +1.因为数列{a n }的各项均不为零,所以a n +1=2,所以S 2n +1=(a 1+a 2n +1)(2n +1)2=2×a n +1×(2n +1)2=4n +2.故选A.7.已知等差数列5,427,347,…,则前n 项和S n =________.解析:由题知公差d =-57,所以S n =na 1+n (n -1)2d =514(15n -n 2).答案:514(15n -n 2)8.已知{a n }为等差数列,S n 为其前n 项和.若a 1=6,a 3+a 5=0,则S 6=________. 解析:∵a 3+a 5=2a 4,∴a 4=0. ∵a 1=6,a 4=a 1+3d ,∴d =-2. ∴S 6=6a 1+6×(6-1)2d =6×6-30=6.答案:69.等差数列{a n }中,已知a 5>0,a 4+a 7<0,则{a n }的前n 项和S n 的最大值为________.解析:∵⎩⎪⎨⎪⎧ a 4+a 7=a 5+a 6<0,a 5>0,∴⎩⎪⎨⎪⎧a 5>0,a 6<0,∴S n 的最大值为S 5.答案:S 510.在等差数列{a n }中,公差d =12,前100项的和S 100=45,则a 1+a 3+a 5+…+a 99=________.解析:因为S 100=1002(a 1+a 100)=45,所以a 1+a 100=910,a 1+a 99=a 1+a 100-d =25,则a 1+a 3+a 5+…+a 99=502(a 1+a 99)=502×25=10.答案:1011.(2018·全国卷Ⅱ)记S n 为等差数列{a n }的前n 项和,已知a 1=-7,S 3=-15. (1)求{a n }的通项公式; (2)求S n ,并求S n 的最小值. 解:(1)设{a n }的公差为d , 由题意得3a 1+3d =-15. 又a 1=-7,所以d =2.所以{a n }的通项公式为a n =2n -9.(2)由(1)得S n =n (a 1+a n )2=n 2-8n =(n -4)2-16,所以当n =4时,S n 取得最小值,最小值为-16.12.(2019·山东五校联考)已知等差数列{a n }为递增数列,其前3项的和为-3,前3项的积为8.(1)求数列{a n }的通项公式; (2)求数列{a n }的前n 项和S n .解:(1)设等差数列{a n }的公差为d ,d >0,∵等差数列{a n }的前3项的和为-3,前3项的积为8,∴⎩⎪⎨⎪⎧3a 1+3d =-3,a 1(a 1+d )(a 1+2d )=8, ∴⎩⎪⎨⎪⎧a 1=2,d =-3或⎩⎪⎨⎪⎧a 1=-4,d =3.∵d >0,∴a 1=-4,d =3,∴a n =3n -7.(2)∵a n =3n -7,∴a 1=3-7=-4,∴S n =n (-4+3n -7)2=n (3n -11)2.B 级1.设a n =(n +1)2,b n =n 2-n (n ∈N *),则下列命题中不正确的是( )A .{a n +1-a n }是等差数列B .{b n +1-b n }是等差数列C .{a n -b n }是等差数列D .{a n +b n }是等差数列 解析:选D 对于A ,因为a n =(n +1)2, 所以a n +1-a n =(n +2)2-(n +1)2=2n +3, 设c n =2n +3,所以c n +1-c n =2.所以{a n +1-a n }是等差数列,故A 正确; 对于B ,因为b n =n 2-n (n ∈N *),所以b n +1-b n =2n , 设c n =2n ,所以c n +1-c n =2,所以{b n +1-b n }是等差数列,故B 正确; 对于C ,因为a n =(n +1)2,b n =n 2-n (n ∈N *), 所以a n -b n =(n +1)2-(n 2-n )=3n +1, 设c n =3n +1,所以c n +1-c n =3, 所以{a n -b n }是等差数列,故C 正确; 对于D ,a n +b n =2n 2+n +1,设c n =a n +b n ,c n +1-c n 不是常数,故D 错误.2.(2019·武汉调研)设等差数列{a n }满足a 3+a 7=36,a 4a 6=275,且a n a n +1有最小值,则这个最小值为________.解析:设等差数列{a n }的公差为d ,∵a 3+a 7=36, ∴a 4+a 6=36,又a 4a 6=275,联立,解得⎩⎪⎨⎪⎧ a 4=11,a 6=25或⎩⎪⎨⎪⎧ a 4=25,a 6=11,当⎩⎪⎨⎪⎧ a 4=11,a 6=25时,可得⎩⎪⎨⎪⎧ a 1=-10,d =7,此时a n =7n -17,a 2=-3,a 3=4,易知当n ≤2时,a n <0,当n ≥3时,a n >0,∴a 2a 3=-12为a n a n +1的最小值; 当⎩⎪⎨⎪⎧ a 4=25,a 6=11时,可得⎩⎪⎨⎪⎧a 1=46,d =-7,此时a n =-7n +53,a 7=4,a 8=-3,易知当n ≤7时,a n >0,当n ≥8时,a n <0,∴a 7a 8=-12为a n a n +1的最小值. 综上,a n a n +1的最小值为-12. 答案:-123.(2018·辽宁五校协作体模考)已知数列{a n }是等差数列,且a 1,a 2(a 1<a 2)分别为方程x 2-6x +5=0的两个实根.(1)求数列{a n }的前n 项和S n ;(2)在(1)中,设b n =S n n +c,求证:当c =-12时,数列{b n }是等差数列. 解:(1)∵a 1,a 2(a 1<a 2)分别为方程x 2-6x +5=0的两个实根, ∴a 1=1,a 2=5,∴等差数列{a n }的公差为4,∴S n =n ×1+n (n -1)2×4=2n 2-n . (2)证明:当c =-12时,b n =S n n +c =2n 2-n n -12=2n , ∴b n +1-b n =2(n +1)-2n =2,b 1=2. ∴数列{b n }是以2为首项,2为公差的等差数列.。
完整版等差数列知识点总结等差数列是数学中的重要概念,它在各个领域都有广泛的应用。
本文将对等差数列的定义、通项公式、前n项和等差数列的性质等知识点进行全面总结。
一、等差数列的定义等差数列是指一个数列中相邻两项之差都相等的数列。
数列中的每一项我们称之为等差数列的项,其中第一项通常用a1表示,等差用d表示。
例如,数列2,5,8,11,14就是一个等差数列,其中a1=2,d=3。
二、等差数列的通项公式等差数列通项公式是指根据等差数列的首项和公差,求出任意一项的求值公式。
通项公式的推导有多种方法,这里我们介绍其中一种常用的方法。
设等差数列的首项是a1,公差是d,第n项是an,则通项公式可以表示为:an = a1 + (n-1)d根据这个公式,我们可以轻松地求得等差数列中任意一项的值。
三、等差数列前n项和公式在等差数列中,求前n项和也是一个常见的问题。
我们可以通过求和公式来解决这个问题。
设等差数列的首项是a1,公差是d,第n项是an,前n项和用Sn表示,则前n项和公式可以表示为:Sn = (n/2)(a1 + an)利用前n项和公式,我们可以方便地求得等差数列的前n项和。
四、等差数列的性质等差数列具有一些特点和性质,我们在解题过程中可以利用它们来简化计算。
1. 通项差是公差的倍数:an - an-1 = d这个性质意味着等差数列中,相邻两项之差都是公差的倍数。
2. 对称性:an = a1 + (n-1)d,an+k = a1 + (n+k-1)d根据等差数列的通项公式,我们可以发现等差数列具有对称性。
一个等差数列中的第k项和倒数第k项之和等于第一项与最后一项之和。
3. 求和公式与项数有关:Sn = (n/2)(a1 + an)求和公式中的项数n对和值Sn有影响,这个公式可以帮助我们快速计算一个等差数列的前n项和。
五、等差数列的应用领域等差数列在数学中有广泛的应用,它们不仅仅出现在数学题目中,还出现在其他许多领域。
等差数列是一种常见的数列,也是一种重要的数列,是指从第2项起,每一项与它的前一项的差都等于同一个常数的数列.与等差数列有关的题目一般主要考查等差数列的通项公式、性质、前n 项的和公式.本文主要谈一谈与等差数列有关的常见题型及其解法.一、求等差数列的通项公式求等差数列的通项公式问题主要考查等差数列的通项公式和性质.这类题目一般较为简单,只要结合题意,灵活运用等差数列的通项公式和性质便能顺利解题.例1.已知等差数列{a n }为递增数列,前3项的和为-3,前3项的积为8.求数列{a n }的通项公式.解:设等差数列{a n }的公差为d ,d >0,∵等差数列{a n }的前3项的和为-3,前3项的积为8,∴ìíî3a 1+3d =-3,a 1(a 1+d )(a 1+2d )=8,∴ìíîa 1=2,d =-3,或ìíîa 1=-4,d =3,∵d >0,∴a 1=-4,d =3,∴a n =3n -7.要想顺利解答本题,需要结合题意,根据等差数列的通项公式列出方程组,通过解方程组求得数列的首项和公差,然后利用等差数列的通项公式求解.例2.各项均不为0的数列{a n }满足a n +1(a n +a n +2)2=a n +2⋅a n ,且a 3=2a 8=18.求数列{a n }的通项公式.解:依题意得,a n +1a n +a n +2a n +1=2a n +2a n ,两边同时除以a n a n +1a n +2,可得1a n +2+1a n =2a n +1,故数列{}1a n 是等差数列,设数列{}1a n的公差为d .因为a 3=2a 8=15,所以1a 3=5,1a 8=10,所以1a 8-1a 3=5=5d ,即d =1,所以1a n =1a 3+(n -3)d =n +2,故a n =1n +2.题目只告知数列各项之间的关系式,需要将已知关系式化简、转化,才能解题.首先将a n +1(a n +a n +2)2=a n +2a n ,两边同时除以a n a n +1a n +2,构造出等差数列,然后求出数列的首项和公差,再利用等差数列的通项公式求得原数列的通项公式.二、求等差数列的前n 项和或最值求等差数列的前n 项和问题是一类常见的问题,主要考查等差数列的前n 项和公式以及求最值的方法.例3.设数列{a n }的前n 项和为S n ,且a n =-2n +1,则数列{}S nn的前11项和为______.解:∵a n =-2n +1,∴数列{a n }是以-1为首项,-2为公差的等差数列,∴S n =n [-1+(-2n +1)]2=-n 2,∴S n n =-n 2n =-n ,∴数列{}S nn 是以-1为首项,-1为公差的等差数列,∴数列{}S nn 的前11项和为11×(-1)+11×102×(-1)=-66.解答等差数列的前n 项和问题的关键是,首先判定数列是等差数列,求出数列的首项、公差,然后利用等差数列的前n 项和公式求得结果.例4.等差数列{a n }中,S n 为前n 项和,且a 1=25,S 17=S 9,请问:数列前多少项的和最大?解法一:∵a 1=25,S 17=S 9,∴17a 1+17×162d =9a 1+9×82d ,解得d =-2.∵a 1=25>0,由ìíîa n =25-2(n -1)≥0,a n +1=25-2n ≤0,得ìíîïïn ≤1312,n ≥1212.∴当n =13时,S n 有最大值.解法二:∵a 1=25,S 17=S 9,∴17a 1+17×162d =9a 1+9×82d ,解得d =-2.从而S n =25n +n (n -1)2(-2)=-(n -13)2+169.故前13项之和最大.求等差数列的前n 项和的最值问题较为复杂,求解此类问题一般有两种方法.①通项变号法:当a 1>0,d <0时,若ìíîa m ≥0,a m +1≤0,则S n 的最大值为S m ;当a 1<0,d >0时,若ìíîa m ≤0,a m +1≥0,则S n 的最小值为S m .②二次函数法:利用等差数列前n 项和的函数表达式S n =an 2+bn ,通过配方或借助图象求得二次函数最值的方法来求解.当然,与等差数列有关的问题还有很多.但无论遇到哪种问题,同学们都要仔细分析题意,灵活运用等差数列的通项公式、性质、前n 项的和公式,以及函数思想和转化思想来解题.(作者单位:江苏省南通市海安实验中学)解题宝典46。
等差数列题型总结是数学中的一种基本数列形式,它在学习数学的过程中经常出现。
掌握的基本概念和解题方法,对于提高数学水平是非常重要的。
本文将对常见的题型进行总结,以帮助读者理解和应用。
一、的基本概念是指一个数列中后一项与前一项之差恒等于一个常数,这个常数称为公差。
例如,数列1,3,5,7,9就是一个,公差为2。
在中,首项通常用a表示,公差用d表示,第n项用an表示。
因此,可以表示为:a,a+d,a+2d,a+3d,...二、的求和公式对于来说,求和是一个常见问题。
如果我们知道了的首项、公差和项数,可以通过求和公式来计算的和。
的求和公式为:Sn = (2a + (n-1)d) * n / 2其中,Sn表示的和,a表示首项,d表示公差,n表示项数。
三、常见的题型1. 求的第n项要求的第n项,可以利用的通项公式:an = a + (n-1)d。
通过给定的首项、公差和项数,可以轻松求得的第n项。
例如,已知的首项为2,公差为3,求该数列的第6项。
根据通项公式可知,a6 = 2 + (6-1) * 3 = 2 + 15 = 17。
2. 求的前n项和要求的前n项和,可以利用求和公式Sn = (2a + (n-1)d) * n / 2。
通过给定的首项、公差和项数,可以计算的前n项和。
例如,已知的首项为1,公差为2,求该数列的前10项和。
根据求和公式可知,S10 = (2 * 1 + (10-1) * 2) * 10 / 2= (2 + 18) * 10 / 2= 20 * 10 / 2= 100因此,的前10项和为100。
3. 求中满足某个条件的项数有时候,我们需要求解中满足某个条件的项数。
在这种情况下,我们可以利用的通项公式,设定一个方程,然后解方程来找到满足条件的项数。
例如,已知的首项为3,公差为5,项数大于等于7且小于等于100的项数中,满足an = 40的项数有多少个?根据通项公式可知,an = 3 + (n-1) * 5 = 3n + 2。
等差数列知识点总结与基本题型一、基本概念1、等差数列的概念(1)定义:如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常用字母d 表示。
1n n a a d +-=(d 为常数),()11n a a n d =+- (2)对于公差d ,需强调的是它是每一项与它前一项的差(从第2项起)要防止把被减数与减数弄颠倒。
(3)0d>⇔等差数列为递增数列0d =⇔等差数列为常数列 0d <⇔等差数列为递减数列(4)一个等差数列至少由三项构成。
2、等差数列的通项公式(1)通项公式:1(1)n a a n d =+-,(当1n =时,等式也成立); (2)推导方法:①不完全归纳法:在课本中,等差数列的通项公式是由1234,,,,a a a a 归纳而得,这种利用一些特殊现象得出一般规律的方法叫不完全归纳法。
②迭加法:也称之为逐差求和的方法:2132,,a a d a a d -=-=431,,n n a a d a a d --=-=,上述式子相加,1(1)n a a n d -=-,即1(1)n a a n d =+-。
③迭代法:1223()2()2n n n n n a a d a d d a d a d d ----=+=++=+=++ 313(1)n a d a n d -=+==+-。
(3)通项公式的应用与理解①可根据d 的情况来分析数列的性质,如递增数列,递减数列等。
②用于研究数列的图象。
11(1)()n a a n d dn a d =+-=+-,∴(Ⅰ)0d ≠时,n a 是n 的一次函数,由于n N *∈,因此,数列{}n a 的图象是直线1()n a dn a d =+-上的均匀排开的无穷(或有穷)个孤立点。
(Ⅱ)0d =时,1n a a =,表示平行于x 轴的直线上的均匀排开的无穷(或有穷)个孤立点。
等差数列及其前n 项和教学目标:1、熟练掌握等差数列定义;通项公式;中项;前n 项和;性质。
2、能熟练的使用公式求等差数列的基本量,证明数列是等差数列,解决与等差数列有关的简单问题。
知识回顾:1.定义:一般地,如果一个数列从第 2 项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫等差数列,这个常数叫做等差数列的公差,公差通常用字母 d 表示。
用递推公式表示为( 2)a n n 或a n 1 a n d(n 1) 。
(证明数列是等差数列的关键)a 1 d n2.通项公式:等差数列的通项为:a n a1 (n 1)d ,当d 0时,a n 是关于n 的一次式,它的图象是一条直线上自然数的点的集合。
推广:a n a m (n m)d3.中项:如果a ,A,b 成等差数列,那么A叫做a 与b 的等差中项;其中a bA 。
24.等差数列的前n项和公式n(a a ) n(n 1)1 nS na d 可以整理成S n=n 12 2 d22+ a d )nn ( 1 。
当d≠0时是n 的一个常数2项为0的二次函数。
5.等差数列项的性质(1)在等差数列a中,若m ,n ,p ,q N 且m n p q,则am a n a p a q ;特n别的,若m ,p ,q N 且2m p q ,则2a m a p a q 。
(2)已知数列a n , b n 为等差数列,S n ,T n 为其前n 项和,则anbnS2nT2n11(3)若等差数列的前n 项和为S n ,则n, S S ,S S ,S 也成等差数列,公差d n d' 22n n 3n 2n;S ,(n 1)1an S S(4),(n 2)n n 1;(5)若数列{ a n }是公差为 d 的等差数列,则数列S nn 也是等差数列,且公差为______。
快乐每一天,收获多一点。
第 1 页共7 页考点分析考点一:等差数列基本量计算例 1、等差数列 {a n } 中, a 1 3a 8 a 15 120 ,则 3a 9 a 11 的值为 练习 (1)设 S n 是等差数列 a 的前 n 项和.已知 a 2 =3, a 6 =11,则 S 7 等于nA .13B .35C .49D .63 (2)数列 a n 为等差数列,且 aa, a 30 ,则公差 d =72 41A .-2B .- 12 C . 1 2D .2(3)在等差数列 a 中,已知 a 3 2 ,则该数列的前 5 项之和为nA .10B .16C .20D .32(4)若等差数列 { a n } 的前 5 项和 S 5=25,且 a 2=3,则 a 7 等于 ()A .12B .13C .14D .151(5)记等差数列 { a 2,S 4=20,则 S 6 等于()n } 的前 n 项和为 S n ,若 a 1=A .16B .24C .36D .48(6) a 的前 n 项和为 nS ,若 a 1 2 , S 3 12 ,则 na 等于 ()6A .8B .10C .12D .14考点二:等差数列性质应用例 1、等差数列 a 中, 3( a 3 a 5 ) 2(a 7 a 10 a 13) 24 ,则该数列前 13 项的和是 ()nA .13B .26C .52D .156练习 1、在等差数列 a n 中, a 1 a 9 10 ,则 a 5 的值为A .5B .6C .8D .64 2、在等差数列 { a } 中, naa a ,则 12, 3 5 10a()7A .5B .8C .10D .143、设数列 { a n } 是等差数列,若 a 3+a 4+a 5=12,则 a 1+a 2+⋯ + a 7 等于()快乐每一天,收获多一点。
第2页共 7 页A.14 B.21 C.28 D.35例2、设等差数列{a n} 的前n 项和为S n,若S3=9,S6=36,则a7+a8+a9 等于( )A.63 B.45 C.36 D.27练习、已知等差数列{ a n} 的前n 项和为S n,且S10=10,S20=30,则S30=________.S2 014 例3、已知S n 是等差数列{a n}的前n 项和,若a1=-2 014 ,2 014 ________.S2 008-2 008=6,则S2 016 =练习、(1) 已知等差数列{a n} 的前n 项和为Sn,且满足S3 S2-=1,则数列{a n} 的公差是3 2( )A. 12 B.1 C.2 D.3例4、设S n ,T n 分别是等差数列a n 、b n 的前n项和,S7n 2n ,则T n 3na5b5。
例5、已知等差数列a的公差为2,项数是偶数,所有奇数项之和为15,所有偶数项之n和为25,则这个数列的项数为________。
练习1、若一个等差数列前 3 项的和为34,最后 3 项的和为146,且所有项的和为390,则这个数列有()A.13 项B.12 项C.11项D.10 项2、等差数列a的公差d 2,a1 a4 a7 a97 50,那么a3 a6 a9 a99 =nA.-78 B.-82 C.-148 D.-182考点三:等差数列的证明例1:在数列{ a n} 中,a1 1, an 1114an,bn22a 1n,其中n N * .(1)求证:数列{ b n} 是等差数列;(2)求证:在数列{ a n } 中对于任意的*n N ,都有a n a n 1快乐每一天,收获多一点。
第 3 页共7 页练习1、数列a满足a1 1,a2 2,a n 2 2a n 1 a n 2 。
n(1)设b 1 ,证明b n 是等差数列;n a an n(2)求数列a的通项公式。
n2、已知数列{ a n} 中,a1=35,a n =2-1( n≥2,n∈N n} 满足b*) ,数列{ bn=a n-11( n∈a n-1N n}是等差数列;* ) .求证:数列{ b2an3、数列a n 满足:a1 2 , 1 n N 。
求证:a n ,a 2n1an是等差数列;小结与拓展:(1)定义法:a n 1 a d (n N ,d 是常数)a n 是等差数列;n(2)中项法:2a n 1 a n a n 2 ( n N ) a n 是等差数列;(3)通项公式法: a kn bn (k,b是常数)a n 是等差数列;(4)前n 项和法:S n= 2kn +bn(k, b 是常数)a n 是等差数列值考点四:等差数列前n 项和的最快乐每一天,收获多一点。
第4页共7 页(1)a1 0 ,d 0时,S n 有最大值;a1 0 ,d 0时,S n 有最小值;(2)S n 最值的求法:①若已知S n ,可用二次函数最值的求法(n N );②找到正负项分界的是第几项。
例1、数列a中,an 2n 49 ,当数列a n 的前n项和S n 取得最大值时,nn练习1、设等差数列a的前n 项和为Sn ,若a1 11,a4 a6 6,则当S n 取最小值时nn 等于( )A.6 B.7 C.8 D.92、若等差数列a n 满足a7 a8 a9 0 ,a8 a9 0 ,则当n ________时a n 的前n项和最大。
例2、在等差数列a中,a1 7,公差为d,前n 项和为S n ,当且仅当n=8 时,S n 取得n最大值,则 d 的取值范围为________。
例3、等差数列a中,a1 0 ,前n项和为S n ,且仅当S5 S12 ,则当n 时,S n 取最大n值。
练习1、设数列a是等差数列,且a2 8 ,a15 5 ,S n 是数列a n 的前n 项和,则()nA.S10 S11 B.S10 S11 C.S9 S10 D.S9 S102.设a n (n N ) 是等差数列,S n 是其前n 项的和,且S5 S6 , S6 S7 S8 则下列结论错.误.的是()A.d 0 B..a7 0 C.S9 S5 D.S6 与S7 均为S n 的最大值考点五:等差数列和项转换 an a1Sn( nSn1)(n12)12 ,求例1、已知数列a n 的前n 项和为S n nn 2 a 。
n2练习1、已知数列a n 的前n 项和为n 2 ,求a n 。
S n快乐每一天,收获多一点。
第 5 页共7 页2、设数列{ a n} 的前n 项和 2S n ,则a8 的值为()nA.15 B.16 C.49 D.64习题15.2 1、在等差数列a n 中,(1)已知a1 2,d 3,n 10,求a ;n(2)已知a a n 21, d 2,求 n3,1 ;(3)已知a 12, a 27,求d1 ;6(4)已知1d ,a7 8,求a 。
132、在等差数列{ a n }中,(1)已知S8 48, S12 168,求a1, 和d(2)已知a6 10, S5 5 ,求a8 和S8(3)a1 20, a n 54, S n 599, 求 d 及n;(4)1d , n 37, S n 629,求a1及an3;5 1(5)a ,d,S n 5,求n及a n1 ;6 6(6) d 2,n 15, an 10, 求a1及S 。
n3、等差数列{ a n } 的前n 项和记为S n ,已知a10 30, a20 50 。
(1)求通项公式{ a n} ;快乐每一天,收获多一点。
第 6 页共7 页(2)若S 242 ,求n 。
n4、设S n 为等差数列{ a n} 的前n项和,若S3 3,S6 24 ,则a95、等差数列{a n } 的前n 项和S n ,若a1 2, S3 12 ,则a6 ( )A.8 B.10 C.12 D.146、已知道单调递增的等差数列a n 的前三项和为21,前三项积为231,则a n7、在等差数列a n 中,a5 120 ,则a2 a4 a6 a88、数列a中,a n 2n 49 ,当数列n a 的前n项和S n 取得最大值时,nn9、数列a n 是首项为23,公差为整数的等差数列,且第六项为正,第七项为负. (1)求数列的公差;(2)求前n 项和S n 的最大值;(3)当S 0 时,求n 的最大值。
n快乐每一天,收获多一点。
第7 页共7 页。