第五章稳定性定义
- 格式:ppt
- 大小:791.00 KB
- 文档页数:20






Chp.5系统稳定性基本要求1.了解系统稳定性的定义、系统稳定的条件;2.掌握Routh判据的必要条件和充要条件,学会应用Routh判据判定系统是否稳定,对于不稳定系统,能够指出系统包含不稳定的特征根的个数;3.掌握Nyquist 判据;4.理解Nyquist 图和Bode 图之间的关系;5.掌握Bode 判据;6.理解系统相对稳定性的概念,会求相位裕度和幅值裕度,并能够在Nyquist 图和Bode 图上加以表示。
重点与难点本章重点1.Routh 判据、Nyquist 判据和Bode 判据的应用;2.系统相对稳定性;相位裕度和幅值裕度求法及其在Nyquist图和Bode 图的表示法。
本章难点Nyquist 判据及其应用。
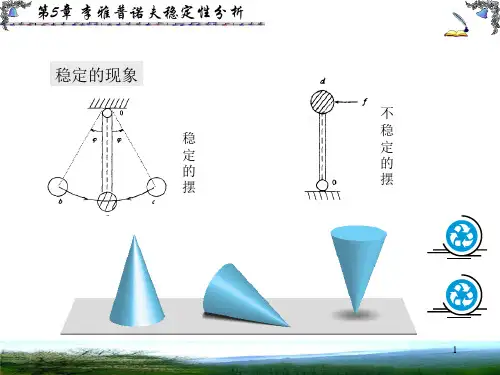
§1 概念示例:振摆1、稳定性定义:若系统在初始条件影响下,其过渡过程随时间的推移逐渐衰减并趋于0,则系统稳定;反之,系统过渡过程随时间的推移而发散,则系统不稳定。
(图5.1.2)讨论:①线性系统稳定性只取决于系统内部结构和参数,是一种自身恢复能力。
与输入量种类、性质无关。
②系统不稳定必伴有反馈作用。
(图5.1.3)若x0(t)收敛,系统稳定;若x0(t)发散,则系统不稳定。
将X0(s)反馈到输入端,若反馈削弱E(s) →稳定若反馈加强E(s) →不稳定③稳定性是自由振荡下的定义。
即x i(t)=0时,仅存在x i(0-)或x i(0+)在x i(t)作用下的强迫运动而系统是否稳定不属于讨论范围。
2、系统稳定的条件:对[a n p n+a n-1p n-1+…a1p+a0]x0(t)=[b m p m+b m-1p m-1+…b1p+b0]x i(t)令B(s)= a n p n+a n-1p n-1+…a1p+a0 A(s)= b m p m+b m-1p m-1+…b1p+b0初始条件:B0(s) A0(s)则B(s)X0(s)- B0(s)= A(s)X i(s)- B0(s)X i(s)=0,由初始条件引起的输出:L-1变换根据稳定性定义,若系统稳定须满足,即z i为负值。




第五章系统的稳定性讲授内容5.1系统稳定的初步概念一、稳定性的定义系统稳定性是指系统在干扰作用下偏离平衡位置,当干扰撤除后,系统自动回到平衡位置的能力。
若系统在初始状态的影响下,由它所引起的系统的时间响应随着时间的推移,逐渐衰减并趋向于零(即回到平衡位置),则称系统为稳定的;反之,由它所引起的系统的时间响应随着时间的推移而发散(即偏离平衡位置越来越远),则称系统为不稳定的。
线性系统的稳定性是系统的固有特性,仅与系统的结构及参数有关;而非线性系统的稳定性不仅与系统的结构及参数有关,而且还与系统的输入有关。
二、系统稳定的充要条件系统稳定的充要条件是的系统所有特征根的实部全都小于零,或系统传递函数的所有极点均分布在s平面的左半平面内。
若系统传递函数的所有极点中,只有一个位于虚轴上,而其它极点均分布在s平面的左半平面内,则系统临界稳定。
而临界稳定的系统极易因为系统的结构或参数的细微变化而变成不稳定的系统。
因此,临界稳定往往也归结为不稳定的一种。
5.2 (劳斯)稳定判据Routh Routh 判据是判别系统特征根分布的一个代数判据。
一、系统稳定的必要条件要使系统稳定,即系统全部特征根均具有负实部,就必须满足以下两个条件:1)特征方程的各项系数都不等于零。
2)特征方程的各项系数的符号都相同。
此即系统稳定的必要条件。
按习惯,一般取最高阶次项的系数为正,上述两个条件可以归结为一个必要条件,即系统特征方程的各项系数全大于零,且不能为零。
二、系统稳定的充要条件系统稳定的充要条件是表的第一列元素全部大于零,且不能等于零。
Routh 运用判据还可以判定一个不稳定系统所包含的具有正实部的特征根的个数为表第一列元素中符号改变的次数。
Routh Routh 运用判据的关键在于建立表。
建立表的方法请参阅相关的例题或教材。
运用判据判定系统的稳定性,需要知道系统闭环传递函数或系统的特征方程。
Routh Routh Routh Routh 在应用判据还应注意以下两种特殊的情况:Routh 1.如果在表中任意一行的第一个元素为0,而其后各元不全为0,则在计算下一行的第一个元时,该元将趋于无穷大。
稳定性理论5.1 外部稳定性和内部稳定性运动稳定性分为基于I/O 描述的外部稳定性和基于状态空间描述的内部稳定性。
内容包括 外部稳定性 内部稳定性内部稳定性和外部稳定性关系(1)外部稳定性考虑以I/O 描述的线性因果系统,假定初始条件为零,外部稳定性定义如下:定义5.1 称一个因果系统为外部稳定,如果对任意有界输入u (t ),对应输出y (t )均有界,即 102(),[,]()u t t t y t ββ∀≤<∞∈∞⇒≤<∞外部稳定也称为BIBO 稳定。
定理5.1 对零初始条件线性时变系统,t 0时刻BIBO 稳定的充分必要条件是 01212(,),,,,;,,,tij t h t d i q j pττβ≤<∞==∫L L证明:先证SISO 情形。
充分性,已知脉冲响应函数绝对可积,证明系统BIBO 稳定。
由基于脉冲响应的输出关系式,有ττβττττττd u d u t h d u t h t y tt tt tt ∫∫∫≤⋅≤=000)()(),()(),()(因此,对任意有界输入u (t ) ∞<≤1β)(t u ∞<≤≤⇒∫10ββττβd u t y tt )()(即系统BIBO 稳定。
再证必要性,已知系统BIBO 稳定,反设有t 1,使得 ∞=∫ττd t h t t 11),(构造有界输入 ⎪⎩⎪⎨⎧<−=>+==0100011111),(,),(,),(,),(sgn )(ττττt h t h t h t h t u∞===⇒∫∫τττττd t h d u t h t y tt t t 1010111),()(),()(这与系统BIBO 稳定矛盾,必要性得证。
MIMO 情形:对输出的每一分量,有 pj q i dt t h ij ,,,;,,,,)(L L 21210==∞<≤∫∞β定理5.2 对零初始条件线性时不变系统,BIBO 稳定的充分必要条件是,传递函数矩阵G (s )所有极点均具负实部。