第五章测量误差及测量平差.
- 格式:docx
- 大小:61.73 KB
- 文档页数:10




现在的位置:课程介绍 >> 理论部分 >> 电子讲稿第五章误差基本知识5.1误差的来源和分类一、定义:观测值与真值之差,记为:X为真值,即能代表某个客观事物真正大小的数值。
为观测值,即对某个客观事物观测得到的数值。
为观测误差,即真误差。
二、误差的来源1、测量仪器一是仪器本身的精度是有限的,不论精度多高的仪器,观测结果总是达不到真值的。
二是仪器在装配、使用的过程中,仪器部件老化、松动或装配不到位使得仪器存在着自身的误差。
如水准仪的水准管轴不平行视准轴,使得水准管气泡居中后,视线并不水平。
水准尺刻划不均匀使得读数不准确。
又如经纬仪的视准轴误差、横轴误差、竖盘指标差都是仪器本身的误差。
2、观测者是由于观测者自身的因素所带来的误差,如观测者的视力、观测者的经验甚至观测者的责任心都会影响到测量的结果。
举例:如水准尺倾斜、气泡未严格居中、估读不准确、未精确瞄准目标都是观测误差。
3、外界条件测量工作都是在一定的外界环境下进行的。
例如温度、风力、大气折光、地球曲率、仪器下沉都会对观测结果带来影响。
上述三项合称为观测条件a.等精度观测:在相同的观测条件下进行的一组观测。
b.不等精度观测:在不同的观测条件下进行的一组观测。
测量误差的分类根据测量误差表现形式不同,误差可分为系统误差、偶然误差和粗差。
1、系统误差定义:误差的符号和大小保持不变或者按一定规律变化,则称其为系统误差。
如:钢尺的尺长误差。
一把钢尺的名义长度为30m,实际长度为30.005m,那么用这把钢尺量距时每量一个整尺段距离就量短了5mm,也就是会带来-5mm的量距误差,而且量取的距离越长,尺长误差就会越大,因此系统误差具有累计性。
如:水准仪的i角误差,由于水准管轴与视准轴不平行,两者之间形成了夹角i,使得中丝在水准尺上的读数不准确。
如果水准仪离水准尺越远,i角误差就会越大。
由于i角误差是有规律的,因此它也是系统误差。
正是由于系统误差具有一定的规律性,因此只要找到这种规律性,就可以通过一定的方法来消除或减弱系统误差的影响。




第七章测量误差基本知识内容:了解测量误差来源及产生的原因;掌握系统误差和偶然误差的特点及其处理方法;理解精度评定的指标(中误差、相对误差、容许误差)的概念;了解误差传播定律的应用。
重点:系统误差和偶然误差的特点及其处理方法。
难点:中误差、相对误差、容许误差的概念;误差传播定律的应用。
§ 5.1 测量误差的概念测量误差按其对测量结果影响的性质,可分为系统误差和偶然误差。
一、系统误差 (system error)1、定义:在相同观测条件下,对某量进行一系列观测,如误差出现符号和大小均相同或按一定的规律变化,这种误差称为系统误差。
2、特点:具有积累性,对测量结果的影响大,但可通过一般的改正或用一定的观测方法加以消除。
二、偶然误差 (accident error)1、定义:在相同观测条件下,对某量进行一系列观测,如误差出现符号和大小均不一定,这种误差称为偶然误差。
但具有一定的统计规律。
2、特点:(1)具有一定的范围。
(2)绝对值小的误差出现概率大。
(3)绝对值相等的正、负误差出现的概率相同。
(4)数学期限望等于零。
即:误差概率分布曲线呈正态分布,偶然误差要通过的一定的数学方法(测量平差)来处理。
此外,在测量工作中还要注意避免粗差 (gross error) (即:错误)的出现。
偶然误差分布频率直方图§ 5.2 衡量精度的指标测量上常见的精度指标有:中误差、相对误差、极限误差。
一、中误差方差:——某量的真误差, [] ——求和符号。
规律:标准差估值(中误差 m )绝对值愈小,观测精度愈高。
在测量中,n为有限值,计算中误差 m 的方法,有:1、用真误差( true error )来确定中误差——适用于观测量真值已知时。
真误差Δ——观测值与其真值之差,有:标准差中误差(标准差估值), n 为观测值个数。
[ 例题 ] :对 10 个三角形的内角进行了观测,根据观测值中的偶然误差(三角形的角度闭合差,即真误差),计算其中误差。


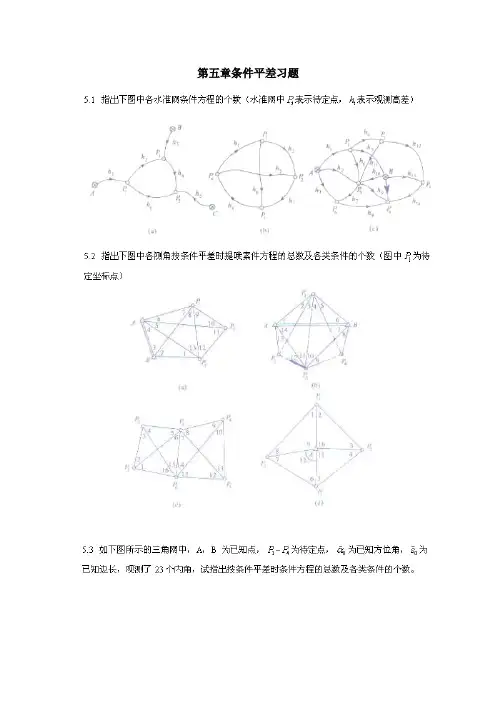
第五章条件平差习题第五章思考题参考答案5.1(a)n=6,t=3,r=3(b)n=6,t=3,r=3(c)n=14,t=5,r=95.2(a)n=13,t=6,r=7共有7个条件方程,其中有5个图形条件,2个极条件。
(b)n=14,t=8,r=6共有6个条件方程,其中有3个图形条件,3个极条件。
(c)n=16,t=8,r=8共有8个条件方程,其中有6个图形条件,2个极条件。
(d)n=12,t=6,r=6共有6个条件方程,其中有4个图形条件,1个圆周条件,1个极条件。
5.3n=23,t=6,r=17共有17个条件方程,其中有9个图形条件,1个圆周条件,1个固定角条件,1个固定边条件,5个极条件。
5.4 (1)n=22,t=9,r=13:7个图形条件,1个圆周条件,2个极条件,2个边长条件,一个基线条件。
(2)12837941314121520111718195610166101119910111213510ˆˆˆ1800ˆˆˆ1800ˆˆˆ1800ˆˆˆ1800ˆˆˆˆ1800ˆˆˆˆ1800ˆˆˆˆ1800ˆˆˆˆˆ1800ˆˆˆsin sin sin L L L L L L L L L L L L L L L L L L L L L L L L L L L L L L L L ++-=++-=++-=++-=+++-=+++-=+++-=++++-=171961116203614184715192211151217121318124ˆsin 1()ˆˆˆˆsin sin sin sin ˆˆˆˆsin sin sin sin 1()ˆˆˆˆsin sin sin sin ˆˆ()ˆˆˆˆsin sin sin sin ˆˆ(ˆˆˆˆsin sin sin sin FG FG L L L L L L L L L L L L L S S S S L L L L S S L L L L ===→=以大地四边形中心为极以中点四边形D 点为极的边长条件1213611891719ˆˆ)ˆˆˆˆsin sin sin sin ˆˆˆˆsin sin sin sin FG AB S S L L L L S S L L L L →=的边长条件(基线条件)5.5 n=8,t=4,r=4;有多种条件方程的列法,其中之一为:1001000100110000120001001104000011014V ⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥-=⎢⎥⎢⎥--⎢⎥⎢⎥---⎣⎦⎣⎦(注意常数项单位为mm ) 5.6 (1)P=3/2,(2)P=15.7 (1)P B =1.6,P C =2.1,P D =2.1,P E =1.6(2)P hCD =1.85.8 []ˆ 2.4998 1.9998 1.3518 1.8515h=2P σ=0.32(mm)5.9 1234561110009100110900101016V V V V V V ⎡⎤⎢⎥⎢⎥-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥+=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎢⎥⎢⎥⎢⎥⎣⎦ []045452TV mm =---[]ˆ 1.576 2.219 3.7950.867 2.443 1.352T h m =--- 5.10 (1)1ˆ10.3556h m = 2ˆ15.0028h m = 3ˆ20.3556h m = 4ˆ14.5008h m =5ˆ 4.6472h m = 6ˆ 5.8548h m = 7ˆ10.5020h m =(2)±2.2mm。
第五章 测量误差及测量平差§5.1 测量误差概述一、测量误差的概念某量的各测量值相互之间或观测值与理论值之间的往往存在着某些差异,说明观测中存在误差。
观测值与真值之差称为测量误差,也叫真误差。
X l i i -=∆ (i =1、2、……、n ) X 为真值。
二、研究测量误差的目的分析测量误差的产生原因、性质和积累规律;正确地处理测量成果,求出最可靠值;评定测量结果的精度;为选择合理的测量方法提供理论依据。
三、测量误差产生的原因1.测量仪器因素2.观测者的因素3.外界条件的因素测量观测条件——测量仪器、观测人员和外界条件这三方面的因素综合起来称为测量观测条件。
等精度观测——测量观测条件相同的各次观测称为等精度观测。
非等精度观测——测量观测条件不相同的各次观测称为非等精度观测。
四、测量误差的分类1.系统误差在相同的观测条件下对某量作一系列观测,如果误差的大小、符号表现出系统性,或按一定的规律变化,或保持不变,这种误差称为系统误差。
其特点:具有累积性,但可以采用适当的观测方法或加改正数来消除或减弱其影响。
2.偶然误差在相同的观测条件下对某量作一系列观测,如果误差的大小和符号不定,表面上没有规律性,但实际上服从于一定的统计规律性,这种误差称为偶然误差。
偶然误差单个的出现上没有规律性,不能采用适当的观测方法或加改正数来消除或减弱其影响。
因此,观测结果中偶然误差占据了主要地位,是偶然误差影响了观测结果的精确性。
五、减少测量误差的措施对系统误差,通常采用适当的观测方法或加改正数来消除或减弱其影响。
对偶然误差,通常采用多余观测来减少误差,提高观测成果的质量。
§5.2 偶然误差的特性一、精度的含义1.准确度准确度是指在对某一个量的多次观测中,观测值对该量真值的偏离程度。
2.精密度精密度是指在对某一个量的多次观测中,各观测值之间的离散程度。
3.精度精度也就是精确度,是评价观测成果优劣的准确度与精密度的总称,表示测量结果中系统误差与偶然误差的综合影响的程度。
第5章测量误差基本知识测量工作使用仪器进行测量,在测量过程中不可避免的出现误差,为了提高测量精度及精度评定,需要了解测量误差的来源,促进测量工作方法的改进,和测量精度的提高。
误差—在一定观测条件下,观测值与真值之差。
精度—观测误差的离散程度。
5-1 误差的基本概念讨论测量误差的目的:用误差理论分析,处理测量误差,评定测量成果的精度,指导测量工作的进行。
▼▼▼▼产生测量误差的原因,▼▼测量误差的分类和处理原则,▼▼偶然误差的特性一、测量误差的来源仪器原因:仪器精度的局限,轴系残余误差等。
人的原因:判别力和分辨率的限制,经验等。
外界影响:气象因素(温度变化,风、大气折光)等。
有关名词:观测条件,等精度观测:上述三大因素总称观测条件,在上述条件基本一致的情况下进行各次观测,称等精度观测。
结论:观测误差不可避免(粗差除外)二、测量误差的分类两类误差:系统误差偶然误差粗差(错误排除)1、系统误差-- 误差出现大小、符合相同,或按规律变化,具有积累性。
处理方法①检校仪器,把仪器的系统误差降到最小程度;②求改正数,对测量结果加改正数消除;③对称观测,使系统误差对观测成果的影响互为相反数,以便外业操作时抵消。
例:误差处理方法钢尺尺长误差△D K 计算改正钢尺温度误差△Dt 计算改正水准仪视准轴误差I 操作时抵消(前后视等距)经纬仪视准轴误差C 操作时抵消(盘左盘右取平均)●结论:系统误差可以消除。
2、偶然误差-- 误差出现的大小,符合各部相同,表面看无规律性。
例:估读误差—气泡居中判断,瞄准,对中等误差,导致观测值产生误差。
◎偶然误差:是由人力不能控制的因素所引起的误差。
◎特点:具有抵偿性。
◎处理原则:采用多余观测,减弱其影响,提高观测结果的精度。
3、粗差—指在一定的观测条件下超过规定限差值。
对于粗差,应当分析原因,通过补测等方法加以消除。
三、偶然误差的特性1、偶然误差的定义:设某量的真值X对该量进行n次观测得n次的观测值l1,l2,l3……l n则产生了n个真误差真误差:△I = X-l i2、偶然误差的特性☎当观测次数很多时,偶然误差的出现,呈现统计学上的规律性,偶然误差具有正态分布的特性。
§ 5.1测量误差概述一、测量误差的概念某量的各测量值相互之间或观测值与理论值之间的往往存在着某些差 异,说明观测中存在误差。
观测值与真值之差称为测量误差,也叫真误差。
X 为真值。
二、研究测量误差的目的分析测量误差的产生原因、性质和积累规律;正确地处理测量成果,求 出最可靠值;评定测量结果的精度;为选择合理的测量方法提供理论依据。
三、 测量误差产生的原因1. 测量仪器因素2. 观测者的因素3. 外界条件的因素测量观测条件一一测量仪器、观测人员和外界条件这三方面的因素综合 起来称为测量观测条件。
等精度观测一一测量观测条件相同的各次观测称为等精度观测。
非等精度观测一一测量观测条件不相同的各次观测称为非等精度观测。
四、 测量误差的分类1. 系统误差在相同的观测条件下对某量作一系列观测,如果误差的大小、符号表现 出系统性,或按一定的规律变化,或保持不变,这种误差称为系统误差。
其特点:具有累积性,但可以采用适当的观测方法或加改正数来消除或 减弱其影响。
2. 偶然误差在相同的观测条件下对某量作一系列观测, 如果误差的大小和符号不定, 表面上没有规律性,但实际上服从于一定的统计规律性,这种误差称为偶然 误差。
偶然误差单个的出现上没有规律性,不能采用适当的观测方法或加改正 数来消除或减弱其影响。
因此,观测结果中偶然误差占据了主要地位,是偶 然误差影响了观测结果的精确性。
五、 减少测量误差的措施对系统误差,通常采用适当的观测方法或加改正数来消除或减弱其影响。
对偶然误差,通常采用多余观测来减少误差,提高观测成果的质量。
第五章 测量误差及测量平差i l i X (i=1、2、 .......... 、 n )§ 5.2偶然误差的特性一、精度的含义1. 准确度准确度是指在对某一个量的多次观测中,观测值对该量真值的偏离程度。
2. 精密度精密度是指在对某一个量的多次观测中,各观测值之间的离散程度。
3. 精度精度也就是精确度,是评价观测成果优劣的准确度与精密度的总称,表示测量结果中系统误差与偶然误差的综合影响的程度。
由于系统误差总是可以采用适当的观测方法或加改正数来消除或减弱其影响,我们认为观测结果中的误差主要是偶然误差。
实际测量中通常真值是不知道的,所以测量中所讲的精度,通常指的是精密度。
测量学上研究的误差是偶然误差。
二、偶然误差的特性通过对偶然误差统计规律的分析,来找出其具有的特性。
本例以对一三角形内角和观测结果(独立观测162次)来说明。
真误差观测值与真值的差值。
△ i= I-X , i=1,2,…,162将162个真误差先进行统计分析,取误差区间d△为0.2〃,各误差区间的个数为k,相对个数为k/n,n为总个数,见表5-1。
从表5-1中可以看出一些规律。
为了更直观表示误差的分布情况,可用直方图的形式来表示。
A 其方程式为:1 厶f(x)L2式中:x= △,^ =m(中误差),即标准偏差。
根据以上分析,偶然误差有以下特性:1. 在一定的观测条件下,偶然误差的绝对值不会超过一定的限值。
2. 绝对值较小的误差比绝对值较大的误差出现的机会多。
3. 绝对值相等的正、负误差出现的机会均等。
4. 偶然误差的算术平均值随观测次数的无限增加而趋向于零,即:lim 口 0 n n§ 5.3 衡量测量精度的指标精度一一误差分布的密集或离散程度衡量测量精度的指标主要有中误差、相对中误差和极限误差。
、中误差 各个真误差的平方的平均值的平方根,称为中误差,用 m J 」 I n式中:[△△戶△ 12+ △ 22+ ……+ △ n 2m 值越大,精度越低,m 值越小,精度越高。
、相对中误差评价测距精度时,用以上绝对的误差值是不能反映实际精度的高低, 而应用相对中误差来评价。
相对中误差是观测值中误差的绝对值与观测值之比,通常化成分子 为1的分数式。
T 值越小,三、极限误差极限误差也称为容许误差或限差。
根据偶然误差的特性,在一定的 观测条件下偶然误差不会超过一定的限度,这个限值即为极限误差。
统计表明,△ >m 的概率为32%△ >2m 的概率为5% △ >3m 的概率为0.3%因此,通常取三倍中误差作为偶然误差的极限值,即△容二 3m要求严格时,也常取二倍中误差作为极限误差,即△容=2mm 表示。
l M表示精度越高,即 M 越大,精度越高。
§ 5.4 误差传播定律有些未知量是不能直接测定的,而是要通过观测值按一定的函数关 系计算而得,那么,函数中误差与观测值中误差的关系如何呢? 误差传播定律:阐述函数中误差与观测值中误差之间的关系。
、观测值一般函数的中误差 设有函数Z = f (X 1 ,X 2,…,X n ) 对函数取全微分得:f f 丄dX n X n 令观测值X 1, X 2,…,X n 的真误差为△X 1,^X 2,…,△ X n ,函数Z 的真误差为△ Z ,由于真误差一般都很小,故上式可写成: f f X ——X 1 X 2 X l X 2当函数关系确定时,偏导数为常数, k 1 , k 2, ,X 2 X ndz ——dX 1 -------- d X 2X i X 2 一 X n X n 则令: k n X i 则 △ Z=k l A X 1+ k 2^ X 2+ …+ k n ^X n设对观测值X 1, X 2,…,X n 进行了 n 次等精度观测,则有 ;△ Z=k l A X 11+ k 2^ X 21+ …+ k n ^ X n1△ Z=k 1 △ X 12+ k 2^ X 22+ …+ k n ^ X n2 △ Z=k 1^ X 1n + k 2^ X 2n + …+ k n ^ X nn把上式两边平方,相加后再除以 k 22』 n [X 2n 得:- 2, [z] k 2 [ X1 ]n n [X i X 2] n2k 1k 2 2k 2k 3X s ] n4,上式写成:根据偶然误差的特性 2 2[z] &2[ X i ] &2[ X 2 ] n n n根据中误差的定义,有:2 2 2 2 2 2m z =k i m Xi + k 2 m X2 + …+ k n mk n 即:mZ沉(三曲k n 2k n2[[X n 2] n X n 2] n(丄)2^2例:量得一球体的直径为10.5cm ,已知其量测中误差为± 0.5mm ,求 该球的体积及其中误差。
解:峠)2m D 2=± 8659mm 3 =± 8.659cm 3、求观测值函数中误差的基本步骤1. 按问题的要求,列出具体的函数关系式;2. 对各观测值求偏导数;3. 写出函数中误差与观测值中误差的关系;4. 计算相应函数值的中误差。
三、几种观测值典型函数的中误差1. 和差函数的中误差设有函数 Z= X 1 ± X 2±・・・± X 2若 m i =m 2=・-=m n贝y : m z mUn2. 倍数函数的中误差 设倍数函数 Z=kx 则有 m z =km说明所求值与观测值是倍数关系的话,其中误差也是倍数关系。
3. 线性函数的中误差设有线性函数 Z=k i x i ± k 2X 2 土…土 k n X n则有:函数关系为:3 R 3 3(D )3606.1cm 3rni v2mD mDI 2 2m zv m im 22m nm zJk 12m 12 k 22m 22k n 2m n 2n 次等精度观测,观测值为|1,|2,…,|n ,则这些观测值的 |l |2x -------------n2. 等精度观测值的最可靠值算术平均值有什么作用呢?设该量的真值为X,则有:「△ 1=11—X△ 2=| 2— X△ n =|n — X上式相加得:1 2n即:———Xn n 根据偶然误差的特性4,当 时,算术平均值就是该值的真值, 下,算术平均值与真值之间只差一个微小量[△] 测值的最可靠值。
二、精度评定当被观测量的真值知道时,可用下式计算中误差:[]n若被观测量的真值不知道时,则应用下式计算中误差: m[VV]m J -----------V n 1 v 为观测值的改正数。
§ 5.6等精度观测的直接平差、求最可靠值1.算术平均值若对某一量进行 算术平均值x 为:l l l 2nn -x 时,即X= x ,表明当观测次数无限多 实际上观测次数总是有限的,在这种情况 /n ,所以算术平均值是观1.观测值的改正数观测值的算术平均值与观测值之差,称为观测值的改正数。
当观测次数 为n 时,有:v 1 = X —11 v 2= X — 12 V n = X — I n将上式相加得:[v ]= n • X — [l ]=0,2.观测值的中误差在实际测量中,某量的真值往往是不知道的,因此要先求出算术平均值, 再得出改正数,按下式计算中误差:其推导过程为:设对真值为X 的某一量进行n 次等精度观测,则有⑵—⑴并移项得:k △ 1 = — V 1 — (X — X ) J △ 2=— V 2 —(X — X ) j △ n = — v n — (X — X )⑶式两边平方后再相加得:[△△ ]=[vv]+n(X — X )2+2(X — X )[v] 即得[△△ ]=[vv]+n(X — X )2式中(X-x )是算术平均值的真误差,无法求得,用算术平均值中误差 M代替,上式两边同除该式即为当真值未知时用改正数计算观测值中误差的计算公式。
n-1为多即[V ] =0,用于计算检核。
‘ △ = = 11 -X 斗△ 2 ==12— -X 、△ n ==In— -X ……⑵……⑶n 得:将m 2整理得:m[vv] nn」代入上式,得:n [vv] m 2n n f[vv] \ n 1余观测数。
U —1|1 1|2nn nMJ n (-)2m 2V n即M 乎 v n从上式可看出,取多次观测值的平均值可以提高观测结果的精度。
在实际测量工作中,不能单凭增加观测次数来提高精度,而应选用适当的 观测方法和观测次数来达到要求。
P.100例:已知DJ6光学经纬仪一测回方向值中误差为± 6〃,现用DJ6光学经 纬仪观测某单角,使最后得到的角值中误差达到± 4〃,问需要观测几各测回?解:根据误差传播定理,一测回观测单角的中误差为:例:对某距离丈量了5次,结果为: 15.154m ,15.158m ,15.155m ,15.156m, 15.157m 。
求观测值中误差及相对中误差。
解:先求出算术平均值:x [L] 15154 0 4 12 3n再求改正数:V 12=(15156-15154)2=4 [vv]=1015156mm 15.156mV 22=4 ,V 32 = 1 , V 42=0 , V 52 = 1/[vv] (20_ V n 1 *511 9600J2.5 1.58mm3.算术平均值的中误差设对某量进行n 次等精度观测,观测值中误差为 m ,则算术平均值的中误差M 为:Mm ,其推导过程如下:v nMj (n )2m 12(丄)n 2 2 m 2(-)2m n 2 n m,则有:(m 2VT因为m j m 2m 3测量学(甲)第五章测量误差及测量平差赵良荣再根据作业题:习题五: 2、6、9、10、11、13、l4V 2 ( 6)28.5则有2耳 4.5M所以要观测5个测回。