圆与组合图形的面积与周长

组合图形的面积周长计算
组合图形
1、求下列组合图形阴影部分的面积。

2、①求它的周长和面积。

（单位：厘米）②圆的
周长是18.84cm，求阴影部分面积。

③长方形的面积和圆的面积相等，已知圆④求直角
三角形中阴影部分的面积。

的半径是3cm，求阴影部分的周长和面积。

（单位：分米）
⑤下图中长方形长6cm，宽4cm，已知阴影⑥图中阴
影①比阴影②面积小48平方厘米，
①比阴影②面积少3cm2，求EC的长。

AB=40cm，求BC的长。

⑦平行四边形的面积是30cm2，⑧一个圆的半
径是4cm，求阴影部分面积。

求阴影部分的面积。

⑨已知AB=8cm，AD=12cm，三角形ABE和三角形ADF的面积，
各占长方形ABCD的1/3，求三角形AEF的面积。

⑩梯形上底8cm，下底16cm，阴影⑾求阴
影部分面积。

（单位：cm）
部分面积64cm2，求梯形面积。

⑿梯形面积是48平方厘米，阴影部分比空白⒀阴影部分比空白部分大6cm2，求S阴。

部分12平方厘米，求阴影部分面积。

3、求下列图形的体积。

（单位：厘米）。

一、选择题
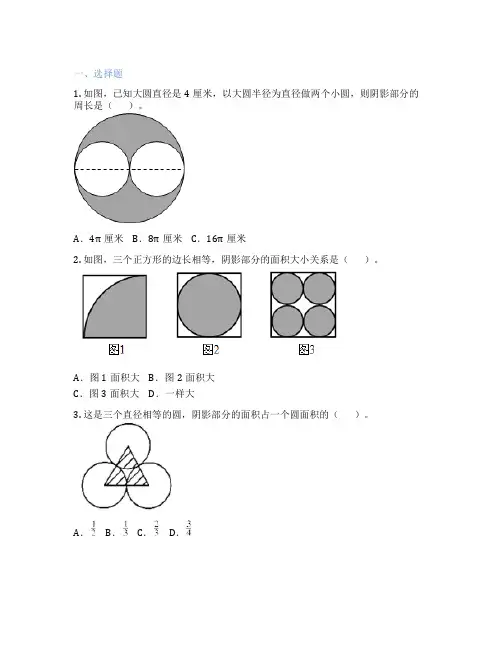
1. 如图，已知大圆直径是4厘米，以大圆半径为直径做两个小圆，则阴影部分的周长是（）。

A．4π厘米B．8π厘米C．16π厘米
2. 如图，三个正方形的边长相等，阴影部分的面积大小关系是（）。

A．图1面积大B．图2面积大
C．图3面积大D．一样大
3. 这是三个直径相等的圆，阴影部分的面积占一个圆面积的（）。

A．B．C．D．
4. 观察图形，对于两个图中阴影部分的叙述，（）是正确的。

A．周长、面积都不相等
B．周长、面积都相等
C．周长相等，面积不相等
D．周长不相等，面积相等
5. 如图图形中正方形的边长相等，阴影部分的面积比较，（）。

A．甲大B．乙大C．阴影面积样大
二、填空题
6. 如图，在一个长方形中画有两个一样大的圆。

已知长方形的周长是18厘米，那么一个圆的面积是( )平方厘米。

7. 要剪一个面积是12.56平方厘米的圆形纸片，至少需要面积是( )平方厘米的正方形纸片（π取3.14）。

8. 下图中阴影部分面积占正方形面积的。

9. 如图所示，阴影部分的面积是______cm2。

10. 学校运动场的两端是半圆形，中间是长方形（如下图），这个运动场的周长是( )米，面积是( )平方米。

三、解答题
11. 用一张长6分米、宽3分米的长方形铁皮，剪出一个最大的半圆，剩下的铁皮的面积是多少平方分米？
12. 两个圆的半径是1厘米，且图中两块阴影部分的面积相等，AB的长为多少厘米？
13. 在图中，AB=BC=CD=16cm，求阴影部分面积．
14. 如图，在正方形中画一个最大的圆，请求出阴影部分的面积。

（单位：厘米）。

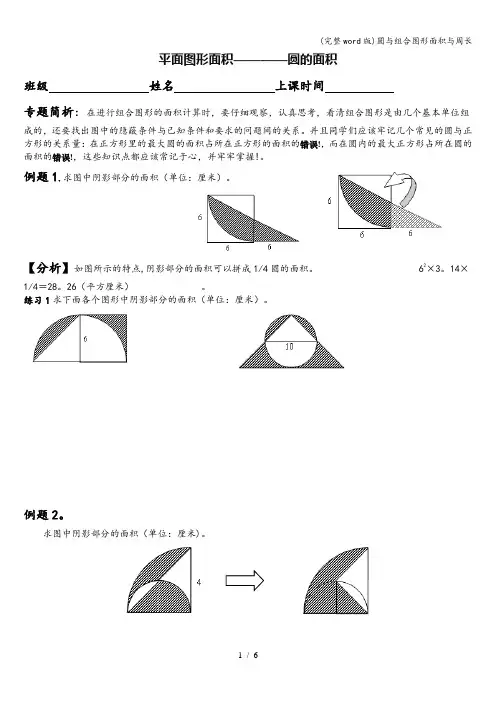
平面图形面积————圆的面积班级姓名上课时间专题简析：在进行组合图形的面积计算时，要仔细观察，认真思考，看清组合图形是由几个基本单位组成的，还要找出图中的隐蔽条件与已知条件和要求的问题间的关系。

并且同学们应该牢记几个常见的圆与正方形的关系量：在正方形里的最大圆的面积占所在正方形的面积的错误!，而在圆内的最大正方形占所在圆的面积的错误!，这些知识点都应该常记于心，并牢牢掌握!。

例题1.求图中阴影部分的面积（单位：厘米）。

【分析】如图所示的特点,阴影部分的面积可以拼成1/4圆的面积。

62×3。

14×1/4＝28。

26（平方厘米）。

练习1求下面各个图形中阴影部分的面积（单位：厘米）。

例题2。

求图中阴影部分的面积（单位：厘米)。

【分析】阴影部分通过翻折移动位置后，构成了一个新的图形（如图所示）。

从图中可以看出阴影部分的面积等于大扇形的面积减去大三角形面积的一半。

3。

14×42×1/4－4×4÷2÷2＝8.56(平方厘米）练习2：计算下面图形中阴影部分的面积（单位:厘米，正方形边长4）。

例题3。

在正方形ABCD中，AC＝6厘米。

求阴影部分的面积。

【分析】这道题的难点在于正方形的边长未知，这样扇形的半径也就不知道。

但我们可以看出，AC是等腰直角三角形ACD的斜边。

根据等腰直角三角形的对称性可知，斜边上的高等于斜边的一半（如图所示）,我们可以求出等腰直角三角形ACD的面积，进而求出正方形ABCD的面积，即扇形半径的平方。

这样虽然半径未求出,但可以求出半径的平方,也可以把半径的平方直接代入圆面积公式计算.既是正方形的面积，又是半径的平方为：6×（6÷2）×2＝18（平方厘米）阴影部分的面积为：18－18×3。

14÷4＝3。

87（平方厘米）答：阴影部分的面积是3.87平方厘米。

练习3 1、如图所示，图形中正方形的面积是50平方厘米，分别求出每个图形中阴影部分的面积。

专题01 圆的周长和面积（组合图形）注意事项：1．答题前，填写好自己的姓名、班级、考号等信息，请写在答题卡规定的位置上。

2．所有题目必须在答题卡上作答，在试卷上作答无效。

3．考试结束后将试卷和答题卡一并交回。

一．计算题（共20小题）1．计算下面图形阴影部分的周长和面积。

（单位：厘米）2．如图中，大圆的半径等于小圆的直径。

请计算阴影部分的周长。

3．计算下面图形的周长与面积。

4．计算下边图形的周长和面积。

5．计算如图形阴影部分的周长和面积。

（单位：dm）6．求下面各图中阴影部分的周长和面积。

（1）（2）7．求阴影部分的周长。

（单位：)cm8．计算图中阴影部分的面积。

（单位：)cm9．求阴影部分的周长。

10．求如图阴影部分的周长（单位：厘米）．11．求阴影部分的周长。

（大圆 4.5R =，小圆2r =，单位：)cm12．求图中形阴影部分的面积．（可以直接用π表示，也可以π取3.14)13．如图，求阴影部分的周长。

(π取3.14)14．计算右图的面积（单位：)dm 。

15．已知三角形的面积是29m，求圆的面积。

16．按要求计算下列各题。

（1）求图中图形的周长。

（2）求图中阴影部分的面积。

17．求阴影部分的面积：（单位：)cm18．求阴影部分的周长。

（单位：)cm19．求下列阴影部分的面积．20．求如图阴影部分面积。

（单位：厘米）专题01 圆的周长和面积（组合图形）答案解析一．计算题（共20小题）1．计算下面图形阴影部分的周长和面积。

（单位：厘米）【分析】根据题意，圆的直径为（4×3）厘米，阴影部分的周长等于圆的周长的一半加上5条4厘米长的线段之和，利用圆的周长公式：C＝πd，代入数据即可求出阴影部分的周长；阴影部分的面积等于圆的面积的一半减去边长为4厘米的正方形面积，分别利用圆的面积和正方形的面积公式求出这两个图形的面积，再相减即可得解。

××÷+×【解答】3.14(43)245×÷+＝3.1412220+＝18.8420＝38.84（厘米）2××÷÷−×3.14(432)244＝2×÷−3.146216×÷−＝3.1436216−＝56.5216＝40.52（平方厘米）即阴影部分的周长是38.84厘米，面积是40.52平方厘米。

圆和简单组合图形的面积一、填空。

(每空2分，共30分)1. 我们先把一个圆平均分成若干份，再拼成一个近似的长方形，这个近似的长方形的长相当于()，宽相当于()，因为长方形的面积等于()，所以圆的面积＝()。

2. 用圆规画一个圆，如果圆规两脚之间的距离是6厘米，那么画出的这个圆的周长是()厘米，这个圆的面积是()平方厘米。

3. 把一个圆形铁片剪成两个相同的半圆形，如果周长增加了12 cm，那么这个圆形铁片的面积是()cm2。

4. 甲圆半径是乙圆半径的3倍，甲圆周长是乙圆周长的()倍，甲圆面积是乙圆面积的()倍。

5. 一个能自动旋转的喷水龙头的有效射程是10米，那么它的喷洒面积最大是()平方米。

6. 圆的半径由6厘米增加到9厘米，圆的面积增加了()平方厘米。

7. 在一张边长为10厘米的正方形纸板里剪出一个最大的圆，剩下的面积是()。

8. 一根铁丝可围成边长是3. 14厘米的正方形，如果用这根铁丝围成一个圆，那么圆的半径是()厘米，面积是()平方厘米。

9. 一种钟表的表面是圆形，它的周长是25. 12厘米，它的面积是()平方厘米。

二、判断。

(对的在括号里打“√”，错的打“×”。

每题2分，共8分)1. 半径是2 cm的圆，它的面积和周长相等。

()2. 一个圆的半径扩大到原来的3倍，面积也扩大到原来的3倍。

()3. 由几个同心圆组成的图形有无数条对称轴。

()4. 周长相等的长方形、正方形和圆，面积最大的是圆。

()三、选择。

(将正确答案的字母填在括号里。

每题2分，共10分)1. 一个圆的面积是28. 26平方厘米，它的半径是()。

A. 3厘米B. 4. 5厘米C. 6厘米D. 9厘米2. 如果一个圆的面积扩大到原来的4倍，那么它的直径()。

A. 扩大到原来的2倍B. 扩大到原来的4倍C. 扩大到原来的8倍D. 扩大到原来的16倍3. 车轮转动一周所行的路程是车轮的()。

A. 半径B. 直径C. 周长D. 面积4. 一个圆的直径与正方形的边长相等。

平面图形面积————圆的面积班级 姓名 上课时间专题简析：在进行组合图形的面积计算时，要仔细观察，认真思考，看清组合图形是由几个基本单位组成的，还要找出图中的隐蔽条件与已知条件和要求的问题间的关系。

并且同学们应该牢记几个常见的圆与正方形的关系量：在正方形里的最大圆的面积占所在正方形的面积的3.144 ,而在圆内的最大正方形占所在圆的面积的23.14,这些知识点都应该常记于心，并牢牢掌握！.例题1。

求图中阴影部分的面积（单位：厘米）。

【分析】如图所示的特点，阴影部分的面积可以拼成1/4圆的面积。

62×3.14×1/4＝28.26（平方厘米） .练习1求下面各个图形中阴影部分的面积（单位：厘米）。

例题2。

求图中阴影部分的面积（单位：厘米）。

【分析】阴影部分通过翻折移动位置后，构成了一个新的图形（如图所示）。

从图中可以看出阴影部分的面积等于大扇形的面积减去大三角形面积的一半。

3.14×42×1/4－4×4÷2÷2＝8.56（平方厘米）练习2: 计算下面图形中阴影部分的面积（单位：厘米，正方形边长4）。

例题3。

在正方形ABCD中，AC＝6厘米。

求阴影部分的面积。

【分析】这道题的难点在于正方形的边长未知，这样扇形的半径也就不知道。

但我们可以看出，AC是等腰直角三角形ACD的斜边。

根据等腰直角三角形的对称性可知，斜边上的高等于斜边的一半（如图所示），我们可以求出等腰直角三角形ACD的面积，进而求出正方形ABCD的面积，即扇形半径的平方。

这样虽然半径未求出，但可以求出半径的平方，也可以把半径的平方直接代入圆面积公式计算。

既是正方形的面积，又是半径的平方为：6×（6÷2）×2＝18（平方厘米）阴影部分的面积为：18－18×3.14÷4＝3.87（平方厘米）答：阴影部分的面积是3.87平方厘米。

六年级数学上册组合图形的周长和面积例1.求阴影部分的面积。

(单位:厘米)解：这是最基本的方法：圆面积减去等腰直角三角形的面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。

设圆的半径为r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。

(单位:厘米)解：最基本的方法之一。

用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。

例4.求阴影部分的面积。

(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。

(单位:厘米)解：这是一个用最常用的方法解最常见的题，为方便起见，我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形，π()×2-16=8π-16=9.12平方厘米另外：此题还可以看成是1题中阴影部分的8倍。

例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π()=100.48平方厘米（注：这和两个圆是否相交、交的情况如何无关）例7.求阴影部分的面积。

(单位:厘米)解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5所以阴影面积为：π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)解：右面正方形上部阴影部分的面积，等于左面正方形下部空白部分面积，割补以后为圆，所以阴影部分面积为：π()=3.14平方厘米例9.求阴影部分的面积。

(单位:厘米)解：把右面的正方形平移至左边的正方形部分，则阴影部分合成一个长方形，所以阴影部分面积为：2×3=6平方厘米例10.求阴影部分的面积。

圆旳组合图形面积姓名：【知识与措施】要解决与圆有关旳题目，需要注意如下几点：1、纯熟掌握有关圆旳概念和面试公式：圆旳面积= 圆旳周长=扇形旳面积= 扇形旳弧长=（n是圆心角旳度数）2、掌握解题技巧和解题措施：加减法、分割重组法、旋转平移法、对折法、抵消法、等积变形法、等量代换法、添辅助线法。

例1.求阴影部分旳面积。

(单位:厘米)解：这是最基本旳措施：圆面积减去等腰直角三角形旳面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分旳面积。

(单位:厘米)解：这也是一种最基本旳措施用正方形旳面积减去圆旳面积。

设圆旳半径为r，由于正方形旳面积为7平方厘米，因此=7，因此阴影部分旳面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分旳面积。

(单位:厘米)解：最基本旳措施之一。

用四个圆构成一种圆，用正方形旳面积减去圆旳面积，因此阴影部分旳面积：2×2-π＝0.86平方厘米。

例4.求阴影部分旳面积。

(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例5.求阴影部分旳面积。

(单位:厘米)解：这是一种用最常用旳措施解最常用旳题，为以便起见，我们把阴影部分旳每一种小部分称为“叶形”，是用两个圆减去一种正方形，π()×2-16=8π-16=9.12平方厘米此外：此题还可以当作是1题中阴影部分旳8倍。

例6.如图：已知小圆半径为2厘米，大圆半径是小圆旳3倍，问：空白部分甲比乙旳面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π()=100.48平方厘米（注：这和两个圆与否相交、交旳状况如何无关）例7.求阴影部分旳面积。

(单位:厘米)解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5。

圆的周长和面积公式1、（1）在同一个圆内或等圆内，有无数条半径，有无数条直径。

所有的半径都相等，所有的接近长方形。

长方形的长相当于圆的周长的一半，长方形的宽相当于圆的半径。

（2）拼出的图形与圆的周长和半径的关系。

圆的半径=长方形的宽圆的周长的一半=长方形的长2、圆面积的计算方法：因为长方形面积=长×宽，所以圆的面积=圆周长的一半×圆的半径。

即S圆=C÷2×r=πr×r=πr2圆的面积公式：S圆=πr2→r2=S圆÷π3、环形的面积：一个环形，外圆的半径用字母R表示，内圆的半径用字母r表示。

（R=r+环的宽度）S环=πR2-πr2或环形的面积公式：S环=π（R2-r2）（建议用这个公式）。

4、一个圆，半径扩大或缩小多少倍，直径和周长也扩大或缩小相同的倍数。

而面积扩大或缩小的倍数是这倍数的平方倍。

5、两个圆：半径比=直径比=周长比；而面积比等于这比的平方。

6、任意一个正方形与它内切圆的面积之比都是一个固定值，即4 :π。

7、当长方形，正方形，圆的周长相等时，圆面积最大，正方形居中，长方形面积最小。

反之，面积相同时，长方形的周长最长，正方形居中，圆的周长最短。

8、常用各π值结果：π= 3.14；2π= 6.28；5π=15.79、外方内圆（内切圆）公式S=0.86r2推导过程：S=S正-S圆=d2-πr2=2r×2r-πr2=4r2-πr2=r2×（4-π）=0.86r210、外圆内方（外切圆）公式S=1.14r2推导过程：S=S圆-S正=πr2-2r2=r2×（π-2）=1.14r2（把正方形看成两个面积相等的三角形，三角形的底就是直径，高是半径）11、一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。

顶点在圆心的角叫做圆心角。

扇形的面积与圆心角大小和半径长短有关。

12、S扇=S圆×n/360°；S扇环=S环×n/360°13、扇形也是轴对称图形，有一条对称轴。