第二章 试井分析的理论基础及方法论
- 格式:doc
- 大小:340.50 KB
- 文档页数:17








第一节:试井分析中的一些基本概念第二章 试井分析的基础理论及基本方法第一节 试井分析中的一些基本概念1、无因次量2、压力降落与压力恢复试井3、井筒存储效应4、表皮效应5、试井曲线与曲线特征6、压力导数7、探测半径8、试井模型9、流动状态1、无因次量无量纲化的优点是:①便于数学模型的推导与应用②数学模型具有普遍意义③便于建立试井典型曲线图版④便于求解物理问题并得出通用性认识2、压力降落与压力恢复试井压降曲线示意图2、压力降落与压力恢复试井压力恢复曲线示意图3、井筒存储系数(1)生产过程中,环形空间没有充满液体,关井后继续流入井中,液面上升;(2)井筒中充满液体,关井后受压缩,继续流入井中。
油井刚开井或关井时,由于原油具有压缩性等多种原因,地面与井底产量不等,在进行压力恢复试井时,由于地面关井,因此关井一段时间内地层流体继续流入井筒,简称续流(Afterflow)其原因:开井生产时,将先采出井筒中原来储存的被压缩的流体,简称为井筒存储。
井筒存储和续流的影响近似是等效的,称为井筒存储效应。
在压力降落与压力恢复曲线分析时都可用存储效应与相应的井筒存储系数表征。
用井筒存储系数表示井筒存储效应的强弱程度,用C表示: 即井筒原油的弹性能所储存或释放的原油的能力。
¾C的物理意义:压力每改变单位压力井筒所储存或释放的流体的体积。
dv V C dp PΔ==Δ3、井筒存储系数若原油是单相的(并充满井筒) ,则:式中C 0为井筒中原油的压缩系数, V为井筒有效容积。
00VC p V C VC p pΔΔ===ΔΔ0V VC p Δ=Δ¾上式计算的C称为“由完井资料计算的井筒存储系数”,记作C 完井。
它是在井筒中充满单相原油,封隔器密封,井筒周围没有与井筒相连通的裂缝等条件下算得的。
因此C 完井是井筒存储系数的最小值。
试井分析中的一些重要概念-井筒存储系数3、井筒存储系数④液面不到井口(井筒不充满液体)的情形, C值会更大。


试井分析第一部分:试井简介试井的分类:稳定试井产能试井试井等时试井不稳定试井一、基本定义1、产能试井:改变若干次测试井的工作制度,测量在各个不同工作制度下的稳定产量及与之相对应的井底压力,从而确定井的产能方程,无阻流量,动态曲线,合理产量等。
2、不稳定试井:改变测试井的产量,从而在油层中形成一个压力扰动或变化,并测量由此所引起的井底压力随时间的不稳定变化过程。
二、试井目的估算完井效率、井底污染情况,判断是否需要采取增产措施,分析增产措施效果,估算地层压力、控制储量或原始地质储量,地层参数,判断边界情况,连续性等。
第二部分:产能试井方法及解释试井方法一、稳定试井测试方法:连续以3~4个不同的稳定产量生产(由大到小),每个产量生产都要求流压达到稳定;测量每个稳定产量及相应的稳定流压、油压、气油比和出砂量等,最后终关井测底层压力。
测试前要求先清井及初关井。
二、回压试井回压试井针对气井,其测试方法与油井的稳定试井相同。
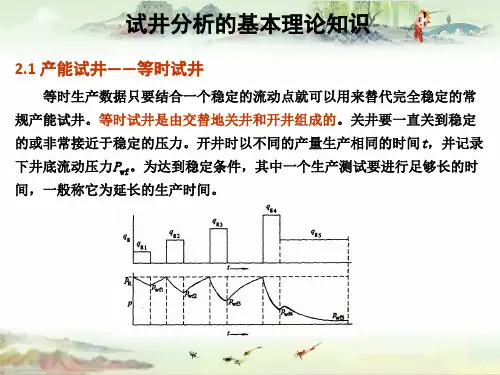
三、等时试井测试方法:连续以3~4个稳定产量开井生产相同的时间,而不管流压是否达到稳定,但要求一定要进入径向流阶段。
在每个不同气嘴生产之间都插入一个关井压力恢复,而且要恢复到地层压力。
最后一次生产要延续很长时间,一直到流压稳定,称为延时测试,最后终关井得到地层压力。
四、修正等时试井测试方法:连续以3~4个稳定产量开井生产相同的时间,而不管流压是否达到稳定,在每个油嘴开井生产之间插入的关井时间相同,且关井时间常与开井时间相同。
同样有延时测试和终关井。
试井解释试井解释分为绘制产能曲线,写出产能方程,绘制流入动态曲线。
产能方程有指数式产能方程和二项式产能方程。
一、指数式产能方程n wf R g p p C q )(22-= (1) 式中:n —渗流指数,15.0≤≤n ,当1=n 时,气体为层流;当5.0=n 时,气体为纯湍流。
g q —气体流量 R p —地层压力 wf p —井底流压 对(1)式两边取对数有)lg(lg lg 22wf R g p p n C q -+= (2) 变形得C nq n p p g wf R lg 1lg 1)lg(22-=- (3)在双对数坐标纸上绘制)(22wf R p p -与g q 的关系曲线(直线)。
试精分析方法《试井分析方法》内容简述第一章绪论第一节试井的概念、分类&用途第二节试井的发展历史一、试井方法、试井分析理论的发展历史二、试井分析理论的发展方向:1.水驱油藏2.水驱气藏3.非牛顿流体 4.低渗透油气藏 5.异常高压气藏6. 凝析气藏7.复杂结构井8.数值试井9.井筒动力学对试井的影响。
第二章产能试井分析方法第一节油井产能试井分析方法:一、产能试井原理二、测试方法:1.工作制度; 2.测试程序:1)测地层压力2)工作制度顺序3)关井测压三、稳定试井曲线:1.指示曲线(p R-p wf)与q的关系曲线(直线型·曲线形·混合型·异常型)2.系统试井曲线: q、p wf、含水率f w 、含沙量S ct 、GOR与工作制度(油嘴)之间的关系3.流入动态关系曲线p wf与q之间的关系曲线,简称IPR曲线,对油井的生产动态预测四、产能试井分析方法:1.服从达西流动的分析方法2.服从非达西流动的分析方法:1) 二项式分析方法2)指数式分析方法3.产能试井分析步骤:1)整理试井质料2)确定产能方程3)作流入动态关系曲线4)确定合理工作制度五、应用实例:1-直线型指示曲线2-曲线形指示曲线第二节油气两相流产能试井分析方法一、地层压力低于饱和压力(p R二、井底压力低于饱和压力(p wf<=p b,p r>p b)三、应用实例:1-测试点流压全小于饱和压力2-部分测试点流压小于饱和压力第三节气井产能试井分析方法一、拟压力:1-拟压力定义2-拟压力的简化3-拟压力的计算二、气井产能试井分析方法:1-回压试井: 1)测试方法;2)测试资料分析方法:(1)二项式分析方法:1.二项式产能方程确定方法;2.二项式产能方程的用途:计算无阻流量,预测产能(拟压力方法|拟压力平方方法) 3.应用实例(2)指数式分析方法: 1.指数式产能方程确定方法;2.指数式产能方程的用途:(3)IPR曲线及其应用。
试井分析复习试井分析复习第⼀章绪论1、什么是试井?试井有哪些分类?答:(⼀)试井:以油⽓渗流⼒学为理论基础,以压⼒、温度、和产量测试为⼿段,研究油⽓藏地质和油⽓井⼯程参数的⼀种⽅法。
(⼆)分类:两⼤类,产能试井和不稳定试井。
(1)产能试井:回压试井、等时试井、修正等时试井、⼀点法试井。
(2)不稳定试井:单井试井(压⼒降落试井、压⼒恢复试井、探边试井)、多井试井(⼲扰试井、脉冲试井)。
2、什么是产能试井?什么是不稳定试井?答:(⼀)产能试井:是改变若⼲次测试井的⼯作制度,测量在各个不同⼯作制度下的稳定产量及与相应的井底压⼒,利⽤稳定试井分析理论研究测试井⽣产能⼒的⼀种动态⽅法。
(确定测试井(或测试层)的产能⽅程和⽆阻流量)(⼆)不稳定试井:改变测试井的产量,并测量由此⽽引起的井底压⼒随时间的变化,利⽤不稳定试井分析理论研究测试井测试层特性参数的⼀种动态⽅法。
3、阐述产能及不稳定试井的主要⽤途。
答:(⼀)产能试井:确定测试井的产能;对单井进⾏动态预测。
(⼆)不稳定试井:确定油⽓藏类型(孔隙结构性质);确定原始地层压⼒;确定地下流体流动能⼒;判断完井效果;确定措施井及层位,确定是否需要采取增产改造措施;判断增产改造措施的效果;推算探测范围和估算单井控制储量;判断边界性质、距离、形状和⽅位等;判断井间连通情况,确定连通厚度及连通渗透率⼤⼩;判断地层渗透率的⽅向性发育情况。
(10条)4、产能及不稳定试井的类型有哪些?(同上)5、⽬前试井存在的问题答:由于油⽓藏及其中流体流动的复杂性,因此,⽬前在许多复杂流体流动和复杂介质中的试井分析理论与⽅法还没有得到很好的解决。
(⽔驱油藏、⽔驱⽓藏、⾮⽜顿流体、低渗油⽓藏、异常⾼压油⽓藏、凝析⽓藏、复杂结构井、数值试井、井筒动⼒学对试井的影响)多相流动:⽬前已投⼊开发的绝⼤多数油⽓藏都进⼊了⾼含⽔期,油(⽓)⽔关系复杂,多井⼲扰问题突出,储层孔隙结构可能已发⽣变化。
多层合采:多个⼩层合采、层间存在⼲扰。
第二章试井分析的理论基础及方法论试井分析是建立在弹性渗流理论基础之上的,它涉及到了许多复杂的数学问题,并且与地质、工程有关。
第一节理论基础一、不可压缩液体的稳定流动1、稳定流动与不稳定流动稳定流动:流动仅为坐标的函数,q、p不随t变而变。
不稳定流动:q或V渗流和P不仅是坐标的函数,而且也是时间的函数。
2、单相流和平面径向流单相流:流线彼此平行,各处渗流面积不变;垂直流线截面的各点压力相同,渗流速度相同,压力和速度都为流动方向上X轴的函数即符合达西定律V X = - K/μ* dP/dX平面径向流:流线在平面上向中心汇聚,并以井眼轴线为中心的各同心圆上,各点压力相同,速度相同,以井眼轴线为中心的极坐标上,各点压力和速度只与半径R有关,即V = K/U *DP/DR3、不可压缩与可压缩流体不可压缩流体:流体V不随P的变化而变化。
可压缩流体:可压缩流体的体积随P的变化而变化。
M = ρυ,C = -1/V * dV/dp; 从而可导出:ρ= ρo e c(p-po) ,此式据麦克劳林级数展开,取前二项近似,可得:ρ= ρO((1 + C(P - P O ))1、稳定渗流的应用V = K/U *DP/DR ,据初始条件及内外边界条件,可推得:q = 5.429*102kh/Bulnr e/r w * (P e - P wf)此式为系统试井或称为稳定试井的理论基础,据此式可得油井指示曲线公式:q = PI*ΔP , 式中:PI为采油指数,ΔP为生产压差。
稳定试井的目的是确定井的合理工作制度,确定井的地层参数以及了解油井生产能力。
气井的稳定试井也称为产能试井。
P = P e– qu/2πkh * ln r e / r压力分布呈压降漏斗。
二、弹性液体的不稳定渗流1、渗流过程⑴不稳定期(遇到外边界之前)⑵过渡期(遇到外边界之后,在拟稳定期开始之前;图上的晚期不稳定段)⑶拟稳定期(对封闭地层而言,DP/DT = 常数;对定压边界而言,DP/DT = 0 ; 满足这一条件,就意味着拟稳定期开始。
)2、基本微分方程和压降公式⑴ 基本微分方程油藏的岩性比较均一、岩石颗粒分选性、磨圆度以及孔隙结构比较均一,没有裂缝,即我们所称的均质油藏。
从物理模型而言,在不考虑微层理的影响下,可作如下假设: ① 均质地层(h 、k 、Ф为常数)和均质流体(μ为常数);② 压力梯度小;③ 流体是弱可压缩,压缩系数为常数;④ 不考虑重力作用和流体惯性力,井筒储集系数不变,流体流动符合达西定律。
相应的数学模型:① 运动方程 υr = k / μ * dp/dr② 状态方程 ρ = ρo ( 1 + C (P - P o ))③ 连续性方程(质量守恒定律)()()ρρυΦ∂∂-=∂∂tr r r r 1 考虑上述假使条件后,可推出扩散方程:tp k C r p r r p t ∂∂Φ=∂∂+∂∂6.312μ 式中:g g w w o o r t S C S C S C C C +++=η:水力扩散系数或导压系数,表示渗流阻力的大小,单位m 2/h 上式为不稳定试井的基础。
⑵ 压降公式无限大地层中液体向一口井作平面径向流,且定产量生产,此时初始条件:p (r,0)= p i外边界条件:p (∞,t )=p i 内边界条件:wr r r p r B kh q =⎪⎭⎫ ⎝⎛∂∂=μπ8.172 或 khqB r p r w r r πμ8.172=⎪⎭⎫ ⎝⎛∂∂= 求解此方程请参阅《油气井测试》P 21~23。
结果为:()⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛---==t r E kh qB p t r p p i i ηπμ4.146.345,2E i (X )为Exponential Integral Function 幂积分函数,定义如下: ()μμμd e x E x i ⎰∞--=-当X<0.01时,可近似表示为:()()x x x E i 781.1ln 57721566.0ln ≈+≈-当wf w p p r r ==,时的解为:⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛--=-=∆S t r E kh qB p p p w i wfi 24.146.3452ηπμ 当01.04.142〈t r w η时(该条件很容易满足),有⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛++⨯-+⨯-=⎪⎪⎭⎫ ⎝⎛+-=--S r C k kh qB p t kh qB S r t kh B q p p w t i w i wf 8686.09077.0lg 10121.2lg 10121.22085.8ln 6.3452332φμμμηπμ此式为压降试井的理论基础。
3、叠加原理与应用⑴ Supperposition Theorem or Principle of Supperposition Method 叠加原理源自数学,其意思是:在线性关系的变量中,总体的变化等于各简单的变化总和(可参阅教材P4)。
这意味着可将一个复杂的解分解成几个简单的解或者说几个简单的解的叠加可得到一个复杂的解。
压降叠加原理:地层中任何一点处的总压降等于油藏中每一口井因生产或注水在该点产生的压力降的总和。
⑵ 应用① 压力恢复公式假设情况如右图q t t p ∆+ 1p ∆-q t ∆ 2p ∆21p p p ∆+∆=∆用压降公式可导出下式:tt t kh qB p t p p p p i ws i ∆∆+⨯-=∆-=∆-lg 10121.2)(3μ 上式是由霍纳于1953年提出的即著名的霍纳公式;若以)(p wf t p 为基值,则可推出如下公式:⎪⎪⎭⎫ ⎝⎛++Φ⨯-===∆-S r C kt kh B q p t p t p w t p i p wf ws 8686.09077.0lg 10121.2)()0(23μμ 因而可得到:⎪⎪⎭⎫ ⎝⎛++Φ+∆∆+-⨯+=∆-S r C kt t t t kh B q t p t p w t p p p wf ws 8686.09077.0lg lg 10121.2)()(23μμ当max t t p ∆〉〉时,1,≈∆+≈∆+p p p p t tt t t t ,此时有⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛++Φ⨯++∆⨯=⎪⎪⎭⎫ ⎝⎛++∆⨯+≈∆---S r C k kh B q t p t kh B q S r C t k kh B q t p t p w t p wf w t p wf ws 8686.09077.0lg 10121.2)(lg 10121.28686.09077.0lg 10121.2)()(23323μμμφμμ上式为简化的霍纳公式,1950年由Miller 、Dyes 、Hutchinson 三人提出,故也称为MDH 公式。
② 变产量情形的处理(第三章第一节中讲)③ 两井或多井同时生产的压降叠加(自学)④ 模拟无流动边界(断层)(在第三章第二节中讲)第二节 一些重要的基本概念一、无因次量(Dimensionless Quantities )一般来说,引进的无因次物理量是该物理量与别的一些物理量的组合,并和该物理量本身成正比。
试井上常见的无因次量有: Bq p kh p D μ310842.1-⨯∆= 26.3w t D r C kt t φμ= , 22wt D hr C C C πφ= ,w D r r r = 26.3we t De r C kt t φμ=,A C kt t t DA φμ6.3= ,26.3f t Df x C kt t φμ= 通过使用无因次量后,无限大地层压降解和扩散方程可分别写成:⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛--=D D i D t r E p 4212 , D D D D D D D t p r p r r p ∂∂=∂∂+∂∂122 使用无因次量的优点:1、由于若干有关的因子已经包含在无因次量的定义之中,所以往往使得关系式变得很简单,因而易于推导、记忆和应用。
2、由于使用的是无因次量,所以导出的公式不受单位制的影响和限制,因而使用更为方便。
3、可以使得某种前提下的讨论具有普遍意义,这就是说,使得讨论的结果可以适用于满足该前提的任何实际场合即解释图版成为可能。
二、井筒储集常数(Wellbore Storage Constant )1、概念井筒储集效应:是指井筒系统内的流体(油、气),由于井筒压力变化而产生弹性能量的释放或聚集所引起的该井流量的变化。
井筒储集系数:是描述井筒储集效应的强弱程度,可定义为在井筒条件下单位压力变化时的井筒流体体积变化量,pv C ∆∆= ,13-MPa m 2、C 的求法⑴ 井筒充满单相液体时(如油),因为p v v C o ∆∆=1 ,pv c ∆∆= 所以,wb wb o C v c vC c ==或⑵ 井筒未充满单相液体时,因为lp p l v v 31080665.9,-⨯=∆=∆μ,所以 M P a m v p v c /,10665.8.933ρμ-⨯=∆∆=⑶ t p ∆-∆关系图,因为在纯井筒储集阶段,24qt v =∆,∴ pqt p v c ∆=∆∆=24 ; t c q p 24=∆ ;所以,对纯C 的数据作关系图,得斜率m ,从而求出c 。
如果直线不过原点,则要对时间进行校正,使其过原点。
m qB c 24=三、表皮效应与表皮系数(Skin Effect & Skin Factor )31.84210s kh p S q Bμ-∆=⨯ 地层污染评价标准:均质油藏 S=0无污染,大于0有污染,小于0增产措施有效;双重介质油藏 S=-3无污染,大于-3有污染,小于-3增产措施有效无污染。
第三节试井分析方法论(Problem-Solving Phylosophy)一、试井分析实质内容试井分析实质上就是将不稳定试井中记录的信息进行分析处理,获取由这些信息反映出的地层特征。
不同试井所获取的信息可用不同的分析手段即试井分析方法进行处理。
尽管油藏形状各异,性质千差万别,但由于油藏系统是一个未知系统,而对未知系统的分析总是按固定的模式去进行的。
因此,不同试井分析方法所遵循的解决问题过程,实质上是固定不变的,这种分析过程从系统分析的角度来看,就十分明显了。
正问题:I×S=O 反问题:O/I=S如何解正问题呢?1、先假设某一已知系统属于未知系统;2、对该系统施加输入信号(即进行试井);3、建立这一已知系统在A信号下的物数模型;4、求解物数模型;5、得出A信号下反映该假设已知系统的特征信息(可以以数据形式,也可以是曲线的形式等)实质上,上述为试井分析的理论工作。
如何解反问题呢?目前需对一未知油藏系统进行分析,由于油藏系统的有限性,尽管目前性质未知,但它必属于已知(并求出了其特性)的那些系统中的某一种,如何判断它属于那种已知系统呢?1、 对该井未知系统施加一定的信息(试井或变产量或变压力)2、得出反映该未知系统特性的输出信息(压力和产量变化史),一般来说,对于一个系统,施加某一输入,一定能得到某一输出;但对于不同的系统,施加同样的信号,一般将得到不同的输出。