土的自重应力

自重应力的分布规律
由土体本身自重在地基土体中引起的应力称为自重应力。

分布规律随深度增加而呈线性增大，按三角形分布。

均质土的自重应力沿深度呈线性分布；非均质土的自重应力沿深度呈折线分布。

地下水位以上土层采用天然重度，地下水位以下土层采用浮重度。

地下水位下降会引起自重应力的变化，使地基中原地下水位以下部分土的有效自重应力增加，从而造成地表大面积附加下沉；地下水位上升，使原来位于地下水位以上的土体处于地下水位之下，会使这部分土体压缩量增大，抗剪强度降低，引起附加沉降。

正应力x、y、z ：
x
3P 2
x2z
R5
1 2 3
R2 Rz z2 R3(R z)
x2(2R z)
R3
(R
z)2
y
3P 2
y2z R5
1 2 3
R2 Rz z 2 R3(R z)
y2 (2R z)
R
3
(
R
z
)
2
z
3P
2
z3 R5
3P
2R2
cos3
x、y、z — 分别平行于x、y、z座标轴的正应力；
基底平均附加压力 (kPa)按下式计算 ：
p0 p c p 0d
p — 基底平均压力设计值(kPa)
c — 土中基底处自重应力
§4.3 地基中的附加应力
附加应力是由于修建建筑物以后在地基内新增加 的应力。
附加应力是使地基发生变形，引起建筑物沉降。
§4.3 地基中的附加应力
假定地基土是连续、均质、各向同性的半无限空 间弹性体，在深度和水平方向上都是无限延伸的。
二、均布矩形荷载下的地基附加应力：
均布矩形荷载角点下
的附加应力z：
角点下的地基附加应力：
d z
3
2
x2
p0 z3 y2 z2
5/2
dxdy
z
d z
A
3 p0 z 3
2
lb 00
x2
1 y2
z2
5 2
dxdy
p0
lbz l 2 b2 2z2
arctan
lb
2 l2 z2 b2 z2 l2 b2 z2
中，竖向正应力z具有特别重要的意义，它是
，

2
土中自重应力 2、基本前提
土体是均匀的半无限体，且假定天然地面为无限 大的水平面。
在自身重力作用下土体任一竖直平面均是对称面， 切面上不存在剪应力。
自重作用下土体只能产生竖向变形而无侧向位移 和剪切变形。
3
土中自重应力 3、竖向自重应力
土体中任意深度处的竖向自重应力等于单位面积上土柱 的有效重量。
土中应力计算
中自重应力
单位：石家庄铁道大学 主讲人：熊保林副教授
1
土பைடு நூலகம்自重应力 1、定义
自重应力：由于土体本身自重引起的应力
确定土体初 始应力状态
土体在自重作用下，在漫长的地质历史时期，已经压 缩稳定，因此，土的自重应力不再引起土的变形。但 对于新沉积土层或近期人工填土应考虑自重应力引起 的变形。
4
土中自重应力
5
土中自重应力 4、水平向自重应力
6
土中自重应力 4、水平向自重应力
表2-1 K0的经验值
7

平均自重应力平均自重应力是指单位面积上所承受的重力大小，是一个土力学中的重要概念。

本文将从平均自重应力的定义、计算公式、影响因素以及工程中的应用等方面进行探讨。

一、平均自重应力的定义平均自重应力是指土体内单位面积上由于土体自身重力所产生的应力。

在垂直于地表的方向上，土体受到的重力会使土体内部发生应力传递，从而形成平均自重应力。

平均自重应力是土体的基本应力状态之一，对土体的力学性质和稳定性具有重要影响。

平均自重应力的计算公式为：σ = γ * h，其中σ表示平均自重应力，γ表示土体的单位重量，h表示土体的深度。

这个公式表明，平均自重应力与土体的单位重量和深度成正比，单位重量越大、深度越深，则平均自重应力越大。

三、平均自重应力的影响因素1.土体的物理性质：土体的单位重量是影响平均自重应力的重要因素之一。

不同种类的土体具有不同的单位重量，例如黏土的单位重量通常较大，而砂土的单位重量较小。

2.土体的深度：土体的深度也是影响平均自重应力的因素之一。

深度越大，土体受到的重力越大，从而平均自重应力也越大。

3.土体的湿度：土体的湿度也会对平均自重应力产生影响。

湿度较大时，土体的单位重量会增加，从而平均自重应力也会增大。

四、平均自重应力在工程中的应用平均自重应力是土力学中的重要参数，广泛应用于工程实践中。

在土体力学分析和设计中，平均自重应力是计算土体稳定性、承载力和变形等问题的基础。

例如，在地基工程中，计算地基承载力时需要考虑土体的平均自重应力；在挖掘工程中，需要对土体的平均自重应力进行评估，以保证工程的稳定性。

总结起来，平均自重应力是土体内单位面积上由于土体自身重力所产生的应力。

它的计算公式为σ = γ * h，受到土体的物理性质、深度和湿度等因素的影响。

在工程中，平均自重应力是土体力学分析和设计的基础，对于保证工程的稳定性和可靠性起着重要作用。

通过对平均自重应力的研究和应用，可以更好地理解土体力学的基本原理，为工程实践提供科学依据。

有效自重应力计算公式
1.排水条件下的有效自重应力计算公式：
排水条件下土体中的孔隙水可以自由排出，因此只有颗粒重力起作用，有效自重应力可用以下公式计算：
σ'=γ*H
其中，σ'表示有效自重应力，γ表示土体的单位重量，H表示土体
的有效高度。

单位重量γ可以通过实测实验获得，有效高度H是指土体
堆积的高度减去排水带（即浸水线以下的部分）的高度。

2.非排水条件下的有效自重应力计算公式：
非排水条件下，土体中的孔隙水不能自由排出，有效自重应力计算需
要考虑孔隙水压力。

σ'=(γ-u)*H
其中，σ'表示有效自重应力，γ表示土体的单位重量，H表示土体
的有效高度，u表示孔隙水压力。

孔隙水压力的计算可以采用以下公式：
u=u0+Δu
其中，u0表示孔隙水静压力，可以通过水压力计等仪器测量得到；
Δu表示孔隙水动压力，可以根据土体的应力路径和试验结果进行估算。

需要注意的是，在进行有效自重应力计算时，需要使用土体的干重而
不是含水量较高的湿重或全重。

此外，有效自重应力的计算公式还要考虑
土体颗粒大小和形状等因素的影响，因此不同的土体类型可能有不同的计算方法。

总之，有效自重应力的计算公式可根据排水条件和非排水条件进行选择，通过合理的应力路径和试验数据的获取，可以得到更准确的有效自重应力值，为工程设计和安全评估提供重要依据。

土的自重应力
《土的自重应力》
一、土的自重应力
土的自重应力是指因土体自身的重力而制造出的土体内部的静力和外部的土体表面的分布应力。

自重应力受土体的形状和密度、外部加载及水力作用的影响，可以用数值计算来计算出自重应力的大小和方向。

它与其他应力的大小有关，是基本力中最大的单个应力，不受荷载而产生的自重应力是支撑和构筑建筑物的基础，所以对于建筑物的抗滑能力和抗压能力有决定性的作用。

二、自重应力的计算
1、计算土体自身的重力：
自重应力的大小取决于土体的形状、密度和体积。

由土体的自然重力可以计算出它的自重应力，自重应力的计算公式为：
F=m*g
其中，m为土体的质量，g为重力加速度。

2、计算外部力和水力作用：
除了土体的自身重量之外，还需要计算外部力和水力的作用，这些外部因素可以使自重应力改变。

外部力的大小取决于土体的形状、大小和它周围的支撑条件，以及水力作用的大小，取决于土体的渗透性和孔隙内水的数量。

三、自重应力的应用
1、土堆积工程：
土堆积工程是指土堆的弹性变形模式，在这种情况下，土体的自重应力对支撑土堆或保护土堆稳定性有重要的作用。

2、基础工程：
基础工程是指地基和桩基础，这类工程对自重应力也有较高的要求，它包括滑动稳定、沉降和破坏的抗压能力。

3、墙体工程：
墙体工程则指墙体的稳定性，墙体的自重应力在很大程度上取决于墙体的重量，墙体的重量又取决于它的施工方法和厚度。

P r
m
⑴在集中力P作用线上，r=0,当z=0 时，附加应力趋于无穷；随着深度 的增加，逐渐减少。 ⑵在r＞0的竖直线上，当z=0时， 附加应力为零，随着深度的增加， 附加应力从零逐渐增大，至一定深 度后又随着深度的增加逐渐变小。 ⑶在z为常数的平面上，附加应力在 集中力作用线上最大，并随着r的增 加而逐渐减小，随着深度增加，这 一分布趋势保持不变，但会随着r增 加而降低的速率变缓。
z
■
应力叠加原理
当地基表面 作用有几个 集中力时， 可分别算出 各集中力在 地基中引起 的附加应力， 然后根据应 力叠加原理 求出附加应 力的总和
Pa
Pb
z
a c
b
空间问题的附加应力计算 设基础长度为L,宽度为b，当l/b＜10时， 其地基附加应力的计算属于空间问题。 ⑴竖直均布荷载作用下矩形基底角点下 的附加应力
dA
z
0 0 l b
2 x 2 y 2 z 2
3z 3 p dxdy
dP L b x
52
p m 1 m 1 1 tg 2 2 2 2 2 2 1 m2 n2 m n 1 n n 1 m n Kc p
cx cy K0 cz
K0—土的侧压力系数，可通过试验求得，无 试验资料时可按经验公式推算
2.2 基底压力
概述 基底压力是计算地基中附加应力的外荷载， 也是计算基础结构内力的外荷载，因此，在计 算地基附加应力和基础内力时，都必须首先研 究基底压力的分布规律和计算方法。
基底压力：指上部结构荷载和基础自重通过基础传递， 在基 础底面处施加于地基上的单位面积压力。 基底反力：地基反向施加于基础底面上的压力。 基底附加压力：基底压力扣除因基础埋深所开挖的自重应力 之后在基底处施加于地基上的单位面积压力。

§3 土体中的应力计算 § 土体自重应力的计算
一. 水平地基中的自重应力
定义：在修建建筑物以前，地基中由土体本身的有效重量而产生的应力。 目的：确定土体的初始应力状态
假定：水平地基半无限空间体半无限弹性体 有侧限应变条件一维问题
计算：地下水位以上用天然容重，地下水位以下用浮容重
§3 土体中的应力计算 § 土体自重应力的计算
均质地基
1 (1 2) 2 2
成层地基
H2
地下水位以下用浮容重γ’
γ3 H3
思考题：水位骤降后，原水位到现水位之间 的饱和土层用什么容重？
§3 土体中的应力计算 § 土体自重应力的计算
一. 水平地基中的自重应力
2. 分布规律
▪自重应力分布线的斜率是容重； ▪自重应力在等容重地基中随深度呈直线分布； ▪自重应力在成层地基中呈折线分布； ▪在土层分界面处和地下水位处发生转折。
一. 水平地基中的自重应力
1.计算公式
均质地基 成层地基
竖直向：sz z
sz W A zA A z
பைடு நூலகம்
水平向：sx sy K0sz
K0 1
竖直向： sz iHi sz 1H1 2H2 3H3;
γ1
Z γ2
H1 水平向： sx sy K0sz K0 iHi
容重：地下水位以上用天然容重γ

自重应力(overburden stress)：
土体变形或地基变形的主要 原因，是导致土体强度破坏 和失稳的重要原因。
建筑物修建以前，地基 中由土体本身的有效重 量所产生的应力。
附加应力(additional stress)：
建筑物修建以后，建筑物重量等 外荷载在地基中引起的应力，所 谓的“附加”是指在原来自重应 力基础上增加的压力。
当e<l/6时，pmax，pmin>0，基底压力呈梯形分布
当e=l/6时，pmax>0，pmin=0，基底压力呈三角形分布
当e>l/6时，pmax>0，pmin<0，基底出现拉应力，基底压力重分
布
pmax
pmin
e<l/6
pmax
pmin=0
pmax
pmin<0 基底压力重分布pmax
e>l/6
e=l/6
§4.3 基底压力 Contact pressure
一、概述
1.概念 基底压力是建筑物荷载通过基础传递给地基的单位面积压力。 作用于地基上的是基底压力 作用于基础上的是地基反力 基底压力为接触压力
2.学习研究的意义 是确定地基强度条件的前提
二、基底压力的分布
1. 基底压力的分布与基础的刚度有关
柔性基础
p0 p cd
❖保证坑底土质不发生浸水膨胀条件
有了基底附加压力，可把它作为作用于弹性半空间表面上的 局部荷载，根据弹性力学计算地基中的附加应力
§4.4 地基中的附加应力
附加应力：新增外加荷载在地基土体中引起的应力
计算基本假定：
地基土是连续、 均匀、各向同性 的半无限完全弹 性体
x, z的函数
不同地基中 应力分布各 有其特点 x, y, z的函数

w
h w
例题 2-1
某土层及其物理性质指标如图所示，地下水位 在地表下1.0 m，计算土中自重应力并绘出分布
a 点：s cz h 0
b
s
点：
cz 1h1
18.6 1
18.6kpa
s cz 1h1 2h2
c 点： 18.6 (18.8 10) 1
地下水位以上的土层取天然重度γ，地下水位 以下的土层取有效重度γ`( γ` = γsat- γw) γ w=10kN/m3或9.8kN/m3
二、 成层地基土的自重应力
s cz 1h1 2h2 3h3 i hi
成层土地基中，竖 直向自重应力也是 随深度的增加而增 大，但沿铅垂线的 分布图是一条折线， 转折点在不同土层 的分界面上
应力的变化？如何影响？
第三节 基础底面压力
建筑物荷载通过基础传递给地基的压力称为 基底压力，与此相对应的地基土对基础底面的 反作用力称为地基反力。
F
基础
G
地基
第三节 基础底面压力
建筑物荷载通过基础传递给地基的压力称为
基底压力，与此相对应的地基土对基础底面的
反作用力称为地基反力。
F
基础
基础
基底压 力
2、偏心荷载作用下基底压力:
A
pmax F G M F G ( 1 6e )
pmin
AW
lb
b
Fk—作用在基础顶面形心的竖向力值. Gk-基础自重及台阶回填土总重，
Gk G Ad G 20kN / m 3
式中l，b为基底平面的长边与宽边尺寸。
在b方向偏心.
荷载偏心方向边长为b.

地基土往往是成层 的，各层土具有不 同的重度。 计算自重应力时， 当地下水位位于同 一土层中，地下水 位面也应作为分层 的界面。

图5-2 成层土中竖向 自重应力沿深度的 分布
二、土自重应力

成层土自重应力的计算公式为：
c


1
n
i
hi
(44)

式中 c —天然地面下任意深度z处的竖向有效自重应力 (kPa)； n —深度z范围内的土层总数 hi —第i层土的厚度(m)； i —第i层土的天然重度，对地下水位以下的土层取有效 重度。
注意：当e
L/6时，
基底附加压力 ：

新增加于地基表面的基底压力，称为基底附加压 力。 如果基础砌置在天然地面上，那末全部基底压力 就是新增加于地基表面的基底附加压力。 埋置在天然地面下一定深度处的的基底压力中应 扣除基底标高处原有的土中自重应力后，才是基 底平面处新增加于地基的基底附加压力 ，

3P y 2 z 1 2 R 2 Rz z 2 y 2 (2R z) 3 3 y 5 2 2 3 R (R z) R ( R z) R
3P z 3 3P 3 z 5 cos 2 2 R 2R

对于计算点不位于角点下的情况，可利用式 z K c p0 角点法和叠加原理求得。 上图列出计算点不位于矩形荷载面角点下的四种 情况(在图中o点以下任意深度z处)。计算时通过 o点把荷载面分成若干个矩形，这样，o点就必 然是划分出的各个矩形的公共角点，然后再按式 (5-21)计算每个矩形角点下同一深度z处的附加 应力z，并求其代数和。
埋置在天然地面下一定深度处的的基底压力中应扣除基底标高处原有的土中自重应力后才是基底平面处新增加于地基的基底附加压力基底平均附加压力kpa按下式计算土中基底处自重应力43地基中的附加应力附加应力是由于修建建筑物以后在地基内新增加的应力

3dP z 3 3 p z 3 d z dxdy 5 5 2 R 2 R
将它对整个矩形荷载面A进行积分：
3 p0 z 3 z d z 2 A
得：
z Kc p0
1 2 dxdy 2 2 5/2 (x y z ) 0 0
上海市土力学与地基基础精品课程
p0 p c p 0d
基底附加压力
上部荷载F 基础自重G
基底压力
地基中各点附加压力
式中：p —基底平均压力设计值(kPa)； c —土中自重应力标准值，基底处: c 0d (kPa) 0 —基础底面标高以上天然土层的加权重度， 0 i hi / hi 其中地下水位下土层的重度取有效重度； d —基础埋深，必须从天然地面算起，对于新填土场地则应 从老天然地面起算，d=h1+h2+...+hn(m)。
均布矩形荷载下任意点的应力计算
利用角点下的应力计算公式和应力叠加原理，推求地基中 任意点的时加应力的方法称为
计算点在荷载面内：
p II I z
III IV
o
III IV
o
II I
z K cⅠ KcⅡ Kc Ⅲ K cⅣ p
上海市土力学与地基基础精品课程
/sub/soil/new/index.php
/sub/soil/new/index.php
分析步骤I：
F=400kN/m 0.1m M=20kN •m
1.5m 2m
0 ＝18.5kN/m3
荷载偏心距 e=M/(F+G)
基础及上覆 土重G= GAd
1.基底压力计算
条形基础取单 位长度计算
pmax pmin

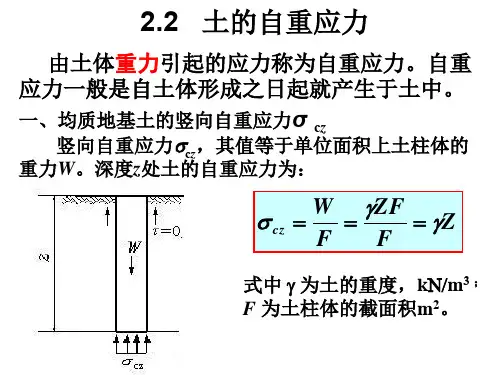
土的自重应力土是地球表面最常见的材料之一，它是由矿物质、有机物和水分组成的。

土的自重应力是指土体自身重力所产生的应力。

在土工工程中，土的自重应力是一个非常重要的参数，它对土体的稳定性和承载力有着重要的影响。

土的自重应力是由土体的密度和重力加速度决定的。

在地球表面，重力加速度的大小约为9.8米/秒²。

因此，土的自重应力可以通过以下公式计算：σ = γ × h其中，σ是土的自重应力，γ是土的单位重量，h是土体的深度。

单位重量是指单位体积土的重量，通常用千克/立方米或克/立方厘米表示。

土的密度是由土壤颗粒的种类、大小和排列方式决定的。

不同种类的土壤具有不同的密度。

例如，砂土的密度通常在1.5-1.7克/立方厘米之间，而黏土的密度通常在1.2-1.5克/立方厘米之间。

因此，不同种类的土壤在相同深度下的自重应力也会有所不同。

土的自重应力对土体的稳定性和承载力有着重要的影响。

在土工工程中，土的自重应力是计算土体承载力和稳定性的重要参数。

例如，在计算土体的承载力时，需要考虑土的自重应力对土体的压缩和变形的影响。

在计算土体的稳定性时，需要考虑土的自重应力对土体的抗剪强度和抗压强度的影响。

土的自重应力还对土体的水分运移和土壤侵蚀有着重要的影响。

在土壤侵蚀过程中，土的自重应力会影响土壤颗粒的运动和沉积，从而影响土壤侵蚀的速度和规模。

在土壤水分运移过程中，土的自重应力会影响土壤孔隙水的压力和流动速度，从而影响土壤水分的分布和运移。

土的自重应力是土工工程中一个非常重要的参数，它对土体的稳定性、承载力、水分运移和土壤侵蚀等方面都有着重要的影响。

在土工工程中，需要对土的自重应力进行准确的计算和分析，以保证工程的安全和可靠性。

基底处土中自重应力符号介绍基底处土中自重应力符号是一个在岩土工程中经常使用的术语，用于描述岩土体在受到自身重力作用时所产生的应力。

在地下工程设计、土力学和地质工程等领域中，了解和计算基底处土中的自重应力符号对于工程设计和稳定性分析非常重要。

自重应力自重应力是指岩土体由于受到重力作用而产生的内部应力。

在岩土工程中，土体的重力是由于土体单元的重量所引起的。

自重应力符号用于表示基底处土体的自重应力。

它是在地面之下的一层土体中的应力分布，其中位于土体深度为Z处的土体单元受到来自于上面的土体单元的重力作用。

自重应力符号通常用斜体符号σ表示，可以分为有效应力符号σ’和总应力符号σ。

有效应力符号表示在没有饱和的情况下，土体中仅考虑固体颗粒之间的接触力所产生的应力。

总应力符号表示在考虑饱和条件下，土体中既考虑固体颗粒之间的接触力，也考虑水分对土体的承压力。

计算公式基底处土中自重应力符号的计算可以通过以下公式进行：σ = γ * Z其中，γ代表土体的单位重量，Z代表土体的深度。

单位重量是指土体的单位体积所承受的重量，通常使用千克/立方米或千牛/立方米作为单位。

在实际工程中，由于土体的性质和地质条件的不同，γ的值可能会有所不同。

因此，在计算基底处土中自重应力符号时，需要根据具体的工程情况和土体性质来确定合适的γ值。

一般来说，可以通过实地调查和实验室试验来获取土体的实际情况和性质，从而确定合适的γ。

影响因素基底处土中自重应力符号的大小受到多种因素的影响，包括土体的深度、土体的密度、土体的类型以及地下水位等。

下面是一些影响基底处土中自重应力符号的主要因素：土体的深度土体的深度是决定基底处土中自重应力符号大小的重要因素。

一般来说，土体的深度越大，受到的上层土体单元的重力就越大，从而使得基底处土中的自重应力符号增加。

土体的密度土体的密度也是影响基底处土中自重应力符号的重要因素。

当土体的密度增加时，单位体积土体所承受的重量也增加，从而使得基底处土中的自重应力符号增加。

在均质土层中,土的竖向自重应力沿深度的分布规律摘要：一、均质土层中竖向自重应力的概念与特点二、竖向自重应力沿深度的分布规律1.分布形式2.影响因素三、实际应用与工程意义正文：在均质土层中，土的竖向自重应力是指土体由于自身重量而在某个位置上产生的应力。

竖向自重应力的分布规律对工程建设中的地基设计、基础施工以及土体稳定性分析等方面具有重要的指导意义。

一、均质土层中竖向自重应力的概念与特点竖向自重应力在土层中沿深度的分布规律是工程界长期研究的问题。

一般来说，竖向自重应力随着深度的增加而逐渐增大。

这是因为在土层深处的土体受到上层土体的约束，无法完全自由沉降。

此外，竖向自重应力还与土的性质、土层厚度、地下水位等因素密切相关。

二、竖向自重应力沿深度的分布规律1.分布形式在均质土层中，竖向自重应力的分布形式通常为线性增加。

也就是说，深度每增加一层，竖向自重应力相应地增加一个固定比例。

2.影响因素竖向自重应力的分布规律受到以下几个因素的影响：（1）土的性质：不同类型的土壤其竖向自重应力分布规律有所差异。

例如，黏性土中的竖向自重应力分布相对较均匀，而砂性土中的竖向自重应力分布则受到土颗粒排列、密度等因素的影响。

（2）土层厚度：土层厚度越大，竖向自重应力分布的线性增长趋势越明显。

（3）地下水位：地下水位以下的土层在计算竖向自重应力时，需要扣除浮力影响。

三、实际应用与工程意义竖向自重应力的分布规律在实际工程中具有重要意义，它有助于：1.地基设计：根据竖向自重应力的分布规律，合理选择地基材料，优化地基设计。

2.基础施工：指导基础施工，确保基础承载力的安全性和稳定性。

3.土体稳定性分析：通过研究竖向自重应力的分布规律，评估土体的稳定性和变形特性，为工程决策提供依据。

总之，了解均质土层中竖向自重应力的分布规律，对于工程设计、施工及土体稳定性分析具有重要的参考价值。