销售中的利润问题

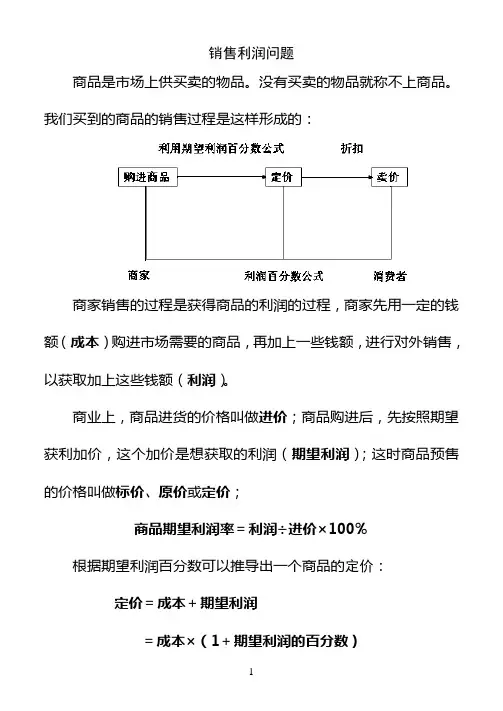
销售利润问题商品是市场上供买卖的物品。

没有买卖的物品就称不上商品。

我们买到的商品的销售过程是这样形成的：商家销售的过程是获得商品的利润的过程，商家先用一定的钱额（成本）购进市场需要的商品，再加上一些钱额，进行对外销售，以获取加上这些钱额（利润）。

商业上，商品进货的价格叫做进价；商品购进后，先按照期望获利加价，这个加价是想获取的利润（期望利润）；这时商品预售的价格叫做标价、原价或定价；商品期望利润率＝利润÷进价×100％根据期望利润百分数可以推导出一个商品的定价：定价＝成本＋期望利润＝成本×（1＋期望利润的百分数）商家在销售过程中，为了获取更高额的利润，会对原订的价格适当地调整，即按一定的折扣降价销售；商品实际卖出的价格叫做售价或卖价，如果降价折扣确定不好，会直接影响到消费者的购买的数量。

折扣数＝售价÷定价 每101或10%叫“一折”，打八折是108或80%。

根据折扣的关系式还能够推导其他的关系式：商品售价＝商品定价×折扣数此时获取的利润是卖价与成本的差，其中，商品利润＝售价－成本商品利润率＝商品利润÷成本×100％＝（售价－成本）÷成本×100％由此能够推导的关系式：售价＝成本×（1＋利润百分率）就必须熟练运用利润百分数，折扣等公式，制定合适的商品价格幅度，确定使用哪种促销方式，制定自己的销售策略，才能在商海中立于不败之地。

解答商品销售利润问题的应用题必须熟知商品销售的过程及相应的关系式，运抓不变量(一般情况下成本是不变量)，用分数或百分数应用题的解答分析步骤求解。

常见的几种题型如下：（一）已知进价、售价，求利润率【例1】电脑产品的进价是10000元，售价为12000元，此商品的利润率是多少？分析与解答：电脑产品的商品利润是（12000－10000＝）2000元，由“商品利润率＝利润÷进价×100％”求得商品利润率为（2000÷10000×100％＝）20％。

销售利润问题1.某种文化衫，平均每天销售40件，每件利润20元，若每件降价1元，则每天可多售出10件，如果每天要盈利1080元，每件应降价多少元？2.某商店从厂家以每件21元的价格购进一批商品，该商品可以自行定价。

若每件商品售价为a元，则可卖出（350—10a）件，但物价局限定每件商品价不能超过进价的20%，商店计划要赚400元，需要卖出多少件商品？每件商品的售价为多少元？3.商店销售核桃，其进价为每千克40元，接每千克60元出售，平均每天可售出100千克，后来经过商场调查发现，单价每降低2元，则平均每天的销售量可增加20千克，若该专卖店销售的这种核桃想要平均每天获利2240元(1).每千克核桃应降价多少元？(2).在平均每天获利不变的情况下，为尽可能让利于顾客，赢得市场。

该店应按原售价的几折出售？4.某花圃用花盆培育某种花圃，经过试验，发现每盆的盈利与每盆的株数构成一定的关系。

每盆植入3株时，平均单株盈利3元；以同样的栽培件，若每盆增加1株，平均盈利就减少0.5元，要使每盆的盈利 10元，每盆应该植多少株？5.商场某种商品平均每天可销售30件，每件盈利50元，为了尽快减少库存是商场决定采取适当的降价措施，经调查发现，每件商品每降价1元，商场平均每天可多售出2件。

正常情况下，每件商品降价多少元是盈利可达6.（基训17页10题）某批发商以每件50元购进800件T恤，第一个月以单价80元销售，售出200件，第二个月如果单价不变，预计可售出200件。

据市场调查，单价每降1元，可售出10件，但最低单价必须高于进价。

第二个月结束后，批发商对余下T恤进行一次性清仓销售。

单价为40元，如果批发商要获利9000元。

那么第二个月T 恤单价为多少元？7、某水果批发商销售每箱进价为40元的苹果，物价部门规定每箱的售价不得高于55元，市场调查发现，若每箱以50元的价格销售，平均每天销售90箱，价格每提高1元，平均每天少销售3箱。

商品销售利润问题一、销售问题中的常见术语：进价、成本价、定价、售价、标价、原价、获利（盈利）、亏损、打折、提价、降价二、销售问题的基本公式（自己回忆）：单件利润= -总利润= -= ×打折后的价格=三、销售问题练习题1、某商品打八折后售价为96元，则该商品原价为元。

2、某商品进价500元，提高40%后标价出售，则售价为；3、某商品的进价200元，将进价提高20%后标价出售，则售出此商品后获利元。

4、某商品的标价为120元，若以9折降价出售，相对于进价仍可获利20%，则此商品的进价为。

5、某商店一套服装的进价为200元，若按标价的80％销售可获利72元，则该服装的标价为元。

6、一件商品按成本价提高20%标价，又以九折销售，售价为270元，这种商品的成本价是元。

7、某商店打折销售商品，如果按定价的6折出售，将赔20元，若按定价的8折出售，将赚15元，这种商品的定价为元。

8、某商品原价每个150元,先降价30%后又涨价30%,最后商品的销售价格是。

9、某商场将进价为800元的商品按此商品标价的8折出售，仍获利10%，则该商品的标价为元。

10、一家商店将某件商品按成本价提高50%后，标价为450元，又以8折出售，则售出这件商品可获利润元．四、例题：某种服装，平均每天可销售20件，每件盈利44元。

若每件降价1元，则每天可多销售5件，如果每天要盈利1600元，每件应降价多少元？五、练习：1、某商场销售一批名牌衬衫，平均第天可售出20件，每件盈利45元，为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当降价措施。

经调查发现，如果每件衬衫每降价1元，商场平均每天多售出4件，若该商场平均每天盈利2100元，则每件衬衫应降价多少元？2、某水果批发商经销一种高档水果，如果每千克盈利10元，每天可售出500千克，经市场调查发现，在进价不变的前提下，若每千克涨价1元，日销售量将减少20千克，现该商场要保证每天盈利6000元，同时又要尽可能使顾客得到实惠，那么每千克水果应涨价多少元？3、某商店购进一种商品，单价30元，试销中发现这种商品每天的销售量P（件）与每件的销售价X（元）满足关系：P=100-2X，若商店每天销售这种商品要获得200元的销售利润，那么每件商品的售价应为多少元？每天要售出这种商品多少件？4、西瓜经营户以2元每千克的价格购进一批小西瓜，以3元每千克的价格出售，每天可出售200千克为了促销，该营销户决定降价销售，经调查发现，这种小西瓜每降价0.1元每千克每天可多售出40千克，另外，每天的房租等固定成本共24元，该经营户要想每天盈利200元，应将每千克小型西瓜的售价降低多少元？5、某批发商以每件50元的价格购进800件T恤，第一个月以单价80元销售，售出了200件；第二个月如果单价不变，预计仍可售出200件，批发商为增加销售量，决定降价销售，根据市场调查，单价每降低1元，可多售出10件，但最低单价应高于购进的价格；第二个月结束后，批发商将对剩余的T恤一次性清仓销售，清仓是单价为40元，设第二个月单价降低x元。

3.4(21)--销售中与利润率相关的盈亏问题一．【知识要点】1.与销售相关的等量关系： （1）销售总额=单价×销售量（2）现价=原价×（1+提价率）；现价=原价×（1-降价率）（3）利润=售价-进价 （4）=100%⨯利润利润率进价（5）利润=进价×利润率 （6）售价=进价×（1+利润率） （7）=10⨯折扣数实际售价标价 二．【经典例题】1.填空：（1）某商品原售价是100元，现降价10%，降价后售价是 元.（2）某商品进价是160元，售价是180元，则利润是 元.（3）某商品进价是160元，售出后盈利40元，则利润率是（3）某商品进价是160元，售出后亏损40元，则利润率是（4）某商品原来进价是100元, 利润率是30%,则利润是 .（5）某商品原来每件进价是100元, 盈利30%,则售价是 元.（6）某商品原来每件进价是100元, 亏损20%,则售价是 元.（7）商品原价是200元，九折出售，卖价是 元。

（8）商品原价是200元，七五折出售，卖价是 元。

2．某商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%,卖出这两件衣服总的是盈利还是亏损,或是不盈不亏?3.某商店购进甲.乙两件服装共用去600元，为获得较大利润，商店老板决定将甲服装按50%的利润定价，乙按40%的利润定价，在实际销售中，两件均按九折出售，共获利174元，两件服装的进价各是多少？4.某校七年级社会实践小组去商场调查商品销售情况，了解到该商场以每件80元的价格购进了某品牌衬衫500件，并以每件120元的价格销售了400件，商场准备采取促销措施，将剩下的衬衫降价销售。

请你帮商场计算一下，每件衬衫降价多少元时，销售完这批衬衫正好达到盈利45%的预期目标?三．【题库】【A】1.列方程解决下列各题：①安踏运动鞋打八折后是220元，设原价是x元,列方程：。

利润问题核心公式：（1）利润＝销售价（卖出价）－成本（2）利润率＝成本利润＝成本成本销售价-＝成本销售价－1（3）销售价＝成本×（1＋利润率）或者 成本＝利润率销售价11、一件商品如果以八折出售，可以获得相当于进价20%的毛利，那么如果以原价出售，可以获得相当于进价百分之几的毛利?2、一种衣服过去每件进价60元，卖掉后每件的毛利润是40元。

现在这种衣服的进价降低，为了促销，商家将衣服八折出售，毛利润却比过去增加了30%，请问现在每件衣服进价是多少元?3、一种衣服过去每件进价60元，卖掉后每件的毛利润是40元。

现在这种衣服的进价降低，为了促销，商家将衣服八折出售，毛利润却比过去增加了30%，请问现在每件衣服进价是多少元?4、出售甲种产品的利润是25%，乙种产品利润是20%，如果分别各用2000元购进甲、乙两种产品，共获利多少元？如果两种产品一起买可以优惠15%，此时的售价是多少？5、一件商品按30%的利润定价，然后又按八折出售，结果赚了64元，这件商品的成本是多少元？6、一件商品如果按原价出售可以盈利25%，如果降价30%出售，则要亏本30元，那么这件产品的进价是多少元？7、某商品按定价出售，每个可获得45元的利润。

已知按定价打八五折出售8个获得的利润与按定价每个减少35元出售12个所获得的利润一样多。

这种商品每个定价多少元？8、某商店从外地购进360个玻璃制品，运输时损坏了40个，剩下的按进价以117%售出，商店可盈利百分之几？9、一家商店将某种服装按成本价提高40％后标价，又以8折 (即按标价的80％)优惠卖出，结果每件仍获利15元，那么这种服装每件的成本是多少元?10、若进货价降低8％，而售价不变，那么利润可由目前的p％增加到(p+10)％，求p．。

一、销售利润问题商品的进货价格叫做进价。

商品预售的价格叫做标价或原价。

商品实际卖出的价格叫做售价。

商品利润=商品售价-商品进价。

商品售价=商品原价（或标价）×折数。

商品利润率=商品利润/商品进价=（商品售价-商品进价）/商品进价。

常见的利润问题有：（一）已知进价、售价、求利润率例1．脑产品的进价是10000元，售价为12000元，此商品的利润率是多少？解：设此商品利润率为x%，根据题意得：（12000-10000）/10000=x%解之得：x=20答：此商品的利润率为20%。

（二）已知进价和利润率，求标价或原价例2．某商品的进价是250元，按标价的9折销售时，利润率为15.2%，商品的标价是多少？解：设商品的标价是x元，根据题意得：（90%x-250）/250=15.2%解之得：x=320答：商品的标价是320元（三）已知进价、标价及利润率，求标价或原价的折数例3．某名牌西装进价是1000元，标价是1500元，某商场要以利润率不低于5%的价格销售，问售货员可以打几折出售此商品？解：设售货员可打x折出售此商品，根据题意得：（1500·x/10-1000）/1000=5%解之得：x=7答：打7折出售该商品。

在这一类求折数的应用题中，以前通常都是设打x折，然后在列式时把售价列为"1500x"，最后x=0.7=7折。

但我认为x=0.7的话，就说明是打0.7折，而不能说是7折，因此这种做法不妥当。

打7折就是原价的7/10，打8折就是原价的8/10。

按照这一原则，列式时我认为应将售价"1500x"列为"1500×x/10",这样才比较合理。

设商品打x折，方程的解x=7，那么商品就是打7折。

这样前后就显得比较一致.（四）已知利润率、标价求进价例4．商场对某一商品作调价，按原价的8折出售，此时商品的利润率是10%，已知商品标价为1375元，求进价。

一、销售利润问题解答这类应用题除了遵循解答应用题的一般步骤之外，还必须注意抓住以下数量的概念及关系式：商品的进货价格叫做进价。

商品预售的价格叫做标价或原价。

商品实际卖出的价格叫做售价。

商品利润 =商品售价 -商品进价。

商品售价 =商品原价（或标价）×折数。

商品利润率 =商品利润 /商品进价 =（商品售价 -商品进价） /商品进价。

常见的利润问题有：（一）已知进价、售价、求利润率1．脑产品的进价是10000 元，售价为12000 元，此商品的利润率是多少？2．某商品的进价是250 元，按标价的9 折销售时，利润率为15.2% ，商品的标价是多少？（三）已知进价、标价及利润率，求标价或原价的折数3．某名牌西装进价是1000 元，标价是1500 元，某商场要以利润率不低于5% 的价格销售，问售货员可以打几折出售此商品？（四）已知利润率、标价求进价4．商场对某一商品调价，按原价的8 折出售，此时商品的利润率是10% ，已知商品标价为1375 元，求进价。

5．一商场将每台VCD 先按进价提高40% 标出销售价，然后再以八五折优惠价出售，结果还赚了228 元，那么每台 VCD 进价多少元？x% 出售，6．商店购进某种商品的进价是每件 8 元，销售价是每件 10 元，现为扩大销量，将每件的售价降低但要求卖出每一件商品所获利润是降低前所获利润的 90% ，问售价降低了多少？7.“五一”期间，某商场搞优惠促销，决定由顾客抽奖定折扣,某顾客购买甲、乙两种商品，分别抽七折和九折优惠券，共付款 386 元，这两种商品原销售价之和为500 元，这两种商品原销售价分别是多少？8.抗“非典”期间，个别商贩将原来每桶价格 a 元的过氧乙酸消毒液提高20％后出售，市政府及时采取措施，使每桶价格在涨价后以八五折出售，那么现在每桶价格是多少？9.某商店将每台彩电先按进价提高40 ％标出售价，然后广告宣传将以八折的优惠价出售，结果每台彩电赚了300 元，则经销这种彩电的利润率是多少？10. 某商品的进价是 500 元，标价是 750 元，商品要求以利润率不低于 5％的售价打折出售，售货员最低可以打几折出售此商品？11. 甲乙两件服装的成本共500 元，商店老板为获取利润，决定将甲服装按50 ％的利润定价，乙服装按 40 ％的利润定价，在实际出售时，应顾客要求，两件服装均按9 折出售，商店共获利157 元，求甲、乙两件服装的成本各是多少？12. 某商品把进价提高后标价为1200 元，为了吸引顾客，再按九折出售，利润能盈利10％，这件商品的进价是多少？13. 某商品的进价为800 元，标价为1200 元，由于商品积压，准备打折出售，但要保持利润率不低于 5 ％，则最低可以打几折？14.某商店有进价不同的两个计算器都卖 64 元，其中一个盈利 60 ％，另一个亏本 20％，在这次买卖中，这家商店是赚还是赔？。

销售问题中利润的求法
在销售问题中，利润是指销售收入与销售成本之间的差额。

计算利润的基本公式为：利润 = 售价 - 成本。

售价指的是商品的销售价格，成本则包括商品的生产成本、运营成本、税费等。

在某些情况下，成本可能仅指商品的进价，即商家从供应商处购买商品的价格。

除了基本公式外，还有一些相关的公式和概念：
1. 利润率：表示利润与成本或售价之间的比例关系。

利润率 = 利润÷成本或者利润率 = (售价 - 成本) ÷售价。

2. 打折销售：在打折销售中，售价 = 标价×折扣。

例如，如果一件商品的标价是100元，打8折销售，那么售价就是80元。

3. 总利润：当销售多个商品时，总利润 = 总销售收入- 总成本。

需要注意的是，在实际应用中，销售问题可能涉及更复杂的情境和因素，如市场需求、竞争状况、营销策略等。

因此，在计算利润时，还需要考虑这些因素对售价和成本的影响。

10利润问题利润赢亏问题〔1〕销售问题中常出现的量有：进价、售价、标价、利润等〔2〕有关关系式：商品利润=商品售价—商品进价=商品标价×折扣率—商品进价商品利润率=商品利润/商品进价商品售价=商品标价×折扣率〔1〕利润=售价-进价〔2〕利润率=进价利润=进价进价售价-〔3〕利润=利润率×成本 〔4〕打折销售中的售价=标价×10折数〔5〕售价=成本+利润+成本×〔1+利润率〕 1.某商品按定价的八折出售，售价14.80元，那么原定价是__18.5_元。

2.、某商品的进货价为每件x 元，零售价为每件900元，为了适应市场竞争，商店按零售价的九折让利40元销售，仍可获利10%，那么x 为〔A 〕A 、700元B 、约733元C 、约736元D 、约856元3、一家商店将某种服装按成本价提高40%后标价，又以8折〔也就是按标价的80%〕卖出，结果每件仍获得利润15元，这种服装每件的成本价是多少元？〔提示：每件服装的利润＝售价－成本价〕等量关系：利润=折扣后价格—进价,折扣后价格－进价=15解：这种服装每件的成本价是x 元，依题意，得(140%)80%15x x +⨯-=解得x=125答：这种服装每件的成本价是125元4、某商店对一种商品调价，按原价的八折出售，打折后的利润率是20﹪，该商品的原价是63元，求该商品的进价。

解：设该商品的进价为x 元，根据题意，得〔1+20%〕x=63×0.8解得x=42答：5、某商店以每3盒16元钱的价格购进一批录音带，又从另外一处以每4盒21元钱的价格购进比前一批数量多一倍的录音带，如果以每3盒k 元的价格全部出售，可得到所投资20%的利润、求k 的值、解：设第一次购进的数量为a,根据题意，得)2421316%)(201(33a a k a ⨯++=⨯ 6、某商店经营一种商品，由于进货价降低5%，出售价不变，使得利润率由m%提高到〔m+6〕%,求m 的值？解：设该商品的进价为a 元，那么售价为〔a+am%〕或a(1-5%)+a(1-5%)(m+6)%根据题意，得(1-5%)a+a(1-5%)(m+6)%=a+am%或a(1+m%)=a(1-5%)〔1+(m+6)%〕解得m=14、∴m%=14%、7、某种商品进价为800元，出售时标价为1200无，后来由于该商品积压，商店准备打折出售，但要保持利润率为5%，那么应打几折出售？解：设应打x 折出售，根据题意，得%)51(800101200+=⨯x 8、某商场售货员同时卖出两件上衣，每件都以135元售出，假设按成本计算，其中一件赢利25%，另一件亏损25%，问这次售货员是赔了还是赚了？解：设盈利25%的那件进价为x 元，根据题意，得〔1+25%〕x=135解得x=108设亏损25%的那件进价为y 元，根据题意，得〔1-25%〕y=135解得y=180∴135×2-108-180=-18即亏损18元9、市场鸡蛋按个数计价，一商贩以每个0.24元购进一批鸡蛋，但在贩运途中，不慎碰坏了12个，剩下的蛋以每个0.28元售出，结果获利11.2元，问商贩当初买进多少鸡蛋？ 解：设商贩当初买进x 个鸡蛋，根据题意，得0.28〔x-12〕=0.24x+11.210、甲乙两店对同一种原价为3000元的彩电进行优惠促销，甲商店的优惠方式是对此彩电降价20%销售，乙商店那么是先降价12%，再降价8%。

专题05 函数实际问题之销售中的利润问题（解析版）一、利润中的几个等量关系：售价=进价+利润；售价=标价×折扣；总利润=单件（单个商品）利润×总销量；二、需要注意的是，在利用函数解答实际问题的过程中，一定要注意自变量的取值范围，以及在这个取值范围内的函数值的最大值及最小值；切不可直接用原函数的最值当作实际问题的最值；避免出现错误的方法是：作出示意图，由图象分析函数值的最值.题型一、利润问题应用题1. （2019·江苏连云港中考）某工厂计划生产甲、乙两种产品共2500吨，每生产1吨甲产品可获得利润0.3万元，每生产1吨乙产品可获得利润0.4万元．设该工厂生产了甲产品x（吨），生产甲、乙两种产品获得的总利润为y（万元）．（1）求y与x之间的函数表达式；（2）若每生产1吨甲产品需要A原料0.25吨，每生产1吨乙产品需要A原料0.5吨．受市场影响，该厂能获得的A原料至多为1000吨，其它原料充足．求出该工厂生产甲、乙两种产品各为多少吨时，能获得最大利润．【答案】见解析.【解析】解：（1）y=0.3x+0.4(2500－x)=－0.1x+1000，（2）由题意得：0.25x+0.5（2500－x）≤1000，解得：x≤2500，即1000≤x≤2500，由（1）知，y=－0.1x+1000，∵－0.1<0，∴y随x的增大而减小，当x=1000时，y取最大值，此时甲产品1000吨，乙产品1500吨时能获得最大利润.2. （2019·江苏宿迁中考）超市销售某种儿童玩具，如果每件利润为40元（市场管理部门规定，该种玩具每件利润不能超过60元），每天可售出50件.根据市场调查发现.销售单价每增加2元，每天销售量会减少1件. 设销售单价增加x元，每天售出y件.（1）请写出y与x之间的函数表达式；（2）当x为多少时，超市每天销售这种玩具可获利润2250元？（3）设超市每天销售这种玩具可获利w元，当x为多少时w最大，最大值是多少？【答案】见解析.【解析】解：（1）y=12-x+50.（2）由题意得：y（x+40）=2250，即（12-x+50）（x+40）=2250，解得：x=50（舍）或x=10，即当x=10时，超市每天销售这种玩具可获利润2250元. （3）由题意知，w= y（x+40）=（12-x+50）（x+40）=12-（x－30）2+2450，∵12-<0，对称轴为x=30，∴当0≤x≤20时，w随x的增大而增大，即当x=20时，w取最大值，最大值为：2400.3. （2019·湖北鄂州中考）“互联网+”时代，网上购物备受消费者青睐. 某网店专售一款休闲裤，其成本为每条40元，当售价为每条80元时，每月可销售100条.为了吸引更多顾客，该网店采取降价措施. 据市场调查反映：销售单价每降1元，则每月可多销售5条. 设每条裤子的售价为x元（x为正整数），每月的销售量为y条.（1）直接写出y与x的函数关系式；（2）设该网店每月获得的利润为w元，当销售单价降低多少元时，每月获得的利润最大，最大利润是多少？（3）该网店店主热心公益事业，决定每月从利润中捐出200元资助贫困学生. 为了保证捐款后每月利润不低于4220元，且让消费者得到最大的实惠，该如何确定休闲裤的销售单价？【答案】见解析.【解析】解：（1）y＝100+5（80－x）或y＝－5x+500（2）由题意，得：W=(x-40)( －5x+500)=-5x2+700x-20000=-5(x-70)2+4500，∵a=-5<0，∴w有最大值即当x=70时，w最大值＝4500∴应降价80－70＝10（元）（3）由题意，得：-5(x-70)2+4500＝4220+200解得：x1＝66，x2 ＝74∵抛物线开口向下，对称轴为直线x=70，∴当66≤x≤74时，符合该网店要求，而为了让顾客得到最大实惠，故x＝66∴当销售单价定为66元时，即符合网店要求，又能让顾客得到最大实惠.题型二、图表类利润最值问题4. （2019·青岛中考）某商店购进一批成本为每件 30 元的商品，经调查发现，该商品每天的销售量y（件）与销售单价x（元）之间满足一次函数关系，其图象如图所示.（1）求该商品每天的销售量y与销售单价x之间的函数关系式；（2）若商店按单价不低于成本价，且不高于 50 元销售，则销售单价定为多少，才能使销售该商品每天获得的利润w（元）最大？最大利润是多少？（3）若商店要使销售该商品每天获得的利润不低于 800 元，则每天的销售量最少应为多少件？【答案】见解析.【解析】解：（1）设商品每天的销售量y与销售单价x之间的函数关系式为y=kx+b，由题意知，30100 4570k bk b+=⎧⎨+=⎩，解得，2160kb=-⎧⎨=⎩，即y关于x的函数解析式是：y＝﹣2x+160；（2）30≤x≤50，w=（x－30）y=（x－30）（﹣2x+160）=－2（x－55）2+1250∵30≤x≤50，∴当x=50时，w取最大值为1200元；（3）w≥800，w=－2（x－55）2+1250的图象如下所示，元，∴－2（x－55）2+1250=800，解得：x1=40，x2=70，∴40≤x≤70时，每天的利润不低于800元，故每天的销售量最少应为﹣2×70+160=20件.5. （2019·成都中考）随着5G技术的发展，人们对各类5G产品的使用充满期待. 某公司计划某地区销售一款5G产品，根据市场分析，该产品的销售价格将随销售周期的变化而变化. 设产品在第x（x为正整数）个销售周期每台的销售价格为y元，y与x之间满足如图所示的一次函数关系.（1）求y与x之间的关系式；（2）设产品在第x 个销售周期的销售数量为p （万台），p 与x 之间的关系为: 1122p x =+,根据以上信息，试问:哪个销售周期的销售收入最大？此时该产品的销售价格是多少元？【答案】见解析.【解析】解：（1）设y 与x 之间的关系式为y =kx +b ，由题意知，∴700055000k b k b +=⎧⎨+=⎩，解得：5007500k b =-⎧⎨=⎩， 即y 与x 之间的关系式为：y =－500x +7500；（2）设第x 个销售周期的销售收入为w 元，则w =yp =（－500x +7500）（1122x +） =－250（x －7）2+16000，∴在第7个销售周期的销售收入最大，销售价格为：4000元.6. （2019·浙江嘉兴中考）某农作物的生长率p 与温度t (C )有如下关系：如图1，当10≤t ≤25时可近似用函数11505p t =-刻画；当25≤t ≤37 时可近似用函数21()0.4160p t h =--+刻画． (1)求h 的值．(2)按照经验，该作物提前上市的天数m (天)与生长率p 满足函数关系：①请运用已学的知识，求m 关于p 的函数表达式；②请用含t 的代数式表示m (3)天气寒冷，大棚加温可改变农作物生长速度．在(2)的条件下，原计划大棚恒温20℃时，每天的成本为200元，该作物30天后上市时，根据市场调查：每提前一天上市售出(一次售完)，销售额可增加600元．因此给大棚继续加温，加温后每天成本w (元)与大棚温度t (C )之间的关系如图2．y问提前上市多少天时增加的利润最大？并求这个最大利润（农作物上市售出后大棚暂停使用）．图1 图2【答案】见解析.【解析】解：（1）将（25,0.3）代入21()0.4160p t h =--+得，h =29或h =21， ∵h >25,∴h =29，（2）①由题意知m 是p 的一次函数，设m =kp +b ， 可得：0.200.310k b k b +=⎧⎨+=⎩，解得：k =100，b =－20， ∴m =100p －20，②当10≤t ≤25时，11505p t =-， ∴m =2t －40，当25<t ≤37时，21(29)0.4160p t =--+， ∴m =25(29)208t --+，(3)①当20≤t ≤25时，由（20,200），（25,300）可得：w =20t －200，∴增加利润为：600m +[200×30－w (30－m )]=40t 2－600t －4000=40（t －7.5）2－6250∴当t =25时，利润最高为：6000元；②当25<t ≤37时，w =300，增加利润为：600m +[200×30－w (30－m )]=21125(29)150002t --+， ∴当t =29时，增加利润取最大值为：15000元，综上所述，当t =29时，提前上市20天，增加利润最大，为15000元.7. （2019·湖北咸宁中考）某工厂用50天时间生产一款新型节能产品，每天生产的该产品被某网店以每件80元的价格全部订购，在生产过程中，由于技术的不断更新，该产品第x 天的生产成本y （元/件）与x （天）之间的关系如图所示，第x 天该产品的生产量z （件）与x （天）满足关系式z =－2x +120.（1）第40天，该厂生产该产品的利润是 元；（2）设第x 天该厂生产该产品的利润为w 元.①求w 与x 之间的函数关系式，并指出第几天的利润最大.最大利润是多少？②在生产该产品的过程中，当天利润不低于2400元的共有多少天？【答案】见解析.【解析】解：（1）由图象可知，第40天时的成本为40元，此时的产量为z ＝﹣2×40+120＝40则第40天的利润为：（80﹣40）×40＝1600元故答案为：1600.（2）①设直线AB 的解析式为y ＝kx +b （k ≠0），把（0，70）（30，40）代入得：304070k b b +=⎧⎨=⎩，解得170k b =-⎧⎨=⎩∴直线AB 的解析式为y ＝﹣x +70.（Ⅰ）当0＜x ≤30时w ＝[80﹣（﹣x +70）]（﹣2x +120）＝﹣2x 2+100x +1200＝﹣2（x ﹣25）2+2450∴当x ＝25时，w 最大值＝2450.（Ⅱ）当30＜x ≤50时， w ＝（80﹣40）×（﹣2x +120）＝﹣80x +4800∵w 随x 的增大而减小∴当x ＝31时，w 最大值＝2320.∴()()()222524500308048003050x x w x x ⎧--+<≤⎪=⎨-+<≤⎪⎩，，， ∴第25天的利润最大，最大利润为2450元.②（i ）当0＜x ≤30时，令﹣2（x ﹣25）2+2450＝2400，解得：x 1＝20，x 2＝30∵抛物线w ＝﹣2（x ﹣25）2+2450开口向下，由其图象可知，当20≤x ≤30时，w ≥2400，此时，当天利润不低于2400元的天数为：30﹣20+1＝11天，（ii ）当30＜x ≤50时，由①可知这些天中的日利润均低于2400元，综上所述，当天利润不低于2400元的共有11天．8. （2019·湖北黄冈中考）某县积极响应市政府加大产业扶贫力度的号召，决定成立草莓产销合作社，负责扶贫对象户种植草莓的技术指导和统一销售，所获利润年底分红。

初一数学利润问题Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】一、销售利润问题商品的进货价格叫做进价。

商品预售的价格叫做标价或原价。

商品实际卖出的价格叫做售价。

商品利润=商品售价-商品进价。

商品售价=商品原价（或标价）×折数。

商品利润率=商品利润/商品进价=（商品售价-商品进价）/商品进价。

常见的利润问题有：（一）已知进价、售价、求利润率例1．脑产品的进价是10000元，售价为12000元，此商品的利润率是多少？解：设此商品利润率为x%，根据题意得：（12000-10000）/10000=x%解之得：x=20答：此商品的利润率为20%。

（二）已知进价和利润率，求标价或原价例2．某商品的进价是250元，按标价的9折销售时，利润率为15.2%，商品的标价是多少？解：设商品的标价是x元，根据题意得：（90%x-250）/250=15.2%解之得：x=320答：商品的标价是320元（三）已知进价、标价及利润率，求标价或原价的折数例3．某名牌西装进价是1000元，标价是1500元，某商场要以利润率不低于5%的价格销售，问售货员可以打几折出售此商品？解：设售货员可打x折出售此商品，根据题意得：（1500·x/10-1000）/1000=5%解之得：x=7答：打7折出售该商品。

在这一类求折数的应用题中，以前通常都是设打x折，然后在列式时把售价列为"1500x"，最后x=0.7=7折。

但我认为x=0.7的话，就说明是打0.7折，而不能说是7折，因此这种做法不妥当。

打7折就是原价的7/10，打8折就是原价的8/10。

按照这一原则，列式时我认为应将售价"1500x"列为"1500×x/10",这样才比较合理。

设商品打x折，方程的解x=7，那么商品就是打7折。

这样前后就显得比较一致.（四）已知利润率、标价求进价例4．商场对某一商品作调价，按原价的8折出售，此时商品的利润率是10%，已知商品标价为1375元，求进价。

实际应用题------- 销售利润问题销售利润问题中常出现的量有：售价、标价、进价、销量、利润、利润率、折扣等。

涉及的等量关系有：售价=折扣数×10%×标价，利润率=进价售价－进价进价利润=，总利润=（销售单价-进货单价）×销售量。

1.（2019湘潭）湘潭政府工作报告中强调，2019年着重推进乡村振兴战略，做做优做响湘莲等特色农产品品牌。

小亮调查了一家湘潭特产店A ，B 两种湘莲礼盒一个月的销售情况，A 种湘莲礼盒进价72元/盒，售价120元/盒，B 种湘莲礼盒进价40元/盒，这两种湘莲礼盒这个月平均每天的销售总额为2800元，平均每天的总利润为1280元。

（1）求该店平均每天销售这两种湘莲礼盒各多少盒？（2）小亮调查发现，A 种湘莲礼盒售价每降3元可多卖1盒。

若B 种湘莲礼盒的售价和销量不娈，当A 种湘莲礼盒降价多少元/盒时，这两种湘莲盒平均每天的总利润最大，最大是多少元？解：（1）设平均每天销售A 种礼盒为x 盒，B 种礼盒为y 盒， 则有 （120-72）x+(80-40)y=1280,120x+80y=2800,解得 x=10,Y=20.故该店平均每天销售A 种礼盒为10盒，B 种礼盒为20盒。

（3）设A 种湘莲盒降价m 元/盒，利润为W 元，依题意得，总利润W=（120-m-72）（10+3m ）+800， 化简得W=-31m 2+6m+1280=-31(m-9)2+1307. ∵a=-31<0， ∴当m=9时，取得最大值为1307，故当A 湘莲礼盒降价9元/盒时，这两种湘莲礼盒平均每天的总利润最大，最大值为1307元。

2.某文具店购进一批纪念册，每本进价为20元，出于营销考虑，要求每本纪念册的售价不低于20元且不高于28元，在销售过程中发现该纪念册每周的销售量y 本与每本纪念册的售价x 元之间满足一次函数关系：当销售单价为22元时，销售量为35本；当销售单价为24元时，销售量为32本。

22.3（10）---利润问题-分段函数一．【知识要点】1.分段求最值，进行比较。

2.销售利润=（售价-成本价）×销售量．3.解题步骤：（1）.设：设出两变量；（2）.列：列出函数解析式；（3）.定：确定自变量的取值范围；（4）.判：判断存在最大（小）值；（5）.求：求出对称轴，并判断对称轴是否在取值范围；（6）.算：计算最值。

二．【经典例题】1.九(13)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:已知该商品的进价为每件30元,设销售商品的每天利润为y元.(1)求出y与x的函数关系式;(2)问该商品第几天时,当天销售利润最大,最大利润是多少?22018年非洲猪瘟疫情暴发后，专家预测，2019年我市猪肉售价将逐月上涨，每千克猪肉的售价y1（元）与月份x（1≤x≤12，且x为整数）之间满足一次函数关系，如下表所示．每千克猪肉的成本y2（元）与月份x（1≤x≤12，且x为整数）之间满足二次函数关系，且3月份每千克猪肉的成本全年最低，为9元，如图所示．月份x…3456…售价y1/元…12141618…（1）求y1与x之间的函数关系式．（2）求y2与x之间的函数关系式．（3）设销售每千克猪肉所获得的利润为w（元），求w与x之间的函数关系式，哪个月份销售每千克猪肉所获得的利润最大？最大利润是多少元？3.某工厂计划在每个生产周期内生产并销售完某型设备，设备的生产成本为10万元/件． （1）如图，设第x （0＜x ≤20）个生产周期设备售价z 万元/件，z 与x 之间的关系用图中的函数图象表示．求z 关于x 的函数解析式（写出x 的范围）． （2）设第x 个生产周期生产并销售的设备为y 件，y 与x 满足关系式y ＝5x +40（0＜x ≤20）．在（1）的条件下，工厂第几个生产周期创造的利润最大？最大为多少万元？（利润＝收入﹣成本）4.为喜迎佳节，某食品公司推出一种新年礼盒，每盒成本为20元．在元旦节前30天进行销售后发现，该礼盒在这30天内的日销售量p （盒）与时间x （天）的关系如下表：在这30天内，前20天每天的销售价格1y （元/盒）与时间x （天）的函数关系式为11254y x =+（1≤x ≤20，且x 为整数），后10天每天的销售价格2y （元/盒）与时间x （天）的函数关系式为21402y x =-+（21≤x ≤30，且x 为整数）． （1）直接写出日销售量p （盒）与时间x （天）之间的关系式；（2）请求出这30天中哪一天的日销售利润最大？最大日销售利润是多少？（3）元旦放假期间，该公司采取降价促销策略．元旦节当天，销售价格（元/盒）比第30天的销售价格降低a%，而日销售量就比第30天提高了4a%，日销售利润比前30天中的最大日销售利润少380元，求a 的值．三．【题库】【A】1.数学兴趣小组经过市场调查，整理出某种商品在第x（1≤x≤90）天的售价与销量的相关信息如下表：已知该商品的进价为每件30元，设销售该商品的每天利润为y元．（1）求出y与x的函数关系式；（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？（3）该商品在前49天销售中，每销售一件商品就捐赠m元（0＜m＜10）给希望工程，若前49天销售获得的最大日利润为5408元，求出m的值时间x（天）1≤x＜5050≤x≤90售价（元/件）x+4090每天销量（件）200﹣2x【B】1.我县云蒙湖被临沂市人民政府定位“饮用水水源地”，为净化水源，某水产养殖企业在净化水源的同时，为谋求养殖利润最大化，对历年市场行情和水产品养殖情况进行了调查．调查发现这种水产品的每千克售价y1（元）与销售月份x（月）满足关系式y＝﹣x+36，而其每千克成本y2（元）与销售月份x（月）满足的函数关系如图所示．“五•一”之前，月份出售这种品每千克的利润最大．【C】1.（本题满分11分）绵阳经开区“万达广场”开业在即，开发商准备对一楼的40个商铺出租，小王和开发商约定：小王租赁的每个商铺每个月的租金y（元/个.月）与租赁的商铺数量x（个）之间函数关系的图象如图中的折线段ABC 所示（不包含端点A ，但包含端点C ）． （1）求y 与x 之间的函数关系式；（2）已知开发商每个月对每个商铺的投入成本共280元，那么当小王租赁的商铺数量为多少时，开发商在这次租赁中，每个月所获的利润w 最大？最大利润是多少？【D 】1.大学生小张利用暑假50天在一超市勤工俭学，被安排销售一款成本为40元/件的新型商销售单价q （元/件）与x 满足：当1≤x ＜25时q=x+60；当25≤x ≤50时． （1）请分析表格中销售量p 与x 的关系，求出销售量p 与x 的函数关系． （2）求该超市销售该新商品第x 天获得的利润y 元关于x 的函数关系式． （3）这50天中，该超市第几天获得利润最大？最大利润为多少？2.某商场在销售旺季临近时 ，某品牌的童装销售价格呈上升趋势，假如这种童装开始时的售价为每件20元，并且每周（7天）涨价2元，从第6周开始，保持每件30元的稳定价格销售，直到11周结束，该童装不再销售。

销售利润问题随着市场经济的发展，销售利润成为企业经营中的重要指标之一。

本文将从销售利润的定义与计算、影响销售利润的因素以及提高销售利润的方法三个方面进行探讨。

一、销售利润的定义与计算销售利润是指企业在销售商品或服务后，从销售收入中减去相关成本后所得到的盈利金额。

它是企业业务活动中的一项核心指标，直接关系到企业的生存与发展。

计算销售利润时，需要考虑各个成本因素。

首先，需要计算销售成本，包括原材料成本、生产成本、人力成本等。

其次，需要考虑销售费用，如广告宣传费用、市场推广费用等。

最后，还需要计算其他费用，如管理费用、税费等。

将这些成本逐项减去销售收入后，即可得到销售利润。

二、影响销售利润的因素1. 市场竞争力：市场竞争力是影响销售利润的重要因素之一。

在市场竞争激烈的情况下，企业往往需要通过降价等方式来吸引消费者，这会直接影响到销售利润的大小。

2. 产品质量与服务：产品质量和服务水平也会对销售利润产生影响。

质量好、服务好的产品往往能够吸引更多的消费者，从而提高销售额和销售利润。

3. 成本管理：成本管理是提高销售利润的关键。

企业需要通过优化生产流程、降低原材料成本、提高劳动生产率等手段来有效控制成本，从而提高利润水平。

4. 销售策略：销售策略的制定对销售利润也有重要影响。

不同的销售策略会导致销售额和销售利润的差异，企业需要根据市场需求与竞争情况来制定相应的销售策略。

三、提高销售利润的方法1. 产品创新：通过产品创新来提高产品差异化，从而获得更高的产品溢价空间，提高销售利润。

2. 成本控制：通过优化生产流程、降低成本等方式来有效控制企业的经营成本，减少浪费，提高销售利润。

3. 市场定位：准确定位自己的目标市场，制定相应的市场营销策略，从而有效提高销售额和销售利润。

4. 售后服务：加强售后服务，提高客户满意度，增加客户的回购率和口碑效应，进而提高销售利润。

5. 供应链管理：优化供应链管理，减少库存积压和物流成本，提高物流配送效率，降低销售利润受损的风险。

一、销售利润问题商品的进货价格叫做进价。

商品预售的价格叫做标价或原价。

商品实际卖出的价格叫做售价。

商品利润=商品售价-商品进价。

商品售价=商品原价（或标价）×折数。

商品利润率=商品利润/商品进价=（商品售价-商品进价）/商品进价。

常见的利润问题有：（一）已知进价、售价、求利润率例1．脑产品的进价是10000元，售价为12000元，此商品的利润率是多少？解：设此商品利润率为x%，根据题意得：（12000-10000）/10000=x%解之得：x=20答：此商品的利润率为20%。

（二）已知进价和利润率，求标价或原价例2．某商品的进价是250元，按标价的9折销售时，利润率为15.2%，商品的标价是多少？解：设商品的标价是x元，根据题意得：（90%x-250）/250=15.2%解之得：x=320答：商品的标价是320元（三）已知进价、标价及利润率，求标价或原价的折数例3．某名牌西装进价是1000元，标价是1500元，某商场要以利润率不低于5%的价格销售，问售货员可以打几折出售此商品？解：设售货员可打x折出售此商品，根据题意得：（1500·x/10-1000）/1000=5%解之得：x=7答：打7折出售该商品。

在这一类求折数的应用题中，以前通常都是设打x折，然后在列式时把售价列为"1500x"，最后x=0.7=7折。

但我认为x=0.7的话，就说明是打0.7折，而不能说是7折，因此这种做法不妥当。

打7折就是原价的7/10，打8折就是原价的8/10。

按照这一原则，列式时我认为应将售价"1500x"列为"1500×x/10",这样才比较合理。

设商品打x折，方程的解x=7，那么商品就是打7折。

这样前后就显得比较一致.（四）已知利润率、标价求进价例4．商场对某一商品作调价，按原价的8折出售，此时商品的利润率是10%，已知商品标价为1375元，求进价。

销售利润问题应用题基本公式：利润＝售价-进价利润率＝利润/进价例题：某商品打7.5折后，商家仍然可得25%的利润。

如果该商品是以每件16.8元的价格进的，为该商品在货架上的标价是多少？用公式：售价＝进价*（1+利润率）本题中，设标价为x元，则售价为：75%*x进价为16.8元，利润率为25%所以75%*x = 16.8*(1+25%) ,解得：x=28（元）练习：1、商品进价为400元，标价为600元，商店要求以利润率不低于5%的售价打折出售，最低可以打几折出售此商品？2、某种商品进价为1600元，按标价的8折出售利润率为10%，问它的标价是多少？3、甲种运动器械进价1200元，按标价1800元的9折出售，乙种跑步器，进价2000元，按标价3200元的8折出售，哪种商品的利润率更高些？4、一批货物，甲把原价降低10元卖，用售价的10%作资金，乙把原价降低20元，用售价的20%作资金，若两人资金一样多，求原价。

5、某商品的售价780元，为了薄利多销，按售价的9折销售再返还30元礼券，此时仍获利10%，此商品的进价是多少元？6、一商店把彩电按标价的九折出售，仍可获利20%，若该彩电的进价是2400元，那么彩电的标价是多少元？7、某商品的标价为165元，若降价以9折出售（即优惠10%），仍可获利10%（相对于进价），那么该商品的进价是多少？8、某商品的进价是2000元，标价为3000元，商店要求以利润率不低于5%的售价打折出售，售货员最低可以打几折出售此商品？9、某种商品进货后，零售价定为每件900元，为了适应市场竞争，商店按零售价的九折降价，并让利40元销售，仍可获利10%（相对于进价），问这种商品的进价为多少元？0、某商场售货员同时卖出两件上衣，每件都以135元售出，若按成本计算，其中一件赢利25%，另一件亏损25%，问这次售货员是赔了还是赚了？1、市场鸡蛋按个数计价，一商贩以每个0.24元购进一批鸡蛋，但在贩运途中，不慎碰坏了12个，剩下的蛋以每个0.28元售出，结果获利11.2元，问商贩当初买进多少鸡蛋？2、某学校准备组织教师和学生去旅游，其中教师22名，现有甲、乙两家旅行社，其定价相同，并且都有优惠条件，甲旅行社表示教师免费，学生按八折收费；乙旅行社表示教师和学生一律按七五折收费，经核算后，甲、乙实际收费相同，问共有多少学生参加旅游？3、某股民将甲、乙两种股票卖出，甲种股票卖出1500元，获利20%，乙种股票也卖出1500元，但亏损20%，该股民在这次交易中是赢利还是亏损？赢利或亏损多少？4、某商店从某公司批发部购100件Axx商品，80件B种商品，共花去2800元，在商店零售时，每件A种商品加价15%，每件B种商品加价10%，这样全部售出后共收入3140元，问A、B两种商品的买入价各为多少元？5、某种商品因换季准备打折出售，如果按定价的七五折出售，将赔25元，而按定价的九折出售，将赚20元，这种商品的定价为多少元？6、一套家具按成本加6成定价出售，后来在优惠条件下，按照售价的72%降低价格售出可得6336元，求这套家具的成本是多少元？这套家具售出后可赚多少元？7、某种商品标价为226元，现打七折出售，仍可获利13%，这钟商品的进价是多少？8、个体户小张，把某种商品按标价的九折出售，仍可获利20%，若按货物的进价为每件24元，求每件的标价是多少元？9、某商品的进价是3000元，标价是4500元（1）商店要求利润不低于5%的售价打折出售，最低可以打几折出售此商品？（2）若市场销售情况不好，商店要求不赔本的销售打折出售，最低可以打几折售出此商品？（3）如果此商品造成大量库存，商店要求在赔本不超过5%的售价打折出售，最低可以打几折售出此商品？思考题：1. 某地生产蔬菜，若在市场上直接销售，每吨利润1000元。