立体几何的向量法(四)——求点到面距离资料
- 格式:doc
- 大小:99.51 KB
- 文档页数:3

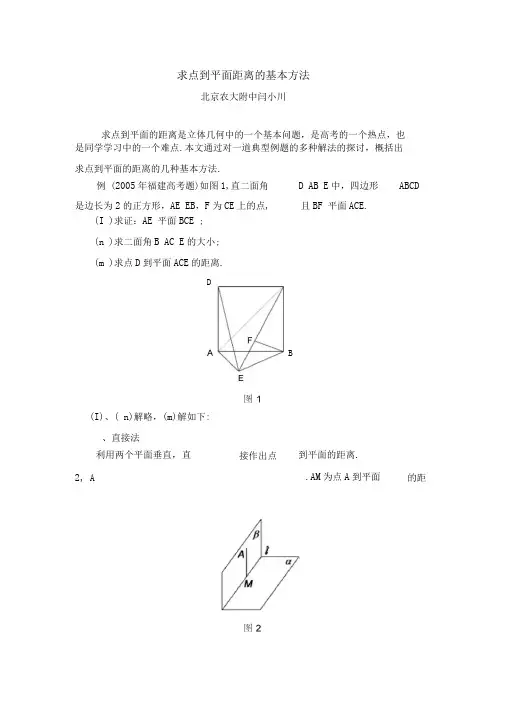
利用两个平面垂直,直接作出点到平面的距离.2, A .AM为点A到平面的距求点到平面距离的基本方法北京农大附中闫小川求点到平面的距离是立体几何中的一个基本问题,是高考的一个热点,也是同学学习中的一个难点.本文通过对一道典型例题的多种解法的探讨,概括出求点到平面的距离的几种基本方法.(I )求证:AE 平面BCE ;(n )求二面角B AC E的大小;(m )求点D到平面ACE的距离.(I)、( n)解略,(m)解如下:、直接法例 (2005年福建高考题)如图1,直二面角 D AB E中,四边形ABCD 是边长为2的正方形,AE EB,F为CE上的点, 且BF 平面ACE.DB解:如图3,过点A 作AG 峑EC ,连结DG,CG ,则平面ADG //平面BCE , •••平面BCE 平面ACE , •••平面ADG 平面ACE ,作DH AG,垂足为H ,则DH 平面ACE.••• DH 是点D 到平面ACE 的距离.二、平行线法,B 为I 上任意一点,AM , BN ,则AM BN . 点A 到平面的距离转化为平行于平面 的直线I 到平面的距离,再转化为直线I 上任意一点B 到平面 的距离.解:如图5,过点D 作DM 屯AE ,连结CM ,则DM //平面ACE , 点D 到平面ACE 的距离转化为直线 DM 到平面ACE 的距离,再转化为点M 到平面ACE 的距离.作MN CE,垂足为N ,在 Rt ADG 中, DHAD DG 2 迈2/3 AG763如图 4, A 1,1 // CB•••平面CEM 平面ACE ,••• MN 平面 ACE ,••• MN 是点M 到平面ACE 的距离.三、斜线法利用平面的斜线及三角形相似,转化为求斜线上的点到平面的距离.如图AOO , A,B l , AM , BN ,若竺 t,则 AM t BN.点 A 到BO平面 的距离转化为求直线I 上的点B 到平面 的距离.解:如图8, BD 与AC 的交点为Q ,即BD 平面ACE Q , ••• DQ BQ ,•••点D 到平面ACE 的距离与点B 到平面ACE 的距离相等. •••平面BCE 平面ACE ,BF 平面ACE , • BF 是点B 到平面ACE 的距离.在 Rt CEM 中,MNEM CM 2 72C E 766、7,lN的一条斜线,A OP , OA l , OP 与 所成的角为A 到平面 的距离为d ,则由斜线和平面所成的角的定义可知,有 d Isin .经过OP 与 垂直的平面与 相交,交线与OP 所成的锐角就是OP 与 所成 的角,这里并不强求要作出A 在 上的射影B ,连结OB 得.解:如图10,v BF 平面ACE , •••平面BDF 平面ACE ,BQF 为DQ 与平面ACE 所成的角为,则点D 到平面ACE 的距离 d DQ sin由(n )知二面角B AC E 的正弦值为,得sin3••• D 到平面ACE 的距离d V2 — 酝33在 Rt BCE 中,BFBC BE 2 迈 2^3CE四、线面角法如图9, OP 为平面屆 3解:女口图 12, •••平面 ACD 平面 ACE AC , DQ 平面 ACD , DQ AC , 设二面角D AC E 的大小为,则点D 到平面ACE 的距离d DQsin由(n )知二面角B AC E 的正弦值为^6,得sin —332P3 ••• D 到平面ACE 的距离d 丘—33五、 二面角法 如图11, 点A到平面的距离AO图10所成二面角的大小为 ,A , AB l , AB a ,d ,则有d as in .也就是二面角的大小,而不强求作出经过AB 的二面角的平面角.B图11六、体积法•••二面角D AB E 为直二面角, ••• E0 丄平面 ABCD.1-AD DC EO• h ——-AE EC 2•••点D 到平面ACE 的距离为沁3B设D 到平面ACE 的距离为h ,V D ACE VE ACD ,h 1SACE h 3SACDE0.AE 平面BCE , ••• AEEC.B解:如图13,过点E 作EOAB 交 AB 于点 0,0E 1.1 22_ 1丘4622J3 3七、向量法解:如图14,以线段AB的中点为原点0, 0E所在直线为x轴,AB所在直线为y轴,过0点平行于AD的直线为z轴,建立空间直角坐标系AE 平面BCE,BE 平面BCE,• •• AE BE ,在Rt AEB中,AB 2,0为AB的中点,••• 0E 1,••• A(0, 1,0),E(1,0,0),C(0,1,2).AE (1,1,0), AC (0,2,2).设平面ACE的一个法向量为n (X, y, z),n0,即x y 0,n 0, 2y 2z 0.令X 1,得n (1, 1,1)是平面ACE的一个法向量.练习: 0 xyz,则AC解得yzX ,AD z AD 2 AD (0,0,2) ACE d |AD||cos AD,n|AD n| 22733 3如图15,已知ABCD是边长为4的正方形,E、F 分别是AB、AD的中点,图14GC垂直于ABCD所在平面,且GC 2,求点B到平面EFG的距离.(答案:2/1)11 )CBE。

点到平面的距离若干求法1定义法求点到平面距离(直接法)定义法求点到平面距离是根据点到平面的定义直接作出或者寻找出点与平面间的垂线段,进而根据平面几何的知识计算垂线段长度而求得点与平面距离的一种常用方法.定义法求点到平面距离的关键在于找出或作出垂线段,而垂线段是由所给点及其在平面射影间线段,应而这种方法往往在很多时候需要找出或作出点在平面的射影。
以下几条结论常常作为寻找射影点的依据:(1)两平面垂直的性质定理:如果两个平面互相垂直,那么在一个平面内垂直于他们交线的直线垂直于另一个平面。
(2)如果一个角所在平面外一点到角的两边的距离相等,那么这个点在该平面内的射影在这个角的角平分线所在的直线上。
(3)经过一个角的顶点引这个角所在平面的斜线。
设斜线和已知两边的夹角为锐角且相等,则这条斜线在这个平面的射影是这个角的角平分线.(4)若三棱锥的三条棱长相等,则顶点在底面上的射影是底面三角形的外心。
例如图4所示,所示的正方体ABCD A B C D''''-棱长为a,求点A'到平面AB D''的距离。
(注:本文所有解法均使用本例)图4解法一(定义法):如图5所示,连结交B D ''于点E ,再连结AE ,过点A '作A H '垂直于AE ,垂足为H ,下面证明A H '⊥平面AB D ''。
图5AA '⊥平面A B C D ''''∴B D ''⊥AA ' 又在正方形A B C D ''''中,对角线B D A C ''''⊥,且AA A C A ''''=AA '⊂平面AA E ', A C ''⊂平面AA E '∴由线面垂直的判定定理知道B D ''⊥平面AA E 'A H '⊂平面AA E '∴A H '⊥B D ''又由A H '的作法知道A H '⊥AE ,且有B D ''AE E =,B D ''⊂平面AB D '',AE ⊂平面AB D ''∴由线面垂直的判定定理知道A H '⊥平面AB D ''根据点到平面距离定义,A H '的长度即为点A '到平面AB D ''的距离,下面求A H '的长度。
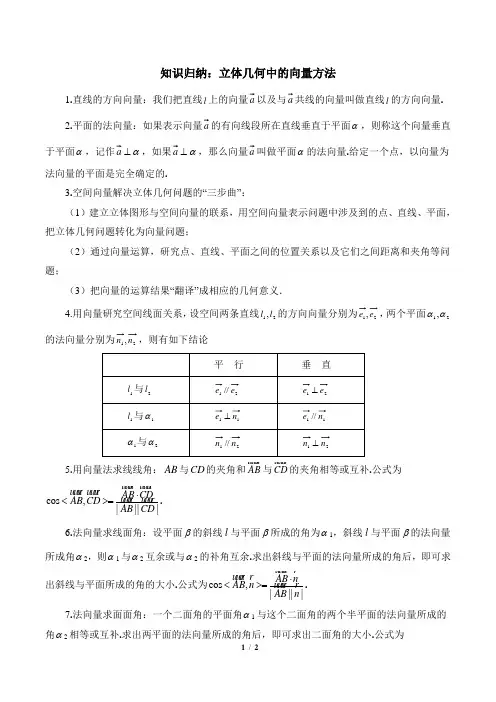
知识归纳:立体几何中的向量方法1.直线的方向向量:我们把直线l 上的向量以及与共线的向量叫做直线l 的方向向量.2.平面的法向量:如果表示向量a 的有向线段所在直线垂直于平面α,则称这个向量垂直于平面α,记作α⊥,如果α⊥,那么向量叫做平面α的法向量.给定一个点,以向量为法向量的平面是完全确定的.3.空间向量解决立体几何问题的“三步曲”:(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及到的点、直线、平面,把立体几何问题转化为向量问题;(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题;(3)把向量的运算结果“翻译”成相应的几何意义.4.用向量研究空间线面关系,设空间两条直线21,l l 的方向向量分别为21,e e ,两个平面21,αα的法向量分别为21,n n ,则有如下结论5.用向量法求线线角:AB 与CD 的夹角和AB 与CD 的夹角相等或互补.公式为cos ,||||AB CDAB CD AB CD ⋅<>=.6.法向量求线面角:设平面β的斜线l 与平面β所成的角为α1,斜线l 与平面β的法向量所成角α2,则α1与α2互余或与α2的补角互余.求出斜线与平面的法向量所成的角后,即可求出斜线与平面所成的角的大小.公式为cos ,||||AB nAB n AB n ⋅<>=.7.法向量求面面角:一个二面角的平面角α1与这个二面角的两个半平面的法向量所成的角α2相等或互补.求出两平面的法向量所成的角后,即可求出二面角的大小.公式为121212cos ,||||n n n n n n ⋅<>=.8.向量法求异面直线间的距离:设分别以这两异面直线上任意两点为起点和终点的向量为,与这两条异面直线都垂直的向量为,则两异面直线间的距离是在方向上的正射影向量的模.公式为d 9.向量法求点到平面的距离:设分别以平面外一点P 与平面内一点M 为起点和终点的向量为,平面的法向量为,则P 到平面的距离d 等于在方向上正射影向量的模.公式为||n d =。

立体几何中的法向量现行高中数学教科书第二册(下B)第九章提到了法向量的定义:如果向量⊥平面α,那么向量a叫做平面α的法向量。
但是对于法向量在立体几何中的运用却没有详细介绍,其实灵活运用法向量去求解某些常见的立几问题如“求点到平面的距离”、“求异面直线间的距离”、“求直线与平面所成的角”、“求二面角的大小”、“证明两平面平行或垂直”等是比较简便的,现介绍如下:一、求点到平面的距离设A是平面α外一点,AB是α的一条斜线,交平面α于点B,而n是平面α的法向量,那么向量BA在n方向上的正射影长就是点A到平面α的距离h,所以h==(1)例1:已知棱长为1的正方体ABCD-A1B1C1D1中,E、F分别是B1C1和C1D1的中点,求点A1到平面DBEF的距离。
解:如图建立空间直角坐标系,=(1,1,0),=(0,21,1),1DA=(1,0,1)设平面DBEF的法向量为n=(x,y,z),则有:n0=⋅DB即x+y=0=⋅21y+z=0令x=1, y=-1, z=21, 取n=(1,-1,21),则A1到平面DBEF的距离1==h注:此题A1在平面DBEF的射影难以确定,给求解增加难度,若利用(1)式求解,关键是求出平面DBEF的法向量。
法向量的求解有多种,可直接利用向量积,在平面内找两个不共线的向量,例如DB和DF,那么n=DB×DF。
但高中教材未曾涉及向量积,这里根据线面垂直的判定定理,设=(x,y,z),通过建立方程组求出一组特解。
二、求异面直线间的距离假设异面直线a、b,平移直线a至a*且交b于点A,那么直线a*和b确定平面α,且直线a∥α,设是平面α的法向量,那么⊥,⊥。
所以异面直线a和b的距离可以转化为求直线a 上任一点到平面α的距离,方法同例1。
例2:已知棱长为1的正方体ABCD -A 1B 1C 1D 1解:如图建立空间直角坐标系,则AC =(-1,1,0),1DA =(1,0,1) 连接A 1C 1,则A 1C 1∥AC,设平面A 1C 1D 的法向量为n =(x ,y ,z ),0=⋅由 可解得=(1,1,-1),又1AA =(0,0,1)01=⋅DA所以点A 到平面A 1C 1D 的距离为33==h ,即直线DA 1和AC 间的距离为33。



知识图谱-利用向量方法求线线角与线面角-利用向量方法求二面角-利用向量方法求距离直线与直线的夹角直线与平面的夹角向量法求二面角含有参数的二面角求法点到点线面的距离线与线面的距离第03讲_立体几何中的向量方法错题回顾利用向量方法求线线角与线面角知识精讲一.用向量方法求线线角与线面角1.两条异面直线所成的角(1)定义:设是两条异面直线,过空间任一点作直线,则与所夹的锐角或直角叫做所成的角;(2)范围:两异面直线所成的角的取值范围是;(3)向量求法:设直线的方向向量为,其夹角为,则有.2.直线与平面所成的角(1)定义:直线与平面所成的角,是指直线与它在这个平面内的射影所成的角;(2)斜线和它在平面内的射影所成的角,是斜线和这个平面内所有直线所称角中最小的角;(3)范围:直线和平面所成角的取值范围是;(4)向量求法:设直线的方向向量为,平面的法向量为,直线与平面所成的角为,与的夹角为,则有或,此外还可以根据定义得到直线与平面所成的角如下图:.三点剖析一.方法点拨1.在用向量法求两条直线的夹角时,如果两条直线方向向量的夹角余弦值是负数时,则取绝对值,要正数,因为两条直线的夹角范围是.2.在用向量法求直线与平面的夹角时,如果算出的是负值时,则线面角的正弦值也需要取正值.题模精讲题模一直线与直线的夹角例1.1、已知是异面直线,,且,则所成的角是( )B、A、C、D、例1.2、如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,A B=,BC=1,PA=2,E为PD的中点.(Ⅰ)求直线AC与PB所成角的余弦值;(Ⅱ)在侧面PAB内找一点N,使NE⊥面PAC,并求出N点到AB和AP的距离.例1.3、如图所示,正四面体的高的中点为的中点为.(1)求证:两两垂直;(2)求.题模二直线与平面的夹角例2.1、若斜线段的长度是它在平面内的射影长的倍,则与所成角的正切值为__________.例2.2、直三棱柱中,底面是等腰直角三角形,,侧棱,分别是的中点,点在平面上的射影是.求与平面所成角的大小(结果用正弦值表示).例2.3、已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=AC=AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.(Ⅰ)证明:CM⊥SN;(Ⅱ)求SN与平面CMN所成角的大小.例2.4、如图,在三棱锥中,底面,,为的中点,为的中点,,.(1)求证:平面;(2)求与平面成角的正弦值;(3)设点在线段上,且,平面,求实数的值.随堂练习随练1.1、若异面直线的方向向量分别是,则异面直线与的夹角的余弦值等于( )A、B、C、D、随练1.2、在棱长为1的正方体中,分别是的中点,在棱上,且,的中点,应用空间向量方法求解下列问题。


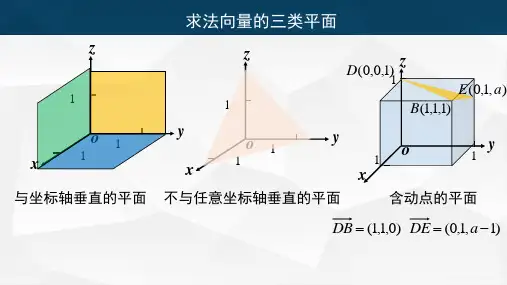
立体几何中几类典型问题的向量解法空间向量的引入为求立体几何的空间角和距离问题、证线面平行与垂直以及解决立体几何的探索性试题提供了简便、快速的解法。
它的实用性是其它方法无法比拟的,因此应加强运用向量方法解决几何问题的意识,提高使用向量的熟练程度和自觉性,注意培养向量的代数运算推理能力,掌握向量的基本知识和技能,充分利用向量知识解决图形中的角和距离、平行与垂直问题。
一、利用向量知识求点到点,点到线,点到面,线到线,线到面,面到面的距离(1)求点到平面的距离除了根据定义和等积变换外还可运用平面的法向量求得,方法是:求出平面的一个法向量的坐标,再求出已知点P 与平面内任一点M 构成的向量MP u u u r的坐标,那么P 到平面的距离cos ,n MP d MP n MP n •=•<>=r u u u r u u u r r u u u rr(2)求两点,P Q 之间距离,可转化求向量PQ uuu r的模。
(3)求点P 到直线AB 的距离,可在AB 上取一点Q ,令,AQ QB PQ AB λ=⊥u u u r u u u r u u u r u u u r或PQ u u u r 的最小值求得参数λ,以确定Q 的位置,则PQ u u u r为点P 到直线AB 的距离。
还可以在AB 上任取一点Q 先求<AB ,cos ,再转化为><,sin ,则PQ u u u r><,sin 为点P 到直线AB 的距离。
(4)求两条异面直线12,l l 之间距离,可设与公垂线段AB 平行的向量n r,,C D 分别是12,l l 上的任意两点,则12,l l 之间距离CD nAB n•=u u u r r r例1:设(2,3,1),(4,1,2),(6,3,7),(5,4,8)A B C D --,求点D 到平面ABC 的距离例2:如图,正方形ABCD 、ABEF 的边长都是1,而且平面ABCD 、ABEF 互相垂直。
立体几何中的向量方法------距离问题一、求点到平面的距离 1.(一般)传统方法:利用定义先作出过这个点到平面的垂线段, 再计算这个垂线段的长度; 2.还可以用等积法求距离; 3.向量法求点到平面的距离.在PAO Rt ∆中,θθsin ||||sin AP d AP =⇒=又|||||sin n AP n AP =θ||n d =∴(其中AP 为斜向量,n 为法向量)二、直线到平面的距离 转化为点到线的距离:||n d =(其中AP 为斜向量,n 为法向量)三、平面到平面的距离也是转化为点到线的距离:||n d =AP 为斜向量,n 为法向量)四、异面直线的距离如图,异面直线也是转化为点到线的距离:||n d =(其中AP 为两条异面直线上各取一点组成的向量,n 是与b a ,都垂直的向量) 例1.如图,在正方体1111D C B A ABCD -中,棱长为1,E 为11D C 的中点,求下列问题: (1) 求1B 到面BE A 1的距离;解:如图,建立空间直角坐标系xyz D -,则•αOP),1,1,0(),0,21,1(11-=-=∴B A E A ,设),,(z y x n =为面BE A 1的法向量则⎪⎩⎪⎨⎧=-=+-⇒⎪⎩⎪⎨⎧=⋅=⋅0210011z y y x B A n E A n 取1=x ,得2,2==z y ,)2,2,1(=∴n选点1B 到面BE A 1的斜向量为)0,1,0(11=B A 得点1B 到面BE A 1的距离为32||11==n d (2)求C D 1到面BE A 1的距离;)2,2,1()1(:1=n BE A 的法向量知平面由解)0,0,1(11=A D 斜向量 311111==∴nn A D d BE A D 的距离为到面点 (3) 求面DB A 1与面11CB D 的距离;)1,1,1(:11-==AC n BD A 的法向量为由图知平面解)0,0,1(11=A D 又斜向量 311111==∴nn A D d BD A D 的距离为到面点 33111的距离为与即面CB D BD A (4) 求异面直线B D 1与E A 1的距离.xyz D -系如图建立空间直角坐标解:)1,1,1(),0,21,1(11-=-=∴B D E Axxxx111(0,0,1),(1,1,0),(1,0,1),(0,,1)2D B AE 则B D E A z y x n 11,),,(是与设=都垂直的向量,则⎩⎨⎧==⇒⎪⎩⎪⎨⎧=⋅=⋅x z x y B D n E A n 320011,取1=x ,得一个法向量为)3,2,1(=n 选11BD E A 与的两点向量)0,0,1(11=A D得11BD E A 与的距离为1414||11==n n A D d 练习1:1.如图在直三棱柱111C B A ABC -中,1==BC AC ,∠ACB 面BC A 1的距离.2.已知棱长为1的正方体1111D C B A ABCD -,求平面11C DA 和平面C AB 1间的距离3.已知棱长为1的正方体1111D C B A ABCD -,求直线1DA 和AC 间的距离。
选修2-1 第三章 空间向量与立体几何§3.2.3 利用法向量解决立体几何中的线面角,求点到平面的距离问题班级 姓名一、目标导引1.会利用法向量解决立体几何中的线面角; 2.会求点到平面的距离问题. 二、教学过程题型一 利用法向量解决立体几何中的线面角 【知识准备】如图,已知PA 为平面α的一条斜线,n 为平面α的一个法向量,过P 作平面α的垂线PO ,连结OA 则PAO ∠为斜线PA 和平面α所成的角,记为θ,则有 ,OP AP θ+<>= ,由此,在Rt AOP ∆中,sin |sin(,)|2OP AP πθ=-<>= = .【注意】直线与平面所成的角的范围是θ∈例1 如图所示,三棱柱ABC -A 1B 1C 1中,CA =CB ,AB =AA 1,∠BAA 1=60°. (1)证明:AB ⊥A 1C ;(2)若平面ABC ⊥平面AA 1B 1B ,AB =CB ,求直线A 1C 与平面BB 1C 1C 所成角的正弦值.11【变式1】在正三棱柱ABC -A 1B 1C 1中,已知AB =1,D 在棱BB 1上,且BD =1,求AD 与平面AA 1C 1C 所成角的正弦值.C1题型二 利用法向量求点到平面的距离问题【知识准备】设P 是平面α外一点,P A 是α的一条斜线,交平面α于点A , n 是平面α的法向量,那么向量PA 在n 方向上的正射影长OP 就是点A 到平面α的距离h ,在Rt AOP ∆中,OP = = .例2 已知正方体ABCD -A 1B 1C 1D 1的棱长为2,E ,F ,G 分别是C 1C ,D 1A 1,AB 的中点,求点A 到平面EFG 的距离.A1【课时作业027】班级 姓名 作业等级A 级 学业水平达标1.在正方体ABCD -A 1B 1C 1D 1中,求直线BC 1与平面A 1BD 所成的角的正弦值.【答案:63】12.正三角形ABC 与正三角形BCD 所在的平面互相垂直,求直线CD 与平面ABD 所成角的正弦值.【答案:155】3.如图所示,在棱长为a 的正方体ABCD -A 1B 1C 1D 1中,E ,F 分别是BC ,A 1D 1的中点.(1)求直线A 1C 与DE 所成角的余弦值;【答案:1515】(2)求直线AD 与平面B 1EDF 所成角的余弦值;【答案:33】(3)求平面B 1EDF 与平面ABCD 所成锐二面角的余弦值.【答案:66】B 级 应试能力达标4.如图,在四棱柱ABCD -A 1B 1C 1D 1中,侧棱AA 1⊥底面ABCD ,AB ∥DC ,AA 1=1,AB =3k ,AD =4k ,BC =5k ,DC =6k (k >0).(1)求证:CD ⊥平面ADD 1A 1; (2)若直线AA 1与平面AB 1C 所成角的正弦值为67,求k 的值.(答案k=1)5.如图,四棱锥P -ABCD 中,P A ⊥底面ABCD ,AB ∥CD ,AD =CD =1,∠BAD =120°,∠ACB =90°.(1)求证:BC ⊥平面P AC ;(2)若二面角D -PC -A 的余弦值为55,求点A 到平面PBC 的距离.(答案32)1选修2-1 第三章 空间向量与立体几何§3.2.3 利用法向量解决立体几何中的线面角,求点到平面的距离问题一、目标导引1.利用法向量解决立体几何中的线面角;2.求点到平面的距离问题二、教学过程题型一 利用法向量解决立体几何中的线面角 【知识准备】如图,已知PA 为平面α的一条斜线,n 为平面α的一个法向量,过P 作平面α的垂线PO ,连结OA 则PAO ∠为斜线PA 和平面α所成的角,记为θ,则有 ,OP AP θ+<>= ,由此,在Rt AOP ∆中,sin |sin(,)|2OP AP πθ=-<>= =【注意】直线与平面所成的角的范围是θ∈例1 如图所示,三棱柱ABC -A 1B 1C 1中,CA =CB ,AB =AA 1,∠BAA 1=60°. ①证明:AB ⊥A 1C ;②若平面ABC ⊥平面AA 1B 1B ,AB =CB ,求直线A 1C 与平面BB 1C 1C 所成角的正弦值. ①证明 取AB 的中点O ,连接OC ,OA 1,A 1B . ∵CA =CB ,∴OC ⊥AB . 由于AB =AA 1,∠BAA 1=60°, 故△AA 1B 为等边三角形,∴OA 1⊥AB .∵OC ∩OA 1=O , ∴AB ⊥平面OA 1C .又A 1C ⊂平面OA 1C ,故AB ⊥A 1C .②解 由①知OC ⊥AB ,OA 1⊥AB .又平面ABC ⊥平面AA 1B 1B ,交线为AB ,OC ⊂平面ABC , 所以OC ⊥平面AA 1B 1B ,故OA ,OA 1,OC 两两垂直.以O 为坐标原点,OA ,OA 1,OC 所在直线分别为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系Oxyz .设AB =2,则A (1,0,0),A 1(0,3,0), C (0,0,3),B (-1,0,0),则BC →=(1,0,3),BB 1→=AA 1→=(-1,3,0), A 1C -→=(0,-3,3). 设n =(x ,y ,z )是平面BB 1C 1C 的法向量,则⎩⎪⎨⎪⎧n ·BC →=0,n ·BB 1→=0,即⎩⎨⎧x +3z =0,-x +3y =0,可取n =(3,1,-1).故cos 〈n ,A 1C -→〉=n ·A 1C -→|n ||A 1C -→|=-105,∴A 1C 与平面BB 1C 1C 所成角的正弦值为105.【变式1】在正三棱柱ABC -A 1B 1C 1中,已知AB =1,D 在棱BB 1上,且BD =1,求AD 与平面AA 1C 1C 所成角的正弦值解析 取AC 的中点E ,连接BE ,则BE ⊥AC ,以B 为坐标原点,BE ,BB 1所在直线分别为x 轴,z 轴,建立如图所示的空间直角坐标系Bxyz ,则A ⎝⎛⎭⎫32,12,0,D (0,0,1),B (0,0,0),E ⎝⎛⎭⎫32,0,0,则AD →=⎝⎛⎭⎫-32,-12,1,BE →=⎝⎛⎭⎫32,0,0. ∵平面ABC ⊥平面AA 1C 1C ,平面ABC ∩平面AA 1C 1C =AC ,BE ⊥AC ,BE ⊂平面ABC , ∴BE ⊥平面AA 1C 1C ,∴BE →=⎝⎛⎭⎫32,0,0为平面AA 1C 1C 的一个法向量.设AD 与平面AA 1C 1C 所成角为α,∵cos 〈AD →,BE →〉=-64,∴sin α=|cos 〈AD →,BE →〉|=64.题型二 利用法向量求点到平面的距离问题【知识准备】设P 是平面α外一点,P A 是α的一条斜线,交平面α于点A ,n 是平面α的法向量,那么向量PA 在n 方向上的正射影长OP 就是点A 到平面α的距离h ,在Rt AOP ∆中,OP = =例2 已知正方体ABCD -A 1B 1C 1D 1的棱长为2,E ,F ,G 分别是C 1C ,D 1A 1,AB 的中点,求点A 到平面EFG 的距离.解 以D 为坐标原点,DA ,DC ,DD 1所在直线分别为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系Dxyz , 则A (2,0,0),E (0,2,1),F (1,0,2),G (2,1,0).所以AG →=(0,1,0),GE →=(-2,1,1),GF →=(-1,-1,2).设n =(x ,y ,z )是平面EFG 的法向量,点A 到平面EFG 的距离为d , 则⎩⎪⎨⎪⎧n ·GE →=0,n ·GF →=0,所以⎩⎪⎨⎪⎧ -2x +y +z =0,-x -y +2z =0,所以⎩⎪⎨⎪⎧x =z ,y =z .令z =1,此时n =(1,1,1),所以d =|AG →·n ||n |=13=33,即点A 到平面EFG 的距离为33.A 级 学业水平达标1.在正方体ABCD -A 1B 1C 1D 1中,求直线BC 1与平面A 1BD 所成的角的正弦值. 【答案:63】解析 以D 为坐标原点,DA →,DC →,DD 1→所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系Dxyz .设正方体的棱长为1,则D (0,0,0),A 1(1,0,1),B (1,1,0),C 1(0,1,1),A (1,0,0),∴BC 1→=(-1,0,1),AC 1→=(-1,1,1),A 1B -→=(0,1,-1), A 1D -→=(-1,0,-1).∴AC 1→·A 1B -→=1-1=0,AC 1→·A 1D -→=1-1=0.∴AC 1⊥A 1B ,AC 1⊥A 1D .又A 1B ∩A 1D =A 1,且A 1B ,A 1D ⊂平面A 1BD ,∴AC 1⊥平面A 1BD . ∴AC 1→是平面A 1BD 的一个法向量.∴cos 〈BC 1→,AC 1→〉=BC 1→·AC 1→|BC 1→||AC 1→|=1+12×3=63.2.正三角形ABC 与正三角形BCD 所在的平面互相垂直,求直线CD 与平面ABD 所成角的正弦值.解析:取BC 的中点O ,连接AO ,DO ,建立如图所示的空间直角坐标系O -xyz .设BC =1,A ⎝⎛⎭⎫0,0,32,B ⎝⎛⎭⎫0,-12,0,C ⎝⎛⎭⎫0,12,0,D ⎝⎛⎭⎫32,0,0,所以BA ―→=⎝⎛⎭⎫0,12,32, BD ―→=⎝⎛⎭⎫32,12,0,CD ―→=⎝⎛⎭⎫32,-12,0. 设平面ABD 的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧n ·BA ―→=0,n ·BD ―→=0,所以⎩⎨⎧12y +32z =0,32x +12y =0,取x =1,则y=-3,z =1,所以n =(1,-3,1),所以cos 〈n ,CD ―→=32+325×1=155,因此直线CD 与平面ABD 所成角的正弦值为155.3.如图所示,在棱长为a 的正方体ABCD -A 1B 1C 1D 1中,E ,F 分别是BC ,A 1D 1的中点.(1)求直线A 1C 与DE 所成角的余弦值;【答案:1515】(2)求直线AD 与平面B 1EDF 所成角的余弦值;【答案:33】(3)求平面B 1EDF 与平面ABCD 所成锐二面角的余弦值.【答案:66】解 以A 为坐标原点,分别以AB ,AD ,AA 1所在直线为x 轴,y 轴,z 轴,建立空间直角坐标系Axyz . 则A 1(0,0,a ),C (a ,a,0),D (0,a,0),E ⎝⎛⎭⎫a ,a2,0, (1) A 1C -→=(a ,a ,-a ),DE →=⎝⎛⎭⎫a ,-a 2,0,∴cos 〈A 1C -→,DE →〉=A 1C -→·DE →|A 1C -→||DE →|=1515,故A 1C 与DE 所成角的余弦值为1515.(2)连接DB 1,∵∠ADE =∠ADF ,∴AD 在平面B 1EDF 内的射影在∠EDF 的平分线上.又B 1EDF 为菱形,∴DB 1为∠EDF 的平分线,故直线AD 与平面B 1EDF 所成的角为∠ADB 1.由DA →=(0,-a,0),DB 1→=(a ,-a ,a ),∴cos 〈DA →,DB 1→〉=DA →·DB 1→|DA →||DB 1→|=33,又直线与平面所成角的范围是⎣⎡⎦⎤0,π2, (3)由已知得ED →=⎝⎛⎭⎫-a ,a 2,0, EB 1→=⎝⎛⎭⎫0,-a 2,a ,平面ABCD 的一个法向量为m =AA 1→=(0,0,a ).设平面B 1EDF的一个法向量为n =(1,y ,z ),由⎩⎪⎨⎪⎧n ·ED →=0,n ·EB 1→=0,得⎩⎪⎨⎪⎧y =2,z =1,∴n =(1,2,1),∴cos 〈n ,m 〉=m ·n |m ||n |=66,∴平面B 1EDF与平面ABCD 所成锐二面角的余弦值为66. B 级 应试能力达标4.如图,在四棱柱ABCD -A 1B 1C 1D 1中,侧棱AA 1⊥底面ABCD ,AB ∥DC ,AA 1=1,AB =3k ,AD =4k ,BC =5k ,DC=6k (k >0).(1)求证:CD ⊥平面ADD 1A 1; (2)若直线AA 1与平面AB 1C 所成角的正弦值为67,求k 的值.[解] (1)证明:取CD 的中点E ,连接BE .∵AB ∥DE ,AB =DE =3k , ∴四边形ABED 为平行四边形,∴BE ∥AD 且BE =AD =4k . 在△BCE 中,∵BE =4k ,CE =3k ,BC =5k , ∴BE 2+CE 2=BC 2,∴∠BEC =90°,即BE ⊥CD .又BE ∥AD ,∴CD ⊥AD . ∵AA 1⊥平面ABCD ,CD ⊂平面ABCD ,∴AA 1⊥CD .又AA 1∩AD =A ,∴CD ⊥平面ADD 1A 1.(2)以D 为坐标原点,DA ―→,DC ―→,DD 1―→的方向分别为x 轴、y 轴、z 轴的正方向建立如图所示的空间直角坐标系,则A (4k,0,0),C (0,6k,0),B 1(4k,3k,1),A 1(4k,0,1),∴AC ―→=(-4k,6k,0),AB 1―→=(0,3k,1),AA 1―→=(0,0,1).设平面AB 1C 的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧AC ―→·n =0,AB 1―→·n =0,即⎩⎪⎨⎪⎧-4kx +6ky =0,3ky +z =0.取y =2,可得平面AB 1C 的一个法向量为n =(3,2,-6k ).设AA 1与平面AB 1C 所成的角为θ,则sin θ=|cos 〈AA 1―→,n 〉|=|AA 1―→·n ||AA 1―→|·|n |=|-6k |36k 2+13=67,解得k =1.故k 的值为1. 5.如图,四棱锥P -ABCD 中,P A ⊥底面ABCD ,AB ∥CD ,AD =CD =1,∠BAD =120°,∠ACB =90°.(1)求证:BC ⊥平面P AC ;(2)若二面角D -PC -A 的余弦值为55,求点A 到平面PBC 的距离.解:(1)证明:∵P A ⊥底面ABCD ,BC ⊂平面ABCD ,∴P A ⊥BC ,∵∠ACB =90°,∴BC ⊥AC ,又P A ∩AC =A , ∴BC ⊥平面P AC .(2)设AP =h ,取CD 的中点E ,则AE ⊥CD ,∴AE ⊥AB .又P A ⊥底面ABCD ,∴P A ⊥AE ,P A ⊥AB ,故建立如图所示的空间直角坐标系,则A (0,0,0),P (0,0,h ),C ⎝⎛⎭⎫32,12,0,D ⎝⎛⎭⎫32,-12,0,B (0,2,0),PC ―→=⎝⎛⎭⎫32,12,-h ,DC ―→=(0,1,0),设平面PDC 的法向量n 1=(x 1,y 1,z 1),则⎩⎪⎨⎪⎧ n 1·PC ―→=0,n 1·DC ―→=0,即⎩⎪⎨⎪⎧32x 1+12y 1-hz 1=0,y 1=0,取x 1=h ,∴n 1=⎝⎛⎭⎫h ,0,32.由(1)知平面P AC 的一个法向量为BC ―→=⎝⎛⎭⎫32,-32,0,∴|cos 〈n 1,BC ―→〉|=32h h 2+34×3=55,解得h =3, 同理可求得平面PBC 的一个法向量n 2=(3,3,2),所以,点A 到平面PBC 的距离为 d =|AP ―→·n 2||n 2|=234=32.。
求点到平面的距离的新方法——向量法
方义成
【期刊名称】《中学数学研究》
【年(卷),期】2005(000)003
【摘要】求点到平面的距离是高中数学中的一个重要知识点,也是一个难点,求解这类问题往往是利用一些技巧(如利用体积相等)来计算的,本文介绍一个求点到平面距离的新方法——向量法。
【总页数】1页(P36)
【作者】方义成
【作者单位】深圳市上海教科院福田实验学校,518000
【正文语种】中文
【中图分类】G633
【相关文献】
1.对“垂面法”求点到平面距离问题的探究 [J], 叶保国
2.对"垂面法"求点到平面距离问题的探究 [J], 叶保国
3.用公式法求立体几何中点到平面的距离 [J], 许乐灵
4.利用向量法求点到平面距离的利与弊 [J], 胡玉莲
5.利用空间向量求点到平面的距离 [J], 张怡临
因版权原因,仅展示原文概要,查看原文内容请购买。