当前位置：文档之家 › 最新46自感和互感

最新46自感和互感

  • 格式：ppt
  • 大小：2.21 MB
  • 文档页数：28

下载文档原格式

  / 28

合集下载

46互感和自感PPT课件

46互感和自感PPT课件
2.自感电动势的方向：增反减同 3.自感电动势的大小:自感电动势正比于电流变化率
E L • I t
4.自感系数： L 简称自感或电感 反映线圈自身
实验表明，线圈越长，越粗，匝数越多， 自感系数越大。
另外，带有铁芯的线圈的自感系数比没
有铁芯时大得多。
（ ）A
A．灯A立即熄灭 B．灯A慢慢熄灭 C．灯A突然闪亮一下再慢慢熄灭 D．灯A突然闪亮一下再突然熄灭
A
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
You Know, The More Powerful You Will Be
（2）自感系数的单位：亨利，简称 亨 符号是 H
常用单位：毫亨（m H） 微亨（μH）
四、磁场的能量
思考：在断电自感的实验中，为什么开关断开 后，灯泡的发光会持续一段时间？甚至会比 原来更亮？试从能量的角度加以讨论。
开关闭合时线圈中有电流，电流产生磁场， 能量储存在磁场中.
开关断开时，线圈作用相当于电源，把磁场 中的能量转化成电能。
结束语
感谢聆听
不足之处请大家批评指导
Please Criticize And Guide The Shortcomings
讲师：XXXXXX XX年XX月XX日
4.6 互感和自感
一、互感现象
1、当一个线圈中电流变化，在另一个线圈中产 生感应电动势的现象，称为互感。互感现象中 产生的感应电动势，称为互感电动势。
2、互感现象不仅发生于绕在同一铁芯上的两个 线圈之间,且可发生于任何两个相互靠近的电 路之间.

4-6自感和互感PPT课件

4-6自感和互感PPT课件

在国际单位制中是亨利，简称亨，符 号是H。 常用的单位还有豪亨（mH)和微亨 （μH） 1H=103 mH=106 μH
如果通过线圈的电流在1秒内改变1安培时，产生的电动 势是1伏特，这个线圈的自感系数就是1亨利。
1 应用： 在交流电路中、在各种用电设备 和无线电技术中有着广泛的应用。如日光灯 的镇流器，LC振荡电路等。 2 防治：在切断自感系数很大、电流很强的 电路的瞬间，产生很高的电动势，形成电弧， 在这类电路中应采用特制的开关。
2 在图-1接通Ｓ，B线圈会不会产生 感应电动势？为什么? 3 在图-2中接通Ｓ，线圈会不会产生 感应电动势？为什么?
A
S
图—2
这种由于导体自身的电流变化 所产生的电磁感应现象是一种 特殊的电磁感应现象
由于导体本身的电流 变化而产生的电磁感应 现象叫自感现象。
通 电 自 感
过 会 儿 亮 呢 ?
L
a
A
b
L
a
b
再看一遍
返回题目
L
a
b
返回题目
例题1
如图所示，L为一个纯电感线圈（直流电阻为零），A为一个灯泡，下列说 法正确的是：（ ）
B
A．开关S接通瞬间无电流通过灯泡
B．开关S接通后，电路稳定时，无电流通过灯泡 C．开关S断开瞬间无电流通过灯泡 D．开关S接通瞬间及接通稳定后，灯泡有由a到b的电流， 而在开关S断开瞬间，灯泡中有从b到a的电流
实例
如图所示，由于两 根平行导线中的电流方 向相反，它们的磁场可 以互相抵消，从而可以 使自感现象的影响减弱 到可以忽略的程度。
自感现象
自 感 现 象
大小:E=LΔI/Δt 作用：总是阻碍电流变化
自感电动势E

4.6 互感和自感

4.6 互感和自感

在法拉第的实验中两个线圈并没有用导 线连接，当一个线圈中的电流变化时， 线连接，当一个线圈中的电流变化时，在另 一个线圈中为什么会产生感应电动势呢？ 一个线圈中为什么会产生感应电动势呢？
一、互感现象
当一个线圈中电流变化， 1、 当一个线圈中电流变化，在另一个线圈中产生 感应电动势的现象，称为互感。互感现象中产生 感应电动势的现象，称为互感。 互感 的感应电动势，称为互感电动势 互感电动势。 的感应电动势，称为互感电动势。 2、互感现象不仅发生于绕在同一铁芯上的两个线圈 之间,且可发生于任何两个相互靠近的电路之间 且可发生于任何两个相互靠近的电路之间. 之间 且可发生于任何两个相互靠近的电路之间 3、利用互感现象，可以把能 利用互感现象， 量从一个线圈传递到另一个 线圈。因此，互感现象在电 线圈。因此， 工技术和电子技术中有广泛 的应用。 的应用。
三、自感系数
1、自感电动势的大小：与电流的变化率成正比 自感电动势的大小：
2、自感系数 L－简称自感或电感 （1）决定线圈自感系数的因素： 决定线圈自感系数的因素：
I E=L t
实验表明，线圈越大，越粗，匝数越多， 实验表明，线圈越大，越粗，匝数越多，自感 系数越大。另外， 系数越大。另外，带有铁芯的线圈的自感系数比 没有铁芯时大得多。 没有铁芯时大得多。 （2）自感系数的单位：亨利，简称亨，符号是 H。 自感系数的单位：亨利，简称亨， 常用单位：毫亨（m H） 微亨（μH） 常用单位：毫亨（ H） 微亨（
A
L S
R
A
课堂训练
4、如图所示，L为自感系数较大的线 、如图所示， 为自感系数较大的线 圈，电路稳定后小灯泡正常发光，当 电路稳定后小灯泡正常发光， 断开电键的瞬间会有 A . 灯A立即熄灭 立即熄灭 B . 灯A慢慢熄灭 慢慢熄灭 C . 灯A突然闪亮一下再慢慢熄灭 突然闪亮一下再慢慢熄灭 D . 灯A突然闪亮一下再突然熄灭 突然闪亮一下再突然熄灭 L A

大学物理自感和互感(二)2024

大学物理自感和互感(二)2024

大学物理自感和互感（二）引言概述：在大学物理中，自感和互感作为电磁学的重要概念，是理解电路和电磁现象的关键。

本文将介绍自感和互感的概念、特性以及在电路中的应用。

通过对这两个概念的深入理解，我们可以更好地理解电磁学原理，并在实践中应用于电路设计和电磁设备。

正文：1. 自感的概念与特性1.1 自感的定义1.2 自感系数的计算方法1.3 自感的单位与量纲1.4 自感的特性及其影响因素1.5 自感在电路中的作用2. 互感的概念与特性2.1 互感的定义2.2 互感系数的计算方法2.3 互感的单位与量纲2.4 互感的特性及其影响因素2.5 互感在电路中的作用3. 自感与互感的数学关系3.1 自感与互感的数学定义3.2 自感与互感的表达式3.3 自感与互感的对立性及作用机制3.4 引入自感与互感的电路方程组3.5 自感与互感的联合应用实例4. 自感和互感在电路分析中的应用4.1 自感与互感对电流、电压的影响4.2 自感与互感对电路能量的转移与储存的影响4.3 自感与互感对电路振荡特性的影响4.4 自感与互感在变压器设计中的应用4.5 自感与互感在电磁传感器中的应用5. 自感和互感的实验验证及工程应用5.1 自感和互感的实验测量方法5.2 自感与互感的实验数据处理与分析5.3 自感和互感在电子工程中的应用案例5.4 自感和互感在电力工程中的应用案例5.5 自感和互感的未来发展方向总结：通过本文的阐述，我们对自感和互感的概念、特性以及在电路中的应用有了较为全面的了解。

自感和互感是电磁学的重要概念，掌握它们的原理和应用，对于电子工程和电力工程领域的学习和实践具有重要意义。

通过进一步的研究和实验，我们可以深入探索自感和互感的机理，并将其应用于更广泛的电磁设备和系统中。

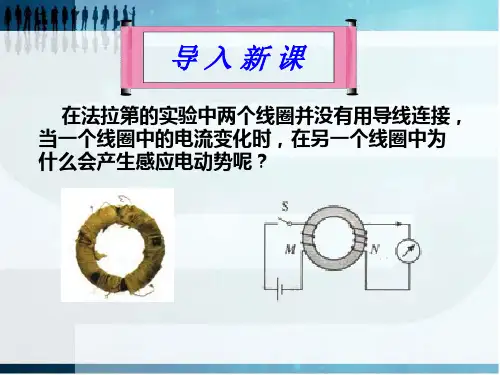
4.6自感和互感

4.6自感和互感

导入新课在法拉第的实验中两个线圈并没有用导线连接，当一个线圈中的电流变化时，在另一个线圈中为什么会产生感应电动势呢？法拉第发现电磁感应现象的第一个成功试验就是互感现象。

到底什么是互感？自感又是怎么回事呢？这节课我们就来学习这方面的内容。

教学目标1.知识与技能知道互感与自感现象都是常见的电磁感应现象。

知道自感电动势的大小由什么因素决定，并理解自感电动势的作用，能解释相关现象。

知道自感系数的单位、决定因素。

2.过程与方法利用已知知识发现问题，提出问题以及设计解决问题的方法，产生创新和设计的冲动。

了解互感现象和自感现象，以及对它们的利用和防止。

培养学生客观全面认识问题的能力。

能够通过电磁感应的有关规律分析通电、断电自感现象的成因及磁场的能量转化问题。

3.情感态度与价值观体验用已知知识去探索未知规律的乐趣，增强成就感。

通过电磁感应的有关规律分析通电、断电自感现象的成因及磁场的能量转化问题。

教学重、难点教学重点自感电动势的作用教学难点断电自感过程对小灯泡闪亮一下的原因解释本节导航1.互感现象2.自感现象3.自感系数4.磁场的能量1.互感现象合F 互感现象1B 2B 2I 1I 当线圈1中的电流变化时,所激发的磁场会在它邻近的另一个线圈2中产生感应电动势。

这种现象称为互感现象。

该电动势叫互感电动势。

注意互感电动势与线圈电流变化快慢有关；与两个线圈结构以及它们之间的相对位置和磁介质的分布有关。

互感系数1B 2B 2I 1I 回路1中的电流在回路2中产生的磁通量1I 12121I M Φ=回路2中的电流在回路1中产生的磁通量2I 21212I M Φ=M 21、M 12是比例系数,M 21称为线圈1对线圈2的互感系数，M 12称为线圈2对线圈1的互感系数。

从能量观点可以证明两个给定的线圈有：M 就叫做这两个线圈的互感系数，简称为互感。

MM M ==21122121212112I ΦI ΦM M M ====注意互感仅与两个线圈形状、大小、匝数、相对位置以及周围的磁介质有关。

4.6 互感和自感

4.6 互感和自感

四、磁场的能量
开关闭合时线圈中有电流，电流产生磁场，能量储存在磁场中；开关断开时，
线圈作用相当于电源，把磁场中的能量转化成电能。
×，断电自感中与原电流方相同
与电流变化快慢有关，
× 与电流变化大小无关。 × 线圈越大，越粗，匝数越多，
带铁芯，自感系数就越大。
√
E L I
t
√
曾经在《4.3 楞次定律习题课》最后一题做过并讲解了， 课后再做一下，不懂的看一下回放。
不能。因为当电流稳定，线圈M产生的磁场稳定，线圈N中的磁场也 不发生变化，不会产生感应电流。
利用互感现象，可以把能量从一个线圈传递到另一个线圈。因此，互感现象在 电工技术和电子技术中有广泛的应用。例如变压器、无线充电。
互感现象是一种常见的电磁感应现象，它不仅发生于绕在同一铁芯上的两个线 圈之间，还可以发生于任何两个相互靠近的电路之间：
实验一：通电自感现象 现象：在闭合开关Ｓ瞬间， 灯A2立刻正常发光，A1却比 A2迟一段时间才正常发光。
原因：由于接通电流瞬间，电流增加，线圈Ｌ自身的磁通量增加而产生了感应 电动势。根据楞次定律，感应电动势总是阻碍磁通量的变化即阻碍线圈中电流 的增加，故A1较慢地亮起来。
结论1:通电自感电动势与线圈的电流方向相反，“ 阻碍”原电流的增加，但最终 没有“阻止”原电流增加。
§4.6 互感和自感
第四章 电磁感应
林老师
1、在法拉第的实验中两个线圈并没有用导线连接。接上电路，如右图，当线圈M 中的开关S闭合时，在另一个线圈N中能否产生感应电流？为什么？
能，S闭合瞬间，电流瞬间增大，线圈M中产生变化的磁场，导致线圈N中的磁 通量发生变化，因此产生了感应电动势。
一、互感现象：
A.t1时，A线圈中电流变化率是零，所 以在B线圈中的磁通变化率为零。在这 一时刻，B中并没有感应电流，没有发 生互感，也不会跟A发生作用，A错。

4,6,1互感和自感-互感

4,6,1互感和自感-互感

手机内部接收端
无线充电器内部
互感的应用
无 线 充 电 器
电
蓝
磁
牙
炉
耳
机
变 压 器
5、防止：互感现象不仅发生于绕在同一铁芯上的两个线圈之间,而 且可以发生于任何两个相互靠近的电路之间。在电力工程中和电子 电路中，互感现象时会影响电路的正常工作，要设法减小互感。
所以平时说的金属壳包装的用电器漏电，有一种是互感引起的。
S2闭合，S1断开时，线圈B中有感应电流，产生电磁感应作用 若S2断开，线圈B中不产生感应电流而起不到延时作用
1．如图甲所示，A、B两绝缘金 属环套在同一铁芯上，A环中电 流iA随时间t的变化规律如图乙所 示，下列说法中正确的是( ) A．t1时刻，两环作用力最大 B．t2和t3时刻，两环相互吸引 C．t2时刻两环相互吸引，t3时刻 两环相互排斥 D．t3和t4时刻，两环相互吸引
一.互感现象
1、互感：在法拉第的实验中，两个线圈之间并没有导线相连，但 当一个线圈中的电流变化时，它所产生的变化磁场会在另一个线 圈中产生感应电动势．这种现象叫做互感．
2、互感电动势：互感现象中产生的感应电动势。
3、理解 (1)互感现象不仅发生于绕在同一铁芯上的两个线圈之间,且可发生于任何 两个相互靠近的电路之间. (2) 利用互感现象可以把能量、信号从一个电路（线圈）传递到另一个电 路（线圈），因此在电工技术和电子技术中有广泛的应用.如：变压器 (3) 在电力工程和电子电路中，互感现象有时会影响电路的正常工作，这 时要求设法减小电路间的互感。
t1时刻感应电流为零，故两环作用力 为零，则A错误
t2和t3时刻A环中电流在减小，则B 环中产生与A环中同向的电流，故 相互吸引，B正确、C错误

《自感和互感》课件

《自感和互感》课件

互感系数：描述互感现象的强 弱，与线圈之间的距离、形状、 材料等因素有关
互感现象：两个或多个线圈之 间通过电磁感应产生的相互影 响
应用：变压器、电感器、电 磁感应加热等
互感现象的影响：可能导致电 路参数变化，影响电路性能和
稳定性
线圈绕组结构：线圈绕组的形状、大小、位置等 线圈材料：线圈的材质、电阻率、磁导率等 线圈电流：线圈中的电流大小、方向、频率等 线圈间距：线圈之间的距离、角度等 线圈环境：温度、湿度、磁场等外部环境因素
线圈形状：线圈的形状和尺寸对自感系数有重要影响 线圈材料：线圈的材料和导电性能对自感系数有影响 线圈匝数：线圈的匝数越多，自感系数越大 线圈放置方式：线圈放置方式对自感系数有影响，如垂直放置、水平放置等 线圈周围环境：线圈周围环境的磁场、温度等对自感系数有影响
自感系数与线圈的匝数、形 状、尺寸、材料等因素有关
互感系数是描述两个线圈之间电磁感应关系的物理量
互感系数的大小与线圈的几何形状、尺寸、材料和位置有关
互感系数的正负号表示两个线圈之间的磁通方向是否相同
互感系数的物理意义在于描述两个线圈之间的电磁感应关系，对于电磁感应现象的研究和应 用具有重要意义。
自感和互感的应用
电流测量：通过自感 现象测量电流大小
感谢您的观看
汇报人：
自感和互感
汇报人：
目录
自感
Байду номын сангаас
互感
自感和互感的应用
自感和互感的区别 与联系
自感
自感是指线圈自身电流变化引起的电磁感应现象
自感现象产生的原因是线圈中的电流变化导致磁场变化，从而产生感应电动势
自感现象在电路中表现为线圈两端的电压变化 自感现象在电磁学中具有重要的应用价值，如电感器、变压器等设备

4.6互感和自感

4.6互感和自感
※ 了解互感现象及互感现象的应用 了解自感现象，认识自感电动势的作 ※ 用 知道自感系数的意义和决定因素．会 ※ 分析自感现象中电流的变化

行驶在大街上的无轨电车拖着两条长的“辫 子”．当道路不平车身颠簸时，“辫子”瞬间 脱离电网线，在“辫子”与电网线之间就会闪 现出电火花，同时发出“啪、啪”的响声．这 是什么原因呢？



1．当一个线圈中的电流变化时， ________________________________ ， 这 种 现象叫做互感． 2．当一个线圈中的电流变化时， ________________________________ ， 这 种 现象叫做自感． 3．自感产生的电动势E＝________，L是比 例系数，它与线圈的大小、形状、圈数，以 及是否有铁芯有关．L越大，越________产生 自感现象．

答案：由于产生断电自感电动势，并且电动 势比较大，故刘伟有被电击感觉，一旦放电 完毕，电动势瞬间消失，李辉无任何感觉也 就不足为怪了．


对“阻碍”含义的正确理解是：当自感电动 势是由于电流增大而引起时，自感电动势阻 碍电流增加，自感电动势方向与原电流方向 相反；当自感电动势是由于电流减小而引起 时，自感电动势阻碍电流减小，自感电动势 方向与原电流方向相同． (3)自感电动势的大小：根据已知条件不同， 自感电动势的大小可以有以下两种算法：
后渐渐变暗

A．①③
B．②③


C．②④
D．①④
解析：在电路(a)中自感线圈L与灯泡D串联，
D与L电流相等，断开S时产生自感电动势将
使D与L中的电流值从稳定状态逐渐减小，D
答案：D 将渐渐变暗，而不是立即熄灭．在电路(b)中，

H4.6互感和自感解读

H4.6互感和自感解读

课堂练习
练习7：如图所示的电路中，A1和A2是完全相同的两只灯泡， 线圈L的电阻可以忽略，下面说法中正确的是（ AD ） A．合上开关S接通电路时，A2先亮，A1后亮，最后一样亮 B．合上开关S接通电路时，A1和A2始终一样亮 C．断开开关S切断电路时，A2立刻熄灭，A1过一会才熄灭 D．断开开关S切断电路时，A1、A2都要延迟一会再熄灭
互感应用
(1)收音机里的“磁性天线”利用互感将广播信号 从一个线圈传送给另一线圈.
(2).
变压器
特别提醒： 互感是一种常见的电磁感应现象！要注意，它 不仅发生于绕在同一铁芯上的两个线圈之间，而且 可以发生于任何相互靠近的电路之间.
B A
S
1
产生电磁感应的条件是什么？
2 在图-1接通Ｓ，B线圈会不会产生 感应电动势？为什么? 3 在图-2中接通Ｓ，线圈会不会产生 感应电动势？为什么?
S
I的变化
B的变化
Φ的变化
E感
阻碍
I的变化
线圈中出现的感应电动势只 是阻碍了原电流的的变化，而非 阻止，所以虽延缓了电流变化的 进程，但最终电流仍然达到最大 值，B最终会正常发光。
二、自感现象
实验2：
如实验1中的电路， （1）传感器测量L的电流，当开关S断开时， 获得L中的电流随时间的变化图像。 （2）观察图像有什么特点？ （3）分析图像为什么有这样的特点。
L
A
R S
二、自感现象
现象：当开关闭合时，L中的电流并没有立刻消失，而是缓慢地减 小到零.
I的变化
B的变化
Φ的变化
E感
阻碍
I的变化
二、自感现象
实验2：
如实验1中的电路， （1）传感器测量R的电流，当开关S断开时， 获得R中的电流随时间的变化图像。 （2）观察图像有什么特点？ （3）分析图像为什么有这样的特点。

自感与互感PPT课件

自感与互感PPT课件
间相互干扰，影响设备正常工作。
知识点精讲
有一电感元件L=1H，通过此电感的电流随时间变化的波形如图4-10-3所示，若电压与电流的参
考方向一致，试计算各段电压并画出电压的波形。
∆
【解析】 = 0 − 4时：1 = ∆ = 1 ×
∆
= 4 − 6时：2 = ∆ = 1 ×
【解析】当电流互感器工作时，副边不允许开路，应将铁壳与副边绕组的一
端接地。电流互感器由升压变压器制成，原边绕组匝数少，副边绕组匝数多。因
此B错误。
知识点精讲
在0.02s内，通过一个线圈的电流由0.6A减小到0.4A，线圈产生5V的自感电动势，则线圈的自感
系数为 0.5
H。

【解析】由 =-L可得L=0.5H。
磁感应定律推导而得
∆
= −
∆
式中
∆——线圈中电流的变化量，单位是安［培］，符号为A；
∆——线圈中电流变化了Δi所用的时间，单位是秒，符号为s；
——线圈的自感系数，单位是亨［利］，符号为H；
——自感电动势，单位是伏［特］，符号为V。
公式中的负号表明自感电动势总是企图阻止电流的变化。
磁与电磁
考纲解读
一、最新考纲要求
1.了解自感现象和互感现象及应用；
2.了解自感和互感电动势；
3.了解自感和互感在生产、生活中的应用与危害。
二、考点解读
必考点：互感现象的产生及应用。
重难点：互感现象的产生及应用。
知识清单
1.自感现象与自感电动势
（1）自感现象
当导体中的电流发生变化时，导体本身就产生感应电动势，这个电动势总是阻碍导体中原来电
决定，与线圈中的电流大小无关。
知识清单

46自感和互感31页PPT

46自感和互感31页PPT

6、自感现象中的能量问题
通电自感：电场能 断电自感：磁场能
磁场能 电场能
[楞次定律的第二种表述] 感应电流的效果总要反抗产生感应电流的原因。 一般用于定性判明感应电流所引起的机械效果。
常见的具体情况有四种：
1、就磁通量而言，总是阻碍原磁通量的变化 （“增反减同”）
2、就相对运动而言，总是阻碍所有导体间的相对运动 （“来斥去吸”）
练习4：
4．如图所示的电路中，L为电阻很小的线圈，G1和G2为零点在表
盘中央的相同的电流表，当开关S闭合时，电流表G1指针偏向右方，
D 那么当开关S断开时，将出Hale Waihona Puke 的现象是（ ）46自感和互感
4.6 自感和互感
回路一
回路二
一、互感现象
1、定义：发生于绕在同一铁芯上的两个线圈之间或两个互相靠 近的电路之间的电磁感应现象。
【互感电动势】这种由互感现象产生的感应电动势叫做互感电动势。 【NOTICE】互感现象不仅发生于绕在同一铁芯上的两个线圈 之间，而且可以发生于任何相互靠近的电路之间。
2．互感的应用和防止
应用：
变压器、收音机的“磁性天线”就是利用互感现象制成。利用互感现象把 广播电台的信号从一个线圈传送到另一个线圈
防止：在电力工程和电子电路中，互感现象 有时会影响电路正常工作。
二、自感现象
【实验探究一】 如图所示电路，先闭合开关S调 节变阻器R，使同样规格的两个 灯泡A1和A2的明亮程度相同， 再调节变阻器R1使两个灯都正常 发光，然后断开开关S，注意观察： 重新闭合开关S的瞬间，两个灯泡 会有什么现象呢？
转15
转11
转11
转11
（2）防止：变压器和电动机
变压器、电动机等设备中有匝数很多 的线圈，当电路中的开关断开时会产 生很大的自感电动势，使得开关中的 金属片之间产生电火花，烧蚀接触点， 甚至引起人身伤害。因此，电动机等 大功率用电器的开关应该装在金属盒 内。最好使用油浸开关，即把开关的 接触点浸在绝缘油中，避免出现电火 花。

[名校联盟]江苏省南通市小海中学高二物理《46互感和自感》课件1

[名校联盟]江苏省南通市小海中学高二物理《46互感和自感》课件1
当线圈通电瞬间和断电瞬间，自感电动势 都要阻碍线圈中电流的变化，使线圈中的电 流不能立即增大到最大值或不能立即减小为 2、电的“惯性”大小与什么有关？ 零 电的“惯性”大小决定于线圈的自感系数
I I I I
t A B
t C
t
D
t
三 、自感系数L
1.自感电动势： 2.自感系数L影响因素：线圈的大小、形状、匝数、有无铁芯 等 3.单位：亨利 符号：Ｈ 常用单位：毫亨（mH) 、微亨（μＨ） 1mH=10-3H 1μH=10-3mH 4.自感系数L：表示线圈的自感特性的物理量
I EL t
课堂例题
例1.实验一中，当电键闭合后， 通过灯泡A1的电流随时间变化的 C 图；通过灯泡A2的电 图像为 ___ A 图。 流随时间变化的图像为___
I I I I
t
A B
t
C
t
D
t
实验二：断电自感
课堂例题
例2.在实验中，若线圈L的电阻RL与灯泡A 的电阻RA相等，则电键断开前后通过线圈 的电流随时间的变化图像为___ A 图，通过灯 泡的电流随时间的变化图像为___ C 图； 若RL远小于RA，则电键断开前后通过线圈的电流随时 B 图，通过灯泡的电流图像为__ 间的变化图像为__ D 图。
二.自感现象： 1.自感:由于导体本身的电流发生变化而产生的电磁 感应现象 2.自感电动势:自感过程中产生的电动势 3.自感电动势的作用：阻碍导体中原电流的变化 1）导体中原电流增大时，自感电动势阻碍它增大。 2）导体中原电流减小时，自感电动势阻碍它减小。 “阻碍”不是“阻止”，电流还是变化的
实验一：通电自感
AD
四、磁场的能量
问题：在断电自感的实验中，为什么开关断开 后，灯泡的发光会持续一段时间？甚至会比原 来更亮？试从能量的角度加以讨论。

2024版高一高教版《电工基础》46电感器教案

2024版高一高教版《电工基础》46电感器教案
谐振法
将电感器与电容器串联或并联组成谐振电路，通过测量谐振频率和 电路参数来计算电感量。
伏安法
在一定频率的交流电压下，测量电感器两端的电压和流过的电流，根 据欧姆定律计算出电感器的阻抗，进而求得电感量。
Q值测量实验设计
实验原理
Q值表示电感器在交流电路中的品质因数，是反映电感器性能的重要参数。通过测量电感器 在谐振状态下的电压、电流和频率，可以计算出Q值。
Q值计算
Q值等于电感器在某一频率下的 感抗XL与其等效电阻R的比值，
即Q=XL/R。
Q值影响因素
电感器的Q值受线圈电阻、磁芯 损耗以及频率等因素的影响。线 圈电阻越小、磁芯损耗越低，Q 值越高；同时，随着频率的升高，
Q值也会逐渐降低。
直流电阻与交流阻抗
01
直流电阻
电感器在直流电路中的电阻，用符号RDC表示。直流电阻的大小取决于
电感振荡电路类型
包括LC振荡电路、RC振荡 电路和晶体振荡电路等。
电感振荡电路特点
频率稳定度高，波形失真 小，适用于产生各种频率 的正弦波信号。
稳压电路中应用
电感稳压原理
01
利用电感的储能作用和自感电动势的产生，与二极管等元件一
起构成稳压电路。
电感稳压电路类型
02
包括串联型稳压电路、并联型稳压电路和开关型稳压电路等。
实验步骤
搭建谐振电路，将电感器置于电路中，调节信号发生器输出一定频率的交流信号，使电路发 生谐振。然后测量电感器两端的电压和流过的电流，记录数据并计算Q值。
注意事项
在测量过程中，需要保持信号发生器的输出稳定，同时注意观察电感器的温升情况，避免温 度过高影响测量结果。
实际应用中性能评估
额定电流下的性能评估
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
D 原生来自断感开电，动电势路，中此电自流感电I0动势2E的R作，用现是将(S闭合，于是电)路中产
A 使电路的电流减小，最后由I0减到零 B 有阻碍电流增大的作用，
最后电流小于I0 C 有阻碍电流增大的作用，
因而电流总保持不变 D 有阻碍电流增大的作用，
但电流还是增大，最后变为2I0
练习7：
7、如图所示：日光灯电路主要由镇流器
启动器和灯管组成，在日光灯正常工作
ABCD 的情况下（
）
A、镇流器给日光灯的开始点燃提供
瞬时高压
B、灯管正常发光时，镇流器起降压限流的作用
C、灯管正常发光情况下，启动器内的两个触片是分离的
D、日光灯点燃瞬间，灯管两端电压大于220V
练习：
1 ．如图所示，两圆环A、B置于同一水平面上，其中A为均匀带电 绝缘环，B为导体环，当A以如图所示的方向绕中心转动的角速度 发生变化时，B中产生如图所示方向的感应电流，则
练习2：
2．如图，电阻R和自感线圈L的电阻值相等，接通S，使电路达
D 到稳定状态，灯泡D发光，则（
）
①在电路（a）中，断开S，D将渐变暗
②在电路（a）中，断开S，D将先变得更亮，然后渐渐变暗
③在电路（b）中，断开S，D将渐变暗
④在电路（b）中，断开S，D将先变得更亮，然后渐渐变暗
A ．①③ B ．②③ C ．②④ D ．①④
练习4：
4．如图所示的电路中，L为电阻很小的线圈，G1和G2为零点在表
盘中央的相同的电流表，当开关S闭合时，电流表G1指针偏向右方，
D 那么当开关S断开时，将出现的现象是（ ）
A．G1和G2指针都立刻回到零点
B．G1指针立刻回到零点，而G2指针
G2
缓慢地回到零点
C．G1指针立刻回到零点，而G2指针先
46自感和互感
回路一
回路二
3、作用 ：阻碍电流的变化
原电流增大时：感应电流与之反向 原电流减小时：感应电流与之同向
4、自感系数L
（1）物理意义 ：阻描述线圈产生自感电动势本领大小的物理量 线圈的横截面积S 大则大
（2）决定因素
线 圈 的 长 度L 大则大 线 圈 的 匝 数N 大则大
会产生一个与原电流方向同向的自感电动势，这个自感电动势与电 源电压加在一起，形成一个瞬时高压，加在灯管两端，使灯管中气 体开始放电，使日光灯管成为电路的通路开始发光。
日光灯正常工作时，要求加在灯管两端的电压小于电源电压 （只需要110V左右 ）由于日光灯使用的是交变电流，电流大小、方 向不断变化，使镇流器线圈中产生自感电动势，总是阻碍交变电流 的变化，这时镇流器又起着镇压限流的作用！
（ BC ）
A ．A可能带正电且转速减小 B ．A可能带正电且转速增大 C ．A可能带负电且转速减小 D ．A可能带负电且转速增大
练习：
2．如图所示，水平放置的两条光滑轨道上有可自由移动的金
属棒PQ、MN，当PQ在外力作用下运动时，MN在磁场力作用下向
BC 右运动，则PQ所做的运动可能是（
）
A．向右匀加速运动
BБайду номын сангаас向左匀加速运动
C．向右匀减速运动
D．向左匀减速运动
练习3：
AD 3．如图所示的电路中，A1和A2是完全相同的灯泡，线圈L的电阻
可以忽略．下列说法中正确的是(
)
A ．合上开关S接通电路时，A2先亮，A1后亮，最后一样亮
B ．合上开关S接通电路时，A1和A2始终一样亮
C ．断开开关S切断电路时，A2立刻熄灭，A1过—会儿熄灭
D ．断开开关S切断电路时，A1和A2都要过一会儿才熄灭
有 无 铁 芯 有则大
（3）单位：亨（利）H mH、 H 1H103mH106 H
5、应用和防止 （1）应用：日光灯
【工作原理】开关S闭合后，由于灯管 中没有电流通过，电源将220V电压全 部加在启动器的两极间，使启动器内 氖气放电而发出辉光，辉光产生的热量 使U行动触片受热膨胀，与静触片接触 而使电路接通。电路接通后氖气停止放 电，U行动触片呢冷却收缩，使电路自 动断开，在这一瞬间通过镇流器的电流 急剧减小，此时，镇流器由于自感现象
3、就闭合导体回路的面积而言，通过改变线圈面积来“反抗”
（“増缩减扩”） 4、阻碍原电流的变化（第六节将学习的自感现象）
（“增反减同”）
自感练习题 互感练习题
练习1： 1．如图所示，L为自感系数较大的线圈，电路稳定后
A 小灯泡正常发光，当断开开关S的瞬间会有（ ）
A
A．灯A立即熄灭 B．灯A慢慢熄灭 C．灯A突然闪亮一下再慢慢熄灭 D．灯A突然闪亮一下再突然熄灭
转15
转11
转11
转11
（2）防止：变压器和电动机
变压器、电动机等设备中有匝数很多 的线圈，当电路中的开关断开时会产 生很大的自感电动势，使得开关中的 金属片之间产生电火花，烧蚀接触点， 甚至引起人身伤害。因此，电动机等 大功率用电器的开关应该装在金属盒 内。最好使用油浸开关，即把开关的 接触点浸在绝缘油中，避免出现电火 花。
6、自感现象中的能量问题
通电自感：电场能 断电自感：磁场能
磁场能 电场能
[楞次定律的第二种表述] 感应电流的效果总要反抗产生感应电流的原因。 一般用于定性判明感应电流所引起的机械效果。
常见的具体情况有四种：
1、就磁通量而言，总是阻碍原磁通量的变化 （“增反减同”）
2、就相对运动而言，总是阻碍所有导体间的相对运动 （“来斥去吸”）
G1
立即偏向左方，然后缓慢地回到零点
D．G1指针先立即偏向左方，然后缓慢 地回到零点，而G2指针缓慢地回到零点
练习5：
5．如图所示的电路，开关原先
闭合，电路处于稳定状态，在某
一时刻突然断开开关S，则通过
电阻R1中的电流I1随时间变化的
D 图线可能是图中的(
)
练习6：
6．如图所示两个电阻均为R，L的电阻及电池内阻均可忽略，S