函数训练题B

一次函数培优训练知识掌握：（一）两个一次函数平行与垂直：当平面直角坐标系中两直线平行时，其函数解析式中k的值（即一次项系数）相等；当平面直角坐标系中两直线垂直时，其函数解析式中k的值互为负倒数（即两个k值的乘积为-1）。

注意：与y轴平行的直线没有函数解析式，与x轴平行的直线的解析式为常函数，（二）一次函数知识要点提醒：1.对一次函数概念理解时，不要漏掉一次项系数不为0这一限制条件；2.不要忽略一次函数自变量取值范围；（三）一次函数的对称：（1）若直线l与直线y=kx+b关于x轴对称，则直线l的解析式为y=-kx-b；（2）若直线l与直线y=kx+b关于y轴对称，则直线l的解析式为y=-kx+b；（3）若直线l与直线y=kx+b关于直线y=x对称，则直线l的解析式为y=1/kx-b/k；（4）若直线l与直线y=kx+b关于直线y=-x对称，则直线l的解析式为y=1/kx+b/k；（5）若直线l与直线y=kx+b关于原点对称，则直线l的解析式为y=kx-b.课堂训练：1．已知，直线y=2x+3与直线y=﹣2x﹣1．（1）求两直线与y轴交点A，B的坐标；（2）求两直线交点C的坐标；（3）求△ABC的面积．2．如图，直线y=2x+3与x轴相交于点A，与y轴相交于点B．（1）求A、B两点的坐标；（2）过B点作直线BP与x轴相交于P，且使AP=2OA，求△BOP的面积．3．（10分）我区A，B两村盛产荔枝，A村有荔枝200吨，B村有荔枝300吨．现将这些荔枝运到C，D两个冷藏仓库，已知C仓库可储存240吨，D仓库可储存260吨；从A村运往C，D两处的费用分别为每吨20元和25元，从B村运往C，D两处的费用分别为每吨15元和18元．设从A 村运往C仓库的荔枝重量为x吨，A，B两村运往两仓库的荔枝运输费用分别为y A元和y B元．B与x之间的函数关系式；（3）考虑到B村的经济承受能力，B村的荔枝运费不得超过4830元．在这种情况下，请问怎样调运，才能使两村运费之和最小？求出这个最小值．4．（10分）已知一次函数y=kx+b的图象是过A（0，﹣4），B（2，﹣3）两点的一条直线．（1）求直线AB的解析式；（2）将直线AB向左平移6个单位，求平移后的直线的解析式．（3）将直线AB向上平移6个单位，求原点到平移后的直线的距离．5．（10分）如图，直线l1的解析式为y=﹣3x+3，且l1与x轴交于点D，直线l2经过点A（4，0）、B（3，），直线l1、l2交于点C．（1）求直线l2的解析式；（2）求△ADC的面积；（3）试问：在直线l2上是否存在异于点C的另一点P，使得△ADP与△ADC的面积相等？若存在，请直接写出点P的坐标；若不存在，请说明理由．6．一次函数y=mx+1与y=nx+2的图象相交于x轴上一点，那么m：n=．7．点P（3，a）、Q（，b）在一次函数y=﹣x+c的图象上，则a与b的大小关系是．8．为表彰在某活动中表现积极的同学，老师决定购买文具盒与钢笔作为奖品．已知5个文具盒、2支钢笔共需100元；3个文具盒、1支钢笔共需57元．（1）每个文具盒、每支钢笔各多少元？（2）若本次表彰活动，老师决定购买10件作为奖品，若购买x个文具盒，10件奖品共需w元，求w与x的函数关系式．如果至少需要购买3个文具盒，本次活动老师最多需要花多少钱？9．某服装厂接到生产一种工作服的订货任务，要求在规定期限内完成，按照这个服装厂原来的生产能力，每天可生产这种服装150套，按这样的生产进度在客户要求的期限内只能完成订货的；现在工厂改进了人员组织结构和生产流程，每天可生产这种工作服200套，这样不仅比规定时间少用1天，而且比订货量多生产25套，求订做的工作服是几套？要求的期限是几天？10．（10分）如图，直角坐标系中，点A的坐标为（1，0），以线段OA为边在第四象限内作等边△AOB，点C为x正半轴上一动点（OC＞1），连接BC，以线段BC为边在第四象限内作等边△CBD，直线DA交y轴于点E．（1）△OBC与△ABD全等吗？判断并证明你的结论；（2）随着点C位置的变化，点E的位置是否会发生变化？若没有变化，求出点E的坐标；若有变化，请说明理由．11．某物流公司的甲、乙两辆货车分别从A、B两地同时相向而行，并以各自的速度匀速行驶，途径配货站C，甲车先到达C地，并在C地用1小时配货，然后按原速度开往B地，乙车从B地直达A地，如图是甲、乙两车间的距离y（千米）与乙车出发x（时）的函数的部分图象．（1）A、B两地的距离是千米，乙车出发小时与甲相遇；（2）求乙车出发1.5小时后直至到达A地的过程中，y与x的函数关系式及x的取值范围；（3）乙车出发多长时间，两车相距100千米？12．如图，直线和x轴、y轴的交点分别为B、C，点A的坐标是（，0），另一条直线经过点A、C．（1）求直线AC所对应的函数表达式；（2）动点M从B出发沿BC运动，运动的速度为每秒1个单位长度．当点M运动到C点时停止运动．设M运动t秒时，△ABM的面积为S．①求S与t的函数关系式；②当t为何值时，（注：S△ABC表示△ABC的面积），求出对应的t值；③当t=4的时候，在坐标轴上是否存在点P，使得△BMP是以BM为直角边的直角三角形？若存在，请直接写出P点坐标；若不存在，请说明理由．（友情提醒：在解题过程中可以直接运用以下结论：在直角三角形中，30°的角所对的直角边的长等于斜边长的一半）13．已知一次函数y=+m（O＜m≤1）的图象为直线l，直线l绕原点O旋转180°后得直线l′，△ABC三个顶点的坐标分别为A（﹣，﹣1）、B（，﹣1）、C（0，2）．（1）直线AC的解析式为，直线l′的解析式为（可以含m）；（2）如图，l、l′分别与△ABC的两边交于E、F、G、H，当m在其范围内变化时，判断四边形EFGH中有哪些量不随m的变化而变化？并简要说明理由；（3）将（2）中四边形EFGH的面积记为S，试求m与S的关系式，并求S的变化范围；（4）若m=1，当△ABC分别沿直线y=x与y=x平移时，判断△ABC介于直线l，l′之间部分的面积是否改变？若不变，请指出来；若改变，请写出面积变化的范围．（不必说明理由）。

函数的单调性专题训练一、选择题1．若函数f (x )在区间(a ，b )上是增函数，在区间(b ，c )上也是增函数，则函数f (x )在区间(a ，b )∪(b ，c )上( )A ．必是增函数B ．必是减函数C ．是增函数或减函数D ．无法确定单调性2．设(a ，b )，(c ，d )都是f (x )的单调增区间，且x 1∈(a ，b )，x 2∈(c ，d )，x 1<x 2，则f (x 1)与f (x 2)的大小关系为( )A ．f (x 1)<f (x 2)B ．f (x 1)>f (x 2)C ．f (x 1)＝f (x 2)D ．不能确定3．设f (x )＝(2a －1)x ＋b 在R 上是减函数，则有( )A ．a ≥12B ．a ≤12C ．a >－12D ．a <124．下列四个函数在(－∞，0)上为增函数的是( )①y ＝|x |＋1； ②y ＝|x |x ； ③y ＝－x 2|x |； ④y ＝x ＋x |x |. A ．①② B ．②③ C ．③④ D ．①④5．已知函数f (x )＝⎩⎪⎨⎪⎧ a －3 x ＋5，x ≤1，2a x ，x ＞1是R 上的减函数，则实数a 的取值范围是( )A ．(0,3)B ．(0,3]C ．(0,2)D ．(0,2]二、填空题6．函数f (x )＝|x －1|＋2的单调递增区间为________．7．如果二次函数f (x )＝x 2－(a －1)x ＋5在区间⎝ ⎛⎭⎪⎫12，1上是增函数，则实数a 的取值范围为________． 8．函数f (x )是定义域上的单调递减函数，且过点(－3，2)和(1，－2)，则使|f (x )|<2的自变量x 的取值范围是________．三、解答题9．已知函数f (x )＝⎩⎪⎨⎪⎧ －x ＋3－3a ，x <0，－x 2＋a ，x ≥0满足对任意的x 1，x 2∈R ，(x 1－x 2)[f (x 1)－f (x 2)]<0，求a的取值范围．10．已知函数f(x)＝1x2－1.(1)设f(x)的定义域为A，求集合A；(2)判断函数f(x)在(1，＋∞)上的单调性，并用定义加以证明．11．讨论函数f(x)＝x＋ax(a＞0)的单调性．12．已知f(x)＝xx－a(x≠a)．(1)若a＝－2，试证f(x)在(－∞，－2)内单调递增；(2)若a>0且f(x)在(1，＋∞)内单调递减，求a的取值范围．函数的单调性专题训练答案一、选择题1．若函数f (x )在区间(a ，b )上是增函数，在区间(b ，c )上也是增函数，则函数f (x )在区间(a ，b )∪(b ，c )上( )A ．必是增函数B ．必是减函数C ．是增函数或减函数D ．无法确定单调性解析：选D 函数在区间(a ，b )∪(b ，c )上无法确定单调性．如y ＝－1x在(0，＋∞)上是增函数， 在(－∞，0)上也是增函数，但在(－∞，0)∪(0，＋∞)上并不具有单调性．2．设(a ，b )，(c ，d )都是f (x )的单调增区间，且x 1∈(a ，b )，x 2∈(c ，d )，x 1<x 2，则f (x 1)与f (x 2)的大小关系为( )A ．f (x 1)<f (x 2)B ．f (x 1)>f (x 2)C ．f (x 1)＝f (x 2)D ．不能确定解析：选 D 根据单调函数的定义，所取两个自变量必须是同一单调区间内的任意两个自变量，才能由该区间上函数的单调性来比较出函数值的大小，而本题中的x 1，x 2不在同一单调区间，故f (x 1)与f (x 2)的大小不能确定，选D.3．设f (x )＝(2a －1)x ＋b 在R 上是减函数，则有( )A ．a ≥12B ．a ≤12C ．a >－12D ．a <12解析：选D ∵f (x )在R 上是减函数，故2a －1<0，即a <12. 4．下列四个函数在(－∞，0)上为增函数的是( )①y ＝|x |＋1； ②y ＝|x |x ； ③y ＝－x 2|x |； ④y ＝x ＋x |x |. A ．①② B ．②③ C ．③④ D ．①④解析：选 C ①y ＝|x |＋1＝－x ＋1(x <0)在(－∞，0)上为减函数；②y ＝|x |x ＝－1(x <0)在(－∞，0)上既不是增函数，也不是减函数；③y ＝－x 2|x |＝x (x <0)在(－∞，0)上是增函数；④y ＝x ＋x |x |＝x －1(x <0)在(－∞，0)上也是增函数．5．已知函数f (x )＝⎩⎪⎨⎪⎧ a －3 x ＋5，x ≤1，2a x ，x ＞1是R 上的减函数，则实数a 的取值范围是( )A ．(0,3)B ．(0,3]C ．(0,2)D ．(0,2]解析：选D 依题意得实数a 满足⎩⎪⎨⎪⎧ a －3＜0，2a ＞0，a －3 ＋5≥2a ，解得0＜a ≤2.二、填空题 6．函数f (x )＝|x －1|＋2的单调递增区间为________．解析：f (x )＝⎩⎪⎨⎪⎧ x ＋1，x ≥1，3－x ，x <1，显然函数f (x )在x ≥1时单调递增．答案：[1，＋∞)7．如果二次函数f (x )＝x 2－(a －1)x ＋5在区间⎝ ⎛⎭⎪⎫12，1上是增函数，则实数a 的取值范围为________． 解析：∵函数f (x )＝x 2－(a －1)x ＋5的对称轴为x ＝a －12且在区间⎝ ⎛⎭⎪⎫12，1上是增函数， ∴a －12≤12，即a ≤2. 答案：(－∞，2]8．函数f (x )是定义域上的单调递减函数，且过点(－3，2)和(1，－2)，则使|f (x )|<2的自变量x 的取值范围是________．解析：∵f (x )是定义域上的减函数，f (－3)＝2，f (1)＝－2，∴当x >－3时，f (x )<2，当x <1时，f (x )>－2，则当－3<x <1时，|f (x )|<2.答案：(－3,1)三、解答题9．已知函数f (x )＝⎩⎪⎨⎪⎧ －x ＋3－3a ，x <0，－x 2＋a ，x ≥0满足对任意的x 1，x 2∈R ，(x 1－x 2)[f (x 1)－f (x 2)]<0，求a的取值范围．解：由对任意的x 1，x 2∈R ，(x 1－x 2)[f (x 1)－f (x 2)]<0知函数f (x )在R 上为减函数．当x <0时，函数f (x )＝－x ＋3－3a 为一次函数，且为减函数，则此时f (x )>f (0)＝3－3a ；当x ≥0时，函数f (x )＝－x 2＋a 为二次函数，也为减函数，且有f (x )≤f (0)＝a .要使函数f (x )在R 上为减函数，则有a ≤3－3a ，解得a≤34.所以a 的取值范围是⎝⎛⎦⎥⎤－∞，34. 10．已知函数f (x )＝1x 2－1. (1)设f (x )的定义域为A ，求集合A ；(2)判断函数f (x )在(1，＋∞)上的单调性，并用定义加以证明．解：(1)由x 2－1≠0，得x ≠±1，所以函数f (x )＝1x 2－1的定义域为A ＝{x ∈R|x ≠±1}． (2)函数f (x )＝1x 2－1在(1，＋∞)上单调递减． 证明：任取x 1，x 2∈(1，＋∞)，设x 1<x 2，则Δx ＝x 2－x 1>0，Δy ＝y 2－y 1＝1x 22－1－1x 21－1＝ x 1－x 2 x 1＋x 2 x 21－1 x 22－1 ， ∵x 1>1，x 2>1，∴x 21－1>0，x 22－1>0，x 1＋x 2>0.又x 1<x 2，所以x 1－x 2<0，故Δy <0.因此，函数f (x )＝1x 2－1在(1，＋∞)上单调递减．11．讨论函数f (x )＝x ＋a x (a ＞0)的单调性．解：f (x )＝x ＋a x (a ＞0)．∵定义域为{x |x ∈R ，且x ≠0}，∴可分开证明，设x 1＞x 2＞0，则f (x 1)－f (x 2)＝x 1＋ax 1－x 2－a x 2＝(x 1－x 2)⎝ ⎛⎭⎪⎫1－a x 1x 2. 当0＜x 2＜x 1≤a 时，恒有a x 1x 2＞1， 则f (x 1)－f (x 2)＜0，故f (x )在(0，a ]上是减函数；当x 1＞x 2＞a 时，恒有0＜a x 1x 2＜1， 则f (x 1)－f (x 2)＞0，故f (x )在(a ，＋∞)上是增函数．同理可证f (x )在(－∞，－a )上是增函数，在[－a ，0)上是减函数．综上所述，f (x )在(－∞，－a )，(a ，＋∞)上是增函数，在[－a ，0)，(0，a ]上是减函数．12．已知f (x )＝xx －a (x ≠a )．(1)若a ＝－2，试证f (x )在(－∞，－2)内单调递增；(2)若a >0且f (x )在(1，＋∞)内单调递减，求a 的取值范围． 解：(1)证明： 设x 1<x 2<－2，则f (x 1)－f (x 2)＝x 1x 1＋2－x 2x 2＋2＝2 x 1－x 2 x 1＋2 x 2＋2 . ∵(x 1＋2)(x 2＋2)>0，x 1－x 2<0，∴f (x 1)<f (x 2)，∴f (x )在(－∞，－2)内单调递增．(2)设1<x 1<x 2，则f (x 1)－f (x 2)＝x 1x 1－a －x 2x 2－a ＝a x 2－x 1 x 1－a x 2－a . ∵a >0，x 2－x 1>0，∴要使f (x 1)－f (x 2)>0，只需(x 1－a )(x 2－a )>0恒成立，∴a ≤1. 综上所述a 的取值范围是(0,1]．。

函数的表示方法 测试题〔2〕一、制卷人：歐陽文化、歐陽理複；制卷時間：二O 二二年二月七日一、 选择题：1、函数x x x y ||+=的图像是以下图中的 〔 〕2、函数⎪⎩⎪⎨⎧<+=>-=)0(1)0(0)0(1)(x x x x x x f ，那么)]21([f f 的值是 〔 〕 A.21 B.21- C.23 D. 23- 3、以下各组函数中)(x f 和)(x g 一样的是 〔 〕A.0)(,1)(x x g x f ==B.x x x g x f ==)(,1)( C.⎩⎨⎧-∞∈-+∞∈==)0,(,),0(,)(|,|)(x x x x x g x x f D. 02)3)(3()(,3)3()(++=++=x x x g x x x f4.如右图,在直角梯形OABC 中,AB ∥OC,BC ⊥OC,且AB=1,OC=BC=2,直线l:x=ｔ,截此梯形所得位于l 左方的图形面积为S,那么函数S=f(t)的大致图象是以以下图形中( )5、 设函数f(x)=,假设f(-4)=f(0),f(-2)=-2,那么关于x 的方程f(x)=x的解的个数为( ).A.1B.2二、填空题： 6、函数2][)(+=x x f ，那么=)35(f ___________.7、⎩⎨⎧∈-∈=]2,1((2]1,0[()(x x x x x f 的定义域为_________,值域为___________. 8、f(x)=⎩⎨⎧>-≤0,0,x x x x ,1)(+=x x g ，那么=)]([x g f ___________________. 三、解答题：9、设⎩⎨⎧>≤=)0(1)0(0)(x x x H 画出函数y ＝H(x －1)的图象10、函数的图象由两条射线及开口向下的抛物线(包括端点)组成，如下图，试求函数的表达式。

参考答案：1，C ；2，A ；3， D ；4，C ；5，C ；6，3；7，[0，2]，[0，1]；8，{1111-≤+->--x x x x ；9，略； 10，解：设左射线所在直线的表达式为y ＝kx ＋b∵ (1，1)，(0，2)在直线上，故∴ 左射线的表达式为y ＝－x ＋2，x ＜1．同理可得右射线的表达式 为y ＝x －2，x ＞3再设抛物线的表达式为y ＝a(x －2)2＋2 ∵ 点(1，1)在此抛物线上，∴a＋2＝1a ＝－1∴ 中间抛物线的表达工为y ＝－(x －2)2＋2＝－x 2＋4x －2 1≤x≤3 总上所述，所求函数表达式为y ＝制卷人：歐陽文化、歐陽理複；制卷時間：二O 二二年二月七日。

(完整版)高一函数大题训练带答案解析一、解答题1．（附加题，本小题满分10分，该题计入总分）已知函数()y f x =，若在区间()2,2-内有且仅有一个0x ，使得0()1f x =成立，则称函数()f x 具有性质M ．（1）若()sin 2f x x =+，判断()f x 是否具有性质M ，说明理由； （2）若函数2()221f x x mx m =+++具有性质M ，试求实数m 的取值范围．2．已知函数()y f x =，若存在实数(),0m k m ≠，使得对于定义域内的任意实数x ，均有()()()m f x f x k f x k ⋅=++-成立，则称函数()f x 为“可平衡”函数，有序数对(),m k 称为函数()f x 的“平衡”数对.（1）若1m =，判断()sin f x x =是否为“可平衡”函数，并说明理由；（2）若a R ∈，0a ≠，当a 变化时，求证：()2f x x =与()2xg x a =+的“平衡”数对相同；（3）若12,m m R ∈，且1,2m π⎛⎫ ⎪⎝⎭、2,4m π⎛⎫ ⎪⎝⎭均为函数()2cos f x x =的“平衡”数对.当04x π<≤时，求2212m m +的取值范围.3．已知定义在R 上的函数()x ϕ的图像是一条连续不断的曲线，且在任意区间上()x ϕ都不是常值函数.设011i i n a t t t t t b -=<<<<<<=，其中分点121n t t t -、、、将区间[],a b 任意划分成()*n n N ∈个小区间[]1,i i t t -，记{}()()()()()()01121,,n n M a b n t t t t t t ϕϕϕϕϕϕ-=-+-++-，称为()x ϕ关于区间[],a b 的n 阶划分“落差总和”.当{},,M a b n 取得最大值且n 取得最小值0n 时，称()x ϕ存在“最佳划分”{}0,,M a b n . (1)已知()x x ϕ=，求{}1,2,2M -的最大值0M ；(2)已知()()a b ϕϕ<，求证：()x ϕ在[],a b 上存在“最佳划分”{},,1M a b 的充要条件是()x ϕ在[],a b 上单调递增.(3)若()x ϕ是偶函数且存在“最佳划分”{}0,,M a a n -，求证：0n 是偶数，且00110i i n t t t t t -+++++=.4．已知集合M 是满足下列性质的函数()f x 的全体；在定义域内存在实数t ，使得(2)()(2)f t f t f +=+．（1）判断()32f x x =+是否属于集合M ，并说明理由； （2）若2()lg2af x x =+属于集合M ，求实数a 的取值范围； （3）若2()2x f x bx =+，求证：对任意实数b ，都有()f x M ∈．5．对于定义域为D 的函数()y f x =，如果存在区间[],m n D ⊆，其中m n <，同时满足： ①()f x 在[],m n 内是单调函数：②当定义域为[],m n 时，()f x 的值域为[],m n ，则称函数()f x 是区间[],m n 上的“保值函数”，区间[],m n 称为“保值区间”.（1）求证：函数()22g x x x =-不是定义域[]0,1上的“保值函数”；（2）若函数()2112f x a a x=+-（,0a R a ∈≠）是区间[],m n 上的“保值函数”，求a 的取值范围；（3）对（2）中函数()f x ，若不等式()22a f x x ≤对1≥x 恒成立，求实数a 的取值范围.6．定义：若存在常数k ，使得对定义域D 内的任意两个不同的实数12,x x ，均有：1212()()f x f x k x x -≤-成立，则称()f x 在D 上满足利普希茨(Lipschitz)条件．（1）试举出一个满足利普希茨(Lipschitz)条件的函数及常数k 的值，并加以验证； （2）若函数()1f x x =+在[0,)+∞上满足利普希茨(Lipschitz)条件，求常数k 的最小值； （3)现有函数()sin f x x =，请找出所有的一次函数()g x ，使得下列条件同时成立： ①函数()g x 满足利普希茨(Lipschitz)条件；②方程()0g x =的根也是方程()0f x =的根，且()()()()g f t f g t =； ③方程(())(())f g x g f x =在区间[0,2)π上有且仅有一解．7．定义在D 上的函数()y f x =，如果满足：对任意x D ∈，存在常数0M >，都有|()|f x M ≤成立，则称函数()y f x =是D 上的有界函数，其中M 称为函数的上界.已知函数1112()1,()2412x xx xm f x a g x m -⋅⎛⎫⎛⎫=+⋅+= ⎪ ⎪+⋅⎝⎭⎝⎭. （1）当1a =时，求函数()y f x =在(,0)-∞上的值域，并判断函数()y f x =在(,0)-∞上是否为有界函数，请说明理由；（2）若函数()y f x =在[0,)+∞上是以3为上界的有界函数，求实数a 的取值范围； （3）若0m >，函数()y g x =在[]0,1上的上界是()T m ，求()T m 的解析式. 8．已知函数11()(,0)f x b a b R a x a x a=++∈≠-+且. （1）判断()y f x =的图象是否是中心对称图形？若是，求出对称中心；若不是，请说明理由；（2）设()(1)g x b x =+，试讨论()()y f x g x =-的零点个数情况. 9．已知函数()y f x =的定义域D ，值域为A .（1）下列哪个函数满足值域为R ，且单调递增？（不必说明理由）①()1tan[()],(0,1)2f x x x π=-∈，②()1lg(1),(0,1)g x x x =-∈.（2）已知12()log (21),()sin 2,f x x g x x =+=函数[()]f g x 的值域[1,0]A =-，试求出满足条件的函数[()]f g x 一个定义域D ；（3）若D A ==R ，且对任意的,x y R ∈，有()()()f x y f x f y -=-，证明：()()()f x y f x f y +=+.10．已知函数()()2xf x x R =∈，记()()()g x f x f x =--．⑴解不等式：()()26f x f x -≤；⑵设k 为实数，若存在实数(]01,2x ∈，使得()()20021g x k gx =⋅-成立，求k 的取值范围；⑶记()()()22h x f x a f x b =++⋅+(其中a ，b 均为实数)，若对于任意的[]0,1x ∈，均有()12h k ≤，求a ，b 的值． 11．已知平面直角坐标系xOy ，在x 轴的正半轴上，依次取点1A ，2A ，3A ，()*n A n N ⋯∈，并在第一象限内的抛物线232y x =上依次取点1B ，2B ，3B ，⋯，()*n B n N ∈，使得()*1k k k A B A k N -∈都为等边三角形，其中0A 为坐标原点，设第n 个三角形的边长为()f n ．⑴求()1f ，()2f ，并猜想()(f n 不要求证明)；⑵令()98n a f n =-，记m t 为数列{}n a 中落在区间()29,9m m 内的项的个数，设数列{}m t 的前m 项和为m S ，试问是否存在实数λ，使得2m S λ≤对任意*m N ∈恒成立？若存在，求出λ的取值范围；若不存在，说明理由； ⑶已知数列{}n b满足：11n b b +={}n满足：111,n nc c +==，求证：12n n n b f c +π⎛⎫<< ⎪⎝⎭．12．对于函数f （x ），若f （x 0）=x 0，则称x 0为f （x ）的“不动点”；若f [f （x 0）]=x 0，则称x 0为f （x ）的“稳定点”满足函数f （x ）的“不动点”和“稳定点”的集合分别记为A 和B ，即A ={x |f （x ）=x }，B ={x |f [f （x ）]=x }． （Ⅰ）设f （x ）=x 2-2，求集合A 和B ； （Ⅱ）若f （x ）=x 2-a ，且满足∅A =B ，求实数a 的取值范围．13．已知集合M 是满足下列性质的函数()f x 的全体：在定义域内存在0x 使得()()()0011f x f x f +=+成立．（1）函数()21f x x=+是否属于集合M ？请说明理由； （2）函数()2ln1af x x =∈+M ，求a 的取值范围； （3）设函数()23x f x x =+，证明：函数()f x ∈M ．14．对于函数()f x ，若在定义域内存在实数0x ，满足00()()f x f x -=-，则称()f x 为“M 类函数”.（1）已知函数()sin()3f x x π=+，试判断()f x 是否为“M 类函数”？并说明理由；（2）设()2x f x m =+是定义在[1,1]-上的“M 类函数”，求是实数m 的最小值；（3）若22log (2)()3x mx f x ⎧-=⎨-⎩,2,2x x ≥<为其定义域上的“M 类函数”，求实数m 的取值范围.15．已知函数()21log 21mx f x x x +⎛⎫=- ⎪-⎝⎭()m 为常数是奇函数. (1)判断函数()f x 在1,2x ∞⎛⎫∈+ ⎪⎝⎭上的单调性,并用定义法证明你的结论;(2)若对于区间[]2,5上的任意值,使得不等式()2xf x n ≤+恒成立,求实数的取值范围.【参考答案】一、解答题1．（Ⅰ）()f x 具有性质M ; （Ⅱ）23m ≤-或2m >或0m =【解析】 【详解】试题分析：（Ⅰ）()sin 2f x x =+具有性质M ．若存在()022x ∈﹣，，使得()01f x =，解方程求出方程的根，即可证得；（Ⅱ）依题意，若函数()2221f x x mx m =+++具有性质M ，即方程2220x mx m ++=在()22﹣，上有且只有一个实根．设()222h x x mx m =++，即()222h x x mx m =++在()22﹣，上有且只有一个零点．讨论m 的取值范围，结合零点存在定理，即可得到m 的范围．试题解析：（Ⅰ）()sin 2f x x =+具有性质M ．依题意，若存在0x ∈(2,2)-，使0()1f x =，则0x ∈(2,2)-时有0sin 21x +=，即0sin 1x =-，022x k ππ=-，k Z ∈．由于0x ∈(2,2)-，所以02x π=-．又因为区间(2,2)-内有且仅有一个02x π=-，使0()1f x =成立，所以()f x 具有性质M 5分（Ⅱ）依题意，若函数2()221f x x mx m =+++具有性质M ，即方程2220x mx m ++=在(2,2)-上有且只有一个实根．设2()22h x x mx m =++，即2()22h x x mx m =++在(2,2)-上有且只有一个零点． 解法一：（1）当2m -≤-时，即2m ≥时，可得()h x 在(2,2)-上为增函数， 只需(2)0,{(2)0,h h -<>解得2,{2,3m m >>-交集得2m >．（2）当22m -<-<时，即22m -<<时，若使函数()h x 在(2,2)-上有且只有一个零点，需考虑以下3种情况：（ⅰ）0m =时，2()h x x =在(2,2)-上有且只有一个零点，符合题意． （ⅱ）当20m -<-<即02m <<时，需(2)0,{(2)0,h h -≤>解得2,{2,3m m ≥>-交集得∅．（ⅲ）当02m <-<时，即20m -<<时，需(2)0,{(2)0,h h ->≤解得2,{2,3m m <≤-交集得223m -<≤-．（3）当2m -≥时，即2m ≤-时，可得()h x 在(2,2)-上为减函数 只需(2)0,{(2)0,h h -><解得2,{2,3m m <<-交集得2m ≤-．综上所述，若函数()f x 具有性质M ，实数m 的取值范围是23m ≤-或2m >或0m = 14分 解法二： 依题意，（1）由(2)(2)0h h -⋅<得，(42)(64)0m m -+<，解得23m <-或2m >． 同时需要考虑以下三种情况： （2）由22,{0,m -<-<∆=解得0m =． （3）由20,{(2)0,m h -<-<-=解得02,{2,m m <<=不等式组无解． （4）由02,{(2)0,m h <-<=解得20,{2,3m m -<<=-解得23m =-． 综上所述，若函数()f x 具有性质M ，实数m 的取值范围是23m ≤-或2m > 或0m = 14分．考点：1．零点存在定理；2．分类讨论的思想．2．（1）()sin f x x =是“可平衡”函数,详见解析（2）证明见解析（3）221218m m <+≤【解析】 【分析】(1)利用两角和差的正弦公式求解即可.(2)根据题意可知,对于任意实数x ,()()22222=22mx x k x k x k ++-=+,再列式利用恒成立问题求解即可.(3)根据“平衡数对”的定义将12,m m 用关于x 的三角函数表达,再利用三角函数的取值范围求解即可. 【详解】（1）若1m =,则()sin m f x x ⋅=,()()()()sin sin f x k f x k x k x k ++-=++-2sin cos x k =,要使得()f x 为“可平衡”函数,需使故()12cos sin 0k x -⋅=对于任意实数x 均成立,只有1cos 2k =,此时23k n ππ=±,n Z ∈,故k 存在,所以()sin f x x =是“可平衡”函数.（2）()2f x x =及()2xg x a =+的定义域均为R ,根据题意可知,对于任意实数x ,()()22222=22mx x k x k x k ++-=+,即22222mx x k =+,即()22220m x k --=对于任意实数x 恒成立,只有2m =,0k =,故函数()2f x x =的“平衡”数对为()2,0,对于函数()2xg x a =+而言,()222x x k x k m a a a +-⋅+=+++()2222x k k a -=+⋅+, 所以()()22222x x k km a a -⋅+=+⋅+,()()22220xkkm a m -⎡⎤⋅-++⋅-=⎣⎦,()2220k k m a m -⎧=+⎪⎨⋅-=⎪⎩, 即22m m ≥⎧⎨=⎩,故2m =,只有0k =,所以函数()2xg x a =+的“平衡”数对为()2,0, 综上可得函数()2f x x =与()2xg x a =+的“平衡”数对相同.（3）2221cos cos cos 22m x x x ππ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭,所以221cos 2sin m x x =,2222cos cos cos 44m x x x ππ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭,所以22cos 1m x =,由于04x π<≤,所以21cos 12x ≤<,故(]212tan 0,2m x =∈,(]22sec 1,2m x =∈, ()22224121tan 4tan m m x x +=++()22222145tan 2tan 15tan 55x x x ⎛⎫=++=++ ⎪⎝⎭, 由于04x π<≤,所以20tan 1x <≤时,2116tan 555x <+≤, ()2212tan 238x <+-≤,所以221218m m <+≤.【点睛】本题主要考查了新定义的函数问题,需要根据题意列出参数满足的关系式,利用恒成立问题或表达出参数满足的解析式再分析求范围等.属于难题. 3．(1)3；(2)见解析；(3)见解析 【解析】 【分析】(1)直接利用题中给的定义求解即可；(2)利用函数的单调性和数列的信息应用求出充要条件；(3)利用函数的奇偶性和存在的最佳划分，进一步建立函数的单调区间，最后求出函数的关系式.(1)()()()()010023M ϕϕϕϕ=--+-=； (2)若()x ϕ在[],a b 上单调递增，则{}()()()(){}11,,,,1ni i i M a b n t t b a M a b ϕϕϕϕ-==-=-=⎡⎤⎣⎦∑，故()x ϕ在[],a b 上存在“最佳划分”{},,1M a b若()x ϕ在[],a b 上存在“最佳划分”{},,1M a b ，倘若()x ϕ在[],a b 上不单调递增， 则存在[]()()121212,,,,x x a b x x x x ϕϕ∈<>.由()()()()()()()()1122a b a x x x x b ϕϕϕϕϕϕϕϕ-≤-+-+-（*）等号当且仅当()()()()()()11220,0,0a x x x x b ϕϕϕϕϕϕ-≥->-≥时取得，此时()()()()()()()()()()11220a b a x x x x b a b ϕϕϕϕϕϕϕϕϕϕ-=-+-+-=-<，与题设矛盾，舍去，故（*）式中等号不成立，即：增加分点12,x x 后，“落差总和”会增加，故{},,M a b n 取最大值时n 的最小值大于1，与条件矛盾. 所以()x ϕ在[],a b 上单调递增；(3)由(2)的证明过程可知，在任间区间[],a b 上，若()x ϕ存在最佳划分{},,1a b ，则当()()a b ϕϕ=时，()x ϕ为常值函数（舍）；当()()a b ϕϕ<时，()x ϕ单调递增；当()()a b ϕϕ>时，()x ϕ单调递减，若()x ϕ在[],a b 上存在最佳划分{}0,,M a b n ，则此时在每个小区间[]()10,1,2,,i i t t i n -=上均为最佳划分{}1,,1i i M t t -.否则，添加分点后可使()x ϕ在[],a b 上的“落差总和”增大，从而{}0,,M a b n 不是“落差总和”的最大值，与“()x ϕ在[],a b 上存在最佳划分{}0,,M a b n ”矛盾，故()x ϕ在每个小区间[]()10,1,2,,i i t t i n -=上都是单调，若()x ϕ在[],a b 上存在最佳划分{}0,,M a b n ，则()x ϕ在相邻的两个区间[][]11,,i i i i t t t t -+、上具有不同的单调性，否则，()()()()()()11111i i i i i t t t t t t ϕϕϕϕϕϕ-+-+-=-+-，减少分点i t ，“落差总和”的值不变，而n 的值减少1，故n 的最小值不是0n ，与“()x ϕ在[],a b 上存在最佳划分{}0,,M a b n ”矛盾，()x ϕ存在“最佳划分”{}0,,M a a n -，故()x ϕ在每个小区间[]()10,1,2,,i i t t i n -=上都单调，而()x ϕ是偶函数，故()x ϕ在y 轴两侧的单调区间对称，共有偶数个单调区间，且当000,1,,2n i j n i ⎛⎫+== ⎪⎝⎭时，0i j t t +=，从而有00120n t t t t ++++=.【点睛】本题是信息给予题，考查了数学阅读能力，考查了函数和数列的综合应用能力，考查了数学运算能力.4．（1）不属于,理由详见解析；（2）[12-+；（3）详见解析.【分析】（1）利用f （x ）＝3x +2，通过f （t +2）＝f （t ）+f （2）推出方程无解，说明f （x ）＝3x +2不属于集合M ； （2）由()22a f x lgx =+属于集合M ，推出()222622a a a lg lg lg x x =++++有实解，即（a ﹣6）x 2+4ax +6（a ﹣2）＝0有实解，对参数分类讨论，利用判断式求解即可；（3）当f （x ）＝2x +bx 2时，方程f （x +2）＝f （x ）+f （2）⇔3×2x +4bx ﹣4＝0，令g （x ）＝3×2x +4bx ﹣4，则g （x ）在R 上的图象是连续的，当b ≥0时，当b ＜0时，判断函数是否有零点，证明对任意实数b ，都有f （x ）∈M ． 【详解】解：（1）当()32f x x =+时，方程(2)()(2)38310f t f t f t t +=+⇔+=+ 此方程无解，所以不存在实数t ，使得(2)()(2)f t f t f +=+， 故()32f x x =+不属于集合M ﹒ （2）由2()lg 2af x x =+，属于集合M ，可得 方程22lglg lg (2)226a a ax x =++++有实解()22(2)262a x x ⎡⎤⇔++=+⎣⎦有实解2(6)46(2)0a x ax a ⇔-++-=有实解，若6a =时，上述方程有实解；若6a ≠时，有21624(6)(2)0a a a ∆=---≥，解得1212a -≤≤+，故所求a 的取值范围是[12-+．（3）当2()2x f x bx =+时，方程(2)()(2)f x f x f +=+⇔ 2222(2)24432440x+x x b x bx b bx ++=+++⇔⨯+-=，令()3244x g x bx =⨯+-，则()g x 在R 上的图像是连续的，当0b ≥时，(0)10g =-<，(1)240g b =+>，故()g x 在(0,1)内至少有一个零点当0b <时，(0)10g =-<，11320bg b ⎛⎫=⨯> ⎪⎝⎭，故()g x 在1,0b ⎛⎫ ⎪⎝⎭内至少有一个零点故对任意的实数b ，()g x 在R 上都有零点，即方程(2)()(2)f x f x f +=+总有解， 所以对任意实数b ，都有()f x M ∈． 【点睛】本题考查抽象函数的应用，函数的零点以及方程根的关系，考查转化思想以及计算能力． 5．（1）证明见详解；（2）32a <-或12a >；（3）112a <≤【解析】 【分析】（1）根据“保值函数”的定义分析即可（2）按“保值函数”定义知()f m m =，()f n n =，转化为,m n 是方程2112x a a x+-=的两个不相等的实根，利用判别式求解即可（3）去掉绝对值，转化为不等式组，分离参数，利用函数最值解决恒成立问题. 【详解】（1）函数()22g x x x =-在[]0,1x ∈时的值域为[]1,0-，不满足“保值函数”的定义， 因此函数()22g x x x =-不是定义域[]0,1上的“保值函数”.（2）因为函数()2112f x a a x=+-在[],m n 内是单调增函数， 因此()f m m =，()f n n =， 因此,m n 是方程2112x a a x+-=的两个不相等的实根， 等价于方程()222210a x a a x -++=有两个不相等的实根.由()222240a a a ∆=+->解得32a <-或12a >.（3）()2212a f x a a x=+-，()22a f x x ≤()22a f x x⇔≤⇔21222a a x x+--≤≤， 即为22122,122,a a x x a a x x ⎧+≤+⎪⎪⎨⎪+≥-⎪⎩对1≥x 恒成立.令()12h x x x=+，易证()h x 在[)1,+∞单调递增， 同理()12g x x x=-在[)1,+∞单调递减. 因此，()()min 13h x h ==，()()min 11g x g ==-.所以2223,21,a a a a ⎧+≤⎨+≥-⎩解得312a -≤≤.又32a <-或12a >，所以a 的取值范围是112a <≤. 【点睛】本题主要考查了新概念，函数的单调性，一元二次方程有解，绝对值不等式，恒成立，属于难题.6．（1）()f x x =,2k =，见解析；（2）min 12k =（3）11(),[,0)(0,]22g x kx k =∈-⋃【解析】 【分析】（1）令()f x x =,可以满足题意，一次函数和常值函数都可以满足； （2）根据定义化简1212()()f x f x x x --12<，得出k 的最小值；（3）由于所有一次函数均满足（1）故设()()0g x kx b k t =+≠是()0g x =的根，推得0b =，若k 符合题意，则k -也符合题意，可以只考虑0k >的情形，分①若1k，②若112k <<，分别验证是否满足题意，可得k 的范围. 【详解】（1）例如令()f x x =,由12122x x x x -≤-知可取2k =满足题意（任何一次函数或常值函数等均可）． （2）()f x =[0,)+∞为增函数∴对任意12,x x R ∈有1212()()f x f x x x --12==<（当120,0x x =→时取到）所以min 12k =（3）由于所有一次函数均满足（1）故设()()0g x kx b k t =+≠是()0g x =的根()0bg t t k∴=⇒=-， 又(())(())(0)(0)0()f g t g f t f g b g x kx =∴=∴=∴=若k 符合题意，则k -也符合题意，故以下仅考虑0k >的情形． 设()(())(())sin sin h x f g x g f x kx k x =-=- ①若1k，则由sin sin 0h k kk πππ⎛⎫=-<⎪⎝⎭且3333sin sin sin 02222k k h k k ππππ⎛⎫=-=+≥⎪⎝⎭所以，在3,2k ππ⎡⎤⎢⎥⎣⎦中另有一根，矛盾．②若112k <<，则由[]sin sin 0,2h k h k k ππππ⎛⎫=-≥⎪⎝⎭sin 2sin 20k k ππ=-< 所以，在,2kππ⎡⎤⎢⎥⎣⎦中另有一根，矛盾．102k ∴<≤以下证明，对任意1(0,],()2k g x kx ∈=符合题意．当(0,]2x π∈时，由sin y x =图象在连接两点()(0,0),,sin x x 的线段的上方知sin sin kx k x >()0h x ∴>当(,]22x kππ∈时，sin sinsin sin ()022k kx k k x h x ππ>≥≥∴>当,22x k ππ⎛⎫∈⎪⎝⎭时，sin 0,sin 0,()0kx x h x >∴ 综上：()0h x =有且仅有一个解0x =，()g x kx ∴=在1(0,]2k ∈满足题意． 综上所述：11(),[,0)(0,]22g x kx k =∈-⋃, 故得解. 【点睛】本题考查运用所学的函数知识解决新定义等相关问题，关键在于运用所学的函数知识，紧紧抓住定义，构造所需要达到的定义式，此类题目综合性强，属于难度题.7．（1）见解析；（2）51a -≤≤；（3）1,01()12,12m m mT m m m m ⎧-<≤⎪+⎪=⎨-⎪>⎪+⎩.【解析】 【分析】（1）通过判断函数()y f x =的单调性，求出()y f x =的值域，进而可判断()y f x =在(,0)-∞上是否为有界函数；（2）利用题中所给定义，列出不等式，换元，转化为恒成立问题，通过分参求构造函数的最值，就可求得实数a 的取值范围；（3）通过分离常数法求()y g x =的值域，利用新定义进而求得()T m 的解析式． 【详解】（1）当1a =时，11()124xxf x ⎛⎫⎛⎫=++ ⎪ ⎪⎝⎭⎝⎭，由于()f x 在(,0)-∞上递减，∴()(0)3,f x f >=∴函数()y f x =在(,0)-∞上的值域为(3,)+∞，故不存在常数0M >，使得|()|f x M ≤成立，∴函数()y f x =在(,0)-∞上不是有界函数 （2）()y f x =在[0,)+∞上是以3为上界的有界函数，即|()|3f x ≤，令12xt ⎛⎫= ⎪⎝⎭，则1131324xxa ⎛⎫⎛⎫-≤+⋅+≤ ⎪ ⎪⎝⎭⎝⎭，即2313,01at t t -≤++≤<<由213at t ++≤得2(01)a t t t≤-<<， 令2()(01)h t t t t=-<<，()h t 在(0,1)上单调递减，所以()(1)1h t h >= 由213at t ++≥-得4(01)a t t t ⎛⎫≥-+<< ⎪⎝⎭，令4()(01)h t t t t ⎛⎫=-+<< ⎪⎝⎭，()h t 在(0,1)上单调递增，所以()(1)5h t h <=-所以51a -≤≤；（3）122()1,0,01,()1221x x xm g x m x g x m m -⋅==->≤≤∴+⋅⋅+在[]0,1上递减， (1)()(0)g g x g ∴≤≤，即121()121m mg x m m--≤≤++， 当1121|2m m m m --≥++时，即当0m <≤1|()|1m g x m -≤+当1121|2m m m m --<++时，即当m >时，12|()|12m g x m -≤+∴1,01()12,12m m mT m m m m ⎧-<≤⎪+⎪=⎨-⎪>⎪+⎩. 【点睛】本题主要考查学生利用所学知识解决创新问题的能力，涉及到函数求值域的有关方法，以及恒成立问题的常见解决思想．8．（1）()y f x =的图象是中心对称图形，对称中心为：()0,b ；（2）当0b >或22b a <-时，有3个零点；当220b a -≤≤时，有1个零点 【解析】 【分析】（1）设()()h x f x b =-，通过奇偶性的定义可求得()h x 为奇函数，关于原点对称，从而可得()f x 的对称中心，得到结论；（2）()()0y f x g x =-=，可知0x =为一个解，从而将问题转化为222b x a =-解的个数的讨论，即22222a b x a b b+=+=的解的个数；根据b 的范围，分别讨论不同范围情况下方程解的个数，从而得到零点个数，综合得到结果. 【详解】（1） 设()()11h x f x b x a x a=-=+-+ ()h x ∴定义域为：{}x x a ≠± ()()1111h x h x x a a x x a x a ⎛⎫-=+=-+=- ⎪---+-⎝⎭()h x ∴为奇函数，图象关于()0,0对称()y f x ∴=的图象是中心对称图形，对称中心为：()0,b （2）令()()110y f x g x bx x a x a=-=+-=-+ ()()20x b x a x a ⎡⎤∴-=⎢⎥-+⎢⎥⎣⎦，可知0x =为其中一个解，即0x =为一个零点 只需讨论222b x a =-的解的个数即可①当0b =时，222b x a =-无解 ()()y f x g x ∴=-有且仅有0x =一个零点②当0b >时 ，2220x a b =+> x ∴=222b x a =-的解()()y f x g x ∴=-有x =0x =共3个零点 ③当0b <时，22222a bx a b b+=+=（i ）若220a b +<，即22b a <-时，220a bb+>x ∴=222b x a =-的解()()y f x g x ∴=-有x =0x =共3个零点 （ii ）若220a b +=，即22b a =-时，222b x a =-的解为：0x = ()()y f x g x ∴=-有且仅有0x =一个零点（iii ）若220a b +>，即220b a -<<时，220a bb+<，方程222b x a =-无解 ()()y f x g x ∴=-有且仅有0x =一个零点 综上所述：当0b >或22b a <-时，有3个零点；当220b a -≤≤时，有1个零点 【点睛】本题考查函数对称性的判断、函数零点个数的讨论.解决本题中零点个数问题的关键是能够将问题转化为方程222b x a =-根的个数的讨论，从而根据b 的不同范围得到方程根的个数，进而得到零点个数，属于较难题. 9．（1）见解析；（2）见解析；（3）见解析 【解析】 【分析】（1）由正切函数与对数函数的性质可直接判断；（2）由()()[]12log 2sin211,0f g x x ⎡⎤=+∈-⎣⎦，得[]2sin211,2x +∈，进而利用正弦函数的性质列式求解即可；（3）利用反证法，假设存在,a b 使得()()()f a b f a f b +≠+，结合条件推出矛盾即可证得. 【详解】（1）()()1tan ,0,12f x x x π⎡⎤⎛⎫=-∈ ⎪⎢⎥⎝⎭⎣⎦满足.()()1lg 1,0,1g x x x ⎛⎫=-∈ ⎪⎝⎭不满足.（2）因为()()[]12log 2sin211,0f g x x ⎡⎤=+∈-⎣⎦，所以[]2sin211,2,x +∈ 即1sin20,2x ⎡⎤∈⎢⎥⎣⎦，所以][522,22,2,.66x k k k k k Z πππππππ⎡⎤∈+⋃++∈⎢⎥⎣⎦所以][5,,,,12122x k k k k k Z πππππππ⎡⎤∈+⋃++∈⎢⎥⎣⎦ 满足条件的0,12D π⎡⎤=⎢⎥⎣⎦（答案不唯一）.（3）假设存在,a b 使得()()()f a b f a f b +≠+ 又有()()()()()(),f a f a b f b f b f a b f a =+-=+-， 所以()()()()()(),f a f a b f b f b f a b f a -=+--=+-，结合两式：()()(),0f a f b f a b =+=，所以()()()0f b f a f a b --=+=， 故()()()f a f b f a -==.由于()()()f a b f a f b +≠+知：()0f a ≠.又()()12222a a a f f a f f f a ⎛⎫⎛⎫⎛⎫=-⇒= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. 类似地，由于()0f a -≠，()22a a f f a f ⎛⎫⎛⎫-=--- ⎪ ⎪⎝⎭⎝⎭得()()11222a f f a f a ⎛⎫-=-= ⎪⎝⎭.所以()022a a f a f f ⎛⎫⎛⎫=--= ⎪ ⎪⎝⎭⎝⎭，与()0f a ≠矛盾，所以原命题成立. 【点睛】本题主要考查了复合函数的性质及反证法的证明，属于难题. 10．(1) (]2,log 3-∞(2) 27119,2259k ⎡⎫∈⎪⎢⎣⎭(3)12a =-，172b = 【解析】 【分析】⑴函数()2xf x =，()()26f x f x -≤，即为22260x x --≤，即为()()22230x x +-≤，可得解集；⑵根据()()20021g x k gx =⋅-，利用换元法，求解最值，即可求解k 的取值范围；⑶根据()()()22h x f x a f x b =++⋅+(其中a ，b 均为实数)，[]0,1x ∈，均有()12h k ≤，建立关系即可求解a ，b 的值．⑴函数()2xf x =，()()26f x f x -≤， 即为22260x x --≤，即为()()22230x x+-≤，即有23x ≤，解得2log 3x ≤， 即解集为(]2,log 3-∞；⑵存在实数(]01,2x ∈，使得()()20021g x k g x =⋅-成立，即为()000022212222x x x x k --+-=-， 设022x x t -=-，在(]1,2递增，可得31524t <≤， ()00002222222224x x x x t --+=++=+，即有21kt +，则21k t =+ 设21m t =，164,2259m ⎡⎫∈⎪⎢⎣⎭，即有y m =，在164,2259m ⎡⎫∈⎪⎢⎣⎭递增， 可得27119,2259y ⎡⎫∈⎪⎢⎣⎭， 即有27119,2259k ⎡⎫∈⎪⎢⎣⎭. ⑶()()()22h x f x a f x b =++⋅+ ()22222422x x xx a b a b +=+⋅+=+⋅+，令2x v =，[]0,1x ∈，[]1,2v ∴∈，()()24h x v v av b ϕ∴==++．若对于任意的[]0,1x ∈，均有()12h x ≤， 即对任意[]1,2v ∈，()2142v v av b ϕ=++≤． 214211622161162a b a b b a ⎧⎪++≤⎪⎪∴++≤⎨⎪⎪-≤⎪⎩①②③，解得：12a =-，172b =．本题主要考查了函数恒成立问题的求解，分类讨论以及转化思想的应用，二次函数闭区间是的最值以及单调性的应用．11．⑴()11f =，()22f =,()f n n =；⑵3λ≤；⑶详见解析 【解析】 【分析】()()111f =，()22f =，进而猜想出()f n ． ()298n a n =-.由21218899899999m m m m n n --<-<⇒+<<+，可得191m n -=+，192m -+，⋯，219m -，21199.m m m t --=-利用等比数列的求和公式即可得出m S .根据2mS λ≤对任意*m N ∈恒成立即可得出λ范围．()13sin4b π=，记1sin ,4n n b πθθ==，可得()*11sin sin 22n n n n n N θπθθ++=⇒=∈，1tan 4c π=，记1tan ,4n n c πϕϕ==，可得()*11sec 1tan tan tan 22n n n n n n n N ϕϕπϕϕφ++-==⇒=∈，根据当0,2x π⎛⎫∈ ⎪⎝⎭时，sin tan x x x <<即可得出． 【详解】解：()()111f =，()22f = 猜想()f n n =()298n a n =-，由21218899899999m m m m n n --<-<⇒+<<+， 191m n -∴=+，192m -+，⋯，219m -21199m m m t --∴=-()()()()35221191999999m m m S --∴=-+-+-+⋯+-()()35212199991999m m --=+++⋯+-+++⋯+()()22129191991091191980m mm m +---⋅+=-=--2m S λ≤对任意*m N ∈恒成立()1min 283m S S λλ⇒≤==⇒≤⑶证明：1sin 4b π=，记1sin ,4n n b πθθ==，则()*11sin sin 22n n n n n N θπθθ++==⇒=∈ 1tan4c π=，记1tan ,4n n c πϕϕ==，则()*11sec 1tan tan tan 22n n n n n n n N ϕϕπϕϕφ++-==⇒=∈ 11sin,tan 22n n n n b c ππ++∴==，当0,2x π⎛⎫∈ ⎪⎝⎭时，sin tan x x x <<可知：1111sin tan 2222n n n n n n b f c ππππ++++⎛⎫=<=<= ⎪⎝⎭，【点睛】本题考查了数列与函数的关系、等比数列的通项公式与求和公式及其性质、三角函数求值及其性质，考查了推理能力与计算能力，属于难题．12．（Ⅰ）A ={-1，2}；B -13}（Ⅱ）[-14，34]【解析】 【分析】（Ⅰ）由f （x ）=x 得x 2-x -2=0，解得x =-1，x =2，故A ={-1，2}；由f （f （x ））=x ，可得f （x 2-2）=x ，即（x 2-2）2-（x 2-2）-2=x ；求解x 可得集合B ．（Ⅱ）理解A =B 时，它表示方程x 2-a =x 与方程（x 2-a ）2-a =x 有相同的实根，根据这个分析得出关于a 的方程求出a 的值． 【详解】（Ⅰ）由f （x ）=x 得x 2-x -2=0，解得x =-1，x =2，故A ={-1，2}； 由f （f （x ））=x ，可得f （x 2-2）=x ，即（x 2-2）2-（x 2-2）-2=x ； 即x 4-2x 3-6x 2+6x +9=0，即（x +1）（x -3）（x 2-3）=0，解得x =-1，x =3，x x B -13}； （Ⅱ）∵∅A =B ，∴x 2-a =x 有实根，即x 2-x -a =0有实根，则△=1+4a ≥0，解得a ≥-14由（x 2-a ）2-a =x ，即x 4-2ax 2-x +a 2-a =0的左边有因式x 2-x -a ， 从而有（x 2-x -a ）（x 2+x -a +1）=0． ∵A =B ，∴x 2+x -a +1=0要么没有实根，要么实根是方程x 2-x -a =0的根． 若x 2+x -a +1=0没有实根，则a ＜34；若x 2+x -a +1=0有实根且实根是方程x 2-x -a =0的根， 由于两个方程的二次项系数相同，一次项系数不同， 故此时x 2+x -a +1=0有两个相等的根-12，此时a =34方程x 2-x -a =0可化为：方程x 2-x -34=0满足条件，故a 的取值范围是[-14，34]．【点睛】本题考查对新概念的理解和运用的能力，同时考查了集合间的关系和方程根的相关知识，解题过程中体现了分类讨论的数学思想．13．（1）见解析；（2）[33a ∈+；（3）见解析 【解析】 【分析】（1）直接进行验证或用反证法求解；（2）由()2ln 1af x x =∈+M 得到方程()22lnlnln 1211aa ax x =++++在定义域内有解，然后转化成二次方程的问题求解；（3）验证函数()f x 满足()()()0011f x f x f +=+即可得到结论成立． 【详解】 （1）()21f x M x=+∉．理由如下： 假设()21f x M x=+∈， 则在定义域内存在0x ，使得()()()0011f x f x f +=+成立， 即00221131x x +=+++， 整理得2003320x x ++=， ∵方程2003320x x ++=无实数解，∴假设不成立， ∴()21f x M x=+∉． （2）由题意得()2ln +1af x M x =∈， ()22lnlnln 1211aa ax x ∴=++++在定义域内有解， 即()222220a x ax a ---+=在实数集R 内有解，当2a =时，12x =-，满足题意；当2a ≠时，由0∆≥，得2640a a -+≤，解得33a ≤2a ≠，综上33a ≤∴实数a的取值范围为33⎡⎣．（3）证明：∵()23x f x x =+，∴()()()()()000212000003113134232x x x f x f x f x x x +⎛⎫+-+=++---=+- ⎪⎝⎭，又函数3x y =的图象与函数32y x =-+的图象有交点，设交点的横坐标为a ，则3302aa +-=， ∴003302xx +-=，其中0x a =， ∴ 存在0x 使得()()()0011f x f x f +=+成立， ∴()f x M ∈． 【点睛】本题以元素与集合的关系为载体考查函数与方程的知识，解题的关键是根据题意中集合元素的特征将问题进行转化，然后再结合方程或函数的相关知识进行求解，考查转化能力和处理解决问题的能力．14．（1）函数()sin()3f x x π=+是“M 类函数”；（2）54-；（3）[1,1)-.【解析】 【详解】试题分析：(1) 由()()f x f x -=-，得sin()sin()33x x ππ-+=-+整理可得02x R π=∈满足00()()f x f x -=-(2) 由题存在实数0[1,1]x ∈-满足00()()f x f x -=-，即方程2220x x m -++=在[1,1]-上有解.令12[,2]2xt =∈分离参数可得11()2m t t =-+，设11()()2g t t t =-+求值域，可得m 取最小值54-(3) 由题即存在实数0x ，满足00()()f x f x -=-，分02x ≥，022x -<<，02x ≤-三种情况讨论可得实数m 的取值范围.试题解析：（1）由()()f x f x -=-，得：sin()sin()33x x ππ-+=-+0x = 所以存在02x R π=∈满足00()()f x f x -=-所以函数()sin()3f x x π=+是“M 类函数”，（2）因为()2x f x m =+是定义在[1,1]-上的“M 类函数”， 所以存在实数0[1,1]x ∈-满足00()()f x f x -=-， 即方程2220x x m -++=在[1,1]-上有解. 令12[,2]2xt =∈则11()2m t t =-+，因为11()()2g t t t =-+在1[,1]2上递增，在[1,2]上递减所以当12t =或2t =时，m 取最小值54-（3）由220x mx ->对2x ≥恒成立，得1m <因为若22log (2)()3x mx f x ⎧-=⎨-⎩,2,2x x ≥<为其定义域上的“M 类函数”所以存在实数0x ，满足00()()f x f x -=-①当02x ≥时，02x -≤-，所以22003log (2)x mx -=--，所以00142m x x =- 因为函数142y x x=-（2x ≥）是增函数，所以1m ≥- ②当022x -<<时，022x -<-<，所以33-=，矛盾③当02x ≤-时，02x -≥，所以2200log (2)3x mx +=，所以00142m x x =-+因为函数142y x x=-+(2)x ≤-是减函数，所以1m ≥-综上所述，实数m 的取值范围是[1,1)-点睛:已知方程有根问题可转化为函数有零点问题，求参数常用的方法和思路有： (1)直接法：直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围； (2)分离参数法：先将参数分离，转化成函数的值域问题解决；(3)数形结合法：先对解析式变形，在同一个平面直角坐标系中，画出函数的图像，然后数形结合求解.15．(1)()1,2f x x ∞⎛⎫∈+ ⎪⎝⎭在上为单调减函数;证明见解析 (2)25log 63n ≥- 【解析】 【详解】试题分析：(1)利用奇偶性，确定函数的解析式，然后利用函数单调性的定义，判断函数的单调性；(2)利用函数的单调性，结合不等式恒成立问题，求解参数的取值范围. 试题解析：(1)由条件可得()()0f x f x -+=,即 2211log log 02121mx mx x x -+⎛⎫⎛⎫+= ⎪ ⎪---⎝⎭⎝⎭化简得222114m x x -=-,从而得2m =±;由题意2m =-舍去,所以 2m =即()212log 21x f x x x +⎛⎫=- ⎪-⎝⎭, ()1,2f x x ∞⎛⎫∈+ ⎪⎝⎭在上为单调减函数,证明如下:设1212x x <<<+∞, 则()()12f x f x -=122122121212log log 2121x x x x x x ⎛⎫⎛⎫++--+ ⎪⎪--⎝⎭⎝⎭因为1212x x <<<+∞,所以210x x ->,12210,210x x ->->; 所以可得1212122112112x x x x +-⋅>-+,所以()()120f x f x ->,即()()12f x f x >;所以函数()f x 在1,2x ∞⎛⎫∈+ ⎪⎝⎭上为单调减函数, (2)设()()2x g x f x =- ,由(1)得()f x 在1,2x ∞⎛⎫∈+ ⎪⎝⎭上为单调减函数, 所以()()2x g x f x =-在[]2,5上单调递减;所以()()2x g x f x =-在[]2,5上的最大值为()252log 63g n =≥-. 由题意知()n g x ≥在[]2,5上的最大值,所以25log 63n ≥-.。

高中数学第三章函数的概念与性质专项训练题单选题1、若定义在R 上的函数f (x )对任意两个不相等的实数a ，b ，总有f(a)−f(b)a−b>0成立，则必有（ ）A ．f (x )在R 上是增函数B ．f (x )在R 上是减函数C ．函数f (x )先增后减D ．函数f (x )先减后增 答案：A分析：根据条件可得当a <b 时，f (a )<f (b )，或当a >b 时，f (a )>f (b )，从而可判断. 由f(a)−f(b)a−b>0知f (a )-f (b )与a -b 同号，即当a <b 时，f (a )<f (b )，或当a >b 时，f (a )>f (b )，所以f (x )在R 上是增函数. 故选：A.2、若函数y =√ax 2+4x +1的值域为[0,+∞)，则a 的取值范围为（ ） A ．(0,4)B ．(4,+∞)C ．[0,4]D ．[4,+∞) 答案：C分析：当a =0时易知满足题意；当a ≠0时，根据f (x )的值域包含[0,+∞)，结合二次函数性质可得结果. 当a =0时，y =√4x +1≥0，即值域为[0,+∞)，满足题意； 若a ≠0，设f (x )=ax 2+4x +1，则需f (x )的值域包含[0,+∞)， ∴{a >0Δ=16−4a ≥0，解得：0<a ≤4；综上所述：a 的取值范围为[0,4]. 故选：C.3、若函数f (x )=x α的图象经过点(9,13)，则f (19)=（ ） A ．13B ．3C ．9D ．8答案：B分析：将(9,13)代入函数解析式，即可求出α，即可得解函数解析式，再代入求值即可.解：由题意知f (9)=13，所以9α=13，即32α=3−1，所以α=−12，所以f (x )=x −12，所以f (19)=(19)−12=3.故选：B4、已知幂函数y =x m 2−2m−3(m ∈N ∗)的图象关于y 轴对称，且在(0,+∞)上单调递减，则满足(a +1)−m3<(3−2a )−m 3的a 的取值范围为（ ）A ．(0,+∞)B ．(−23,+∞) C ．(0,32)D ．(−∞,−1)∪(23,32)答案：D分析：由条件知m 2−2m −3<0，m ∈N ∗，可得m ＝1．再利用函数y =x −13的单调性，分类讨论可解不等式. 幂函数y =x m2−2m−3(m ∈N ∗)在(0,+∞)上单调递减，故m 2−2m −3<0，解得−1<m <3．又m ∈N ∗，故m ＝1或2．当m ＝1时，y =x −4的图象关于y 轴对称，满足题意； 当m ＝2时，y =x −3的图象不关于y 轴对称，舍去，故m ＝1． 不等式化为(a +1)−13<(3−2a )−13，函数y =x −13在(−∞,0)和(0,+∞)上单调递减，故a +1>3−2a >0或0>a +1>3−2a 或a +1<0<3−2a ，解得a <−1或23<a <32．故应选：D ．5、已知函数f (x +1)的定义域为(−1,1)，则f (|x |)的定义域为（ ） A ．(−2,2)B ．(−2,0)∪(0,2) C ．(−1,0)∪(0,1)D ．(−12,0) 答案：B分析：根据抽象函数定义域的求法求得正确答案. 依题意函数f (x +1)的定义域为(−1,1)， −1<x <1⇒0<x +1<2， 所以0<|x |<2，解得−2<x<0或0<x<2，所以f(|x|)的定义域为(−2,0)∪(0,2).故选：B6、已知函数f(x)是定义在R上的偶函数，f(x)在[0,+∞)上单调递减，且f(3)=0，则不等式(2x−5)f(x−1)<0的解集为（）A．(−2,52)∪(4,+∞)B．(4,+∞)C．(−∞,−2)∪[52,4]D．(−∞,−2)答案：A分析：根据偶函数的性质及区间单调性可得(−∞,0)上f(x)单调递增且f(−3)=f(3)=0，进而确定f(x)的区间符号，讨论{2x−5>0f(x−1)<0、{2x−5<0f(x−1)>0求解集即可. 由题设，(−∞,0)上f(x)单调递增且f(−3)=f(3)=0，所以(−∞,−3)、(3,+∞)上f(x)<0，(−3,3)上f(x)>0，对于(2x−5)f(x−1)<0，当{2x−5>0f(x−1)<0，即{x>52x−1<−3或{x>52x−1>3，可得x>4；当{2x−5<0f(x−1)>0，即{x<52−3<x−1<3，可得−2<x<52；综上，解集为(−2,52)∪(4,+∞).故选：A7、已知函数f(x)是定义在R上的奇函数，且x>1时，满足f(2−x)=−f(x)，当x∈(0,1]时，f(x)=x2，则f(−2021)+f(2022)=（）A．−4B．4C．−1D．1答案：C分析：由已知条件可得x>1时f(x+2)=f(x)，然后利用f(−2021)+f(2022)=−f(1)+f(0)求解即可.因为函数f(x)是定义在R上的奇函数，且x>1时，满足f(2−x)=−f(x)，所以f(0)=0，f(2−x)=−f(x)=f(−x)，即可得x>1时f(x+2)=f(x)，因为当x∈(0,1]时，f(x)=x2，所以f(−2021)+f(2022)=−f(2×1010+1)+f(2×1011+0)=−f(1)+f(0)=−1+0=−1， 故选：C 8、函数f (x )=√−x 2+5x+6x+1的定义域（ ）A ．(−∞,−1]∪[6,+∞)B ．(−∞,−1)∪[6,+∞)C ．(−1,6]D ．[2,3] 答案：C分析：解不等式组{−x 2+5x +6≥0x +1≠0得出定义域.{−x 2+5x +6≥0x +1≠0，解得−1<x ⩽6即函数f (x )的定义域(−1,6] 故选：C 多选题9、对任意两个实数a,b ，定义min{a ，b}={a,a ≤b,b,a >b,若f (x )=2−x 2，g (x )=x 2，下列关于函数F (x )=min {f (x ),g (x )}的说法正确的是（ ） A ．函数F (x )是偶函数 B ．方程F (x )=0有三个解C ．函数F (x )在区间[−1,1]上单调递增D ．函数F (x )有4个单调区间 答案：ABD分析：结合题意作出函数F (x )=min {f (x ),g (x )}的图象，进而数形结合求解即可.解：根据函数f (x )=2−x 2与g (x )=x 2，，画出函数F (x )=min {f (x ),g (x )}的图象，如图． 由图象可知，函数F (x )=min {f (x ),g (x )}关于y 轴对称，所以A 项正确； 函数F (x )的图象与x 轴有三个交点，所以方程F (x )=0有三个解，所以B 项正确；函数F (x )在(−∞,−1]上单调递增，在[−1,0]上单调递减，在上单调递增，在[1,+∞)上单调递减，所以C[0,1]项错误，D项正确．故选：ABD10、下列各组函数是同一函数的是（）A．y=|x|x与y=1B．y=√(x−1)2与y=x−1C．y=(√x)2x 与y=(√x)2D．y=x3+xx2+1与y=x答案：CD分析：根据同一函数的概念，逐一分析各个选项，即可得答案.对于A：函数y=|x|x的定义域为x≠0，函数y=1定义域为R，两函数定义域不同，故不是同一函数；对于B：函数y=√(x−1)2定义域为R，化简可得y=|x−1|，与y=x−1解析式不同，故不是同一函数；对于C：函数y=(√x)2x 定义域为x>0，化简可得y=1(x>0)，函数y=(√x)2定义域为x>0，化简可得y=1(x>0)，故为同一函数；对于D：函数y=x3+xx2+1定义域为R，化简可得y=x，与y=x为同一函数.故选：CD11、如图所示是函数y=f(x)的图象，图中x正半轴曲线与虚线无限接近但是永不相交，则以下描述正确的是（）A．函数f(x)的定义域为[−4,4)B．函数f(x)的值域为[0,+∞)C．此函数在定义域内是增函数D．对于任意的y∈(5,+∞)，都有唯一的自变量x与之对应答案：BD分析：利用函数的图象判断.由图象知：A.函数f(x)的定义域为[−4,0]∪[1,4)，故错误；B.函数f(x)的值域为[0,+∞)，故正确；C. 函数f(x)在[−4,0]，[1,4)上递增，但在定义域内不单调，故错误；D.对于任意的y∈(5,+∞)，都有唯一的自变量x与之对应，故正确；故选：BD12、已知函数y=(m−1)x m2−m为幂函数，则该函数为（）A．奇函数B．偶函数C．区间(0,+∞)上的增函数D．区间(0,+∞)上的减函数答案：BC分析：由幂函数的概念可得m的值，根据幂函数的性质可得结果.由y=(m−1)x m2−m为幂函数，得m−1=1，即m=2，则该函数为y=x2，故该函数为偶函数，且在区间(0,+∞)上是增函数，故选：BC.13、已知函数f(x)是定义在[−4,0)∪(0,4]上的奇函数，当x∈(0,4]时，f(x)的图象如图所示，那么满足不等式f(x)−3x+1−3≥0的x的可能取值是（）3A ．－4B ．－1C ．12D ．2 答案：AC分析：把“求f(x)−3x+1−33≥0的解集”转化为“求f (x )≥3x −1的解集”，进而转化为观察两个函数图象的特征，即可求出不等式的解集．因为函数f (x )是定义在[−4,0)∪(0,4]上的奇函数，由题意，画出函数f (x )在[−4,0)∪(0,4]上的图象（如图），在同一坐标系内画出y =3x −1的图象，因为f (2)=89，所以f (−2)=−f (2)=−89=3−2−1，又f (1)=2=31−1，所以f (x )的图象与y =3x −1的图象交于(−2,−89)和(1,2)两点，f (x )−3x+1−33≥0即为f (x )≥3x −1，由图象可得，只需−4≤x ≤−2或0<x ≤1，故A ，C 可能取到故选：AC ． 填空题14、函数y =√x 2−1的单调递减区间为___________. 答案：(−∞,−1](或(−∞,−1)都对)解析：利用复合函数的单调性，同增异减，即可得到答案； 令t =x 2−1，则y =√t ，∵ t =x 2−1在(−∞,−1)单调递减，y =√t 在(0,+∞)单调递增， 根据复合函数的单调性可得：y =√x 2−1在(−∞,−1)单调递减，所以答案是：(−∞,−1).15、为满足人民对美好生活的向往，环保部门要求相关企业加强污水治理，排放未达标的企业要限期整改，的大小评价在[a,b]这段时间内企业污水治理设企业的污水排放量W与时间t的关系为W=f(t)，用−f(b)−f(a)b−a能力的强弱，已知整改期内，甲、乙两企业的污水排放量与时间的关系如下图所示.给出下列四个结论：①在[t1,t2]这段时间内，甲企业的污水治理能力比乙企业强；②在t2时刻，甲企业的污水治理能力比乙企业强；③在t3时刻，甲、乙两企业的污水排放都已达标；④甲企业在[0,t1],[t1,t2],[t2,t3]这三段时间中，在[0,t1]的污水治理能力最强．其中所有正确结论的序号是____________________．答案：①②③分析：根据定义逐一判断，即可得到结果表示区间端点连线斜率的负数，−f(b)−f(a)b−a在[t1,t2]这段时间内，甲的斜率比乙的小，所以甲的斜率的相反数比乙的大，因此甲企业的污水治理能力比乙企业强；①正确；甲企业在[0,t1],[t1,t2],[t2,t3]这三段时间中，甲企业在[t1,t2]这段时间内，甲的斜率最小，其相反数最大，即在[t1,t2]的污水治理能力最强．④错误；在t2时刻，甲切线的斜率比乙的小，所以甲切线的斜率的相反数比乙的大，甲企业的污水治理能力比乙企业强；②正确；在t3时刻，甲、乙两企业的污水排放量都在污水打标排放量以下，所以都已达标；③正确；所以答案是：①②③小提示：本题考查斜率应用、切线斜率应用、函数图象应用，考查基本分析识别能力，属中档题.16、已知幂函数f(x)的图象过点(3,13)，则此函数的解析式为______．答案：f(x)=x−1##f(x)=1x分析：设出幂函数f(x)，代入点(3,13)即可求解.由题意，设f(x)=xα，代入点(3,13)得13=3α，解得α=−1，则f(x)=x−1.所以答案是：f(x)=x−1.解答题17、已知函数f(x)=x2x2+1(1)证明：f(x)为偶函数；(2)判断g(x)=f(x)+x的单调性并用定义证明；(3)解不等式f(x)−f(x−2)+2x>2答案：(1)证明见解析(2)g(x)为R上的增函数，证明见解析(3)(1,+∞)分析：（1）根据奇偶性的定义证明即可；（2）首先得到g(x)的解析式，再利用定义法证明函数的单调性，按照设元、作差、变形、判断符号，下结论的步骤完成即可；（3）根据函数的单调性将函数不等式转化为自变量的不等式，解得即可；（1）证明：f(x)的定义域为R，又f(−x)=(−x)2(−x)2+1=x2x2+1=f(x)，故f(x)为偶函数；（2）解：g(x)=f(x)+x=x2x2+1+x，所以g(x)为R上的增函数，证明：任取x1，x2∈R，且x1>x2，g(x1)−g(x2)=x12x12+1+x1−(x22x22+1+x2)=x1−x2+x12x12+1−x22x22+1=x1−x2+x12(x22+1)−x22(x12+1) (x12+1)(x22+1)=x1−x2+x12−x22(x12+1)(x22+1)=(x1−x2)[1+x1+x2(x12+1)(x22+1)]=(x1−x2)[x12x22+x12+x22+1+x1+x2 (x12+1)(x22+1)]=(x1−x2)[x12x22+(x1+12)2+(x2+12)2+12(x12+1)(x22+1)].∵x1>x2，∴x2−x2>0，又x12x22+(x1+12)2+(x2+12)2+12(x12+1)(x22+1)>0，∴(x1−x2)[x12x22+(x1+12)2+(x2+12)2+12(x12+1)(x22+1)]>0，即g(x1)>g(x2)，∴g(x)为R上的增函数；（3）解：不等式f(x)−f(x−2)+2x>2，等价于f(x)+x>f(x−2)+2−x=f(2−x)+2−x即g(x)>g(2−x)，∵g(x)为R上的增函数，∴x>2−x，解得x>1，故不等式的解集为(1,+∞).18、函数f(x)对任意x，y∈R，总有f(x+y)=f(x)+f(y)，当x<0时，f(x)<0，且f(1)=13．（1）证明f(x)是奇函数；（2）证明f(x)在R上是单调递增函数；（3）若f(x)+f(x−3)≥−1，求实数x的取值范围．答案：（1）证明见解析；（2）证明见解析；（3）[0,+∞)．分析：（1）先用赋值法求出f(0)=0，令y=−x，即可根据定义证明f(x)是奇函数；（2）利用定义法证明f(x)是R上的增函数；（3）先把f(x)+f(x−3)≥−1转化为f(2x−3)≥f(−3)，利用单调性解不等式即可．（1）令x =y =0，则f (0)=f (0)+f (0)，解得f (0)=0，令y =−x ，则f (0)=f (x )+f (−x )，即f (x )+f (−x )=0，即f (−x )=−f (x )， 易知f (x )的定义域为R ，关于原点对称，所以函数f (x )是奇函数；（2）任取x 1，x 2∈R ，且x 1<x 2，则x 1−x 2<0，因为当x <0时，f (x )<0，所以f (x 1−x 2)<0，则f (x 1)−f (x 2)=f (x 1)+f (−x 2)=f (x 1−x 2)<0，即f (x 1)<f (x 2)，所以函数f (x )是R 上的增函数；（3）由f (1)=13，得f (2)=23，f (3)=1，又由f (x )是奇函数得f (−3)=−1. 由f (x )+f (x −3)≥−1，得f (2x −3)≥f (−3)，因为函数f (x )是R 上的增函数， 所以2x −3≥−3，解得x ≥0，故实数x 的取值范围为[0,+∞)．。

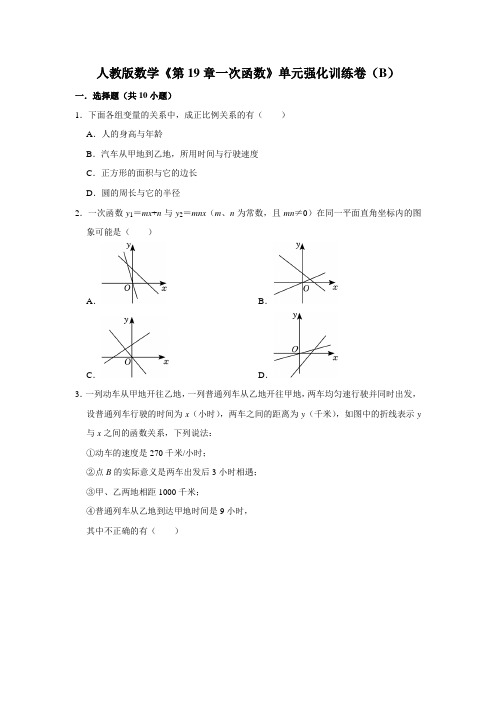
人教版数学《第19章一次函数》单元强化训练卷（B）一．选择题（共10小题）1．下面各组变量的关系中，成正比例关系的有（）A．人的身高与年龄B．汽车从甲地到乙地，所用时间与行驶速度C．正方形的面积与它的边长D．圆的周长与它的半径2．一次函数y1＝mx+n与y2＝mnx（m、n为常数，且mn≠0）在同一平面直角坐标内的图象可能是（）A．B．C．D．3．一列动车从甲地开往乙地，一列普通列车从乙地开往甲地，两车均匀速行驶并同时出发，设普通列车行驶的时间为x（小时），两车之间的距离为y（千米），如图中的折线表示y 与x之间的函数关系，下列说法：①动车的速度是270千米/小时；②点B的实际意义是两车出发后3小时相遇；③甲、乙两地相距1000千米；④普通列车从乙地到达甲地时间是9小时，其中不正确的有（）A．1个B．2个C．3个D．4个4．一次函数y=−x+12的图象不经过下列哪个象限（）A．第一象限B．第二象限C．第三象限D．第四象限5．若P（m，y1），Q（m﹣1，y2）是一函数y＝﹣x+3图象上的两点，则y1与y2的大小关系是（）A．y1＜y2B．y1＞y2C．y1＝y2D．不能确定6．在弹性限度内，弹簧伸长的长度与所挂物体的质量成正比．某弹簧不挂物体时长15cm；当所挂物体质量为3kg时，弹簧长16.8cm．则弹簧长度y（cm）与所挂物体质量x（kg）之间的函数表达式为（）A．y＝﹣0.6x+15B．y＝0.6x﹣15C．y＝﹣0.6x﹣15D．y＝0.6x+157．在平面直角坐标系中，已知一次函数y＝﹣x+5的图象经过A（﹣3，y1），B（2，y2）两点，则y1，y2的大小关系为（）A．y1＜y2B．y1＞y2C．y1＝y2D．无法确定8．满足k＞0，b＝3的一次函数y＝kx+b的图象大致是（）A．B．C．D．9．已知A（﹣1，a），B（2，b）两点都在关于x的一次函数y＝﹣x+m的图象上，则a，b 的大小关系为（）A．a≥b B．a＞b C．a＜b D．无法确定10．正比例函数y＝kx（k≠0）和一次函数y＝x﹣k在同一个直角坐标系内的图象大致是（）A．B．C．D．二．填空题（共5小题）11．如图，已知A地在B地正南方3千米处，甲乙两人同时分别从A，B两地向正北方向匀速直行，他们与A地的距离s（千米）与所行的时间t（小时）之间的函数关系图象用如图所示的AC和BD表示，当他们行走3小时后，他们之间的距离为千米．12．如图，直线y＝2x与y＝kx+b相交于点P（m，2），则关于x的方程2x＝kx+b的解是．13．在y＝（k﹣1）x+k2﹣1中，若y是x的正比例函数，则k值为．14．如图，在平面直角坐标系中，一次函数y＝2x﹣2的图象分别交x、y轴于点A、B，将直线AB绕点B按顺时针方向旋转45°，交x轴于点C，则直线BC的函数表达式是．15．甲、乙两车分别从A，B两地同时相向匀速行驶．当乙车到达A地后，继续保持原速向远离B的方向行驶，而甲车到达B地后立即掉头，并保持原速与乙车同向行驶，经过一段时间后两车同时到达C地．设两车行驶的时间为x（小时），两车之间的距离为y（千米），y与x之间的函数关系如图所示，当甲车到达B地时，乙车距离A地千米．三．解答题（共8小题）16．东明一中门口有甲乙两个图书超市，他们都经营同一种练习本，两个超市的标价都是1元．甲超市的优惠条件是：购买10本以上，从第11本开始按标价的7折卖；乙超市的优惠条件是：从第1本开始就按标价的8.5折卖．（1）请分别求出购买的数量x（本）与所花的钱数y甲（元），y乙（元）之间的函数表达式；（2）小明要买22的练习本，到哪家超市购买较省钱？17．已知一次函数y＝kx+b的图象经过点A（﹣4，0），B（2，6）两点．（1）在平面直角坐标系中，画出这个函数的图象；（2）求一次函数y＝kx+b的表达式．18．为了节能减排，我市某校准备购买某种品牌的节能灯，已知3只A型节能灯和5只B 型节能灯共需50元，1只A型节能灯和3只B型节能灯共需26元．（1）求1只A型节能灯和1只B型节能灯的售价各是多少元；（2）学校准备购买这两种型号的节能灯共200只，要求购买A型号的节能灯a只，记购买两种型号的节能灯的总费用为W元．①求W与a的函数关系式；②当a＝80时，求购买两种型号的节能灯的总费用是多少？19．一个正比例函数的图象经过点A（﹣3，6），B（2，a），C（b，﹣1），求a，b的值．20．如图，已知直线y＝kx+b的图象经过点A（0，﹣4），B（3，2），且与x轴交于点C．（1）求直线y＝kx+b的解析式；（2）求△BOC的面积．21．已知，点P（2，m）是第一象限内的点，直线P A交y轴于点B（0，2），交x轴负半轴于点A．联结OP，S△AOP＝6．（1）求△BOP的面积；（2）求点A的坐标和m的值．22．小明在学习一次函数后，对形如y＝k（x﹣m）+n（其中k，m，n为常数，且k≠0）的一次函数图象和性质进行了探究，过程如下：【特例探究】（1）如图所示，小明分别画出了函数y＝（x﹣1）+2，y＝﹣（x﹣1）+2，y＝2（x﹣1）+2的图象．请你根据列表、描点、连线的步骤在图中画出函数y＝﹣2（x﹣1）+2的图象．【深入探究】（2）通过对上述几个函数图象的观察、思考，你发现y＝k（x﹣1）+2（k为常数，且k ≠0）的图象一定会经过的点的坐标是．【得到性质】（3）函数y＝k（x﹣m）+n（其中k、m、n为常数，且k≠0）的图象一定会经过的点的坐标是．【实践运用】（4）已知一次函数y＝k（x+2）+3（k为常数，且k≠0）的图象一定过点N，且与y轴相交于点A ，若△OAN 的面积为2，则k 的值为 ．23．小明、小刚两人同时从家步行到乙地游玩，小明开始以50m /min 的速度行走，行走了一段路程后开始加快速度，两人到小明家的距离s （m ）与行走时间t （min ）之间的函数图象如图所示，根据图象提供的信息解答下列问题．（1）a ＝ min ．（2）若小刚的速度是小明提速后速度的35． ①小刚到达乙地的时间为 min ；②求两人相遇时离乙地的距离．。

函数的表示法训练题（附答案）1．下列各图中，不能是函数f(x)图象的是()解析：选C.结合函数的定义知，对A、B、D，定义域中每一个x都有唯一函数值与之对应；而对C，对大于0的x而言，有两个不同值与之对应，不符合函数定义，故选C.2．若f(1x)＝11＋x，则f(x)等于()A.11＋x(x≠－1)B.1＋xx(x≠0)C.x1＋x(x≠0且x≠－1)D．1＋x(x≠－1)解析：选C.f(1x)＝11＋x＝1x1＋1x(x≠0)，∴f(t)＝t1＋t(t≠0且t≠－1)，∴f(x)＝x1＋x(x≠0且x≠－1)．3．已知f(x)是一次函数，2f(2)－3f(1)＝5,2f(0)－f(－1)＝1，则f(x)＝() A．3x＋2B．3x－2C．2x＋3D．2x－3解析：选B.设f(x)＝kx＋b(k≠0)，∵2f(2)－3f(1)＝5,2f(0)－f(－1)＝1，∴k－b＝5k＋b＝1，∴k＝3b＝－2，∴f(x)＝3x－2.4．已知f(2x)＝x2－x－1，则f(x)＝________.解析：令2x＝t，则x＝t2，∴f(t)＝t22－t2－1，即f(x)＝x24－x2－1.答案：x24－x2－11．下列表格中的x与y能构成函数的是()A.x非负数非正数y1－1B.x奇数0偶数y10－1C.x有理数无理数y1－1D.x自然数整数有理数y10－1解析：选C.A中，当x＝0时，y＝±1；B中0是偶数，当x＝0时，y＝0或y＝－1；D中自然数、整数、有理数之间存在包含关系，如x＝1∈N(Z，Q)，故y的值不唯一，故A、B、D均不正确．2．若f(1－2x)＝1－x2x2(x≠0)，那么f(12)等于()A．1B．3C．15D．30解析：选C.法一：令1－2x＝t，则x＝1－t2(t≠1)，∴f(t)＝－－1，∴f(12)＝16－1＝15.法二：令1－2x＝12，得x＝14，∴f(12)＝16－1＝15.3．设函数f(x)＝2x＋3，g(x＋2)＝f(x)，则g(x)的表达式是()A．2x＋1B．2x－1C．2x－3D．2x＋7解析：选B.∵g(x＋2)＝2x＋3＝2(x＋2)－1，∴g(x)＝2x－1.4．某学生离家去学校，由于怕迟到，所以一开始就跑步，等跑累了再走余下的路程，在下图中纵轴表示离学校的距离，横轴表示出发后的时间，则下图中较符合此学生走法的是()解析：选D.由于纵轴表示离学校的距离，所以距离应该越来越小，排除A、C，又一开始跑步，速度快，所以D符合．5．如果二次函数的二次项系数为1且图象开口向上且关于直线x＝1对称，且过点(0,0)，则此二次函数的解析式为()A．f(x)＝x2－1B．f(x)＝－(x－1)2＋1C．f(x)＝(x－1)2＋1D．f(x)＝(x－1)2－1解析：选D.设f(x)＝(x－1)2＋c，由于点(0,0)在函数图象上，∴f(0)＝(0－1)2＋c＝0，∴c＝－1，∴f(x)＝(x－1)2－1.6．已知正方形的周长为x，它的外接圆的半径为y，则y关于x的函数解析式为()A．y＝12x(x>0)B．y＝24x(x>0)C．y＝28x(x>0)D．y＝216x(x>0)解析：选C.设正方形的边长为a，则4a＝x，a＝x4，其外接圆的直径刚好为正方形的一条对角线长．故2a＝2y，所以y＝22a＝22×x4＝28x. 7．已知f(x)＝2x＋3，且f(m)＝6，则m等于________．解析：2m＋3＝6，m＝32.答案：328.如图，函数f(x)的图象是曲线OAB，其中点O，A，B的坐标分别为(0,0)，(1,2)，(3,1)，则的值等于________．解析：由题意，f(3)＝1，∴＝f(1)＝2.答案：29．将函数y＝f(x)的图象向左平移1个单位，再向上平移2个单位得函数y＝x2的图象，则函数f(x)的解析式为__________________．解析：将函数y＝x2的图象向下平移2个单位，得函数y＝x2－2的图象，再将函数y＝x2－2的图象向右平移1个单位，得函数y＝(x－1)2－2的图象，即函数y＝f(x)的图象，故f(x)＝x2－2x－1.答案：f(x)＝x2－2x－110．已知f(0)＝1，f(a－b)＝f(a)－b(2a－b＋1)，求f(x)．解：令a＝0，则f(－b)＝f(0)－b(－b＋1)＝1＋b(b－1)＝b2－b＋1.再令－b＝x，即得f(x)＝x2＋x＋1.11．已知f(x＋1x)＝x2＋1x2＋1x，求f(x)．解：∵x＋1x＝1＋1x，x2＋1x2＝1＋1x2，且x＋1x≠1，∴f(x＋1x)＝f(1＋1x)＝1＋1x2＋1x＝(1＋1x)2－(1＋1x)＋1.∴f(x)＝x2－x＋1(x≠1)．12．设二次函数f(x)满足f(2＋x)＝f(2－x)，对于x∈R恒成立，且f(x)＝0的两个实根的平方和为10，f(x)的图象过点(0,3)，求f(x)的解析式．解：∵f(2＋x)＝f(2－x)，∴f(x)的图象关于直线x＝2对称．于是，设f(x)＝a(x－2)2＋k(a≠0)，则由f(0)＝3，可得k＝3－4a，∴f(x)＝a(x－2)2＋3－4a＝ax2－4ax＋3.∵ax2－4ax＋3＝0的两实根的平方和为10，∴10＝x21＋x22＝(x1＋x2)2－2x1x2＝16－6a，∴a＝1.∴f(x)＝x2－4x＋3.。

函数概念与性质1.函数定义域1、函数x x x y +-=)1(的定义域为A ．{}0≥x x B ．{}1≥x x C ．{}{}01 ≥x x D ．{}10≤≤x x2、函数x x y +-=1的定义域为A ．{}1≤x x B ．{}0≥x x C ．{}01≤≥x x x 或 D ．{}10≤≤x x3、若函数)(x f y =的定义域是[]2,0，则函数1)2()(-=x x f x g 的定义域是A ．[]1,0B ．[)1,0C ．[)(]4,11,0D ．()1,04、函数的定义域为)4323ln(1)(22+--++-=x x x x xx f A ．(][)+∞-∞-,24, B ．()()1,00,4 - C ．[)(]1,00,4 - D ．[)()1,00,4 -5、函数)20(3)(≤<=x x f x 的反函数的定义域为A ．()+∞,0 B ．(]9,1 C ．()1,0 D ．[)+∞,96、函数41lg)(--=x xx f 的定义域为 A ．()4,1 B ．[)4,1 C ．()()+∞∞-,41, D ．(]()+∞∞-,41,7、函数21lg )(x x f -=的定义域为A ．[]1,0 B ．()1,1- C ．[]1,1- B ．()()+∞-∞-,11,8、已知函数xx f -=11)(的定义域为M ，)1ln()(x x g +=的定义域为N ，则=N MA ．{}1->x xB ．{}1<x xC ．{}11<<-x xD ．Φ9、函数)13lg(13)(2++-=x xx x f 的定义域是A ．⎪⎭⎫ ⎝⎛+∞-,31 B ．⎪⎭⎫ ⎝⎛-1,31 C ．⎪⎭⎫ ⎝⎛-31,31 D ．⎪⎭⎫ ⎝⎛-∞-31,10、函数的定义域2log 2-=x y 是A ．()+∞,3 B ．[)+∞,3 C ．()+∞,4 D ．[)+∞,411、函数的定义域x y 2log =是A ．(]1,0 B ．()+∞,0 C ．()+∞,1 D ．[)+∞,112、函数)1(log 12)(2---=x x x f 的定义域为 ．2.函数与值域练习题一、填空题1、定义在R 上的函数()f x 满足()()()2(,),(1)2f x y f x f y xy x y R f +=++∈=，则(0)f = ，(2)f -= 。

高中同步测控优化训练(十)第二章 函数(二)(B 卷)说明：本试卷分为第Ⅰ、Ⅱ卷两部分，共100分，考试时间90分钟.第Ⅰ卷(选择题 共30分)一、选择题(本大题共10小题，每小题3分，共30分)1.设f :x →y =2x 是A →B 的映射，已知集合B ={0,1,2,3,4},则A 满足 A.A ={1，2，4，8，16} B.A ={0，1，2，log 23} C.A ⊆{0,1,2,log 23} D.不存在满足条件的集合 解析:A 中每个元素在集合中都有象，令2x =0，方程无解. 分别令2x =1,2,3,4,解得x =0,1,log 23,2. 答案:C2.若a 、b 是任意实数,且a ＞b ,则 A.a 2＞b 2B.a b ＜1 C.lg(a －b )＞0 D.(21)a ＜(21)b答案:D3.设1＜x ＜a ，那么log a x 2、(log a x )2、log a (log a x )之间的大小顺序是 A.log a x 2＜(log a x )2＜log a (log a x ) B.log a x 2＜log a (log a x )＜(log a x )2 C.log a (log a x )＜(log a x )2＜log a x 2 D.(log a x )2＜log a x 2＜log a (log a x )解法一:令x =2,a =4,则log a x 2=log 44=1, (log a x )2=(log 42)2=41log a (log a x )=log 4(log 42)=－21，∴log a (log a x )＜(log a x )2＜log a x 2. 解法二:∵1＜x ＜a ，∴0＜log a x ＜1. log a x 2=2log a x ＞log a x ＞0,0＜(log a x )2＜log a x ,log a (log a x )＜log a 1=0, ∴log a (log a x )＜(log a x )2＜log a x 2. 答案:C 4.已知函数f (x )=⎩⎨⎧≤>0),(x 3),0(log2xx x 则f ［f (41)］的值是A.9B.91C.－9D.－91解析:f (41)=log 241=－2,f (－2)=3－2=91.答案:B5.当函数f (x )=2－|x －1|－m 的图象与x 轴有交点时，实数m 的取值范围是 A.－1≤m ＜0 B.0≤m ≤1 C.0＜m ≤1 D.m ≥1解析:函数f (x )=2－|x －1|－m 的图象与x 轴有交点，即方程2－|x －1|－m =0有解，∴m=2－|x －1|. ∴0＜m ≤1. 答案:C6.已知f (x )=a x ,g (x )=log a x (a >0且a ≠1)，若f (3)g (3)<0,则f (x )与g (x )在同一坐标系内的图象可能是ABC解析:∵f (3)=a 3>0,∴g (3)=log a 3<0. ∴0<a <1. 答案:C 7.若函数y =21log(2－log 2x )的值域是(－∞,0)，则其定义域是A.x <2B.0<x <2C.0<x <4D.2<x <4 解析:令2－log 2x =u ,由题意知u >1log 2x <1,故0<x <2. 答案:B8.世界人口已超过56亿,若按千分之一的年增长率计算,则两年增长的人口就可相当于 一个A.新加坡(270万)B.香港(560万)C.瑞士(700万)D.上海(1200万) 解析:本题考查指数型函数的应用.若按10001的年增长率计算,则两年后增长的人口数y =560000(1+10001)2－560000≈1120.56(万).答案:D9.已知f (x )的图象关于y 轴对称,且它在［0,+∞)上是减函数,若f (lg x )＞f (1),则x 的取值范围是A.(101,1) B.(0,101)∪(1,+∞)C.( 101,10)D.(0,1)∪(10,+∞)解析:若函数f (x )的图象关于y 轴对称,则在y 轴两侧的对称区间上 ,它们的单调性相反. 由题可知,0≤|lg x |＜1, 即－1＜lg x ＜1,lg 101＜lg x ＜lg10,所以101＜x ＜10.答案:C现准备用下列函数中的一个近似地表示这些数据满足的规律，其中最接近的一个是A.v =log 2tB.v =21logtC.v =212-t D.v =2t －2解析:五组数据，取近似值1.99≈2;4.04≈4;5.1≈5,18.01≈18，代入验证可知v =212-t最接近.答案:C第Ⅱ卷(非选择题 共70分)二、填空题(本大题共4小题，每小题4分，共16分) 11.方程log 3(1－2·3x )=2x +1的解x =_______. 解析:32x +1=1－2·3x ，即3(3x )2+2·3x －1=0. 解得3x =31,故x =－1.答案:－112.3log9(lg2－1)2+5log25(log0.5－2)2等于_________.解析:3log9(log2－1)2+5log25(log0.5－2)2=22529)25.0(lg log21)12(lg log 21259-∙-∙+=9log9(1－lg2)+25log25(2－lg0.5)=1－lg2+2－lg0.5=3－lg(2×0.5)=3. 答案:313.国家规定的个人稿酬纳税方法是：不超过800元的不纳税；超过800元而不超过4000元的按超过800元的14%纳税；超过4000元按全部稿酬的11%纳税.某人出版了一本书，共纳税420元，他的稿费为_______元.解析:若其稿费为4000元，则应纳税3200×14%=448>420. 故稿费应小于4000元，设为x 元. 则(x －800)14%=420,解得x =3800(元).答案:380014.若函数f (x )=lg(x 2+ax －a －1)在区间［2,+∞)上单调递增,则实数a 的取值范围是_________.解析:本题考查复合函数单调性的判定方法,要注意判断函数的单调性必须在函数的定义域内进行.∵函数f (x )在区间［2,+∞)上单调递增,∴－2a ≤2,且x =2时,x 2+ax －a －1＞0,即⎪⎩⎪⎨⎧>--+≤-,0124,22a a a∴⎩⎨⎧->-≥.3,4a a ∴a ＞－3,即实数a 的取值范围是(－3,+∞). 答案:(－3,+∞)三、解答题(本大题共5小题，共54分.解答应写出文字说明、证明过程或演算步骤) 15.(本小题满分8分)某摩托车生产企业,上年度生产摩托车的投入成本为1万元/辆,出厂价为1.2万元/辆,年销售量为1000辆.本年度为适应市场需求,计划提高产品档次,适当增加投入成本.若每辆车投入成本增加的比例为x (0＜x ＜1),则出厂价相应的提高比例为0.75x ,同时预计年销售量增加的比例为0.6x .(1)写出本年度预计的年利润y 与投入增加的比例x 的关系式;(2)为使本年度的年利润比上年有所增加,问投入成本增加的比例x 应在什么范围内. 分析:年利润=(出厂价－投入成本)×年销售量.解:(1)由题意,得y =［1.2(1+0.75x )－1×(1+x )］×1000(1+0.6x )(0＜x ＜1). 整理,得y =－60x 2+20x +200(0＜x ＜1).(2)要保证本年度的利润比上年度有所增加,只需⎩⎨⎧<<>⨯--,10,01000)12.1(x y 即⎩⎨⎧<<>+-,10,020602x x x 解得0＜x ＜31,即为保证本年度的利润比上年度有所增加,投入成本的比例应满足0＜x ＜31.16.(本小题满分10分)已知y =log 4(2x +3－x 2). (1)求定义域；(2)求f (x )的单调区间；(3)求y 的最大值，并求取最大值时x 的值. 解:(1)由2x +3－x 2>0,解得－1<x <3. ∴f (x )的定义域为{x |－1<x <3}. (2)令u =2x +3－x 2，则u >0,y =log 4u . 由于u =2x +3－x 2=－(x －1)2+4.再考虑定义域可知，其增区间是(－1，1)，减区间是［1，3).又y =log 4u 在(0,+∞)上为增函数，故该函数单调递增区间为(－1，1)，减区间为［１，３］.(3)∵u =2x +3－x 2=－(x －1)2+4≤4,∴y =log 4u ≤log 44=1.故当x =1，u 取最大值4时，y 取最大值1.17.(本小题满分12分)某电器公司生产A 型电脑.1993年这种电脑每台平均生产成本为5000元,并以纯利润20%确定出厂价.从1994年开始,公司通过更新设备和加强管理,使生产成本逐年降低.到1997年,尽管A 型电脑出厂价仅是1993年出厂价的80%,但却实现了50%纯利润的高效益.(1)求1997年每台A 型电脑的生产成本;(2)以1993年的生产成本为基数,求1993年至1997年生产成本平均每年降低的百分数.(精确到0.01,以下数据可供参考:5=2.236,6=2.449)分析:出厂价=单位商品的成本+单位商品的利润.解:(1)一方面可以根据1993年的出厂价求得1997年的出厂价;另一方面根据题意可把1997年的出厂价用1997年的生产成本表示,列出方程求解.设1997年每台电脑的生产成本为x 元,依题意,得 x (1+50%)=5000×(1+20%)×80%,解得x =3200(元).(2)因为1993年至1997年四年间成本平均每年降低的百分率相等,因此可把1997年每台的生产成本用这个百分率来表示,而这个量应与第(1)问中求得的1997年每台电脑的生产成本相等,据此列出方程求解.设1993年至1997年间每年平均生产成本降低的百分率为y ,则依题意,得5000(1－y )4=3200,解得y 1=1－552,y 2=1+552(舍去).所以,y =1－552≈0.11=11%.即1997年每台电脑的生产成本为3200元,1993年至1997年生产成本平均每年降低11%. 18.(本小题满分12分)已知二次函数f (x )的二次项系数为负数，且对任意x 恒有f (2－x )=f (2+x )成立，解不等式f ［21log(x 2+x +21)］＞f ［21log(2x 2－x +85)］.解:因为对任意x ，恒有f (2－x )=f (2+x )成立，可得二次函数f (x )的对称轴是x =2. ∵x 2+x +21=(x +21)2+41≥41,2x 2－x +85=2(x －41)2+21≥21,∴21log(x 2+x +21)≤21log41=2,21log(2x 2－x +85)≤21log(21)=1.∵二次函数f (x )的二次项系数为负数， ∴在对称轴左侧f (x )为增函数.∴21log(x 2+x +21)＞21log(2x 2－x +85)x 2+x +21＜2x 2－x +85x 2－2x +81＞0x ＜－4144-或x ＞4144+.故不等式的解集为(－∞,4414-)∪(4144+,+∞).19.(本小题满分12分)已知函数f (x )=xx ax122-+的定义域恰为不等式log 2(x +3)+21logx ≤3的解集，且f (x )在定义域内单调递减，求实数a 的取值范围.解:由log 2(x +3)+ 21logx ≤3得log 2(x +3)≤3+log 2x =log 28x . ∴⎩⎨⎧->+≥.3,38x x x ∴x ≥73.设x 2＞x 1≥73,f (x 2)－f (x 1)=112122221212x x ax x x ax-+--+=212121))(1(x x x x x ax -+.∵f (x )在［73，+∞)上单调递减,∴f (x 2)＜f (x 1)，即212121))(1(x x x x x ax -+＜0.∵x 1x 2＞0,x 1－x 2＜0,∴ax 1x 2+1＞0，即a ＞－211x x .由x 2＞x 1≥73知x 1x 2＞499,∴－211x x ＜－949∴a ≥－949.。

高三数学函数专题训练题（附详解）第1卷（选择题）一、单选题1. 已知定义在R 上的可导函数f(x)的导函数为f(x)，满足f '(x) < f(x)，且f(-x) = f(2+x)，f(2)=1，则不等式f(x)< e x 的解集为（ ） A.（-∞，2） B.（2，+∞） C.（1，+∞） D.（0，+∞）2. 函数y=sinx+2|sinx|，x ∈[0，2x]的图像与直线y=k 有且仅有两个不同的交点，则k 的取值范围为（ ）A. k ∈ [0，3]B. k ∈ [1，3]C. k ∈（1，3）D. k ∈（0，3） 3. 已知sina 1+cosa= 2，则 tana =（ ）A. - 43B. - 34C. 43D. 24. 定义在R 上的奇函数f(x)满足f(x+4) = f(x)，当x ∈(0，2)时，f(x)=3x -1，则f(2022)+f(2023)=（ ）A. -2023B. -1C. 1D. 32022 5. 设a=log 20.3，b=0.2，c=（12）0.2，则a,b,c 三者的大小关系为（ ） A. a<b<c B. c<a<b C. b<c<a D. a<c<b6. 设函数f(x)(x ∈R)的导函数为f '(x)，满足f '(x)>f(x)，则当a>0时，f(a)与e a f(0)的大小关系为（ ）A. f(a)>e a f(0)B. f(a)<e a f(0)C. f(a)=e a f(0)D. 不能确定7. 已知f(x)=2x2x +1+ax+cos2x ，若f (π3)=2，则f(-π3)等于（ ）A. -2B. -1C. 0D. 18. 已知函数f(x)=√3sin(ωx+φ)(ω>0,-π2<φ<π2)，A （13，0）为f(x)图像的对称中心，B 、C 是该图像上相邻的最高点和最低点，且|BC|=4，则下列结论正确的是（ ） A. 函数f(x)的对称轴方程为x=43+4k(k ∈Z)B. 若函数f(x )在区间(0，m)内有5个零点，则在此区间内f(x )有且只有2个极小值点C. 函数f(x )在区间(0，2)上单调递增D. f(x -π3)的图象关于y 轴对称9. 已知函数f(x)={|x|x+4√x 36−x，−4<x<2，2≤x<6,若方程f(x)+αx 2=0有5个不等实根，则实数α的取值范围是（ ）A. (-∞，- √24) ∪ {- 13}B. [- 13，- 14] C. [13，√24] D. ( √24，+∞)∪ { 13} 10. 已知F 1，F 2分别为双曲线x 2-y 23=1的左、右焦点，直线l 过点F 2，且与双曲线右支交于A ，B 两点，O 为坐标原点，△AF 1F 2、△BF 1F 2的内切圆的圆心分别为O 1，O 2，则△OO 1O 2面积的取值范围是（ ） A. (1，2√33) B. [1，2√33)C. [1，2√33] D. (1，2√33] 11. 设定义在R 上的函数f(x)与g(x)的导函数分别为f '(x)和g'(x)，若g(x)-f(3-x)=2，f '(x)=g'(x-1)，且g(x+2)为奇函数，g(1)=1。