Rt三角形的性质

第1章直角三角形§1.1直角三角形的性质和判定（Ⅰ）一、复习提问：（1）什么叫直角三角形？（2）直角三角形是一类特殊的三角形，除了具备三角形的性质外，还具备哪些性质? （一）直角三角形性质定理1：直角三角形的两个锐角互余。

练习1（1）在直角三角形中，有一个锐角为520，那么另一个锐角度数（2）在Rt△ABC中，∠C=900，∠A -∠B =300，那么∠A= ，∠B= 。

练习2 在△ABC中，∠ACB=900，CD是斜边AB上的高，那么，（1）与∠B互余的角有（2）与∠A相等的角有。

（3）与∠B相等的角有。

（二）直角三角形的判定定理1提问：“在△ABC中，∠A +∠B =900那么△ABC是直角三角形吗？”归纳：有两个锐角互余的三角形是直角三角形练习3:若∠A= 600，∠B =300，那么△ABC是三角形。

（三）直角三角形性质定理2直角三角形斜边上的中线等于斜边的一半。

三、巩固训练：练习4：在△ABC中，∠ACB=90 °，CE是AB边上的中线，那么与CE相等的线段有_________，与∠A相等的角有_________，若∠A=35°，那么∠ECB= _________。

练习5：已知：∠ABC=∠ADC=90O，E是AC中点。

求证：（1）ED=EB(2)∠EBD=∠EDB（3）图中有哪些等腰三角形？练习6 已知：在△ABC中，BD、CE分别是边AC、AB上的高， M是BC的中点。

如果连接DE,取DE的中点 O,那么MO 与DE有什么样的关系存在?§1.1直角三角形的性质和判定（Ⅰ）EDCBA提出命题：直角三角形斜边上的中线等于斜边的一半 证明命题：（教师引导，学生讨论，共同完成证明过程）推理证明思路： ①作点D 1 ②证明所作点D 1 具有的性质 ③ 证明点D 1 与点D 重合 应用定理：例1、已知：如图，在△ABC 中，∠B=∠C ，AD 是∠BAC 的平分线，E 、F 分别AB 、AC 的中点。

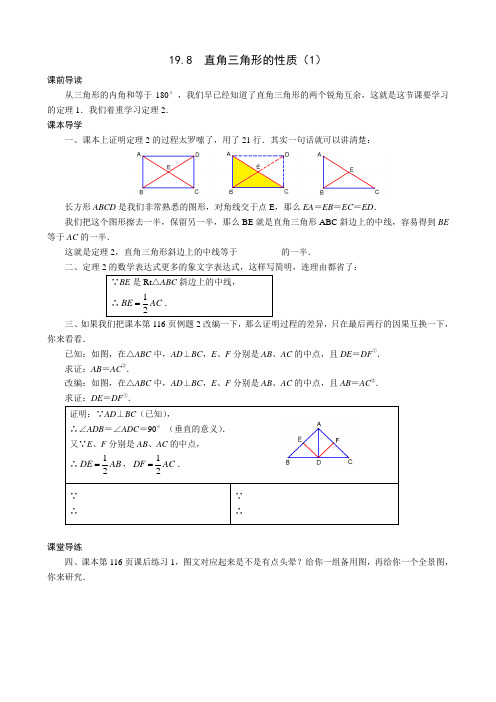
19.8 直角三角形的性质（1）课前导读从三角形的内角和等于180°，我们早已经知道了直角三角形的两个锐角互余，这就是这节课要学习的定理1．我们着重学习定理2．课本导学一、课本上证明定理2的过程太罗嗦了，用了21行．其实一句话就可以讲清楚：长方形ABCD是我们非常熟悉的图形，对角线交于点E，那么EA＝EB＝EC＝ED．我们把这个图形擦去一半，保留另一半，那么BE就是直角三角形ABC斜边上的中线，容易得到BE 等于AC的一半．这就是定理2，直角三角形斜边上的中线等于__________的一半．二、定理2的数学表达式更多的象文字表达式，这样写简明，连理由都省了：三、如果我们把课本第116页例题2改编一下，那么证明过程的差异，只在最后两行的因果互换一下，你来看看．已知：如图，在△ABC中，AD⊥BC，E、F分别是AB、AC的中点，且DE＝DF①．求证：AB＝AC②．改编：如图，在△ABC中，AD⊥BC，E、F分别是AB、AC的中点，且AB＝AC②．求证：DE＝DF①．课堂导练四、课本第116页课后练习1，图文对应起来是不是有点头晕？给你一组备用图，再给你一个全景图，你来研究．五、课本第117页课后练习2，可能是这本书里图形最复杂，书写过程最简短的一道典型题了，因此它是上镜率也很高哦．我们把图形拆分开来好理解．∵MD、ME分别是Rt△DB C和Rt△EBC斜边上的中线，∴______________，______________．∴___________．又∵N是DE的中点，∴____________（等腰三角形的“____________”）．六、图解课本第117页课后练习3的思路．原图中点E，得BE＝DE全等，得OE＝OF三线合一，得BD⊥EF七、图解课本第117页课后练习4的思路：设F为Rt△CDE的斜边DE的中点．。

直角三角形知识点一、直角三角形的性质1、Rt△的两个锐角互余（∠A+∠B=90°）2、斜边上的中线等于斜边的一半（若D为斜边AB的中点，则CD＝12AB）3、30°角所对直角边等于斜边的一半（若∠A＝30°，∠C=90°，CB=12AB）4、勾股定理：两直角边的平方和等于斜边的平方（若∠C=90°，则222a b c+=）二、直角三角形的判定1、有两个锐角互余的△是直角三角形。

2、如果一个三角形中，一条边上的中线等于这条边的一半，那么这条边所对的角为90°3、勾股定理的逆定理：如果三角形三边满足222a b c+=，则∠C＝90°。

用法：（1）选出最大边；（2）计算较小两边的平方和；（3）比较最大边的平方与较小两边的平方和；（4）如果两者相等，则最大边所对的角为直角。

三、常用几个结论：（1）（2）直角三角形斜边上的高＝两直角边乘积除以斜边。

公式为c abhc=（3）常见的勾股数：（3k，4k，5k）（5k，12k，13k）（7k，24k，25k）（8k，15k，17k）（9k，40k，41k）（4）在求曲面上的最短距离时，先把曲面展开成平面图形，画出起点到终点的线段，就是最短距离，一般需要用到勾股定理。

（1）蚂蚁沿着圆柱表面爬行，最短距离例1 如图1有一个圆柱,它的高等于12cm ,底面周长为10cm，在圆柱的下底面A点上有一只蚂蚁，他想吃到上底面上与A点相对的B点处的食物，需要爬行的最短路程是多少?分析：可以把圆柱的侧面展开，其展开图为矩形，如图3所示。

连接AC，则AC即为小虫爬行的最短路线，可用勾股定理求得其长。

解：①若沿着曲面走，则：AB=12×10=5，BC=12，所以AC=13=图1 图2半周长②若走折线A=>D=>C ，则AC+DC=12+10π∵12+10π>13∴最短路程为13cm 。

直角三角形的性质、判定（HL ）1、如果一个△ABC 有一个角是直角，则它是直角三角形，记作Rt △ABC 。

直角三角形两锐角互余。

2、直角三角形的判定定理：如果两个直角三角形的斜边和一条直角边对应相等，则这个两个直角三角形全等，简称HL 。

3、直角三角形性质定理(一):在直角三角形中，斜边上的中线等于斜边的一半.4、直角三角形性质定理(二):在直角三角形中,如果一个锐角等于30°，则它所对的直角边等于斜边的一半;5、直角三角形性质的逆定理（1）:如果一个三角形一边上的中线，等于这条边的一半，则这个三角形式直角三角形.（2）在直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的角为30°.二、知识运用典型例题例1：已知:△ABC 中,∠ACB=90°,CD 是高, ∠A=30°.求证:BD=14AB.例2：已知:如图, △ABC 中,AB=AC,BD ⊥AC 于D 点,BD=12AC. 则∠A=_____.例3：已知:如图,AD 为△ABC 的高,E 为AC 上的一点,BE 交AD 于F,且有BF=AC,FD=CD, 求证:BE ⊥AC.例4：如图3，AD 是ΔABC 的中线，DE ⊥AB 于E ，DF ⊥AC 于F ，且BE=CF ， 求证：（1）AD 是∠BAC 的平分线AD CBAE DC BF 12 A12（2）AB=AC例5：已知如图，AE ⊥ED ，AF ⊥FD ，AF=DE ，EB ⊥AD ，FC ⊥AD ，垂足分别为B 、C.试说明EB=FC.例6：如图，已知BE ⊥AD ，CF ⊥AD ，且BE ＝CF ．请你判断AD 是△ABC 的中线还是角平分线？请说明你判断的理由．三、知识运用课堂训练1、△ABC 中各角的度数之比如下,能够说明△ABC 是直角三角形的是( ) A.1:2:3 B.2:3:4 C.3:4:5 D.3:2:52、直角三角形中,两锐角的角平分线相交所成的角的度数为 .3、等腰三角形一腰上的高等于该三角形一条边长度的一半,则其顶角为 .4、如图,CD 为△ABC 的中线,∠ACB=90°,CE ⊥AB 于E, AE=ED,则图中30°的角有 个.ABCD FEABCD E5、如图,AC=BD,AD ⊥AC,BC ⊥BD,求证:AD=BC.6、如图所示，D 是△ABC 的边BC 上的中点，DE ⊥AC ，DF ⊥AB ，垂足分别为E 、F ，且BF ＝CE 。

Rt三角形表示的为直角三角形
拓展：
直角三角形（right triangle 缩写Rt三角形）是一个几何图形，是有一个角为直角的三角形，有普通的直角三角形和等腰直角三角形两种。

其符合勾股定理，具有一些特殊性质和判定方法。

等腰直角三角形是一种特殊的三角形等腰直角三角形是一种特殊的三角形，具有所有三角形的性质：具有稳定性、内角和为180°。

两直角边相等，两锐角为45°，斜边上中线，角平分线、垂线三线合一，等腰直角三角形斜边上的高为此三角形外接圆的半径R。

第七讲 直角三角形的边角关系一、知识点快速归纳理解：考点一、直角三角形的性质 1、直角三角形的两个锐角互余可表示如下：∠C=90°⇒∠A+∠B=90°2、在直角三角形中，30°角所对的直角边等于斜边的一半。

∠A=30°可表示如下： ⇒BC=21AB ∠C=90°3、直角三角形斜边上的中线等于斜边的一半 ∠ACB=90°可表示如下： ⇒CD=21AB=BD=AD D 为AB 的中点 4、勾股定理直角三角形两直角边a ，b 的平方和等于斜边c 的平方，即222c b a =+ 5、射影定理在直角三角形中，斜边上的高线是两直角边在斜边上的摄影的比例中项，每条直角边是它们在斜边上的摄影和斜边的比例中项∠ACB=90° BD AD CD •=2⇒ AB AD AC •=2CD ⊥AB AB BD BC •=2 6、常用关系式由三角形面积公式可得：AB •CD=AC •BC考点二、直角三角形的判定1、有一个角是直角的三角形是直角三角形。

2、如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形。

3、勾股定理的逆定理如果三角形的三边长a ，b ，c 有关系222c b a =+，那么这个三角形是直角三角形。

考点三、锐角三角函数的概念 1、如图，在△ABC 中，∠C=90°①锐角A 的对边与斜边的比叫做∠A 的正弦，记为sinA ，即casin =∠=斜边的对边A A②锐角A 的邻边与斜边的比叫做∠A 的余弦，记为cosA ， 即cbcos =∠=斜边的邻边A A③锐角A 的对边与邻边的比叫做∠A 的正切，记为tanA ，即b atan =∠∠=的邻边的对边A A A④锐角A 的邻边与对边的比叫做∠A 的余切，记为cotA ，即abcot =∠∠=的对边的邻边A A A2、锐角三角函数的概念锐角A 的正弦、余弦、正切、余切都叫做∠A 的锐角三角函数 3、一些特殊角的三角函数值 三角函数 0° 30°45°60° 90° sinα21 22 23 1cos α 123 22 21 0tan α 0 33 13不存在cot α 不存在 3133 04、各锐角三角函数之间的关系（1）互余关系： sinA=cos(90°—A)，cosA=sin(90°—A)tanA=cot(90°—A)，cotA=tan(90°—A) （2）平方关系： 1cos sin 22=+A A （3）倒数关系： tanA •tan(90°—A)=1 （4）弦切关系： tanA=AAcos sin 5、锐角三角函数的增减性 当角度在0°~90°之间变化时， （1）正弦值随着角度的增大（或减小）而增大（或减小） （2）余弦值随着角度的增大（或减小）而减小（或增大） （3）正切值随着角度的增大（或减小）而增大（或减小） （4）余切值随着角度的增大（或减小）而减小（或增大） 考点四、解直角三角形 1、解直角三角形的概念2、解直角三角形的理论依据在Rt △ABC 中，∠C=90°，∠A ，∠B ，∠C 所对的边分别为a ，b ，c（1）三边之间的关系：222c b a =+（勾股定理） （2）锐角之间的关系：∠A+∠B=90° （3）边角之间的关系：ba B ab Bc a B c b B a b A b a A c b A c a A ========cot ,tan ,cos ,sin ;cot ,tan ,cos ,sin二、知识点练习题方式方法及技巧渗透1．如图，小颖利用有一个锐角是30°的三角板测量一棵树的高度，已知她与树之间的水平距离BE 为5m ，AB 为1.5m （即小颖的眼睛距地面的距离），那么这棵树高是（ ） A ．（53332+）m B ．（3532+）m C ． 533m D ．4m 2．如图，在等腰Rt △ABC 中，∠C =90o ，AC =6，D 是AC 上一点，若tan ∠DBA =51，则AD 的长为（ ） （A ） 2 （B ）3 （C ）2 （D ）13．已知在ABC △中，90C ∠=o，设sinB n =，当B ∠是最小的内角时，n 的取值范围是（ ）A ．202n <<B ．102n << C ．303n << D ．302n << 4．如图，小正方形的边长都为1，A 、B 、C 是小正方形的顶点，则∠ABC 的度数为（ ）A ．90°B ．60°C ．45°D ．30°5．如图，已知一商场自动扶梯的长z 为10米，该自动扶梯到达的高度h 为6米，自动扶梯与地面所成的角为θ，则tan θ的值等于( )6．如图，矩形ABCD 中，AB ＞AD ，AB =a ，AN 平分∠DAB ，DM ⊥AN 于点M ，CN ⊥AN 于点N ．则DM +CN 的值为（用含a 的代数式表示）( )A ．aB ．a 54C ．a 22D ． a 23 7．在△ABC 中，∠C ＝90°，sinA ＝45，则tanB ＝ （ ） A ．43 B ．34 C ．35 D ．458．在正方形网格中，ABC △的位置如图所示，则cos B ∠的值为（ ）A ．12B ．22C ．32D ．33aNM CDAB（第6题）BA ED C30°第1题第2题CA第4题图第5题图9．计算2sin 45°的结果等于（ ）A ．2B ．1C ．22 D ．21 10．在Rt △ABC 中,∠C=90°,若AC=2BC,则sin A 的值是( )A ．12B ．2C ．5D ．5 11．在Rt △ABC 中，∠C=90°，sinA=54，则cosB 的值等于（ ） A ．53 B. 54 C. 43D. 5512．在△ABC 中，∠C ＝90°，sinA ＝45，则tanB ＝（ ） A ．43 B ．34 C ．35 D ．4513．在7,35,90,==∠=∠∆AB B C ABC Rt οο中，则BC 的长为 （ ）（A ）ο35sin 7（B ）ο35cos 7（C ）ο35cos 7 （D ）．ο35tan 714．如上右第9题图，在梯形ABCD 中，AD//BC ，AC ⊥AB ，AD=CD 54cos =∠DCA ，BC=10，则AB 的值是（ ） A ．9 B ．8 C ．6 D ．315．如图，小明为了测量其所在位置A 点到河对岸B 点之间的距离，沿着与AB 垂直的方向走了m 米，到达点C ，测得∠ACB ＝α，那么AB 等于（ ）(A) m ·sin α米 (B) m ·tan α米 (C) m ·cos α米 (D) αtan m米16．如图，△ABC 的三个顶点分别在正方形网格的格点上，则A ∠tan 的值是 （ ）A ．56 B ．65 C ．3102 D ．1010317．sin30︒的值等于 （ ） （A ）12（B ）2 （C ）3 （D ）118．已知在Rt ABC △中，390sin 5C A ∠==°，，则tan B 的值为（ ） A ．43B ．45C ．54D ．3419．如图，为测量一幢大楼的高度，在地面上距离楼底O 点20 m 的点A 处，测得楼顶B 点的仰角∠OAB A BC m α(第15题图)D BC E ＝65°，则这幢大楼的高度为 （ ） （结果保留3个有效数字）． （A ）42.8 m（B ）42.80 m （C ）42.9 m （D ）42.90 m20．如图，在正方形ABCD 中，O 是CD 边上一点，以O 为圆心，OD 为半径的半圆恰好与以B 为圆心，BC 为半径的扇形的弧外切，则∠OBC 的正弦值为 ．21．如图，已知直线1l ∥2l ∥3l ∥4l ，相邻两条平行直线间的距离都是1，如果正方形ABCD 的四个顶点分别在四条直线上，则sin α= ．22．已知：如图，梯形ABCD 中，AB//CD ，∠A=600 ，AD=5cm ，DC=6cm ，AB=10cm 。