四川省成都七中实验学校2018_2019学年高二数学10月月考试题(无答案)

2018-2019学年四川省成都市七中实验学校高二数学文联考试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 数列的前n项和为，，则数列的前100项的和为（）。

(A) (B) (C) (D)参考答案：A略2. 复数，则（）A. 1B.C.D. 2参考答案：B【分析】先化简z，然后结合复数模长计算公式，即可。

【详解】,所以,故选B.【点睛】本道题考查了复数的四则运算和复数模长计算公式，难度较易。

3. 设0＜m≤2，已知函数，对于任意，都有，则实数m的取值范围为（）A. B. C. D.参考答案：B【分析】根据题意，设，求出其导数，得到函数的单调性，结合m的范围分析可得在上为减函数，进而可得函数在上也为减函数，据此求出在上的最大值与最小值；结合题意分析可得必有，即，变形解可得m的取值范围，即可得答案．【详解】根据题意，设，其导数，当时，，即函数在上为增函数，当时，，即函数在上为减函数，当时，，即函数在上为增函数，又由，则，则在上，为减函数，又由，则函数在上也为减函数，则，，若对于任意，，都有，则有，即，变形可得：，可得：或，又由，则m的取值范围为；故选：B．【点睛】本题主要考查导数在函数中的综合应用，以及恒成立问题的求解，着重考查了转化与化归思想、逻辑推理能力与计算能力，对于恒成立问题，通常要构造新函数，利用导数研究函数的单调性，求出最值，进而得出相应的含参不等式，从而求出参数的取值范围；也可分离变量，构造新函数，直接把问题转化为函数的最值问题．4. 已知命题p：?x∈R，x2﹣2x+4≤0，则?p为（）A．?x∈R，x2﹣2x+4≥0B．C．?x?R，x2﹣2x+4≤0D．参考答案：B【考点】命题的否定．【专题】计算题；规律型；简易逻辑．【分析】利用全称命题的否定是特称命题写出结果即可．【解答】解：因为全称命题的否定是特称命题，所以，命题p：?x∈R，x2﹣2x+4≤0，则?p为：．故选：B．【点评】本题考查命题的否定，特称命题与全称命题的否定关系，是基础题．5. 在空间直角坐标系Oxyz中，点(1，－2，4)关于y轴对称的点为A.(－1，－2，－4)B.(－1，－2，4)C.(1，2，－4)D.(1，2，4)参考答案：A6. 下列说法正确的个数是( )①若，其中。

花落知多少四川省成都市第七中学2018-2019学年高二数学上学期半期考试试题理（满分：150 分，考试时间：120 分钟）一、选择题（本题共 12 小题，每小题 5 分，共 60 分。

在每小题给出的四个选项中，只有一项是符合题目要求的.）1.不在曲线上的点的坐标是（）2.抛物线的焦点到准线的距离等于（）3.双曲线的渐近线方程为（）4.直线在x 轴上的截距为（）5.直线与坐标轴围成的三角形的周长为（）6.若x,y 满足约束条件，则的最小值为（）7.设P 为双曲线上任一点，，则以FP 为直径的圆与以双曲线实轴长为直径的圆（）相切相交相离内含8.已知P 为椭圆上一点，为椭圆焦点，且，则椭圆离心率的范围是（）9.点满足关系式，则点M 的轨迹是（）椭圆双曲线双曲线的一支线段10.圆关于直线对称的圆的方程为（）.x2+y2+3y+1=011.设点，直线相交于点M，且它们的斜率之积为k，对于结论：①当时，点M 的轨迹方程为；x2 9y2②当时，点M 的轨迹方程为-=1(x ≠±5);25100③当时，点M 的轨迹方程为.其中正确结论的个数为（）0 1 2 312．设A,B,M 为椭圆上的三个点，且以AB 为直径的圆过原点O，点N 在线段AB 上，且，则的取值范围是（）二、填空题(本大题共 4 小题，每小题 5 分，共 20 分．把答案填在答卷横线上)13.双曲线的实轴长为.⎨⎩⎧2x +y - 2 ≥0,14．已知x,y 满足约束条件⎪x -2y + 4 ≥ 0, 则的最大值为.⎪3x -y - 3 ≤0.15.直线l 过抛物线的焦点F 交抛物线于A,B 两个点，则1+1= .FA FB16.点为椭圆x2 y2+=1上一点，F1,F2为椭圆的两个焦点，则∆F1MF2的内心的轨迹方程为9 5.三、解答题（17 题 10 分，18～22 每小题 12 分，共 70 分．解答应写出文字说明，证明过程或演算步骤.）17.已知圆C 的圆心在直线上，并且与x 轴的交点分别为.（1）求圆C 的方程；（2）若直线l 过原点且垂直直线，直线l 交圆C 于M,N，求的面积.x2 y218.已知双曲线E:-a2b2=1(a > 0, b > 0) 的渐近线方程为y=±，焦距为 3 .过点作直线l 交双曲线E 于A,B 两点，且M 为AB 的中点.（1）求双曲线E 的方程；（2）求直线l 的方程.19.一个化肥厂生产甲、乙两种混合肥料，生产 1 车皮甲种肥料的主要原料是磷酸盐 4t，硝酸盐 18t，生产 1 车皮乙种肥料需要的主要原料是磷酸盐 1t，硝酸盐 15t，现库存磷酸盐 10t，硝酸盐 66t，在此基础上生产这两种肥料，若生产 1 车皮甲种肥料，产生的利润为10000 元，生产 1 车皮乙种肥料，产生的肥料为 5000 元，那么分别生产甲、乙两种肥料各多少车皮，能够产生最大的利润？20.已知圆 P 过.（1）求圆 P 的方程； （2）若过点的直线 l 被圆 P 所截得的弦长为 8，求直线 l 的方程.21.从抛物线上各点向 x 轴作垂线，垂线段中点的轨迹为 E .（1）求曲线 E 的方程; （2）若直线与曲线 E 相交于 A ,B 两点，求证：OA ⊥OB ；（3）若点 F 为曲线 E 的焦点，过点Q (2, 0) 的直线与曲线 E 交于 M ,N 两点，直线 MF ,NF 分别与曲线 E 交于 C , D 两点，设直线 MN , CD 的斜率分别为 k 1 ,k 2 ，求 k 2 的值.k 122.已知椭圆 的离心率为 ，短轴长为 4，直线 AB 过原点 O 交椭圆于A ,B ，，直线 AP ,BP 分别交椭圆于 C ,D ，且直线 AD ,BC交于点 M ，图中所有直线的斜率都存在. （1）求椭圆方程；（2）求证：;（3）求 的值.成都七中 2018～2019 学年度上期高 2020 届 数学半期考试（理科）参考答案一、选择题（共 12 题，每题 5 分，共 60 分）二、 13. 8 14. 13 15. 1 16.x 2 5 y 2 + = 1( y ≠ 0) 4 4 三、解答题17.解：（1）线段 AB 的中垂线方程为：,由，得,∴圆心 C 为 ,又半径,∴圆 C 的方程为. ……5 分（2）直线 l 的方程为：,所以点 C 到直线 l 的距离为：，∴，∴. ……10 分b18.解：（1）由已知得 = a2 ， 2c = 23 ，解得 a = 1, b = 2.∴双曲线 E 的方程为. ……4 分（2）设直线 l 方程为:，，.由，得……6 分∴…①……8 分∴，由为AB 的中点，得，解得，适合①……10 分∴直线l 的方程为，即 (12)分说明：学生也可以用点差法求解，如果没有检验∆> 0 的学生，扣1 分.19.解：设生产甲种肥料x 车皮，乙种肥料y 车皮，能够产生利润z 万元，目标函数为,其中x，y 满足以下条件：……4 分可行域如右图：……6 分把变形为，……8 分得到斜率为，在y 轴上的截距为 2z，随z 变化的一族平行直线，当直线经过可行域上的点M 时，截距 2z 最大，即z 最大，联立方程得. ……10 分∴……11 分答：生产甲、乙两种肥料各 2 车皮，能够产生最大利润，最大利润为 3 万元 (12)分20.解：（1）设圆P 的方程为：.∵A,B,C 都在圆上,∴, 解得.∴所求圆P 的方程为.……6 分（2）由，知圆心，半径，如右图，由直线l 被圆p 截得的弦长为 8，得圆心距……8 分当直线l 与x 轴不垂直时，设直线l 方程为：,即,∴圆心P 到直线l 距离，化简得，则.∴直线l 方程为：，即. (10)分当直线轴时，直线l 方程为，代入圆方程得，解得，，∴弦长仍为8,满足题意 (11)分综上，直线l 的方程为,或 (12)分21.解：（1）令抛物线上一点,设.由已知得,∵满足，∴,则，即.∴曲线 E 的方程为：.……4 分（2）由，可得，设，由于∆=122-4⨯16 >0,由韦达定理可知：，，∴，∴OA⊥OB.……8 分22.解：（1）由 2b=4，得b=2.由e=，得，解得.∴椭圆的方程为.……3 分（2）设，则.∴由得：,即，，即. ……7 分（3）设,由（2）知,又,,∴,∴…③同理,又, ,∴,∴…④由化简得：,∴，即. ……12 分。

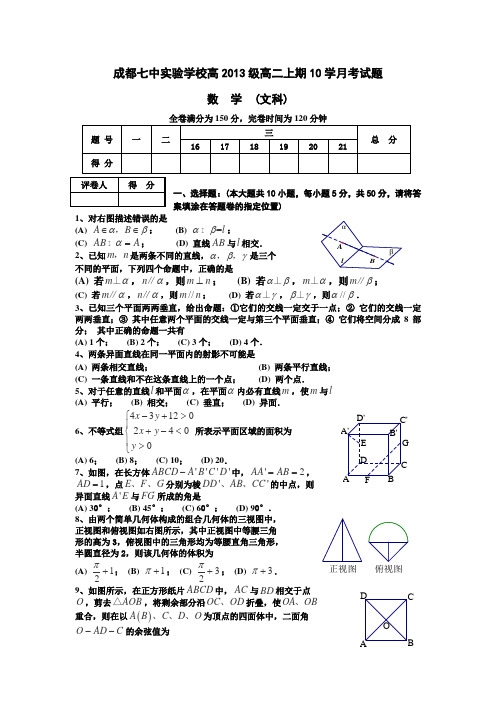
成都七中实验学校高2013级高二上期10学月考试题数 学 (文科)全卷满分为150分，完卷时间为120分钟一、选择题：(本大题共10小题，每小题5分，共50分，请将答案填涂在答题卷的指定位置)1、对右图描述错误的是(A) A B αβ∈∈，； (B) =l αβ；(C) AB A α=； (D) 直线AB 与l 相交． 2、已知m n ，是两条不同的直线，αβγ，，是三个不同的平面，下列四个命题中，正确的是(A) 若m α⊥，n α∥，则m n ⊥； (B) 若αβ⊥，m α⊥，则m β∥； (C) 若m α∥，n α∥，则//m n ； (D) 若αγ⊥，βγ⊥，则//αβ．3、已知三个平面两两垂直，给出命题：①它们的交线一定交于一点；② 它们的交线一定两两垂直；③ 其中任意两个平面的交线一定与第三个平面垂直；④ 它们将空间分成8部分； 其中正确的命题一共有(A) 1个； (B) 2个； (C) 3个； (D) 4个． 4、两条异面直线在同一平面内的射影不可能是(A) 两条相交直线； (B) 两条平行直线； (C) 一条直线和不在这条直线上的一个点； (D) 两个点．5、对于任意的直线l 和平面α，在平面α内必有直线m ，使m 与l (A) 平行； (B) 相交； (C) 垂直； (D) 异面．6、不等式组⎪⎩⎪⎨⎧><-+>+- 004201234y y x y x 所表示平面区域的面积为(A) 6； (B) 8； (C) 10； (D) 20．7、如图，在长方体''''ABCD A B C D -中，'2AA AB ==， 1AD =，点E F G 、、分别为棱''DD AB CC 、、的中点，则 异面直线'A E 与FG所成的角是(A) 30°；(B) 45°；(C) 60°； (D) 90°． 8、由两个简单几何体构成的组合几何体的三视图中， 正视图和俯视图如右图所示，其中正视图中等腰三角 形的高为3，俯视图中的三角形均为等腰直角三角形， 半圆直径为2，则该几何体的体积为 (A)12π+； (B) 1π+； (C)32π+； (D) 3π+．9、如图所示，在正方形纸片ABCD 中，AC 与BD 相交于点 O ，剪去AOB △，将剩余部分沿OC OD 、折叠，使OA OB 、 重合，则在以()A B C D O 、、、为顶点的四面体中，二面角O AD C --的余弦值为俯视图正视图O DCBAD'C'B'A'G FE D CB A(A)(B) ；(C)(D) 10、已知一动点P 在棱长为2的正方体1111ABCD A B C D -的内部，且点P 到棱1AB AD AA 、、的距离的平方和为2，则动点P 的轨迹和正方体的侧面所围成的几何体的体积为 (A) 6π； (B)3π； (C)43π； (D) 83π．二、填空题：(本大题共5小题，每小题5分，共25分，请将答案填写在答题卷的指定位置)11、与同一平面所成角均为45°的两条直线的位置关系是 ．12、若实数y x 、满足不等式组⎪⎩⎪⎨⎧≥≤+≤02y y x x y ，则目标函数y x z 3+=的最大值为 ．13、如右图所示，网格纸的小正方形的边长是1，在其上 用粗线画出了某多面体的三视图，则这个多面体最长的一 条棱与底面所成角的正弦值为 ．14、若=∠=∠=∠CPABPC APB 60°，则直线PA 与平面PBC 所成角的余弦值为 ．15、在长方体1111ABCD A B C D -中，1AB AD ==，12AA =， 给出下列结论： ① 直线1AC 与BD 互相垂直；② 二面角1A BD C --的余弦值为13-；③ 1AC 与平面1A BD 的交点是线段1A C 的一个三等分点；④ 1AC 与平面1A BD 的交点是1A BD △的外心； ⑤ 1AC 与平面1A BD ． 其中正确的结论有(请写出所有正确结论的序号)．三、解答题：(本大题共6小题，共75分．请在答题卷的指定位置作答，解答应写出文字说明、证明过程或演算步骤．)16、(12分) 如图，在棱长为1的正方体1111ABCD A B C D -中，E 为棱11A B 的中点，作出过点A C E 、、的截面与正方体各侧面的交线，并求出正方体被该平面截得的较小部分的体积．D 1C 1B 1A 1D CB A1A17、(12分) 如图，在棱长为2的正方体1111ABCD A B C D 中，E F 、分别为棱11AD C D 、的中点， (I) 分别作出四边形1BED F 在平面1111ABCD ABB A BCC B 、、内的投影，并求出投影的面积；投影一的面积为 ；投影二的面积为 ；投影三的面积为 ；(II) 直线BF 与1ED 相交吗？ 答案： ；求直线BE 与1D F 所成角的正弦值．F ED 1C 1B 1A 1DCBAA B B 1A 1BC C 1B 1D CBA18、(12分) 右图为正方体1111D C B A ABCD -的平面展开图，其中E M N 、、分别为111A D BC CC 、、的中点，(I) 作出该正方体的水平放置直观图； (II) 求证：平面∥1BEC 平面MN D 1．19、(12分) 已知不等式组330210270x y x y x y --≥⎧⎪--≤⎨⎪+-≤⎩表示的区域为D ，(I) 在坐标系中作出区域D (用阴影部分表示)；(II) 若在可行域D 内，使目标函数z kx y =-的取得最小值的最优解有无数个，求实数k 的取值范围．20、(13分) 如图，在三棱柱111ABC A B C -中，1A A ⊥平面ABC ，D 为棱1AA 的中点，1AB AC AD ===，(I) 求证：平面1DBC ⊥平面11BCC B ； (II) 若直线1A B 与11B C 所成角为75°， 求二面角1B AA C --的余弦值．C 1B 1A 1D CBA y x 11O21、(14分) 在如图所示的几何体中，EA ⊥平面ABC ，DB ⊥平面ABC ，AC BC ⊥，2AC BC BD AE ===，M 是AB 的中点，(I) 求证：CM EM ⊥； (II) 求CM 与平面CAE 所成角的大小；(III) 求平面ABC 与平面CDE 所成锐二面角的余弦值．M E D C A。

成都市第七中学2018—2018学年度上学期10月阶段性考试高二数学理试题考试时间：120分钟总分：150分一、选择月（每小题5分，共60分，在每小题给出的四个选项中，只有一项符合要求，把答案填在答题卡上．）1、右图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（）A ．9πB．10π C ．11πD．12π2、过不重合的A（m2＋2，m2一3），B（3一m一m2，2m）两点的直线l倾斜角为450，则m的取值为（）A．m＝一1 B．m＝一2 C．m＝一1或2 D．m＝l或m ＝－23、利用斜二测画法得到的①三角形的直观图是三角形。

②平行四边形的直观图是平行四边形。

③正方形的直观图是正方形。

④菱形的直观图是菱形。

以上结论，正确的是（）A．①②B．①④C．③④D．①②③④4、若直线l沿x轴向左平移3个单位，再沿y轴向上平移1个单位后，回到原来位置，则直线l的斜率为（）A．13 B、一13C、一3 D．35、己知圆C1：x2十y2＋2x＋8y一8＝0，圆C2：x2十y2－4x－4y 一2＝0，圆C1与圆C2的位置关系为（）A．外切B．内切C．相交D．相离6、己知变量x，y满足约束条件，则z＝3x十y的最大值为（）A．12 B．11 C．3 D．一l7、己知点A（l，3），B（3，l），C（一1，0），则△ABC的面积为（）A．5 B．10 CD．78、若圆x2十y2一4x一4y一10＝0上至少有三个不同的点，到直线l：y＝x＋b的距离为b取值范围为（）A．（一2，2）B．［一2，2］C．［0，2］D．［一2，2）9、若直线a x十2by一2＝0（a＞0，b＞0）始终平分圆x2十y2一4x 一2y 一8＝0的周长，则 12ab+的最小值为（）A ．1B ．5C ．D ．3＋10、己知函数f （x ）＝（x 一l ）（log 3a ）2一6（log 3a ）x ＋x ＋l 在x ∈0，l ］内恒为正值，则a 的取值范围是（） A 一1＜a ＜13B 、a ＜13C 、aD ·13＜a 11、平面上到定点A （l ，2）距离为1且到定点B （5，5）距离为d 的直线共有4条，则d 的取值范是（）A ．（0，4）B ．（2，4）C ．（2，6）D ．（4，6）12、实数a ，b 满足这三个条件，则｜a 一b 一6｜的范围是（ ） A ．［2，4＋B ．［32，7］C ．［32，4＋2D ．［4－2，7］二、填空题（本大题共4小题，每题4分，共16分，把答案填在答题卡的横线上．）13、长、宽、高分别为3，4，5的长方体，沿相邻面对角线截取一个三棱锥（如图），剩下 几何体的体积为 。

成都七中高2020届高二下期入学考试数学试卷（理科）考试时间：120分钟 满分：150分一、选择题（共12题，每题5分，满分60分．在每题给出的四个选项中，只有一项是符合题目要求的．请把答案填涂在答题卷上）1．抛物线2=4y x 的准线方程为（ ）A ．1y =-B ．1y =C ．1x =-D ．1x =2．双曲线221124x y -=的焦距为（ ）A．B ． 8C．D ．43．过点(2,1)的直线中，被圆22(1)(2)5x y -++=截得的最长弦所在的直线方程为（ ）A ．3x －y －5＝0B ．3x ＋y －7＝0C ．x ＋3y －5＝0D ．x －3y ＋1＝04．已知p：“a =q ：“直线0x y -=与圆22()1x y a +-=相切”，则p 是q 的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 5．为了测试小班教学的实践效果，任课教师对A 、B 两班的学生进行了阶段测试，并将所得成绩统计 如图所示；记本次测试中，A 、B 两班学生的平均成绩分别为A x ，B x ，A 、B 两班学生成绩的方差分别为2A s ，2B s ，则观察茎叶图可知（ ）A ．A x <B x ， 2A s <2B s B ．A x >B x ， 2A s <2B sC ．A x <B x ， 2A s >2B sD ．A x >B x ， 2A s >2B s6．某高中在校学生有2000人．为了响应“阳光体育运动”号召，学校举行了跑步和登山比赛活动．每人都参加而且只限参与了其中一项比赛，各年级参与比赛人数情况如下表：其中::2:3:5a b c =，全校参与登山的人数占总人数的60%，为了了解学生对本次活动的满意程度， 现用分层抽样从中抽取了一个100人的样本进行调查，则从高二年级参与跑步的学生中应抽取（ ）A.6人B.12人C.18人D.24人7．在区间[0，2π]上随机取一个数x ，则事件“sin cos x x ≥”发生的概率为（ ）A ．14B ．13C ．12D ．238．右面程序框图是为了求出满足321000n n ->的最小偶数n ，那么两个空白框中可以分别填入（ ） A ．A >1000? 和 n =n +1 B ．A >1000? 和 n =n +2 C ．A ≤1000? 和 n =n +1 D ．A ≤1000? 和 n =n +29．双曲线221916x y -=的左顶点为A ，右焦点为F ，过点F 作平行于双曲线的一条渐近线的直线l ，则点A 到直线l 的距离为（ ）A. 815B. 325C. 3215D. 8510．已知椭圆的左焦点为1F ，有一质点A 从1F 处以速度v 开始沿直线运动，经椭圆内壁反射（无论经过几次反射速率始终保持不变），若质点第一次回到1F 时，它所用的最长时间是最短时间的7倍，则椭圆的离心率e 为（ ） A.23 B. 34 C. 35 D. 5711．已知点E 是抛物线2:2(0)C y px p =>的对称轴与准线的交点，点F 为抛物线C 的焦点，点在抛物线C 上．在EFP ∆中，若sin sin EFP FEP μ∠=⋅∠，则μ的最大值为（ ）A ．B ．C D12．如图， 12,A A 为椭圆22195x y +=长轴的左、右端点， O 为坐标原点， ,,S Q T 为椭圆上不同于12,A A 的三点，直线12,,,QA QA OS OT 围成一个平行四边形OPQR ，则22OS OT +=（ ）A. 7B. 9C. 12D. 14二、填空题（共4题，每题5分，满分20分．请把答案填写在答题卷上）13．若双曲线2213616x y -=的焦点分别是1F ，2F ，点P 是C 上任意一点，则12PF PF -=________．14．如图是抛物线形拱桥，此时水面宽4米，拱顶离水面2米．当水位下降1米后，则水面宽为_________米．15．已知直线l 过椭圆C ：2212x y +=的左焦点F 且交椭圆C 于A 、B 两点，O 为坐标原点．若以线段AB为直径的圆经过点O ，则点O 到直线AB 的距离为_________．16．已知椭圆222:1(0)x y a aΓ+=>，圆222:6C x y a +=-在第一象限有公共点P ，设圆C 在点P 处的切线斜率为1k ，椭圆Γ在点P 处的切线斜率为2k ，则12k k 的取值范围为_________． 三、解答题（共6题，满分70分．第17题10分，第18～22题每题12分；解答应写出文字说明，证明过程或演算步骤．请将解答过程写在答题卷的相应题号的下面）17．命题p ：方程22124x y m m +=+-表示椭圆；命题q ：双曲线222:1(0)4x y C m m -=>的虚轴长于实轴． （1）当简单命题p 为真命题时，求实数m 的取值范围； （2）当复合命题 “p ∧q ”为真命题时，求实数m 的取值范围．18． 过抛物线x y 82=的焦点作倾斜角为045的直线，交抛物线于A 、B 两点，求：（1）被抛物线截得的弦长AB ； （2）线段AB 的中点到直线02=+x 的距离．19． 2019年的流感来得要比往年更猛烈一些．据四川电视台SCTV -4“新闻现场”播报，近日四川省人民医院一天的最高接诊量超过了一万四千人，成都市妇女儿童中心医院接诊量每天都在九千人次以上．这些浩浩荡荡的看病大军中，有不少人都是因为感冒来的医院．某课外兴趣小组趁着寒假假期空闲，欲研究昼夜温差大小与患感冒人数之间的关系，他们分别到成都市气象局与跳伞塔社区医院抄录了去年1到6月每月20日的昼夜温差情况与患感冒就诊的人数，得到如下资料：该兴趣小组确定的研究方案是：先从这六组数据中选取2组,用剩下的4组数据求线性回归方程，再用被选取的2组数据进行检验．（1） 若选取的是1月与6月的两组数据，请根据2月至5月份的数据，求出y 关于x 的线性回归方程y bx a=+；（2） 若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的，试问该小组所得线性回归方程是否理想？(参考公式: 1122211()(),()n niii ii i nni i i i x x y y x y nx yb a y bx x x x nx====---===---∑∑∑∑)20．如图，已知圆22:(1)(2)2C x y -+-=，点P 坐标为(2,1)-， 过点P 作圆C 的切线，切点为A ，B ．（1）求直线PA ，PB 的方程； （2）求过P 点的圆的切线长； （3）求直线AB 的方程．21．某市电视台为宣传所在城市，随机对该市15～65岁的人群抽取了n 人调查，回答预设答案的问题“本市著名旅游景点有哪些？”，统计结果如下列表格和频率分布直方图所示：（1）分别求出题设或表格中n ，a ，b ，x 和y 的值；（2）根据频率分布直方图估算这组数据的中位数（保留小数点后两位）和平均数；（3）若第1组回答正确的人员中有两名女性，其余均为男性，现从中随机抽取两名，求至少抽中一名女性的概率．22．已知椭圆x 2a 2＋y 2b 21(a ＞b ＞0)过点(0,1)，其长轴、焦距和短轴的长的平方依次成等差数列．直线l 与x轴正半轴和y 轴分别交于Q ，P ，与椭圆分别交于点M ，N ，各点均不重合且满足PM ―→＝λ1MQ ―→，PN ―→＝λ2NQ ―→．（1）求椭圆的标准方程；（2）若λ1＋λ2＝－3，求证：直线l 过定点，并求出该定点．(第20题)成都七中高2020届高二下期入学考试数学试卷（理科）参考答案一、选择题：1～5：CBAAB 6～10：BCDBD 11～12：CD ． 二、填空题：13．12 14． 15． 16. （3，5）． 三、解答题：17. 解：（1）当命题p 是真命题时，满足20m +>，40m ->，且24m m +≠-时，得24m -<<且1m ≠，即(2,1)(1,4)m ∈-⋃时，方程表示椭圆； ……………5 分 （2）当命题q 是真命题时，满足22b a >，则有420m >>，即(0,2)m ∈时， 虚轴长于实轴， 当复合命题“p ∧q ”为真命题时，则p 、q 都是真命题，则有(0,1)(1,2)m ∈⋃． ……………10分 18. 解：（1）抛物线的焦点为（2，0），则直线方程为：2-=x y ………2分联立方程组得：4,12041228212122==+⇒=+-⇒⎩⎨⎧-==x x x x x x x y x y ………6分 因此 164)(2)(2)()(21221221221221=-+=-=-+-=x x x x x x y y x x AB …………8分（2）法一：该点到02=+x 的距离为：82421=++=x x d ；……………12分法二：线段AB 的中点为)2,2(2121y y x x ++，由（1）可得中点为（6，4）， 所以该点到02=+x 的距离为：8=d ．………………………12分20.解：(1)设过P 点圆的切线方程为y ＋1＝k (x －2)，即kx ―y ―2k ―1＝0．因为圆心C (1，2)到直线的距离为2，1＋ 3 － － 2k k ＝2， 解得k ＝7，或k ＝－1．故所求的切线方程为7x ―y ―15＝0，或x ＋y －1＝0． ……………4 分(2)在Rt △PCA 中，因为|PC |＝222 － 1 － ＋ 1 － 2)()(＝10，|CA |＝2，所以|PA |2＝|PC |2－|CA |2＝8．所以过点P 的圆的切线长为22． ……………8 分(3)法一：容易求出k PC ＝－3，所以k AB ＝31．如图，由CA 2＝CD ·PC ，可求出CD ＝PC CA 2＝102．设直线AB 的方程为y ＝31x ＋b ，即x －3y ＋3b ＝0．由102＝23 ＋ 1 3 ＋ 6 － 1 b 解得b ＝1或b ＝37(舍)．所以直线AB 的方程为x －3y ＋3＝0． ……………12 分法二：由四边形对角互补，易知P ,A ,C ,B 四点共圆，且以线段PC 为直径，设该圆圆心为M ，则31(,)22M ，半径122r PC ==，则圆M 标准方程为22315()()222x y -+-=，即2230x y x y +--=， 又知圆C 方程的方程为222430x y x y +--+=，∴ 圆M 和圆C 方程之差即为两相交圆之公共弦所在直线AB 的方程是x －3y ＋3＝0．…………12 分20(0.0101030(0.02010)40(0.03010)50(0.02510)60(0.03010)26.......1212.5941.58x =⨯⨯++⨯⨯+⨯⨯+⨯⨯+⨯⨯=++++=分315,32,,,1,252,),(,),(,1),(,2),(,),(,1),(,2),(,1),(,2),(1,2)10(,1),(,2),(,1),(,2),(,1),(,2),(1,2)7a a b c a b a c a a b c b b c c A a a b b c c =（）由（）知则第一组中回答正确的人员中有名男性，名女性，男性分别记为女性分别为记，先从人中随机抽取人，共有（个基本事件，记“至少抽中一名女性”为事件，共有个7() (1210)P A =基本事件，则分22. 解：（1）设椭圆的焦距为2c ，由题意知b ＝1，且(2a )2＋(2b )2＝2(2c )2， 又a 2＝b 2＋c 2，所以a 2＝3．所以椭圆的方程为x 23＋y 2＝1．……………4 分(2)由题意设P (0，m )，Q (x 0,0)，M (x 1，y 1)，N (x 2，y 2)，直线l 的方程为x ＝t (y －m )，由PM ―→＝λ1MQ ―→ ，知(x 1，y 1－m )＝λ1(x 0－x 1，－y 1)，∴y 1－m ＝－y 1λ1，由题意y 1≠0，∴λ1＝my 1－1．同理由PN ―→＝λ2NQ ―→知λ2＝my 21．∵λ1＋λ2＝－3，∴m y 1－1＋my 2－1＝－3，∴y 1y 2＋m (y 1＋y 2)＝0，……① 联立2233()x y x t y m ⎧+=⎨=-⎩，得(t 2＋3)y 2－2mt 2y ＋t 2m 2－3＝0，∴由题意知Δ＝4m 2t 4－4(t 2＋3)(t 2m 2－3)＞0，……②且有y 1＋y 2＝2mt 2t 2＋3，y 1y 2＝t 2m 2－3t 2＋3，……③ 将③代入①得t 2m 2－3＋2m 2t 2＝0，∴(mt )2＝1，由题意mt ＜0，∴mt ＝－1，满足②，故直线l 的方程为x ＝ty ＋1， 过定点(1,0)，即Q 为定点．……………12 分。

成都七中2018～2019 学年度上期高2020 届数学半期考试试题（理科）（满分：150分，考试时间：120分钟）一、选择题（本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的.）1.不在曲线上的点的坐标是（）2.抛物线的焦点到准线的距离等于（）3.双曲线的渐近线方程为（）4.直线在x轴上的截距为（）5.直线与坐标轴围成的三角形的周长为（）6.若x,y满足约束条件，则的最小值为（）7.设P为双曲线上任一点，，则以FP为直径的圆与以双曲线实轴长为直径的圆（）相切相交相离内含8.已知P为椭圆上一点，为椭圆焦点，且，则椭圆离心率的范围是（）9.点满足关系式，则点M的轨迹是（）椭圆双曲线双曲线的一支线段10.圆关于直线对称的圆的方程为（）.x2+y2+3y+1=011.设点，直线相交于点M，且它们的斜率之积为k，对于结论：①当时，点M的轨迹方程为；x2 9y2②当时，点M的轨迹方程为-=1(x≠±5);25 100③当时，点M的轨迹方程为.其中正确结论的个数为（）0 1 2 312．设A,B,M为椭圆上的三个点，且以AB为直径的圆过原点O，点N在线段AB上，且，则的取值范围是（）⎨⎩二、填空题(本大题共4小题，每小题5分，共20分．把答案填在答卷横线上)13.双曲线的实轴长为.⎧2x+y-2≥0,14．已知x,y满足约束条件⎪x-2y+4≥0,则的最大值为.⎪3x -y-3≤0.15.直线l过抛物线的焦点F交抛物线于A,B两个点，则1+1= .FA FB16.点为椭圆x 2 y2+ =1上一点，F1,F2为椭圆的两个焦点，则∆F1MF2的内心的轨迹方程为9 5.三、解答题（17题10分，18～22每小题12分，共70分．解答应写出文字说明，证明过程或演算步骤.）17.已知圆C的圆心在直线上，并且与x轴的交点分别为.（1）求圆C的方程；（2）若直线l过原点且垂直直线，直线l交圆C于M,N，求的面积.x2 y218.已知双曲线E:-a2b2=1(a>0,b>0)的渐近线方程为y=±，焦距为作直线l交双曲线E于A,B 两点，且M为AB的中点.（1）求双曲线E的方程；（2）求直线l的方程.19.一个化肥厂生产甲、乙两种混合肥料，生产1车皮甲种肥料的主要原料是磷酸盐4t，硝酸盐18t，生产1车皮乙种肥料需要的主要原料是磷酸盐1t，硝酸盐15t，现库存磷酸盐10t，硝酸盐66t，在此基础上生产这两种肥料，若生产1车皮甲种肥料，产生的利润为10000元，生产1车皮乙种肥料，产生的肥料为5000元，那么分别生产甲、乙两种肥料各多少车皮，能够产生最大的利润？20.已知圆P 过.（1）求圆P 的方程；（2）若过点的直线l 被圆P 所截得的弦长为8，求直线l 的方程.21.从抛物线上各点向x 轴作垂线，垂线段中点的轨迹为E .（1）求曲线E 的方程;（2）若直线与曲线E 相交于A ,B 两点，求证：OA ⊥OB ；（3）若点F 为曲线E 的焦点，过点Q (2,0)的直线与曲线E 交于M ,N 两点，直线MF ,NF 分 别与曲线E 交于C ,D 两点，设直线MN ,CD 的斜率分别为k 1,k 2 ，求k 2 的值.k 122.已知椭圆的离心率为，短轴长为4，直线AB 过原点O 交椭圆于A ,B ，，直线AP ,BP 分别交椭圆于C ,D ，且直线AD ,BC交于点M ，图中所有直线的斜率都存在.（1）求椭圆方程；（2）求证：;（3）求的值.成都七中2018～2019 学年度上期高2020届数学半期考试（理科）参考答案一、 选择题（共12题，每题5分，共60分）二、填空题（共4题，每题5分，共20分）13.814.1315. 116.x 2 5y 2+ =1(y ≠0)4 4三、 解答题17.解：（1）线段AB 的中垂线方程为：,由，得,∴圆心C 为 ,又半径,∴圆C 的方程为.……5分（2）直线l 的方程为：,所以点C 到直线l 的距离为：，∴，∴. ……10分b18.解：（1）由已知得= a2，2c =2 3，解得a =1,b =2.∴双曲线E 的方程为.……4分（2）设直线l 方程为:，，.由，得……6分∴…①……8分∴，由为AB的中点，得，解得，适合①……10分∴直线l的方程为，即……12分说明：学生也可以用点差法求解，如果没有检验∆>0的学生，扣1分.19.解：设生产甲种肥料x车皮，乙种肥料y车皮，能够产生利润z万元，目标函数为,其中x，y满足以下条件：……4分可行域如右图：……6分把变形为，……8分得到斜率为，在y轴上的截距为2z，随z变化的一族平行直线，当直线经过可行域上的点M时，截距2z最大，即z最大，联立方程得.……10分∴……11分答：生产甲、乙两种肥料各2车皮，能够产生最大利润，最大利润为3万元.……12分20.解：（1）设圆P的方程为：.∵A,B,C都在圆上,∴, 解得.∴所求圆P的方程为.……6分（2）由，知圆心，半径，如右图，由直线l被圆p截得的弦长为8，得圆心距……8分当直线l与x轴不垂直时，设直线l方程为：,即,∴圆心P到直线l距离，化简得，则.∴直线l方程为：，即.……10分当直线轴时，直线l方程为，代入圆方程得，解得，，∴弦长仍为8,满足题意.……11分综上，直线l的方程为,或.……12分21.解：（1）令抛物线上一点,设.由已知得,∵满足，∴,则，即.∴曲线E的方程为：.……4分（2）由，可得，设，由于∆=122 -4⨯16>0,由韦达定理可知：，，∴，∴OA⊥OB.……8分22.解：（1）由2b=4，得b=2.由e=，得，解得.∴椭圆的方程为.……3分（2）设，则.∴由得：,即，，即. ……7分（3）设,由（2）知,又,,∴,∴…③同理,又, ,∴,∴…④由化简得：,∴，即.……12分。

成都七中2018～2019学年度上期高2020届数学半期考试试题（文科）参考答案一、选择题（共12题，每题5分，共60分）二、填空题（共4题，每题5分，共20分）13. 8 14. 2 15. 45 16.2291(0)5y x y +=≠三、解答题17.解：（1）线段AB 的中垂线方程为：x =2,由{x =2 3x +2y =0，得y =−3,∴圆心C 为(2,−3), 又半径r =|AC|=5,∴圆C 的方程为(x −2)2+(y +3)2=25. ……5分（2）直线l 的方程为：2x −3y =0,所以点C 到直线l 的距离为：d =4+9√4+9√13，∴|MN |==4√3，∴S △MCN =12×|MN |×d =12×4√3×√13=2√39. ……10分18.解：（1）由已知得b a =2c =，解得1,a b ==∴双曲线E 的方程为x 2−y 22=1. ……4分（2）设直线l 方程为:y −1=k(x −2)，A(x 1,y 1)，B(x 2,y 2).由{y =kx +(1−2k )x 2−y 22=1 ，得(2−k 2)x 2+2k (2k −1)x −(1−2k)2−2=0 (∗)……6分∴{2−k 2≠0 Δ=4k 2(2k −1)2+4(2−k 2)[(1−2k )2+2]>0…①……8分 ∴x 1+x 2=2k (2k−1)k 2−2，由M(2,1)为AB 的中点，得x 1+x 22=k (2k−1)k 2−2=2，解得k =4，适合①……10分∴直线l 的方程为y −1=4(x −2)，即4x −y −7=0……12分说明：学生也可以用点差法求解，如果没有检验0∆>的学生，扣1分.19.解：（1）令抛物线上一点P(x 0,y 0),设E(x,y).由已知得x 0=x,y =12y 0,∵P(x 0,y 0)满足y 2=16x ，∴y 02=16x 0,则4y 2=16x ，即y 2=4x .∴曲线E 的方程为：y 2=4x . ……6分（2）由{y =x −4y 2=4x，可得x 2−12x +16=0， 设A (x 1,y 1),B (x 2,y 2)，由于2124160,∆=-⨯> 由韦达定理可知：x 1+x 2=12,x 1x 2=16，y 1y 2=(x 1−4)(x 2−4)=x 1x 2−4(x 1+x 2)+16=−16，∴OA ⃗⃗⃗⃗⃗ ∙OB⃗⃗⃗⃗⃗ =x 1x 2+y 1y 2=0， ∴OA ⊥OB . ……12分20.解：设生产甲种肥料x 车皮，乙种肥料y 车皮，能够产生利润z 万元，目标函数为z =x +0.5y ,其中x ，y 满足以下条件：{4x +y ≤1018x +15y ≤66x ≥0y ≥0……4分 可行域如右图：……6分把z =x +0.5y 变形为y =−2x +2z ，……8分得到斜率为−2，在y 轴上的截距为2z ，随z 变化的一族平行直线，当直线y =−2x +2z 经过可行域上的点M 时，截距2z 最大，即z 最大，联立方程{4x +y =1018x +15y =66,得M(2,2). ……10分 ∴z max =2+1=3. ……11分答：生产甲、乙两种肥料各2车皮，能够产生最大利润，最大利润为3万元. ……12分21.解：（1）设圆P 的方程为：x 2+y 2+Dx +Ey +F =0.∵A ,B ,C 都在圆上,∴ {29+5D −2E +F =09+3E +F =017+4D +E +F =0 , 解得{D =0E =4F =−21. ∴所求圆P 的方程为x 2+y 2+4y −21=0. ……6分（2）由x 2+(y +2)2=25，知圆心P(0,−2)，半径r =5，如右图，由直线l 被圆p 截得的弦长为8，得圆心距d =22=3 ……8分当直线l 与x 轴不垂直时，设直线l 方程为：y +3=k(x +3),即kx −y +3k −3=0,∴圆心P 到直线l 距离d =|3k−1|2=3，化简得−6k =8，则k =−43. ∴直线l 方程为：y +3=−43(x +3)，即4x +3y +21=0. ……10分 当直线l ⊥x 轴时，直线l 方程为x =−3，代入圆方程得y 2+4y −12=0，解得y 1=−6，y 2=2，∴弦长仍为8,满足题意. ……11分 综上，直线l 的方程为4x +3y +21=0,或x =−3. ……12分22.解：（1）由2b =4，得b =2.由e =√53=c a ，得a 2−4a 2=59，解得a 2=9. ∴椭圆的方程为x 29+y 24=1. ……3分（2）设A (x 0,y 0),D (x 1,y 1)，则B (−x 0,−y 0).∴{x 029+y 024=1…①x 129+y 124=1…②由①−②得：(x 0−x 1)(x 0+x 1)9+(y 0−y 1)(y 0+y 1)4=0, 即(x 0−x 1)(x 0+x 1)9=−(y 0−y 1)(y 0+y 1)4，−49=(y 0−y 1)(y 0+y 1)(x 0−x 1)(x 0+x 1)， 即k AD ∙k BD =−49. ……7分（3）由（2）知k AD ∙k BD =−49，设A (3cos θ,2sin θ),则B (−3cos θ,−2sin θ).又k BD =k BP =2sin θ1+3cos θ,则k AD =−2(1+3cos θ)9sin θ, ∴直线AD 方程为：y −2sin θ=−2(1+3cosθ)9sinθ(x −3cos θ) …③ 同理k BC ∙k AC =−49,又k AC =k AP =2sin θ3cos θ−1,则k BC =−2(3cosθ−1)9sinθ,∴直线BC 方程为：y +2sin θ=−2(3cos θ−1)9sin θ(x +3cos θ)…④ 由③−④得：−4sin θ=−29sin θ[(1+3cos θ)(x −3cos θ)−(3cos θ−1)(x +3cos θ)],化简得x =9.∴点M 在定直线x =9上. ……12分。

成都七中实验学校2015--2016学年度第一次月考高二数学一、选择题（本题共12小题，每题5分，共60分）1.以下角：①异面直线所成角；②直线和平面所成角；③二面角的平面角； 可能为钝角的有 （ ） A ．0个 B ．1个 C ．2个 D ．3个2. 已知m n 、是不重合的直线，αβ、是不重合的平面，正确的是（ ）A ．若,//n m n αβ=，则//,//m m αβ；B ．若//,m m n α⊥，则n α⊥；C ．若,m m αβ⊥⊥，则//αβD ．若αβ⊥，m α⊥，则m β∥；3. 一个水平放置的平面图形的斜二测直观图是一个底角为45°，腰和 上底长均为1的等腰梯形，则这个平面图形的面积是（ ） A ． 2＋ 2 B ．1＋22 C ．1＋ 2 D ． 12＋224. 某三棱锥的侧视图、俯视图如图所示，则该三棱锥的体积是（ ）A ．3B ．2CD ．1 5. 下面四个说法中，正确的个数为（ ）①三点确定一个平面；②ABC ∆在平面α外，其三边延长线分别和α交于R Q P ,,,则R Q P ,,一定共线；③一个角的两边所在直线分别平行于另一个角的两边所在直线，则这两角相等； ④在三维空间中，三个平面最多把空间分成八部分。

A ．1 B ．2 C ．3 D ．46. 对于任意的直线l 和平面α，在平面α内必有直线m ，使m 与l ( ) A ．平行； B ． 相交； (C) 垂直； (D) 异面．7. 若点P 是两条异面直线a ，b 外一点，则过P 且与a ，b 都平行的平面个数是 个( ) A ．0个 B ．1个 C ．0或1个 D ．无数个8. 如图，若Ω是长方体ABCD －A1B 1C 1D 1被平面EFGH 截去几何体EFGHB 1C 1后得到的几何体，其中E 为线段A 1B 1上异于B 1的点，F 为线段BB 1上异于B 1的点，且EH ∥A 1D 1，则下列结论中不．正确的是( )A ．EH ∥FGB ．四边形EFGH 是矩形C ．Ω是棱柱D ．Ω是棱台9. 如图所示，在正四棱锥S －ABCD (顶点S 在底面ABCD 上的射影是正方形ABCD 的中心)中，E 是BC 的中点，P 点在侧面△SCD 内及其边界上运动，并且总是保持PE ⊥AC .则动点P 的轨迹与△S C D组成的相关图形最有可能是图中的( )10. 在直二面角α－AB －β中,βα∈∈Q P ,,直线PQ 与面FC 1D 1B 1A 1DC004530所成角为，与所成角为βα,则异面直线AB PQ 与所成角为（ ）A ．030B ．060C ．090D ．04511. 如图，已知六棱锥ABCDEF P -的底面是正六边形，AB PA ABC PA 2,=⊥平面则下列结论正确的是（ ）A ．AD PB ⊥ B ． PAB 平面PBC 平面⊥C ． 直线BC ∥PAE 平面D ． 直线ABC PD 与平面所成的角为45°12.在2,,,ABC AB AC AD BC AB BD BC ∆⊥⊥=⋅中若则；类似地有命题：在三棱锥A —BCD 中，⊥AD 面ABC ，若A 点在BCD 内的射影为M ，则有BCD BCM ABC S S S ∆∆∆⋅=2。

成都七中实验学校2018～2019学年上期第一学月考试高二年级数学试题(满分150，考试时间120分钟)一、选择题：(每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合要求，请将答案填涂在答题卡上)1、圆()()22235x y -++=的圆心坐标和半径分别为A ．()235-，　，B ．()23-．()235-，　， D ．()23-，　2、如果直线m ⊂平面a ，直线n ⊂平面a ， M m N n M l N l ∈∈∈∈，，，，则A ．l α⊂B ．l α⊄C ．lM a = D ．l N a = 3、圆()()221114C x y ++-=　：与圆()()2223425C x y -+-=　：的位置关系是A ．相离B ．相交C ．相切D ．内含4、直线1y kx =+与圆224x y +=的位置关系是A ．相交B ．相切C ．相离D ．与k 的取值有关5、“若0232=+-x x ，则2=x ”为原命题，则它的逆命题、否命题与逆否命题中真命题的个数是A ．0B ．2C ．3D ．4 6、若x y R ∈，，则1x y ≥，是122≤+y x 成立的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件7、已知某棱锥的三视图如图所示，则该棱锥的表面积为A ．52+B ．253+ C ．252+ D ．53+ 8、已知点()()0P a b ab ≠，是圆222O x y r +=：内一点，直线l 的方程为20ax by r ++=，那么直线l 与圆O 的位置关系是A ．相离B ．相切C ．相交D ．不确定9、已知三棱柱111C B A ABC -的侧棱与底面垂直，体积为94，若P 为底面111C B A 的中心，则PA 与平面ABC 所成角的大小为A ．512πB ．3πC ．4πD ．6π 10、圆C 的方程为015822=+-+x y x ，若直线2-=kx y 上至少存在一点，使得以该点为圆心，1为半径的圆与圆C 有公共点，则k 的最大值是A ．0B ．34C ．21 D ．1- 11、若直线()22000ax by a b -+=>>，被圆222410x y x y ++-+=截得的弦长为4，则11a b+的最小值为 A ．14 B ．12 C ．2 D ．4 12、四面体BCD A -中，10==CD AB ，342==BD AC ，412==BC AD ，则四面体BCD A -外接球的表面积为A ．π50B ．π100C ．π200D ．π300二、填空题：(每小题5分，共20分，请将答案填写在答题卡上)13、在正方体1111D C B A ABCD -各条棱所在的直线中，与直线1AA 垂直的条数共有 条．14、圆2224150x y x y +++-=上到直线20x y -= .15、在底面是正方形的长方体1111ABCD A BC D -中，12AA AB =，则异面直线1A B 与1AD 所成角的余弦值为 .16、过点()12P ，　作圆122=+y x 的切线分别交圆于A B 、两点，则AB 所在直线方程是 ．三、解答题：(17题10分，18～22每小题12分，共70分．解答应写出文字说明，证明过程或演算步骤)17、(1) 求过点()22M ，　且与012=++y x 垂直的直线方程；(2) 求过点()21P ，　且在两坐标轴上截距相等的直线方程．18、如图，ABCD 是边长为2的正方形，O 是正方形的中心，PO ⊥底面ABCD，PO E 是PC 的中点，(1) 求证：PA ∥平面BDE ；(2) 直线PA 与平面PBD 所成的角．19、已知圆C 经过()32A ，　和()16B ，　两点，且圆心在直线x y 2=上．(1) 求圆C 的方程；(2) 若直线l 经过点()13P -，　且与圆C 相切，求直线l 的方程．DABC O E P20、如图，四面体ABCD 中，O E 、分别为BD BC 、的中点，AB AD ==2CA CB CD BD ====，(1) 求证：AO ⊥平面BCD ；(2) 求点E 到平面ACD 的距离.21、如图所示，在四棱锥P ABCD -中，底面ABCD 是边长为2的正方形，侧面PAD 为正三角形，且面PAD ⊥面ABCD ， E F 、分别为棱AB PC 、的中点，(1) 求证： EF ∥平面PAD ；(2) (文科) 求三棱锥B EFC -的体积；(理科) 求二面角P EC D --的正切值．22、在平面直角坐标系xOy 中，已知圆C 的方程为224xy +=，点()23M -，　, (1) 求过点M 且与圆C 相切的直线方程；(2) 过点M 任作一条直线与圆C 与交于A B 、两点，圆C 与x 轴正半轴的交点为P ，求证：直线PA 与直线PB 的斜率之和为定值．。