当前位置：文档之家 › 2-统计数据的描述

2-统计数据的描述

  • 格式：pptx
  • 大小：1.28 MB
  • 文档页数：87

下载文档原格式

  / 87

合集下载

2统计描述(集中趋势的描述)

2统计描述(集中趋势的描述)

4.13 4.28 4.91 3.95 4.23
2.78 3.26 3.18 5.08 3.57
4.26 3.50 3.68 4.53 4.83
3.58 2.70 4.83 3.92 3.52
4.34 4.61 3.87 3.58 3.84
4.84 4.75 3.95 5.35 4.50
4.41 2.91 3.91 3.84 3.96
第三章: 统计描述
一、数值变量资料的统计描述
1、频数分布 2、集中趋势的统计描述 3、离散趋势的统计描述 4、正态分布及其应用
二、分类变量资料的统计描述
2
概述 ：
统计描述:用适当的统计图(表)和统计指 标来描述资料的分布规律及其数量特征. 资料性质
离散型：变量取值可以列举，如心跳、脉搏 连续型：变量取值不能明确列举，如血糖
1．描述频数分布的 类型 （1）对称分布 ： (2) 偏态分布
25 20
人数
15
Æ µ Ê ý
10 5
0
2.45
3.05
3.65
4.25
4.85
5.45
6.10
Ñ ª Ç å × Ü µ ¨¹ Ì ´ ¼ £ ¨mmol/L£ ©
Í ¼ 2 - 1 101 à û Õ ý ³ £ ³ É Ä ê Å ® Ó ×Ñ ª Ç å Ü ×µ ¨¹ Ì ´ ¼ µ Ä Æ µ Ê ý Ö ·² ¼
4.34 4.61 3.87 3.58 3.84
4.84 4.75 3.95 5.35 4.50
4.41 2.91 3.91 3.84 3.96
4.50 3.27 4.52 3.19 4.59 3.75 3.98 4.13 4.26 3.63 3.87 5.71 3.30 4.73 4.17 5.13 3.78 4.57 3.80 3.93 3.78 3.99 4.48 4.28 4.06 5.26 5.25 3.98 5.03 3.51 3.86 3.02 3.70 4.33 3.29 3.25 4.15 4.36 4.95 3.00 3.26

实训项目2-描述性统计的SPSS软件实现方法

实训项目2-描述性统计的SPSS软件实现方法

【实践教学具体实施过程】
1. 教师先对理论知识进行梳理、讲授并演示 操作过程。
2. 学生实训：学生根据实训内容基于SPSS软 件进行实训操作——对调查资料进行描述 性统计。
实训二 描述性统计的SPSS软件实现方法
见第二章例2-3，利用SPSS，根据表2-1资 料绘制直方图，对该资料进行正态性检验， 计算集中趋势和离散趋势指标，并计算该 地8岁女孩身高均值95%的医学参考值范围 和置信区间。
【实训步骤】
1. 启动SPSS。 2. 单击SPSS界面左下角的“变量视图”标签，
定义变量，变量名为“身高”、数值型、 宽度为2、小数位数为1(实训图1)。 3. 单击左下角的“数据视图”标签，在“身 高”变量内录人数据。
实训二
描述性统计的SPSS 软件实现方法
【教学目标】
通过实训项目的操作，详细讲解描述性统 计在医学研究中的应用，做到理论指导与 实践操作相结合，从而避免统计学理论与 实际运算脱节的困扰。
【实训目的】
运用SPSS“分析”菜单中“描述统计”选 项，将调查或试验搜集来的原始资料进行 整理，编制频数表，检验其分布类型，绘 制直方图，揭示资料的分布特征，计算统 计指标。
数据分布的直方图
【实训步骤】
6. ②勾选“含检验的正态图”,单击“继续”按钮。 ③在“统计”对话框中勾选“描述”选项，并 设置置信区间百分比为95%，单击“继续”按 钮。单击“确定”按钮，得到分析结果。
正态性检验结果
带正态曲线的直方图
描述性结果
【实训步骤】
7. ①单击“分析”→“描述统计”→“频率”弹 出对话框。②点击“统计”选项，勾选“百分 位数”，输入“2.5”点击添加，接着输入 “97.5”点击添加，单击“继续”按钮。③单 击“确定”按钮，得到95%医学参考值的分析 结果。

统计学(第二版)课后答案

统计学(第二版)课后答案

附录1：各章练习题答案第1章绪论（略）第2章统计数据的描述2.1 （1）属于顺序数据。

（2）频数分布表如下：服务质量等级评价的频数分布服务质量等级家庭数（频率）频率%A1414B2121C3232D1818E1515合计100100（3）条形图（略）2.2 （1）频数分布表如下：（2）某管理局下属40个企分组表按销售收入分组（万元）企业数（个）频率（%）先进企业良好企业一般企业落后企业11119927.527.522.522.5合计40 100.0 2.3 频数分布表如下：某百货公司日商品销售额分组表按销售额分组（万元）频数（天）频率（%）25～30 30～35 4610.015.035～40 40～45 45～50 159637.522.515.0合计40 100.0 直方图（略）。

2.4 （1）排序略。

（2）频数分布表如下：100只灯泡使用寿命非频数分布按使用寿命分组（小时）灯泡个数（只）频率（%）650~660 2 2660~670 5 5670~680 6 6680~690 14 14690~700 26 26700~710 18 18710~720 13 13720~730 10 10730~740 3 3740~750 3 3合计100 100 直方图（略）。

2.5 （1）属于数值型数据。

（2）分组结果如下：分组天数（天）-25~-20 6-20~-15 8-15~-10 10-10~-5 13-5~0 120~5 45~10 7合计60（3）直方图（略）。

2.6 （1）直方图（略）。

（2）自学考试人员年龄的分布为右偏。

（2）A 班考试成绩的分布比较集中，且平均分数较高；B 班考试成绩的分布比A 班分散，且平均成绩较A 班低。

2.82.9 （1）x =274.1（万元）；Me=272.5 ；Q L =260.25；Q U =291.25。

（2）17.21=s （万元）。

2.10 （1）甲企业平均成本＝19.41（元），乙企业平均成本＝18.29（元）；原因：尽管两个企业的单位成本相同，但单位成本较低的产品在乙企业的产量中所占比重较大，因此拉低了总平均成本。

统计学原理(第二章)

统计学原理(第二章)

数据的计量和类型
一、数据的计量尺度 4.定比尺度：又称为比例尺度或是比较水平， 是对事物之间比值的一种测度，它是最高层 次的测量，可用于参数和非参数统计推断。 它是与定距尺度属于同一层次的一种计量尺 度，但其功能比定距尺度更强一些。
在日常生活中，大多数情况下使用的都是 定比尺度。例如，年龄、收入、某地区每年的 失业人数、罪犯人数等。
数值数据的描述
一、数值数据的 分组
为什么要进行数据的分组？
品质数据的描述
某电脑公司50名销售代表某季度电脑销售量按从小 到大排序如下表：
107 108 108 110 112 112 113 114 115 117 117 117 118 118 118 119 120 120 121 122 122 122 122 123 123 123 123 124 124 124 125 125 126 126 126 127 127 128 128 129 130 131 133 133 134 134 135 139 139 139
204 80.00% 105 41.17%
235 92.16% 51 20%
255 100% 20 7.84%
— 100% —
品质数据的描述
二、品质数据的 图示 1.条形图：是用宽度相同的条形的高度或长 短来表示数据变动的图形，横置的称为带形 图，纵置的称为柱形图（直方图）。
柱形图（直方图）
120 100 80 60 40 20
定类变量、定序变量、 数值型变量（离散变量、连续变量）
第二节 品质数据的描述
一、品质数据的描述 二、数据的类型品质数据的图示 三、品质数据的分布特征描述
品质数据的描述
一、品质数据的 描述 1.频数：是落在某一特定类别（或组）中的 数据的个数。把各个类别及其相应的频数全 部列出来则形成频数分布。

统计数据的描述实训报告

统计数据的描述实训报告

一、实训背景随着我国经济的快速发展，统计数据在政府决策、企业管理和学术研究等方面发挥着越来越重要的作用。

为了提高我们对统计数据的理解和应用能力，本次实训旨在通过实际操作，学习如何对统计数据进行分析、描述和解释。

二、实训目的1. 掌握统计数据的收集、整理和描述方法；2. 熟悉常用的统计图表和统计指标；3. 培养对统计数据的分析和解释能力；4. 提高运用统计方法解决实际问题的能力。

三、实训内容1. 统计数据的收集本次实训以某地区2019年居民消费水平调查数据为例，通过查阅相关资料和实际调查，收集到以下数据：（1）居民消费水平（元/年）（2）居民收入水平（元/年）（3）居民教育程度（4）居民年龄2. 统计数据的整理对收集到的数据进行整理，主要包括以下几个方面：（1）对数据进行分类和分组，以便更好地分析；（2）计算各组的频数、频率和众数；（3）计算平均值、中位数、极差和标准差等统计指标。

3. 统计数据的描述（1）绘制统计图表根据整理后的数据，绘制以下统计图表：①居民消费水平分布图②居民收入水平分布图③居民教育程度分布图④居民年龄分布图（2）计算统计指标①计算居民消费水平、收入水平、教育程度和年龄的平均值、中位数、极差和标准差；②计算居民消费水平与收入水平的相关系数。

4. 统计数据的分析（1）分析居民消费水平与收入水平的关系；（2）分析居民教育程度与消费水平的关系；（3）分析居民年龄与消费水平的关系。

四、实训结果与分析1. 居民消费水平与收入水平的关系通过相关系数计算，得出居民消费水平与收入水平的相关系数为0.85，说明两者之间存在较强的正相关关系。

即收入水平越高，消费水平也越高。

2. 居民教育程度与消费水平的关系从居民教育程度分布图可以看出，高教育程度的居民在消费水平上普遍较高。

这说明教育程度对消费水平有一定的影响。

3. 居民年龄与消费水平的关系通过分析居民年龄分布图和消费水平分布图，可以得出以下结论：（1）青年群体（18-35岁）消费水平较高，这与他们的收入水平和消费观念有关；（2）中年群体（36-55岁）消费水平相对稳定，这与他们的生活需求和消费能力有关；（3）老年群体（56岁以上）消费水平相对较低，这与他们的收入水平和消费观念有关。

统计数据的描述

统计数据的描述

统计数据的描述在我们的日常生活和工作中，统计数据无处不在。

从市场调研的销售数据，到医学研究中的患者症状统计，再到学校里的学生成绩分析，统计数据为我们提供了宝贵的信息，帮助我们做出更明智的决策。

然而，要真正理解和利用这些数据，首先需要学会对其进行准确的描述。

那么，什么是统计数据的描述呢？简单来说，就是用一些特定的方法和指标，将一堆看似杂乱无章的数据转化为有意义、易于理解和分析的形式。

这就像是给一堆未经雕琢的原石进行打磨和雕琢，让它们展现出内在的价值和美丽。

描述统计数据时，最常用的方法之一就是使用集中趋势的度量指标。

这包括平均数、中位数和众数。

平均数，大家应该都很熟悉，就是将所有数据相加，然后除以数据的个数。

比如说，一个班级里 5 名学生的考试成绩分别是 80 分、90 分、85 分、75 分和 95 分，那么他们的平均成绩就是（80 ＋ 90 ＋ 85 ＋ 75 ＋ 95）÷ 5 ＝ 85 分。

平均数能够反映出数据的总体水平，但它也有一个缺点，就是容易受到极端值的影响。

比如，如果这 5 名学生中，有一个人的成绩是 20 分，那么平均成绩就会被拉低很多。

这时候，中位数就派上用场了。

中位数是将数据按照从小到大或从大到小的顺序排列后，位于中间位置的那个数。

如果数据的个数是奇数，那么中位数就是中间的那个数；如果数据的个数是偶数，那么中位数就是中间两个数的平均值。

继续上面的例子，将成绩从小到大排列为 75 分、80 分、85 分、90 分、95 分，中间的数是 85 分，所以中位数就是 85 分。

即使有极端值，中位数也不会受到太大影响，它更能反映数据的中间水平。

众数则是数据中出现次数最多的那个值。

比如在一组数据 1, 2, 2, 3, 3, 3, 4 中，众数就是 3，因为 3 出现的次数最多。

众数可以帮助我们了解数据中最常见的情况。

除了集中趋势，数据的离散程度也是描述统计数据的重要方面。

离散程度反映了数据的分布范围和波动情况。

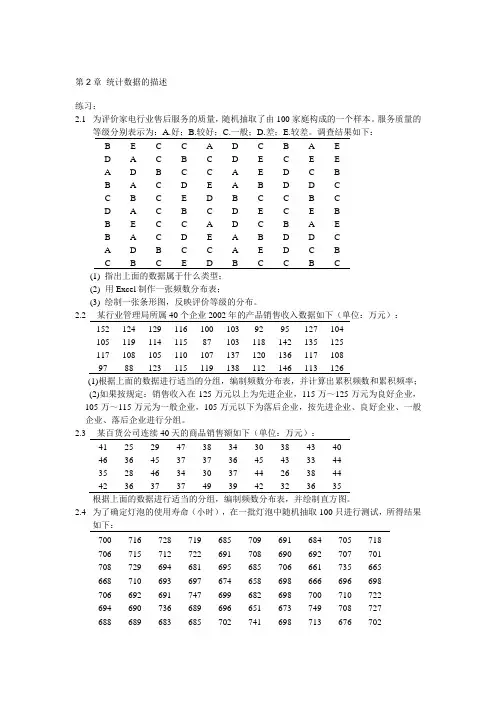
统计学 第2章 统计数据的描述

第2章统计数据的描述练习：2.1为评价家电行业售后服务的质量，随机抽取了由100家庭构成的一个样本。

服务质量的等级分别表示为：A.好；B.较好；C.一般；D.差；E.较差。

调查结果如下：B EC C AD C B A ED A C B C DE C E EA DBC C A ED C BB ACDE A B D D CC B C ED B C C B CD A C B C DE C E BB EC C AD C B A EB ACDE A B D D CA DBC C A ED C BC B C ED B C C B C(1) 指出上面的数据属于什么类型；(2)用Excel制作一张频数分布表；(3) 绘制一张条形图，反映评价等级的分布。

2.2某行业管理局所属40个企业2002年的产品销售收入数据如下（单位：万元）：152 124 129 116 100 103 92 95 127 104105 119 114 115 87 103 118 142 135 125117 108 105 110 107 137 120 136 117 10897 88 123 115 119 138 112 146 113 126(1)根据上面的数据进行适当的分组，编制频数分布表，并计算出累积频数和累积频率；(2)如果按规定：销售收入在125万元以上为先进企业，115万～125万元为良好企业，105万～115万元为一般企业，105万元以下为落后企业，按先进企业、良好企业、一般企业、落后企业进行分组。

2.3某百货公司连续40天的商品销售额如下（单位：万元）：41 25 29 47 38 34 30 38 43 4046 36 45 37 37 36 45 43 33 4435 28 46 34 30 37 44 26 38 4442 36 37 37 49 39 42 32 36 35根据上面的数据进行适当的分组，编制频数分布表，并绘制直方图。

第2章统计数据的描述

第二章统计数据的描述一、单项选择题1.下列中，最粗略、计量层次最低的计量尺度是（）A.间隔尺度B.顺序尺度C.比例尺度D.列名尺度2.将全国人口按“民族”划分为汉、白、彝、回、藏…..，这里使用的计量尺度是（）A.比例尺度B.列名尺度C.间隔尺度D.顺序尺度3.某个人对某一事物的态度可以划分为非常同意、同意、保持中立、不同意、非常不同意，这里使用的计量尺度是（）A.列名尺度B.间隔尺度C.顺序尺度D.比例尺度4.下列中，计量层次的最高、最精确的计量尺度是（）A.比例尺度B.间隔尺度C.顺序尺度D.列名尺度5.下列调查方式中，只能调查一些最基本、最一般现象的调查方式是（）A.抽样调查B.重点调查和典型调查C.统计报表D.普查6.实际中应用最为广泛的一种调查方式是（）A.重点调查B.统计报表C.普查D.抽样调查7.某城市拟对占全市储蓄额4/5的几个大储蓄所进行调查，以了解全市储蓄的一般情况，则这种调查方式是（）A.抽样调查B.典型调查C.重点调查D.普查8.一次性调查是指（）A.只做过一次的调查B.调查一次以后不再调查C.间隔一段时间在进行一次调查D.只隔一年就进行一次的调查9.在统计分析中，对累积的次数分配用得最直接的是（）A.供给曲线B.需求曲线C.洛伦茨曲线D.边际需求曲线10.专门用来衡量和反映收入分配平均程度的统计指标是（）A.基尼系数B.可决系数C.相关系数D.离散系数11.一般认为，基尼系数在（）之间是比较恰当的。

A.0.1—0.2B.0.2—0.4C.0.4—0.6D.0.6—0..812.一般认为，基尼系数等于（）是收入分配不公平的警戒线。

A.0.2B.0.6C.0.4D.0.813.利用公式计算众数的基本假定之一是众数组的频数在该组内呈（）A.正态分布B.t分布C.均匀分布D.偏态分布14.计算中位数时，假定中位数所在组的频数在该组内呈（）A.左偏分布B.正态分布C.右偏分布D.均匀分布15.反映数据分布集中趋势的最主要的测度值是（）A.众数B.中位数C.均值D.几何平均数16.各个变量值与均值的离差之和（）A.大于0B.小于0C.等于0D.等于一个不为0的常数17.各个变量值与均值的离差平方和（）A.为最大B.为最小C.为0D.为一个不为0的常数18.下列中，专门用来衡量众数代表性大小的离散程度测度值是（）A.异众比率B.四分位差C.方差或标准差D.极差19.下列中，专门用来衡量中位数代表性大小的离散程度测度值是（）A.方差和标准差B.内距C.异众比率D.平均差20.下列中，适用于列名数据的集中趋势测度值是（ ）A.众数B.中位数C.均值D.几何均值21.描述数据离散程度最简单的测度值是（ ）A.平均差B.方差和标准差C.极差D.四分位差22.经验法则表明，当一组数据呈对称分布时，大约有95%的数据在（ ）范围之内。

统计学第2章 统计数据的描述(1)


（4）组中值：上下限之间中点的值。
组中值=（上限+下限）/2=上限-组距/2 =下限+组距/2
“××以上”、“××以下”这样的组叫开口组。一般假 定开口组的组距与其相邻组的组距相等。其组中值计算如下： 缺下限最小组的组中值=上限-相邻组组距/2 缺上限最大组的组中值=下限+相邻组组距/2 见第37页的表2.15
第三节 统计整理
一、统计整理的概念和步骤
概念：统计整理是根据统计研究的目的和要求，把统计调查 从而得到反映事物总体特征资料的过程。
步骤： 第一，统计资料审核。包括及时性(整个工作期限、搜 集资料的时间、资料所属的时间)；准确性(事实求地反映 实际情况、计算正确)；完整性(规定应调查的总体单位、 每个调查单位应调查的内容)等方面的审核。 第二，统计分组 第三，统计汇总 第四，编制统计表或绘制统计图
提供统计数据的部分政府网站
美国政府机构 人口普查局 联邦储备局 预算编制办公室 商务部 网 址 数据内容
人口和家庭等 http://www.bog.frb.fed. 货币供应、信誉、 us 汇率等 http://www.whitehouse. 财政收入、支出、 gov/omb 债券等 商业、工业等
统计数据的来源主要有两个： 一是直接来源，即来源于直接的调查和科学试验， 得到第一手数据。 二是间接来源，即来源于别人调查或试验的数 据，得到第二手数据。
见第8-9页
一、统计数据的直接来源 1、普查
（1）概念 为了某一特定目的而专门组织的一次性全面调查。 （2）特点 ①具有一次性和周期性。
“一次性”是指调查现象在某一时点上的数据。
（1）对称分布：以变量值的中点为对称轴的对称分布。
（2）偏态分布:

2-数值变量与分类变量的统计描述分析

实习二统计描述第164～180页实习二统计描述医学统计资料类型¾数值变量资料：又称为计量资料。

变量值是定量的，有单位的，表示为数值的大小。

¾无序分类资料：又称为计数资料。

变量值是定性的，没有单位，表示为相互独立的类别。

¾有序分类资料：又称为等级资料。

变量值是定性的，没有单位，各类别具有程度上的差异。

注：不同类型的资料，统计方法不同；各种类型的资料之间是可以相互转化的。

一、数值变量资料的统计描述统计描述包括两个方面：集中趋势的描述和离散趋势的描述一、数值变量资料的统计描述（一）数值变量资料的频数表频数表（frequency table）：当变量值或者观测值较多时，将变量值分为适当的组段，统计各组段中相应的频数（或者人数），以描述数值变量资料的分布特征和分布类型。

一、数值变量资料的统计描述（一）数值变量资料的频数表频数表的用途1.描述数值变量资料的分布特征集中趋势（central tendency）：频数最多的组段代表了中心位置（平均水平），从两侧到中心，频数分布是逐渐增加的。

离散趋势（tendency of dispersion）：从中心到两侧，频数分布是逐渐减少的。

反映了数据的离散程度或者变异程度。

一、数值变量资料的统计描述（一）数值变量资料的频数表频数表的用途2.描述数值变量资料的分布类型正态分布：集中位置居中，左右两侧频数基本对称。

常见近似正态分布。

偏态分布：集中位置偏向一侧，频数分布不对称。

正偏态分布：集中位置偏向数值小的一侧或者左侧，有较长的右尾部。

负偏态分布：集中位置偏向数值大的一侧或者右侧，有较长的左尾部。

一、数值变量资料的统计描述（二）数值变量资料的频数分布图及正态曲线直方图及近似正态分布直方图及正偏态分布（二）数值变量资料的频数分布图及正态曲线一、数值变量资料的统计描述（三）集中趋势指标描述1.算数均数（均数mean ）适用于正态分布或者近似正态分布总体均数：µ；样本均数：一、数值变量资料的统计描述一、数值变量资料的统计描述（三）集中趋势指标描述2.几何均数（geometric mean，G）适用于一种特殊的偏态分布资料：等比资料（常见于抗体滴度）。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2. 各类经济信息中心、信息咨询机构、
专业调查机构等提供的数据
Internet
3. 各类专业期刊、报纸、书籍所提供的 资料。
4. 各种会议，如博览会、展销会、交易
会及专业性、学术性研讨会上交流的
中 国中
有关资料。
人国 口市 统场
计统
5. 从互联网或图书馆查阅到的相关资料 。
年计 鉴年
鉴
系统内部的数据
分类的变量
投资数量
百分比
(in thousands $)
46.5
42.27
32
29.09
15.5
14.09
16
14.55
110
100
统计表的构造
•序号：写在表的左上方。 •名称：是一个表的名称，应写在表的上方。 •标目：一般在表的上面一行和左侧一列。
统计表构造
数字：是统计表的语言，又称统计指标。 它占据统计表的大部分空间，书写一定 要整齐划一，位数要上下对齐，小数点 后缺位的要补零。
频数分布的实际状况
数据描述
分类数据
列联表 综合统计表
统计图
条形图
圆形图 其它图
统计表
•统计表的作用 •统计表可以给人以一目了然、简洁、清晰
的印象，表中的数据易于比较分析，是 经济与社会科学研究报告整理数据时普 遍采用的方法。
综合统计表
(例：表 1 某一投资者的证券组合表)
投资方式分类
股票 债券 CD 储蓄 合计
全面、详细地 反映总体情况
专门调查 或定期报 表
选择在总体 标志总量中 占绝大比重 的单位
粗略反映 总体的基 本情况
专门调查 ，有时也 采用报表 形式
按主观选 择具有一 定代表性 的单位
粗略估计 总体的情 况
专门调查
按随机性原 则选择的样 本单位
可以在一定 的可靠程度 保证下推断 总体。
Data Sources 数据来源
已存在来源（Existing Sources） 某一特定应用数据或许存在于公司或组织中 大量的商务和经济数据可从专门收集和维护数 据的组织中得到 政府机构是另一个重要的数据来源 数据可从许多行业组织和有些特定兴趣的组织 中得到
Data Sources 数据来源
互联网（Internet） 互联网在成为一个重要的数据来源 大多数收集和处理数据的政府机构通过网上站点 提供服务() 公司在其网站向公众提供信息()， 商品种类，价格等
3.求组距：指每一组的间距，用符号i表示。
4.定组限：指各组数据在数值上的起点值和终点值。 5.求组中值：各组实际上限数值与实际下限数值的中
点数值，即上、下限数值的平均值。 6.归类划记：将原始观测值按照一定的顺序逐一归组。 7.记录各组次数（f）。 8.核对，抄录新表。
有90个学生的语文成绩
编制次数分布表的步骤
检查应调查的单位或个体是否有遗漏 所有的调查项目或指标是否填写齐全
2. 准确性审核
检查数据是否真实反映客观实际情况，内 容是否符合实际
检查数据是否有错误，计算是否正确等
数据的审核—原始数据
(raw data)
审核数据准确性的方法
1. 逻辑检查
从定性角度，审核数据是否符合逻辑，内容是否 合理，各项目或数字之间有无相互矛盾的现象
1. 业务资料，如与业务经营活动有关的 各种单据，记录；
2. 经营活动过程中的各种统计报表； 3. 各种财务，会计核算和分析资料等。
中 国中 人国 口市 统场 计统 年计 鉴年
鉴
一、统计数据的搜集（续）
数据的直接来源(原始数据)
1. 调查数据
通过调查方法获得的数据 通常是对社会现象而言 通常取自有限总体
组中值
下限值+上限值 =
2
组距分组与不等距分组
(在表现频数分布上的差异)
1. 等距分组
各组频数的分布不受组距大小的影响 可直接根据绝对频数来观察频数分布的特征
2. 不等距分组
各组频数的分布受组距大小不同的影响 各组绝对频数的多少不能反映频数分布的实际
状况 需要用频数密度（频数密度=频数/组距）反映
Data Acquisition Considerations 获得数据的考虑
▪ 时间要求（Time Requirement） 获得数据信息是很费时间的 信息当得到是或许已经没有用了
▪ 得到数据的成本（Cost of Acquisition） 组织要对数据收取费用
▪ 数据误差（Data Errors） 收集数据不小心会导致得到的数据不准确或 不真实
表注：写于表的下面。不是统计表的必要 组成部分。如果需要可对标题补充说明。 数据来源、附记等都可作为表注的内容， 文字可长可短。
次数分布表
•对于一组大小不同的数据划出等距的分组区间
（称为组距），然后将数据按其数值大小列入各 个相应的组别内，便可以出现一个有规律的表式。 这种统计表称之为次数分布表或频次分布表。 •编制次数分布表与绘制次数分布图，对于了解一 组数据的分布情况，平均水平，差异情况等非常 有用，是对连续随机变量进行初步整理的重要步 骤。
各组区间可写为：35~39，40~44，45~49，50~54，55~59，60~64， 65~69，70~74，75~79，80~84，85~89，90~94，95~99，最高组 95~99，亦可将最高分97包括进去。 各分组区间用整数表示，是为书写方便。在对数据进行分组时，一定要
按各组的精确限：34.5－39.5，39.5－44.5…以下类推。
尽可能使用最新的数据
3. 确认是否必要做进一步的加工整理
统计资料整理的程序
统计资料的分组 •统计资料的汇总 •统计图表的制作
统计资料的分组
统计资料的分组，即根据研究的任务及统 计事项内在的特征，按一定的标志把数 据资料进行归类，将性质相同的数据归 为一类。
•分组应该注意以下两个问题： •要分类正确。必须查明被研究现象的本质，
分组方法
分组方法
单变量值分组
组距分组 等距分组 异距分组
单变量值分组
(要点)
1. 将一个变量值作为一组
2. 适合于离散变量
☺
☺ 3. 适合于变量值较少的情况
☺
☺
组距分组
(要点)
1. 将变量值的一个区间作为一组 ☺ ~ ☺
2. 适合于连续变量
☺~ ☺
3. 适合于变量值较多的情况
☺~ ☺
二、统计数据的整理（续）
统计数据的整理的内容：
数据的审核； 根据研究目的和任务的要求选择整理的指标；
并根据分析的需要确定具体的分组； 对各调查项目的资料进行综合汇总，计算各
组和总体指标； 通过统计表、统计图等形式对整理的结果进
行描述。
数据审核—原始数据
(raw data)
审核的内容 1. 完整性审核
2. 实验数据
通过实验方法得到的数据 通常是对自然现象而言 也被广泛运用到社会科学中，如社会学、经济
学、管理学等
一、统计数据的搜集（续）
统计调查的方式 ：专门调查和统计报表 专门调查 ：
普查——是专门组织的为了某一特定目的的一 次性全面调查。
一、统计数据的搜集（续）
重点调查——是指只在调查对象中选择一部分重点单 位进行调查，借以了解基本情况的一种非全面调查。
中国统计出版社 中国信息报社 中国统计出版社 中国统计出版社 中国统计出版社 中国统计出版社 中国统计出版社 中国统计出版社 中国统计出版社 中国统计出版社 中国统计出版社 中国统计出版社 中国财政经济出版社 中国社会科学出版社 中华人民共和国海关总署
系统外部的数据
1. 统计部门和政府部门公布的有关资料， 如各类统计年鉴。
掌握被研究现象的本质是分类的基础。 •分类标志要明确，要能包括所有的数据。
统计资料的汇总
统计资料的汇总，是指在统计分组的基 础上，根据已经确定的分组标志和分组 数目，把总体中各单位归纳到相应的各 组中去，并计算出各组和总体的单位数 或指标值。 统计图表的制作，统计资料整理的最后 一步，是把统计资料汇总的结果整理成 表格，即统计表。
编制次数分布表的步骤
第五步，按照各组的精确下限和精确上限，计算 每组的组中值。 计算得到各组的组中值为：37，42，47，52， 57，62，67，72，77，82，87，92，97。
编制次数分布表的步骤
1.求全距 从最大值的数据中减去最小值的数据，所得差数
就是全距。用符号R表示。 2.定组数
分组数目要看数据的多少，如果数据个数在100个 以上，习惯上一般分10—20组。如果数据的总体分布 为正态，可用下面的经验公式计算组数（K），这样可 使分组满足渐近最优关系。
编制次数分布表的步骤
4. 需要遵循“不重不漏”的原则
5. 可采用等距分组，也可采用不 ☺ ~ ☺
等距分组
☺~ ☺
组距分组
(步骤)
1. 确定组数：组数的确定应以能够显示数据的分布特
征和规律为目的。在实际分组时，可以按斯塔奇斯 （Sturges） 提出的经验公式来确定组数K
2. 确定组距：组距(Class Width)是一个组的上限与下 限之差，可根据全部数据的最大值和最小值及所分 的组数来确定，即
典型调查 ——是根据调查的目的和要求，在对研究 对象进行初步全面分析的基础上，有意识地选择部分 有代表性的单位进行周密、系统地调查，以达到对事 物本质规律的认识，也是一种非全面调查。
抽样调查 ——是指根据随机原则从调查总体中抽取 部分单位进行观察并根据其结果推断总体数量特征的 一种非全面调查。
统计调查方式比较 ：
调查方式 比较项目
普查