测量坐标计算及高程计算

三四等水准测量计算程序在进行三、四等水准测量时，需要进行一系列的计算来确定高程差和坐标的测量结果。

以下是一个用于三、四等水准测量计算的程序，示例中使用的是简化的计算方法。

首先，我们需要定义一些变量：-P：已知点的高程-D：中间点的读数差-S：视线长度-T：观测仪器常数-L：目标点的高程差-B：倒角仪观测的读数差-C：倒角仪的常数-H：目标点的高程-R：目标点基准高程程序计算的步骤如下：1.计算中间点的高程差：-L=D+((P-D)*S/T)2.计算目标点的高程：-H=(B/100)*C3.计算目标点的绝对高程：-R=P+L+H通过上述计算步骤，可以得出目标点的绝对高程。

下面是示例程序的代码：```python#定义已知点的高程P=100.0#定义中间点读数差D=2.0#定义视线长度S=50.0#定义观测仪器常数T=100.0#定义目标点读数差B=5.0#定义倒角仪常数C=0.6#计算中间点的高程差L=D+((P-D)*S/T)#计算目标点的高程H=(B/100)*C#计算目标点的绝对高程R=P+L+H#输出结果print("目标点的绝对高程为：", R)```上述程序中假设已知点的高程为100.0，中间点的读数差为2.0，视线长度为50.0，观测仪器的常数为100.0，倒角仪的读数差为5.0，倒角仪的常数为0.6、通过计算，得出目标点的绝对高程为107.0。

这只是一个简化的示例程序，实际应用中还需要考虑更多的因素和计算步骤。

同时，还需要注意测量过程中的误差与精度要求。

在实际的三、四等水准测量中，还会涉及到更多的数据处理和参数调整，程序的实现也会更加复杂。

因此，需要根据具体的测量任务和要求进行适当的修改和完善。

高程精度的检测计算公式引言。

高程精度的检测计算在地理测量和工程测量中起着至关重要的作用。

高程精度的检测计算可以帮助工程师和测量员准确地确定地表的高程，从而为工程设计和规划提供重要的数据支持。

本文将介绍高程精度的检测计算公式及其在实际工程中的应用。

高程精度的检测计算公式。

在地理测量和工程测量中，高程精度的检测计算通常采用以下公式进行计算：ΔH = √(ΔX^2 + ΔY^2 + ΔZ^2)。

其中，ΔH表示高程精度，ΔX、ΔY和ΔZ分别表示测量点的X、Y和Z坐标的误差。

这个公式可以帮助测量员计算出测量点的高程精度，从而评估测量数据的可靠性和准确性。

在实际工程中，测量员通常会通过GPS、全站仪等测量设备获取测量点的X、Y和Z坐标，并根据这些数据计算出高程精度。

通过高程精度的检测计算，工程师可以评估工程设计和规划中所使用的地形数据的可靠性，从而确保工程施工的准确性和安全性。

高程精度的检测计算在道路、桥梁、隧道、水利工程等工程项目中具有重要的应用价值。

通过对地表高程的精确测量和计算，工程师可以更好地了解地形地貌的特征，从而为工程设计和规划提供重要的参考依据。

实际应用。

在实际工程中，高程精度的检测计算通常需要结合地形地貌的特点和工程设计的要求进行综合分析。

工程师通常会根据工程项目的具体情况选择合适的测量设备和方法，并根据测量数据计算出高程精度。

在道路工程中，高程精度的检测计算可以帮助工程师准确地确定道路的坡度和高程变化，从而为道路设计和施工提供重要的数据支持。

在桥梁工程中，高程精度的检测计算可以帮助工程师确定桥梁的高程和地基的稳定性，从而确保桥梁的安全性和稳定性。

在水利工程中，高程精度的检测计算可以帮助工程师确定水利设施的高程和水流的流向，从而为水利工程设计和规划提供重要的数据支持。

结论。

高程精度的检测计算是地理测量和工程测量中的重要内容，对于工程设计和规划具有重要的应用价值。

通过高程精度的检测计算，工程师可以准确地确定地表的高程，从而为工程设计和规划提供重要的数据支持。

工程测量坐标的计算方法在工程测量中，确定地物或工程物体的位置和坐标是非常重要的。

通过测量，我们可以确定物体在水平面和垂直面上的位置，计算出其准确的坐标。

本文将介绍工程测量中常用的坐标计算方法。

1. 水平方向坐标计算1.1 几何坐标法几何坐标法主要是通过测量物体在水平面上的距离和方向来确定其坐标。

这种方法适用于小范围测量，通常使用全站仪、经纬仪、电子测距仪等仪器进行测量。

具体步骤如下：1.设置测站：选择一个稳定的点作为测站，并用全站仪或经纬仪记录其坐标作为基准点。

2.目标测量：使用测量仪器测量目标物体与测站之间的水平距离和方向角。

3.计算坐标：根据基准点坐标和测量距离、方向角，利用三角函数计算目标物体的坐标。

1.2 平差计算法平差计算法是一种通过多个测量点之间的相互关系来计算坐标的方法。

该方法适用于大范围的测量，可以消除个别测量误差对结果的影响，提高计算的准确性。

具体步骤如下：1.设置基准点：选择一个已知坐标的点作为基准点。

2.进行测量：使用仪器对各个目标测点进行水平测量，得到其相对于基准点的距离和方向角。

3.建立观测方程：将各个目标测点与基准点之间的距离和方向角建立观测方程。

4.进行平差计算：通过最小二乘法或最小二乘平差法对观测方程进行计算，得到各个目标测点的坐标。

2. 垂直方向坐标计算垂直方向的坐标计算主要是确定物体在垂直方向上的高程。

常用的计算方法有如下两种：2.1 水平法加测高法在这种方法中，首先测量目标物体与基准点的水平距离和方向角，然后测量目标物体的高程差。

通过这些测量数据，可以计算出目标物体的高程。

具体步骤如下：1.设置基准点：选择一个已知高程的点作为基准点。

2.进行水平测量：使用测量仪器测量目标物体与基准点之间的水平距离和方向角。

3.测量高程差：使用水准仪等仪器测量目标物体的高程差。

4.计算目标物体的高程：根据基准点的高程和水平距离、方向角、高程差，利用三角函数计算出目标物体的高程。

测绘常用计算公式
测绘是一门综合性学科，涉及到许多不同的测量和计算工作。

以下是一些测绘中常用的计算公式的示例：
1.距离测量：
-直角三角形定理：a^2+b^2=c^2（勾股定理），其中a和b是直角三角形的两条边，c是斜边的长度。

-视差公式：d=(hxb)/H，其中d是距离，h是测量点的高度差，b是视差（即测量点到目标的水平距离），H是测量点的仰角。

2.面积测量：
-自由多边形面积计算：根据测得的各个角点坐标，使用边积法或三角形面积法计算多边形的面积。

-圆形地块面积计算：A=πr^2，其中A是圆形地块的面积，r是圆的半径。

3.高程测量：
- 水平线测量高程变化：h = d x tan(α)，其中h是高程变化，d 是水平距离，α是斜度角。

- 三角高程测量：H = D x tan(θ)，其中H是高程变化，D是水平距离，θ是俯角。

4.坐标转换：
-大地平面坐标转高斯投影坐标：X=X0+N+ΔX，Y=Y0+N+ΔY，其中X 和Y是高斯投影坐标，X0和Y0是中央子午线的投影坐标，N是正算的纵向坐标增量，ΔX和ΔY是由于地球椭球体引起的坐标改正数。

-高斯投影坐标转大地平面坐标：N=Y-Y0-ΔY，E=X-X0-ΔX，其中N 和E是大地平面坐标，Y0和X0是中央子午线的投影坐标，ΔX和ΔY是由于地球椭球体引起的坐标改正数。

以上仅是一些测绘中常用的计算公式的示例，在实际测量和计算中可能还会使用其他公式和方法。

同时，注意在使用这些公式时，需要根据具体的测量条件和要求进行相应的修正和适用性验证。

已知坐标如何计算高程在地理信息系统（GIS）中，高程是地球表面上某一点相对于某一基准面的垂直距离。

它是地形和地貌分析以及水文学研究等领域中至关重要的数据。

当我们已知某一点在二维坐标系中的位置时，我们可以通过一些方法来计算该点的高程。

根据地形图查询地形图是一种展示地表地形特征的地图，通常以等高线的形式表现。

我们可以通过查阅已有的地形图，找到坐标对应位置处的等高线，并确定所在点的高程。

首先，寻找目标位置（已知坐标）附近的地形图。

以该位置为中心，扩大搜索范围，找到合适的地形图。

在地形图上寻找与已知坐标附近的等高线，例如30米等高线。

根据等高线的分布情况，我们能够初步估计该点的高程。

如果需要更加准确的高程数据，可以通过与地图上标注的高程值进行比对，推测出该点的具体高程。

使用全球定位系统（GPS）全球定位系统（GPS）是一种基于卫星定位的导航系统，可以提供位置和时间等信息。

当我们已知某一点的经纬度坐标时，我们可以使用GPS来获取该点的高程。

通过GPS接收器，我们可以获取到当前位置的经纬度坐标信息。

利用相关的GPS测量数据和高程数据库，可以计算出该点的高程值。

在此过程中，我们可以利用差分GPS等方法提高高程数据的精度。

利用数字高程模型（DEM）数字高程模型（DEM）是一种用来表示地表高程信息的数学模型。

它按照一定的间隔进行采样，能够准确地表示一个地理区域的高程变化。

当我们已知某一点的二维坐标，可以通过数字高程模型来计算该点的高程。

首先，找到对应区域的DEM数据集。

然后，使用DEM数据集中的高程值进行插值计算，确定目标点的高程。

插值方法可以有多种选择，如最近邻插值、反距离权重插值等。

通过地形测量仪器测量在现实世界中，我们可以使用一些专业的地形测量仪器来测量某一点的高程。

这些仪器可以直接测量地面的高程变化，提供准确的高程数据。

常用的地形测量仪器包括全站仪、水准仪等。

通过在已知坐标处进行测量，我们可以得到该点的高程值。

导线测量常用计算公式导线测量是土木工程或电气工程中的一项重要工作，主要用于确定建筑物的位置、土地边界以及计算地形的变化等。

在导线测量中，有很多常用的计算公式可以帮助工程师或测量师进行精确的测量和计算。

以下是一些常用的导线测量计算公式：1.距离计算公式：-垂直平距（垂距）：D=SQRT((ΔN)^2+(ΔE)^2)-水平平距：H=SQRT((ΔN)^2+(ΔE)^2+(ΔH)^2)-斜距：L=SQRT((ΔN)^2+(ΔE)^2+(ΔH)^2)- 仰角：A = arctan(ΔH / H)-前视高差：h1=H1-H0-反视高差：h2=H0-H22.坐标计算公式：- 相对平差量：ΔX = (ΔN * cosα) + (ΔE * sinα)- 相对平差量：ΔY = (ΔN * sinα) - (ΔE * cosα)-新坐标X=X0+∑(ΔX)-新坐标Y=Y0+∑(ΔY)3.角度计算公式：- 方位角：I = arctan((ΔE2 - ΔE1) / (ΔN2 - ΔN1))-转角：θ=I2-I1-内角和：∑θ=∑(Ii)-外角和：∑θ=n*180°-∑(Ii)4.高程计算公式：-平均高程：H=(H0+H1+H2)/3-高程改正：ΔHi=Hi-H-净高差：Nh=h1+ΔH5.线性状况计算公式：-输沙率：Q=W/(T*B)其中，Q为输沙率，W为沙子的质量，T为时间，B为河道截面积。

6.面积计算公式：-梯形法计算面积：A={0.5*(a+b)*h}- 辛普森法计算面积：A = {h / 3 * (y0 + 4y1 + 2y2 + 4y3 + ... + yn)}7.建筑斜率计算公式：-百分比斜率：P=(ΔH/L)*100- 度数斜率：s = tan^-1(ΔH / L)这些计算公式是导线测量中常用的工具，可以帮助工程师或测量师在实际工作中准确地计算测量结果。

需要根据具体的测量需求和情况选择合适的公式进行计算，并注意测量文档中的单位和精度要求，以确保测量结果的准确性。

高程实测与计算方法与测绘技术指南高程测量是地理信息领域中不可或缺的一部分，它在土地开发、规划设计、水利工程、交通运输等众多领域都扮演着重要的角色。

而高程实测与计算方法以及测绘技术则为我们提供了准确、高效的高程数据，为各项工作的顺利进行提供了有力保障。

一、高程实测方法实测是获取准确高程数据的关键步骤之一，目前常见的高程测量方法主要包括水准测量和GPS测高。

水准测量是利用重力作用下物体受力平衡状态的基本原理测定地表高程的一种方法。

它通过测量基准点与目标点之间的高差来获取高程信息，适用于长距离、高精度的高程测量。

水准测量的主要仪器设备有水准仪、三脚架和测站杆。

GPS测高则是利用卫星导航系统进行高程测量的方法。

它通过接收多颗卫星发射的信号，通过计算信号传播时间来获得高程信息。

GPS测高准确度高、速度快，适用于短距离、中精度的高程测量。

GPS测高的主要设备有GPS接收机和测高杆。

二、高程计算方法高程计算是基于高程实测数据进行精确的计算和处理，以获取更加准确的高程数值。

常见的高程计算方法主要有水准网平差法和拟合曲面法。

水准网平差法是根据一系列水准测量数据建立水准网，通过精确的计算和平差，得到各点的坐标高程值。

水准网平差法的优点是高程计算结果具有全局一致性和较高的精度。

在实际应用中，水准网平差法通常结合GPS测高数据来进行高程计算，以提高效率和精确度。

拟合曲面法则是将一系列离散测量点的高程数据拟合成一条平滑曲面，从而实现对整个测区的高程计算。

拟合曲面法通过数学模型来描述测区的高程分布规律，如多项式函数、样条函数等。

拟合曲面法的优点是计算速度快、适用于大范围的高程计算。

但也需要注意模型的选取和合理性。

三、测绘技术指南为了确保高程实测与计算的准确性和可靠性，测绘技术在其中起着重要的作用。

下面简要介绍几种常用的测绘技术：1. 数据采集与处理技术：包括GPS、全站仪等测量仪器的使用和数据导入、处理的技术。

通过科学合理的数据采集与处理，可以提高高程测量的准确度和效率。

在测量岗位工作已经有三个月到时间了，三个月的时间学习和收获了许多，现对这三个月的工作学习做一下总结。

测量工作容主要有以下两个方面：测量放线（坐标计算），高程控制。

一、测量放线测量放线到主要技术包括坐标计算和仪器使用。

坐标计算包括直线段坐标计算和曲线段坐标计算。

1、直线段坐标计算。

直线坐标计算分为中桩坐标计算和边桩坐标计算。

1）中桩坐标计算。

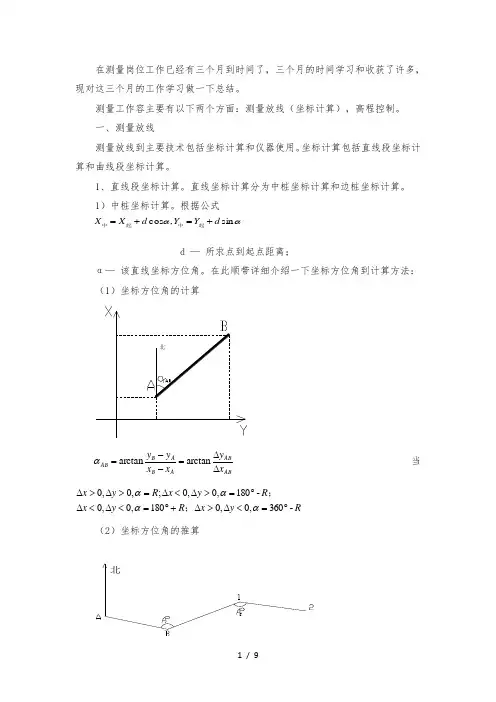
根据公式ααsin ,cos d Y Y d X X +=+=起中起中d — 所求点到起点距离；α— 该直线坐标方位角。

在此顺带详细介绍一下坐标方位角到计算方法： （1）坐标方位角的计算ABABA B A B AB x yx x y y ∆∆=--=arctan arctanα当Ry x R y x R y x R y x -360,0,0180,0,0-180,0,0;,0,0︒=<∆>∆+︒=<∆<∆︒=>∆<∆=>∆>∆αααα；；（2）坐标方位角的推算北，，218021*********βαβααβαβαα-︒+=-=+︒+=+=B B AB BA B 由此推出：βαα±︒+=180后前（“左”→“+”，“右”→“-”），计算中，若α值大于360°，应减去360°；若小于0°，则加上360°。

2）边桩坐标计算应用公式 )90sin(90cos(︒±+=︒±+=ααl y y l x x 中边中边）， 进行边桩坐标到计算。

北客站为直线车站，坐标计算较简单，现以位于机场线第二段底板的变电所夹层东北角C 点为例进行计算：以机场线右线为基准来计算中、边桩坐标。

已知起点坐标A （22264.4009，11553.2031），终点坐标B （22180.2655，11279.0739），起点里程为YDK0+255.275,C 点里程为YDK0+286.075,偏距为15.33m ，则由以上公式计算C 点坐标：α=arctan(（11279.0739-11553.2031）/（22180.2655-22264.4009）)+180°=252.938°，=中x 22264.4009+（286.075-255.275）*cos252.938°=22255.3640 =中y 11553.2031+（286.075-255.275）*sin252.938°=11523.7586 =c x 中x +15.33*cos （252.938°+90°）=22270.0193=c y 中y +15.33*sin （252.938°+90°）=11519.2606，则可求出C（22270.0193，11519.2606）。

全站仪测量高程计算方法全站仪是现代测量工程中常用的精密测量仪器，它可以用来测量各种地形、建筑物和其他工程项目的高程。

全站仪不仅可以提供高度测量的精确结果，还可以通过自动化的功能简化测量过程。

本文将介绍全站仪测量高程的计算方法。

1. 基本原理全站仪基于三角测量原理进行高程测量。

它通过测量目标点与测站的水平角和垂直角，以及目标点与测站之间的距离来计算高程。

全站仪内置的电子仪器能够自动记录和计算这些测量数据，并根据预设的坐标系进行转换和纠正。

2. 实际操作步骤使用全站仪进行高程测量需要以下步骤：2.1 设置仪器在开始测量之前，首先需要设置全站仪的参数，包括工作单位、坐标系和参考高程等。

根据具体测量要求进行设置。

2.2 进行垂直角测量在确定好测站位置后，需要通过全站仪测量目标点与测站之间的垂直角。

将全站仪对准目标点，观测仪器显示的垂直角，并记录下来。

2.3 进行水平角测量在完成垂直角测量后，需要通过全站仪测量目标点与测站之间的水平角。

将全站仪对准目标点，观测仪器显示的水平角，并记录下来。

2.4 进行距离测量在垂直角和水平角测量完成后，全站仪还可以测量目标点与测站之间的水平距离。

通过仪器上的测距功能进行测量，并记录下来。

2.5 计算高程根据测量得到的垂直角、水平角和距离数据，可以使用三角测量原理进行计算。

通过一些基本的三角函数关系，可以将观测数据转化为目标点的高程值。

全站仪内置的计算功能能够自动完成这个过程，并给出最终的高程结果。

3. 注意事项在进行全站仪测量高程时，有一些注意事项需要注意：•确保测站位置稳定，并尽量选择平坦的地面进行测量，以减小测量误差。

•在目标点与测站之间的测量距离较长时，需要注意大气折射的影响，并进行补偿。

•在进行长距离测量时，应使用更精确的测量方法，如追踪测距法，以提高测量精度。

•在进行多点测量时，需要根据测量数据的准确性进行数据处理，如采用平均值方式来获得更准确的结果。

•在测量过程中，注意仪器的保养和校准，以确保测量结果的准确性。

CASIO 9860G SD线元法隧道三维（坐标正反计算、高程）计算程序1. A（此为主程序）Lbl 0：〝1.LC=>XY〝：〝2.XY=>LC〝：〝3.ZHZL=>GC〝：〝PB=>V=1,2,3〞？→V：If V=1：Then GOTO 1 ：IfEnd ：If V=2：Then GOTO 2 ：IfEnd ：If V=3：Then GOTO 3 ：Else GOTO 0 ：IfEnd：Lbl 3：〝ZH=H〝？→H ：〝SDZF=Z〝？→Z：Prog〝ZGCZCX〝：GOTO 0：Lbl 1 ：〝ZH=L〝？→L：If L>173000 And L<174661.96：Then GOTO 4 ：Else GOTO 0 ：IfEnd ：Lbl 4：L→L：〝SDZF=Q〝？→Q：〝XLZJ,-Z+Y=Q〝：Q+0.125→Q：Prog 〝ZBQXYS〝：〝JSJD=J〝：90→J▲Prog 〝ZSZB〝：〝X=〝：X ▲ 〝Y=〝：Y▲〝FWJ=O〝：O▼DMS▲L→H：Q-0.125→Z：Prog 〝ZGCZCX〝：GOTO 0：Lbl 2：〝XO=M〝?→M：〝YO=R〝?→R：173300→L：If M>3845505.273 And M<3846506.099And R>499371.832 And R<500352.224 ：Then GOTO 5：Else GOTO 2：IfEnd ：Lbl 5：0→Q：0→J：Prog 〝ZBFS〝：〝LC=L〝：L ▲〝JL=Q〝：Q▲ 〝SDZJ，-Z+Y=Q〝：Q-0.125→Q ▲L→H：Q→Z：Prog 〝ZGCZCX〝：GOTO 02.正算坐标ZBZS( L-S ) / 4→H：90/π→F：HHF（1/T-1/I）/（K-S）→U：2HF/ I→D：C+4D+16 U→Ｏ：O+J→P ：C+ D+ U→E：C+2D+4U→W：C+3D+9U→G：A+AbsH/3*(cosC+4(cosG+cosE)+2cosW+cosO)+Qcos P→X ：B+AbsH/3*(sinC+4(sinG+sinE)+2sinW+sinO)+Qsin P→Y3.反算坐标：ZBFSLbl 0：Prog 〝ZBQXYS〝：Prog 〝ZBZS〝：O-90→Z：(R-Y)cosZ-(M-X) sinZ→P ：L+P→L：If Abs P≥0.001：Then GOTO 0 ：Else GOTO 1：IfEnd ：Lbl 1： (R-Y)cosO-(M-X) sinO→Q4. 曲线元要素数据库：ZBQXYSIf L≥S And L＜K ：Then **→ S：**→ A：**→ B：**→ C：**→ I：**→ K：* *→ T IfEnd ：If L≥S And L＜K ：Th en **→ S：**→ A：**→ B：**→ C：**→ I：**→ K：* *→ T IfEnd ：If L≥S And L＜K ：Then **→ S：**→ A：**→ B：**→ C：**→ I：**→ K：* *→ T IfEnd ：If L≥S And L＜K ：Then **→ S：**→ A：**→ B：**→ C：**→ I：**→ K：* *→ T IfEnd ：If L≥S And L＜K ：Then **→ S：**→ A：**→ B：**→ C：**→ I：**→ K：* *→ T IfEnd ：……………………………If L≥S And L＜K ：Then **→ S：**→ A：**→ B：**→ C：**→ I：**→ K：* *→ T IfEnd ┘(注：如有多个曲线元要素继续添加入数据库ZBQXYS中)5 高程计算主程序ZGCZCX (后有修改说明)Lbi1 ：〝SCGC=X〝？→X：〝R=M〝：5.98→M：〝CS=N〝：1.603→N：Prog＂GC SJK＂：C-D→F：Abs(RF÷2) →T：R AbsF÷F→R：If H≤B-T ：Then 0→K：GOTO 2：IfEnd ：If H>B-T And H<B+T ：Then H-B+T→K ：GOTO 2：IfEnd ：If H≥B+T ：Then 0→K：D→C：GOTO 2：IfEnd ：Lbi 2 ：〝XLZG=G〝：A-（B-H）C-K^2÷2R→G▲If Z≥0：Then If X>100 Then 〝YO1XGC=J〝：G+N→J▲〝YGCFSKD=J〝：Abs√(M^2-(X-（G+N）)^2) →J▲〝YKDCQ,+C,-Q=J〝：J- Abs (Z+0.000) →J▲〝YSBSJGC=J〝：G+N+√(M^2-(Z+0.000)^2) →J▲〝YGCCQ,C+,Q-=J〝：X-J→J▲Else〝YO1XGC=J〝：G+N→J▲〝YSBSJGC=J〝：G+N+√(M^2-(Z+0.000)^2) →J▲ IfEnd ：Else 〝ZO1XGC=J〝：G+N→J▲If X>100 ：Then〝ZGCFSKD=J〝：Abs√(M^2-(X-（G+N）)^2) →J▲〝ZKDCQ,+C,-Q=J〝：J- Abs (Z+0.000) →J▲〝ZSBSJGC=J〝：G+N+√(M^2-(Z+0.000)^2) →J▲〝ZGCCQ,C+,Q-=J〝：X-J→J▲Else〝ZSBSJGC=J〝：G+N+√(M^2-(Z+0.000)^2) →J ▲IfEnd ：IfEnd6高程计算主程序子程序：GCSJKIf H>起点桩号 And H≤第一个竖曲线起点桩号Then 第一竖曲线交点高程→A：第一竖曲线交点桩号→B：第一竖曲线前坡度→C：第一竖曲线后坡度→D：第一竖曲线半径→R：IfEnd：If H>第一竖曲线止点桩号 And H≤第二竖曲线起点桩号Then 第一竖曲线交点高程→A：第一竖曲线交点桩号→B：第一竖曲线前坡度→C：第一竖曲线后坡度→D：第一竖曲线半径→R：IfEnd：If H>第一竖曲线止点桩号 And H≤第二竖曲线起点桩号Then 第一竖曲线交点高程→A：第一竖曲线交点桩号→B：第一竖曲线前坡度→C：第一竖曲线后坡度→D：第一竖曲线半径→R：IfEnd………………………(继续添加要素)说明：第一部分坐标部分（1、2、3、4）V=1进入坐标正算 V=2进入坐标反算V=3进入单独的高程计算当V不等于1、2、3时，则返回程序，要求再次输入V值。

工程测量坐标计算公式工程测量是工程建设的重要环节，准确的坐标计算是保证工程质量和施工安全的基础。

本文将介绍工程测量中常用的坐标计算公式，帮助读者更好地理解并应用于实践中。

一、坐标计算的基础知识在工程测量中，常用的坐标系统有直角坐标系和大地坐标系。

直角坐标系以某一点为原点，建立笛卡尔坐标系，用x、y、z三个轴线表示空间位置。

大地坐标系则以地球为基准，通过经度、纬度和高程来确定点的相对位置。

二、坐标计算公式1. 直角坐标系的坐标计算公式在直角坐标系中，常用的坐标计算公式有：- 两点间距离计算公式：设A点坐标为(x1, y1, z1)，B点坐标为(x2, y2, z2)。

则两点间的距离d计算公式如下：d = √((x2-x1)^2 + (y2-y1)^2 + (z2-z1)^2)- 点到直线距离计算公式：设点A的坐标为(x1, y1, z1)，直线方程为Ax + By + Cz + D = 0。

则A点到直线的距离d计算公式如下：d = |Ax1 + By1 + Cz1 + D| / √(A^2 + B^2 + C^2)- 点到平面距离计算公式：设点A的坐标为(x1, y1, z1)，平面方程为Ax + By + Cz + D = 0。

则A点到平面的距离d计算公式如下：d = |Ax1 + By1 + Cz1 + D| / √(A^2 + B^2 + C^2)2. 大地坐标系的坐标计算公式在大地坐标系中，常用的坐标计算公式有：- 两点间距离计算公式：根据两点的经纬度计算其球面距离，公式如下：d = R * arccos(sinφ1*sinφ2 + cosφ1*cosφ2*cos(λ2-λ1))其中，R为地球半径，φ为纬度，λ为经度。

- 两点间方位角计算公式：根据两点经纬度计算其中一点相对于另一点的方位角，公式如下：α = arctan((sinΔλ * cosφ2) / (cosφ1*sinφ2 -sinφ1*cosφ2*cosΔλ))其中，φ为纬度，λ为经度，Δλ为两点经度差。

全站仪计算坐标的公式全站仪是一种常用的地理测量仪器，用于测量地物的空间坐标。

它能够通过观测目标点和测站的角度和距离信息，计算出目标点的空间坐标。

计算坐标的公式是全站仪测量中的关键部分，下面将介绍全站仪计算坐标的公式。

1. 基本原理全站仪计算坐标的基本原理是三角测量方法。

它利用目标点和测站的观测角度和距离，通过三角关系计算目标点的坐标。

全站仪观测角度时，会测量水平角和垂直角，测量距离时，常用的方法是通过自动跟踪仪器观测目标点，测量目标点和仪器之间的水平距离。

2. 水平角的计算全站仪观测水平角时，通常通过测量水平角的方向和水平角的量值来确定目标点的方位角。

水平角的计算公式如下：方位角 = 测站方位角 + 观测水平角方向 × 180°其中，测站方位角是指测站和正北方向之间的水平角度，观测水平角方向是指观测时旋转到正对目标点的方向的角度差。

3. 垂直角的计算全站仪观测垂直角时，通过测量垂直角的仰角和俯角，可以计算出目标点的高程。

垂直角的计算公式如下：高程角 = 观测垂直角仰角 - 观测垂直角俯角4. 距离的计算在全站仪中，常用的方法测量水平距离是通过自动跟踪仪器观测目标点。

观测时，会记录测站和目标点之间的水平距离。

距离的计算公式如下：距离 = 观测距离 - 目标仪器高程 + 测站仪器高程其中，观测距离是指测站和目标点之间的水平距离，目标仪器高程是指目标点相对于仪器的高度，测站仪器高程是指测站相对于仪器的高度。

5. 坐标的计算在得到目标点的方位角、高程和距离后，即可计算出目标点的空间坐标。

坐标的计算公式如下：X坐标 = 测站X坐标 + 距离 × sin(方位角)Y坐标 = 测站Y坐标 + 距离 × cos(方位角)Z坐标 = 测站Z坐标 + 高程角其中，测站X、Y、Z坐标是指测站的空间坐标。

通过这些公式，可以计算出目标点的水平坐标和高程坐标。

总结一下，全站仪计算坐标的公式包括水平角的计算、垂直角的计算、距离的计算以及坐标的计算。

工程测量常用计算公式一、 方位角的计算公式二、 平曲线转角点偏角计算公式三、 平曲线直缓、缓直点的坐标计算公式 四、 平曲线上任意点的坐标计算公式 五、 竖曲线上点的高程计算公式 六、 超高计算公式七、 地基承载力计算公式 八、 标准差计算公式一、 方位角的计算公式1. 字母所代表的意义：x 1：QD 的X 坐标 y 1：QD 的Y 坐标 x 2：ZD 的X 坐标 y 2：ZD 的Y 坐标 S：QD～ZD 的距离 α：QD～ZD 的方位角 2. 计算公式：212212y y x x S1）当y 2- y 1>0，x 2- x 1>0时：1212x x y y arctg2）当y 2- y 1<0，x 2- x 1>0时：1212360x x y y arctg3）当x 2- x 1<0时：1212180x x y y arctg二、 平曲线转角点偏角计算公式 1. 字母所代表的意义：α1：QD～JD 的方位角 α2：JD～ZD 的方位角 β：JD 处的偏角β＝α2-α1（负值为左偏、正值为右偏）三、 平曲线直缓、缓直点的坐标计算公式1. 字母所代表的意义：U：JD 的X 坐标 V：JD 的Y 坐标A：方位角（ZH～JD）T：曲线的切线长，2322402224R L L D tg R L R T s s sD：JD 偏角，左偏为-、右偏为+ 2. 计算公式：直缓（直圆）点的国家坐标：X′=U+Tcos(A+180°)Y′=V+Tsin(A+180°)缓直（圆直）点的国家坐标：X″=U+Tcos(A+D)Y″=V+Tsin(A+D)四、 平曲线上任意点的坐标计算公式1. 字母所代表的意义：P：所求点的桩号B：所求边桩～中桩距离，左-、右+ M：左偏-1，右偏+1 C：JD 桩号 D：JD 偏角 L s ：缓和曲线长A：方位角（ZH～JD） U：JD 的X 坐标 V：JD 的Y 坐标T：曲线的切线长，2322402224R L L D tg R L R T s s sI=C-T：直缓桩号J=I+L：缓圆桩号s L DRJ H 180：圆缓桩号K=H+L：缓直桩号1）当P<I 时中桩坐标：X m =U+(C-P)cos(A+180°) Y m =V+(C-P)sin(A+180°) 边桩坐标：X b =X m +Bcos(A+90°) Y b =Y m +Bsin(A+90°)2）当I<P<J 时s230RL I P MA O 2390R I P I P G中桩坐标：X m =U+Tcos(A+180°)+GcosOY m =V+Tsin(A+180°)+GsinOs290RL I P W边桩坐标：X b =X m +Bcos(A+MW+90°) Y b =Y m +Bsin(A+MW+90°)3）当J<P<H 时R J P L M A R J P R L M A O s s909090 RJ P R G 90sin2 中桩坐标： O G R L M A R L L A T U X s ss m cos 30cos 90180cos 23O G R L M A R L L A T V Y s ss m sin 30sin 90180sin 23RJ P W90边桩坐标：X b =X m +Bcos(O+MW+90°) Y b =Y m +Bsin(O+MW+90°)4）当H<P<K 时sRL K P MMD A O 230180 2390R P K P K G中桩坐标：X m =U+Tcos(A+MD)+GcosOY m =V+Tsin(A+MD)+GsinOs290RL K P W边桩坐标：X b =X m +Bcos(A+MD-MW+90°) Y b =Y m +Bsin(A+MD-MW+90°)5）当P>K 时中桩坐标：X m =U+(T+P-K)cos(A+MD) Y m =V+(T+P-K)sin(A+MD) 边桩坐标：X b =X m +Bcos(A+MD+90°) Y b =Y m +Bsin(A+MD+90°)注：计算公式中距离、长度、桩号单位：“米”；角度测量单位：“度”；若要以“弧度”为角度测量单位，请将公式中带°的数字换算为弧度。

角度坐标测量计算公式细则文件编码（008-TTIG-UTITD-GKBTT-PUUTI-WYTUI-8256）计算细则1、坐标计算：X1=X+Dcosα,Y1=Y+Dsinα。

式中 Y、X为已知坐标，D为两点之间的距离，Α为方位角。

2、方位角计算：1）、方位角=tan=两坐标增量的比值，然后用计算器按出他们的反三角函数（±号判断象限）。

2）、方位角：arctan（y2-y1)/(x2-x1)。

加减180（大于180就减去180（还大于360就在减去360）、小于180就加180如果x轴坐标增量为负数，则结果加180°。

如果为正数，则看y轴的坐标增量，如果Y轴上的结果为正，则算出来的结果就是两点间的方位角，如果为负值，加360°。

S=√（y2-y1)+(x2-x1),1)、当y2-y1>0，x2-x1>0时；α=arctan（y2-y1)/(x2-x1)。

2)、当y2-y1<0，x2-x1>0时；α=360°+arctan（y2-y1)/(x2-x1)。

3)、当x2-x1<0时；α=180°+arctan（y2-y1)/(x2-x1)。

再用两点之间的距离公式可算距离(根号下两个坐标距离差的平方相加）。

拨角：arctan（y2-y1)/(x2-x1)1、例如：两条巷道要互相平行掘进的话，求它们的拨角：方法（前视边方位角减后视边方位）在此后视边方位要加减180°，若拨角结果为负值为左偏“逆时针”（+360°就可化为右偏，正值为右偏“顺时针”。

2、在图上标识方位的方法：就是导线边与Y轴的夹角。

3、高程计算：目标高程=测点高程+h+仪器高—占标高。

4、直角坐标与极坐标的换算：（直角坐标用坐标增量表示；极坐标用方位角和边长表示）1）、坐标正算（极坐标化为直角坐标）已知一个点的坐标及该点至未知点的距离和方位角，计算未知点坐标方位角，知A(Xa,Ya)、Sab、αab，求B(Xa,Ya)解：Xab=Sab×COSαab 则有Xb=Xa+XabYab=Sab×SINαab Yb=Ya+Yab2)、坐标反算，已知两点的坐标，求两点的距离（称反算边长）和方位角(称反算方位角）的方法已知A(Xa,Ya)、B(Xb,Yb),求αab、Sab。

工程测量计算公式总结工程测量是指在工程建设过程中，通过测量仪器仪表对施工位置、尺寸、形状、高程、坐标以及土壤、岩石等物理和力学性质等进行测量和计算的一项工作。

工程测量涉及到很多计算公式，下面将对一些常见的工程测量计算公式进行总结。

1.直线测量直线测量是测量工程中最常见的一种测量方式，其中包括距离和角度的测量。

(1)间接测距公式：L=ExK其中，L为实际测定的距离值，E为仪器测得的读数，K为仪器常数。

(2)斜距计算公式：L = sqrt (ar^2 + hp^2)其中，L为斜距，ar为水平投影，hp为垂直投影。

(3)曲线长度计算公式：其中，L为曲线长度，a为切差，b为中线长，θ为转角。

2.高程测量高程测量是指对地面或其他物体的高度进行测量的过程。

(1)高差计算公式：ΔH=H1-H2其中，ΔH为高程差，H1为较高点的高程，H2为较低点的高程。

(2)三等水准测量公式：ΔH=Hi-Hn=L1+L2+...+Ln其中，ΔH为起点和终点的高差，Hi为每个高差的累加，L为每个边长。

3.角度测量角度测量是工程测量中常用的一种测量方式。

(1)方位角计算公式：Z = arctan ( Y / X ) + 360°其中，Z为方位角，Y为北向坐标差值，X为东向坐标差值。

(2)三角高程计算公式：H = D x sin(θ)其中，H为高程值，D为斜距，θ为水平方向与竖直方向的夹角。

4.面积和体积计算面积和体积的计算是工程测量中常见的计算任务。

(1)矩形面积计算公式：A=LxW其中，A为面积，L为长度，W为宽度。

(2)三角形面积计算公式：A=0.5xBxH其中，A为面积，B为底边长，H为高。

(3)平面多边形面积计算公式：A=1/2x(X1Y2+X2Y3+...+XnY1-Y1X2-Y2X3-...-YnX1)其中，A为面积，Xi为顶点的x坐标，Yi为顶点的y坐标，n为顶点数量。

(4)长方体体积计算公式：V=LxWxH其中，V为体积，L为长度，W为宽度，H为高度。

工程测量常用计算公式工程测量是指通过测量手段获取工程项目的相关数据，以便进行设计、施工和监测等工作。

在工程测量中，常常需要用到一些计算公式来进行数据处理和分析。

下面是一些常用的工程测量计算公式：1.距离测量相关公式：- 直线距离计算公式：d=sqrt((x2-x1)^2+(y2-y1)^2)，其中(x1,y1)和(x2,y2)分别为直线两个点的坐标。

- 准线距离计算公式：d=(s/n)*sqrt((m1)^2+(m2)^2+...+(mn)^2)，其中s为总长度，n为总测次数，m1、m2、..、mn分别为各测次的测量值。

- 斜距计算公式：d=sqrt((HC+ΔH)^2-(n1-n2)^2)，其中HC为水平视距，ΔH为高差，n1和n2分别为测站的高程。

2.角度测量相关公式：- 三角测量公式：tanA=(a/b)，其中A为角度，a为A边长，b为B边长。

-方位角计算公式：Az=At+Δ，其中Az为目标点的方位角，At为测站的方位角，Δ为目标点相对测站的方位角修正数。

- 高程角计算公式：V=(100/π)*atan((n2-n1)/d)，其中V为高程角，n1和n2分别为测站和目标点的高程，d为水平距离。

3.面积和体积测量相关公式：- 面积计算公式：S=(1/2)*(x1y2+x2y3+...+xn-1yn+xny1-x2y1-x3y2-...-xn-yn-1-x1yn)，其中(x1,y1)到(xn,yn)为多边形边界点的坐标。

-体积计算公式：V=S*H，其中V为体积，S为横截面面积，H为高度。

4.坐标转换公式：- 平面坐标转换公式：X=x0+R*sin(A)，Y=y0+R*cos(A)，其中(x0,y0)为原点坐标，R为距离，A为方位角。

-大地坐标转换公式：B=B0+ΔB，L=L0+ΔL，其中(B0,L0)为基准点的大地坐标，ΔB和ΔL分别为相对于基准点的纬度和经度差值。

这些计算公式只是工程测量中的一部分，在实际应用中还可以根据具体测量需求进行更多的计算和推导。

水准仪在测量工程中是如何计算高程2010-11-28 02:44:45| 分类：工程测量|举报|字号订阅水准仪在测量工程中是如何计算高程实测标高=后视读数+后视标高-前视读数高程的计算有两种方法 1 已知高程+高差=待测高程(高差法)高差=前视度数-后视觉读数2 已知高程+已知高程点读数=HH - 待测点读数=待测高程(等高法)表格中有: 观测点站点每站的前/后视读数高差高差闭合差高程结果qq:35542491 我会尽我所能地面高+后视读数=仪器高度仪器高度-塔尺读数=塔尺处的高程<必须知道一个已知的地面高,你自己设一个也是可以的>后视器高中间视前视高程备注1.100 180.695 179.5951.200 179.495179.595+1.1=180.695180.695-1.2=179.495高层建筑沉降观测技术的应用摘要：随着社会的不断进步，物质文明的极大提高及建筑设计施工技术水平的日臻成熟完善，同时，也因土地资源日渐减少与人口增长之间日益突出的矛盾，高层及超高层建(构)筑物越来越多。

为了保证建构筑物的正常使用寿命和建（构）筑物的安全性，并为以后的勘察设计施工提供可靠的资料及相应的沉降参数，建（构）筑物沉降观测的必要性和重要性愈加明显。

关键词：高层沉降观测随着社会的不断进步，物质文明的极大提高及建筑设计施工技术水平的日臻成熟完善，同时，也因土地资源日渐减少与人口增长之间日益突出的矛盾，高层及超高层建(构)筑物越来越多。

为了保证建构筑物的正常使用寿命和建（构）筑物的安全性，并为以后的勘察设计施工提供可靠的资料及相应的沉降参数，建（构）筑物沉降观测的必要性和重要性愈加明显。

现行规范也规定，高层建筑物、高耸构筑物、重要古建筑物及连续生产设施基础、动力设备基础、滑坡监测等均要进行沉降观测。

特别在高层建筑物施工过程中应用沉降观测加强过程监控，指导合理的施工工序，预防在施工过程中出现不均匀沉降，及时反馈信息为勘察设计施工部门提供详尽的一手资料，避免因沉降原因造成建筑物主体结构的破坏或产生影响结构使用功能的裂缝，造成巨大的经济损失。