共轭梯度法程序及调试结果分析

一、实验目的:1、掌握求解无约束最优化问题的 F-R 共轭梯度法，以及约束最优化问题 Wolfe 简约梯度法。

2、学会用MATLAB 编程求解问题，并对以上方法的计算过程和结果进行分析。

二、实验原理与步骤: 1、F-R 共轭梯度法基本步骤是在点)(k X 处选取搜索方向)(k d , 使其与前一次的搜索方向)1(-k d关于A 共轭，即(1)()(1),0k k k d d Ad --<>=然后从点)(k X 出发，沿方向)(k d 求得)(X f 的极小值点)1(+k X ,即)(m in )()()(0)1(k d X f X f k k λλ+=>+如此下去, 得到序列{)(k X }。

不难求得0,)1()(>=<-k k Ad d的解为)()1()1()()()()1(,,k k k k k k k d Ad d d AX b XX><>-<+=--+注意到)(k d 的选取不唯一，我们可取)1(1)()()(--+-∇=k k k k d X f d β由共轭的定义0,)1()(>=<-k k Add 可得： ><><-=----)1()1()1()(1,,k k k k k Ad d Ad r β共轭梯度法的计算过程如下：第一步：取初始向量)0(X , 计算⎪⎪⎩⎪⎪⎨⎧+=><><-=-=-∇==(0)0(0)(1))0()0()0()0(0(0)(0)(0)(0)d X X ,,X )X (r d λλAd d Ad r A b f第1+k 步：计算⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧+=><><-=+=><><-=-=-∇=+------(k)0(k)1)(k )()()()()1(1(k))()1()1()1()(1(k)(k)(k)d X X ,,r ,,X )X (r λλββk k k k k k k k k k k k k Ad d Ad r d d Ad d Adr A b f2、Wolfe 简约梯度法Wolfe 基本计算步骤：第一步：取初始可行点 x 0∈X l ,给定终止误差ε>0 ，令k:=0；第二步：设 I B k是x k 的 m 个最大分量的下标集，对矩阵A 进行相应分解 A =(B k ,N k )；第三步：计算 ∇f(x k)=(∇B f(x k )∇Nf(x k )) ,然后计算简约梯度r N k=−(B k −1N k )T ∇B f(x k )+∇N f(x k )；第四步：构造可行下降方向 p k . 若||p k ||≤ε ，停止迭代，输出x k 。

一、共轭梯度法共轭梯度法（Conjugate Gradient）是共轭方向法的一种，因为在该方向法中每一个共轭向量都是依靠赖于迭代点处的负梯度而构造出来的，所以称为共轭梯度法。

由于此法最先由Fletcher和Reeves （1964）提出了解非线性最优化问题的，因而又称为FR 共轭梯度法。

由于共轭梯度法不需要矩阵存储，且有较快的收敛速度和二次终止性等优点，现在共轭梯度法已经广泛地应用于实际问题中。

共轭梯度法是一个典型的共轭方向法，它的每一个搜索方向是互相共轭的，而这些搜索方向d仅仅是负梯度方向与上一次迭代的搜索方向的组合，因此，存储量少，计算方便，效果好。

二、共轭梯度法的原理设有目标函数f（X）=1/2X T HX+b T X+c 式1 式中，H作为f（X）的二阶导数矩阵，b为常数矢量，b=[b1,b2,b3,...b n]T 在第k次迭代计算中，从点X（k）出发，沿负梯度方向作一维搜索，得S(K)=-∆f（X（k））式2 X(k+1)=X(k)+ɑ(k)S(k) 式3在式中，ɑ（k）为最优步长。

设与S(k）共轭的下一个方向S(k+1)由点S(k）和点X(k+1)负梯度的线性组合构，即S (k+1)=-∆f （X （k+1））+β(k)S (k) 式4 根据共轭的条件有[S (k)]T ∆2f （X (k)）S (k+1)=0 式5 把式2和式4带入式5，得-[∆f(X (k))]T ∆2f （X (k)）[-∆f （X （k+1））+β(k)S (k) ]=0 式6 对于式1，则在点X (k)和点X (k+1)的梯度可写为∆f(X (k))=HX (k)+b 式7 ∆f （X （k+1）)=HX (k+1)+b 式8 把上面两式相减并将式3代入得ɑ(k)H S (k)=∆f （X （k+1）)-∆f(X (k)) 式9 将式4和式9两边分别相乘，并代入式5得-[∆f （X （k+1）)+β(k)∆f(X (k))]T [∆f （X （k+1）)-∆f(X (k)]=0 式10 将式10展开，并注意到相邻两点梯度间的正交关系，整理后得 β（k ）=22||))((||||))1((||k X f k X f ∆+∆ 式11把式11代入式4和式3，得 S （k+1）=-∆f （X (k)）+β（k ）S （k ）X (k+1)=X （k ）+ɑ（k ）S （k ）由上可见，只要利用相邻两点的梯度就可以构造一个共轭方向。

共轭梯度法实验报告
实验报告：共轭梯度法
引言：
实验目的：
1.了解共轭梯度法的基本原理和步骤；
2.掌握共轭梯度法的具体实现方法；
3.比较共轭梯度法和其他方法的解的精确度和收敛速度；
4.验证共轭梯度法在求解大规模线性方程组中的优势。

实验步骤：
1.阐述共轭梯度法的原理和步骤；
2.设定一个线性方程组，并使用共轭梯度法进行求解；
3.通过计算实验结果与理论结果的误差，评估共轭梯度法的精确度；
4.将共轭梯度法与其他迭代方法进行对比，分析其收敛速度；
5.设定一个大规模的线性方程组，比较共轭梯度法在求解大规模方程组时的性能。

实验结果与分析：
根据实验步骤中的设定，实验结果显示，共轭梯度法成功求解了所设定的线性方程组，并且与理论结果的误差很小，说明共轭梯度法的精确度很高。

此外，将共轭梯度法与其他迭代方法进行对比发现，共轭梯度法的
收敛速度相对较快，需要的迭代次数较少。

在求解大规模线性方程组时，共轭梯度法表现出了较大的优势，可以显著减少计算时间。

结论：
共轭梯度法是一种求解线性方程组的高效方法，其精确度和收敛速度优于其他迭代方法。

在实际应用中，共轭梯度法可以被广泛应用于求解大规模的线性方程组，提高计算效率。

值得指出的是，共轭梯度法在求解非对称方程组时效果不佳，需要使用相关的改进方法来解决。

因此，在实际使用共轭梯度法时，需根据方程组的特点来选择合适的方法。

2. Saad Y. Iterative methods for sparse linear systems [M]. SIAM, 200
3.。

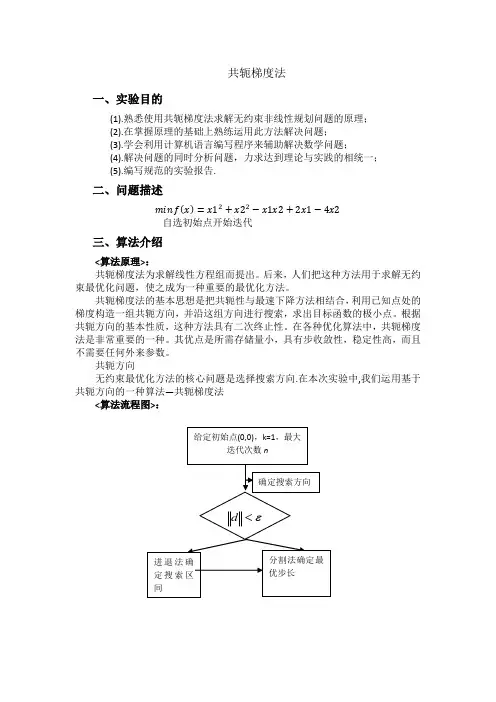
共轭梯度法一、实验目的(1).熟悉使用共轭梯度法求解无约束非线性规划问题的原理；(2).在掌握原理的基础上熟练运用此方法解决问题；(3).学会利用计算机语言编写程序来辅助解决数学问题；(4).解决问题的同时分析问题，力求达到理论与实践的相统一；(5).编写规范的实验报告.二、问题描述自选初始点开始迭代三、算法介绍<算法原理>：共轭梯度法为求解线性方程组而提出。

后来，人们把这种方法用于求解无约束最优化问题，使之成为一种重要的最优化方法。

共轭梯度法的基本思想是把共轭性与最速下降方法相结合，利用已知点处的梯度构造一组共轭方向，并沿这组方向进行搜索，求出目标函数的极小点。

根据共轭方向的基本性质，这种方法具有二次终止性。

在各种优化算法中，共轭梯度法是非常重要的一种。

其优点是所需存储量小，具有步收敛性，稳定性高，而且不需要任何外来参数。

共轭方向无约束最优化方法的核心问题是选择搜索方向.在本次实验中,我们运用基于共轭方向的一种算法—共轭梯度法<算法流程图>：四、程序%¾«È·ÏßËÑË÷,ÌݶÈÖÕÖ¹×¼Ôòfunction [ m,k,d,a,X,g1,fv] = GETD( G,b,c,X,e,method)if nargin<6error('ÊäÈë²ÎÊý±ØÐëΪ6');endn=length(G);if n==2format long e%ratsyms x1x2f=1/2*[x1,x2]*G*[x1;x2]+b'*[x1;x2]+c;g=[diff(f,x1);diff(f,x2)];g1=subs(subs(g,x1,X(1,1)),x2,X(2,1));d=-g1;a=-(d'*g1)/(d'*G*d);% a=-((X(:,1)'*G*d+b'*d)/(d'*G*d)); a=g1(:,1)'*g1(:,1)/(d(:,1)'*G*d(:,1));X(:,2)=X(:,1)+a*d;g1=[g1 subs(subs(g,x1,X(1,2)),x2,X(2,2))];m1=norm(g1(:,1));m=norm(g1(:,2));i=2;k=zeros(1);switch methodcase'FR'while m>=ek(i-1)=(m/m1)^2;d(:,i)=-g1(:,i)+k(i-1)*d(:,i-1);a(i)=-(d(:,i)'*g1(:,i))/(d(:,i)'*G*d(:,i));%a1(i)=-((X(:,i)'*G*d(:,i)+b'*d(:,i))/(d(:,i)'*G*d(:,i)));a (i)=g1(:,i)'*g1(:,i)/(d(:,i)'*G*d(:,i));X(:,i+1)=X(:,i)+a(i)*d(:,i);g1=[g1 subs(subs(g,x1,X(1,i+1)),x2,X(2,i+1))];m1=m;m=norm(g1(:,i+1));i=i+1;endcase'PRP'while m>=ek(i-1)=g1(:,i)'*(g1(:,i)-g1(:,i-1))/(norm(g1(:,i-1)))^2;d(:,i)=-g1(:,i)+k(i-1)*d(:,i-1);a(i)=-(d(:,i)'*g1(:,i))/(d(:,i)'*G*d(:,i));X(:,i+1)=X(:,i)+a(i)*d(:,i);g1=[g1 subs(subs(g,x1,X(1,i+1)),x2,X(2,i+1))];i=i+1;endcase'HS'while m>=ek(i-1)=g1(:,i)'*(g1(:,i)-g1(:,i-1))/(d(:,i-1)'*(g1(:,i)-g1(:,i-1))); d(:,i)=-g1(:,i)+k(i-1)*d(:,i-1);a(i)=-(d(:,i)'*g1(:,i))/(d(:,i)'*G*d(:,i));X(:,i+1)=X(:,i)+a(i)*d(:,i);g1=[g1 subs(subs(g,x1,X(1,i+1)),x2,X(2,i+1))];m=norm(g1(:,i+1));i=i+1;endcase'DY'while m>=ek(i-1)=g1(:,i)'*g1(:,i)/(d(:,i-1)'*(g1(:,i)-g1(:,i-1)));d(:,i)=-g1(:,i)+k(i-1)*d(:,i-1);a(i)=-(d(:,i)'*g1(:,i))/(d(:,i)'*G*d(:,i));X(:,i+1)=X(:,i)+a(i)*d(:,i);g1=[g1 subs(subs(g,x1,X(1,i+1)),x2,X(2,i+1))];m=norm(g1(:,i+1));i=i+1;endcase'LS'while m>=ek(i-1)=g1(:,i)'*(g1(:,i)-g1(:,i-1))/(d(:,i-1)'*(-g1(:,i-1)));d(:,i)=-g1(:,i)+k(i-1)*d(:,i-1);a(i)=-(d(:,i)'*g1(:,i))/(d(:,i)'*G*d(:,i)); %a(i)=-((X(:,i)'*G*d(:,i) +b'*d(:,i))/(d(:,i)'*G*d(:,i)));X(:,i+1)=X(:,i)+a(i)*d(:,i);g1=[g1 subs(subs(g,x1,X(1,i+1)),x2,X(2,i+1))];m=norm(g1(:,i+1));i=i+1;endcase'CD'while m>=ek(i-1)=g1(:,i)'*g1(:,i)/(d(:,i-1)'*(-g1(:,i-1)));d(:,i)=-g1(:,i)+k(i-1)*d(:,i-1);a(i)=-(d(:,i)'*g1(:,i))/(d(:,i)'*G*d(:,i));X(:,i+1)=X(:,i)+a(i)*d(:,i);g1=[g1 subs(subs(g,x1,X(1,i+1)),x2,X(2,i+1))];i=i+1;endcase'WYL'while m>=ek(i-1)=g1(:,i)'*(g1(:,i)-(m/m1)*g1(:,i-1))/(m1^2);d(:,i)=-g1(:,i)+k(i-1)*d(:,i-1);a(i)=-(d(:,i)'*g1(:,i))/(d(:,i)'*G*d(:,i)); %a(i)=-((X(:,i)'*G*d(:,i) +b'*d(:,i))/(d(:,i)'*G*d(:,i)));X(:,i+1)=X(:,i)+a(i)*d(:,i);g1=[g1 subs(subs(g,x1,X(1,i+1)),x2,X(2,i+1))];m1=m;m=norm(g1(:,i+1));i=i+1;endendfv=subs(subs(f,x1,X(1,i)),x2,X(2,i));endl1=X(1,i);l2=X(2,i);w1=X(1,1);w2=X(2,1);v1=min(l1,w1)-abs(l1-w1)/10:abs(l1-w1)/10:max(l1,w1)+abs(l1-w1)/10;v2=min(l2,w2)-abs(l2-w2)/10:abs(l2-w2)/10:max(l2,w2)+abs(l2-w2)/10; [x,y]=meshgrid(v1,v2);s=size(x);z=zeros(size(x));for i=1:s(1)for j=1:s(2)z(i,j)=1/2*[x(i,j),y(i,j)]*G*[x(i,j);y(i,j)]+b'*[x(i,j);y(i,j)]+c;endend[px,py] = gradient(z,.2,.2);contour(v1,v2,z), hold on, quiver(v1,v2,px,py)[C,h] = contour(x,y,z);set(h,'ShowText','on','TextStep',get(h,'LevelStep')*2)x1=X(1,:);y1=X(2,:);plot(x1,y1,'r*:');五、计算结果如图所示，输入>> G=[2,-1;-1,2];>> b=[2;-4];>> c=0;X=[1;1];e=1e-3;method='FR';表示正定矩阵为G，b为一次元系数矩阵，c为常数0，X是初始迭代点，e 为精度，method为共轭梯度的公式方法。

共轭梯度实验报告共轭梯度实验报告引言：共轭梯度是一种常用的优化算法，广泛应用于数值计算和机器学习等领域。

本实验旨在探究共轭梯度算法的原理和应用，并通过实验验证其在解决线性方程组和最小二乘问题中的有效性和优越性。

一、共轭梯度算法的原理共轭梯度算法是一种迭代法，用于求解对称正定矩阵的线性方程组。

其基本思想是通过选择一组互相共轭的搜索方向，以最小化目标函数的二次型形式。

共轭梯度算法的核心步骤包括初始化、计算搜索方向、计算步长和更新解向量等。

二、共轭梯度算法在线性方程组求解中的应用共轭梯度算法在求解线性方程组方面具有独特的优势。

相比于传统的直接求解方法，共轭梯度算法不需要存储整个矩阵，仅需存储向量和少量中间变量，节省了内存空间。

同时，共轭梯度算法具有较快的收敛速度，能够在有限的迭代次数内得到较精确的解。

三、共轭梯度算法在最小二乘问题中的应用最小二乘问题是一类常见的优化问题，广泛应用于数据拟合和参数估计等领域。

共轭梯度算法在最小二乘问题中的应用主要体现在正规方程法和QR分解法的改进上。

通过共轭梯度算法，可以有效地求解最小二乘问题，得到更准确的拟合结果。

四、实验设计与结果分析本实验选择了一组线性方程组和最小二乘问题进行测试，分别使用共轭梯度算法和传统直接求解方法进行比较。

实验结果表明，共轭梯度算法在求解线性方程组和最小二乘问题时，具有更快的收敛速度和更高的精度。

尤其在大规模问题上，共轭梯度算法的优势更加明显。

结论：共轭梯度算法是一种有效的优化算法，适用于求解对称正定矩阵的线性方程组和最小二乘问题。

通过选择互相共轭的搜索方向，共轭梯度算法能够在有限的迭代次数内得到较精确的解。

在实际应用中，共轭梯度算法具有较快的收敛速度和较高的精度，是一种值得推广和应用的算法。

总结：通过本次实验，我们深入了解了共轭梯度算法的原理和应用，并通过实验验证了其在线性方程组和最小二乘问题中的有效性和优越性。

共轭梯度算法作为一种常用的优化算法，在数值计算和机器学习等领域具有广泛的应用前景。

共轭梯度算法分析与实现
梯度下降是一种常用的优化算法，用于求解优化问题。

它通过迭代的
方式不断沿着梯度的反方向更新参数，以最小化损失函数。

然而，梯度下
降算法在处理大规模数据时会变得非常慢，因为它需要计算全部训练样本
的梯度。

为了解决这个问题，共轭梯度算法被提出。

共轭梯度算法是一种适用于解决对称正定矩阵形式下的线性方程组的
优化算法。

它在每一步更新参数时，会按照预先选择好的方向进行更新。

这些方向通常是互相共轭的，这意味着每一个方向都是相对于其他方向来
说是正交的。

共轭梯度算法的原理是，通过每次迭代选择共轭方向来加速
梯度下降算法的收敛速度。

具体而言，共轭梯度算法中的每一步迭代可以分为四个部分：初始化、步长、更新参数和计算残差。

首先，在初始化阶段设定初始参数和初始残差，并选择一个适当的共轭方向。

然后，在步长阶段，通过线方法选择一
个合适的步长。

接下来，在更新参数阶段，根据步长和共轭方向更新参数。

最后，在计算残差阶段，计算新的残差，并检查是否达到停止条件。

如果
没有达到停止条件，那么就继续迭代进行和更新。

共轭梯度算法相对于梯度下降算法有几个优点。

首先，它不需要计算
全部训练样本的梯度，这样可以加速算法的收敛速度。

其次，它可以解决
对称正定矩阵形式下的线性方程组，这在很多实际问题中非常常见。

最后，共轭梯度算法在存储以及计算量上都比较少，所以可以处理大规模数据。

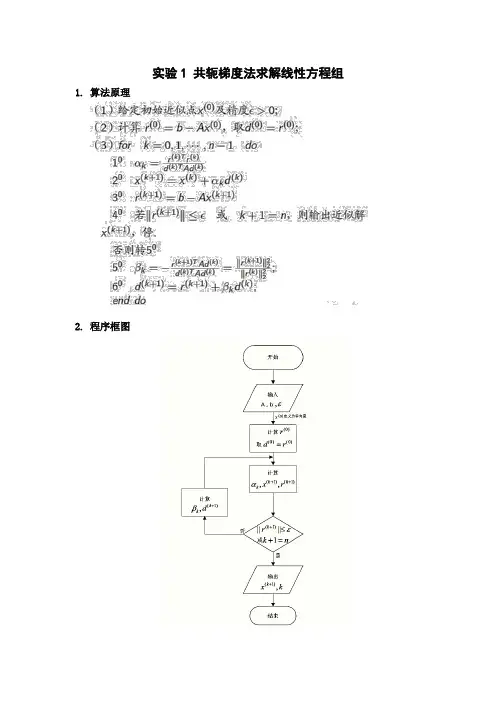
实验1 共轭梯度法求解线性方程组1.算法原理2.程序框图3.程序使用说明。

本程序使用MATLAB来求解线性方程组Ax b源程序文件“gongetidu1.m”为共轭梯度法源程序，x为方程组的解，k为迭代次数，A为方程组的系数矩阵，b为方程组的右端项，ep为精度。

定义A, b，ep后，在命令窗口输入[x,k] = gongetidu1(A,b,ep)，回车后即可算出方程组的解和迭代次数。

源程序文件“gongetidu2.m”为共轭梯度算例3.2中构造A，b矩阵的程序。

定义阶数n的数值后，在命令窗口输入[A,b] = gongetidu2(n)即可算出A, b矩阵。

4.算例计算结果此算例为课本113页计算实习3.2.首先，设定MATLAB的数值格式为“long”。

当n=100时，在命令窗口中输入“[A,b]=gongetidu2(100)”，回车后可得到A 和b的矩阵；假设精度ep = 10-3，然后在命令窗口输入“[x,k] = gongetidu1(A,b,10^-3)”即可算出方程组的解x和迭代次数k。

x=( 0.999999999999988,0.999999999999995,1.000000000000009，···0.9999 99999999997,0.999999999999998 )T（x向量一共有100个元素）k=49.同理，可以算出n=200,400的结果。

n=200时，同样假设精度ep = 10-3，结果为：x=( 0.999999999999974,1.000000000000023,0.999999999999935,···1.000000 000000029, 0.999999999999987)T （x向量一共有200个元素）k=99.n=400时，同样假设精度ep = 10-3，结果为：x=( 1.000000000000017,0.999999999999846,1.000000000000039,···0.99999999 9999881,1.000000000000062)T （x向量一共有400个元素）k=199。

共轭梯度法matlab程序共轭梯度法是一种用于求解无约束优化问题的迭代算法。

以下是一个简单的MATLAB 程序示例，用于实现共轭梯度法：matlab复制代码function[x, fval, iter] = conjugate_gradient(A, b, x0, tol,max_iter)% A: 矩阵% b: 向量% x0: 初始解% tol: 容忍度% max_iter: 最大迭代次数r = b - A*x0;p = r;x = x0;fval = A*x - b;iter = 0;while (norm(r) > tol) && (iter < max_iter)Ap = A*p;alpha = dot(p, r) / dot(p, Ap);x = x + alpha*p;r = r - alpha*Ap;if iter == 0fval_new = dot(r, r);elsebeta = dot(r, r) / dot(p, Ap);p = r + beta*p;fval_new = dot(r, r);endif fval_new < fvalfval = fval_new;enditer = iter + 1;endend该程序接受一个矩阵A、一个向量b、一个初始解x0、一个容忍度tol和一个最大迭代次数max_iter作为输入，并返回最终解x、目标函数值fval和迭代次数iter。

使用该函数时，您需要将要优化的目标函数转换为矩阵形式，并调用该函数来找到最优解。

例如，假设您要最小化一个函数f(x)，可以将该函数转换为矩阵形式A*x - b，其中A是目标函数的雅可比矩阵，b是目标函数的常数项向量。

然后，您可以调用该函数来找到最优解，例如：matlab复制代码A = jacobian(f); % 计算目标函数的雅可比矩阵b = [1, 2, 3]; % 目标函数的常数项向量x0 = [0, 0, 0]; % 初始解向量tol = 1e-6; % 容忍度max_iter = 1000; % 最大迭代次数[x, fval, iter] = conjugate_gradient(A, b, x0, tol, max_iter); % 调用共轭梯度法函数求解最优解。

编号:_ 09《最优化方法》课程设计题目：共轭梯度算法分析与实现院系：数学与计算科学学院专业：数学与应用数学姓名学号：指导教师：日期：2013 年12 月23 日摘要在最优化计算中，共轭梯度法是非常重要的一种方法。

共轭梯度法是一种改进的最速下降法，介于最速下降法与牛顿法之间的一种无约束优化算法,是为求解目标函数为二次函数的问题而设计的一类算法。

它利用目标函数的梯度逐步产生共轭方向并将其作为搜索方向的方法，收敛速度快。

共轭梯度法仅需利用一阶导数信息，避免了牛顿法需要存储和计算Hesse矩阵并求逆的缺点，具有二次终止性。

关键词：共轭梯度法；牛顿法；二次函数；无约束优化AbstractIn the calculation of optimization method, conjugate gradient method is a very important one. The conjugate gradient method is a unconstrained optimization method between the steepest descent method and Newton method, and sove the objective function for the original quadratic function problems and design for a class of algorithm. Conjugate gradient method using only first derivative information, to avoid the Newton method requires storage and computing the inverse Hesse matrix and shortcomings, this method has the quadratic termination.Keywords: Conjugate gradient method; Newton method;Unconstrained optimization目录1、引言 (1)2、共轭梯度算法的描述 (1)2.1 无约束优化问题概述 (1)2.2 共轭方向 (1)2.3 共轭梯度法 (1)2.4 共轭梯度算法的步骤 (2)3、数值实验 (2)3.1 代码实现 (2)3.2 算法测试 (3)3.3 结果分析 (5)4、算法比较 (5)4.1 最速下降法描述 (6)4.1.1最速下降方向 (6)4.1.2 最速下降法 (6)4.2 最速下降法实现 (6)4.3 最速下降法测试 (7)4.4共轭梯度法与最速下降法比较 (8)5、总结 (8)5.1 总结概括 (8)5.2 个人感言 (9)6、参考文献： (9)1、引言共轭梯度法最早是由Hesternes 和Stiefle(1952)提出来的，用于解正定系数矩阵的线性方程组，在这个基础上，Fletcher 和Reeves(1964)首先提出了解非线性最优化问题的共轭梯度法。