下载文档原格式
第1章控制系统概述【课后自测】1-1 试列举几个日常生活中的开环控制和闭环控制系统，说明它们的工作原理并比较开环控制和闭环控制的优缺点。
解：开环控制——半自动、全自动洗衣机的洗衣过程。
工作原理：被控制量为衣服的干净度。
洗衣人先观察衣服的脏污程度，根据自己的经验，设定洗涤、漂洗时间，洗衣机按照设定程序完成洗涤漂洗任务。
系统输出量（即衣服的干净度）的信息没有通过任何装置反馈到输入端，对系统的控制不起作用，因此为开环控制。
闭环控制——卫生间蓄水箱的蓄水量控制系统和空调、冰箱的温度控制系统。
工作原理：以卫生间蓄水箱蓄水量控制为例，系统的被控制量（输出量）为蓄水箱水位（反应蓄水量）。
水位由浮子测量，并通过杠杆作用于供水阀门（即反馈至输入端），控制供水量，形成闭环控制。
当水位达到蓄水量上限高度时，阀门全关（按要求事先设计好杠杆比例），系统处于平衡状态。
一旦用水，水位降低，浮子随之下沉，通过杠杆打开供水阀门，下沉越深，阀门开度越大，供水量越大，直到水位升至蓄水量上限高度，阀门全关，系统再次处于平衡状态。
开环控制和闭环控制的优缺点如下表1-2 自动控制系统通常有哪些环节组成？各个环节分别的作用是什么？解：自动控制系统包括被控对象、给定元件、检测反馈元件、比较元件、放大元件和执行元件。
各个基本单元的功能如下：（1）被控对象—又称受控对象或对象，指在控制过程中受到操纵控制的机器设备或过程。
（2）给定元件—可以设置系统控制指令的装置，可用于给出与期望输出量相对应的系统输入量。
（3）检测反馈元件—测量被控量的实际值并将其转换为与输入信号同类的物理量，再反馈到系统输入端作比较，一般为各类传感器。
（4）比较元件—把测量元件检测的被控量实际值与给定元件给出的给定值进行比较，分析计算并产生反应两者差值的偏差信号。
常用的比较元件有差动放大器、机械差动装置和电桥等。
（5）放大元件—当比较元件产生的偏差信号比较微弱不足以驱动执行元件动作时，可通过放大元件将微弱信号作线性放大。
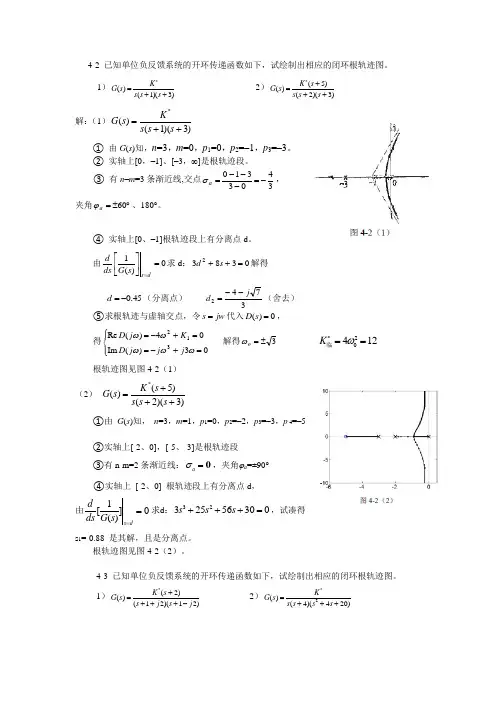
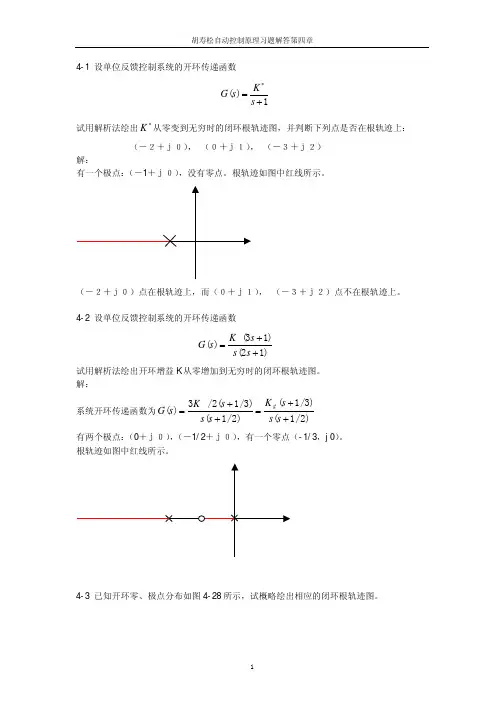
4-2 已知单位负反馈系统的开环传递函数如下，试绘制出相应的闭环根轨迹图。
1）*()(1)(3)K G s s s s =++ 2）*(5)()(2)(3)K s G s s s s +=++解：（1）()(1)(3)*K G s s s s =++① 由G (s )知，n =3，m =0，p 1=0，p 2=–1，p 3=–3。
② 实轴上[0，–1]、[–3，∞]是根轨迹段。
③ 有n –m =3条渐近线,交点3403310-=---=a σ， 夹角︒±=60a ϕ、180°。
④ 实轴上[0、–1]根轨迹段上有分离点d 。
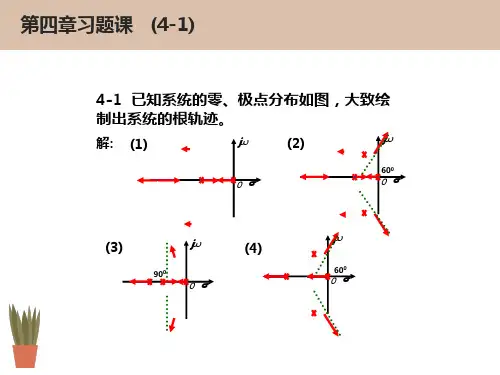
由0)(1=⎥⎦⎤⎢⎣⎡=ds s G ds d 求d ：03832=++s d 解得 45.0-=d （分离点） 3742j d --=（舍去） ⑤求根轨迹与虚轴交点，令jw s =代入0)(=s D ，得⎪⎩⎪⎨⎧=+-==+-=03)(Im 04)(Re 312ωωωωωj j j D K j D 解得3±=o ω 20412*K ω==临根轨迹图见图4-2（1）（2） *(5)()(2)(3)K s G s s s s +=++①由 G (s )知， n =3，m =1，p 1=0，p 2=–2，p 3=–3，p 4=–5②实轴上[-2、0]，[-5、-3]是根轨迹段 ③有n-m=2条渐近线：0a σ=，夹角ϕa =±90°④实轴上 [-2、0] 根轨迹段上有分离点d ， 由1[]0()s dd ds G s ==求d ：3232556300s s s +++=，试凑得 s 1=-0.88 是其解，且是分离点。
根轨迹图见图4-2（2）。
4-3 已知单位负反馈系统的开环传递函数如下，试绘制出相应的闭环根轨迹图。
1）*(2)()(12)(12)K s G s s j s j +=+++- 2）*2()(4)(420)K G s s s s s =+++解：（1）*(2)()(12)(12)K s G s s j s j +=+++-根轨迹图见图4-3（1）（2）*2()(4)(420)K G s s s s s =+++① n =4，m =0，p 1=0，p 2=–4，p 3、4=–2±j 4② p 1、p 2连线中点正好是p 3、p 4实部，开环极点分布对称于垂线s=–2，根轨迹也将对称于该垂线。
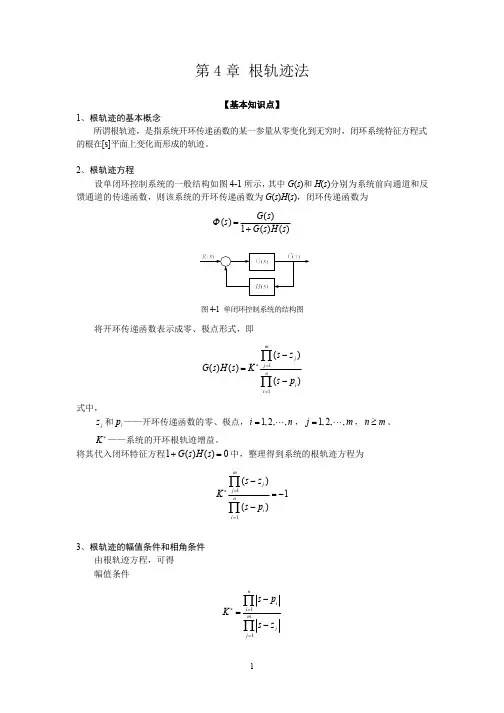
11习题二2-1 试求题2-1图所示电路的微分方程和传递函数。
题2-1图2-2 试证明题2-2图所示的电路(a )与机械系统(b )具有相同的数学模型。
题2-2图2-3 试求题2-3图所示运算放大器构成的电路的传递函数。
题2-3图2-4 如题2-4图所示电路，二极管是一个非线性元件，其电流d i 与d u 间的关系为)1(10026.06-=-du d e i 。
假设电路中的Ω=310R ，静态工作点V u 39.20=，A i 301019.2-⨯=，试求在工作点),(00i u 附近)(d d u f i =的线性化方程。
题2-4图2-5 试简化题2-5图中各系统结构图，并求传递函数C (s )/R (s )。
题2-5图2-6试求题2-6图所示系统的传递函数C1(s)/R1(s)，C2(s)/R1(s)，C1(s)/R2(s)及C2(s)/R2(s)。
题2-6图2-7试绘制题2-7图所示系统的信号流图，并用Mason公式求系统的传递函数C(s)/R(s)。
题2-7图2-8试绘制题2-8图所示系统的信号流图，并用Mason公式求系统的传递函数C(s)/R(s)。
题2-8图2-9已知系统结构图如题2-9图所示，试写出系统在给定R(s)及扰动N(s)同时作用下输出C(s)的表达式。
题2-9图2-10系统的信号流图如题2-10图所示，试求系统的传递函数C(s)/R(s)。
题2-10图2-11已知单位负反馈系统的开环传递函数(1)试用MATLAB求系统的闭环传递函数；(2)将闭环传递函数表示为零极点形式和部分分式形式。
2-12如题2-12图所示系统结构图(1)试用MATLAB简化结构图，并计算系统的闭环传递函数；(2)绘制闭环传递函数的零极点图。
题2-12图。
自动控制原理第二版第四章课后答案【篇一：《自动控制原理》第四章习题答案】4-1 系统的开环传递函数为g(s)h(s)?k*(s?1)(s?2)(s?4) 试证明点s1??1?j3在根轨迹上，并求出相应的根轨迹增益k*和开环增益k。
解若点s1在根轨迹上，则点s1应满足相角条件?g(s)h(s)??(2k?1)?，如图解4-1所示。
对于s1= -1+j3，由相角条件?g(s1)h(s1)?0??(?1?j3?1)??(?1?j3?2)??(?1?j3?4)? 0??2??3??6???满足相角条件，因此s1= -1+j3在根轨迹上。
将s1代入幅值条件： g(s1)h（s1?k*?1?1?j3?1??1?j3?2??1?j3?4k8*解出： k=12 ，k=*?324-2 已知开环零、极点如图4-2 所示，试绘制相应的根轨迹。
解根轨如图解4-2所示：4-3 单位反馈系统的开环传递函数如下，试概略绘出系统根轨迹。
⑴ g(s)?ks(0.2s?1)(0.5s?1)k(s?5)s(s?2)(s?3)* ⑵ g(s)?⑶ g(s)?k(s?1)s(2s?1)解⑴ g(s)?ks(0.2s?1)(0.5s?1)=10ks(s?5)(s?2)系统有三个开环极点：p1?0,p2= -2,p3 = -5①实轴上的根轨迹：???,?5?, ??2,0?0?2?57?????a??33②渐近线： ????(2k?1)????,?a?33?③分离点：1d?1d?5?1d?2?0解之得：d1??0.88，d2?3.7863(舍去)。
④与虚轴的交点：特征方程为 d(s)=s3?7s2?10s?10k?0?re[d(j?)]??7?2?10k?0令 ? 3im[d(j?)]????10??0?解得?????k?7。
根轨迹如图解4-3(a)所j）与虚轴的交点（0，?示。
⑵根轨迹绘制如下：①实轴上的根轨迹：??5,?3?, ??2,0?0?2?3?(?5)????0a??2②渐近线： ????(2k?1)????a?22?③分离点： 1d?1d?2?1d?3?1d?5用试探法可得 d??0.886。
第四章4-1已知单位反馈系统的开环传递函数为()(1)(2)KG s s s s =++ 试绘制该系统在正、负反馈情况下的根轨迹图。
解：（1）负反馈情况令(1)(2)=0s s s ++，解得 3个开环极点1230,1,2p p p ==-=-根轨迹分支数为3，起点分别为(0,0),(1,0),(2,0)j j j -- 终点均为无穷远处。
在实轴上的根轨迹为(][],2,1,0-∞--两段。
由n=3,m=0得轨迹有3条渐近线，它们在实轴上的交点坐标111n mi ji j a p zn mσ==-==--∑∑渐近线与实轴正方向的夹角为2121=3a k k n m ππϕ++=-（）（），（k=0,1,2）当k=0,1,2时，计算得a ϕ分别为60°，180°，-60° 确定分离点，由111++=012d d d ++解得120.42, 1.58d d =-=-由于2d 不是根轨迹上的点，故不是分离点，分离点坐标为1d确定根轨迹与虚轴的交点：控制系统特征方程3232=0s s s K +++令=s j ω 代入上式得3232=0j j K ωωω--++ 写出实部和虚部方程233=020K ωωω⎧-⎪⎨-=⎪⎩可求得=006K K ωω⎧⎧=⎪⎨⎨==⎪⎩⎩因此，根轨迹在ω=6K =；另外实轴上的根轨迹分支在0ω=处与虚轴相交。
负反馈系统根轨迹如下图所示（2）正反馈情况令(1)(2)=0s s s ++，解得 3个开环极点1230,1,2p p p ==-=-根轨迹分支数为3，起点分别为(0,0),(1,0),(2,0)j j j -- 终点均为无穷远处。
在实轴上的根轨迹为[](]2,1,0,--+∞两段。
由n=3,m=0得轨迹有3条渐近线，它们在实轴上的交点坐标111n mi ji j a p zn mσ==-==--∑∑渐近线与实轴正方向的夹角为2=3a k πϕ，（k=0,1,2）当k=0,1,2时，计算得a ϕ分别为0°，120°，-120° 确定分离点，由111++=012d d d ++解得120.42, 1.58d d =-=-由于1d 不是根轨迹上的点，故不是分离点，分离点坐标为2d确定根轨迹与虚轴的交点：控制系统特征方程3232-=0s s s K ++将=s j ω 代入上式得3232-=0j j K ωωω--+ 写出实部和虚部方程23-3=020K ωωω⎧-⎪⎨-=⎪⎩可求得=00-6K K ωω⎧⎧=⎪⎨⎨==⎪⎩⎩ 因此，根轨迹在0ω=处与虚轴相交。
正反馈系统根轨迹如下图所示 4-2设系统的开环传递函数为(+)()(s)()()K s z G s H z p s s p =>+绘制根轨迹图，证明根轨迹的复数部分是圆，并求出圆的圆心和半径。
解：系统实轴上的根轨迹为[](],,,0z p -∞- 根轨迹分离点坐标满足111+=d d p d z++解得12d z d z =-=- 系统闭环特征方程2()+=0s p K s Kz ++解得1,2=-2p Ks +±令=-,2p Kx y +=2222222()()=(z-)()244()()44p K p K x z z z p K Kz p K p K y Kz +++=-++-++==-两式相加得222()=x z y z zp ++- 又分离点d到开环零点距离r=d z -=即2222()r =()x z y d z ++=-故根轨迹的复数部分是圆，圆心为零点，半径为零点到分离点之间的距离。
根轨迹图如下：4-3已知单位负反馈系统的开环传递函数，试绘制根轨迹图。
（1）(2)()(1)(3)K s G s s s s +=++ （2）2(1)()(0.11)K s G s s s +=+（3）(5)()(1)(3)K s G s s s +=++ （4）2(1)()K s G s s += （5）2(4)()(1)K s G s s +=+ （6）2(0.2)()( 3.6)K s G s s s +=+解：（1）由开环传递函数可知，系统有1个开环零点12z =- 3个开环极点1230,1,3p p p ==-=-根轨迹分支数为3，起点分别为(0,0),(1,0),(3,0)j j j -- 一个终点为(2,0)j - 另两个终点为无穷远处。
在实轴上的根轨迹为(][]3,2,1,0---两段。
由n=3,m=1得轨迹有2条渐近线，它们在实轴上的交点坐标111n mi ji j a p zn mσ==-==--∑∑渐近线与实轴正方向的夹角为2121=2a k k n m ππϕ++=-（）（），（k=0,1）当k=0,1时，计算得a ϕ分别为-90°，90° 则系统根轨迹如下图所示（2）由开环传递函数可知，系统有1个开环零点11z =- 3个开环极点1230,0,10p p p ===-根轨迹分支数为3，起点分别为(0,0),(0,0),(10,0)j j j - 一个终点为(1,0)j - 另两个终点为无穷远处。
在实轴上的根轨迹为[]10,1--段。
由n=3,m=1得轨迹有2条渐近线，它们在实轴上的交点坐标114.5n mi ji j a p zn mσ==-==--∑∑渐近线与实轴正方向的夹角为2121=2a k k n m ππϕ++=-（）（），（k=0,1）当k=0,1时，计算得a ϕ分别为-90°，90° 确定分离点，由1111++=101d d d d ++解得124, 2.5d d =-=- 确定根轨迹与虚轴的交点：控制系统特征方程320.1=0s s Ks K +++将=s j ω 代入上式可求得=0K ω⎧⎨=⎩则系统根轨迹如下图所示（3）由开环传递函数可知，系统有1个开环零点15z =- 2个开环极点121,3p p =-=-根轨迹分支数为2，起点分别为(1,0),(3,0)j j --，终点分别为(5,0)j -和无穷远处。
在实轴上的根轨迹为(][],5,3,1-∞---两段。
轨迹有1条渐近线，它与实轴上的交点坐标111n mi ji j a p zn mσ==-==-∑∑渐近线与实轴正方向的夹角为21=21a a k k n mπϕπϕπ+=+=-（）（），（k=0）则确定分离点，由111+=135d d d +++解得1255d d =-+=-- 确定根轨迹与虚轴的交点：控制系统特征方程2(4)35=0s K s K ++++将=s j ω代入上式可求得=0,3-45K K ωω⎧⎧⎪⎪⎨⎨==-⎪⎩⎪⎩均舍去 则系统根轨迹如下图所示（4）由开环传递函数可知，系统有1个开环零点11z =- 2个开环极点120,0p p ==根轨迹分支数为2，起点分别为(0,0),(0,0)j j ，终点分别为(1,0)j -和无穷远处。
在实轴上的根轨迹为(],1-∞-段。
轨迹有1条渐近线，它与实轴上的交点坐标111n mi ji j a p zn mσ==-==-∑∑渐近线与实轴正方向的夹角为21=21a a k k n mπϕπϕπ+=+=-（）（），(k=0)则确定分离点，由111+=1d d d +解得2d =-，则分离点为()2,0j - 则系统根轨迹如下图所示（5）由开环传递函数可知，系统有1个开环零点14z =- 2个开环极点121,1p p =-=-根轨迹分支数为2，起点分别为(1,0),(1,0)j j --，终点分别为(4,0)j -和无穷远处。
在实轴上的根轨迹为(],4-∞-段。
轨迹有1条渐近线，它与实轴上的交点坐标112n mi ji j a p zn mσ==-==-∑∑渐近线与实轴正方向的夹角为21=21a a k k n mπϕπϕπ+=+=-（）（），(k=0)则确定分离点，由111+=114d d d +++解得7d =- 则系统根轨迹如下图所示（6）由开环传递函数可知，系统有1个开环零点10.2z =- 3个开环极点1230,0, 3.6p p p ===-根轨迹分支数为3，起点分别为(0,0),(0,0),( 3.6,0)j j j -，终点分别为(0.2,0)j -和无穷远处。
在实轴上的根轨迹为(]3.6,0.2--段。
轨迹有2条渐近线，它与实轴上的交点坐标111.7n mi ji j a p zn mσ==-==--∑∑渐近线与实轴正方向的夹角为2121=22a a k k n m πππϕϕ++==±-（）（），(k=0,1)则确定分离点，由1111+=3.60.2d d d d +++解得121.67,0.43d d =-=-则系统根轨迹如下图所示4-5已知系统如下图所示，试绘制根轨迹图。
解：由图可知系统的开环传递函数为32()()22KG s H s s s s=++令3222=0s s s ++，解得 3个开环极点1230,1,1p p j p j ==-+=--根轨迹分支数为3，起点分别为(0,0),(1,)(1,)j j j ---和，终点分别为(5,0)j -和无穷远处。
在实轴上的根轨迹为(],0-∞段。
轨迹有3条渐近线，它与实轴上的交点坐标1123n mi ji j a p zn mσ==-==--∑∑ 渐近线与实轴正方向的夹角为2121=3a k k n m ππϕ++=-（）（），（k=0,1,2）当k=0,1,2时，计算得a ϕ分别为60°，180°，-60° 确定分离点，由111++=0(1)(1)d d j d j --+---无解得 无分离点 确定根轨迹与虚轴的交点：控制系统特征方程3222=0s s s K +++将=s j ω代入上式可求得=0=,04K K ωω⎧⎧⎪⎨⎨==⎪⎩⎩由11(21)()m npi zjpi pjpi j j j ik θπϕθ==≠=++-∑∑得出射角为321,,44p p p ππθθθπ==-=则系统根轨迹如下图所示。
