当前位置：文档之家 › 矢量场与标量场以及计算方法资料

矢量场与标量场以及计算方法资料

  • 格式：ppt
  • 大小：2.20 MB
  • 文档页数：60

下载文档原格式

  / 60

合集下载

标量场和矢量场

标量场和矢量场

2、矢量相加和相减可用平行四边形法则求解：
A B
B
A
B
A
AB
B
矢量的乘法
1）矢量与标量相乘
v kA
evx
kAx
evykAy
evzkAz
evAvk
v A
标量与矢量相乘只改变矢量的大小，不改变方向。
2）矢量与矢量点乘
A B | A || B | cosAB Ax Bx Ay By Az Bz
设矢量 A与三个坐标轴 x, y, z 的夹角分别为, , ，则
z
Ax Acos
Ay Acos
v Az
v A
Az Acos
A A(ex cos ey cos ez cos ) 任一方向的单位矢量为
v Ax
o
eA ex cos ey cos ez cos x
v Ay
y
2
2.位置矢量
R2 [(x x)2 ( y y)2 (z z)2 ]
3
3.矢量的代数运算
v A
evx
Ax
evy
Ay
evz
Az
v B
evx
Bx
evyLeabharlann ByevzBz
矢量的加法和减法
v A
v B
evx
( Ax
Bx
)
evy (Ay
By
)
evz
( Az
Bz
)
说明：
1、矢量的加法符合交换律和结合律：
vv vv vv v v vv A B B A (A B) C A (B C)
A B | A || B | sin AB en Ax
Ay
Az

矢量分析【电磁场与波+电子科技大学】

矢量分析【电磁场与波+电子科技大学】

面元矢量与此矢量相合时，极限值为最大值，也就是
该矢量的模。这个矢量称为 的旋度(curl)，记为
或
，故有
其中 是 在面元矢量 (用 表示其方向)上的投影。
第47页
电磁场与电磁波 第一章__矢量分析
旋度：若在矢量场 中的一点M 处存在矢量 ， 的方向
是 在该点环流面密度最大的方向，它的模就是这个最大
的环流面密度。矢量 称为矢量场 在点M 的旋度，记
为
或
。
说明：
① 在流体力学中，旋度表示了旋转的强弱即大小；在电磁场中，
不存在旋转强弱的意义；
② 旋度与环流中C 的形状、取向无关，只与场在M 点的量 本身有关；
③ 旋度场： 与矢量场 中的点一一对应得到的新的矢量场
第48页
电磁场与电磁波 第一章__矢量分析
第23页
电磁场与电磁波 第一章__矢量分析 1.3.2/3 方向导数和梯度 方向导数意义：表示场沿某方向的空间变化率
梯度的意义：描述标量场在某点的最大变化率及其 变化最大的方向
第24页
电磁场与电磁波 第一章__矢量分析
定义算符:
←哈密顿算符
数量场u 的梯度是矢量(是空间坐标点的函数) 梯度的大小为该点标量函数u 的最大变化率，即最大方向导数 梯度的方向为该点最大方向导数的方向 梯度场：数量场u 中每点都有一个梯度而形成的矢量场
第25页
电磁场与电磁波 第一章__矢量分析 直角坐标梯度: 圆柱坐标梯度: 球 坐 标 梯度:
第26页
电磁场与电磁波 第一章__矢量分析
梯度运算公式：
k为常数
第27页
电磁场与电磁波 第一章__矢量分析
{例} 考虑一个二维标量场 求此标量场的等值面，求u 的梯度 任取一闭合的积分回路,证明

矢量分析

矢量分析
性质
∇ × ∇ϕ = 0
梯度
三、矢量场的通量、散度
1、通量
r 定义：若矢量场 A 分布于空间中，在空间中存在任意曲面 S
r 上。定义 A 在曲面上的积分为通量。
r r Ψ = ∫ A ⋅ dS
s
曲面 S 的方向 开表面： 作一封闭线圈，选定绕行方向后，沿绕行方向 按右手螺旋法则，拇指方向为开表面方向 闭合面：外法线方向
s l
无旋场 性质
r ∇× A = 0
r ∇ ⋅ (∇ × A) = 0
旋度
例题讲解（课本） 例题1-8 例题1-9 例题1-10
例题
五、亥姆霍兹定理
内容：位于空间有限区域内的矢量场，当它的散度，旋度 以及它在区域边界上的场分布给定之后，该矢量场就被唯 一确定；对于无限大空间，如果矢量在无限远处减少至零 则该矢量由其散度和旋度唯一确定。
基础
矢量表示式
r r r r A = er Ar + eϕ Aϕ + e z Az
微分长度
r r r r dl = er dr + eϕ rdϕ + e z dz
微分面积
r r dS r = er rdϕdz r r dS ϕ = eϕ drdz r r dS z = e z rdrdϕ
微分体积
dV = rdrd ϕdz
只改变大小，不改变方向 矢量与矢量点乘
s r r r A ⋅ B = A B cosθ AB = Ax Bx + Ay B y + Az Bz
r r r r A⋅B = B⋅A
基础
说明： 1、两个矢量的标量积或点积，是一个标量 。 2、Θ是A、B之间较小的夹角，小于Π弧度。 3、其结果表示一个矢量的模和另一个矢量在该矢量 上的投影和乘积。 矢量与矢量叉乘

1-矢量分析与场论

1-矢量分析与场论

ex ex 0, ey ey 0, ez ez 0
ex ey ez , ey ez ex , ez ex ey
A B A B en AB
A// B A B 0
A B Axex Ayey Azez Bxex Byey Bzez
如果要了解场的局部特性，即考虑场在空间每 个点沿各个方向的变化情况，
对于标量场，需要引入方向导数和梯度的概念；
对于矢量场，需要引入散度和旋度的概念。
从数学上看，场是定义在空间区域上的函数：
静态标量场和矢量场可分别表示为：
u(x, y, z)、F(x, y, z)
时变标量场和矢量场可分别表示为：
矢量的叉积不符合交换律，但符合分配律 A B B A A(B C) A B AC
两个矢量的叉积为矢量
矢量运算恒等式
A (B C) B (C A) C (A B) A(BC) B(AC) C(A B)
混合积 双重矢量积
几个特殊结论
假设 M(x, y, z) 为矢量线上任一点，则过点 M沿矢量 线的位移元 dl 与矢量 A(x, y, z)共线。
共线矢量dl 与 A(x, y, z) 满足方程
dl A 0 或
dx dy dz Ax Ay Az
矢量形式
标量形式
A
M
dl r r dr
上面这两个方程称为矢量线方程
M0
而 l 的方向余弦为 cos
2
2
12 22 22 3
cos cos
2
2

12 22 22 3
1
1
12 22 22 3

第01章 矢量分析和场论基础

第01章 矢量分析和场论基础
ϕ
cos ϕ e y
− sin ϕ e x
cos ϕ e x ϕ
e ρ cos ϕ sin ϕ 0 e x e = − sin ϕ cos ϕ 0 e ϕ y ez 0 0 1 e z − sin ϕ cos ϕ 0 0 e ρ 0 eϕ 1 e z
第一章 矢量分析与场论基础
电磁场与电磁波理论基础
3.体、面和线微分元 体 体微分元 dV = ρ d ρ dϕ dz
dS ρ = ρ dϕ dze ρ 面微分元 dSϕ = d ρ dz eϕ dS = ρ d ρ dϕ e z z
Z
ez
线微分元 dl = d ρ e ρ + ρ dϕ eϕ + dze z
P( ρ ,θ , ϕ )
er eϕ
θ是位矢 与正 轴之间的夹角， 是位矢r与正 轴之间的夹角， 与正Z轴之间的夹角
θ
in rs
eθ
r sin θ sin ϕ
(1-17)
式中 n 是一垂直于由矢量 A 和 B 构成的平面的单位矢量， 构成的平面的单位矢量，并遵循 右手螺旋法则，见图1-3。 右手螺旋法则，见图 。
图1-3 矢量的标积和矢积
矢量的矢积不满足交换律： 矢量的矢积不满足交换律： A × B = −B × A (1-18) 矢积满足分配律和数乘， 矢积满足分配律和数乘，即
ϕ
ez
P( ρ , ϕ , z )
ρ
eϕ
eρ
图1-10 圆柱坐标
0 ≤ ρ < +∞ 取值范围 0 ≤ ϕ ≤ 2π −∞ < z < +∞
z = 常数

矢量场,标量场,散度,梯度,旋度的理解

矢量场,标量场,散度,梯度,旋度的理解

1。

梯度gradient设体系中某处的物理参数（如温度、速度、浓度等）为w，在与其垂直距离的dy处该参数为w+dw，则称为该物理参数的梯度，也即该物理参数的变化率.如果参数为速度、浓度或温度，则分别称为速度梯度、浓度梯度或温度梯度。

在向量微积分中，标量场的梯度是一个向量场。

标量场中某一点上的梯度指向标量场增长最快的方向，梯度的长度是这个最大的变化率.更严格的说，从欧氏空间Rn到R的函数的梯度是在Rn某一点最佳的线性近似。

在这个意义上，梯度是雅戈比矩阵的一个特殊情况。

在单变量的实值函数的情况，梯度只是导数,或者，对于一个线性函数,也就是线的斜率. 梯度一词有时用于斜度，也就是一个曲面沿着给定方向的倾斜程度。

可以通过取向量梯度和所研究的方向的点积来得到斜度.梯度的数值有时也被成为梯度.在二元函数的情形，设函数z=f（x，y）在平面区域D内具有一阶连续偏导数,则对于每一点P（x,y）∈D，都可以定出一个向量（δf/x)*i+（δf/y)*j这向量称为函数z=f（x,y）在点P(x，y）的梯度，记作gradf（x,y）类似的对三元函数也可以定义一个：（δf/x）*i+（δf/y）＊j+（δf/z）*k 记为grad［f(x,y，z）]2.散度气象学中指：散度指流体运动时单位体积的改变率。

简单地说,流体在运动中集中的区域为辐合，运动中发散的区域为辐散。

用以表示的量称为散度，值为负时为辐合，此时有利于天气系统的的发展和增强，为正时表示辐散，有利于天气系统的消散。

表示辐合、辐散的物理量为散度.微积分学→多元微积分→多元函数积分中:设某量场由A(x，y，z）= P(x,y,z)i + Q(x.y，z)j + R（x，y,z）k 给出，其中P、Q、R 具有一阶连续偏导数，∑是场内一有向曲面，n 是∑在点（x,y，z) 处的单位法向量，则∫∫A·ndS 叫做向量场A 通过曲面∑向着指定侧的通量，而δP/δx + δQ/δy + δR/δz 叫做向量场A 的散度,记作div A，即div A = δP/δx + δQ/δy + δR/δz。

矢量场与标量场以及计算方法资料

矢量场与标量场以及计算方法资料

图 1-5 矢量管
矢量管：
通过场域某一曲面s上的所有点的矢量 线的全体构成的管状区域。
0.2 标量场的梯度
Gradient of Scalar Field
1.方向导数：设一个标量函数 (x，y，z)，若函数 在点 P 可微，则 在点P 沿任意方向 l 的变化率称
为方向导数，即
l
（
x
ex
y
ey
(x2 y2 z2 )3/2
40 r 40r2
0.3 矢量场的通量与散度
Flux and Divergence of Vector 1 通量 ( Flux )
矢量E 沿有向曲面 S 的面积分
Φ S AndS = S A dS
若 S 为闭合曲面Φ S A dS
图0.3.1 矢量场的通量
（设曲面S的单位法向矢量en），An为A在en上的投影
l A dl S ( A) dS
矢量函数的线积分与面积分的相互转化。
在电磁场理论中，高斯定理 和 斯托克斯定理 是 两个非常重要的公式。
例1-12 求矢量场A=x(z-y) ex+y(x-z)ey+z(y-x)ez在点M(1，0，1) 处的旋度以及沿n=2ex+6ey+3ez方向的环量面密度。
lim
V 0
1 V
A dS lim = d =divA
V 0 V dV
根据奥式公式
蜒 S
A dS
S
( Axdydz
Aydzdx
Azdxdy)
V
( Ax x
Ay y
Az )dV z
通量可看成V内各点处的发散强度的体积分
divA
A
Ax x

标量场和矢量场

标量场和矢量场

第 1 章矢量分析1.2 标量场和矢量场1.2.1 场的分类1.2.2 场的表示一. 什么是场-具有某种物理量在空间的分布。

如地球周围的温度场、湿度场、重力场；另外还有气功场；百慕大三角场（洞、汇）-场在数学上用函数表示。

即场中任一个点都有一个确定的标量值或矢量。

场量在占有空间区域中，除开有限个点和某些表面外，是处处连续、可微的。

二. 场的分类标量场：具有标量特征的物理量在空间的分布，如温度场T(x,y,z)、电位Φ(x,y,z)等。

矢量场：具有矢量特征的物理量在空间的分布，如重力场F(x,y,z)、流速场v(x,y,z)等。

标量场和矢量场都有可能随时间变化。

动态场: 场量随时间变化（时变场）f ( x, y, z, t ), A( x, y, z ,t ), 四元函数静态场: 场量不随时间变化（恒定场）f ( x, y, z), A( x, y, z), 三元函数2）图示法u (x,y,z )：等值面、等值线1. 标量场的表示方法1）数学法f = f ( x, y, z)（A ）等高线图（B ）色码图（C ）地势图三. 场的表示方法标量场Scalar Field火星夜间温度图2. 矢量场的表示方法F(x,y,z) = a x F x(x,y,z) + a y F y(x,y,z) + a z F z(x,y,z) 1）数学法2）图示法（A）矢量图箭头方向→场量的方向箭头颜色或长度→场量的大小（A ）矢量图2.图示法（B）场线图切向→场量的方向疏密程度→场量的大小。

（B）场线图（C）纹理图(Grass Seeds)纹理与场方向平行（C）纹理图点电荷产生的电场无限长载流线产生的磁场TE10电场、磁场、电流TE10电场、磁场矢量场和标量场点电荷产生的电场和电位四.场源Source of Field•场是由源产生的，场不能离开场源而存在•不同的场对应不同的源•源有矢量和标量之分（旋度源和散度源）如：温度场由热源产生静止电荷电场运动电荷磁场Note：电荷及电流是产生电磁场唯一的源。

工程电磁场-第1章-矢量分析和场论基础

工程电磁场-第1章-矢量分析和场论基础

04
电磁2
03
静电场
由静止电荷产生的电场， 其电场线不随时间变化。
恒定磁场
由恒定电流产生的磁场， 其磁场线是闭合的，且不 随时间变化。
时变电磁场
由变化的电流或变化的电 荷产生的电场和磁场，其 电场线和磁场线都随时间 变化。
电磁场的分类
按存在形式分类
有源场和无源场。有源场是指其散度非零的场，如静电场和恒定 磁场；无源场是指其散度为零的场，如时变电磁场。
根据场的来源，可以将场分为自然场 和人工场。
场量和场强
场量是描述场中物理量分布的量，如电场强度、磁场强度等 。
场强是描述场作用的强度和方向的物理量，如电场线、磁场 线等。
03
矢量场和标量场
矢量场的性质
02
01
03
矢量场由矢量线组成，具有方向和大小。
矢量场具有旋度或散度，分别表示场中的旋涡或电荷 分布。 矢量场的变化遵循斯托克斯定理和格林定理。
80%
斯托克斯定理
斯托克斯定理是矢量积分的重要 定理之一，它描述了矢量场中某 点处的散度与该点处单位球体体 积内的积分之间的关系。
矢量函数和场
矢量函数
矢量函数是描述空间中矢量场 变化的数学工具，其定义域和 值域都是矢量。
矢量场
矢量场是由空间中一系列点构 成的集合，每个点都有一个与 之相关的矢量。
梯度、散度和旋度
在磁场的边界上，磁场线切线方向的 分量连续，即磁场强度不突变。
05
电磁场的能量和动量
电磁场的能量
电磁场能量的定义
01
电磁场能量是指存在于电磁场中的能量，它与电场和磁场的变
化率有关。
电磁场能量的计算
02
通过计算电场和磁场的能量密度，可以得出整个电磁场的总能

矢量分析

矢量分析

二、方向导数 在实际应用中，不仅需要宏观上了解场在空间的数值，还要知道在不同 方向上场变化的情况。方向导数表征标量场空间中，某点处场沿各个方向变 化的规律。
取等位面 u 1、定义：
x, y , z
增加的方向，相互垂直且满足右手螺旋法则
v ˆ ˆ ˆ 矢量表示： A = e x Ax + e y Ay + e z Az
v 位置矢量： r = e x x + e y y + e z z ˆ ˆ ˆ
v ˆ ˆ ˆ dr = e x dx + e y dy + e z dz 微分长度元：
（2）球面坐标系下矢量运算
v ˆ ˆ ˆ A = er Ar + eθ Aθ + eϕ Aϕ v ˆ ˆ ˆ B = er Br + eθ Bθ + eϕ Bϕ
v v ˆ ˆ ˆ A ± B = er ( Ar ± Br ) + eθ ( Aθ ± Bθ ) + eϕ ( Aϕ ± Bϕ )
v v A• B = Ar Br + Aθ Bθ + Aϕ Bϕ
e 单位矢量：ˆ ρ
ρ
,φ
ˆ , eφ
,z
ˆ , ez
0 ≤ ρ < ∞ , 0 ≤ φ ≤ 2π , − ∞ < z < ∞
ˆ ˆ ˆ e z = e ρ × eφ ˆ ˆ ˆ e ρ = eφ × e z ˆ ˆ ˆ eφ = e z × e ρ
ˆ ˆ ˆ ↑ e ρ 、eφ 、e z
分别代表ρ、φ、z 增加的方向，相互垂直且满足右手螺旋法则
ˆ 由于 θ、ϕ 不是常矢量，与 er
ˆ ∂er ˆ =eθ ∂θ ˆ ∂ eθ ˆ = −er ∂θ ˆ ∂ eϕ = 0 ∂θ

动力学中的标量和矢量标量和矢量物理量的区别与计算方法是什么

动力学中的标量和矢量标量和矢量物理量的区别与计算方法是什么

动力学中的标量和矢量标量和矢量物理量的区别与计算方法是什么动力学中的标量和矢量：标量和矢量物理量的区别与计算方法在物理学中，动力学是研究物体运动以及物体与力之间相互作用的学科。

在动力学的研究中，我们经常会遇到标量和矢量这两种不同类型的物理量。

本文将详细介绍标量和矢量物理量的定义、区别以及计算方法。

一、标量的定义和计算方法在动力学中，标量是指只具有大小而没有方向的物理量。

比如物体的质量、体积、温度等都属于标量物理量。

标量物理量通常用实数或复数来表示，它们可以通过数值的大小来进行比较或计算，而无需考虑方向。

标量的计算方法十分简单，我们直接对数值进行加减乘除运算即可。

例如，若有两个标量物理量A和B，我们可以直接进行加法运算得到它们的和A + B，或者进行乘法运算得到它们的乘积A * B。

二、矢量的定义和计算方法与标量不同，矢量是指既有大小又有方向的物理量。

例如物体的速度、位移、力等都属于矢量物理量。

矢量物理量不仅有大小，还有所指示的方向，因此在进行计算时需要考虑其方向性。

矢量物理量通常用箭头来表示，箭头的长度表示其大小，而箭头的方向表示其方向。

在动力学的研究中，我们使用三维坐标系来描述矢量的方向，通常以x、y、z三个轴来表示。

分别表示矢量在三个轴上的分量，利用这些分量可以准确描述矢量的方向。

矢量的计算方法包括向量相加、向量相减、数量积以及叉积等操作。

向量相加时，我们按照矢量的几何方法进行运算，将两个矢量的起点放在一起，然后将两个矢量相连的箭头就是它们的和。

向量相减的方式类似，只需要将一矢量的箭头取反即可。

数量积（也称为点积）是指两个矢量相乘后加和的结果。

计算数量积的方法是将两个矢量的各个分量分别相乘，并将得到的结果相加。

数量积的结果是一个标量值。

叉积（也称为矢量积）是指两个矢量相乘后的矢量结果。

计算叉积的方法是根据右手定则，将两个矢量的大小和方向进行运算。

叉积的结果是一个新的矢量，其大小由两个矢量的大小以及夹角决定，方向垂直于这两个矢量所在的平面。

矢量运算法则

矢量运算法则

例2： 设
r1 2aˆx aˆy aˆz , r2 aˆx 3aˆy 2aˆz r3 2aˆx aˆy 3aˆz , r4 3aˆx 2aˆy 5aˆz
求： r4 ar1 br2 cr3 中的标量 a、b、c。
解： 3aˆx 2aˆy 5aˆz a(2aˆx aˆy aˆz ) b(aˆx 3aˆy 2aˆz ) c(2aˆx aˆy 3aˆz ) (2a b 2c)aˆx (a 3b c)aˆy (a 2b 3c)aˆz
(，R其,中,)均为 ,
h1 1, h2 R, h3 R sin
正交曲线坐标系：
在正交曲线坐标系中，其坐标变量
不一(定u1都, u是2 ,长u度3 )，其线元必然
有一个修正系数，这些修正系数称为拉梅系数，若已知其拉梅系数
，就
可正确写出其线元、面元和体元。
h1, h2 , h3
R
aˆR

R
aˆ

R sin
aˆ
在任意正交曲线坐标系中：



h1u1
aˆu1


h2u2
aˆu 2


h3u3
aˆu3
五、矢量场的散度
1. 矢线（场线）：
在矢量场中，若一条曲线上每一点的切线
方向与场矢量在该点的方向重合，则该曲线称
+
-
为矢线。
2. 通量：
h BC
A C

B
在直角坐标系中：
aˆx aˆy aˆz
A (B C) ( Axaˆx Ayaˆy Azaˆz ) Bx By Bz

《工程电磁场》 (9)

《工程电磁场》 (9)
用两个实数表示， 例如：正弦电压U U
标量场：标量在空间的分布。
例如 电位场： (r,t) (x, y, z,t)
高度场：H
H (r , t)
H (x,
y, z,t)
等值面（线），等位面（线） (r,t) C
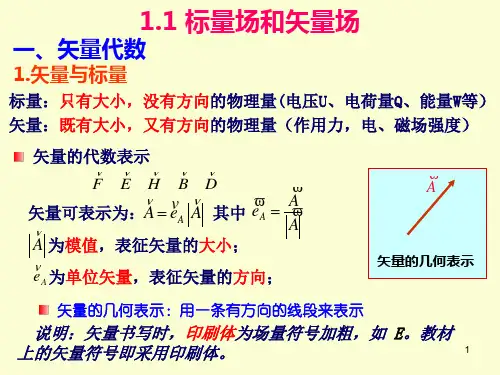
0.1 标量场和矢量场
3. 矢量和矢量场 模
矢量：不仅具有大小，而且具有方向特征的量。
•
在矢量场中，若
F
J
0
,称之为旋度场(或旋涡
场)，
J
称为旋度源(或旋涡源)；
•
若矢量场处处
F
0
，称之为无旋场（保守场）。
旋度的计算公式
C 0
(CF ) C F
(F G) F G
(uF ) u F u F
(F G) G ( F ) F ( G)
Fz z
散度(divergence)
物理意义:
• 矢量的散度是一个标量，是空间坐标点的函数；
• 散度代表矢量场的通量源的分布特性：
divF 0 这点有正源
divF 0
divF 0 连续场，无源场
这点有负源
散度和通量源
F
0
(无源）
F
0 (正源）
F
0(负源）
在矢量场中，若
F
0 ，称之为有源场，
旋度(curl)
在直角坐标系下
ex ey ez
F
x
y
z
Fx Fy Fz
旋度也可描述成单位面积上的环流量
旋度的物理意义
以“流速场”为例，利用一个小浆轮作为“旋度计”。 如图所示：
1. 流速均匀
流速场
2. 流速不均
rotF 0

《矢量分析与场论》知识点归纳

《矢量分析与场论》知识点归纳

⎢⎢a
y
⎥ ⎥
=
⎢⎢sinθ
sin
ϕ
⎢⎣az ⎥⎦ ⎢⎣ cosθ
cosθ cosϕ cosθ sinϕ
− sinθ
− sinϕ cosϕ
− sinϕ cosϕ
0
0⎤⎡aρ ⎤
0⎥⎥
⎢⎢aϕ
⎥ ⎥
1⎥⎦⎢⎣az ⎥⎦
（1-2-10）
如果矢量 A 是在圆柱坐标系给定的，根据式（1-2-10）
可以变换成直角坐标系的表达式，反之，若矢量 A 是在直角坐标系给定的，则根据式（1-2-9）
可以变换成圆柱坐标系的表达式。
P 沿 ρ 、ϕ 和 z 方向的长度增量分别为
⎤ ⎥ ⎥
=
⎡sinθ ⎢⎢cosθ
cosϕ cosϕ
⎢⎣aϕ ⎥⎦ ⎢⎣ − sinϕ
sinθ sinϕ cosθ sinϕ
cosϕ
cosθ ⎤⎡ax ⎤
−
sin
θ
⎥ ⎥
⎢⎢a
y
⎥ ⎥
0 ⎥⎦⎢⎣az ⎥⎦
同样，将上式求逆即可得到由球坐标变换到直角坐标的关系式
（1-2-23）
⎡ax ⎤ ⎡sinθ cosϕ
矢量分析与场论
实数域内任一代数即一个只有大小的量称之为标量，而一个既有大小又有方向特性的量 称之为矢量。无论是标量还是矢量，一旦被赋予物理单位，则成为一个具有物理意义的量即 所谓的物理量。物理量数值的无穷集合称为场。如果这个物理量是标量，就称其为标量场； 如果物理量是矢量就称这个场为矢量场。场的一个重要属性是它占有一个空间，而且在该空 间域内，除有限个点或表面外它是处处连续的。如果场中各处物理量不随时间变化，则称该 场为静态场，不然，则称为动态场或时变场。

第0章 矢量分析

第0章 矢量分析

例2. 求 f = 4e 2x− y+ z 在点P1(1,1,−1) 处的由该点指向P2(-3,5,6) 方向上的方 − 向导数。 向导数。 解： ∇f = ∇(4e 2 x-y + z ) = 4∇(e 2 x-y + z )
= 4e 2 x-y + z ∇(2 x − y + z ) = 4e 2 x-y + z (2 e x − e y + e z )
▽算符的特性： 算符的特性： 在不同坐标系下▽算符有不同的表达形式； ① 在不同坐标系下▽算符有不同的表达形式； 算符单独存在没有任何意义； ② ▽算符单独存在没有任何意义； 算符的矢量特性： ③ ▽算符的矢量特性：
∇ ⋅ ∇f = ∇ 2 f
算符的微分特性： ④ ▽算符的微分特性： ∂ ∂ ∂ ∇( fg ) = ( fg )e x + ( fg )e y + ( fg )e z ∂x ∂y ∂z ∂g ∂f ∂f ∂f ∂g ∂g = f + g ex + f + g ey + f + g ez ∂x ∂y ∂z ∂x ∂z ∂y
e12 =
F 在P1处沿 12方向上的方向导数 处沿R
∂f ∂R12 = ∇f
P1 P1
⋅ e12
= 4(2 e x − e y + e z ) ⋅
− 4 ex + 4 e y + 7 ez 9 4 20 = [2 × ( −4) + ( −1) × 4 + 1 × 7] = − 9 9
0.3 矢量场的通量及散度
可见进行梯度运算，只需先按微分公式运算， 可见进行梯度运算，只需先按微分公式运算，d ( fg ) = fd g + g d f 换成▽ 再将 d 换成▽算符即可。

矢量分析与场论

矢量分析与场论

在直角坐标系中称之为哈密顿算子，是一个微分 符号，同时又要当作矢量看待。算子与矢性函数 A 的点积为一标量函数。在直角坐标系中，散度 的表达式可以写为：
Ax Ay Az A i j k Ax i Ay j Az k y z x y z x


矢量的加减运算同向量的加减，符合平行四边 形法则 任意两个矢量的点积是一个标量，任意两个矢 量的叉积是一个矢量 如果两个不为零的矢量的点积等于零，则这两 个矢量必然互相垂直 如果两个不为零的矢量的叉积等于零，则这两 个矢量必然互相平行
1.2 矢量场
1.2.1矢量场的矢量线
矢量场空间中任意一点P处的矢量可用一 个矢性函数A=A（P）来表示。直角坐标中， 可以表示成如下形式：
例: 求矢量场A=xy2i+x2yj+zy2k的矢量线方程。 解： 矢量线应满足的微分方程为
dx dy dz 2 2 2 xy x y y z
dy dx 2 2 xy x y 从而有 dx dz xy 2 y 2 z
解之即得矢量方程
z c x 1 2 2 x y c2
解： 矢量场A的旋度
i rotA A x x( z y )
j
k
y z y ( x z ) z ( y x)
( z y )i ( x z ) j ( y x)k
在点M(1，0，1)处的旋度
A
n方向的单位矢量
M
i + 2j + k
2） 矢量积 任意两个矢量 A 与 B 的矢量积（ Vector Product ） 是一个矢量，矢量积的大小等于两个矢量的大 小与它们夹角的正弦之乘积，其方向垂直于矢 量A与B组成的平面， 如图1所示，记为 C=A×B=anAB sinθ an=aA×aB （右手螺旋）

矢量分析

矢量分析

| 首页 | 目录 | 向前 | 向后 | 资源 | 搜索 | 帮助 | 矢量分析 > 标量场和矢量场 标量场和矢量标量场和矢量场概念标量：只有大小而没有方向的量。

如电压U 、电荷量Q 、电流I 、面积S 等。

矢量：具有大小和方向特征的量。

如电场强度矢量、磁场强度矢量、作用力矢量、速度矢量等。

标量场：在指定的时刻，空间每一点可以用一个标量唯一地描述，则该标量函数定出标量场。

例如物理系统中的温度、压力、密度等可以用标量场来表示。

矢量场：在指定的时刻，空间每一点可以用一个矢量唯一地描述，则该矢量函数定出矢量场。

例如流体空间中的流速分布等可以用矢量场来表示。

标量场 矢量场矢量描述矢量可采用有向线段、文字、单位矢量、分量表示等多种方式来描述。

场的"场图"表示研究标量和矢量场时，用“场图”表示场变量在空间逐点演变的情况具有很大的意义。

对标量场，用等值面图表示。

空间内标量值相等的点集合形成的曲面称为等值面，例如气象图上的等压线，地图上的等高线等。

显然，等值面的方程式为＝常数值对矢量场，则用一些有向曲线来形象表示矢量在空间的分布，称为力线或流线。

力线上任意点的切线方向必定与该点的矢量方向相同，即, 称为力线的微分方程式。

式中为力线切向的一段矢量。

在直角坐标内，力线的微分方程式可写成按统一规则，绘制出力线，则既能根据力线确定矢量场中各点矢量的方向，又可根据各处力线的疏密程度，判别出各处矢量的大小及变化趋势。

P点处的矢量力线图矢量代数平行四边形法则求和差作图法遵循平行四边形法则分量法.求点积（标量积、内积）公式：特点：应用：电通量的计算求矢积（矢量积、外积）公式：特点：应用：磁感应强度的计算|首页|目录|向前|向后|资源|搜索|帮助|矢量分析> 矢量的环流、旋度矢量的环流、矢量的环流定义：矢量沿某一有向闭合曲线的线积分为沿的环流，即。

物理意义：矢量沿闭合曲线的环流反映了闭合曲线内源的性质。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

表明：标量函数 沿l方向的方向导数就是矢量g在l上的投影。
当 ( g,el ) 0 ，
最大
l
也就是只有当l的方向和g的方向一致时，方向导数才取得最 大值。
l的方向和g的方向垂直时，方向导数为零
l的方向和g的方向相反时，方向导数为-1，取得最小值，此
时 减小的最快
2. 梯度
g
x
ex
y
ey
☻ 标量场的梯度函数
建立了标量场与矢 量场的联系，这一 联系使得某一类矢 量场可以通过标量 函数来研究，或者 说标量场可以通过 矢量场的来研究。
形象描绘场分布的工具——场线
(1) 标量场--等值线(面)
其方程为:
(x, y, z) c
该曲面上任一点的函数值相等 等值面充满了场所在的空间
是单值函数，因此等值面不相交
图0.1.1 等高线
思考 在某一高度上沿什么方向高度变化最快？
3矢量场--矢量线（力线）
目的：形象地描绘矢量场A的分布 特点：
电磁场与电磁波
Vector Analysis（矢量分析）
标量场和矢量场 标量场的梯度 矢量场的通量与散度 矢量场的环量与旋度 亥姆霍兹定理 电磁场的特殊形式
1 标量场和矢量场
补充： 01.矢性函数
在二维空间或三维空间内的任一点P， 它是一个既存在 大小(或称为模)又有方向特性的量，故称为实数矢量，一般用
•
C=A×B=enAB sinθ
•
en=eA×eB （右手螺旋）
矢量的叉积不服从交换律，但服从分配律
A×B= -B×A
C
eann O eaBB
eaAA
B
A
C＝A×B B
A
(a)
(b)
图 1 - 3 矢量积的图示及右手螺旋
(a) 矢量积
(b) 右手螺旋
1. 标量场和矢量场
场： 如果在某一空间区域内的每一点，都对应着某个物理量 的一个确定的值，则称在此区域内确定了该物理量的一个场。
1） 标量积
任意两个矢量A与B的标量积
(Scalar Product)是一个标量，
B
它等于两个矢量的大小与它
们夹角的余弦之乘积，如图
1-2所示， 记为
Bcos
A
•A·B=AB cosθ
图1-2 标量积
2） 矢量积
任 意 两 个 矢 量 A 与 B 的 矢 量 积 （ Vector Product）是一个矢量，矢量积的大小等于两 个矢量的大小与它们夹角的正弦之乘积，其 方向垂直于矢量A与B组成的平面， 如图1-3 所示，记为
z
ez）•（ex
cos
ey
cos
ez
cos ）
cos cos cos
x
y
z
式中 , , 分别是任一方向 l 与 x, y, z 轴的夹角
设
g x ex y ey z ez ,
el
ex cos ey cos ez cos
则有：
l
g el
|
g
| cos( g, el )
换句话说， 在某一空间区域中，物理量的无穷集合表示 一种场。如在教室中温度的分布确定了一个温度场，在空间电 位的分布确定了一个电位场。（物理量的值可相等）
场的一个重要的属性是它占有一定空间，而且在该空间
域内， 除有限个点和表面外，其物理量应是处处连续 的。 若该物理量与时间无关，则该场称为静态场； 若该物理
设t是一数性变量，A为变矢，对于某一区间G［a, b］ 内的每一个数值t, A都有一个确定的矢量A (t)与之对应，则 称A为数性变量t的矢性函数。记为
A A(t)
而G为A的定义域。矢性函数A(t)在直角坐标系中的三个坐 标分量都是变量t的函数，分别为Ax(t)、Ay(t)、Az(t)，则矢性函 数A (t)也可用其坐标表示为
黑体A表示。
若用几何图形表示，它是从该点出发画一条带有箭头的 直线段，直线段的长度表示矢量A的模，箭头的指向表示该矢 量A的方向。
矢量一旦被赋予物理单位，便成为具有物理意义的矢量， 如电场强度E、磁场强度H、速度v等等。
若某一矢量的模和方向都保持不变， 此矢量称为常矢， 如某物体所受到的重力。
而在实际问题中遇到的更多的是模和方向或两者之一会 发生变化的矢量，这种矢量我们称为变矢，如沿着某一曲线 物体运动的速度v等。
例如，在直角坐标下：
(x,
y,
z)
4π [(x
1)2
5 (
y
2)2
z2]
标量场
然而在许多物理系统中， 其状态不仅需要 确定其大小，同时还需确定它们的方向，这就 需要用一个矢量场来描述。例如电场、磁场、 流速场等等。
A(x, y, z) 2xy2ex x2 zey xyzez
矢量场
2.标量场的等值面
(1)它上面每一点处的切线方向都与矢量场在该点的 方向相同
(2)矢量场中的矢量线也充满了整个场域，但它们互
不相交
其方程为：
A dl 0
在直角坐标下：
二维场 三维场
Ax Ay dx dy Ax Ay Az dx dy dz
图0.1.2 矢量线
•物理意义：矢量线和场量的变化方向一致
图 1-4 矢量场的矢量线
图 1-5 矢量管
矢量管：
通过场域某一曲面s上的所有点的矢量 线的全体构成的管状区域。
0.2 标量场的梯度
Gradient of Scalar Field
1.方向导数：设一个标量函数 (x，y，z)，若函数 在点 P 可微，则 在点P 沿任意方向 l 的变化率称
为方向导数，即
l
（
x
ex
y
ey
量与时间有关，则该场称为动态场或称为时变场。
场是一个标量或一个矢量的位置函数，即场中 任一个点都有一个确定的标量或矢量。
在研究物理系统中温度、 压力、 密度等在一定
空间的分布状态时，数学上只需用一个代数变量来描 述， 这些代数变量(即标量函数)所确定的场为标量场， 如温度场T(x, y, z)、电位场φ(x, y, z)、高度场等。
A Ax (t)ex Ay (t)ey Az (t)ez
其中ex、ey、ez为x轴、y轴、z轴正向单位矢量。
•终点一般称为矢性函数A(t)的矢端曲线。
z
Z
P(X, Y, Z)
r
Aazz
Aaxx O
Y Aayy
y
X
x
图1-1 直角坐标系中一点的投影
02. 矢量的乘积
•矢量的乘积包括标量积和矢量积。
z
ez
grad
——梯度(gradient)
式中
ex
x
ey
y
ez
z
•
del(代尔)梯度的意义源自——哈密顿算子 图0.1.3
”
nabla (那勃拉)”)
等温线分布
标量场的梯度是一个矢量，是空间坐标点的函数。
梯度的大小为该点标量函数 的最大变化率，即
最大方向导数。 梯度的方向为该点最大方向导数的方向。