函数的平均变化率解读

变化率简介变化率是学习导数的前提，它在描述各种变化规律的过程中起着非常重要的作用，速度和加速度就是两个典型例子.新教材人教A 版中，对于变化率主要从以下两个方面介绍：1、平均变化率；2、瞬时变化率.一、平均变化率函数()y f x =在区间00[,]x x x +∆或（00[,]x x x +∆）上的平均变化率是商yx∆∆，其中x ∆是自变量x 在0x 处的改变量，可正可负，但不能为0，y ∆是函数值相应的改变量，即00()()y f x x f x ∆=+∆-（y ∆为正、负、零均可）所以00()()f x x f x y x x+∆-∆=∆∆，下面通过举例来进一步加深对概念的理解。

例1、求332-=x y 在0x 到x x ∆+0之间的平均变化率.解：当自变量从0x 到x x ∆+0之间变化时，函数的平均变化率为：x f∆∆=∆-∆+=x x f x x f )()(00xx x x ∆---∆+=]33[]3)(3[2020 x x xx x x ∆+=∆∆+∆⋅=36)(3602评注：此类题目只需要紧扣定义式，注意运算过程就可以了. 评注：⑴函数平均变化率的求法可分两步：①求y ∆；②求yx∆∆.⑵不论0x 、x ∆中的哪一个变化，都会引起函数平均变化率的变化。

拓展：函数()y f x =的平均变化率的几何意义为其图象上割线的斜率。

即：函数()y f x =的图象为曲线C ，曲线C 上有一点00(,)P x y 及邻近一点00(,)Q x x y y +∆+∆，则割线PQ 的斜率0000y y y yk x x x x+∆-∆==+∆-∆。

利用平均变化率的几何意义，可解决一些实际问题，举例如下：例2、某电视机厂有甲、乙两条生产流水线，产量S （单位：台）与时间t （单位：天）的关系如图所示，问：（1）0t 天内，甲、乙两条生产线的平均日产量哪个大？（2）在接近0t 天时，甲、乙两条生产线谁的日产量大？0,)x y y ∆+∆解析：（1） 0t 天内，甲、乙两条生产线的平均日产量，即函数1()S f t =与2()S f t =在0[0,]t 内的平均变化率，其都为直线OA 的斜率，所以0t 天内，甲、乙两条生产线的平均日产量相同。

1 变化的快慢与变化率
1.平均变化率：上述问题中的变化率可用式子 表示,称为函数f (x )从x 1到x 2的平均变化率。

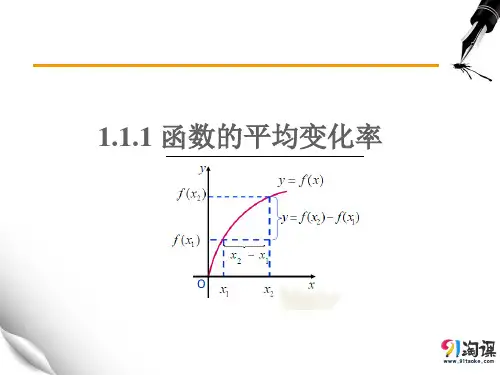
1．函数的平均变化率的概念：一般地，给出函数()f x 在区间12[]x x ，上的平均变化率2121
()()f x f x x x --； 2. 平均变化率的几何意义：直线的斜率；
3．平均变化率的实际作用：反映了函数某个区间上的平均变化率（变化快慢）；或者说在某个区间上曲线的陡峭程度．平均变化率是曲线陡峭程度的“数量化”，曲线陡峭程度是平均变化率的“视觉化”．
提醒：平均变化率有局限．我们知道平均变化率只能反映函数在某个区间内的平均变化，而无法精确反映某一点的变化状态
1 已知函数x x x f +-=2)(的图象上的一点)2,1(--A 及
临近一点)2,1(y x B ∆+-∆+-则
=∆∆x
y . 【解析】
)1()1(22x x y ∆+-+∆+--=∆+- ∴x x
x x x y ∆-=∆-∆+-+∆+--=∆∆32)1()1(2 2 求2x y =在0x x =附近的平均变化率.
【解析】
2
020)(x x x y -∆+=∆
所以x x x x x y ∆-∆+=∆∆2020)(x x x x x x x x ∆+=∆-∆+∆+=020202022 1
212)()(x x x f x f --
所以2x y =在0x x =附近的平均变化率为x x ∆+02。

§3.1 导 数3．1.1 函数的平均变化率学习目标 1.理解平均变化率的意义.2.会求函数在某一点附近的平均变化率．知识点 函数的平均变化率假设如图是一座山的剖面示意图，并建立如图所示的平面直角坐标系．A 是出发点，H 是山顶．爬山路线用函数y ＝f (x )表示．自变量x 表示某旅游者的水平位置，函数值y ＝f (x )表示此时旅游者所在的高度．设点A 的坐标为(x 1，y 1)，点B 的坐标为(x 2，y 2)．思考1 若旅游者从点A 爬到点B ，自变量x 和函数值y 的改变量分别是多少？ 答案 自变量x 的改变量为x 2－x 1，记作Δx ，函数值y 的改变量为y 2－y 1，记作Δy . 思考2 怎样用数量刻画弯曲山路的陡峭程度？ 答案 对山路AB 来说，用Δy Δx ＝y 2－y 1x 2－x 1可近似地刻画其陡峭程度． 思考3 观察函数y ＝f (x )的图象，平均变化率Δy Δx ＝f (x 2)－f (x 1)x 2－x 1表示什么？答案 观察图象可看出，ΔyΔx 表示曲线y ＝f (x )上两点(x 1，f (x 1))，(x 2，f (x 2))连线的斜率．梳理 (1)函数的平均变化率的定义已知函数y ＝f (x )在点x ＝x 0及其附近有定义，令Δx ＝x －x 0；Δy ＝y －y 0＝f (x )－f (x 0)＝f (x 0＋Δx )－f (x 0)．则当Δx ≠0，比值f (x 0＋Δx )－f (x 0)Δx ＝ΔyΔx 叫做函数y ＝f (x )在x 0到x 0＋Δx 之间的平均变化率．(2)平均变化率的实质：函数值的改变量与自变量的改变量之比． (3)作用：刻画函数在区间[x 0，x 0＋Δx ]上变化的快慢．(4)几何意义：已知P 1(x 1，f (x 1))，P 2(x 2，f (x 2))是函数y ＝f (x )的图象上两点，则平均变化率ΔyΔx ＝f (x 2)－f (x 1)x 2－x 1表示割线P 1P 2的斜率．(1)在平均变化率的定义中，自变量x 的增量Δx ＞0.( × )(2)对于函数f (x )在区间[x 1，x 2]内的平均变化率也可以表示为f (x 2)－f (x 1)x 2－x 1.( √ )(3)Δy Δx ＝f (x 0＋Δx )－f (x 0)Δx 是f (x )在区间[x 0，x 0＋Δx ](Δx ＞0)上的平均变化率，也可以说是f (x )在x ＝x 0处的变化率．( × )类型一 求函数的平均变化率例1 已知函数y ＝f (x )＝3x 2＋5，求f (x )： (1)在0.1到0.2之间的平均变化率； (2)在x 0到x 0＋Δx 之间的平均变化率． 考点 题点解 (1)因为f (x )＝3x 2＋5，所以在0.1到0.2之间的平均变化率为f (0.2)－f (0.1)0.2－0.1＝3×0.22＋5－3×0.12－50.2－0.1＝0.9.(2)Δy ＝f (x 0＋Δx )－f (x 0) ＝3(x 0＋Δx )2＋5－(3x 20＋5)＝3x 20＋6x 0Δx ＋3(Δx )2＋5－3x 20－5＝6x 0Δx ＋3(Δx )2，函数y ＝f (x )在x 0到x 0＋Δx 之间的平均变化率为Δy Δx ＝6x 0Δx ＋3(Δx )2Δx＝6x 0＋3Δx . 反思与感悟 求平均变化率的主要步骤 (1)先计算函数值的改变量Δy ＝f (x 2)－f (x 1)． (2)再计算自变量的改变量Δx ＝x 2－x 1. (3)得平均变化率Δy Δx ＝f (x 2)－f (x 1)x 2－x 1.跟踪训练1 (1)已知函数f (x )＝2x 2＋3x －5.①求：当x 1＝4，x 2＝5时，函数增量Δy 和平均变化率ΔyΔx； ②求：当x 1＝4，x 2＝4.1时，函数增量Δy 和平均变化率ΔyΔx.(2)求函数y ＝f (x )＝x 2在x ＝1,2,3附近的平均变化率，取Δx 都为13，哪一点附近的平均变化率最大？考点 平均变化率的概念 题点 求平均变化率解 (1)因为f (x )＝2x 2＋3x －5， 所以Δy ＝f (x 1＋Δx )－f (x 1)＝2(x 1＋Δx )2＋3(x 1＋Δx )－5－(2x 21＋3x 1－5) ＝2[(Δx )2＋2x 1Δx ]＋3Δx ＝2(Δx )2＋(4x 1＋3)Δx .Δy Δx ＝2(Δx )2＋(4x 1＋3)Δx Δx＝2Δx ＋4x 1＋3. ①当x 1＝4，x 2＝5时，Δx ＝1，Δy ＝2(Δx )2＋(4x 1＋3)Δx ＝2＋19＝21，ΔyΔx ＝21.②当x 1＝4，x 2＝4.1时，Δx ＝0.1， Δy ＝2(Δx )2＋(4x 1＋3)Δx ＝0.02＋1.9＝1.92. ΔyΔx＝2Δx ＋4x 1＋3＝19.2. (2)在x ＝1附近的平均变化率为k 1＝f (1＋Δx )－f (1)Δx ＝(1＋Δx )2－1Δx＝2＋Δx ；在x ＝2附近的平均变化率为k 2＝f (2＋Δx )－f (2)Δx ＝(2＋Δx )2－22Δx ＝4＋Δx ；在x ＝3附近的平均变化率为k 3＝f (3＋Δx )－f (3)Δx ＝(3＋Δx )2－32Δx ＝6＋Δx .当Δx ＝13时，k 1＝2＋13＝73，k 2＝4＋13＝133，k 3＝6＋13＝193.由于k 1<k 2<k 3，所以在x ＝3附近的平均变化率最大． 类型二 求物体的平均速度例2 一质点做直线运动，其位移s 与时间t 的关系为s (t )＝t 2＋1，求该质点在t ＝1,2,3附近，Δt ＝13时，平均速度的值，并比较在哪一时刻附近的平均速度最大．考点 题点解 s (t )在t 0到t 0＋Δt 之间的位移增量为s (t 0＋Δt )－s (t 0)＝(t 0＋Δt )2＋1－(t 20＋1)＝2t 0Δt ＋(Δt )2， Δs Δt ＝2t 0Δt ＋(Δt )2Δt＝2t 0＋Δt ， 将t 0＝1,2,3，Δt ＝13分别代入上式得，当t 0＝1时，平均速度Δs Δt ＝73；当t 0＝2时，平均速度Δs ＝133；当t 0＝3时，平均速度Δs Δt ＝193.由上面的计算知，t ＝3附近的平均速度最大． 引申探究若该质点在2到2＋Δt 之间的平均速度不大于5，则Δt (Δt ＞0)的取值范围是什么？解 s (t )在t 0到t 0＋Δt 之间的位移增量为s (t 0＋Δt )－s (t 0)＝(t 0＋Δt )2＋1－(t 20＋1)＝2t 0Δt ＋(Δt )2. Δs Δt ＝2t 0Δt ＋(Δt )2Δt＝2t 0＋Δt . 当t 0＝2时，由题意，得4＋Δt ≤5，得Δt ≤1. 又因为Δt ＞0，故Δt 的取值范围是(0,1]．反思与感悟 已知物体的运动方程，即知道物体运动过程中位移与时间的函数关系，求其在[t 0，t 0＋Δt ]内的平均速度，根据平均速度的意义可知就是求这个函数在[t 0，t 0＋Δt ]内的平均变化率．跟踪训练2 动点P 沿x 轴运动，运动方程为x ＝10t ＋5t 2，式中t 表示时间(单位：s)，x 表示距离(单位：m)，求在20≤t ≤20＋Δt 时间段内动点的平均速度，其中 (1)Δt ＝1；(2)Δt ＝0.1；(3)Δt ＝0.01. 考点 题点解 动点在20≤t ≤20＋Δt 时间段内的平均速度为 v ＝10(20＋Δt )＋5(20＋Δt )2－10×20－5×202Δt＝210Δt ＋5(Δt )2Δt＝5Δt ＋210，(1)当Δt ＝1时，v ＝5×1＋210＝215(m/s)． (2)当Δt ＝0.1时，v ＝5×0.1＋210＝210.5(m/s)．(3)当Δt ＝0.01时，v ＝5×0.01＋210＝210.05(m/s).1．一物体的运动方程是s ＝3＋2t ，则在[2,2.1]这段时间内的平均速度是( ) A ．0.4 B ．2 C ．0.3 D ．0.2 考点 平均变化率的概念 题点 求平均变化率 答案 B解析 s (2.1)－s (2)2.1－2＝3＋2×2.1－(3＋2×2)0.1＝2.2．如图，函数y ＝f (x )在1到3之间的平均变化率为( )A ．1B ．－1C ．2D ．－2 考点 题点 答案 B 解析 Δy Δx ＝1－33－1＝－1.3．在曲线y ＝f (x )＝x 2＋2的图象上取一点(2,6)及邻近一点(2＋Δx ,6＋Δy )，则ΔyΔx 为( )A ．Δx ＋1Δx ＋4B ．Δx －1Δx －4C ．Δx ＋4D ．4＋Δx －1Δx考点 题点 答案 C解析 Δy Δx ＝f (2＋Δx )－f (2)Δx ＝(2＋Δx )2－4Δx＝Δx ＋4.4．将半径为R 的球加热，若半径从R ＝1到R ＝m 时球的体积膨胀率为28π3，则m 的值为________． 考点 题点 答案 2解析 ΔV ＝4π3m 3－4π3×13＝4π3(m 3－1)，∴ΔV ΔR ＝4π3(m 3－1)m －1＝28π3. ∴m 2＋m ＋1＝7， ∴m ＝2或m ＝－3(舍)．理解平均变化率要注意以下几点：(1)平均变化率f (x 2)－f (x 1)x 2－x 1表示点(x 1，f (x 1))与点(x 2，f (x 2))连线的斜率，是曲线陡峭程度的“数量化”．(2)为求点x 0附近的平均变化率，上述表达式常写为f (x 0＋Δx )－f (x 0)Δx的形式．(3)函数的平均变化率可以表现出函数的变化趋势．自变量的改变量Δx 取值越小，越能准确体现函数的变化情况．一、选择题1．如果质点M 按规律s ＝3＋t 2运动，则在时间[2，2.1]内的平均速度是( ) A ．4 B ．4.1 C ．0.41 D ．3 考点 平均变化率的概念 题点 求平均变化率 答案 B解析 v ＝(3＋2.12)－(3＋22)0.1＝4.1.2.甲、乙两厂污水的排放量W 与时间t 的关系如图所示，则治污效果较好的是( )A ．甲B ．乙C ．相同D ．不确定考点 平均变化率的概念 题点 平均变化率的应用 答案 B解析 在t 0处，虽然W 1(t 0)＝W 2(t 0)， 但是在t 0－Δt 处，W 1(t 0－Δt )<W 2(t 0－Δt )， 即⎪⎪⎪⎪⎪⎪W 1(t 0)－W 1(t 0－Δt )Δt <⎪⎪⎪⎪⎪⎪W 2(t 0)－W 2(t 0－Δt )Δt ，所以在相同时间Δt 内，甲厂比乙厂的平均治污率小． 所以乙厂的治污效果较好．3．已知函数f (x )＝2x 2－1的图象上一点(1,1)及附近一点(1＋Δx ，f (1＋Δx ))，则ΔyΔx等于( ) A ．4 B ．4＋2Δx C ．4＋2(Δx )2 D ．4x考点 题点 答案 B解析 Δy ＝f (1＋Δx )－f (1)＝[2(1＋Δx )2－1]－1＝4Δx ＋2(Δx )2，∴Δy Δx ＝4Δx ＋2(Δx )2Δx＝4＋2Δx . 4．函数y ＝f (x )在x 0到x 0＋Δx 之间的平均变化率f (x 0＋Δx )－f (x 0)Δx 中，Δx 不可能( )A ．大于0B ．小于0C ．等于0D ．大于0或小于0考点 题点 答案 C5．函数y ＝f (x )＝x 2＋x 在x ＝1到x ＝1＋Δx 之间的平均变化率为( ) A ．Δx ＋2 B ．2Δx ＋(Δx )2 C ．Δx ＋3 D ．3Δx ＋(Δx )2 考点 题点 答案 C 解析Δy Δx ＝f (1＋Δx )－f (1)Δx＝(1＋Δx )2＋(1＋Δx )－(12＋1)Δx＝Δx ＋3.6．函数f (x )＝x 2在x 0到x 0＋Δx 之间的平均变化率为k 1，在x 0－Δx 到x 0之间的平均变化率为k 2，则k 1，k 2的大小关系是( ) A ．k 1＜k 2 B ．k 1＞k 2 C ．k 1＝k 2 D ．无法确定考点 题点 答案 D解析 k 1＝f (x 0＋Δx )－f (x 0)Δx ＝2x 0＋Δx ，k 2＝f (x 0)－f (x 0－Δx )Δx ＝2x 0－Δx .又因为Δx 可正可负且不为0， 所以k 1，k 2的大小关系不确定．二、填空题7.汽车行驶的路程s 和时间t 之间的函数图象如图所示，在时间段[t 0，t 1]，[t 1，t 2]，[t 2，t 3]上的平均速度分别为v 1，v 2，v 3，则三者的大小关系为________________．(用“＜”连接)考点 平均变化率的概念 题点 平均变化率的应用 答案 v 1<v 2<v 3解析 v 1＝k OA ，v 2＝k AB ，v 3＝k BC ， 由图象知，k OA <k AB <k BC .8．函数f (x )＝x 2－x 在区间[－2，t ]上的平均变化率为2，则t ＝________. 考点 平均变化率的概念 题点 平均变化率的应用 答案 5解析 函数f (x )＝x 2－x 在区间[－2，t ]上的平均变化率是Δy Δx ＝f (t )－f (－2)t －(－2)＝t 2－t －(－2)2－2t ＋2＝2，即t 2－t －6＝2t ＋4，所以t 2－3t －10＝0， 解得t ＝5或t ＝－2(舍去)．所以当函数f (x )＝x 2－x 在区间[－2，t ]上的平均变化率是2时，t 的值是5.9．在曲线y ＝2x 2＋1的图象上取一点(1,3)及邻近一点(1＋Δx ,3＋Δy )，则ΔyΔx ＝________.考点 题点 答案 2Δx ＋4解析 Δy Δx ＝2(1＋Δx )2＋1－3Δx＝2Δx ＋4.10．已知圆的面积S 与其半径r 之间的函数关系为S ＝πr 2，其中r ∈(0，＋∞)，则当半径r ∈[1,1＋Δr ]时，圆的面积S 的平均变化率为________．考点题点答案 2π＋πΔr解析 当r ∈[1,1＋Δr ]时，圆的面积S 的平均变化率为ΔS Δr ＝π(1＋Δr )2－πΔr ＝π＋2π·Δr ＋(Δr )2π－πΔr＝2π＋πΔr .三、解答题11．过曲线y ＝f (x )＝x 3＋2x 上两点P (1,3)和Q (1＋Δx ，3＋Δy )作曲线的割线，求出当Δx ＝0.2时割线的斜率．考点题点解 由条件可知，当Δx ＝0.2时，k PQ ＝3＋Δy －31＋Δx －1＝Δy Δx＝(1＋Δx )3＋2(1＋Δx )－(13＋2×1)Δx＝(Δx )2＋3Δx ＋5＝0.22＋3×0.2＋5＝5.64.故当Δx ＝0.2时，割线的斜率为5.64.12．求函数y ＝f (x )＝3x 2＋2在区间[x 0，x 0＋Δx ]上的平均变化率，并求当x 0＝2，Δx ＝0.1时平均变化率的值．考点题点解 函数y ＝f (x )＝3x 2＋2在区间[x 0，x 0＋Δx ]上的平均变化率为f (x 0＋Δx )－f (x 0)(x 0＋Δx )－x 0＝[3(x 0＋Δx )2＋2]－(3x 20＋2)Δx ＝6x 0·Δx ＋3(Δx )2Δx＝6x 0＋3Δx . 当x 0＝2，Δx ＝0.1时，函数y ＝3x 2＋2在区间[2,2.1]上的平均变化率为6×2＋3×0.1＝12.3.13．以初速度v 0竖直向上抛一物体的位移s 与时间t 的关系为s (t )＝v 0t －12gt 2(g 为物体的重力加速度)．(1)求物体从时刻t 0到时刻t 0＋Δt 这段时间内的平均速度v ；(2)求物体在t ＝10 s 到10.4 s 这段时间内的平均速度．考点题点解 (1)由t 0到t 0＋Δt ，则改变量为Δt .因为Δs ＝s (t 0＋Δt )－s (t 0)＝v 0(t 0＋Δt )－12g (t 0＋Δt )2－v 0t 0＋12gt 20 ＝v 0Δt －gt 0·Δt －12g (Δt )2， 所以v ＝Δs Δt ＝v 0Δt －gt 0·Δt －12g (Δt )2Δt＝v 0－gt 0－12g Δt . (2)当t 0＝10 s 时，Δt ＝0.4 s ，则物体在t ＝10 s 到10.4 s 这段时间内的平均速度 v ＝v 0－10g －12×g ×0.4＝v 0－10.2g . 四、探究与拓展14．婴儿从出生到第24个月的体重变化如图，则第二年婴儿体重的平均变化率为________千克/月．考点题点答案 0.25解析 第二年婴儿体重的平均变化率为14.25－11.2524－12＝0.25(千克/月)． 15．若函数y ＝f (x )＝－x 2＋x 在[2,2＋Δx ](Δx >0)上的平均变化率不大于－1，求Δx 的取值范围． 考点 平均变化率的概念题点 平均变化率的应用解 ∵函数f (x )在[2,2＋Δx ]上的平均变化率为 Δy Δx ＝f (2＋Δx )－f (2)Δx＝－(2＋Δx )2＋(2＋Δx )－(－4＋2)Δx＝－3－Δx ，∴由－3－Δx ≤－1，得Δx ≥－2.又∵Δx >0，∴Δx 的取值范围是(0，＋∞)．。

利用函数的导数解决变化率问题函数的导数在解决变化率问题中发挥着重要的作用。

在数学和应用领域中，我们经常需要计算事物随时间、空间或其他变量的变化速率。

这些问题可以通过函数的导数来求解，下面将介绍一些常见的变化率问题以及如何利用函数的导数来解决它们。

一、平均变化率平均变化率是描述函数在某个区间内的平均变化速率。

假设有一个函数f(x)，我们想要求解它在区间[a, b]上的平均变化率。

这可以通过计算函数值的差异除以自变量的变化量得到：平均变化率 = (f(b) - f(a)) / (b - a)二、瞬时变化率瞬时变化率是指函数在某一点上的变化速率。

函数的导数可以用来计算瞬时变化率。

给定一个函数f(x)，我们可以通过求解其导函数f'(x)来得到瞬时变化率。

瞬时变化率 = f'(x)三、最大和最小变化率函数的导数还可以帮助我们找到函数在某个区间内的最大和最小变化率。

通过找到函数的导数的最大和最小值，我们可以确定在哪些点上函数的变化率达到最大或最小。

最大和最小变化率 = f'(x) = 0四、应用实例以物理学中的运动问题为例，假设一个物体的位移随时间的变化关系可以用函数f(t)表示。

我们想要求解该物体在某一时刻的瞬时速度。

可以通过计算函数f(t)的导函数f'(t)来得到瞬时速度。

瞬时速度 = f'(t)五、其他变化率问题除了上述提到的问题，函数的导数还可以应用于其他各种变化率问题，比如计算人口增长率、温度变化率、经济增长率等。

只要有一个与时间或其他变量相关的函数，就可以利用函数的导数来解决相应的变化率问题。

总结：通过函数的导数，我们可以解决各种变化率问题，包括平均变化率、瞬时变化率、最大和最小变化率等。

函数的导数可以帮助我们更好地理解和分析事物的变化过程，并且应用广泛。

无论是在数学领域还是其他应用领域，函数的导数都是一个强大的工具，能够提供准确的变化率信息，帮助我们更好地理解和解决问题。