曲线拟合
- 格式:doc
- 大小:645.00 KB
- 文档页数:20

曲线拟合归一化
目录
1.曲线拟合的定义和作用
2.归一化的定义和作用
3.曲线拟合和归一化在数据处理中的应用
4.曲线拟合和归一化的优缺点
5.结论
正文
曲线拟合是一种数学方法,用于在给定数据集上找到最佳匹配的曲线。
它可以帮助我们在数据中发现模式和趋势,从而更好地理解数据。
拟合的曲线可以是线性的,也可以是非线性的,具体取决于数据的特性。
曲线拟合在许多领域都有应用,包括经济学、物理学、生物学等。
归一化是一种数据处理的技术,它的主要目的是将数据转换到一个标准范围内,使得不同的特征之间的值可以进行直接的比较。
归一化的方法包括最大值和最小值归一化,以及标准差归一化等。
归一化可以提高模型的性能,特别是在数据量纲不同的情况下。
曲线拟合和归一化在数据处理中都有重要的应用。
曲线拟合可以用于拟合出数据集的函数关系,而归一化则可以将数据转换到同一量纲,方便后续的处理。
例如,在机器学习中,我们常常需要对输入数据进行归一化,以保证模型的稳定性和准确性。
曲线拟合和归一化都有其优缺点。
曲线拟合的优点是可以找出数据中的模式和趋势,但在数据量较少或者噪声较大的情况下,拟合的曲线可能会不准确。
归一化的优点是可以将数据转换到同一量纲,方便后续处理,但也可能会损失数据的原始信息。
总的来说,曲线拟合和归一化都是数据处理中常用的方法,它们可以帮助我们更好地理解和处理数据。

计算机曲线拟合公式
拟合曲线是指在已知一组数据的前提下,通过一定的数学方法,找出一个代表这组数据的曲线方程。
这个曲线方程可以用于对数据进行预测、分析和优化等操作。
常见的曲线拟合公式包括线性拟合、多项式拟合、指数拟合等。
1. 线性拟合
线性拟合是指拟合一个一次函数y=kx+b,其中k和b分别为
拟合曲线的斜率和截距。
通常使用最小二乘法来求解k和b。
最小二乘法是指通过最小化误差平方值的方法来确定k和b的值,误差平方值=∑(yi-(kxi+b))^2,其中yi为实际的数据值,
xi为自变量的取值。
通过求解误差平方值的导数,可以得到k
和b的值。
2. 多项式拟合
多项式拟合是指将一个多项式函数拟合到一组数据上。
多项式函数的一般形式为y=a0+a1*x+a2*x^2+…+an*x^n。
多项式拟
合的主要目的是通过多项式来描述数据中的非线性趋势。
常见的拟合方法包括最小二乘法、牛顿法、拉格朗日法等。
3. 指数拟合
指数拟合是指将一个指数函数y=a*exp(b*x)拟合到数据上。
这
种拟合常用于数据呈现出指数增长或衰减趋势的情况。
指数拟合的关键是通过对数变换将指数函数转化为线性函数,然后再进行线性拟合。
具体方法是对数据进行对数变换,然后用线性拟合的方法求解出a和b的值,再通过指数函数进行反推,得
到拟合曲线的方程。
以上是常见的曲线拟合公式及方法,拟合的具体选择要根据不同的数据趋势和实际需求进行决定。

mathcad曲线拟合曲线拟合是指通过一些已知数据点,找到在数据点集上近似逼近的一条曲线。
在许多实际问题中,我们常常需要通过一组离散的数据来确定系统的行为规律。
曲线拟合提供了一种以数学模型近似描述或预测数据的方法,具有广泛的应用领域。
Mathcad是一款强大的数学计算软件,可用于曲线拟合问题。
Mathcad提供了诸多曲线拟合的方法和工具,常用的方法包括最小二乘法、多项式拟合、指数拟合和对数拟合等。
在曲线拟合中,最常用的方法是最小二乘法。
最小二乘法是通过最小化残差平方和来确定最佳拟合曲线的优化方法。
在Mathcad中,使用最小二乘法进行曲线拟合可以通过数值计算工具箱中的“拟合曲线”功能实现。
这个功能提供了一系列曲线拟合方法,例如多项式拟合、有理函数拟合、傅里叶级数拟合等等。
为了说明曲线拟合的使用,我们可以考虑一个简单的例子。
假设我们有一组离散的数据点,我们希望通过曲线拟合来找到一个函数,能够近似描述这些数据点的分布规律。
我们首先在Mathcad中导入这些数据点,然后利用最小二乘法进行曲线拟合。
假设我们的数据点是(x1,y1),(x2,y2),(x3,y3),......,(xn,yn),其中x和y是变量。
我们可以使用Mathcad的拟合曲线功能,选择一个适当的曲线拟合方法,例如多项式拟合。
对于多项式拟合,我们需要选择多项式的阶数,例如2阶,3阶或者更高阶。
Mathcad中的拟合曲线功能会自动计算出最佳拟合曲线的参数,使得拟合曲线和原始数据点的残差平方和最小。
我们可以通过拟合曲线的参数来获得拟合曲线的方程,从而可以进行进一步的分析和预测。
曲线拟合不仅仅局限于多项式拟合,还可以使用其他拟合方法进行精确拟合。
例如,指数函数拟合适用于需要分析指数增长或衰减行为的数据。
对数函数拟合则适用于处理呈现对数增长或对数衰减行为的数据。
此外,Mathcad还提供了其他拟合方法,例如多项式拟合、样条插值、非线性拟合等。

曲线拟合、分布拟合
曲线拟合和分布拟合都是在数据分析中常见的拟合方法。
曲线拟合是指通过拟合一个函数或模型来描述一组数据之间的依赖关系。
通常,我们使用最小二乘法或其他优化方法来找到最佳拟合曲线。
在曲线拟合中,我们需要选择一个函数形式,例如线性、二次、指数、对数等等,来拟合数据。
分布拟合则是通过拟合一个概率分布来描述一组数据的概率分布情况。
常见的分布包括正态分布、泊松分布、指数分布等等。
在分布拟合中,我们需要选择一个合适的概率分布模型,并使用最大似然估计法或其他方法来估计模型的参数。
曲线拟合和分布拟合之间存在一些区别。
曲线拟合通常关注的是找到一个函数形式来描述数据之间的依赖关系,而分布拟合则是关注的是找到一个概率分布模型来描述数据的概率分布情况。
此外,曲线拟合通常是在一组离散数据点上进行,而分布拟合则是在一组连续数据上进行。
在某些情况下,曲线拟合和分布拟合可以相互转化。
例如,如果我们有一组满足某种分布的随机变量,那么我们可以使用分布拟合来估计该分布的参数。
同样地,如果我们有一组离散数据点,我们可以使用曲线拟合来找到一个最佳拟合曲线。
总之,曲线拟合和分布拟合都是常用的数据分析方法,它们在不同的情况下有不同的应用。
在具体的应用中,我们需要根据实际问题的特点来选择合适的方法。

曲线拟合方法曲线拟合方法是在数据分析中应用广泛的一种数学模型,它能够有效地拟合一组数据,从而推断出它背后的现象,同时推断出现象的规律。
曲线拟合方法是最常用的无比可以满足实际应用要求的符号方法之一,在实际应用中可以清楚地看到它的优越性。
一、曲线拟合方法的定义曲线拟合方法是一种用来拟合数据的数学方法,即将一组数据拟合到一条曲线上,从而求解出拟合曲线的方程。
一般来说,曲线拟合方法是根据给定的数据集,通过最小二乘法来拟合出曲线的方程,以表述和描述该数据的特征。
曲线拟合方法给我们提供了一种比较直观和有效的数据分析工具,可以有效地发现数据中不同特征之间的关系,从而推断出它们背后的现象及其规律。
二、曲线拟合方法的基本思想曲线拟合方法的基本思想是将一组数据以曲线的形式,以拟合精度最高的方式拟合出曲线的方程。
有多种拟合方法,比如线性拟合、参数拟合、二次拟合、多项式拟合等,可以根据实际的数据特点,选择合适的拟合方法。
拟合方法的最终目的是使拟合曲线越接近原始数据,越接近实际情况,以此来求解出拟合曲线的方程,并且能够有效地反映出数据的规律特征。
三、曲线拟合方法的应用曲线拟合方法在实际工程中被广泛应用,它的应用非常广泛,可以用于各种数据的拟合,其中包括统计学中的数据拟合、物理学中拟合各种非线性函数曲线,以及优化、控制理论中根据给定数据拟合控制参数等。
曲线拟合方法可以有效地发现数据中不同特征之间的关系,从而推断出它们背后的现象,以及它们背后的规律,因此,曲线拟合方法在预测及数据分析中具有重要的作用。
四、曲线拟合方法的优缺点曲线拟合方法的优点在于它的拟合效果好,能够有效地发现数据中不同特征之间的关系,从而推断出它们背后的现象,以及它们背后的规律,因此它可以提供丰富、有价值的数据分析以及预测服务。
但是,曲线拟合方法也有一些缺点,比如它拟合的曲线不一定能够代表实际情况,有可能导致拟合出错误的结果,因此在使用时要注意控制拟合精度。

拟合曲线的拟合曲线是一种数学方法,通过寻找最符合给定数据集的数学模型,以近似描述数据的趋势或规律。
拟合曲线可以用于理解数据的变化趋势、预测未来趋势以及找出数据背后的规律。
常见的拟合曲线方法包括:1.线性拟合(Linear Regression):使用线性模型拟合数据,例如通过最小二乘法找到一条直线,使其在数据点附近误差最小化。
2.多项式拟合(Polynomial Regression):使用多项式函数来拟合数据,可以是二次、三次或更高次的多项式模型,适用于非线性数据。
3.最小二乘法(Least Squares Fitting):一种常用的拟合方法,通过最小化实际观测值和模型预测值之间的误差平方和来找到最佳拟合曲线。
4.非线性拟合(Non-linear Regression):使用非线性模型来拟合数据,例如指数函数、对数函数、高斯函数等,适用于复杂的非线性关系。
5.局部拟合(Local Regression):通过在数据的不同区域内分别拟合局部模型,来更好地适应数据的变化。
拟合曲线的步骤通常包括:●数据收集和准备:收集数据并对数据进行清洗和预处理,确保数据质量和一致性。
●选择模型:根据数据的特征和问题的需求选择合适的拟合模型。
●拟合曲线:使用所选的拟合方法,在数据集上拟合出最优的曲线或模型。
●评估拟合:对拟合模型进行评估,检查模型的拟合程度和预测能力。
●应用和解释:将拟合曲线应用于数据预测、分析趋势或发现数据背后的规律,并进行解释和应用。
拟合曲线是数据分析和建模中常用的技术之一,但在选择模型和解释结果时需要小心谨慎。
不同的拟合方法适用于不同类型的数据和问题,正确选择适合数据特征的模型是非常重要的。
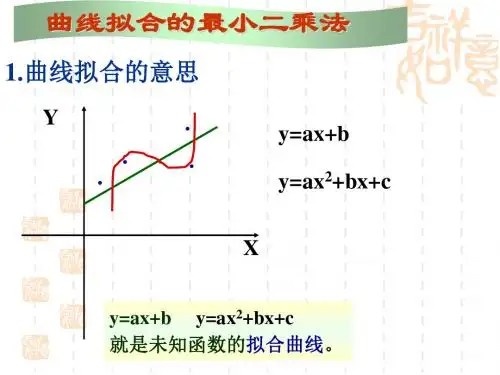

常用的曲线拟合方法常用的曲线拟合方法1. 多项式拟合•多项式拟合是最常见的曲线拟合方法之一,通过使用多项式函数来逼近实际数据的曲线。
•多项式拟合可以使用最小二乘法来确定最佳的拟合曲线。
•多项式拟合的优点是计算简单,易于理解和实现。
•多项式拟合的缺点是容易产生过拟合的问题,特别是在高次多项式的情况下。
2. 线性回归•线性回归是一种拟合直线的方法,适用于线性关系较强的数据。
•线性回归的目标是找到一条直线,使得所有数据点到该直线的距离之和最小。
•线性回归可以使用最小二乘法或者梯度下降法来求解最佳拟合直线。
•线性回归的优点是计算简单,易于解释。
•线性回归的缺点是对非线性关系的数据拟合效果不佳。
3. 指数拟合•指数拟合适用于呈指数增长或者指数衰减的数据。
•指数拟合的目标是找到一个指数函数,使得拟合曲线与实际数据的差异最小。
•指数拟合可以通过最小二乘法来求解最佳拟合曲线。
•指数拟合的优点是适用范围广,可以处理很多不同类型的数据。
•指数拟合的缺点是对于非指数型的数据拟合效果不佳。
4. 对数拟合•对数拟合适用于呈对数增长或者对数衰减的数据。
•对数拟合的目标是找到一个对数函数,使得拟合曲线与实际数据的差异最小。
•对数拟合可以通过最小二乘法来求解最佳拟合曲线。
•对数拟合的优点是适用范围广,可以处理很多不同类型的数据。
•对数拟合的缺点是对于非对数型的数据拟合效果不佳。
5. 非线性拟合•非线性拟合是一种通过使用非线性函数来逼近实际数据的曲线的方法。
•非线性拟合可以使用最小二乘法或者其他优化算法来求解最佳拟合曲线。
•非线性拟合的优点是可以适用于各种形状的数据曲线。
•非线性拟合的缺点是计算复杂度较高,收敛困难。
以上是常用的曲线拟合方法的简要介绍,不同的方法适用于不同类型的数据。
在实际应用中,需要根据数据的特点选取合适的拟合方法来进行数据处理和分析。
6. 平滑拟合•平滑拟合是一种通过平滑算法来逼近实际数据的曲线的方法。
•平滑拟合的目标是去除数据中的噪声和异常值,使得拟合曲线更加平滑。

线性曲线拟合程度计算公式引言。
线性曲线拟合是一种常见的数据分析方法,它可以帮助我们找到数据中的趋势和规律。
在实际应用中,我们经常需要评估线性曲线拟合的程度,以确定拟合是否准确。
本文将介绍线性曲线拟合程度的计算公式,并讨论其在实际应用中的意义和应用。
线性曲线拟合程度计算公式。
线性曲线拟合程度的计算公式通常使用R方值(R-squared)来衡量。
R方值是一个统计量,用于评估拟合模型对观测数据的拟合程度。
它的取值范围在0到1之间,越接近1表示拟合越好,越接近0表示拟合越差。
R方值的计算公式如下:R方 = 1 (Σ(yi ŷi)²) / Σ(yi ȳ)²。
其中,yi表示观测数据的实际值,ŷi表示拟合模型的预测值,ȳ表示观测数据的平均值。
通过计算R方值,我们可以评估拟合模型对观测数据的解释能力,进而确定拟合的程度。
R方值的意义和应用。
R方值是一种常用的拟合程度衡量指标,它在实际应用中具有重要的意义和应用价值。
首先,R方值可以帮助我们评估拟合模型的准确性。
通过比较不同模型的R方值,我们可以确定哪个模型对观测数据的拟合效果更好,从而选择最合适的模型。
其次,R方值还可以帮助我们理解数据的变异性。
当R方值接近1时,说明观测数据的变异性大部分可以由拟合模型解释,反之则说明模型的解释能力较弱。
最后,R方值还可以用于预测模型的可靠性。
当R方值较高时,我们可以认为拟合模型的预测结果比较可靠,反之则需要对模型进行进一步的验证和调整。
实际应用。
线性曲线拟合程度计算公式在实际应用中具有广泛的应用。
例如,在金融领域,我们经常需要对股票价格走势进行拟合分析,以预测未来的价格变化。
通过计算R 方值,我们可以评估拟合模型对股票价格走势的拟合程度,从而确定预测结果的可靠性。
在医学领域,线性曲线拟合也常用于分析药物的剂量-效应关系。
通过计算R方值,我们可以评估拟合模型对药物剂量和效应之间的关系的拟合程度,从而确定最佳的用药方案。

拟合曲线的方法(一)拟合曲线拟合曲线是一种数据分析方法,用于找到最符合给定数据的函数曲线。
在实际应用中,拟合曲线广泛应用于计算机图形学、统计学和机器学习等领域。
不同的方法可以应用于不同类型的数据和问题,下面将介绍几种常见的拟合曲线方法。
线性拟合线性拟合是最简单也是最常见的拟合曲线方法之一。
其基本思想是通过一条直线来拟合数据点。
线性拟合常用于描述两个变量之间的线性关系。
线性拟合的数学模型可以表示为:y=a+bx,其中y是因变量,x是自变量,a是截距,b是斜率。
线性拟合的目标是通过最小化实际数据点和拟合直线之间的误差来确定最佳的a和b。
多项式拟合多项式拟合是一种通过多项式函数来拟合数据点的方法。
多项式函数是由多个幂函数组成的函数,可以适应各种形状的数据。
多项式拟合的数学模型可以表示为:y=a0+a1x+a2x2+⋯+a n x n,其中y是因变量,x是自变量,a0,a1,…,a n是拟合函数的系数。
多项式拟合的目标是通过最小化实际数据点和拟合曲线之间的误差来确定最佳的系数。
曲线拟合曲线拟合是一种通过曲线函数来拟合数据点的方法。
曲线函数可以是任意形状的函数,可以适应各种复杂的数据。
常见的曲线拟合方法包括:贝塞尔曲线拟合贝塞尔曲线拟合是一种用于拟合平滑曲线的方法。
贝塞尔曲线由控制点和节点构成,通过调整控制点的位置来改变曲线的形状。
贝塞尔曲线拟合的目标是通过最小化实际数据点和贝塞尔曲线之间的误差来确定最佳的控制点和节点。
样条曲线拟合样条曲线拟合是一种用于拟合光滑曲线的方法。
样条曲线由多个局部曲线段组成,每个曲线段由一组控制点和节点定义。
样条曲线拟合的目标是通过最小化实际数据点和样条曲线之间的误差来确定最佳的控制点和节点。
非线性拟合非线性拟合是一种用于拟合非线性关系的方法。
非线性关系在现实世界中很常见,例如指数函数、对数函数等。
非线性拟合的数学模型可以表示为:y=f(x,θ),其中y是因变量,x是自变量,θ是模型的参数。

曲线拟合的实用方法与原理曲线拟合是一种常用的数据分析方法,它可以通过寻找最佳拟合曲线来描述一组数据的趋势和关系。
在科学研究、工程技术、金融分析等领域中,曲线拟合被广泛应用于数据模型的建立、预测和优化等方面。
本文将介绍曲线拟合的实用方法和原理,帮助读者更好地理解和运用这一分析工具。
一、曲线拟合的基本概念曲线拟合是指通过一组已知数据点,寻找一条函数曲线来逼近这些数据点的过程。
拟合曲线的选择通常基于拟合误差最小化的原则,即找到一条曲线,使得它与实际数据点之间的误差最小。
二、常见的曲线拟合方法1. 最小二乘法最小二乘法是一种常见的曲线拟合方法,它通过最小化拟合曲线与实际数据点之间的残差平方和来确定最佳拟合曲线。
最小二乘法在实际应用中较为简单和灵活,能够拟合各种类型的曲线,如线性曲线、多项式曲线、指数曲线等。
2. 多项式拟合多项式拟合是一种通过多项式函数来拟合数据点的方法。
它可以通过最小二乘法来确定多项式的系数,从而得到最佳拟合曲线。
多项式拟合可以适用于不同阶数的多项式,阶数越高,拟合曲线越复杂,能够更好地逼近实际数据。
3. 曲线拟合工具除了最小二乘法和多项式拟合外,还有一些专门的曲线拟合工具可供使用。
例如,MATLAB和Python中的Scipy库提供了丰富的曲线拟合函数,可以根据实际需求选择合适的拟合方法和工具。
三、曲线拟合的实际应用曲线拟合在各个领域都有广泛的应用。
以下是几个典型的实际应用案例:1. 经济数据分析曲线拟合可以用于分析经济数据的趋势和关系。
例如,通过对历史GDP数据进行曲线拟合,可以预测未来的经济增长趋势,为政策制定和投资决策提供参考。
2. 工程建模在工程领域,曲线拟合可以用于建立物理模型和优化设计。
例如,通过对实验数据进行曲线拟合,可以得到物质的力学性质曲线,从而优化材料的设计和使用。
3. 股票价格预测曲线拟合可以用于股票价格的预测和交易策略的制定。
通过对历史股票价格数据进行曲线拟合,可以找到潜在的趋势和周期性,从而为投资者提供决策依据。
拟合曲线的方法
拟合曲线是一种数据分析方法,用于找到最适合描述数据的数学函数或曲线。
这种方法主要用于通过已知数据点来估计未知数据点的数值。
在拟合曲线的过程中,有几种常见的方法可以使用。
下面是其中一些常见的方法:
1. 最小二乘法:最小二乘法是一种常见的拟合曲线方法,其目标是通过最小化观测数据点与拟合曲线之间的误差来找到最佳拟合曲线。
这种方法可以应用于线性和非线性函数。
2. 多项式拟合:多项式拟合是一种通过多项式函数来拟合数据的方法。
它通常用于拟合曲线比较平滑的数据集。
多项式拟合方法可以根据数据的复杂度选择合适的多项式阶数,例如线性、二次、三次等。
3. 样条插值:样条插值是一种通过多个分段多项式函数来拟合数据的方法。
这种方法通过将数据集划分为多个小段,并在每个小段上拟合一个多项式函数,从而得到整体的曲线拟合。
4. 非参数拟合:非参数拟合是一种不依赖于特定函数形式的拟合曲线方法。
这种方法主要通过使用核函数或直方图等技术来估计数据的概率密度函数,并从中得到拟合曲线。
总体而言,选择合适的拟合曲线方法取决于数据的特征和对拟合结果的要求。
需要根据数据的分布、噪声水平和所需精度等因素来选择合适的方法。
此外,还可以使用交叉验证等技术来评估拟合曲线的质量,并选择最佳的拟合曲线模型。
名词解释曲线的拟合曲线的拟合是指通过一组已知的离散数据点,找到与这些数据点最匹配的数学函数曲线的过程。
它在许多领域有着广泛的应用,包括数学建模、统计学、机器学习和工程等。
曲线的拟合可以帮助我们理解数据之间的关系、预测未知数据点的值,以及寻找隐含在数据背后的规律和趋势。
在进行曲线的拟合之前,我们首先需要明确所使用的数据点以及期望的拟合函数类型。
常见的拟合函数包括线性函数、多项式函数、指数函数、对数函数等。
其中最简单的情况就是拟合一条直线,被称为线性回归。
而如果拟合的函数是一个高次的多项式,就被称为多项式拟合。
在实际应用中,我们根据数据的特点和需求选择合适的拟合函数类型。
曲线的拟合的关键在于确定拟合参数的取值,使得拟合函数与实际数据点尽可能地吻合。
我们使用拟合误差来衡量拟合的好坏。
拟合误差通常使用最小二乘法来计算,即将实际数据点到拟合函数曲线的距离平方求和最小化。
最小二乘法的优势在于能够将拟合误差平方化,避免正负误差相互抵消的情况产生。
在进行曲线的拟合过程中,我们可以使用一些常见的数学工具和算法。
例如,最小二乘法可以通过解线性方程组或最优化算法来求解最优拟合参数。
而在多项式拟合中,常常使用最小二乘多项式拟合,将实际数据点与多项式函数进行匹配。
此外,还有一些高级的拟合技术,如样条插值、非线性回归和神经网络等,可以在特定情况下提供更加精确和灵活的拟合结果。
曲线的拟合不仅仅是数学方法的应用,更是一门艺术。
在实际拟合过程中,我们需要不断地调整参数和拟合函数的选择,以寻找到最佳的拟合解。
拟合结果的质量取决于多个因素,包括数据的质量、调整参数的准确性,以及拟合函数的合理性等。
因此,拟合过程往往是一个经验丰富和反复试验的过程。
曲线的拟合还涉及到一些限制和问题。
例如,过度拟合是指拟合函数与实际数据点过于吻合,导致对未知数据的预测效果不佳。
解决过度拟合的方法之一是正则化,通过在拟合过程中引入惩罚项来控制模型参数的大小。
excel拟合曲线公式
Excel提供了多种曲线拟合函数,可以根据不同的数据和需求选择适合的函数。
以下是一些常见的曲线拟合函数及其应用:
1.线性拟合(一次多项式):使用最小二乘法拟合一条直线。
函数形式:y = mx + b Excel函数:LI NEST、SLOPE、INTERCEPT
2.多项式拟合(高次多项式):使用最小二乘法拟合一条曲线。
函数形式:y = m1x^n + m2x^(n-1) + ... + mn-1*x + mn Excel函数:LINEST
3.对数拟合:将数据点拟合到一个对数函数曲线上,适用于呈现指数增长或衰减的数据。
函数形式:y = a*ln(x) + b Excel函数:LINEST
4.幂函数拟合:将数据点拟合到一个幂函数曲线上,适用于呈现幂次关系的数据。
函数形式:y = a* x^b Excel函数:LINEST
5.指数拟合:将数据点拟合到一个指数函数曲线上,适用于呈现指数增长或衰减的数据。
函数形式:y = aexp(bx) Excel函数:LINEST
6.正弦拟合:将数据点拟合到一个正弦函数曲线上,适用于呈现周期性变化的数据。
函数形式:y = asin(bx + c) Excel函数:LINEST
要进行曲线拟合,你可以使用Excel提供的数据分析工具或自带的函数,如"LINEST"函数。
使用这些函数可以计算拟合系数并生成拟合曲线。
请注意,拟合的准确性和适用性取决于数据本身和所选择的拟合函数。
同时,可以利用Excel的图表功能来可视化拟合曲线,并通过调整拟合的参数来优化曲线的拟合效果。
拟合曲线算法
拟合曲线算法是一种在平面上用连续曲线近似描述离散数据点之间函数关系的方法。
它可以用于分析和预测数据,从而在科学、工程和数学等领域解决一系列问题。
拟合曲线算法主要包括以下几种:
1.线性拟合:通过最小化误差平方和,找到一条直线或多项式,使得这条直线或多项式与数据点之间的误差最小。
线性拟合常用的工具有最小二乘法、多项式拟合等。
2.非线性拟合:对于非线性数据关系,可以采用非线性函数拟合方法。
常见的非线性拟合算法有:多项式拟合、指数拟合、对数拟合、贝塞尔基函数拟合等。
3.曲线拟合:通过寻找一个连续的函数来近似描述数据点之间的关系。
曲线拟合可以分为一线性曲线拟合和非线性曲线拟合。
线性曲线拟合通常采用最小二乘法,非线性曲线拟合可以采用de Boor算法、Navier-Stokes算法等。
4.插值拟合:插值拟合是通过在数据点之间插入新的点,然后用一个连续的函数来描述这些点之间的关系。
常见的插值方法有拉格朗日插值、牛顿插值、三次样条插值等。
5.优化算法:在拟合曲线过程中,可以使用优化算法来寻找最优的拟合参数。
常见的优化算法有梯度下降、牛顿法、拟牛顿法、信赖域反射算法等。
总的来说,拟合曲线算法是一种通过寻找一个数学函数来描述数据点之间关系的方法,可以根据实际问题和数据特点选择合适的拟合算法。
在实际应用中,曲线拟合算法可以帮助我们更好地理解数据,预测趋势,并为决策提供依据。
在线曲线拟合(最小二乘法)一、简介在线曲线拟合,也被称为最小二乘法,是一种常用的数学优化技术,主要用于数据分析和预测。
通过最小化预测值与实际观测值之间的平方差,找到最佳拟合曲线的参数。
这种方法在各个领域都有广泛的应用,例如经济预测、科学实验数据分析、金融市场分析等。
二、基本原理在线曲线拟合的基本原理是通过最小化预测值与实际观测值之间的平方差和,找到最佳拟合曲线的参数。
具体来说,假设我们有一组数据点(x1, y1), (x2, y2), ..., (xn, yn),我们要找到一条曲线y = f(x),使得这些数据点与曲线之间的偏差最小。
偏差通常用平方差来度量,即∑(yi - f(xi))^2。
我们的目标是找到一组参数,使得这个偏差最小。
三、实现步骤在线曲线拟合的实现步骤如下:1. 收集数据:首先需要收集用于拟合的数据。
这些数据通常是一组观测值,可以是一维或多维的。
2. 设定模型:选择一个合适的数学模型,用于描述数据的内在规律。
模型通常是一条曲线,可以是一次函数、二次函数、指数函数等。
3. 计算偏差:计算每个数据点到拟合曲线的偏差,通常用平方差来度量。
偏差的计算方法取决于所选择的模型和数据点的具体形式。
4. 最小化偏差:通过迭代或优化算法,找到一组参数,使得偏差最小。
这一步通常需要使用数学优化技术,例如梯度下降法、牛顿法等。
5. 评估拟合效果:最后,需要对拟合结果进行评估。
可以通过计算残差、R方值等指标来衡量拟合效果的好坏。
如果拟合效果不理想,可能需要重新设定模型或收集更多的数据。
四、应用示例在线曲线拟合的应用非常广泛,下面举一个简单的例子来说明其应用。
假设我们有一组销售数据,想要通过这些数据来预测未来的销售趋势。
我们可以选择一条线性模型y = ax + b,其中a 和b 是待求解的参数。
通过最小化预测值与实际观测值之间的平方差和,我们可以找到最佳拟合曲线的参数a 和b。
最后,我们可以用这些参数来预测未来的销售趋势。
一种分段曲线拟合方法研究摘要:分段曲线拟合是一种常用的数据处理方法,但在分段点处往往不能满足连续与光滑.针对这一问题,本文给出了一种能使分段点处连续的方法.该方法首先利用分段曲线拟合对数据进行处理;然后在相邻两段曲线采用两点三次Hermite插值的方法,构造一条连结两条分段曲线的插值曲线,从而使分段点处满足一阶连续.最后通过几个实例表明该方法简单、实用、效果较好.关键词:分段曲线拟合Hermite插值分段点连续Study on A Method of Sub-Curve FittingAbstract:Sub-curve fitting is a commonly used processing method of data, but at sub-points it often does not meet the continuation and smooth, in allusion to to solve this problem, this paper presents a way for making sub-point method continuous. Firstly, this method of sub-curve fitting deals with the data; and then uses the way of t wo points’ cubic Hermite interpolation in the adjacent, structures a interpolation curve that links the two sub-curves, so the sub-point meets first-order continuation; lastly, gives several examples shows that this method is simple, practical and effective.Key words:sub-curve fitting Hermite interpolation sub-point continuous前言数据拟合是一种重要的数据处理方法,其中最常用的是多项式曲线拟合.然而当数据点较多时,多项式阶数太低,拟合精度和效果不太理想,要提高拟合精度和效果就需要提高曲线阶数,但阶数太高又带来计算上的复杂性及其他方面的不利.因此,如果只采用一种多项式曲线函数拟合较多的数据点,难以取得较好的拟合精度和效果.为有效地解决上述问题,一般采用分段曲线拟合.以往的分段曲线拟合方法主要是针对在自然科学领域中测量的数据而使用的拟合方法,这些数据的变化一般都遵循一定的规律.因此,在对这些测量数据拟合时,传统的分段曲线拟合方法一般是先根据主观经验对数据分段, 然后进行拟合.但是对于有些实际问题的数据,比如社会、经济生活中的大量统计数据,这些数据变化的机理一般非常复杂,往往不像物理定律那样有着严格的规律,所以变化的不确定性很强.因此,传统的分段曲线拟合根据主观经验对数据进行分段的做法就显现出明显地不足.针对这种不足,国内外许多文献也讨论过,文献[1]研究的是最小二乘法在曲线拟合中的实现,给出了最小二乘法在多元正交基函数拟合中的计算机实现方法,以常见的二次曲线拟合为例说明了程序编制的要点,在实验的数据处理中具有实用价值;文献[2]讨论分段最小二乘曲线拟合方法,本文在一般最小二乘的基础上提出分段最小二乘曲线拟合的方案,讨论了连接分段拟合曲线的方法,并且给出分段最小二乘多项式拟合的计算方法;文献[4]主要介绍基于最小二乘原理的分段曲线拟合法,在最小二乘的基础上,运用实测数据点的分段曲线拟合法,探讨相应的模型以及用不同类型的曲线拟合同时拟合数据点的具体应用,对一实例,应用MATLAB编程设计,完成模型的求解、显著性检验等,可以得到拟合精度比较高的拟合曲线,该方法原理简便,其模型易用MATLAB编程求解;文献[5]研究的是基于最小二乘法的分段三次曲线拟合方法研究,多项式曲线拟合是一种较常用的数据处理方法,但当数据点较多时,只采用一种多项式曲线函数拟合所有数据点难以得到较好的拟合效果,针对传统分段曲线拟合方法中对数据点分段时经验成分较多的不足,提出了一种基于最小二乘法原理的分段三次曲线拟合方法,建立三次拟合曲线方程,通过实际数据的检验,验证了该方法的拟合效果;文献[6,7,8]主要研究基于分段三次曲线拟合的广州周发案量预测,随着城市化进程的不断加快,城市人口不断增多,广州市未来治安形势预警,支持政府部门和政法部门关于治安工作的决策,首先需要对未来时期的发案量做出比较精确的预测,由于目前广州市方案量统计数据比较少,且发案量受农历春节影响较明显,针对传统时间序列预测方法在此情况下应用不足,提出了基于分段三次曲线拟合的周发案量预测模型,并给出了具体的建模、计算步骤,最后通过实际数据的检验,证明了方法预测效果较好;文献[9]提出了分段函数的光滑方法及其在曲线拟合中的应用,在分析复杂实验数据时,采用分段曲线拟合方法,利用此方法在段内可以实现最佳逼近,但在段边界上却可能不满足连续性与可导性.为了克服这种现象,本文主要研究一种能使段边界连续的方法,具有一定的理论和实际意义.在前人的基础上,本文总结分段曲线拟合的方法与步骤,介绍了分段三次曲线的拟合方法和两点三次Hermite插值,然后讨论如何利用Hermite插值方法使得分段拟合曲线在连接点处满足连续方法,最后通过一些实例应用,表明本文所介绍的方法具有一定的应用价值.1 最小二乘曲线拟合1.1 最小二乘法[1]令待求的未知量为12,,,t a a a ,它们可由()n n t ≥个直接测量12,,,n y y y 通过下列函数关系求得:11122212331212(,,,)(,,,)(,,,)(,,,)t t t n n t y f a a a y f a a a y f a a a y f a a a ====若j a 为真值,由上述已知函数求出真值j y ,若其测量值为*j y ,则对应的误差为*,(1,2,)j j j y y j n σ=-= .最小二乘法可定量表示为:21min njj σ==∑ (1.1.1)对不等精度的测量,应加上各测量值的权重因子j p ,即:21min nj jj p σ==∑ (1.1.2)最小二乘法是在随机误差为正态分布时,由最大似然法推出的这个结论.它可使测量误差的平方和最小,因此被视为从一组测量值中求出一组未知量的最可信赖的方法.1.2 最小二乘多项式曲线拟合的基本原理[2]1.2.1 线性拟合原理将拟合函数取线性函数是一种简单的数据拟合方法,将数据点1122(,()),(,()),,(,())m m x f x x f x x f x确定线性拟合函数()x a bx ϕ=+ (1.2.1.1) 称为对数据的线性拟合。
对于线性拟合问题,需要求函数2(,)1[()]ma b k k k S a b x y ==+-∑ (1.2.1.2) 的最小值点,该问题的几何背景是寻求一条直线,使该直线与数据表所确定的平面散点的纵向距离的平方和最小,如图1.2.1-1所示.(图1.2.1-1)由函数对两个变量求导得:12[()],mk k k Sa bx y a =∂=+-∂∑(1.2.1.3) 12[()],mk k k k Sa b x y x b =∂=+-∂∑ (1.2.1.4)其余等于零,得正规方程组112111,m mk k k k m m mk k k k k k k ma x b y x a x b x y =====⎧+=⎪⎪⎨⎪+=⎪⎩∑∑∑∑∑ (1.2.1.5) 也可将其矩阵形式写出来即:112111mm k k k k m m m i k k k k k k m x y a b x x x y =====⎛⎫⎛⎫ ⎪ ⎪⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭ ⎪ ⎪⎝⎭⎝⎭∑∑∑∑∑ 解得,a b 的值,将其代入(1.2.1.1)即可得到拟合线性函数. 1.2.2 多项式拟合原理为了确定数据拟合问题,选用幂函数2{1,,,}n x x x 作为函数类,则2012()nn x a a x a x a x ϕ=++++ (1)n m +< (1.2.2.1)这就是多项式拟合函数.为了确定拟合函数2012()n n x a a x a x a x ϕ=++++ 的系数,需要求解正规方程组011112101111112011111m m mnk k n kk k k m m m mn k k k n k k k k k k m m m mn n n n k k k n k kk k k k ma x a x a y x a x a x a x y x a x a x a x y ===+====+====⎧+++=⎪⎪⎪+++=⎪⎨⎪⎪⎪+++=⎪⎩∑∑∑∑∑∑∑∑∑∑∑ (1.2.2.2) 也可以用矩阵形式表示为11102111111121111m mm n k k k k k k m m m m n k k k k k k k k k n m m mm n n n n k k k k k k k k k m x x y a x x x x y a a x x x x y ===+====+====⎛⎫⎛⎫ ⎪ ⎪⎪ ⎪⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭∑∑∑∑∑∑∑∑∑∑∑ 解得01,,,n a a a 即可,将其代入(1.2.2.1)即可得到拟合多项式.2 分段曲线拟合2.1 分段曲线拟合的基本原理[3]先根据实测数据分布的特点,确定分段数目以及相应拟合曲线类型.拟合函数一般可选为多项式函数,因为在一定范围内,连续函数可用多项式任意逼近,然后再应用最小二乘法原理求得各分段拟合方程的系数.基本步骤为:第一步:将数据点分段,确定基函数01(),(),,()n x x x ϕϕϕ , 第二步:根据题目要求,建立正规方程组, 第三步:解正规方程组,求出待定系数, 第四步:写出拟合函数.下面以分段线性拟合与分段三次曲线拟合为例讨论分段拟合的基本过程. 2.1.1 分段线性拟合我们把给出的数据点分成k 组12,,,k N N N ,即1122***1111121211***2121222222***1122(,),(,),,(,)(,),(,),,(,)(,),(,),(,)k k N N N N k k k k kN kN x y x y x y x y x y x y x y x y x y其中12,,,k N N N 为每组数据的个数.首先考虑线性拟合这种简单的情形,对k 组数据点分别应用最小二乘线性拟合,得到各组数据点所对应的近似线性函数,111()g x a b x =+ 1111()N x x x ≤<222()g x a b x =+ 1212()N N x x x ≤<()k k k g x a b x =+ 11()k k k N kN x x x --≤≤而在整个考虑的拟合区间上就得到了1k -条直线段,现在就这1k -条直线段所在各区间的左端点定义1()()i i i iN i iN g x g x +=,该函数就成为整个区间上的数据拟合函数.这就是分段最小二乘线性拟合问题.然而有些数据组并不是每段都呈线性关系,如数据(,)1,2,,i i x y i n = ,根据其散点图却发现其前m 个点较接近直线,后n m -个点呈现非线性关系,则可分两段拟合.分别以一次多项式1Y 和n 次多项式2Y 进行拟合,即1Y kx b =+ (2.1.1.1) 为了说明具体的方法,不妨选2Y 的阶数为2,即22012Y a x a x a =++ (2.1.1.2) 要保证在边界点(,)m m x y 连续光滑,所以存在两个约束条件2012m m m kx b a x a x a +=++和012m k a x a =+,因此,式(2.1.1.1)和(2.1.1.2)的系数是相关的.解得220m b a a x =-,故式(2.1.1.1)为210102(2)m m Y a x a x a x a =+-+令S 为最小二乘估计量,则2222012001211[(2)]()mnm i mi i i i i i m S a x a x a a x y a xa x a y ==+=++--+++-∑∑通过模型0iSa ∂=∂;0,1,2i =,可求得最小方差S 的012,,a a a 的值,从而确定出式(2.1.1.1)与(2.1.1.2)中的回归系数.最后,通过r =和F 检验值22(2)1n r F r -=-,对回归方程进行显著性检验,式中11ni i y y n ==∑;210102(2)i m i m Y a x a x a x a=+-+;22012i i Y a x a x a =++. 当然,根据不同的数据,可分三段进行拟合,或根据不同的数据特点,采用多次曲线拟合方式.2.1.2 分段三次曲线拟合[4,5]设有N 个数据123,,,N Z Z Z Z .因为四个数据点可确定一条三次曲线,但在选取分段点时,必须考虑分段后相邻曲线必须连续,即边界点连续,因此用五个数据点拟合一条三次曲线.拟合方法:首先对数据进行一定的分段,将第一到第五数据分为第一段,再将第五到第九个数据分为第二段,将第九到第十三个数据分为第三段,依次类推进行分组,即前一段末尾的数据为下一段数据的首位,这样便保证了数据分段的连续性.然后再对个分段数据进行三次曲线拟合即可.令某段数据的三次拟合曲线函数为:23(2,1,0,1,2)t w a bt ct dt t =+++=--可以将此曲线函数分解为奇偶两个函数:奇函数3t v bt dt =+和偶函数2t u a ct =+.下面应用最小二乘法的基本原理求三次拟合曲线的系数[6],由于在每段数据中第一点和最后一点均两次参与拟合,因此,在求一段曲线的拟合方差时需要加权.按照平均分配的原则[7],求方差的权值2212λλ-==,1011λλλ-===,得到该段曲线拟合的方差2222()t t t t S w Z λ=-=-∑ (2.1.2.1)曲线表示为奇偶函数的形式如下,,t t t t t t t w u v u u v v --=+==- (2.1.2.2) 由(2.1.2.2)可以推导出下式11(),()22t t t t t t u w w v w w --=+=- (2.1.2.3)令,,t t t t t t t Z x y x x y y --=+==-则11(),()22t t t t t t x Z Z y Z Z --=+=- (2.1.2.4)因此拟合方差为222222222222222()() ()() t t t t t t t t t t t t t t t t t t S w Z u v x y u x v y S S λλλλ=-=-=-=-=-=+--=-+-=+∑∑∑∑奇偶(2.1.2.5)即t w 对t Z 的平滑可以看作是奇函数和偶函数分别平滑的叠加.从(2.1.2.5)式中可知奇函数拟合的方差.222223212212() 2() 2()(28)t t t t tt t S x y bt dty b d y b d y λλ=-=-=-=--=+-++-∑∑奇(2.1.2.6)令120280b d y b d y +-=⎧⎨+-=⎩, 解出2112(2)6(8)6b y y d y y =-⎧⎨=-⎩. 因此0S =奇,即奇函数的拟合方差为0,达到最佳逼近.同样,从(2.1.2.5)式中可知偶函数拟合方差为2222220122()()2()(4)t t t t Su x a x a c x a c xλ=-=-=-++-++-∑偶(2.1.2.7) 由(2.1.2.3)式得知在边界点上2221()42u w w a c -=+=+. 考虑到边界点连续这一约束条件,令4e a c =+ (2.3.2.8)因此由式(2.3.2.7)可令2222212012201(4)()2()31()2()44S S a c x a x a c x a x a e x =-+-=-++-=-++-偶 (2.1.2.9) 解令210S a∂=∂,有01312()3()044a x a e x -++-=,得 10(1283)17a x x e =+- (2.1.2.10)从(2.1.2.10)式可知三次曲线函数的系数,a c 的取值与边界点值有关,将(2.1.2.10)式代入(2.1.2.9)式中可得222222122011(4)()(34)17S S a c x S e x x e x =-+-=--=+-偶偶 .所以得出2222011()(34)17S e x x e x =-++-偶,再令20S e∂=∂偶,有20122()(34)017e x x e x -++-=,解得102431718x x x e -+=. (2.1.2.11)联立式(2.1.2.8)、式(2.1.2.10)、式(2.1.2.11),解得012(34)6a x x x =+-012(325)18c x x x =--+最后得到三次拟合曲线表达式为230120122112(34)(325)(2)(8)66186t x x x x x x y y y y w t t t+---+--=+++.3 基于两点三次Hermite 插值的分段曲线拟合3.1 插值的定义定义3.1.1[9] 设函数()y f x =在区间[,]a b 上有定义,且已知在点012n a x x x x b ≤<<<<≤ 处的函数值(),(0,1,2,,)j j y f x j n == ,若存在n 次多项式2012()n n n p x a a x a x a x =++++ (3.1.1) 使得(),(0,1,2,,)n j j p x y j n == (3.1.2) 成立,则称()n p x 为()f x 的插值多项式,012,,,,n x x x x 为插值结点,()f x 为插值函数.3.2 Hermite 插值方法Hermite 插值方法可以处理插值条件中合导数值的插值问题,即知道插值结点处的函数值以及导数值,求插值多项式的插值问题. 3.2.1 三次Hermite 插值考虑两个插值结点的情形,设01a x x b ≤<≤,函数()[,]f x c a b '∈且已知00110011(),(),(),()f x y f x y f x m f x m ''====, 在区间[,]a b 上求三次插值函数230123()H x a a x a x a x =+++ (3.2.1.1) 使其满足插值条件(),(),(0,j j j j H x y H x m j '===. (3.2.1.2)定理3.2.1.1[9] 满足插值条件(3.2.1.2)的三次Hermite 插值多项式是存在且唯一的.证明:由插值条件得线性方程组2300000231111122000231111101230123a y x x x a y x x x a m x x a m x x ⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪ ⎪⎪ ⎪= ⎪⎪ ⎪ ⎪⎪⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ (3.2.1.3)考虑系数矩阵行列式,利用行列式的拉普拉斯展开定理,可得230002341111020021111()01230123x x x x x x x x x x x x =-- (3.2.1.4) 故系数矩阵非奇异,线性方程组(3.1.2.3)有唯一解,从而三次多项式存在且唯一.例 1 求满足插值条件0011()1,()0,()0,()0x x x x αααα''====的三次插值多项式()x α,以及满足插值条件0101()0,()0,()1,()0x x x x ββββ''====的三次插值多项式()x β.解:由于1x 是三次多项式()x α的二重零点,故可设2121)()()(x c x x x c α+-=由插值条件00)1,()0(x x αα'==得210201)()1(x c x x c +-=, 210110201()2()()0x x c x c x x c -++-=求解得012323010101221,()()()x c x x x x x x c =-=+--- 代入2121)()()(x c x x x c α+-=整理得2011010)()()(12x x x x x x x x x α----=+ 现求()x β,由于1x 是三次多项式()x β的二重零点,0x 是一重零点,故可设201)()()(x x x c x x β-=-由插值条件0()1x β='得2010001)2()()]1[(x x x x x c x -+--=求解得2101()x x c -=所以21010)()()(x x x x x x x β--=- 注:例题中的两个特殊的插值函数实际上是两点Hermite 插值的基函数.定理3.2.1.2[9] 两点Hermite 插值函数可以用基函数的方法表示为00110011()()()()()x y x m x m x H x y ααββ+++=,01,][x x x ∈ (3.2.1.5)其中2010101020111010210010201110()(12)()()(12)()()()()()()()x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x αββα--=+----=+---=---=--注:定理3.2.1.2中的0101(),(),(),()x x x x αββα为Hermite 插值基函数,其中1 () ()00 i j i j i jx x i j αβ=⎧==⎨≠⎩;1 () ()00i j i j i jx x i j βα=⎧''==⎨≠⎩例2 给定(1)0,(1)4,(1)2,(1)0f f f f ''-==-==,求Hermite 插值多项式. 解:30101()0()4()2()0()H x h x h x g x g x =+++. 显然本题不必计算01(),()h x g x .221(1)(1)()12(2)(1)4111(1)x x h x x x ⎛⎫---⎛⎫=+=-+⎪ ⎪----⎝⎭⎝⎭ 2201()((1))(1)(1)411x g x x x x -⎛⎫=--=+- ⎪--⎝⎭310()4()2()H x h x g x =+2231()(2)(1)(1)(1)2H x x x x x =-+++-3.3 基于Hermite 插值的分段曲线拟合基本原理的主要步骤第一步:根据给出的数据做出其散点图,第二步:分析散点图的特点,通过拟合试验确定分段拟合函数, 第三步:采用MATLAB 编程求得分段拟合函数的表达式, 第四步:利用Hermite 插值求出分段边界点的插值多项式, 第五步:将插值多项式与分段拟合函数连接成连续的拟合曲线.4 实例应用例3 在农业生产试验研究中,对某地区土豆的产量与化肥的关系做了一实验, 得到磷肥的施肥量与土豆产量的对应关系如表4-1所示.根据上表的数据给出土豆产量与磷肥的关系做出其散点图,如图4-1所示.土豆产量(公斤)051015202530354045050100150200250300350400土豆产量(公斤)图4-1磷肥的施肥量与土豆产量对应关系的散点图从图可看出从 0 到 98、从 98 到 342 之间分别呈明显的线性关系, 由此可选取所求拟合函数为一分段的线性函数作拟合试验,换言之,用前 5 点作一线性拟合函数,再用后 5个点也作一线性拟合函数.采用MATLAB 编程(见附录1)求得,对磷肥的分段拟合函数0.084432.07710.009039.1303x y x +⎧=⎨+⎩分段拟合图如图4-2所示.图4-2磷肥的施肥量与土豆产量分段拟合曲线图考虑到边界点不连续,采用两点三次Hermite 插值使边界点连续的方法,由于(98)40.3483,(147)40.4533,(98)0.0844,(147)0.0090y y y y ''====,故可以设其Hermite 插值多项式为30101()40.3483()40.4533()0.0844()0.0090()H x h x h x g x g x =+++经计算得2232240.3483(147)(2147)40.4533(98)(3432)()1176490.0844(147)(98)0.0090(98)(147)2401x x x x H x x x x x --+--=--+--+即323()0.00003711550.0144093294 1.839257142936.444499972H x x x x =-+- 将插值多项式与分段边界点连接便可以得到连续的拟合曲线图,达到较好的拟合效果. 拟合曲线图如图4-3所示(程序见附录2).图4-3磷肥的施肥量与土豆产量的Hermite 插值分段拟合曲线图例4 弹簧受力F 的作用伸长x ,F 与x 在一定范围内服从虎克定律:F kx =(x 为弹性系数),呈线性关系;但当F 增加到一定值后,不再服从虎克定律.一次试验测得的数据如表4-2所示,其散点图如图4-4所示.x (cm) 1 3 5 7 9 11 12 14 16 18 F (N)1.95.38.612.115.716.819.220.721.421.8图4-4弹簧受力与伸长量的关系的散点图通过散点图先拟合试验,得出前5个点可用线性拟合,后5个点可作二次函数拟合;同样采用分段拟合的方法,方法同例3(可设211221202,y kx b y a a x a x =+=++).运行程序(见附录3)可得0120.1350; 4.5518;16.5508; 1.7200;0.1200a a a k b =-==-==.同样将拟合函数的边界点采用两点三次Hermite 插值.由(9)15.6000,(11)17.1840,(9) 1.7200,(11) 1.5818y y y y ''====,采用MATLAB 编程(见附录4)求得插值多项式为3230.429449999999999712.91805000000000129.8885499999999 420.1039499999994H x x x=-+-再用插值多项式连接分段拟合曲线的边界点便可得到较好的拟合图形,拟合曲线如图4-5所示(程序见附录5).图4-5弹簧受力与伸长量的Hermite 插值分段拟合曲线图例5 在油页高温分解的过程中,一种苯有机分解成沥青及其他物质,要了解沥青在一定温度下随时间t (分钟)变化的相对浓度y (%)之间的关系.试验如表4-3所示,散点图如图4-6所示.图4-6沥青的相对浓度与时间变化的关系的散点图同样通过散点图先作拟合试验,得出前5个点可采用三次多项式拟合,后5个点可采用二次多项式拟合,可设分段拟合函数为32211121314212223,y a x a x a x a y b x b x b =+++=++ 运行程序(见附录6)得出12341230.0002;0.0285; 1.5456;7.44910.0013;0.1747;16.2750a a a ab b b ==-==-=-== 再将拟合函数的边界点采用两点三次Hermite 插值,由(65)20.4974,(80)22.2531,(65)0.3756,(80)0.3827y y y y ''====采用MATLAB 编程(见附录7)计算求得插值多项式为3230.0023298074074074070.506496444444444036.68982888888888 864.2173592592588H x x x=-+-将插值多项式连接分段拟合曲线的边界点后得到的拟合曲线图,拟合曲线见图4-7(程序见附录8).图4-7沥青的相对浓度与时间变化的关系的Hermite插值分段拟合图5 结束语本文介绍最小二乘多项式曲线拟合的基本原理,在具体介绍线性拟合、多项式拟合的基本及方法的基础上,给出了分段曲线拟合的方法与步骤.分段曲线拟合是一种常用的数据处理方法,但是在分段点处往往不能满足连续与光滑,针对这一问题,本文进一步给出了Hermite插值的基本原理,并采用两点三次Hermite插值连接分段曲线,从而使分段点处满足一阶连续,最后通过三个实例表明该方法的拟合效果较好.另外,本文仅讨论了使用Hermite插值连接分段线性、分段多项式曲线拟合的方法,对其他种类的曲线未作讨论.事实上,两点三次Hermite插值的方法连接其他种类的拟合曲线同样适用.参考文献[1] 聂翔, 张瑞林. 最小二乘法在曲线拟合中的实现[J]. 陕西工学院学报, 2000, 3: 79-82.[2] 张东林. 分段最小二乘曲线拟合[J]. 沈阳大学学报(自然科学版), 1994, 2: 80-83.[3] 刘晓莉, 陈春梅. 基于最小二乘原理的分段曲线拟合法[J]. 伊犁教育学院学报, 2004, 17(3):131-136.[4] 蔡山, 张浩, 陈洪辉, 等. 基于最小二乘法的分段三次曲线拟合方法研究[J]. 科学技术与工程,2007, 7(3): 352-355.[5] 张浩, 任义广, 沙基昌. 基于分段三次曲线拟合的广州周发案量预测[J]. 计算机仿真, 2008, 25(6):257-260.[6] Roychowdhury S. Fuzzy curve fitting using least square principles[J]. IEEE International Conferenceon Systems, Man and Cybemetics, 1998, 4: 4022-4027.[7] 高伟, 姜水生. 分段曲线拟合与离散度加权的数据误差处理方法[J]. 中国测试技术, 2005, 11:55-56.[8] 张兴元. 分段函数的光滑方法及其在曲线拟合中的应用[J]. 西南民族大学学报(自然科学版),2007, 33(3): 486-490.[9] 钟尔杰, 黄延祝. 数值分析(第四版) [M]. 北京: 高等教育出版社, 2004.[10] 韩中庚. 数学建模方法及其应用[M]. 北京: 高等教育出版社, 2005.[11] 刘卫国. MA TLAB程序设计与应用(第二版) [M]. 北京: 高等教育出版社, 2006.致谢经过几个月的努力和忙碌,本次毕业论文即将完成,对为一个本科生的毕业论文,由于经验不足,难免有许多地方考虑不全面,如果没有指导老师的督促与辛勤的指导,以及一起学习的同学们的帮助与支持,想顺利的完成这篇论文比较难.值此论文完成之际,首先对指导老师李军成老师表示最诚挚的感谢与崇高的敬意.李老师严谨的治学态度,深厚渊博的学术素养,敏锐的思维,积极进去的精神,严以律己,宽以待人的崇高品质,乐观向上的人生态度,谦逊和蔼的为人品德,平等的师生关系,尤其是认真负责的工作态度均给我留下了不可磨灭的印象,相信对我今后的学习、工作以及生活都会有着深远的影响.感谢陈国华主任、杨笃庆书记、谭本远主任等数学系领导们,你们认真负责的治学态度和高速度、高效率的办事方式深深的感染了我们,让我们能够时时刻刻提醒自己要认真负责对待每件事情、每一个环节,感谢梁经珑老师、杨涤尘老师、余星老师、李军成老师、邓华老师、钟月娥老师、孙红果老师、李兵老师、龙承星老师等数学系的老师们,你们的授课方式与渊博的知识深化了我们的知识面,拓广了我们的视野,使我们对数学有了更浓厚的兴趣与体会.感谢杜鹃老师、郑丽峰老师,你们热忱的帮助使我们有一个很好的学习氛围来完成论文.在本文的写作过程中,李军成老师,石小芳、彭迪、方其斌等同学提出了许多宝贵的意见,此论文的完成离不开他们的指导,特别是李军成老师;他们渊博的学识与敏锐的头脑让我受益匪浅.再次对帮助我的人表示衷心的感谢.附录1 磷肥的施肥量与土豆产量的分段拟合函数程序x=[0,24,49,73,98,147,196,245,294,342];y=[33.46,32.47,36.06,37.96,41.04,40.09,41.26,42.17,40.36,42.73];plot(x,y,'r+')a1=polyfit(x(1:5),y(1:5),1)a2=polyfit(x(6:10),y(6:10),1)xx1=0:98; yy1=a1(1)*xx1+a1(2);xx2=147:342; yy2=a2(1)*xx2+a2(2);plot(x,y,'r+',xx1,yy1,xx2,yy2)附录2 磷肥的施肥量与土豆产量的Hermite插值的分段拟合曲线图程序x=[0,24,49,73,98,147,196,245,294,342];y=[33.46,32.47,36.06,37.96,41.04,40.09,41.26,42.17,40.36,42.73];plot(x,y,'r+')a1=polyfit(x(1:5),y(1:5),1)a2=polyfit(x(6:10),y(6:10),1)xx1=0:0.01:98; yy1=a1(1)*xx1+a1(2);xx2=147:0.01:342; yy2=a2(1)*xx2+a2(2);xx3=98:0.01:147;yy3=0.0000371155*xx3.^3-0.0144093294*xx3.^2+1.83925 71429*xx3-36.444499972;plot(x,y,'r+',xx1,yy1,xx2,yy2,xx3,yy3)附录3 弹簧受力与伸长量的关系的分段拟合函数程序x=[1,3,5,7,9,11,12,14,16,18];y=[1.9,5.3,8.6,12.1,15.7,16.8,19.2,20.7,21.4,21.8];plot(x,y,'r+')a1=polyfit(x(1:5),y(1:5),1)a2=polyfit(x(6:10),y(6:10),2)xx1=1:0.01:9; yy1=a1(1)*xx1+a1(2);xx2=11:0.01:18; yy2=a2(1)*xx2.^2+a2(2)*xx2+a2(3);plot(x,y,'r+',xx1,yy1,xx2,yy2)附录4 弹簧受力与伸长量的关系的两点三次Hermite插值多项式程序format long eclf,clear,x0=9;x1=11;y0=15.6000;y1=17.1840;m0=1.7200;m1=1.5818;x=linspace(9,11,100);y=linspace(15.6000,17.1840,100);m=2*(y0-y1)+(m0+m1)*(x1-x0);n=3*(x0+x1)*y1-3*(x0+x1)*y0-(2*x1+x0)*m0*(x1-x0)-(2*x0+x1)*(x1-x0)*m1;k=6*x0*x1*(y0-y1)+(x1-x0)*((m0*x1.^2+m1*x0.^2)+2*x1*x0*(m0+m1));q=x1.^2*(x1-3*x0)*y0+x0.^2*(3*x1-x0)*y1-x0*x1*(x1-x0)*(x1*m0+x0*m1);p=(x1-x0).^3;a=m/pb=n/pc=k/pd=q/py=a*x.^3+b*x.^2+c*x+d;plot(x,y,'r-')附录5 弹簧受力与伸长量的Hermite插值的分段拟合曲线图程序x=[1,3,5,7,9,11,12,14,16,18];y=[1.9,5.3,8.6,12.1,15.7,16.8,19.2,20.7,21.4,21.8];plot(x,y,'r+')a1=polyfit(x(1:5),y(1:5),1)a2=polyfit(x(6:10),y(6:10),2)xx1=1:0.01:9; yy1=a1(1)*xx1+a1(2);xx2=11:0.01:18; yy2=a2(1)*xx2.^2+a2(2)*xx2+a2(3);xx3=9:0.01:11;yy3=0.4294499999999997*xx3.^3-12.91805000000000*xx3.^2+129.8885499999999*xx3-420.1039499999994;plot(x,y,'r+',xx1,yy1,xx2,yy2,xx3,yy3)附录6 沥青的相对浓度与时间变化的关系分段拟合函数程序x=[5,15,20,50,65,80,100,120,160,180];y=[0,8.0,15.1,20.1,20.5,22.0,20.9,18.2,11.5,5.5];plot(x,y,'r+')a1=polyfit(x(1:5),y(1:5),3)a2=polyfit(x(6:10),y(6:10),2)xx1=5:0.01:65; yy1=a1(1)*xx1.^3+a1(2)*xx1.^2+a1(3)*xx1+a1(4);xx2=80:0.01:180; yy2=a2(1)*xx2.^2+a2(2)*xx2+a2(3);plot(x,y,'r+',xx1,yy1,xx2,yy2)附录7 沥青的相对浓度与时间变化的两点三次Hermite插值多项式程序format long eclf,clear,x0=65;x1=80;y0=20.4974;y1=22.2531;m0=0.3756;m1=0.3827;x=linspace(65,80,100);y=linspace(20.4974,22.2531,100);m=2*(y0-y1)+(m0+m1)*(x1-x0);n=3*(x0+x1)*y1-3*(x0+x1)*y0-(2*x1+x0)*m0*(x1-x0)-(2*x0+x1)*(x1-x0) *m1;k=6*x0*x1*(y0-y1)+(x1-x0)*((m0*x1.^2+m1*x0.^2)+2*x1*x0*(m0+m1));q=x1.^2*(x1-3*x0)*y0+x0.^2*(3*x1-x0)*y1-x0*x1*(x1-x0)*(x1*m0+x0*m1 );p=(x1-x0).^3;a=m/pb=n/pc=k/pd=q/py=a*x.^3+b*x.^2+c*x+d;plot(x,y,'r-')附录8 沥青的相对浓度与时间变化的Hermite插值的分段拟合曲线图程序x=[5,15,20,50,65,80,100,120,160,180];y=[0,8.0,15.1,20.1,20.5,22.0,20.9,18.2,11.5,5.5];plot(x,y,'r+')a1=polyfit(x(1:5),y(1:5),3)a2=polyfit(x(6:10),y(6:10),2)xx1=5:0.01:65;yy1=a1(1)*xx1.^3+a1(2)*xx1.^2+a1(3)*xx1+a1(4);xx2=80:0.01:180;yy2=a2(1)*xx2.^2+a2(2)*xx2+a2(3);xx3=65:0.01:80;yy3=0.002329807407407407*xx3.^3-0.5064964444444440 *xx3.^2+ 36.68982888888888*xx3-864.2173592592588;plot(x,y,'r+',xx1,yy1,xx2,yy2,xx3,yy3)。