当前位置：文档之家 › 电网络理论第2章

电网络理论第2章

  • 格式：ppt
  • 大小：627.00 KB
  • 文档页数：27

下载文档原格式

  / 27

合集下载

电网络理论 第二章图论

电网络理论 第二章图论

电网络理论第二章图论第二章图论图论是电网络理论的重要分支，主要研究对象是图。

图是由节点和边构成的一种抽象模型，被广泛应用于计算机科学、数学和其他相关领域。

本章将介绍图论的基本概念、常用算法以及在电网络中的应用。

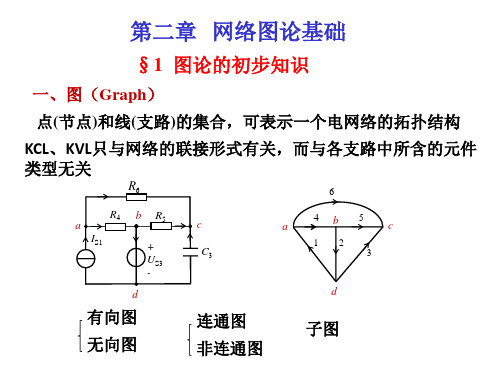
1. 图的定义和表示方式图由节点（也称为顶点）和边组成。

节点表示图中的元素，边表示节点之间的关联关系。

图可以分为有向图和无向图两种类型。

有向图中的边有方向性，表示从一个节点到另一个节点的单向关系。

无向图中的边没有方向性，表示节点之间的无序关系。

图可以用邻接矩阵或邻接表来表示。

邻接矩阵是一个二维数组，用于表示节点之间的关系。

邻接表则是由链表构成的数组，每个节点对应一条链表，链表中记录了该节点与其他节点的关系。

2. 图的基本术语和性质图论中有一些基本的术语和性质，包括：- 路径：指从一个节点到达另一个节点所经过的一系列边和节点。

- 简单路径：路径中不含有重复节点的路径。

- 环：起点和终点相同的路径。

- 连通图：图中任意两个节点之间都存在路径的图。

- 强连通图：有向图中任意两个节点之间都存在路径的图。

- 子图：由图中部分节点和对应的边组成的图。

- 度：节点所连接的边的数量。

- 入度和出度：有向图中节点的入边和出边的数量。

3. 常用图论算法图论中有许多重要的算法，下面介绍其中几个常用算法：- 广度优先搜索（BFS）：用于查找图中从起点到终点的最短路径，同时可以用于遍历图的所有节点。

- 深度优先搜索（DFS）：用于遍历图的所有节点，通过递归的方式沿着路径向前搜索，直到没有未访问的节点。

- 最小生成树（MST）：通过连接图中的所有节点，使得生成的树具有最小的总权重。

- 最短路径算法：例如迪杰斯特拉算法和贝尔曼-福特算法，用于查找图中两个节点之间的最短路径。

- 拓扑排序：用于对有向无环图进行排序，使得图中的节点满足一定的顺序关系。

4. 图论在电网络中的应用图论在电网络领域有广泛的应用，包括：- 网络拓扑分析：通过图论算法可以对电网络的拓扑结构进行分析，了解网络中节点之间的连接关系。

王勤电网络理论第二章

王勤电网络理论第二章

⎧ 1, 若 ⎪ a jk = ⎨ − 1 , 若 ⎪ 0, 若 ⎩
j j j
k k k
② b1 ① b4 b5 ⑤ b7 b6 ④
b1 b2 b3 0 0 1 -1 0 b4 1 0 0 -1 0 b5 -1 0 0 0 1 b6 0 0 0 -1 1 b7 0⎤ 0⎥ ⎥ -1⎥ ⎥ 0⎥ 1⎥ ⎦ 0 ① ⎡1 ⎢− 1 - 1 ② ⎢ 1 ③ ⎢0 ⎢ 0 ④ ⎢0 0 ⑤ ⎢0 ⎣
一般规定： ① 支路的编号采用先连支后树支的顺序； ② 各单连支回路的绕向与相应连支的方向一致； ③ 回路的序号与连支的序号要一致且顺次列写。 Bf=[1l | Bt ] Bt 1l (b-n)×n矩阵 b-n阶单位矩阵 基本回路与树支的关联关系 基本回路与连支的关联关系
② b1 ① b2 b5 ⑤ b7 b6 ④ b3 ③
0 ⎡ 1 ⎢− 1 - 1 A= ⎢ ⎢ 0 1 ⎢ 0 ⎣0
① 按“Aa每一列中只有两个非零元素，一个为+1， 另一个为–1”的关系，可由A还原成Aa 。 ② 故A也与有向图G一一对应。即已知G可唯一地写 出A；已知A也可唯一地画出G 。 ③ 通常采用的是A，且A也简称为关联矩阵。 定理5：连通图G的A的n×n子阵非奇异的充分必 要条件是：此子阵的列所对应的支路形成G的一 个树，且该子阵的行列式之值为±1 定理6：连通图G满足： 秩(Aa )= 秩(A )=n= nt –1
§2—3
一、关联矩阵Aa和A
图的矩阵表示
增广关联矩阵Aa表示G的节点和支路的关联关系 (augmented incidence matrix) Aa=[ajk]是一个nt × b的矩阵。
＋1第k条支路与第j个节点相关联，且支路方向离开节点j；

电网络理论第二章

电网络理论第二章

子图
二、回路（Loop） 路径的起点和终点重合 用支路表示 l(1,3,6)， l(1,2,4) 用节点表示 l(a,d,c,a)， l(a,d,b,a) 三、树（Tree） 包含所有节点；是连通的；不包含任何回路 树支：nt
a
4
6
a
4
b
2
5
c
3
1
d
6
b
2
5
c
a
4
b
2 3
c
a
1
b
2
c
连支: l
d d
可用（n-1)×b阶矩阵Q表示，其中元素qij定义如下：
1 支路j与割集i关联且方向一致 qij = -1 支路j与割集i关联且方向相反 0 支路j与割集i不关联
1 2 3 4 5 6 b
1
3
2 5
1 0 1 Q f = c2 0 1 1 1 0 1 c3 0 0 1 0 1 1
A= i ai1 n-1 a( n 1)1
a1b a2b aib a( n 1) b
2
……
b
b12 b11 b22 2 b21 Bf = bj2 i b j1 b-n+1 b(b n 1)1 a(b n 1)2
k 1
b
（1）回路j不通过节点i
a 、若支路k与回路j有关联，则必与节点i无关联
k j i j i j
i
即bjk 0, aik 0 即aik 0, bjk 0
aik bjk 0 aik bjk 0
b 、若支路k与节点i有关联，则必与回路j无关联
k

第二章 电网络分析与综合

第二章 电网络分析与综合

u 回路l1 u 回路l2 u l3 回路
0 0 0
BU＝0
对图1-4所示的基本割集依次列写KCL方程并写成矩阵形式得
c3
4 2
5 3 6 c1
0 1 1 i4 i1 1 1 1 i i 5 2 1 1 0 i3 i6
说明连支电压可以用树支电压的线性组合表示。 在全部支路电压中，树支电压是一组独立变量， (n 1) 个数等于树支数 取基本回路是列写独立KVL方程的一个充分非 必要条件 。
u 6 u1 u 2
推广到一般情况：在基本回路上列写的基尔霍夫 电压定律方程是一组独立方程，方程的数目等于 连支数，基本回路是一组独立回路。
推广，b条支路，n个节点，第n号节点为参考节点，支路电压和节 点电压列矢量分别记作 则基尔霍夫电压定律的关联矩阵形式是
ATU n U
四、基尔霍夫定律的基本回路矩阵形式
基本回路矩阵(fundamental loop matrix):描述基本回路与各支路的 关联关系，用B表示。B的行对应基本回路、列对应支路，B 是
c2
1
图 1-4 基本割集
连支电流列矢量为
I l [il1 il 2 il ,bl ]T
则基尔霍夫电流定律的基本回路矩阵形式为 B T I l I
五、基尔霍夫定律的基本割集矩阵形式
基本割集矩阵(fundamental cut-set matrix) ：基本割集与各支 路的关联关系，用C表示。矩阵的行对应基本割集，列对应支 路，其元素为:
第二章 网络图论和网络方程
本章是通过线图既点和线联结而成 的几何图形，抽象模拟比较复杂的电网 络，从而对形象直观的线图性质进行研 究，得到各种系统的分析综合方法。

电网络理论全套PPT课件共计210页

电网络理论全套PPT课件共计210页
T
Qf Bf T 0 T Bf Qf 0
关联矩阵与回路矩阵
Aa Ba T 0
T A Ba a 0
A Bf T 0 B f AT 0
25
第1章 电网络概述
b b
证明：
Ba Qa 0
T
令 D Ba Qa
T
b ji qki d jk b ji qik
i 1 i 1
1. 支路电压与节点电压
Vb ATVn
2.
节点电压法
树支电压与连支电压、支路电压
B f Vb 0
Vl 1 Bt V 0 t
割集电压法
Vb Q f TVt
T Vl BV Q t t l Vt
33
第1章 电网络概述
二、各种电流关系
1. 连支电流和树支电流
节点电压列向量
Im
网孔电流列向量
Vt
树支电压列向量
1.7.1 基尔霍夫电流定律的矩阵形式 1.7.2 基尔霍夫电压定律的矩阵形式
30
第1章 电网络概述
1.7.1 基尔霍夫电流定律的矩阵形式
AI b 0 Qa I b 0
独立？
n I 1 I I 1 2 I I I 1 4 5 n I3 I I I I ＝0 3 4 6 2 I I I I4 2 3 5 n I5 I 3 I 6
1 1 1 1 0 0 1234 235 Qf 0 1 1 0 1 0 1 1 0 0 0 1 126
独立
Q f Ql
1
23
第1章 电网络概述

电网络理论-第二章

电网络理论-第二章
T i B il Q i 0
2-25
QB i 0
T l
Q B
T f f
T
0 or
T t
B Q
0
T
0
T t
对同一有向图，任选一树，按先树枝后连枝顺序有：
Q B
B 1 Ql 1
Ql B
§2-3 图的基本矩阵形式
A与Qf 之间的关系 对同一有向图，任选一树，按先树枝后连 枝顺序写出矩阵：
2-26
A At Al B f Bt 1 Q 1 Q l f
§2-3 图的基本矩阵形式
结 支 ② 1 -1 0 1 0 2 3 -1 1 0 -1 0 0 1 0 4 0 -1 1 0 5 0 0 1 -1
2-10
1 Aa= 2 3 4
6 ３ ４ 0 ６ ③ 1 ① ５ 0 ２ -1 ④ 1
降阶关联矩阵A
支路b
A=
结 点 n-1
(n-1) b
§2-3 图的基本矩阵形式
矩阵形式的KVL：[ Qf ]T[ut ]=[u]
§2-3 图的基本矩阵形式 注意 连支电压可以用树支电压表示。 ut 1 T [u ] Qf ut T ut ul Ql ul QlT ut 小结
A KCL KVL B [B ] T [ il ] =[i] Q [Qf][i]=0
un1 un un2 un3
矩阵阵形式KVL
[u ] [ A] [un ]
T
§2-3 图的基本矩阵形式 2. 回路矩阵B
2-13
[B]=
独 立 回 路
支路b
注意

电网络理论2013第二章图论

第2章 网络图论基础
§ 2-1 图论的基本知识
• 图(Graph) 图是拓扑（Topological）图的简称 节点和支路的一个集合
分类：
无向图：未赋以方向的图。 混合图：只有部分支路赋以方向的图。 有向图：所有支路都赋以方向的图。 ::图并不反映支路之间的耦合关系。
元件的图
i1 i2
1 2

1
T ˆ ˆ u i i b ub 0 T b b
T T ˆ ˆb 0 ub i b i b u
或者
ˆ u i k k 0
k 1
b
ˆi u
k 1
b
k k
0
3. 特勒根定理的差分形式
ˆ 具有相同的拓扑结构，在t时刻， N ˆ 设网络N和 N i b， N的支路电压和电 ˆ b和 ˆ 的支路电压和电流分别为 u 流的变化量分别为u b和 i b ，则
u i i ub 0
T b b T b
或者
u i
k 1
b
k k
0
功率守恒定律的证明
T u A un KVL： b

u u A
T b T n
u i u Aib u Aib
T b b T n T n
利用KCL：Ai b 0
u i 0
T b b
i ub 0
2

3 3
二端元件的图
i1 ＋ u1 － i2 ＋ u2 －
三端元件的图

1
2
双口元件的图
连通图
• 连通图 如果图G中的任何两个节点之间都至少存在一 条路径，则G称为连通图(Connected Graph)，否则 称为非连通图。

电力网络


4．电缆线路 电缆线路的优缺点 电缆的构造一般包括三部分，即导体、绝缘层和 包护层 电缆的导体用铝或铜的单股或多股线，通常用多 股线 电缆绝缘层的材料大多用浸渍纸 包护层分内护层和外护层两部分 内护层由铝、铅、聚乙烯、聚氯乙烯制成，用以 保护绝缘不受损伤，防止浸渍剂的外温和水分的 侵入。外护层的作用在于防止外界的机械损伤和 化学腐蚀。
一般线路的等值电路 1．一般线路的等值电路 一般线路，指中等及中等以下长度线路。对架空线路， 这长度大约为州300km；对电缆线路，大约为100km。 线路长度不超过这些数值时，可不考虑它们的分布参数 特性．而只用将线路参数简单地集中起来的电路来表示。 以R( )、x( )、G(s)、B(s)分别表示全线路每相的总电 阻.显然，线路长度为l (km)时：
导线形式：
由于多股线优于单股线，架空线路多半采用绞合的多段导 线。多股导线的标号为J,由内向外，第一层6股，第二层 12股，第三层18股，余类推
1.架空线路的导线和避雷线
由于多股铝线的机械性能差，往往将铝和钢组合 起来制成钢芯铝线。它是将铝线绕在单股或多股 钢线外层作主要载流部分，机械荷载由钢线和铝 线共同承担的导线。 钢芯铝线中，因铝线部分与钢线部分截面积比值 的不同，机械强度也不同，过去曾将其分成三类：
3．关于架空线路的换位问题
换位的目的：减少三相参数的不平衡（1/10的不平 衡电流） 换位的方式：滚式换位和换位杆塔换位
按规定，在中性点直接接地的电力系统中， 长度超过100km的架空线路都应换位。但随 着电压级的升高，换位所遇到困难也愈益增 多，以致对某些超高压线路，如500kv电压 级线路，不得不采取不换位的架设方案。
可设G＝0（正常天气不考虑电晕，及不考虑绝缘 子泄漏
—般线路中，又有短线路和中等长度线路之分 所谓短线路，是指长度不超过100km的架空线路。线 路电压不高时，这种线路电纳B的影响一般不大，可略 去。从而，这种线路的等值电路员简单，只有一串联的 总电抗Z＝R十jX，如图2—36所示。 显然，如电缆线路不长，电纳的影响不大时，也可采 用这种等值电路。

电网络理论1-9


3
2
1-12
建模
1 i1 + u1 – 1'
零器和泛器
u1 u2
i1 + u1 – R1
R1i1 R2 i2
i2 + – + R2 u2 –
R1
R2
2 i2 + u2 – 2'
1
R1
R2
2
1 R1 R2
2
1'
2'
1'
2'
1' (c) 2'
1-12
1
1
零器和泛器
2
2 1
等效联接
1
2
2
u k, i 0 u 0, i k u 0, i 0
1
Z1 Z2
2
1
2
Z1 1 Z2 2 1 2
u k1 ,

i k2
1
2
1
1'
2'
1'
2'
1-12
零器和泛器
C B B C
等效电路
E
E
1 3
1 2
– +
当 u u
A( u u ) uo A A
当u
当 u u

u

• 线性运算放大器 工作在线性区
1-9
受控元件
• 理想的一般运算放大器
+ —

R 负载
1-9
受控元件
• 理想的线性运算放大器
1-9
受控元件
• 若x表示控制变量，（，）表示二端元件的 动态无关变量偶，即 ( , ) (u, i ), (u, q), (i , ), ( , q) 如果二端元件的成分关系为 (t ) f1 ( (t ), x ) 则该二端元件称为受控制变量x控制的受控元件。 受控电阻元件 受控电容元件 受控电感元件

电网络理论补充习题

《电网络理论》补充习题
第一章 电网络性质
补 1.1 确定以下电阻元件的性质：线性与非线性，时变与非时变，压控型或流控型。
(1) i = e−u ,
(2) u + 10i = 0 ,
(3) u = i3 + i ,
(4) u = i2 ,
(5) u = i cos 2t ,
(6) u = 2 + i cos 2t .
1ς 1F
1
2
+
+
u1 1'-
1F
2F 1ς
u2 - 2'
—3—
第五章 状态方程
补 5.1 用端口法列写图示电路的状态方程。
补 5.2 图示电路中，非线性元件的特性为
u1 = 2q12 , u4 = 3(i4 + 2i43 ),
i5 = th(0.5φ5 ),
试用直观法列写状态方程。
L
iS
i
C R3 +
8 9 10
基本割集和基本回路矩阵。
1 6
4
5
补 1.7 设某连通图 G 具有 5 个节点、8 条支路，它的关联矩阵如下：
(1) 不要画图，证明支路集{1, 2, 3, 7}为一树. (2) 对此树(不画图)写出基本回路矩阵。 (3) 确定同一树的基本割集矩阵。
⎢⎣⎡ ⎥⎦⎤ A =
1 1 -1 0 0 0 0 0 0 -1 0 -1 1 1 0 0 0 0 1 0 -1 0 1 0 -1 0 0 1 0 0 0 −1
(2)用该电路实现下列带通函数时求各电阻值(取C 1 =C 2 =0.01μF)．
T (s) =
− 5252s
s 2 + 3184s + 6.632 ×107
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第2章 网络矩阵方程
支路电流、电压特性 Ik Isk Iek Idk Vk Vsk Vek Vdk
矩阵形式
Ib Is Ie Id Vb Vs Ve Vd
Vk
Id GVe Ie
Ie Ye Ve
Ib Is (1 GZe )Ye (1 RYe )1(Vb Vs )
2.4 回路电流法
Ib Is Yb (Vb Vs )
Vb Zb Ib Zb Is Vs
回路电压方程 B fVb 0
B f Zb Ib B f Zb Is B fVs
B f ZbB f T Il B f Zb Is B fVs
Vk
回路阻 抗矩阵
Zl Il El
2.1 节点电压法
2.1.1 复合支路的伏安特性
第2章 网络矩阵方程
Iek Yk Vek
矩阵
Ie Ye Ve
Vk 元件导纳矩阵
Ie Ie1 Ie2 L Iek L Ieb T Ve Ve1 Ve2 L Vek L Veb T Ye diagY1 Y2 L Yk L Yb
b nt 1 q
第2章 网络矩阵方程
2.5 含零泛器网络的节点电压法
2.5.1 零口器、非口器和零器

半导体器件
理想 运放
零值器（Nullator）零口 I 0V 0
泛值器（Norator）非口
I V 任意值
零泛器( Nullor ) 零器
第2章 网络矩阵方程
Q f YbQTfVt Q f YbVs Q f Is
YqVt Jt
注入割 集的电 流源向
量
第2章 网络矩阵方程
网络含p 条纯电压源支路时
已知信息描述为
p
Vt

Vt1
Vt
2

连支和树支1 树支2
纯电 压源 支路
树支1 Qf 树支2
Q11 Q12
Q21
Q22

回路电压 源向量
第2章 网络矩阵方程
网络含q 条纯电流源支路时
阻抗
已知信息描述为
Il

Il1

I
l
2

1 Bf 0
B12
B22

纯电 流源 支路
q
Zb

Zb1

0
q 连支1
Bf 连支2
q
连支1
B11

B21
连支2和树支
B12
B22

p
p
Qf

Q11 Q21
0 1
Yb

Yb1

0
0
Yb 2

p
Vs

Vs1
Vs
2

p
Is

Is1

0

p
第2章 网络矩阵方程
割集方程
QQ1211YYbb11QQ11TT11
Q11Yb1Q2T1 Q21Yb1Q2T1 Yb2

第2章 网络矩阵方程
2.1.3 方程的建立
节点电流方程 AIb 0
Ib Is Yb (Vb Vs )
AIb AYb (Vb Vs ) Is 0
AYb ATVn AYbVs AIs
YnVn Jn
节点导 纳矩阵
注入节 点的电 流源向
量
第2章 网络矩阵方程
0
Zb
2

Is

Is1

I
s
2


q
Vs
0

Vs
2

q
第2章 网络矩阵方程
回路电压方程


Z
b1 B12 Zb2 B1T2 B22 Zb2 B1T2
B12 B22
Zb2 Zb2
B2T2 B2T2

Il1

I
l
2


Zb1Is1 B12 Zb2 Is2
2.2 修正节点电压法
网络含纯电压源支路
导纳
解决方式 将纯电压源支路的电流作为附加变量
Iw Iw1 Iw2 Iw3 T
Vws Vws1
Vws 2
VT ws3
Y nVn J n N
第2章 网络矩阵方程
Jn L
Iws1 Iws1 L
Iw2 Iw2 L Iw3 Iw3 L T
Vd Ve RIe
第2章 网络矩阵方程
Vk
Ib Is (1 GZe )Ye (1 RYe )1(Vb Vs )
复合 支路 伏安 特性
Ib Is Yb (Vb Vs )
Yb (1 GZe )Ye (1 RYe )1

B22 Zb2 Is2




B12Vs 2 B22Vs 2


Il1 Is1 已知 B22 Zb2 B12T Il1 B22 Zb2 B22T Il 2 B22 Zb2 I s2 B22Vs2
待求方程
B22 Zb2 B22T Il 2 B22 Zb（2 I s2 B12T I s1） B22Vs2
第2章 网络矩阵方程
2.1.2 支路导纳矩阵和支路阻抗矩阵
支路导纳矩阵 Yb
Yb (1 GZe )Ye (1 RYe )1
支路阻抗矩阵 Zb 元件导纳矩阵 Ye
Zb Yb1
Ye diagY1 Y2 L Yk L Yb
常用
Yb Ye G Zb Ze R
Vt1 Vt 2


＝Q21YQb1V11Ys1b1VYs1b
2Vs
2


－QQ1211IIss11


已知
Vt 2 Vs2
待求方程
Q11Yb1Q1T1Vt1 Q11Yb（1 Vs1 Q2T1Vt 2 ) Q11I s1
（nt 1 p)
第2章 网络矩阵方程
Y n

AwT
Aw 0


Vn

I
w



Jn Vws


修正节点 电压方程
2.3 割集电压法
Vk
第2章 网络矩阵方程
Ib Is Yb (Vb Vs ) 割集电流方程 Q f Ib 0
Q f YbVb Q f YbVs Q f Is
割集导 纳矩阵
Jn Aw Iw
Aw
00 0 0
L
L
L

i 1 0 0
j 1 0
0

L L L


k0 1 0
l

0
1
0

L L L
m

0
0
1

n 0 0 1
第2章 网络矩阵方程
Y nVn J n Aw Iw
附加方程
AwTVn Vws