线线垂直、线面垂直、面面垂直的习题及答案解析

线线，线面，面面垂直的证明一、线面垂直（共9题；共85分）1.（2021高一下·岑溪期末）如图，四棱锥的底面是边长为2的菱形，底面.（1）求证：平面；2.（2021高一下·和平期末）如图，斜三棱柱中，侧面是菱形，与交于点，E是AB的中点．求证：（2）若，求证：．3.（2021高一下·宁波期末）已知三棱锥，平面，是以为斜边的等腰直角三角形，是以为斜边的直角三角形，为上一点，为上一点，且．（Ⅰ）现给出两个条件：① ；② 为中点．从中任意选一个条件为已知条件，求证：平面；4.（2021高一下·怀化期末）如图，在正方体中.（1）求证：面；5.（2021高一下·绍兴期末）如图，四棱台的底面是矩形，，，，．（Ⅰ）证明：平面；6.（2021高二下·二道期末）如图，在四棱锥P-ABCD中，底面ABCD为正方形，侧面PAD是正三角形，侧面底面ABCD，M是PD的中点.（1）求证：平面PCD；7.（2021高一下·长春期末）如图，AB是的直径，PA垂直于所在的平面，C是圆周上不同于A，B的一动点.8.（2021高一下·河北期末）如图，在正四棱锥中，点E，F分别在棱PB，PD上，且．（1）证明：平面PAC．9.（2021高一下·天津期末）如图，在四棱锥中，平面，底面是菱形，（2）求证：直线平面二、线线垂直（共7题；共70分）10.（2021高一下·海南期末）如图所示，三棱柱中，，，，．（1）证明：；11.（2021·全国甲卷）已知直三棱柱ABC-A1B1C1.中，侧面AA1B1B为正方形，AB= BC = 2，E，F分别为AC和CC1的中点，D为棱A1B1上的点，BF丄A1B1.（1）证明：BF⊥DE；12.（2021·全国甲卷）已知直三棱柱中，侧面为正方形．分别为和的中点，．（2）已知为棱上的点，证明：．13.（2021·新高考Ⅰ）如图，在三棱锥A-BCD中.平面ABD丄平面BCD，AB=AD.O为BD的中点.（1）证明：OA⊥CD：14.（2021高一下·广东期末）如图，在三棱锥中，，点是线段的中点，平面平面.（2）求证：.15.（2021高二下·湖北期末）中国是风筝的故乡，南方称“鹞”，北方称“鸢”，如图，某种风筝的骨架模型是四棱锥，其中于，，，平面．（1）求证：；16.（2021·浙江）如图，在四棱锥中，底面是平行四边形，，M，N分别为的中点，.（1）证明：；三、面面垂直（共9题；共105分）17.（2021·新高考Ⅱ卷）在四棱锥中，底面是正方形，若．（1）证明：平面平面；18.（2021高一下·滨海新期末）如图，在三棱柱中，平面，，是的中点.（2）求证：平面平面；19.（2021高一下·和平期末）如图，在四棱锥中，平面平面，四边形为矩形，，，为的中点．（2）求证：平面平面；20.（2021高一下·龙岩期末）如图，是圆锥的顶点，是底面圆的直径，为底面圆周上异于的点，为的中点．（1）求证：平面平面21.（2021高一下·东丽期末）如图，三棱柱，底面，且为正三角形，，为中点．（2）求证：平面平面．22.（2021高一下·湖北期末）如图，在三棱台中，上底面为等腰直角三角形，，，，在上，.（1）证明：平面平面；23.（2021高一下·重庆期末）如图1，在平行四边形ABCD中，，，，将沿折起，使得平面平面，如图2．（1）证明：平面平面BCD；24.（2021高一下·河北期末）如图，在三棱柱中，，点为的中点，，．（1）证明：平面平面ABC．25.（2021·全国乙卷）如图，四棱锥P-ABCD的底面是矩形，PD 底面ABCD，M为BC的中点，且PB AM.（1）证明：平面PAM 平面PBD；线线，线面，面面垂直的证明参考答案一、线面垂直（共9题；共85分）1.（2021高一下·岑溪期末）如图，四棱锥的底面是边长为2的菱形，底面.（1）求证：平面；【答案】（1）证明：因为四边形ABCD是菱形，所以AC⊥BD，又因为PD⊥平面ABCD，平面ABCD，所以PD⊥AC，又，AC⊥平面PBD2.（2021高一下·和平期末）如图，斜三棱柱中，侧面是菱形，与交于点，E是AB的中点．求证：（2）若，求证：．（2）∵侧面是菱形∴∵，，平面，平面∴平面∵平面∴．3.（2021高一下·宁波期末）已知三棱锥，平面，是以为斜边的等腰直角三角形，是以为斜边的直角三角形，为上一点，为上一点，且．（Ⅰ）现给出两个条件：① ；② 为中点．从中任意选一个条件为已知条件，求证：平面；【答案】解：（Ⅰ）若选①证明：∵平面，平面，∴，又，，∴平面．又平面，∴．又，，∴平面．又平面，∴．又，，∴平面．若选② 为中点证明：∵平面，平面，∴．又，，∴平面．又平面，∴．又，，∴平面．又平面，∴．又为等腰直角三角形斜边中点，则，，∴平面．4.（2021高一下·怀化期末）如图，在正方体中.（1）求证：面；【答案】（1）证明：因为为正方体，所以ABCD为正方形,所以，又因为平面ABCD，平面ABCD，故，又，平面，所以平面．5.（2021高一下·绍兴期末）如图，四棱台的底面是矩形，，，，．（Ⅰ）证明：平面；【答案】解：（Ⅰ）证明：因为底面是矩形，所以，又，，所以平面，又因为，所以平面．6.（2021高二下·二道期末）如图，在四棱锥P-ABCD中，底面ABCD为正方形，侧面PAD是正三角形，侧面底面ABCD，M是PD的中点.（1）求证：平面PCD；【答案】（1）在正方形ABCD中，，又侧面底面ABCD，侧面底面，所以平面PAD，平面PAD，所以，是正三角形，M是PD的中点，所以，又，所以平面PCD.7.（2021高一下·长春期末）如图，AB是的直径，PA垂直于所在的平面，C是圆周上不同于A，B的一动点.（1）证明：BC⊥面PAC；【答案】（1）证明见解析PA垂直于所在的平面PA⊥BCAB是的直径AC⊥BCBC⊥面PAC8.（2021高一下·河北期末）如图，在正四棱锥中，点E，F分别在棱PB，PD上，且．（1）证明：平面PAC．【答案】（1）证明：如图，连接，记，连接PO，由题意可得四边形ABCD是正方形，，则O为AC的中点，且，因为，所以，因为平面，面，且，所以平面，因为，所以，则平面PAC；9.（2021高一下·天津期末）如图，在四棱锥中，平面，底面是菱形，（2）求证：直线平面【答案】（2）因为四边形是菱形，所以又因为平面平面所以又因为所以平面二、线线垂直（共7题；共70分）10.（2021高一下·海南期末）如图所示，三棱柱中，，，，．（1）证明：；【答案】（1）∵，，．∴，∴．∵，，∴．又∵，平面，∴平面．∵平面，∴．11.（2021·全国甲卷）已知直三棱柱ABC-A1B1C1.中，侧面AA1B1B为正方形，AB= BC = 2，E，F分别为AC和CC1的中点，D为棱A1B1上的点，BF丄A1B1.（1）证明：BF⊥DE；【答案】法一法2（1）因为三棱柱是直三棱柱，所以底面，所以因为，，所以，又，所以平面．所以两两垂直．以为坐标原点，分别以所在直线为轴建立空间直角坐标系，如图．所以，．由题设（）．因为，所以，所以．12.（2021·全国甲卷）已知直三棱柱中，侧面为正方形．分别为和的中点，．（2）已知为棱上的点，证明：．（2）由(1)的结论可将几何体补形为一个棱长为2的正方体，如图所示，取棱的中点，连结，正方形中，为中点，则，又，故平面，而平面，从而.13.（2021·新高考Ⅰ）如图，在三棱锥A-BCD中.平面ABD丄平面BCD，AB=AD.O为BD的中点.（1）证明：OA⊥CD：【答案】（1），为中点，，面，面面且面面，面，．14.（2021高一下·广东期末）如图，在三棱锥中，，点是线段的中点，平面平面.（2）求证：.【答案】（2）证明：∵，∴，∴，∵平面平面，且平面平面，平面，∴平面，∵平面，∴.15.（2021高二下·湖北期末）中国是风筝的故乡，南方称“鹞”，北方称“鸢”，如图，某种风筝的骨架模型是四棱锥，其中于，，，平面．（1）求证：；【答案】（1）证明：∵平面，平面，∴，又，，平面，平面，∴平面，又平面．∴．16.（2021·浙江）如图，在四棱锥中，底面是平行四边形，，M，N分别为的中点，.（1）证明：；【答案】（1）证明：在中，，，，由余弦定理可得，所以，．由题意且，平面，而平面，所以，又，所以三、面面垂直（共9题；共105分）17.（2021·新高考Ⅱ卷）在四棱锥中，底面是正方形，若．（1）证明：平面平面；【答案】（1）取的中点为，连接.因为，，则，而，故.在正方形中，因为，故，故，因为，故，故为直角三角形且，因为，故平面，因为平面，故平面平面.18.（2021高一下·滨海新期末）如图，在三棱柱中，平面，，是的中点.（2）求证：平面平面；【答案】（2）∵，是的中点，∴，∵三棱柱中，平面，∴平面∵AD 平面，∴，又､BC是平面内的两条相交直线∴平面∵AD 平面∴平面平面19.（2021高一下·和平期末）如图，在四棱锥中，平面平面，四边形为矩形，，，为的中点．（2）求证：平面平面；【答案】（2）因为平面平面，平面平面，,所以平面，因为平面，所以,又, 平面,所以平面,又平面，所以,又,所以,又平面,所以平面,又平面,所以平面平面；20.（2021高一下·龙岩期末）如图，是圆锥的顶点，是底面圆的直径，为底面圆周上异于的点，为的中点．（1）求证：平面平面【答案】（1）由圆锥的性质可知，底面圆∵在底面圆上，∴，∵在圆上，为直径，∴，又点分别为的中点，∴∴又，且平面，∴平面，又平面，∴平面平面．21.（2021高一下·东丽期末）如图，三棱柱，底面，且为正三角形，，为中点．（2）求证：平面平面．【答案】（2）∵面，面，∴．又，，∴，面，∴面．又面，∴面面．22.（2021高一下·湖北期末）如图，在三棱台中，上底面为等腰直角三角形，，，，在上，.（1）证明：平面平面；【答案】（1）因为三棱台中，因为，所以，由，所以，所以，又由，所以，因为，且平面，所以平面，又因为平面，所以平面平面.23.（2021高一下·重庆期末）如图1，在平行四边形ABCD中，，，，将沿折起，使得平面平面，如图2．（1）证明：平面平面BCD；【答案】（1）在中，因为，，，由余弦定理得，所以，所以，所以如图所示：作于点，因为平面平面，平面平面，所以平面，所以，又因为，所以平面，因为平面，所以，又由，所以平面.所以平面平面BCD；24.（2021高一下·河北期末）如图，在三棱柱中，，点为的中点，，．（1）证明：平面平面ABC．【答案】（1）证明：因为，所以，，在三棱柱中，，所以，又因为，所以平面ABC，又因为平面，所以平面平面ABC；25.（2021·全国乙卷）如图，四棱锥P-ABCD的底面是矩形，PD 底面ABCD，M为BC的中点，且PB AM.（1）证明：平面PAM 平面PBD；【答案】（1）因为底面，平面，所以，又，，所以平面，而平面，所以平面平面．。

1空间线线、线面、面面垂直关系练习题一、填空题1．给出下列三个命题：①“直线a 、b 为异面直线”的充分非必要条件是“直线a 、b 不相交”；②“直线a 垂直于直线b ”的充分非必要条件是“直线a 垂直直线b 在平面β内的射影”；③“直线a 垂直平面β” 的必要非充分条件是“直线a 垂直于平面β内的无数条直线” 其中所有真命题的序号是 ③2．如图，正方形ABCD ，P 是正方形平面外的一点，且P A ⊥平面A BCD 则在△P AB 、△PBC 、△PCD 、△P AD 、△P AC 及△PBD 中，为直角三角形有______5___个．3．在四棱锥P-ABCD 中，P A ⊥底面ABCD ，底面各边都相等，M 是PC 上的一动点，当点M 满足 BM PC ⊥ 时，平面MBD ⊥平面PCD ．4．已知三棱锥ABC S -的底面是正三角形，点A 在侧面SBC 上的射影H 是SBC ∆的垂心，且SA 的长为定值，则下列关于此三棱锥的命题：①点B 在侧面SAC 上的射影是SAC ∆的垂心；②三棱锥ABC S -是一个正三棱锥；③三棱锥ABC S -的体积有最大值；④三棱锥ABC S -的体积有最小值.其中正确命题的序号为 ①②③ . 5．如果a,b 是异面直线，P 是不在a,b 上的任意一点，下列四个结论：（1）过P 一定可作直线L 与a , b 都相交；（2）过P 一定可作直线L 与a , b 都垂直；（3）过P 一定可作平面α与a , b 都平行；（4）过P 一定可作直线L 与a , b 都平行，其中正确的结论有___（2）______．6．给出下列命题：①分别和两条异面直线AB ．CD 同时相交的两条直线AC ．BD 一定是异面直线②同时与两条异面直线垂直的两直线不一定平行③斜线b 在面α内的射影为c ，直线a ⊥c ，则a ⊥b ④有三个角为直角的四边形是矩形，其中真命题是 ① ．7．点P 在直径为2的球面上，过P 作两两垂直的三条弦，若其中一条弦长是另一条弦长的2倍，则这三条弦长之和为最大值是 5702 ． 8．正四面体ABCD的棱长为1，棱AB αα]21,42[l l l βα⊂⊂AC ,60120棱锥D ABCE -的底面是矩形，DE ⊥面ABCE ，3,1, 2.DE EC BC G ===为DA 的中点，Q 为DC 上一点，且EQ ⊥面GBC ，则DQ QC ＝ 32. 11．已知边长为23的正ABC ∆，点,D E 分别在边,AB AC 上，且//DE BC ，以DE 为折痕，把ADE ∆折起至A DE '∆，使点A '在平面BCED 上的射影H 始终落在BC 边上，记2ADE S A H ∆='的面积，则S 的取值范围为 ．【答案】3(,)3+∞【解析】设A 到DE 的距离为x ，则DE 与BC 间距离为3x -，ADE ∴∆的面积为233x ()222369A H x x x '=--=- 2339232x S x x ⎛⎫∴=⋅> ⎪-⎝⎭ S ∴的取值范围为3(,)3+∞． 12．三棱锥ABC P -中，︒=∠=∠=∠90CPA BPC APB ，点M 在△ABC 内，且=∠MPA ︒=∠60MPB ，则MPC ∠的度数是___︒45______．13.如图，AD 与BC 是四面体ABCD 中互相垂直的棱，2=BC ，若c AD 2=，且a CD AC BD AB 2=+=+，其中a 、c 为常数，则四面体ABCD 的体积的最大值是 。

线面垂直练习题及答案线面垂直是几何学中的一项基本概念，用于描述线段、射线、直线和平面之间的垂直关系。

理解线面垂直的概念对于解决几何问题至关重要。

本文将为读者提供一些线面垂直练习题及答案，帮助读者巩固对该概念的理解。

练习题一：1. AB为一条线段，m是一平面。

如果AB与m垂直，判断下列命题的真假：a) 线段AB垂直于平面mb) 平面m垂直于线段ABc) 线段AB平行于平面m2. P是平面XYZ的内点，AP的延长线与平面XYZ有几个交点？练习题二：1. 给出下列命题的定义：a) 垂线b) 垂直平分线c) 垂直平面2. 在平面上画一条线段AB和一条直线l，求证：若线段AB与直线l垂直，则直线l过点A和点B的垂直平分线。

1. 已知直线l与平面P垂直，直线m过l上一点，那么直线m与平面P的关系是什么？2. 在长方形ABCD中，线段AC和线段BD相交于点O。

求证：线段AC与平面ABCD垂直。

答案及解析：练习题一：1. a) 假，线段AB无法垂直于平面m，因为线段只有两个端点而不是无限延伸。

b) 真，平面m可以垂直于线段AB。

c) 假，线段和平面不可能平行。

2. AP的延长线与平面XYZ有且只有一个交点。

练习题二：1. a) 垂线是与给定线段或直线垂直的线段或直线。

b) 垂直平分线是将给定线段或直线垂直平分的线段或直线。

c) 垂直平面是与给定平面垂直的平面。

2. 假设直线l过点A和点B的垂直平分线交线段AB于点M，则根据垂直平分线的定义，我们可以得出线段AM和线段BM的长度相等，且直线l与线段AM和线段BM都垂直。

1. 直线m与平面P平行。

2. 连接线段AC的中点和线段BD的中点，设为点O'。

根据长方形的性质，线段OO'相等且垂直于两个平行线段AC和BD。

因此，线段OO'垂直于平面ABCD，而线段OO'与线段AC相等，所以线段AC与平面ABCD垂直。

通过以上练习题及答案，我们可以加深对线面垂直概念的理解。

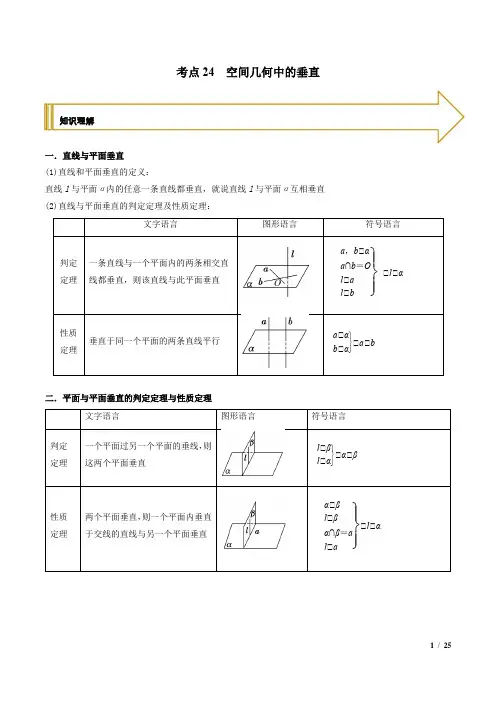
考点24 空间几何中的垂直知识理解一．直线与平面垂直(1)直线和平面垂直的定义：直线l与平面α内的任意一条直线都垂直，就说直线l与平面α互相垂直(2)直线与平面垂直的判定定理及性质定理：二．平面与平面垂直的判定定理与性质定理三．证明线线垂直的思路平行四边形：正方形、菱形、矩形图形三角形：等腰（等边）三角形--取中点正余弦定理边关系或边长勾股逆定理线面垂直的定义面面垂直的性质⎧⎧⎪⎪⎨⎪⎩⎪⎪⎧⎪⎪⎨⎨⎪⎩⎪⎪⎪⎪⎩ 考向一 线面垂直【例1】3．（2021·江西吉安市·高三期末节选）如图，在四棱锥P ABCD -中，底面ABCD 为直角梯形，//AD BC ，90ADC ∠=︒，22AD DC BC ===，PAD △为正三角形，Q 为AD 的中点，求证：AD ⊥平面PBQ【答案】证明见解析【解析】∵PAD △为正三角形，Q 为AD 的中点，∴PQ AD ⊥.∵//AD BC ，2AD DC BC ==，Q 为AD 的中点.∴四边形BCDQ 为平行四边形，∴//BQ CD . 又90ADC ∠=︒，∴90AQB ∠=︒，即BQ AD ⊥.又PQBQ Q =，∴AD ⊥平面PBQ.考向分析【举一反三】1．（2021·河南信阳市节选）如图所示，四棱锥S ABCD -中，//AB CD ，AD DC ⊥，2224CD AD AB SD ====，SD ⊥平面ABCD ，求证:BC ⊥平面SBD【答案】证明见解析【解析】证明://,,2AB CD AD DC AB AD ⊥==，BD BC ∴==又4CD =，222CD BD BC ∴=+，故BC BD ⊥， 又SD ⊥平面,ABCD BC ⊂平面ABCD ，BC SD ∴⊥， 又SD BD D =，BC ∴⊥平面SBD .2．（2021·江西赣州市节选）如图，已知三棱柱111ABC A B C -的所有棱长均为2，13B BA π∠=，证明：1B C ⊥平面1ABC【答案】证明见解析【解析】证明：如图取AB 中点D ，连接1,B D CD ．因为四边形11BCC B 为菱形，所以11B C BC ⊥ 又因为三棱柱的所有棱长均为2，13B BA π∠=，所以ABC 和1ABB △是等边三角形，所以1,B D AB CD AB ⊥⊥因为1,B D CD ⊂平面11,B CD B D CD D ⋂=，所以AB ⊥平面1B CD 所以1B C AB ⊥，而1BC AB B ，所以1B C ⊥平面1ABC3．（2020·山东德州市节选）如图，四棱锥P ABCD -中，四边形ABCD 是边长为2的正方形，PAD ∆为等边三角形，,E F 分别为PC 和BD 的中点，且EF CD ⊥，证明:CD ⊥平面PAD【答案】证明见解析【解析】如图所示，连接AC ，由ABCD 是边长为2的正方形， 因为F 是BD 的中点，可得AC 的中点，在PAC △中，因为,E F 分别是,PC AC 的中点，可得//EF PA ， 又因为EF CD ⊥，所以PA CD ⊥，又由AD CD ⊥，且ADAP A =，所以CD ⊥平面PAD .考向二 面面垂直【例2】（2021·河南高三期末节选）如图，直四棱柱1111ABCD A B C D -的底面ABCD 为平行四边形，3AD =，5AB =，3cos 5BAD ∠=，1BD DD =，E 是1CC 的中点，求证：平面DBE ⊥平面1ADD【答案】证明见解析【解析】由题意可得2222cos 16BD AD AB AB AD BAD =+-⨯∠=， 所以222AD BD AB +=，因此AD BD ⊥. 在直四棱柱1111ABCD A B C D -中，1DD ⊥平面ABCD ，BD ⊂平面ABCD ，所以1.DD BD ⊥又因为1ADDD D =，1,AD DD ⊂平面1ADD ，所以BD ⊥平面1ADD ，因为BD ⊂平面DBE ，所以平面DBE ⊥平面1ADD ． 【举一反三】1．（2021·河南焦作市节选）如图所示，在四棱锥РABCD -中，底面ABCD 是菱形，PA ⊥平面,ABCD 点Q 为线段PC 的中点，求证:平面BDQ ⊥平面PAC【答案】证明见解析【解析】因为四边形ABCD 是菱形，所以,AC BD ⊥ 因为PA ⊥平面,ABCD BD ⊂平面,ABCD 所以,BD PA ⊥ 又因为,PA AC A ⋂=所以BD ⊥平面,PAC 因为BD ⊂平面,BDQ 所以平面BDQ ⊥平面PAC .2．（2021·山东青岛市·高三期末节选）如图，在直角梯形ABED 中，//BE AD ，DE AD ⊥，BC AD ⊥，4AB =，BE =将矩形BEDC 沿BC 翻折，使得平面ABC ⊥平面BCDE ，若BC BE =，证明：平面ABD ⊥平面ACE【答案】证明见解析【解析】证明：连接BD ，因BC BE =所以BD CE ⊥ 因为平面ABC ⊥平面BCDE ，平面ABC 平面BCDE BC =，AC BC ⊥所以AC ⊥平面BCDE因为BD ⊂平面BCDE ，所以AC BD ⊥ 因为ACCE C =，所以BD ⊥平面ACE因为BD ⊂平面ABD ，所以平面ABD ⊥平面ACE3．（2021·安徽马鞍山市节选）如图，BE ，CD 为圆柱的母线，ABC 是底面圆的内接正三角形，M 为BC 的中点，证明：平面AEM ⊥平面BCDE【答案】证明见详解【解析】根据题意可得，AM BC ⊥. 又BE 为圆柱的母线，BE ∴⊥平面ABC .BE AM ∴⊥，BC BE B =，AM ∴⊥平面BCDE .又AM ⊂平面AEM ，∴平面AEM ⊥平面BCDE ．考向三 线线垂直【例3】（2021·江西宜春市·高安中学节选）如图，四棱锥P ABCD -的底面ABCD 是边长为2的菱形，60BAD ∠=，已知2,PB PD PA ===，E 为PA 的中点，求证PC BD ⊥【答案】证明见解析【解析】,AC BD 交点为O ，连接PO ，ABCD 是边长为2的菱形，,AC BD O ∴⊥是,AC BD 的中点，,PD O B BD P P =∴⊥，又PO ⊂平面POC ，AC ⊂平面POC ，POAC O =，BD ∴⊥平面POC ，PC ⊂平面POC ，.C BD P ∴⊥【举一反三】1．（2021·江苏南通市·高三期末节选）如图，在四棱锥A BCDE -中，//BC DE ，22BC DE ==，BC CD ⊥，F 为AB 的中点，BC EF ⊥，求证：AC BC ⊥【答案】证明见解析【解析】取AC 中点M ，连接FM ，DM ，,F M 分别为AB ，AC 中点，12FMBC ∴， 1,2DEBC FM DE ∴， ∴四边形DEFM 是平行四边形，//DM EF ∴，,EF BC DM BC ⊥∴⊥，,,CD DM CD DM ⊥⊂平面ACD ，CD DM D ⋂=，BC ∴⊥平面CDM ，AC ⊂平面CDM ，BC AC ∴⊥；2．（2020·山东德州市节选）如图，已知四棱锥P ABCD -中，底面ABCD 为菱形，60,ABC PA ∠=︒⊥平面,,ABCD E F 分别为,BC PA 的中点.（1）求证:AE PD ⊥; （2）求证://EF 平面PCD .【答案】（1）证明见解析；（2）证明见解析.【解析】证明：（1）连AC ，60ABC ∠=，底面ABCD 为菱形，ABC ∴是等边三角形， BE EC =，AE BC ∴⊥，又//BC AD ，AE AD ∴⊥，又PA ⊥面,ABCD AE ⊂面ABCD ，PA AE ∴⊥， PA AD A ⋂=，AE ∴⊥面,PAD PD ⊂面PAD ，AE PD ∴⊥.()2取PD 的中点M ，连,FM MC ，PF FA =，所以11//,22FM AD FM AD =， 又11//,22EC AD EC AD =， //,FM EC FM EC ∴=， ∴四边形FECM 是平行四边形，//EF MC ∴，又EF ⊄面,PCD MC ⊂面PCD ，//EF ∴面PCD .3．（2021·山东枣庄市节选）如图，四棱锥P ABCD -的侧面PAD △是正三角形，底面ABCD 是直角梯形，90BAD ADC ∠=∠=，22AD AB CD ===，M 为BC 的中点，求证：PM AD ⊥【答案】（1）证明见解析；（2）7. 【解析】证明：取AD 中点N ，连PN ，NM ， 因为PAD △是正三角形，所以PNAD .又M 是BC 中点，所以//NM AB .因为90BAD ∠=，即AB AD ⊥.所以NM AD ⊥，因为NM PN N ⋂=，NM ､PN ⊂平而PMN ， 所以AD ⊥平面PMN ，PM ⊂平面PMN ，所以AD PM ⊥.1．（2021·山东泰安市·高三期末节选）如图，在四棱锥P ABCD -中，底面ABCD 是菱形，60BAD ∠=︒，PB PD =，F 为PC 上一点，过AF 作与BD 平行的平面AEFG ，分别交PD ，PB 于点E ，G ，证明：EG ⊥平面PAC【答案】证明见解析【解析】证明：连接BD ，交AC 于点O ，连接PO ． ∵//BD 平面AEFG ，平面PBD平面AEFG EG =，BD ⊂平面PBD ，∴//EG BD ．∵底面ABCD 是菱形，∴AC BD ⊥，且O 为AC ，BD 中点，强化练习又PB PD =，∴PO BD ⊥，又AC PO O =，,AC PO ⊂平面PAC ，∴BD ⊥平面PAC ，∴EG ⊥平面PAC ．2．（2021·浙江金华市·高三期末节选）在三棱锥P ABC -中，平面PAC ⊥平面ABC ，PA PB AB ====，）证明：PC ⊥平面ABC【答案】证明见解析；【解析】证明：取AB 中点D ，连接PD ，DC∵PA PB =，AC BC =，则AB PD ⊥，AB DC ⊥， 而PD DC D ⋂=，∴AB ⊥平面PDC ， 因为PC ⊂平面PDC ，故AB PC ⊥．在ABC 中，AB ==，故222AB AC BC =+，∴BC AC ⊥．又∵平面PAC ⊥平面ABC ，且交线为AC ，BC ⊂平面ABC ， ∴BC ⊥平面PAC ，因为PC ⊂平面PAC ，故BC PC ⊥． 因为AB BC B ⋂=，∴PC ⊥平面ABC ．3．（2021·河南焦作市节选）如图，四棱锥P ABCD -的底面为正方形，PA ⊥底面ABCD ，E ，F ，H 分别为AB ，PC ，BC 的中点，求证：DE ⊥平面PAH【答案】证明见解析【解析】因为PA ⊥底面ABCD ，DE ⊂底面ABCD ，所以PA DE ⊥，因为E ，H 分别为正方形ABCD 的边AB ，BC 的中点，,,AB DA BH AE HBA EAD ，所以Rt ABH Rt DAE ≌△△，所以BAH ADE ∠=∠，由90AED ADE ∠+∠= 所以90BAH AED ∠+∠=，所以DE AH ⊥， 因为PA ⊂平面PAH ，AH ⊂平面PAH ，PA AH A ⋂=，所以DE ⊥平面PAH .4．（2021·浙江温州市节选）如图，已知三棱锥P ABC -﹐PC AB ⊥，ABC 是边长为形，PB =60PBC ∠=，点F 为线段AP 的中点，证明：PC ⊥平面ABC【答案】证明见解析【解析】在PBC 中，PB =BC =60PBC ∠=，由余弦定理可得2222cos 36PC PB BC PB BC PBC =+-⋅∠=，222PC BC PB ∴+=，PC BC ∴⊥，PC AB ⊥，AB BC B ⋂=，PC ∴⊥平面ABC ；5．（2021·陕西咸阳市·高三一模节选）如图，在三棱锥P ABC -中，平面PAC ⊥平面ABC ，PC AC ⊥，BC AC ⊥，2AC PC ==，4CB =，M 是PA 的中点，求证：PA ⊥平面MBC【答案】证明见解析【解析】平面PAC ⊥平面ABC ，平面PAC 平面ABC =AC ，BC ⊂平面ABC ，BC AC ⊥，∴BC ⊥平面PAC ， ∵PA ⊂平面PAC ， ∴BC PA ⊥，∵AC PC =，M 是PA 的中点， ∴CM PA ⊥， ∵CMBC C =，,CM BC ⊂平面MBC ，∴PA ⊥平面MBC ．6．（2021·浙江金华市节选）如图，在四棱锥P ABCD -中，底面ABCD 为矩形，PD AB ==，平面PCD ⊥平面ABCD ，若E 为PC 的中点，求证：DE ⊥平面PBC【答案】证明见解析【解析】因为平面PCD ⊥平面ABCD ，且平面PCD平面ABCD CD =，底面ABCD 为矩形，所以BC CD ⊥，又CD ⊂平面PDC ，所以BC ⊥平面PDC ，又DE ⊂平面PDC ，所以BC DE ⊥；因为PD AB DC ==，所以PDC △为等腰三角形，E 为PC 的中点，所以DE CP ⊥，因为CPBC C =，,BC CP ⊂面PBC ，所以DE ⊥面PBC7．（2021·西安市铁一中学节选）如图，在底面为菱形的四棱锥P ABCD -中，60,1,ABC PA AC PB PD ︒∠=====，点E 在PD 上，且2PEED=，求证：PA ⊥平面ABCD【答案】证明见详解【解析】因为底面ABCD 是菱形，60ABC ︒∠=， 所以1AB AC AD ===，在PAB △中，1,PA PB ==由222PA AB PB +=，可得PA AB ⊥.同理，PA AD ⊥，又AB AD A ⋂=所以PA ⊥平面ABCD .8．（2021·河南高三期末节选）如图，直四棱柱1111ABCD A B C D -的底面ABCD 为平行四边形，133,5,cos ,,5AD AB BAD BD DD E ==∠==是1CC 的中点，求证：平面DBE ⊥平面1ADD【答案】证明见解析【解析】由题意可得2222cos 16BD AD AB AB AD BAD =+-⨯∠=， 所以222AD BD AB +=，因此AD BD ⊥，在直四棱柱1111ABCD A B C D -中，1DD ⊥平面ABCD ，所以1DD BD ⊥， 又因为1ADDD D =，所以BD ⊥平面1ADD ，因为BD ⊂平面DBE ，所以平面DBE ⊥平面1ADD ．9．（2021·江苏南通市节选）如图，四面体ABCD 中，O 是BD 的中点，点G 、E 分别在线段AO 和BC 上，2BE EC =，2AG GO =，2CA CB CD BD ====，AB AD ==（1）求证：//GE 平面ACD ； （2）求证：平面ABD ⊥平面BCD . 【答案】（1）证明见解析；（2）证明见解析.【解析】证明：（1）连接BG 并延长，交AD 于M ，连接MC ，在ABD △中，O 为BD 中点，G 在AO 上，2AG GO =， ∴G 为ABD △的重心∴21BG GM =， 又21BE EC =∴BG BEGM EC=∴//GE MC ， ∵GE ⊄平面ACD ，AC ⊂平面ACD ， ∴//GE 平面ACD ；（2）在ABD △中，O 为BD 中点，2BD =，AB AD ==∴AO BD ⊥∴1AO ==，在BCD △中，2BC CD BD ===，O 为BD 中点，连接OC ，则OC =又2CA =，∴222OA OC CA +=，∴AO OC ⊥ 由AO OC ⊥，AO BD ⊥，OC BD O =，,OC BD ⊂平面BCD ，得AO ⊥平面BCD ， 又AO ⊂平面ABD ， ∴平面ABD ⊥平面BCD .10．（2021·山西吕梁市·高三一模节选）如图，四棱锥S ABCD -中，//AB CD ，BC CD ⊥，侧面SCD为等边三角形， 4AB BC ==，2CD =，SB =BC SD ⊥【答案】证明见解析【解析】由已知4BC =，2SC =，SB =222SB BC SC =+，所以90BCS ∠=︒，所以BC CS ⊥，又,BC CD CDCS C ⊥=，所以BC ⊥平面SCD ，又SD ⊂平面SCD ，所以BC SD ⊥.11．（2021·云南高三期末）如图所示，在正方体ABCD A B C D ''''-中，点M 为线段B D ''的中点.（1）求证：DD AC '⊥； （2）求证：//BM平面ACD '.【答案】（1）证明见解析；（2）证明见解析. 【解析】（1）在正方体ABCD A B C D ''''-中， ∵DD AD '⊥，DD CD '⊥，且CDAD D =，∴DD '⊥平面ACD ，AC ⊂平面ACD . ∴DD AC '⊥（2）如图所示，连接BD ，交AC 于N ，连接D N '.由题设得：BN MD '=，//BN MD '， ∴四边形BMD N '为平行四边形. ∴//BM ND '.又∵ND '⊂平面ACD '，BM ⊄平面ACD '， ∴//BM平面ACD '.12．（2021·江西景德镇市节选）如图，已知四棱锥S ABCD -，其中//AD BC ，AB AD ⊥，45BCD ∠=，22BC AD ==，侧面SBC ⊥底面ABCD ，E 是SB 上一点，且ECD 是等边三角形，求证：CE ⊥平面SAB【答案】证明见解析 【解析】//AD BC ，AB AD ⊥，AB BC ∴⊥，侧面SBC ⊥底面ABCD ，侧面SBC底面ABCD BC =，AB平面ABCD ，AB ∴⊥平面SBC ，CE ⊂平面SBC ，CE AB ∴⊥，如下图所示，取BC 的中点F ，连接DF 、EF ，2BC AD =，且F 为BC 的中点，则AD BF =，//BC AD ，则//AD BF ，所以，四边形ABFD 为平行四边形，则//DF AB ， DF ⊥∴平面SBC ，EF 、BC ⊂平面SBC ，DF EF ∴⊥，DF BC ⊥，ECD 为等边三角形，则EF CF BF ===，所以，FBE BEF ∠=∠，FCE CEF ∠=∠，由2FBE BEF FCE CEF BEC π∠+∠+∠+∠=∠=，2BEC π∴∠=，即CE SB ⊥，SB AB B =，因此，CE ⊥平面SAB ；13．（2021·江西景德镇市·景德镇一中）如图，在三棱柱111ABC A B C -中，平面11A ACC ⊥平面ABC ，2,AB BC == 30ACB ∠=，13AA =，11BC A C ，E 为AC 的中点.（1）求证：1//AB 平面1C EB ； （2）求证：1A C ⊥平面1C EB .【答案】（1）证明见解析；（2）证明见解析. 【解析】（1）如下图所示，连接1AB 、1B C ，设11B CBC F =，连接EF ，在三棱柱111ABC A B C -中，四边形11BB C C 为平行四边形， 因为11B CBC F =，在点F 为1B C 的中点，又因为点E 为AC 的中点，1//EF AB ∴，1AB ⊄平面1C EB ，EF ⊂平面1C EB ，所以，1//AB 平面1C EB ；（2）AB BC =，E 为AC 的中点，BE AC ∴⊥，因为平面11A ACC ⊥平面ABC ，平面11A ACC ⋂平面ABC AC =，BE ⊂平面ABC ，BE ∴⊥平面11A ACC ，1A C ⊂平面11A ACC ，1A C BE ∴⊥， 11BC AC ⊥，1BE BC B =，1A C ∴⊥平面1C EB .14．（2021·陕西咸阳市）在三棱锥A BCD -中，E 、F 分别为AD 、DC 的中点，且BA BD =，平面ABD ⊥平面ADC .（1）证明：//EF 平面ABC ；（2）证明：BE CD ⊥.【答案】（1）证明见解析；（2）证明见解析.【解析】（1）在ADC 中，E 、F 分别是AD 、DC 的中点，//EF AC ∴.EF ⊄平面ABC ，AC ⊂平面ABC ，//EF ∴平面ABC ；（2）在ABD △中，BA BD =，E 为AD 的中点，BE AD ∴⊥， 又平面ABD ⊥平面ADC ，平面ABD ⋂平面ADC AD =，BE ⊂平面ABD ，BE ∴⊥平面ADC .CD ⊂平面ADC ，BE CD ∴⊥.15．（2021·全国）已知四棱锥P ABCD -中，平面PAB ⊥平面ABCD ，PAB △为等边三角形，底面ABCD 为直角梯形，90DAB ∠=︒且2AB CD =，点M 为PB 的中点，求证：PB DM ⊥.【答案】证明见解析.【解析】因为PAB △为等边三角形，M 为PB 的中点，所以AM PB ⊥，因为平面PAB ⊥平面ABCD ，平面PAB ⋂平面ABCD AB =，DA AB ⊥，DA ⊂平面ABCD ， 所以DA ⊥平面PAB ，因为PB ⊂平面PAB ，所以DA PB ⊥，因为DA AM A ⋂=，所以PB ⊥平面ADM ，因为DM ⊂平面ADM ，所以PB DM ⊥.16．（2020·全国）如图，矩形ABCD 所在平面与半圆弧CD 所在平面垂直，M 是CD 上异于C ，D 的点．（1）证明：平面AMD ⊥平面BMC ；（2）若P 点是线段AM 的中点，求证：//MC 平面PBD ．【答案】（1）证明见解析；（2）证明见解析.【解析】证明：（1）因为矩形ABCD 所在平面与半圆弦CD 所在平面垂直，面ABCD 面CDM CD =，AD DC ⊥，AD ⊂面ABCD ，所以AD ⊥半圆弦CD 所在平面，且CM ⊂半圆弦CD 所在平面，所以CM AD ⊥；又M 是CD 上异于C ，D 的点，所以CM DM ⊥；又DM AD D =，所以CM ⊥平面AMD ；又CM ⊂平面CMB ，所以平面AMD ⊥平面BMC ；（2）由P 是AM 的中点，连接BD 交AC 于点O ，连接OP ，如图所示：由中位线定理得//MC OP ；又MC ⊂/平面BDP ，OP ⊂平面BDP ，所以//MC 平面PBD ．17．（2021·全国高三专题练习）如图，边长为2的正方形ABCD 所在的平面与半圆弧CD 所在平面垂直，M 是CD 上异于C ，D 的点.证明：平面AMD ⊥平面BMC .【答案】证明见解析【解析】由题设知，平面CMD ⊥平面ABCD ，交线为CD .因为BC ⊥CD ，BC ⊂平面ABCD ，所以BC ⊥平面CMD ，故BC ⊥DM .因为M 为CD 上异于C ，D 的点，且DC 为直径，所以DM ⊥CM .又BC CM =C ，所以DM ⊥平面BMC .而DM ⊂平面AMD ，故平面AMD ⊥平面BMC .18．（2020·全国高三专题练习）已知四棱锥P ABCD -中，平面PAB ⊥平面ABCD ，PAB △为等边三角形，底面ABCD 为直角梯形，90DAB ∠=︒且2AB CD =，点M 为PB 的中点，求证：DM PB .【答案】证明见解析.【解析】证明：∵PAB ∆为等边三角形，M 为PB 的中点，∴AM PB ⊥， 又∵平面PAB ⊥平面ABCD ，且平面PAB 平面ABCD AB =， DA AB ⊥，DA ⊂平面ABCD ，∴DA ⊥平面PAB ，又PB ⊂平面PAB ，∴DA PB ⊥，∵DA AM A ⋂=，∴PB ⊥平面ADM ，又DM ⊂平面ADM ，∴PB DM ⊥.19．（2020·江苏苏州市·高三三模）如图，在三棱柱111A B C ABC -中，AB AC =，D 为BC 中点，平面ABC ⊥平面11BCC B ，11BC B D ⊥.（1）求证：1//A C 平面1AB D ；（2）求证：11AB BC ⊥.【答案】（1）证明见解析（2）证明见解析【解析】证明：（1）连结1A B 交1AB 于点O ，连结OD .因为111A B C ABC -是三棱柱，所以11ABB A 是平行四边形，所以O 为1A B 中点. 有因为D 为BC 中点，所以1OD AC . 又1AC ⊄平面1AB D ，OD ⊂平面1AB D ，所以1A C 平面1AB D . （2）因为AB AC =，D 为BC 中点，所以AD BC ⊥.又因为平面ABC ⊥平面11BCC B ，平面ABC 平面11BCC B BC =，AD ⊂平面ABC ， 所以AD ⊥平面11BCC B . 因为1BC ⊂平面11BCC B ，所以1AD BC ⊥. 又因为11BC B D ⊥，1AD B D D ⋂=，AD ⊂平面1AB D ，1B D ⊂平面1AB D ， 所以1BC ⊥平面1AB D . 因为1AB ⊂平面1AB D ，所以11AB BC ⊥.。

.线线垂直、线面垂直、面面垂直局部习及答案1．在四面体ABCD中，△ABC与△DBC都是边长为 4 的正三角形．(1)求证：BC⊥AD；2 如图，在三棱锥S—ABC 中， SA⊥平面ABC，平面 SAB⊥平面 SBC．(第1题)〔1〕求证： AB⊥BC；3.如图，四棱锥 P—ABCD 的底面是边长为 a 的形， PA⊥底面 ABCD，E 为 AB 的中点，且 PA=AB．〔1〕求证：平面 PCE⊥平面 PCD；〔2〕求点 A 到平面 PCE的距离．4.如图 2-4-2 所示，三棱锥 S—ABC 中， SB=AB ，SC=AC，作AD⊥BC 于 D，SH⊥AD 于 H，求证：SH⊥平面ABC.5.如下图， Rt△ABC 所在平面外一点 S，且 SA=SB=SC，点 D为斜边 AC 的中点 .(1)求证： SD⊥平面 ABC；(2)假设 AB=BC，求证： BD⊥平面 SAC.6. 证明：在体 ABCD－A1B1C1 D1中， A1C⊥平面 BC1 DD 1C1A 1B 1D CA B7.如下图，直三棱柱中，∠ ACB=90°，AC=1 ，，侧棱，侧面的两条对角线交点为 D，的中点为 M.求证： CD⊥平面 BDM.8.在三棱锥Ａ－BCD中，BC＝AC，AD＝BD，作 BE⊥CD，Ｅ为垂足，作 AH⊥BE于Ｈ．求证： AH⊥平面 BCD．9. 如图，过 S 引三条长度相等但不共面的线段 SA、SB、SC，且∠ASB=∠ASC=60°，∠BSC=90°，求证：平面 ABC⊥平面 BSC．10.如图，在长方体ABCD—A1B1C1D1中，AB＝2，BB1＝BC＝1，E为D1 C1的中点，连结 ED，EC，EB和 DB．(1)求证：平面EDB⊥平面EBC；(2)求二面角E－DB－C的正切值 .11：直线 PA 垂直于圆 O 所在的平面， A 为垂足， AB 为圆 O 的直径，C 是圆周上异于 A、B 的一点。

空间中的垂直关系专题训练知识梳理一、线线垂直：如果两条直线于一点或经过后相交于一点，并且交角为，则称这两条直线互相垂直.二、线面垂直：1.定义：如果一条直线和一个平面相交，并且和这个平面内的_________________，则称这条直线和这个平面垂直. 也就是说，如果一条直线垂直于一个平面，那么他就和平面内任意一条直线都 .直线l和平面α互相垂直，记作l⊥α.2.判定定理：如果一条直线与平面内的直线垂直，则这条直线与这个平面垂直.推论①：如果在两条平行直线中，有一条垂直于平面，那么另一条直线也于这个平面.推论②：如果两条直线同一个平面，那么这两条直线平行.3.点到平面的距离：长度叫做点到平面的距离.三、面面垂直：1.定义：如果两个相交平面的交线与第三个平面，又这两个平面与第三个平面相交所得的两条交线，就称这两个平面互相垂直.平面α，β互相垂直，记作α⊥β.2.判定定理：如果一个平面经过另一个平面的___________，则这两个平面互相垂直.3.性质定理：如果两个平面互相垂直，那么在一个平面内垂直于直线垂直于另一个平面.四、求点面距离的常用方法：1.直接过点作面的垂线，求垂线段的长，通常要借助于某个三角形.2.转移法：借助线面平行将点转移到直线上某一特殊点到平面的距离来求解.3.体积法：利用三棱锥的特征转换位置来求解.题型一线线垂直、线面垂直的判定及性质例1.如图，在四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°,PA=AB=BC,E是PC的中点.求证：(1)CD⊥AE；(2)PD⊥平面ABE.【变式1】已知：正方体ABCD﹣A1B1C1D1 ，AA1=2，E为棱CC1的中点．（Ⅰ）求证：B1D1⊥AE；（Ⅱ）求证：AC∥平面B1DE．【解答】（Ⅰ）连接BD，则BD∥B1D1，∵ABCD是正方形，∴AC⊥ BD．∵CE⊥平面ABCD，BD⊂平面ABCD，∴CE⊥BD．又∵AC∩CE=C，∴BD⊥面ACE．∵AE⊂面ACE，∴BD⊥AE，∴B1D1⊥AE．﹣﹣﹣（5分）（Ⅱ）证明：取BB1的中点F，连接AF、CF、EF．∵ E、F是C1C、B1B的中点，∴ CE∥B1F且CE=B1F，∴ 四边形B1FCE是平行四边形，∴ CF∥ B1E．∵ 正方形BB1C1C 中，E、F是CC、BB的中点，∴ EF∥BC且EF=BC又∵ BC∥AD且BC=AD，∴ E F∥AD且EF=AD．∴ 四边形ADEF是平行四边形，可得AF∥ED，∵ AF∩CF=C，BE∩ED=E，∴ 平面ACF∥平面B1DE．又∵ AC⊂平面ACF，∴AC∥面B1DE．【变式2】如图，已知四棱锥P﹣ABCD，底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，点E、G分别是CD、PC的中点，点F在PD上，且PF：FD=2：1．（Ⅰ）证明：EA⊥PB；（Ⅱ）证明：BG∥面AFC．【解答】（Ⅰ）证明：因为面ABCD为菱形，且∠ABC=60°，所以△ ACD为等边三角形，又因为E是CD的中点，所以EA⊥AB．又PA⊥平面ABCD，所以EA⊥PA．而AB∩PA=A所以EA⊥面PAB，所以EA⊥PB．（Ⅱ）取PF中点M，所以PM=MF=FD．连接MG，MG∥CF，所以MG∥面AFC．连接BM，BD，设AC∩BD=O，连接OF，所以BM∥OF，所以BM∥面AFC．而BM∩MG=M所以面BGM∥面AFC，所以BG∥面AFC．【变式3】如图，四棱柱ABCD﹣A1B1C1D1的底面ABCD是正方形，O为底面中心，A1O⊥平面ABCD，AB=，AA1=2．（1）证明：AA1⊥BD（2）证明：平面A1BD∥平面CD1B1；（3）求三棱柱ABD﹣A1B1D1的体积．【解答】（1）证明：∵底面ABCD是正方形，∴BD⊥AC，又∵ A1O⊥平面ABCD且BD⊂面ABCD，∴ A1O⊥BD，又∵ A1O∩AC=O，A1O⊂面A1AC，AC⊂面A1AC，∴BD⊥面A1AC，AA1⊂面A1AC，∴ AA1⊥BD．（2）∵ A1B1∥AB，AB∥CD，∴ A1B1∥CD，又A1B1=CD，∴四边形A1B1CD是平行四边形，∴ A1D∥B1C，同理A1B∥CD1，∵ A1B⊂平面A1BD，A1D⊂平面A1BD，CD1⊂平面CD1B1，B1C⊂平面CD1B，且A1B∩A1D=A1，CD1∩B1C=C，∴平面A1BD∥平面CD1B1．（3）∵ A1O⊥面ABCD，∴ A1O是三棱柱A1B1D1﹣ABD的高，在正方形ABCD中，AO=1．在Rt△A1OA中，AA1=2，AO=1，∴ A1O=，∴ V三棱柱ABD﹣A1B1D1=S△ABD•A1O=•（）2•=∴三棱柱ABD﹣A1B1D1的体积为．【变式4】如图，三棱柱ABC﹣A1B1C1中，侧棱AA1⊥底面ABC，AB=BC=AC=AA1=4，点F在CC1上，且C1F=3FC，E是BC的中点．（1）求证：AE⊥平面BCC1B1（2）求四棱锥A﹣B1C1FE的体积；（3）证明：B1E⊥AF．【解答】（1）∵ AB=AC，E是BC的中点，∴AE⊥ BC．在三棱柱ABC﹣A1B1C1，中，BB1∥ AA1，∴ BB1⊥平面ABC，∵ AE⊂平面ABC，∴ BB1⊥ AE，…．（2分）又∵ BB1∩BC=B，…．（3分）BB1，BC⊂平面BB1C1C，∴AE⊥平面BB1C1C，…．（4分）（2）由（1）知，即AE为四棱锥A﹣B1C1FE的高，在正三角形ABC中，AE=AB=2，…在正方形BB1C1C，中，CE=BE=2，CF=1，∴=﹣﹣S△CFE=4×=11．…（6分）∴=•AE==…（7分）（3）证明：连结B1F，由（1）得AE⊥平面BB1C1C，∵ B1E⊂平面BB1C1C，∴AE⊥B1E，…．（8分）在正方形BB1C1C，中，B1F==5，B1E==2，EF==，∵ B1F2=B1E2+EF2，∴ B1E⊥EF…．（9分）又∵AE∩EF=E，…．（10分）AE，EF⊂平面AEF，∴ B1E⊥平面AEF，…．（11分）∵ AF⊂平面AEF，∴ B1E⊥AF．…．（12分）【变式5】如图，四棱锥P﹣ABCD中，PD⊥平面ABCD，底面ABCD为正方形，BC=PD=2，E为PC的中点，G在BC上，且CG=CB（1）求证：PC⊥BC；（2）求三棱锥C﹣DEG的体积；（3）AD边上是否存在一点M，使得PA∥平面MEG？若存在，求AM的长；否则，说明理由．【解答】（1）证明：∵PD⊥平面ABCD，∴PD⊥BC．又∵ABCD是正方形，∴BC⊥CD．又∵PD∩CD=D，∴BC⊥平面PCD．又∵PC⊂平面PCD，∴PC⊥BC．（2）∵BC⊥平面PCD，∴ GC是三棱锥G﹣DEC的高．∵ E是PC的中点，∴ S△EDC=S△PDC==×（×2×2）=1．V C﹣DEG=V G=GC•S△DEC=××1=．﹣DEC（3）连结AC，取AC中点O，连结EO、GO，延长GO交AD于点M，则PA∥平面MEG．证明：∵E为PC的中点，O是AC的中点，∴EO∥PA．又∵EO⊂平面MEG，PA⊄平面MEG，∴PA∥平面MEG．在正方形ABCD中，∵O是AC的中点，BC=PD=2，CG=CB．∴△OCG≌△OAM，∴AM=CG=，∴所求AM的长为．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣【变式6】如图所示，在三棱柱ABC﹣A1B1C1中，BB1⊥底面A1B1C1，A1B1⊥B1C1且A1B1=BB1=B1C1，D为AC的中点．（Ⅰ）求证：A1B⊥AC1（Ⅱ）在直线CC1上是否存在一点E，使得A1E⊥平面A1BD，若存在，试确定E 点的位置；若不存在，请说明理由．【解答】（Ⅰ）证明：连接AB1∵ BB1⊥平面A1B1C1∴ B1C1⊥BB1∵ B1C1⊥A1B1且A1B1∩BB1=B1∴ B1C1⊥平面A1B1BA∴ A1B⊥B1C1 . 又∵ A1B⊥AB1且AB1∩B1C1=B1∴A1B⊥平面AB1C1∴A1B⊥AC1（Ⅱ）存在点E在CC1的延长线上且CE=2CC1时，A1E⊥平面A1BD．设AB=a，CE=2a，∴，∴，，DE=，∴，∴A1E⊥A1D…∵BD⊥AC，BD⊥CC1，AC∩CC1=C，∴BD⊥平面ACC1A1，又A1E⊂平面ACC1A1∴ A1E⊥BD. 又BD∩A1D=D ，∴ A1E⊥平面A1BD【变式7】如图，在直三棱柱ABC﹣A1B1C1中，AC=3，BC=4，AB=5，点D是AB的中点．（1）求证：AC⊥ BC1；（2）求证：AC1∥平面CDB1．【解答】证明：（1）因为三棱柱ABC﹣A1B1C1为直三棱柱，所以C1C⊥平面ABC，所以C1C⊥AC．又因为AC=3，BC=4，AB=5，所以AC2+BC2=AB2，所以AC⊥BC．又C1C∩BC=C，所以AC⊥平面CC1B1B，所以AC⊥ BC1．（2）连结C1B交CB1于E，再连结DE，由已知可得E为C1B的中点，又∵D为AB的中点，∴DE 为△BAC1的中位线．∴AC1∥DE。

线面垂直练习题及答案线面垂直是几何学中一个重要的概念，它涉及到直线和平面之间的关系。

在几何学中，我们经常需要判断线和平面是否垂直，以及如何确定它们的垂直关系。

为了帮助大家更好地理解和掌握线面垂直的概念，本文将介绍一些线面垂直的练习题及答案。

1. 练习题：判断线段和平面是否垂直题目：已知线段AB的两个端点分别为A(1, 2, 3)和B(4, 5, 6)，平面P的法向量为(2, -1, 3)，判断线段AB是否垂直于平面P。

解答：要判断线段AB是否垂直于平面P，只需判断线段AB的方向向量是否与平面P的法向量垂直。

线段AB的方向向量为AB = B - A = (4, 5, 6) - (1, 2, 3) = (3, 3, 3)。

两个向量的点积为3*2 + 3*(-1) + 3*3 = 9，不等于0。

因此，线段AB不垂直于平面P。

2. 练习题：确定两平面之间的垂直关系题目：已知平面P1的法向量为(1, 2, -1)，平面P2的法向量为(2, -1, 3)，判断平面P1和平面P2之间的垂直关系。

解答：两个平面垂直的条件是它们的法向量垂直，即两个法向量的点积为0。

计算两个法向量的点积为1*2 + 2*(-1) + (-1)*3 = 0，等于0。

因此，平面P1和平面P2垂直。

3. 练习题：求垂直平面上的直线题目：已知平面P的方程为2x + 3y - z = 6，求过点A(1, 2, 3)且垂直于平面P的直线的方程。

解答：垂直于平面P的直线的方向向量应该与平面P的法向量垂直。

由平面P的方程可知，平面P的法向量为(2, 3, -1)。

因此，过点A(1, 2, 3)且垂直于平面P 的直线的方向向量为(2, 3, -1)。

直线的方程可以表示为x = 1 + 2t，y = 2 + 3t，z = 3 - t，其中t为参数。

4. 练习题：判断直线和平面是否垂直题目：已知直线L的方程为x = 1 + 2t，y = 2 + 3t，z = 3 - t，平面P的方程为2x + 3y - z = 6，判断直线L是否垂直于平面P。

线线垂直、线面垂直、面面垂直部分习及答案1．在四面体ABCD中，△ABC与△DBC都是边长为4的正三角形．(1)求证：BC⊥AD；2如图，在三棱锥S—ABC中，SA⊥平面ABC，平面SAB⊥平面SBC．(第1题)（1）求证：AB⊥BC；3.如图，四棱锥P—ABCD的底面是边长为a的正方形，PA⊥底面ABCD，E为AB的中点，且PA=AB．4. 如图2-4-2所示，三棱锥S—ABC中，SB=AB，SC=AC，作AD⊥BC于D，SH⊥AD于H，求证：SH⊥平面ABC.5. 如图所示，已知Rt△ABC所在平面外一点S，且SA=SB=SC，点D为斜边AC的中点.(1)求证：SD⊥平面ABC；(2)若AB=BC，求证：BD⊥平面SAC.6. 证明：在正方体ABCD－A1B1C1D1中，A1C⊥平面BC1DD1C1A1B1D CA B7. 如图所示，直三棱柱中，∠ACB=90°，AC=1，，侧棱，侧面的两条对角线交点为D，的中点为M.求证：CD⊥平面BDM.8.在三棱锥Ａ－BCD中，BC＝AC，AD＝BD，作BE⊥CD，Ｅ为垂足，作AH⊥BE于Ｈ．求证：AH⊥平面BCD．9. 如图，过S引三条长度相等但不共面的线段SA、SB、SC，且∠ASB=∠ASC=60°，∠BSC=90°，求证：平面ABC⊥平面BSC．10.如图，在长方体ABCD—A1B1C1D1中，AB＝2，BB1＝BC＝1，E为D1C1的中点，连结ED，EC，EB和DB．(1)求证：平面EDB⊥平面EBC；(2)求二面角E－DB－C的正切值.11：已知直线PA垂直于圆O所在的平面，A为垂足，AB为圆O的直径，C是圆周上异于A、B的一点。

求证：平面PAC 平面PBC。

12..如图1-10-3所示，过点S引三条不共面的直线，使∠BSC=90°，∠ASB=∠ASC=60°，若截取SA=SB=SC.求证：平面ABC⊥平面BSC13.如图1-10-5所示，在四面体ABCD中，BD= a,2AB=AD=BC=CD=AC=a.求证：平面ABD⊥平面BCD.14.如图所示，△ABC 为正三角形，CE ⊥平面ABC ，BD ∥CE ，且CE=AC=2BD ，M 是AE 的中点，求证：(1)DE=DA ；(2)平面BDM ⊥平面ECA ；(3)平面DEA ⊥平面ECA ．15.如图所示，已知PA ⊥矩形ABCD 所在平面，M 、N 分别是AB 、PC 的中点．(1)求证：MN ∥平面PAD ；(2)求证：MN ⊥CD ；(3)若∠PDA=45°，求证：MN ⊥平面PCD ．16. 如图1，在正方体1111ABCD A B C D -中，M 为1CC 的中点，AC 交BD 于点O ，求证：1A O ⊥平面MBD答案与提示：1. 证明：(1)取BC 中点O ，连结AO ，DO ．∵△ABC ，△BCD 都是边长为4的正三角形， ∴AO ⊥BC ，DO ⊥BC ，且AO ∩DO ＝O ， ∴BC ⊥平面AOD ．又AD ⊂平面AOD ， ∴BC ⊥AD ．2. 【证明】作AH ⊥SB 于H ，∵平面SAB ⊥平面SBC ．平面SAB ∩平面SBC=SB ，∴AH ⊥平面SBC ，又SA ⊥平面ABC ，∴SA ⊥BC ，而SA 在平面SBC 上的射影为SB ，∴BC ⊥SB ，又SA ∩SB=S ，∴BC ⊥平面SAB ．∴BC ⊥AB ．3. 【证明】PA ⊥平面ABCD ，AD 是PD 在底面上的射影，又∵四边形ABCD 为矩形，∴CD ⊥AD ，∴CD ⊥PD ，∵AD ∩PD=D ∴CD ⊥面PAD ，∴∠PDA 为二面角P —CD —B 的平面角，∵PA=PB=AD ，PA ⊥AD ∴∠PDA=45°，取Rt △PAD 斜边PD 的中点F ，则AF ⊥PD ，∵AF ⊂面PAD ∴CD ⊥AF ，又PD ∩CD=D ∴AF ⊥平面PCD ，取PC 的中点G ，连GF 、AG 、EG ，则GF21CD 又AE21CD ，∴GF AE ∴四边形AGEF 为平行四边形∴AF ∥EG ，∴EG ⊥平面PDC 又EG ⊂平面PEC ，∴平面PEC ⊥平面PCD ．（2）【解】由（1）知AF ∥平面PEC ，平面PCD ⊥平面PEC ，过F 作FH ⊥PC 于H ，则FH ⊥平面PEC∴FH 为F 到平面PEC 的距离，即为A 到平面PEC 的距离．在△PFH 与 △PCD 中，∠P 为公共角，而∠FHP=∠CDP=90°，∴△PFH ∽△PCD ．∴PC PFCD FH =，设AD=2，∴PF=2，PC=324822=+=+CD PD ，∴FH=362322=⋅∴A 到平面PEC 的距离为36． 4.【证明】取SA的中点E，连接EC ，EB. ∵SB=AB,SC=AC, ∴SA ⊥BE,SA ⊥CE. 又∵CE ∩BE=E, ∴SA ⊥平面BCE.∵BC平面BCE5. 证明：(1)因为SA=SC ，D 为AC 的中点， 所以SD ⊥AC.连接BD. 在Rt △ABC 中，有AD=DC=DB ， 所以△SDB ≌△SDA ， 所以∠SDB=∠SDA ， 所以SD ⊥BD.又AC ∩BD=D ， 所以SD ⊥平面ABC. (2)因为AB=BC ，D 是AC 的中点， 所以BD ⊥AC. 又由(1)知SD ⊥BD ， 所以BD 垂直于平面SAC 内的两条相交直线，所以BD⊥平面SAC.6.证明：连结ACBD AC⊥AC为A1C在平面AC上的射影∴⊥⊥⎫⎬⎭⇒⊥BD A CA C BC A C BC D11111同理可证平面7.证明：如右图，连接、、，则.∵，∴为等腰三角形.又知D 为其底边的中点，∴.∵，，∴.又，∴.∵为直角三角形，D 为的中点，∴，.又，，∴..即CD⊥DM.∵、为平面BDM内两条相交直线，∴CD ⊥平面BDM.8.证明：取AB的中点Ｆ，连结CF，DF．∵AC BC=，∴CF AB⊥．∵AD BD=，∴DF AB⊥．又CF DF F=，∴AB⊥平面CDF．∵CD⊂平面CDF，∴⊥．CD AB又CD BE⊥，BE AB B=，∴CD⊥平面ABE，CD AH⊥．∵AH CD⊥，AH BE=，⊥，CD BE E∴AH⊥平面BCD．9.证明：如图，已知PA=PB=PC=a，由∠APB=∠APC=60°，△PAC，△PAB为正三角形，则有：PA=PB=PC=AB=AC=a，取BC中点为E直角△BPC中，，，由AB=AC ，AE ⊥BC ， 直角△ABE 中，，，， 在△PEA 中，，，∴，平面ABC ⊥平面BPC.10. 证明：(1)在长方体ABCD －A 1B 1C 1D 1中，AB ＝2，BB 1＝BC ＝1，E 为D 1C 1的中点．∴△DD 1E 为等腰直角三角形，∠D 1ED ＝45°．同理∠C 1EC ＝45°．∴︒=∠90DEC ，即DE ⊥EC ．在长方体ABC D －1111D C B A 中，BC ⊥平面11DCC D ，又DE ⊂平面11DCC D ，∴BC ⊥DE ．又C BC EC = ，∴DE ⊥平面EBC ．∵平面DEB 过DE ，∴平面DEB ⊥平面EBC ．(2)解：如图，过E 在平面11DCC D 中作EO ⊥DC 于O ．在长方体ABCD －1111D C B A 中，∵面ABCD ⊥面11DCC D ，∴EO ⊥面ABCD．过O在平面DBC中作OF⊥DB于F，连结EF，∴EF⊥BD．∠EFO为二面角E－D B－C的平面角．利用平面几何知1，(第10题)识可得OF＝5又OE＝1，所以，tan∠EFO＝5．11.（1）【证明】∵C是AB为直径的圆O的圆周上一点，AB是圆O的直径∴BC⊥AC；又PA⊥平面ABC，BC⊂平面ABC，∴BC⊥PA，从而BC⊥平面PAC．∵BC ⊂平面PBC，∴平面PAC⊥平面PBC．.12.证明：如图1-10-4所示,取BC的中点D，连接AD，SD.由题意知△ASB与△ASC是等边三角形，则AB=AC，∴AD⊥BC,SD⊥BC.令SA=a,在△SBC中，SD= a,又AD= = a,∴AD2+SD2=SA2,即AD⊥SD.又∵AD⊥BC，∴AD⊥平面SBC.∵AD平面ABC，∴平面ABC⊥平面SBC.13.证明：取BD的中点E，连接AE，CE.则AE⊥BD,BD⊥CE.在△ABD中，AB=a,BE= BD= ,∴AE= ,同理,CE= .在△AEC中，AE=EC= ,AC=a,∴AC2=AE2+EC2，即AE⊥EC.∵BD∩EC=E,∴AE⊥平面BCD.又∵AE平面ABD，∴平面ABD⊥平面BCD14.证明：((1)取EC的中点F，连接DF．∵CE⊥平面ABC，∴CE⊥BC．易知DF∥BC，CE⊥DF．∵BD∥CE，∴BD⊥平面ABC．在Rt△EFD和Rt△DBA中，∵，，∴Rt△EFD≌Rt△DBA．故DE=AD．(2)取AC的中点N，连接MN、BN，MN CF．∵BD CF，∴MN BD．N平面BDM．∵EC⊥平面ABC，∴EC⊥BN．又∵AC⊥BN，∴BN⊥平面ECA．又∵BN平面MNBD，∴平面BDM⊥平面ECA．(3)∵DM∥BN，BN⊥平面ECA，∴DM⊥平面ECA．又∵DM平面DEA，∴平面DEA⊥平面ECA．15.证明：(1)取PD的中点E，连接AE、EN，则，故AMNE为平行四边形，∴MN∥AE．∵AE平面PAD，MN平面PAD，∴MN∥平面PAD．(2)要证MN⊥CD，可证MN⊥AB．由(1)知，需证AE⊥AB．∵PA⊥平面ABCD，∴PA⊥AB．又AD⊥AB，∴AB⊥平面PAD．∴AB⊥AE．即AB⊥MN．又CD∥AB，∴MN⊥CD．(3)由(2)知，MN⊥CD，即AE⊥CD，再证AE⊥PD即可．∵ PA ⊥平面ABCD ，∴ PA ⊥AD ． 又∠PDA=45°，E 为PD 的中点． ∴ AE ⊥PD ，即MN ⊥PD ． 又MN ⊥CD ，∴ MN ⊥平面PCD ．16.证明：连结MO ，1A M ，∵DB ⊥1A A ，DB ⊥AC ，1A A AC A =，∴DB ⊥平面11A ACC ，而1AO ⊂平面11A ACC ∴DB ⊥1A O ． 设正方体棱长为a ，则22132A O a =，2234MO a =．在Rt △11A C M 中，22194A M a =．∵22211A O MO A M +=，∴1AO OM ⊥．∵OM ∩DB =O ，∴ 1A O ⊥平面MBD ．。

直线、平面垂直的判定及其性质建议用时：45分钟一、选择题1．设m，n是两条不同的直线，α，β是两个不同的平面，则下列说法正确的是()A．若m⊥n，n∥α，则m⊥αB．若m∥β，β⊥α，则m⊥αC．若m⊥β，n⊥β，n⊥α，则m⊥αD．若m⊥n，n⊥β，β⊥α，则m⊥αC[A中，由m⊥n，n∥α可得m∥α或m与α相交或m⊥α，错误；B中，由m∥β，β⊥α可得m∥α或m与α相交或m⊂α，错误；C中，由m⊥β，n⊥β可得m∥n，又n⊥α，所以m⊥α，正确；D中，由m⊥n，n⊥β，β⊥α可得m∥α或m与α相交或m⊂α，错误．] 2．在下列四个正方体中，能得出AB⊥CD的是()A[A选项中，因为CD⊥平面AMB，所以CD⊥AB；B选项中，AB与CD 成60°角；C选项中，AB与CD成45°角；D选项中，AB与CD夹角的正切值为 2.]3．(2019·东北三省三校联考)在四棱锥P-ABCD中，P A⊥平面ABCD，底面ABCD是正方形，且P A＝AB＝2，则直线PB与平面P AC所成角为()A.π6 B.π4 C.π3 D.π2A[连接BD，交AC于点O.因为P A⊥平面ABCD，底面ABCD是正方形，所以BD⊥AC，BD⊥P A.又因为P A∩AC＝A，所以BD⊥平面P AC，故BO⊥平面P AC.连接OP，则∠BPO即为直线PB与平面P AC所成角．又因为P A＝AB＝2，所以PB＝22，BO＝ 2.所以sin∠BPO＝BOPB＝12，所以∠BPO＝π6.故选A.]4．(2017·全国卷Ⅲ)在正方体ABCD-A1B1C1D1中，E为棱CD的中点，则() A．A1E⊥DC1B．A1E⊥BDC．A1E⊥BC1D．A1E⊥ACC[如图．∵A1E在平面ABCD上的投影为AE，而AE不与AC，BD垂直，∴B，D错；∵A1E在平面BCC1B1上的投影为B1C，且B1C⊥BC1，∴A1E⊥BC1，故C正确；(证明：由条件易知，BC1⊥B1C，BC1⊥CE，又CE∩B1C＝C，∴BC1⊥平面CEA1B1.又A1E⊂平面CEA1B1，∴A1E⊥BC1)∵A1E在平面DCC1D1上的投影为D1E，而D1E不与DC1垂直，故A错．] 5．如图所示，在四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°.将△ADB沿BD折起，使平面ABD⊥平面BCD，构成三棱锥A-BCD，则在三棱锥A-BCD中，下列结论正确的是()A．平面ABD⊥平面ABCB．平面ADC⊥平面BDCC．平面ABC⊥平面BDCD．平面ADC⊥平面ABCD[∵在四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°，∴BD⊥CD.又平面ABD⊥平面BCD，且平面ABD∩平面BCD＝BD，故CD⊥平面ABD，则CD⊥AB.又AD⊥AB，AD∩CD＝D，AD⊂平面ADC，CD⊂平面ADC，故AB⊥平面ADC.又AB⊂平面ABC，∴平面ADC⊥平面ABC.]二、填空题6．如图，在长方体ABCD-A1B1C1D1中，AB＝BC＝2，若该长方体的体积为82，则直线AC1与平面BB1C1C所成的角为．30°[连接BC1(图略)，由AB⊥平面BB1C1C知∠AC1B就是直线AC1与平面BB1C1C所成的角．由2×2×AA1＝82得AA1＝22，∴BC1＝BC2＋CC21＝23，在Rt△AC1B中，tan∠AC1B＝ABBC1＝223＝33，∴∠AC1B＝30°.]7．在正四棱柱ABCD-A1B1C1D1中，AA1＝2AB＝2，则点A1到平面AB1D1的距离是．23[如图，△AB1D1中，AB1＝AD1＝5，B1D1＝2，∴△AB 1D 1的边B 1D 1上的高为(5)2－⎝ ⎛⎭⎪⎫222＝322，∴S △AB 1D 1＝12×2×322＝32，设A 1到平面AB 1D 1的距离为h ；则有S △AB 1D 1×h ＝S △A 1B 1D 1×AA 1， 即32h ＝12×2，解得h ＝23.]8．(2016·全国卷Ⅱ)α，β是两个平面，m ，n 是两条直线，有下列四个命题： ①如果m ⊥n ，m ⊥α，n ∥β，那么α⊥β. ②如果m ⊥α，n ∥α，那么m ⊥n . ③如果α∥β，m ⊂α，那么m ∥β.④如果m ∥n ，α∥β，那么m 与α所成的角和n 与β所成的角相等． 其中正确的命题有 ．(填写所有正确命题的编号)②③④ [对于①，α，β可以平行，可以相交也可以不垂直，故错误． 对于②，由线面平行的性质定理知存在直线l ⊂α，n ∥l ，又m ⊥α，所以m ⊥l ，所以m ⊥n ，故正确．对于③，因为α∥β，所以α，β没有公共点．又m ⊂α，所以m ，β没有公共点，由线面平行的定义可知m ∥β，故正确．对于④，因为m ∥n ，所以m 与α所成的角和n 与α所成的角相等．因为α∥β，所以n 与α所成的角和n 与β所成的角相等，所以m 与α所成的角和n 与β所成的角相等，故正确．]三、解答题9．(2018·北京高考)如图，在四棱锥P -ABCD 中，底面ABCD 为矩形，平面P AD ⊥平面ABCD ，P A ⊥PD ，P A ＝PD ，E ，F 分别为AD ，PB 的中点．(1)求证：PE⊥BC；(2)求证：平面P AB⊥平面PCD；(3)求证：EF∥平面PCD.[证明](1)因为P A＝PD，E为AD的中点，所以PE⊥AD.因为底面ABCD为矩形，所以BC∥AD.所以PE⊥BC.(2)因为底面ABCD为矩形，所以AB⊥AD.又因为平面P AD⊥平面ABCD，所以AB⊥平面P AD.所以AB⊥PD.又因为P A⊥PD，所以PD⊥平面P AB.因为PD⊂平面PCD，所以平面P AB⊥平面PCD.(3)取PC中点G，连接FG，DG.因为F，G分别为PB，PC的中点，所以FG∥BC，FG＝12BC.因为四边形ABCD为矩形，且E为AD的中点，所以DE∥BC，DE＝12BC.所以DE∥FG，DE＝FG.所以四边形DEFG为平行四边形，所以EF∥DG.又因为EF⊄平面PCD，DG⊂平面PCD，所以EF∥平面PCD.10．(2019·太原模拟)如图，在直三棱柱ABC-A1B1C1中，D是BC上的一点，AB＝AC，且AD⊥BC.(1)求证：A1C∥平面AB1D；(2)若AB＝BC＝AA1＝2，求点A1到平面AB1D的距离．[解](1)证明：如图，连接BA1，交AB1于点E，再连接DE，据直棱柱性质知，四边形ABB1A1为平行四边形，E为AB1的中点，∵AB＝AC，AD⊥BC，∴D是BC的中点，∴DE∥A1C，又DE⊂平面AB1D，A1C⊄平面AB1D，∴A1C∥平面AB1D.(2)如图，在平面BCC1B1中，过点B作BF⊥B1D，垂足为F，∵D是BC中点，∴点C到平面AB1D与点B到平面AB1D距离相等，∵A1C∥平面AB1D，∴点A1到平面AB1D的距离等于点C到平面AB1D的距离，∴BF长为所求，在Rt△B1BD中，BD＝1，BB1＝2，B1D＝5，∴BF＝25＝255，∴点A1到平面AB1D的距离为255.1．如图，在斜三棱柱ABC-A1B1C1中，∠BAC＝90°，BC1⊥AC，则C1在底面ABC上的射影H必在()A．直线AB上B．直线BC上C．直线AC上D．△ABC内部A[连接AC1(图略)，由AC⊥AB，AC⊥BC1，AB∩BC1＝B，得AC⊥平面ABC1.∵AC⊂平面ABC，∴平面ABC1⊥平面ABC.∴C1在平面ABC上的射影H必在两平面的交线AB上．]2．(2019·唐山模拟)如图，在以下四个正方体中，直线AB与平面CDE垂直的是()①②③④A．①②B．②④C．①③D．②③B[对于①，易证AB与CE所成角为45°，则直线AB与平面CDE不垂直；对于②，易证AB⊥CE，AB⊥ED，且CE∩ED＝E，则AB⊥平面CDE；对于③，易证AB与CE所成角为60°，则直线AB与平面CDE不垂直；对于④，易证ED⊥平面ABC，则ED⊥AB，同理EC⊥AB，可得AB⊥平面CDE.故选B.] 3．如图，P A⊥圆O所在的平面，AB是圆O的直径，C是圆O上的一点，E，F分别是点A在PB，PC上的射影，给出下列结论：①AF⊥PB；②EF⊥PB；③AF⊥BC；④AE⊥平面PBC.其中正确结论的序号是．①②③[由BC⊥AC，BC⊥P A可得BC⊥平面P AC，又AF⊂平面P AC，所以AF⊥BC，又AF⊥PC，则AF⊥平面PBC，从而AF⊥PB，AF⊥BC，故①③正确；由PB⊥AF，PB⊥AE可得PB⊥平面AEF，从而PB⊥EF，故②正确；若AE⊥平面PBC，则由AF⊥平面PBC知AE∥AF与已知矛盾，故④错误．] 4．(2019·西宁模拟)已知三棱柱ABC-A1B1C1，A1在底面ABC上的射影恰为AC的中点D，∠BCA＝90°，AC＝BC＝2，又知BA1⊥AC1.(1)求证：AC1⊥平面A1BC；(2)求点C到平面A1AB的距离．[解](1)证明：∠BCA＝90°得BC⊥AC，因为A1D⊥平面ABC，所以A1D⊥BC，A1D∩AC＝D，所以BC⊥平面A1ACC1，所以BC⊥AC1.因为BA1⊥AC1，BA1∩BC＝B，所以AC1⊥平面A1BC.(2)作DE⊥AB于点E，连接A1E，作DF⊥A1E于点F.因为A1D⊥平面ABC，所以A1D⊥AB，DE⊥AB，DE∩A1D＝D，所以AB⊥平面A1DE，又DF⊂平面A1DE，所以AB⊥DF，由DF⊥A1E，A1E∩AB＝E，所以DF⊥平面A1AB，由(1)及已知得DE＝22，A1D＝3，Rt△A1DE中，DF ＝A 1D ·DE A 1E ＝217， 因为D 是AC 中点，所以C 到面A 1AB 距离2217.1．(2019·衡阳模拟)如图，在四面体ABCD 中，AD ⊥BD ，截面PQMN 是矩形，则下列结论不一定正确的是( )A ．平面BDC ⊥平面ADCB ．AC ∥平面PQMNC ．平面ABD ⊥平面ADCD ．AD ⊥平面BDCD [由PQ ∥MN ，MN ⊂平面ADC ，PQ ⊄平面ADC ，得PQ ∥平面ADC ，又PQ⊂平面ABC，平面ABC∩平面ADC＝AC，∴PQ∥AC，同理QM∥BD，因为PQ⊥QM，∴AC⊥BD，又BD⊥AD，AC∩AD＝A，∴BD⊥平面ADC，∴平面BDC⊥平面ADC，平面ABD⊥平面ADC，∴A和C选项均正确；由PQ∥AC，得AC∥平面PQMN，∴B选项正确．∵不能得到AD⊥DC或AD⊥BC，∴不能得到AD⊥平面BDC，故选项D 不一定正确．故选D.]2．(2019·泉州模拟)如图，在直三棱柱ABC-A1B1C1中，底面ABC是边长为2的正三角形，M，N分别是AB，AA1的中点，且A1M⊥B1N.(1)求证：B1N⊥A1C；(2)求M到平面A1B1C的距离．[解](1)证明：如图，连接CM.在直三棱柱ABC -A 1B 1C 1中，AA 1⊥平面ABC ，CM ⊂平面ABC ， 所以AA 1⊥CM .在△ABC 中，AC ＝BC ，AM ＝BM ，所以CM ⊥AB .又AA 1∩AB ＝A ，所以CM ⊥平面ABB 1A 1.因为B 1N ⊂平面ABB 1A 1，所以CM ⊥B 1N .又A 1M ⊥B 1N ，A 1M ∩CM ＝M ，所以B 1N ⊥平面A 1CM .因为A 1C ⊂平面A 1CM ，所以B 1N ⊥A 1C .(2)法一：连接B 1M .在矩形ABB 1A 1中，因为A 1M ⊥B 1N ，所以∠AA 1M ＝∠A 1B 1N .所以tan ∠AA 1M ＝tan ∠A 1B 1N ，即AM AA 1＝A 1N A 1B 1. 因为△ABC 是边长为2的正三角形，M ，N 分别是AB ，AA 1的中点，所以AM ＝1，CM ＝3，A 1B 1＝2.设AA 1＝x ，则A 1N ＝x 2.所以1x ＝x 22，解得x ＝2.从而S △A 1B 1M ＝12S 正方形ABB 1A 1＝2，A 1C ＝B 1C ＝2 2.在△A 1CB 1中，cos ∠A 1CB 1＝A 1C 2＋B 1C 2－A 1B 212A 1C ·B 1C ＝34，所以sin ∠A 1CB 1＝74，所以S △A 1B 1C ＝12A 1C ·B 1C ·sin ∠A 1CB 1＝7.设点M 到平面A 1B 1C 的距离为d ，由V 三棱锥M -A 1B 1C ＝V 三棱锥C -A 1B 1M ，得13S △A 1B 1C ·d ＝13S △A 1B 1M ·CM ，所以d ＝S △A 1B 1M ·CM S △A 1B 1C ＝2217，即点M 到平面A 1B 1C 的距离为2217. 法二：在矩形ABB 1A 1中，因为A 1M ⊥B 1N ，所以∠AA 1M ＝∠A 1B 1N ，所以tan ∠AA 1M ＝tan ∠A 1B 1N ，即AM AA 1＝A 1N A 1B 1. 因为△ABC 是边长为2的正三角形，M ，N 分别是AB ，AA 1的中点， 所以AM ＝1，CM ＝3，A 1B 1＝2.设AA 1＝x ，则A 1N ＝x 2，所以1x ＝x22，解得x ＝2.如图，取A 1B 1的中点D ，连接MD ，CD ，过M 作MO ⊥CD 于O .在正方形ABB 1A 1中，易知A 1B 1⊥MD ，由(1)可得CM ⊥A 1B 1，又CM ∩MD ＝M ，所以A 1B 1⊥平面CDM .因为MO ⊂平面CDM ，所以A 1B 1⊥MO .又MO ⊥CD ，A 1B 1∩CD ＝D ，所以MO ⊥平面A 1B 1C ，即线段MO 的长就是点M 到平面A 1B 1C 的距离．由(1)可得CM⊥MD，又MD＝2，所以由勾股定理，得CD＝CM2＋MD2＝7.S△CMD＝12·CD·MO＝12·CM·MD，即12×7×MO＝12×3×2，解得MO＝2217，故点M到平面A1B1C的距离为221 7.。

线面垂直判定定理测试题1.如图，在三棱锥P-ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA＝AB＝BC＝2，D为线段AC的中点，E为线段PC上一点．（1）求证：PA⊥BD；（2）求证：平面BDE⊥平面PAC；（3）当PA//平面BDE时，求三棱锥E-BCD的体积．2.如图，在四棱锥P-ABCD中，底面ABCD是正方形．点E是棱PC的中点，平面ABE与棱PD交于点F．（1）求证：AB∥EF；（2）若PA=AD，且平面PAD⊥平面ABCD，求证：AF⊥平面PCD．3.如图，已知AF⊥面ABCD，四边形ABEF为矩形，四边形ABCD为直角梯形，∠DAB=90°，AB∥CD，AD=AF=CD=1，AB=2（1）求证：AF∥面BCE；（2）求证：AC⊥面BCE；（3）求三棱锥E-BCF的体积．4.如图，四面体ABCD中，△ABC是正三角形，AD＝CD．（1）证明：AC⊥BD；（2）已知△ACD是直角三角形，AB＝BD，若E为棱BD上与D不重合的点，且AE⊥EC，求四面体ABCE与四面体ACDE的体积比．5.如图，多面体ABCDS中，面ABCD为矩形，SD⊥AD，且SD⊥AB，AD=1，AB=2，SD=√3．（1）求证：CD⊥平面ADS；（2）求AD与SB所成角的余弦值；（3）求二面角A-SB-D的余弦值．6.如图，在四棱锥P-ABCD中，底面ABCD是矩形，平面PAD⊥平面ABCD，AP=AD，M，N分别为棱PD，PC的中点．求证：（1）MN∥平面PAB；（2）AM⊥平面PCD．7.如图所示四棱锥P-ABCD中，PA⊥底面ABCD，四边形ABCD中，AB⊥AD，BC∥AD，PA=AB=BC=2，AD=4，E为PD的中点，F为PC中点．（Ⅰ）求证：CD⊥平面PAC；（Ⅱ）求证：BF∥平面ACE；（Ⅲ）求直线PD与平面PAC所成的角的正弦值．答案和解析1.【答案】（1）证明：由PA ⊥AB ，PA ⊥BC ，AB ⊂平面ABC ，BC ⊂平面ABC ，且AB ∩BC =B ，可得PA ⊥平面ABC ，由BD ⊂平面ABC ，可得PA ⊥BD ；（2）证明：由AB =BC ，D 为线段AC 的中点，可得BD ⊥AC ，由PA ⊥平面ABC ，PA ⊂平面PAC ，可得平面PAC ⊥平面ABC ，又平面PAC ∩平面ABC =AC ，BD ⊂平面ABC ，且BD ⊥AC ，即有BD ⊥平面PAC ，BD ⊂平面BDE ，可得平面BDE ⊥平面PAC ；（3）解:PA //平面BDE ，PA ⊂平面PAC ，且平面PAC ∩平面BDE =DE ，可得PA //DE ，又D 为AC 的中点，可得E 为PC 的中点，且DE =12PA =1，由PA ⊥平面ABC ，可得DE ⊥平面ABC ，可得S △BDC =12S △ABC =12×12×2×2=1， 则三棱锥E -BCD 的体积为13DE •S △BDC =13×1×1=13．【解析】本题考查空间的线线、线面和面面的位置关系的判断，主要是平行和垂直的关系，注意运用线面平行的性质定理以及线面垂直的判定定理和性质定理，面面垂直的判定定理和性质定理，同时考查三棱锥的体积的求法，考查空间想象能力和推理能力，属于中档题．（1）运用线面垂直的判定定理可得PA⊥平面ABC，再由性质定理即可得证；（2）要证平面BDE⊥平面PAC，可证BD⊥平面PAC，由（1）运用面面垂直的判定定理可得平面PAC⊥平面ABC，再由等腰三角形的性质可得BD⊥AC，运用面面垂直的性质定理，即可得证；（3）由线面平行的性质定理可得PA//DE，运用中位线定理，可得DE的长，以及DE⊥平面ABC，求得三角形BCD的面积，运用三棱锥的体积公式计算即可得到所求值．2.【答案】解：（1）证明：∵底面ABCD是正方形，∴AB∥CD ,又∵AB⊄平面PCD，CD⊂平面PCD，∴AB∥平面PCD ,又∵A，B，E，F四点共面，且平面ABEF∩平面PCD=EF，∴AB∥EF ;（2）证明：在正方形ABCD中，CD⊥AD ,又∵平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD，CD⊂平面ABCD,CD⊄平面PAD∴CD⊥平面PAD ,又∵AF⊂平面PAD ,∴CD⊥AF ,由（1）可知，AB∥EF，又∵AB∥CD，C,D,E,F在同一平面内，∴CD∥EF ,∵点E是棱PC中点，∴点F是棱PD中点,在△PAD中，∵PA=AD，∴AF⊥PD ,又∵PD∩CD=D，PD、CD⊂平面PCD,∴AF⊥平面PCD．【解析】（1）证明AB∥平面PCD，即可得AB∥EF；（2）利用平面PAD⊥平面ABCD，证明CD⊥AF，PA=AD，所以AF⊥PD，即可证明AF⊥平面PCD；本题考查线面平行的性质，平面与平面垂直的性质，考查线面垂直，考查学生分析解决问题的能力，属于中档题．3.【答案】（1）证明：∵四边形ABEF为矩形，∴AF∥BE，∵AF⊄平面BCE，BE⊄平面BCE，∴AF∥面BCE．（2）证明：∵AF⊥面ABCD，四边形ABEF为矩形，∴BE⊥平面ABCD，∵AC⊂平面ABCD，∴AC⊥BE，∵四边形ABCD为直角梯形，∠DAB=90°，AB∥CD，AD=AF=CD=1，AB=2 ∴AC=BC=√12+12=√2，∴AC2+BC2=AB2，∴AC⊥BC，∵BC∩BE=B，∴AC⊥面BCE．（3）解：三棱锥E-BCF的体积：V E-BCF=V C-BEF=13×S△BEF×AD=1 3×12×BE×EF×AD=1 3×12×1×2×1=13．【解析】本题考查线面平行、线面垂直的证明，考查三棱锥的体积的求法，考查推理论证能力、运算求解能力、空间想象能力，考查数形结合思想、转化化归思想，考查数据处理能力和运用意识，是中档题．（1）推导出AF∥BE，由此能证明AF∥面BCE．（2）推导出AC⊥BE，AC⊥BC，由此能证明AC⊥面BCE．（3）三棱锥E-BCF的体积V E-BCF=V C-BEF，由此能求出结果．4.【答案】证明：（1）取AC中点O，连结DO、BO，∵△ABC是正三角形，AD=CD，∴DO⊥AC，BO⊥AC，∵DO∩BO=O，∴AC⊥平面BDO，∵BD⊂平面BDO，∴AC⊥BD．（2）解：连结OE，由（1）知AC⊥平面OBD，∵OE⊂平面OBD，∴OE⊥AC，设AD=CD=√2，则OC=OA=1，EC=EA，∵AE⊥CE，AC=2，∴EC2+EA2=AC2，∴EC=EA=√2=CD，∴E是线段AC垂直平分线上的点，∴EC=EA=CD=√2，由余弦定理得：cos∠CBD=BC2+BD2−CD22BC⋅BD =BC2+BE2−CE22BC⋅BE，即4+4−22×2×2=4+BE2−22×2×BE，解得BE=1或BE=2，∵BE＜BD=2，∴BE=1，∴BE=ED，∵四面体ABCE与四面体ACDE的高都是点A到平面BCD的高h，∵BE=ED，∴S△DCE=S△BCE，∴四面体ABCE与四面体ACDE的体积比为1．【解析】本题考查线线垂直的证明，考查两个四面体的体积之比的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查数形结合思想、化归与转化思想，是中档题．（1）取AC中点O，连结DO、BO，推导出DO⊥AC，BO⊥AC，从而AC⊥平面BDO，由此能证明AC⊥BD．（2）连结OE，设AD=CD=，则OC=OA=1，由余弦定理求出BE=1，由BE=ED，四面体ABCE与四面体ACDE的高都是点A到平面BCD的高h，S△DCE=S△BCE，由此能求出四面体ABCE与四面体ACDE的体积比．5.【答案】解：（I）证明：∵ABCD是矩形，∴CD⊥AD又SD⊥AB，AB∥CD，则CD⊥SD（2分）AD⊥SD∴CD⊥平面ADS（II）矩形ABCD，∴AD∥BC，即BC=1，∴要求AD与SB所成的角，即求BC与SB所成的角在△SBC中，由（1）知，SD⊥面ABCD．∴Rt△SDC中，SC=√(√3)2+22=√7∴CD是CS在面ABCD内的射影，且BC⊥CD，∴SC⊥BCtan∠SBC=SCCB =√71=√7cos∠SBC=√24从而SB与AD的成的角的余弦为√24．（III）∵△SAD中SD⊥AD，且SD⊥AB∴SD⊥面ABCD．∴平面SDB⊥平面ABCD，BD为面SDB与面ABCD的交线．∴过A作AE⊥DB于E∴AE⊥平面SDB又过A作AF⊥SB于F，连接EF，从而得：EF⊥SB∴∠AFB为二面角A-SB-D的平面角在矩形ABCD中，对角线∵√12+22=√5BD=√5∴在△ABD中，AE=AB⋅CDBD =1⋅2√5=2√55由（2）知在Rt△SBC，SB=√(√7)2+12=√8．而Rt△SAD中，SA=2，且AB=2，∴SB2=SA2+AB2，∴△SAB为等腰直角三角形且∠SAB为直角，∴AF=√22AB=√2∴sin∠AFE=AEAF =2√55√2=√105所以所求的二面角的余弦为√155【解析】（1）要证CD⊥平面ADS，只需证明直线CD垂直平面ADS内的两条相交直线AD、SD即可；（2）要求AD与SB所成的角，即求BC与SB所成的角，解三角形可求AD与SB所成角的余弦值；（3）过A作AE⊥DB于E 又过A作AF⊥SB于F，连接EF，说明∠AFB为二面角A-SB-D的平面角，解三角形可求二面角A-SB-D的余弦值．本题考查直线与平面垂直的判定，二面角的求法，异面直线所成的角，考查学生逻辑思维能力，计算能力，是中档题．6.【答案】证明：（1）因为M、N分别为PD、PC的中点，所以MN∥DC，又因为底面ABCD是矩形，所以AB∥DC．所以MN∥AB，又AB⊂平面PAB，MN⊄平面PAB，所以MN∥平面PAB．（2）因为AP=AD，P为PD的中点，所以AM⊥PD．因为平面PAD⊥平面ABCD，又平面PAD∩平面ABCD=AD，CD⊥AD，CD⊂平面ABCD，所以CD⊥平面PAD，又AM⊂平面PAD，所以CD⊥AM．因为CD、PD⊂平面PCD，CD∩PD=D，∴AM⊥平面PCD．【解析】（1）推导出MN∥DC，AB∥DC．从而MN∥AB，由此能证明MN∥平面PAB．（2）推导出AM⊥PD，CD⊥AD，从而CD⊥平面PAD，进而CD⊥AM，由此能证明AM⊥平面PCD．本题考查线面平行、线面垂直的证明，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、数形结合思想，是中档题．7.【答案】（Ⅰ）证明：因为PA⊥底面ABCD，CD⊂面ABCD，所以PA⊥CD，又因为直角梯形ABCD中，AC=2√2，CD=2√2，所以AC2+CD2=AD2，即AC⊥CD，又PA∩AC=A，所以CD⊥平面PAC；（Ⅱ）解法一：如图，连接BD，交AC于O，取PE中点G，连接BG，FG，EO，则在△PCE中，FG∥CE，又EC⊂平面ACE，FG⊄平面ACE，所以FG∥平面ACE，因为BC∥AD，所以BOOD =GEED，则OE∥BG，又OE⊂平面ACE，BG⊄平面ACE，所以BG∥平面ACE，又BG∩FG=G，所以平面BFG∥平面ACE，因为BF⊂平面BFG，所以BF∥平面ACE．解法二：如图，连接BD，交AC于O，取PE中点G，连接FD交CE于H，连接OH，则FG∥CE，在△DFG中，HE∥FG，则GEED =FHHD=12，在底面ABCD中，BC∥AD，所以BOOD =BCAD=12，所以FHHD =BOOD=12，故BF∥OH，又OH⊂平面ACE，BF⊄平面ACE，所以BF∥平面ACE．（Ⅲ）由（Ⅰ）可知，CD⊥平面PAC，所以∠DPC为直线PD与平面PAC所成的角，在Rt△PCD中，CD=2√2，PD=√PA2+AD2=2√5，所以sin∠DPC=CDPD =2√22√5=√105，所以直线PD与平面PAC所成的角的正弦值为√105．【解析】本题考查线面垂直、线面平行，考查线面角，解题的关键是掌握线面垂直、线面平行的判定方法，正确找出线面角．（Ⅰ）证明CD⊥平面PAC，证明PA⊥CD，AC⊥CD即可；（Ⅱ）解法一：连接BD，交AC于O，取PE中点G，连接BG，FG，EO，证明平面BFG∥平面ACE，即可证得BF∥平面ACE；解法二：如图，连接BD，交AC于O，取PE中点G，连接FD交CE于H，连接OH，则证明BF∥OH，即可证得BF∥平面ACE；（Ⅲ）确定∠DPC为直线PD与平面PAC所成的角，在Rt△PCD中，即可求得直线PD与平面PAC所成的角的正弦值．第11页，共11页。

直线、平面垂直的判定及其性质经典例题经典例题透析类型一、直线和平面垂直的定义1．下列命题中正确的个数是( )①如果直线与平面内的无数条直线垂直，则；②如果直线与平面内的一条直线垂直，则；③如果直线不垂直于，则内没有与垂直的直线；④如果直线不垂直于，则内也可以有无数条直线与垂直．A．0B．1 C．2 D．3答案：B解析：当内的无数条直线平行时，与不一定垂直，故①不对；当与内的一条直线垂直时，不能保证与垂直，故②不对；当与不垂直时，可能与内的无数条直线垂直，故③不对；④正确．故选B．总结升华：注意直线和平面垂直定义中的关键词语．举一反三：【变式1】（2010 山东）在空间，下列命题正确的是A．平行直线的平行投影重合B．平行于同一直线的两个平面平行C．垂直于同一平面的两个平面平行D．垂直于同一平面的两条直线平行答案：D解析：A项，平行直线的平行投影也可以是两条平行线；B项，平行于同一直线的两个平面可平行、可相交；C项，垂直于同一平面的两个平面可平行、可相交；D项，正确．总结升华：本题主要考察对基础知识的掌握．类型二、直线和直线、平面垂直的判定2．（2011 广东理18）如图，在椎体P-ABCD中，ABCD是边长为1的菱形，且∠DAB=60，,PB=2, E,F分别是BC,PC的中点．（1）证明：AD 平面DEF;（2）求二面角P-AD-B的余弦值．解析：（1）证明：取AD中点G，连接PG，BG，BD．∵PA=PD，∴，在中，，∴为等边三角形，∴，∴AD⊥平面PBG，∴又PB//EF，得，又∵DE//GB，得AD⊥DE，又，∴AD⊥平面DEF．（2）为二面角P—AD—B的平面角，在，在中，总结升华：要判定一条已知直线和一个平面是否垂直，取决于在这个平面内能否找出两条相交直线和这条直线垂直，至于这两条相交直线是否和已知直线有公共点，则无关紧要.举一反三：【变式1】如图所示，直三棱柱中，∠ACB=90°，AC=1，，侧棱，侧面的两条对角线交点为D，的中点为M．求证：平面CBD ⊥平面BDM．证明：如下图，连接、、，则．∵，∴为等腰三角形．又知D为其底边的中点，∴．∵，，∴．又，∴．∵为直角三角形，D为的中点，∴，．又，，∴．．即CD⊥DM．∵、为平面BDM内两条相交直线，∴CD⊥平面BDM．又∵，∴平面CBD⊥平面BDM．总结升华：处理面面垂直问题转化为处理线面垂直问题，进一步转化为处理线线垂直问题.所以证明平面与平面垂直，只要在一个平面内找到两条相交直线和另一个平面内的一条直线垂直即可.类型三、直线和平面所成的角3．如图所示，已知∠BOC在平面内，OA是平面的斜线，且∠AOB=∠AOC=60°，OA=OB=OC=，BC=，求OA和平面所成的角．解析：∵，∠AOB=∠AOC=60°，∴△AOB、△AOC为正三角形，∴．∵，∴，∴△ABC为直角三角形．同理△BOC也为直角三角形．过A作AH垂直平面于H，连接OH，∵AO=AB=AC，∴OH=BH=CH，H为△BOC的外心．∴H在BC上，且H为BC的中点．∵Rt△AOH中，，∴，∴∠AOH=45°．即AO和平面所成角为45°．总结升华：(1)确定点在平面内的射影的位置，是解题的关键，因为只有确定了射影的位置，才能找到直线与平面所成的角，才能将空间的问题转化为平面的问题来解．(2)求斜线与平面所成的角的程序：①寻找过直线上一点与平面垂直的直线；②连接垂足和斜足得出射影，确定出所求解；③把该角放入三角形计算．(3)直线和平面所成的角，也应考虑到直线和平面垂直、直线和平面平行或在平面内诸情况，也就是直线和平面成90°角和0°角的情况，所以求线面所成角时，应想到以上两种情况．举一反三：【变式1】（2011 全国大纲19）如图，四棱锥中，,，侧面为等边三角形，．(Ⅰ)证明：；(Ⅱ)求与平面所成角的大小．解析：（I）取AB中点E，连结DE、SE，∴四边形BCDE为矩形，DE=CB=2，∵侧面为等边三角形∴又∵SD=1，，∴为直角．又∵，∴AB⊥平面SDE，∴．又SD与两条相交直线AB、SE都垂直．∴SD⊥平面SAB．（II）作垂足为F，FG⊥BC，垂足为G，连结SG∵AB⊥平面SDE，∴平面ABCD⊥平面SED．∴SF⊥平面ABCD，∵∴，又∵FG⊥BC，∴BC⊥平面SFG，∵∴平面SBC⊥平面SFG．作，H为垂足，则FH⊥平面SBC．又∵在中，，在中，∴，即F到平面SBC的距离为．∵ED//BC，∴ED//平面SBC，∴E到平面SBC的距离d也是．设AB与平面SBC所成的角为α，则．∴与平面所成的角为．【变式2】如图所示，在正三棱柱中，侧棱长为，底面三角形的边长为1，则与侧面所成的角是________．答案：解析：如下图．由题取AC中点O，连接BO．则BO⊥平面．故为与平面所成角．又在中，，．∴，∴．类型四、二面角4．如图所示，在四面体ABCD中，△ABD、△ACD、△BCD、△ABC都全等，且，，求以BC为棱，以面BCD和面BCA为面的二面角大小．解析：取BC的中点E，连接AE、DE，∵AB=AC，∴AE⊥BC．又∵△ABD≌△ACD，AB=AC，∴DB=DC，∴DE⊥BC．∴∠AED为二面角的平面角．又∵△ABC≌△BDC，∴AD=BC=2，在Rt△DEB中，DB=，BE=1，∴，同理．在△AED中，∵，，∴，∴∠AED=90°．∴以面BCD和面ABC为面的二面角大小为90°．总结升华：确定二面角的平面角，常常用定义来确定．举一反三：【变式1】已知D、E分别是正三棱柱的侧棱和上的点，且．求过D、E、C1的平面与棱柱的下底面所成的二面角的大小．解析：如图，在平面内延长DE和交于点F，则F是面与面的公共点，为这两个平面的交线，∴所求二面角就是的平面角．∵，且，∴E、分别DF和A1F的中点．∵，∴．又面，面，∴面，而面．∴．∴是二面角的平面角，由已知，∴．总结升华：当所求的二面角没有给出它的棱时，找出二面角的两个面的两个公共点，从而找出它的棱，进而求其平面角的大小即可．类型五、平面与平面垂直的判定5．在四面体ABCD中，，AB=AD=CB=CD=AC=，如图所示．求证：平面ABD⊥平面BCD．证明：∵△ABD与△BCD是全等的等腰三角形，∴取BD的中点E，连接AE、CE，则AE⊥BD，BD⊥CE，∴∠AEC为二面角A-BD-C的平面角．在△ABD中，，，∴．同理．在△AEC中，，，由于，∴AE⊥CE，即∠AEC=90°，即二面角A-BD-C的平面角为90°．∴平面ABD⊥平面BCD．总结升华：利用两个平面互相垂直的定义可以直接判定两个平面垂直，判定的方法是(1)找出两个相交平面的平面角；(2)证明这个平面角是直角；(3)根据定义，这两个平面互相垂直．举一反三：【变式1】如图所示，在空间四边形ABCD中，AB=BC，CD=DA，E、F、G分别为CD、DA和对角线AC的中点，求证：平面BEF⊥平面BGD．证明：∵AB=BC，CD=AD，G是AC的中点，∴BG⊥AC，DG⊥AC，∴AC⊥平面BGD．又EF∥AC，∴EF⊥平面BGD．∵EF平面BEF，∴平面BDG⊥平面BEF．总结升华：证面面垂直的方法：(1)证明两平面构成的二面角的平面角为90°；(2)证明一个平面经过另一个平面的一条垂线,将证明“面面垂直”的问题转化为证明线面垂直的问题.【变式2】如图所示，在Rt△AOB中，，斜边AB=4．Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到，且二面角B-AO-C是直二面角．D是AB的中点．求证：平面COD⊥平面AOB；证明：由题意，CO⊥AO，BO⊥AO，∴∠BOC是二面角B-AO-C的平面角．又∵二面角B-AO-C是直二面角．∴CO⊥BO．又∵AO∩BO=O，∴CO⊥平面AOB．又CO平面COD，∴平面COD⊥平面AOB．【变式3】过点P引三条长度相等但不共面的线段PA、PB、PC，有∠APB=∠APC=60°，∠BPC=90°，求证：平面ABC⊥平面BPC．证明：如图，已知PA=PB=PC=a，由∠APB=∠APC=60°，△PAC，△PAB为正三角形，则有：PA=PB=PC=AB=AC=a，取BC中点为E直角△BPC中，，，由AB=AC，AE⊥BC，直角△ABE中，，，，在△PEA中，，，∴，平面ABC⊥平面BPC．类型六、综合应用6．如图所示，△ABC为正三角形，CE⊥平面ABC，BD∥CE，且CE=AC=2BD，M是AE的中点，求证：(1)DE=DA；(2)平面BDM⊥平面ECA；(3)平面DEA⊥平面ECA．证明：(1)取EC的中点F，连接DF．∵CE⊥平面ABC，∴CE⊥BC．易知DF∥BC，CE⊥DF．∵BD∥CE，∴BD⊥平面ABC．在Rt△EFD和Rt△DBA中，∵，，∴Rt△EFD≌Rt△DBA．故DE=AD．(2)取AC的中点N，连接MN、BN，MN CF．∵BD CF，∴MN BD．N平面BDM．∵EC⊥平面ABC，∴EC⊥BN．又∵AC⊥BN，∴BN⊥平面ECA．又∵BN平面MNBD，∴平面BDM⊥平面ECA．(3)∵DM∥BN，BN⊥平面ECA，∴DM⊥平面ECA．又∵DM平面DEA，∴平面DEA⊥平面ECA．总结升华：本题涉及线面垂直、面面垂直的性质和判定，这里证明的关键是BN⊥平面ECA，应充分体会线线垂直、线面垂直与面面垂直的关系．7．如图所示，已知PA⊥矩形ABCD所在平面，M、N分别是AB、PC的中点．(1)求证：MN∥平面PAD；(2)求证：MN⊥CD；(3)若∠PDA=45°，求证：MN⊥平面PCD．思路点拨：要证明MN∥平面PAD，须证MN平行于平面PAD内某一条直线．注意到M、N分别为AB，PC的中点，可取PD的中点E，从而只须证明MN∥AE即可．证明如下．证明：(1)取PD的中点E，连接AE、EN，则，故AMNE为平行四边形，∴MN∥AE．∵AE平面PAD，MN平面PAD，∴MN∥平面PAD．(2)要证MN⊥CD，可证MN⊥AB．由(1)知，需证AE⊥AB．∵PA⊥平面ABCD，∴PA⊥AB．又AD⊥AB，∴AB⊥平面PAD．∴AB⊥AE．即AB⊥MN．又CD∥AB，∴MN⊥CD．(3)由(2)知，MN⊥CD，即AE⊥CD，再证AE⊥PD即可．∵PA⊥平面ABCD，∴PA⊥AD．又∠PDA=45°，E为PD的中点．∴AE⊥PD，即MN⊥PD．又MN⊥CD，∴MN⊥平面PCD．总结升华：本题是涉及线面垂直、线面平行、线线垂直诸多知识点的一道综合题．(1)的关键是选取PD的中点E，所作的辅助线使问题处理的方向明朗化．线线垂直→线面垂直→线线垂直是转化规律．。

线面垂直面面垂直知识点总结经典例题及解析高考题练习及答案 SANY标准化小组 #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#直线、平面垂直的判定与性质【考纲说明】1、能够认识和理解空间中线面垂直的有关性质和判定定理。

2、能够运用公理、定理和已获得的结论证明一些空间图形的位置关系的简单命题。

【知识梳理】一、直线与平面垂直的判定与性质 1、直线与平面垂直（1）定义：如果直线l 与平面α内的任意一条直线都垂直，我们就说直线l 与平面α互相垂直，记作l ⊥α，直线l 叫做平面α的垂线，平面α叫做直线l 的垂面。

如图，直线与平面垂直时,它们唯一公共点P 叫做垂足。

（2）判定定理：一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直。

结论：如果两条平行直线中的一条垂直于一个平面，那么另一条也垂直于这个平面，记作.//a b b a αα⎫⇒⊥⎬⊥⎭（3）性质定理：垂直于同一个平面的两条直线平行。

即,//a b a b αα⊥⊥⇒.由定义知：直线垂直于平面内的任意直线。

2、直线与平面所成的角平面的一条斜线和它在平面上的射影所成的锐角叫做这条直线和这个平面所成的角。

一条直线垂直于平面，该直线与平面所成的角是直角；一条直线和平面平行，或在平面内，则此直线与平面所成的角是00的角。

3、二面角的平面角从一条直线出发的两个半平面所组成的图形叫做二面角，这条直线叫做二面角的棱，这两个半平面叫做二面角的面。

如果记棱为l ，那么两个面分别为αβ、的二面角记作l αβ--.在二面角的棱上任取一点，以该点为垂足，在两个半平面内分别作垂直于棱的射线，则两射线所构成的角叫做叫做二面角的平面角。

其作用是衡量二面角的大小；范围：000180θ<<.二、平面与平面垂直的判定与性质1、定义：一般地，两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面垂直.2、判定：一个平面过另一个平面的垂线，则这两个平面垂直。

四、关于线线、线面及面面垂直的问题：典型例题：例1.已知矩形ABCD ，1AB =，BC =ABD ∆沿矩形的对角线BD 所在的直线进行翻折，在翻折过程中，【 】A ．存在某个位置，使得直线AC 与直线BD 垂直B ．存在某个位置，使得直线AB 与直线CD 垂直C ．存在某个位置，使得直线AD 与直线BC 垂直D ．对任意位置，三对直线“AC 与BD ”，“AB 与CD ”，“AD 与BC ”均不垂直 【答案】B 。

【考点】空间中直线与直线之间的位置关系。

【解析】 如图，AE ⊥BD ，CF ⊥BD ，依题意，1AB =，BC =AE =CF3BE EF FD ===。

A ，若存在某个位置，使得直线AC 与直线BD 垂直，则∵BD ⊥AE ，∴BD ⊥平面AEC ，从而BD ⊥EC ，这与已知矛盾，排除A ；B ，若存在某个位置，使得直线AB 与直线CD 垂直，则CD ⊥平面ABC ，平面ABC ⊥平面BCD 。

取BC 中点M ，连接ME ，则ME ⊥BD ，∴∠AEM 就是二面角A BD C --的平面角，此角显然存在，即当A 在底面上的射影位于BC 的中点时，直线AB 与直线CD 垂直，故B 正确；C ，若存在某个位置，使得直线AD 与直线BC 垂直，则BC ⊥平面ACD ，从而平面ACD ⊥平面BCD ，即A 在底面BCD 上的射影应位于线段CD 上，这是不可能的，排除C ；D ，由上所述，可排除D 。

故选 B 。

例2.如图，三棱柱ABC －A 1B 1C 1中，侧棱垂直底面，∠ACB=90°，AC=BC=12AA 1，D 是棱AA 1的中点(Ｉ)证明：平面BDC 1⊥平面BDC（Ⅱ）平面BDC 1分此棱柱为两部分，求这两部分体积的比。

【答案】解：(Ｉ)证明：∵由题设，三棱柱ABC －A 1B 1C 1中，侧棱垂直底面，∠ACB=90°，∴BC⊥CC 1，BC⊥AC，CC 1AC=C ，∴BC⊥平面ACC 1A 1。

立体几何平行与垂直专题（附经典解析）1垂直证明习题——线面垂直⇒面面垂直1. 如图所示，三棱柱中，，平面．证明：平面平面．2. 如图，在四棱锥中，底面是菱形，且，，，分别为，的中点，且．求证：平面平面．3. 如图所示，△ABC 为正三角形，CE ⊥平面ABC ，BD ∥CE ，且CE ＝AC ＝2BD ，M 是AE 的中点．求证：平面BDM ⊥平面ECA ．111ABC A B C -90BCA ∠=°1AC ⊥1A BC ABC ⊥11ACCA P ABCD -ABCD 2PA AD ==120PAD BAD ∠=∠=︒E FPDBD 2EF =PAD ⊥ABCD垂直证明习题——线面垂直⇒面面垂直（教师版）1. 如图所示，三棱柱中，，平面．证明：平面平面．【解析】证明：平面，．，，平面．又平面，平面平面．2. 如图，在四棱锥中，底面是菱形，且，，，分别为，的中点，且．求证：平面平面．【解析】过P 作PO ⊥AD ，垂足为O ，连结AO ，BO ， 由∠PAD=120°，得∠PAO=60°，111ABC A B C -90BCA ∠=°1AC ⊥1A BC ABC ⊥11ACCA 1AC ⊥1A BC 1AC BC ∴⊥90BCA ∠︒＝BC AC ∴⊥BC ∴⊥11ACC A BC ⊂ABC ∴ABC ⊥11ACC A P ABCD -ABCD 2PA AD ==120PAD BAD ∠=∠=︒E FPDBD EF =PAD ⊥ABCD立体几何平行与垂直专题（附经典解析）3∴在Rt △PAO 中，PO=PAsin ∠PAO=2sin60°=2×，∵∠BAO=120°，∴∠BAO=60°，AO=AO ，∴△PAO ≌△BAO ，∴∵E ，F 分别是PA ，BD 的中点，EF=∴EF是△PBD 的中位线，∴PB=2EF=2×，∴PB 2=PO 2+BO 2，∴PO ⊥BO ，∵AD∩BO=O ，∴PO ⊥平面ABCD ， 又PO ⊂平面PAD ，∴平面PAD ⊥平面ABCD ．3. 如图所示，△ABC 为正三角形，CE ⊥平面ABC ，BD ∥CE ，且CE ＝AC ＝2BD ，M 是AE 的中点．求证：平面BDM ⊥平面ECA ．【解析】取AC 的中点N ，连接MN 、BN ，则MN //CF ．∵BD //CF ，∴MN //BD ， ∴N ∈平面BDM ．∵EC ⊥平面ABC ，∴EC ⊥BN ．又∵AC ⊥BN ，EC ∩AC ＝C ，∴BN ⊥平面ECA ． 又∵BN ⊂平面BDM ，∴平面BDM ⊥平面ECA ．222。

高中数学直线与平面垂直的性质、平面与平面垂直的性质精选题目（附答案）1．直线与平面垂直的性质定理(1)文字语言：垂直于同一个平面的两条直线平行．(2)图形语言：(3)符号语言：⎭⎬⎫a ⊥αb ⊥α⇒a ∥b . (4)作用：①线面垂直⇒线线平行；②作平行线．2．平面与平面垂直的性质定理(1)文字语言：两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直．(2)图形语言：(3)符号语言：⎭⎬⎫α⊥βα∩β＝l a ⊂αa ⊥l ⇒a ⊥β.(4)作用：①面面垂直⇒线面垂直；②作面的垂线．一、线面垂直性质定理的应用1.如图，已知正方体A 1C .(1)求证：A 1C ⊥B 1D 1.(2)M ，N 分别为B 1D 1与C 1D 上的点，且MN ⊥B 1D 1，MN ⊥C 1D ，求证：MN ∥A 1C .[证明] (1)如图，连接A 1C 1.∵CC 1⊥平面A 1B 1C 1D 1，B 1D 1⊂平面A 1B 1C 1D 1，∴CC 1⊥B 1D 1.∵四边形A 1B 1C 1D 1是正方形，∴A 1C 1⊥B 1D 1.又∵CC 1∩A 1C 1＝C 1，∴B1D1⊥平面A1C1C.又∵A1C⊂平面A1C1C，∴B1D1⊥A1C.(2)如图，连接B1A，AD1.∵B1C∥AD，∴四边形ADC1B1为平行四边形，∴C1D∥AB1.∵MN⊥C1D，∴MN⊥AB1.又∵MN⊥B1D1，AB1∩B1D1＝B1，∴MN⊥平面AB1D1.由(1)知A1C⊥B1D1.同理可得A1C⊥AB1.又∵AB1∩B1D1＝B1，∴A1C⊥平面AB1D1.∴A1C∥MN.注：(1)若已知一条直线和某个平面垂直，证明这条直线和另一条直线平行，可考虑利用线面垂直的性质定理，证明另一条直线和这个平面垂直，证明时注意利用正方形、平行四边形及三角形中位线的有关性质．(2)直线与平面垂直的其他性质：①如果一条直线和一个平面垂直，则这条直线和这个平面内任一条直线垂直．②若两条平行线中的一条垂直于一个平面，则另一条也垂直于这个平面．③若l⊥α于A，AP⊥l，则AP⊂α.④垂直于同一条直线的两个平面平行．⑤如果一条直线垂直于两个平行平面中的一个，则它必垂直于另一个平面．2.如图所示，在正方体ABCD-A1B1C1D1中，M是AB上一点，N是A1C的中点，MN⊥平面A1DC.求证：(1)MN∥AD1；(2)M 是AB 的中点．证明：(1)∵四边形ADD 1A 1为正方形，∴AD 1⊥A 1D .又∵CD ⊥平面ADD 1A 1，∴CD ⊥AD 1.∵A 1D ∩CD ＝D ，∴AD 1⊥平面A 1DC .又∵MN ⊥平面A 1DC ，∴MN ∥AD 1.(2)连接ON ，在△A 1DC 中，A 1O ＝OD ，A 1N ＝NC ，∴ON=12CD=12AB .∴ON ∥AM .又∵MN ∥OA ，∴四边形AMNO 为平行四边形．∴ON ＝AM .∵ON ＝12AB ，∴AM ＝12AB .∴M 是AB 的中点.二、面面垂直性质定理的应用3.已知P 是△ABC 所在平面外的一点，且P A ⊥平面ABC ，平面P AC ⊥平面PBC ，求证：BC ⊥AC .[证明] 如图，在平面P AC 内作AD ⊥PC 于点D ，∵平面P AC ⊥平面PBC ，AD ⊂平面P AC ，且AD ⊥PC ，∴AD ⊥平面PBC ，又BC ⊂平面PBC ，∴AD ⊥BC .∵P A ⊥平面ABC ，BC ⊂平面ABC ，∴P A ⊥BC ，∵AD ∩P A ＝A ，∴BC ⊥平面P AC ，又AC ⊂平面P AC ，∴BC ⊥AC .注： 若所给题目中有面面垂直的条件，一般要利用面面垂直的性质定理将其转化为线面垂直、线线垂直．应用面面垂直的性质定理，注意三点：①两个平面垂直是前提条件；②直线必须在其中一个平面内；③直线必须垂直于它们的交线．4.如图所示，P是四边形ABCD所在平面外的一点，四边形ABCD是边长为a的菱形，且∠DAB＝60°.侧面P AD为正三角形，其所在平面垂直于底面ABCD.(1)若G为AD的中点，求证：BG⊥平面P AD；(2)求证：AD⊥PB.证明：(1)如图，在菱形ABCD中，连接BD，由已知∠DAB＝60°，∴△ABD为正三角形，∵G是AD的中点，∴BG⊥AD.∵平面P AD⊥平面ABCD，且平面P AD∩平面ABCD＝AD，∴BG⊥平面P AD.(2)如图，连接PG.∵△P AD是正三角形，G是AD的中点，∴PG⊥AD，由(1)知BG⊥AD.又∵PG∩BG＝G.∴AD⊥平面PBG.而PB⊂平面PBG，∴AD⊥PB.三、垂直关系的综合应用4.如图，在△BCD中，∠BCD＝90°，BC＝CD＝1，AB⊥平面BCD，∠ADB＝60°，E，F分别是AC，AD上的动点，且AEAC＝AFAD＝λ(0<λ<1)．(1)求证：无论λ为何值，总有平面BEF⊥平面ABC.(2)当λ为何值时，平面BEF⊥平面ACD?[解](1)证明：∵AB⊥平面BCD，CD⊂平面BCD，∴AB⊥CD.∵CD⊥BC，AB∩BC＝B，∴CD⊥平面ABC.又∵AEAC＝AFAD＝λ(0<λ<1)，∴无论λ为何值，恒有EF∥CD，∴EF⊥平面ABC.又∵EF⊂平面BEF，∴无论λ为何值，总有平面BEF⊥平面ABC.(2)由(1)知BE⊥EF，∵平面BEF⊥平面ACD，平面BEF∩平面ACD＝EF，∴BE⊥平面ACD.又∵AC⊂平面ACD，∴BE⊥AC.∵BC＝CD＝1，∠BCD＝∠ABD＝90°，∠ADB＝60°，∴BD＝2，∴AB＝2tan 60°＝6，∴AC＝AB2＋BC2＝7.由Rt△AEB∽Rt△ABC，得AB2＝AE·AC，∴AE＝67，∴λ＝AEAC＝67.故当λ＝67时，平面BEF⊥平面ACD.注：(1)空间中的垂直关系有线线垂直、线面垂直、面面垂直，这三种关系不是孤立的，而是相互关联的．它们之间的转化关系如下：线线垂直判定定理线面垂直定义线面垂直判定定理性质定理面面垂直(2)空间问题化成平面问题是解决立体几何问题的一个基本原则，解题时，要抓住几何图形自身的特点，如等腰(边)三角形的三线合一、中位线定理、菱形的对角线互相垂直等．还可以通过解三角形，产生一些题目所需要的条件，对于一些较复杂的问题，注意应用转化思想解决问题．5.如图(1)，在直角梯形ABCD中，AD∥BC，∠BAD＝π2，AB＝BC＝12AD＝a，E是AD的中点，O是AC与BE的交点．将△ABE沿BE折起到图(2)中△A1BE 的位置，得到四棱锥A1-BCDE.(1)证明：CD⊥平面A1OC；(2)当平面A1BE⊥平面BCDE时，四棱锥A1-BCDE的体积为362，求a的值．解：(1)证明：在图(1)中，因为AB＝BC＝12AD＝a，E是AD的中点，∠BAD＝π2，所以BE⊥AC.即在图(2)中，BE⊥A1O，BE⊥OC，从而BE⊥平面A1OC.又CD∥BE，所以CD⊥平面A1OC.(2)由已知，平面A1BE⊥平面BCDE，且平面A1BE∩平面BCDE＝BE，又由(1)可得A1O⊥BE，所以A1O⊥平面BCDE. 即A1O是四棱锥A1-BCDE的高．由图(1)知，A1O＝22AB＝22a，平行四边形BCDE的面积S＝BC·AB＝a2，从而四棱锥A1-BCDE的体积为V＝13S·A1O＝13×a2×22a＝26a3.由26a3＝362，得a＝6.巩固练习：1．设l是直线，α，β是两个不同的平面()A．若l∥α，l∥β，则α∥βB．若l∥α，l⊥β，则α⊥βC．若α⊥β，l⊥α，则l⊥βD．若α⊥β，l∥α，则l⊥β2．已知平面α，β和直线m，l，则下列命题中正确的是()A．若α⊥β，α∩β＝m，l⊥m，则l⊥βB．若α∩β＝m，l⊂α，l⊥m，则l⊥βC．若α⊥β，l⊂α，则l⊥βD．若α⊥β，α∩β＝m，l⊂α，l⊥m，则l⊥β3．在四棱柱ABCD-A1B1C1D1中，已知平面AA1C1C⊥平面ABCD，且AB＝BC，AD＝CD，则BD与CC1()A．平行B．共面C．垂直D．不垂直4.如图，设平面α∩平面β＝PQ，EG⊥平面α，FH⊥平面α，垂足分别为G，H.为使PQ⊥GH，则需增加的一个条件是()A．EF⊥平面αB．EF⊥平面βC．PQ⊥GED．PQ⊥FH5．设m，n是两条不同的直线，α，β，γ是三个不同的平面，给出如下命题：①若α⊥β，α∩β＝m，n⊂α，n⊥m，则n⊥β；②若α⊥γ，β⊥γ，则α∥β；③若α⊥β，m⊥β，m⊄α，则m∥α；④若α⊥β，m∥α，则m⊥β.其中正确命题的个数为()A．1 B．2C．3 D．41.解析：选B对于选项A，两平面可能平行也可能相交；对于选项C，直线l可能在β内也可能平行于β；对于选项D，直线l可能在β内或平行于β或与β相交．2.解析：选D选项A缺少了条件：l⊂α；选项B缺少了条件：α⊥β；选项C缺少了条件：α∩β＝m，l⊥m；选项D具备了面面垂直的性质定理的全条件．3.解析：选C如图所示，在四边形ABCD中，∵AB＝BC，AD＝CD.∴BD⊥AC.∵平面AA1C1C⊥平面ABCD，平面AA1C1C∩平面ABCD＝AC，BD⊂平面ABCD，∴BD⊥平面AA1C1C.又CC1⊂平面AA1C1C，∴BD⊥CC1，故选C.4.解析：选B因为EG⊥平面α，PQ⊂平面α，所以EG⊥PQ.若EF⊥平面β，则由PQ⊂平面β，得EF⊥PQ.又EG与EF为相交直线，所以PQ⊥平面EFHG，所以PQ⊥GH，故选B.5.解析：选B根据平面与平面垂直的性质知①正确；②中，α，β可能平行，也可能相交，不正确；③中，α⊥β，m⊥β，m⊄α时，只可能有m∥α，正确；④中，m与β的位置关系可能是m∥β或m⊂β或m与β相交，不正确．综上，可知正确命题的个数为2，故选B.6.如图，平面ABC⊥平面ABD，∠ACB＝90°，CA＝CB，△ABD是正三角形，O为AB中点，则图中直角三角形的个数为________．解析：∵CA＝CB，O为AB的中点，∴CO⊥AB.又平面ABC⊥平面ABD，交线为AB，∴CO⊥平面ABD.∵OD⊂平面ABD，∴CO⊥OD，∴△COD为直角三角形．所以图中的直角三角形有△AOC，△COB，△ABC，△AOD，△BOD，△COD 共6个．答案：67.如图，直二面角α-l-β，点A∈α，AC⊥l，C为垂足，B∈β，BD⊥l，D为垂足，若AB＝2，AC＝BD＝1，则CD的长为________．解析：如图，连接BC，∵二角面α-l-β为直二面角，AC⊂α，且AC⊥l，∴AC⊥β.又BC⊂β，∴AC⊥BC，∴BC2＝AB2－AC2＝3，又BD⊥CD，∴CD＝BC2－BD2＝ 2.答案： 28．已知m，n是直线，α，β，γ是平面，给出下列说法①若α⊥β，α∩β＝m，n⊥m，则n⊥α或n⊥β；②若α∥β，α∩γ＝m，β∩γ＝n，则m∥n；③若m不垂直于α，则m不可能垂直于α内的无数条直线；④若α∩β＝m，n∥m且n⊄α，n⊄β，则n∥α且n∥β.其中正确的说法序号是________(注：把你认为正确的说法的序号都填上)．解析：①错，垂直于交线，不一定垂直平面；②对；③错，凡是平面内垂直于m的射影的直线，m都与它们垂直；④对．答案：②④9.如图：三棱锥P-ABC中，已知△ABC是等腰直角三角形，∠ABC＝90°，△P AC是直角三角形，∠P AC＝90°，∠ACP＝30°，平面P AC⊥平面ABC.求证：平面P AB⊥平面PBC.证明：∵平面P AC⊥平面ABC，平面P AC∩平面ABC＝AC，P A⊥AC，∴P A ⊥平面ABC.又BC⊂平面ABC，∴P A⊥BC.又∵AB⊥BC，AB∩P A＝A，AB⊂平面P AB，P A⊂平面P AB，∴BC⊥平面P AB.又BC⊂平面PBC，∴平面P AB⊥平面PBC.10.如图，边长为2的正方形ACDE所在的平面与平面ABC垂直，AD与CE的交点为M，AC⊥BC，且AC＝BC.(1)求证：AM⊥平面EBC；(2)求直线EC与平面ABE所成角正弦值．解：(1)证明：∵平面ACDE⊥平面ABC，平面ACDE∩平面ABC＝AC，BC⊥AC，∴BC⊥平面ACDE.又AM⊂平面ACDE，∴BC⊥AM.∵四边形ACDE是正方形，∴AM⊥CE.又BC∩CE＝C，∴AM⊥平面EBC.(2)取AB的中点F，连接CF，EF.∵EA⊥AC，平面ACDE⊥平面ABC，平面ACDE∩平面ABC＝AC，∴EA⊥平面ABC，∴EA⊥CF.又AC＝BC，∴CF⊥AB.∵EA∩AB＝A，∴CF⊥平面AEB，∴∠CEF即为直线EC与平面ABE所成的角．在Rt△CFE中，CF＝2，FE＝6，tan∠CEF＝26＝33.11．在圆柱的一个底面上任取一点(该点不在底面圆周上)，过该点作另一个底面的垂线，则这条垂线与圆柱的母线所在直线的位置关系是() A．相交B．平行C．异面D．相交或平行12．已知m，n是两条不同直线，α，β是两个不同平面，则下列命题正确的是()A．若α，β垂直于同一平面，则α与β平行B．若m，n平行于同一平面，则m与n平行C．若α，β不平行．．．，则在α内不存在．．．与β平行的直线D．若m，n不平行．．．，则m与n不可能．．．垂直于同一平面13．设m，n是两条不同的直线，α，β是两个不同的平面．下列命题中正确的是()A．若α⊥β，m⊂α，n⊂β，则m⊥nB．若α∥β，m⊂α，n⊂β，则m∥nC．若m⊥n，m⊂α，n⊂β，则α⊥βD．若m⊥α，m∥n，n∥β，则α⊥β14．在三棱锥P-ABC中，平面P AC⊥平面ABC，∠PCA＝90°，△ABC是边长为4的正三角形，PC＝4，M是AB边上的一动点，则PM的最小值为() A．2 3 B．27C．4 3 D．47参考答案：11.解析：选B∵圆柱的母线垂直于圆柱的底面，所作的垂线也垂直于底面，由线面垂直的性质定理可知，二者平行．12.解析：选D A项，α，β可能相交，故错误；B项，直线m，n的位置关系不确定，可能相交、平行或异面，故错误；C项，若m⊂α，α∩β＝n，m∥n，则m∥β，故错误；D项，假设m，n垂直于同一平面，则必有m∥n，所以原命题正确，故D项正确．13.解析：选D A中m，n可能为平行、垂直、异面直线；B中m，n可能为异面直线；C中m应与β中两条相交直线垂直时结论才成立．14.解析：选B连接CM，则由题意PC⊥平面ABC，可得PC⊥CM，所以PM＝PC2＋CM2，要求PM的最小值只需求出CM的最小值即可，在△ABC中，当CM⊥AB时CM有最小值，此时有CM＝4×32＝23，所以PM的最小值为27.15.如图，若边长为4和3与边长为4和2的两个矩形所在的平面互相垂直，则cos α∶cos β＝________.解析：由题意，两个矩形的对角线长分别为5,25，所以cos α＝525＋4＝529，cos β＝2529，所以cos α∶cos β＝5∶2.答案：5∶216．经过平面α外一点和平面α内一点与平面α垂直的平面有________个．解析：设面外的点为A，面内的点为B，过点A作面α的垂线l，若点B恰为垂足，则所有过AB的平面均与α垂直，此时有无数个平面与α垂直；若点B不是垂足，则l与点B确定唯一平面β满足α⊥β.答案：1或无数17.如图，四棱锥P-ABCD的底面是边长为a的菱形，∠BCD＝120°，平面PCD⊥平面ABCD，PC＝a，PD＝2a，E为P A的中点．求证：平面EDB⊥平面ABCD.证明：设AC∩BD＝O，连接EO，则EO∥PC.∵PC＝CD＝a，PD＝2a，∴PC2＋CD2＝PD2，∴PC⊥CD.∵平面PCD⊥平面ABCD，平面PCD∩平面ABCD＝CD，∴PC⊥平面ABCD，∴EO⊥平面ABCD.又EO⊂平面EDB，故有平面EDB⊥平面ABCD.18.如图所示，在斜三棱柱A1B1C1-ABC中，底面是等腰三角形，AB＝AC，D是BC的中点，侧面BB1C1C⊥底面ABC.(1)求证：AD⊥CC1；(2)过侧面BB1C1C的对角线BC1的平面交侧棱于点M，若AM＝MA1，求证：截面MBC1⊥侧面BB1C1C；(3)若截面MBC1⊥平面BB1C1C，则AM＝MA1吗？请叙述你的判断理由．解：(1)证明：∵AB＝AC，D是BC的中点，∴AD⊥BC.∵底面ABC⊥平面BB1C1C，底面ABC∩平面BB1C1C＝BC，∴AD⊥平面BB1C1C.又CC1⊂平面BB1C1C，∴AD⊥CC1.(2)证明：延长B1A1与BM交于点N，连接C1N.∵AM＝MA1，∴NA1＝A1B1.∵A1C1＝A1N＝A1B1，∴C1N⊥B1C1，∴C1N⊥侧面BB1C1C.∴截面MBC1⊥侧面BB1C1C；(3)结论正确．证明如下：过M作ME⊥BC1于点E，连接DE. ∵截面MBC1⊥侧面BB1C1C，∴ME⊥侧面BB1C1C.又AD⊥侧面BB1C1C，∴ME∥AD，∴M，E，D，A四点共面．∵MA∥侧面BB1C1C，∴AM∥DE.∴四边形AMED是平方四边形，又AM∥CC1，∴DE∥CC1.∵BD＝CD，∴DE＝12CC1，∴AM＝12CC1＝12AA1.∴AM＝MA1.。