试验设计初步· 二、正交试验的应用》

正交实验的原理应用正交实验（Orthogonal experiment）是一种通过在各个试验条件上进行全面系统且彼此独立的设计和排列试验，以获取最大化信息的试验方法。

该方法既能减少试验次数，又能得到准确的统计结果，被广泛应用于工程、科学、管理和医药等领域。

正交实验的原理是基于多因素多水平的统计方法。

试验中的多个因素是一个系统中的相互作用因素，通过对每个因素设计多个水平进行试验，可以得到不同水平下因素之间的关系。

而正交实验的排列设计能够使得每个因素的每个水平在试验中均匀分布，将不同的水平组合起来进行试验，从而减少冗余试验次数，提高实验效率。

1.产品设计：在产品设计中，正交实验能通过全面探索不同因素之间的相互关系，找到最优的设计方案。

通过对产品的多个参数进行多水平设计，可以确定最佳组合，从而提高产品的性能和质量，并降低成本。

2.工程管理：在工程管理中，正交实验可以帮助确定最佳的资源配置和进度安排。

通过考虑不同的因素如人员、设备、时间等的组合和配比，可以找到最优的方案，提高工程效率和质量。

3.制造过程优化：在制造过程中，正交实验可以辅助确定不同因素对产品质量的影响程度，以及最佳参数设置。

通过对尺寸、材料、工艺等多个因素进行正交实验，可以找到最佳的组合，确保产品的一致性和可靠性。

4.医药研发：在医药研发中，正交实验可以辅助确定不同因素对药物疗效的影响，并确定最佳的配方和用量。

通过对不同药物成分、剂型、剂量等因素进行正交实验，可以找到最佳的组合，提高药物的疗效和安全性。

5.营销策略：在市场营销中，正交实验可以辅助确定不同因素对市场反应的影响，以及最佳策略的制定。

通过对产品特性、价格、促销等因素进行正交实验，可以找到最佳的组合，提高市场份额和盈利能力。

总之，正交实验作为一种全面且高效的试验方法，可以应用到各个领域中。

通过对多个因素进行全面的探索和分析，可以帮助决策者找到最佳的方案和决策，提高工作效率和质量。

正交试验设计的理论分析方法及应用一、本文概述正交试验设计是一种高效、系统的试验设计方法，广泛应用于工程、农业、医学等多个领域。

本文旨在深入探讨正交试验设计的理论分析方法及其应用。

我们将对正交试验设计的基本概念进行简要介绍，包括正交表、正交性等关键要素。

随后，本文将重点阐述正交试验设计的理论分析方法，包括试验设计原则、误差分析、方差分析等方面。

通过这些理论分析方法，我们可以有效地评估试验结果的可靠性和有效性。

在应用领域方面，本文将通过具体案例展示正交试验设计在多个领域的实际应用。

例如，在工程领域，正交试验设计可用于优化产品设计参数，提高产品质量；在农业领域，正交试验设计可用于研究作物生长条件，提高农作物产量；在医学领域，正交试验设计可用于药物筛选和临床试验，提高药物研发效率。

通过这些案例，我们将展示正交试验设计在实际问题中的独特优势和广泛应用价值。

本文还将对正交试验设计的未来发展进行展望，探讨其在新技术、新领域的应用前景。

通过本文的阐述，我们期望能够帮助读者更好地理解和应用正交试验设计，为推动相关领域的研究和实践提供有益的参考。

二、正交试验设计的基本原理与特点正交试验设计是一种高效、系统的试验设计方法，其核心原理在于通过正交表来安排试验，使得试验点分布均匀且具有代表性。

正交表是一种特殊类型的表格，其每一行代表一种试验条件组合，每一列则代表一个试验因素的不同水平。

通过正交表，研究者可以方便地选择出具有代表性的试验点，从而有效地减少试验次数，提高试验效率。

均衡分散性：正交表的设计保证了试验点在试验范围内分布均匀，每个试验点都具有代表性，从而能够全面反映试验因素与试验指标之间的关系。

整齐可比性：由于正交表的特殊结构，不同试验点之间具有良好的可比性。

这使得研究者可以方便地比较不同试验条件下的试验结果，从而得出准确的结论。

灵活性：正交试验设计可以根据实际需要进行调整和优化。

例如，当试验因素或水平发生变化时，可以通过调整正交表来适应新的试验需求。

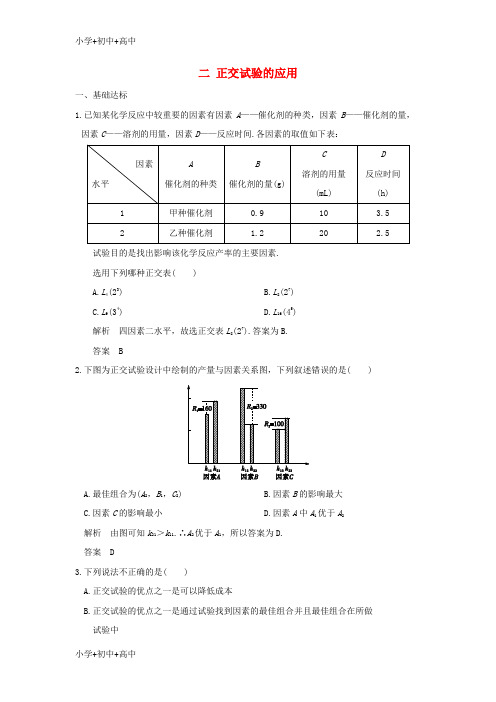
二正交试验的应用一、基础达标1.已知某化学反应中较重要的因素有因素A——催化剂的种类，因素B——催化剂的量，因素C——溶剂的用量，因素D——反应时间.各因素的取值如下表：试验目的是找出影响该化学反应产率的主要因素.选用下列哪种正交表( )A.L4(23)B.L8(27)C.L9(34)D.L16(45)解析四因素二水平，故选正交表L8(27).答案为B.答案 B2.下图为正交试验设计中绘制的产量与因素关系图，下列叙述错误的是()A.最佳组合为(A2，B1，C2)B.因素B的影响最大C.因素C的影响最小D.因素A中A1优于A2解析由图可知k21＞k11.∴A2优于A1，所以答案为D.答案 D3.下列说法不正确的是( )A.正交试验的优点之一是可以降低成本B.正交试验的优点之一是通过试验找到因素的最佳组合并且最佳组合在所做试验中C.正交试验的优点之一是用最少次数的试验结合统计分析，确定影响试验结果的主要因素D.正交试验的优点之一是对影响试验结果的因素进行全面考察解析正交试验是部分试验代替全面试验，可能会影响结果的判断，故最佳组合不一定在所做的试验中，B错.答案 B4.关于正交表的特性，下列说法不正确的是( )A.任一因素的任一水平与其他因素的每一水平相碰一次，且仅碰一次，搭配均匀B.各因素的最优水平组合，一定是正交表中某一试验号的搭配组合C.每一列中，不同的数字出现的次数相等，即同一因素的任一水平在试验中出现的机会相等D.任意两列，任何两因素的各种水平搭配，在试验中出现的机会均相等解析正交试验目的是找出各因素对试验结果影响的大小，从而找到各因素最优水平的组合，但最优组合一般不会是在正交表中某一试验点的搭配组合.答案 B5.用正交表对某化学反应中的反应结果进行分析，所得部分的数据已填写在下表：则这个化学反应中，最优组合是__________.解析因为k11＞k21，k12＞k22，k23＞k13，所以最佳组合为A1B1C2.答案A1B1C26.用正交表对某化学反应中的反应结果进行分析，所得部分的数据已填写在下表：则表中a ＋b ＝__________，b ＋d ＝__________.解析 由表可知⎩⎪⎨⎪⎧K 11＝a ＋b ，K 22＝b ＋d .又∵K 11＝2k 11＝122，K 22＝2k 22＝126， ∴a ＋b ＝122，b ＋d ＝126. 答案 122 126 二、能力提升7.下面给出的正交试验结果表中，已知K 12＝125，k 23＝39，指标值越大越好，则y 4＝__________，y 9＝__________.解析 ∵K 12＝125＝45＋y 4＋44，∴y 4＝36.k 23＝13(33＋y 4＋y 9)＝13(69＋y 9)＝39，∴y 9＝48.答案 36 488.如果一个3因素2水平的正交试验表如下：完成上表，找出最优组合，并指出影响试验结果的最主要因素. 解最佳组合为(A 2，B 1，C 1).∵R 1＞R 2＞R 3， ∴最主要因素为A .9.某化工厂为提高产品的产量，经过分析研究，决定考察反应温度A，反应时间B，催化剂C对产品质量的影响，每个因素选取3个不同的水平，选用正交表L9(34)安排试验，根据试验结果，得到如图所示的.(1)求k pq，p，q＝1，2，3；(2)求R1，R2，R3；(3)确定影响产量的主要因素；(4)确定使产量最高的最优生产条件.解(1)由因果关系图可知k11＝15.3，k21＝17.4，k31＝21.3，k12＝17.1，k22＝19.5，k32＝17.4，k13＝16.5，k23＝20.1，k33＝17.4.(2)R1＝max{15.3，17.4，21.3}－min{15.3，17.4，21.3}＝21.3－15.3＝6.0，R2＝max{17.1，19.5，17.4}－min{17.1，19.5，17.4}＝19.5－17.1＝2.4，R3＝max{16.5，20.1，17.4}－min{16.5，20.1，17.4}＝20.1－16.5＝3.6.(3)因为R1＞R3＞R2，故3个因素的主次关系为→C→.(4)因为max{k11，k21，k31}＝k31，max{k12，k22，k33}＝k22，max{k13，k23，k33}＝k23，故根据直观分析法得到的使产量最高的最优生产条件为A3B2C2.三、探究与创新10.某厂生产液体葡萄糖，要对生产工艺进行优选试验，因素及其水平如下表：试验指标为产量(kg)，越高越好，用正交表L9(34)安排试验，将各因素依次放在正交表的1～4列上.9次试验所得结果依次如下：498，568，568，577，512，540，501，550，510.请找出最好的生产方案及影响结果中的最主要的因素.解将各数据及有关计算值列表如下：从表中可知，最好的生产方案是(A1，B2，C2，D3)，即选用粉浆浓度为16%，粉浆酸度为pH＝2，稳压时间为5 min，工作压强为3.2×105 Pa.各因素中影响最主要的是工作压强.。

正交试验设计及其应用正交试验设计是一种常用于实验研究的设计方法，通过合理地选择试验因素，确定不同水平的组合，并根据正交表的设计原理，使得各个试验因素对试验结果的影响相互独立，从而有效提高实验效率。

正交试验设计广泛应用于工程、科学和统计学等领域，具有较高的实用价值。

正交试验设计的核心是正交表。

正交表是按照特定规则构造的由一系列因素水平组成的表格，保证各个因素对试验结果的影响相互独立。

正交表可以通过数学方法或者计算机程序生成。

常见的正交表包括正交四因素表、正交八因素表等，不同的正交表适用于不同的试验设计需求。

正交试验设计的主要应用之一是优化工程设计。

在工程设计中，需要确定各个设计因素对产品性能的影响程度，并在保障产品质量的前提下，寻找最佳的设计方案。

通过正交试验设计，可以在较小的试验次数下，全面地测试各个设计因素及其水平，分析其对产品性能的影响，从而确定最佳设计方案。

正交试验设计还可以通过分析试验样本数据，建立数学模型，进一步优化产品设计。

正交试验设计还可应用于药物研发领域。

在药物研发中，需要确定药物成分、剂型、工艺参数等因素对药物性能的影响，以及它们之间的相互作用。

通过正交试验设计，可以系统地研究各个因素的影响，并确定最佳的组合方案，以提高药物的疗效和稳定性。

此外，正交试验设计还可以应用于社会科学研究。

在社会科学中，往往存在多个影响因素，这些因素之间可能存在复杂的相互作用关系。

通过正交试验设计，可以确保各个因素的影响相互独立，减少干扰因素的影响，从而更加准确地分析各个因素的作用和相互关系。

正交试验设计在市场调查、心理学实验等领域有很好的应用效果。

总之，正交试验设计作为一种高效、可靠的实验设计方法，被广泛应用于不同领域。

通过合理选择试验因素和利用正交表进行试验设计，可以最大程度地提高实验效率，准确分析各个因素的作用和相互关系，为决策提供科学依据，为实际问题的解决提供有效支持。