湖南省益阳市箴言中学2017届高三上学期第三次模拟考试(11月)数学(文)试题Word版含答案.doc

益阳市箴言中学2017-2018学年高三第三次模拟考试英语试题时量：120分钟总分：150分时量：120分钟总分：150分第I卷（选择题共100分）第一部分听力（共两节，满分30分）做题时，先将答案划在试卷上。

录音内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题卡上。

第一节（共5小题；每小题1.5分，满分7.5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1. Where does the conversation probably take place?A. In a restaurant.B. In a furniture store.C. In the woman's company.2. What does the man want to do first?A. See the elephants.B. Have a cup of tea.C. Watch the dolphin show.3. What is the woman probably going to do?A. Make a list.B. Do some shopping.C. Make a chocolate pie.4. Why does the woman look upset?A. She experienced a theft.B. She was given a parking ticket.C. She couldn't find a parking space.5. How will the woman go to the city church?A. By bike.B. By bus.C. By car.第二节（共15小题：每小题1.5分，满分22.5分）听下面5段对话或独白。

益阳市箴言中学2016届高三第三次模拟考试理科数学试题时量 120分钟 总分 150分一、选择题（每小题5分，共60分）1. 已知M ＝{x |x －a ＝0}，N ＝{x |ax －1＝0}，若M∩N ＝N ，则实数a 的值为（ ）A ．1B ．－1C ．1或－1D ．0或1或－1 2. 记等比数列{}n a 的公比为q ，则“q >1”是“1+n a >n a (n ∈N *)”的（ ）A ．充分不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件 3. 已知sin (4π＋θ)＝53，则sin 2θ的值为（ ）A ．2519-B ．257-C ．2516-D ．2574. 函数)(x f ＝A sin (ωx ＋ϕ)(A>0，ω>0，|ϕ|<2π)的部分图象如图所示，则ω，ϕ的值分别为（ ）A ．2，3πB ．3，6πC ．3，3πD ．2，6π5. 若直线x ·cos θ＋y ·sin θ－1＝0与圆161)()1(22=-+-θsin y x 相切，且θ为锐角，则该直线的斜率是（ ） A ．－33 B ．－3 C ．33 D ．36. 设函数)(x f ＝⎩⎨⎧>-≤-1,11,221x x log x x ，则满足)(x f ≤2的x 的取值范围是（ ）A ．[－1，2]B ．[0，2]C ．[1，＋∞)D ．[0，＋∞) 7. 正四棱锥S —ABCD 的侧棱长为2，底面边长为3，E 为SA 中点，则异面直线BE 与SC 所成的角是（ ）A ．30°B ．45°C ．60°D ．90°8. 曲线y ＝2+x ax 在点(－1，a )处的切线方程为2x －y ＋b ＝0，则（ ）A ．a ＝1，b ＝－1B ．a ＝1，b ＝1C ．a ＝1，b ＝3D ．a ＝－1，b ＝－2BDC ASE9. 在平面直角坐标系中，若不等式组⎪⎩⎪⎨⎧≥+-≤-≥-+010101y ax x y x (a 为常数)所表示的平面区域的面积等于2，则a 的值为（ ）A ．－5B ．1C ．2D ．3 10. 下列不等式恒成立的个数有（ ）①ab ≤2)2(b a +≤222b a +(a ，b ∈R )； ②222c b a ++≥ab ＋bc ＋ca (a ，b ，c ∈R )； ③若实数a >1，则a ＋14-a ≥5； ④若实数a >0，则lga ＋a lg 1≥2.A ．1个B ．2个C ．3个D ．4个11. 空间四点A 、B 、C 、D 均在同一球面上，其中△ABC 是正三角形，AD ⊥平面ABC ，AD＝2AB ＝6，则该球的体积为（ ）A ．323π B ．48π C ．643π D ．163π12. 已知满足条件22y x +≤1的点(x ，y )构成的平面区域的面积为S 1，满足条件22][][y x +≤1的点(x ，y )构成的平面区域的面积为S 2，其中[x ]、[y ]分别表示不大于x 、y 的最大整数，例如：[－0.3]＝－1，[1.2]＝1等，则S 1与S 2的关系是（ ） A ．S 1＋S 2＝π＋3 B ．S 1＝S 2 C ．S 1>S 2 D ．S 1<S 2二、填空题（每小题5分，共20分） 13. 在△ABC 中，若(3b －c )·cos A=a ·cos C ，则cos A= .14. 设p ：函数)(x f ＝||2a x -在区间(4，＋∞)上单调递增；q ：2a log <1，如果“⌝p ”是真命题，“p 或q ”也是真命题，则实数a 的取值范围为 .15. 某几何体的三视图如图所示，其中正视图是腰长为2的等腰三角形，侧视图是半径为1的半圆，该几何体的体积为 .16. 满足条件AB=6，AC=2BC 的三角形ABC 的面积的最大值为 .正视图 侧视图 俯视图三、解答题：17. （本小题满分10分）设函数)(x f =x cos 4－2a ·sinx ·cosx －x sin 4的图象的一条对称轴的方程为x =－8π.（1）求实数a 的值；（2）对于x ∈[0，2π]，求函数)(x f 的最小值及取得最小值时的x 的值.18. （本小题满分10分）已知方程2x ＋2y －2x －4y ＋m ＝0.（1）若此方程表示圆，求实数m 的取值范围；（2）若（1）中的圆与直线x ＋2y －4＝0相交于M ，N 两点，且OM ⊥ON （O 为坐标原点），求m 的值；（3）在（2）的条件下，求以MN 为直径的圆的方程.19. （本小题满分12分）已知数列{a n }的首项a 1＝32，a n ＋1＝12+n na a （n ∈N *） （1）设nb ＝11-na ，求数列}{nb 的通项公式；（2）求数列{na n }的前n 项和S n .20. （本小题满分12分）一艘轮船在航行中的燃料费和它的速度的立方成正比，已知在速度为每小时10km 时的燃料费是每小时6元，而其他与速度无关的费用是每小时96元，问此轮船以多大速度航行时，能使行驶每千米的费用总和最小？21. （本小题满分13分）如图所示的几何体ABCDE 中，DA ⊥平面EAB ，CB ∥DA ，EA=DA=AB=2CB ，EA ⊥AB ，M 是EC 的中点.（1）求证：DM ⊥EB ；（2）求二面角M —BD —A 的余弦值.22. （本小题满分13分）设)(x f ＝xx ln )1( （x >0）. （1）判定函数)(x f 的单调性；（2）是否存在实数a ，使得关于x 的不等式ln (1＋x )<ax 在（0，＋∞）上恒成立？若存在，求出a 的范围，若不存在，说明理由.DA EBCM理科数学试题——参考答案一、选择题：DDBD ADCC DCAD二、填空题： 13、【33】；14、【a >4】；15、【33π】；16、【12】；三、解答题：17、解：（1）∵)(x f =cos 2x －a ·sin 2x =21a +cos (2x +ϕ)，又图象的一条对称轴x =－8π，∴)8(π-f =±21a +，即22(1+a )=±21a +，解得：a =1.（2）由（1）得：)(x f =2cos (2x +4π)，又由x ∈[0，2π]得：4π≤2x +4π≤45π，∴－1≤cos (2x +4π)≤22，∴)(x f min=－2，当且仅当2x +4π=π，即x =83π，∴)(x f 的最小值为－2，此时x =83π.18、解：（1）由D 2＋E 2－4F>0得：04)4()2(22>--+-m ，解得m <5；（2）设M(1x ，1y )，N(2x ，2y )，由x ＋2y －4＝0得：x ＝4－2y ；将x ＝4－2y 代入2x ＋2y－2x －4y ＋m ＝0得：52y －16y ＋8＋m ＝0，∴1y ＋2y ＝516，1y 2y ＝58m +，∵OM ⊥ON ，∴2211x y x y ⋅＝－1，即1x 2x ＋1y 2y ＝0，∵1x 2x ＝(4－21y )(4－22y )＝16－8(1y ＋2y )＋41y 2y ，∴1x 2x ＋1y 2y ＝16－8(1y ＋2y )＋51y 2y ＝0，即(8＋m )－8×516＋16＝0，解得m＝58；（3）设圆心C 的坐标为(a ，b )，则a ＝21(1x ＋2x )＝54，b ＝21(1y ＋2y )＝58，半径r ＝|OC|＝554，∴所求圆的方程为：516)58()54(22=-+-y x .19、解：（1）由a n ＋1＝12+n na a 得：11+n a ＝21＋n a 21，∴111-+n a ＝21(11-n a )，∴1+n b ＝21n b又1b =111-a ＝23－1＝21≠0，∴n b ≠0，∴nn b b1+=21（常数），∴数列{n b }是以21为首项，以21为公比的等比数列，∴n b =n⎪⎭⎫ ⎝⎛21.（2）由（1）知：11-n a ＝n ⎪⎭⎫ ⎝⎛21，∴n a 1＝n⎪⎭⎫ ⎝⎛21＋1， ∴n a n ＝n ＋n n 2，∴S n ＝11a ＋22a ＋…＋na n ＝（1＋2＋···＋n ）＋[1×21＋2×(21)2＋···＋n ×(21)n ]，令T n ＝1×21＋2×(21)2＋···＋n ×(21)n ，得：T n ＝2－121-n －nn 2（“差比”数列求和） ∴S n ＝2－n n 22+＋2)1(+n n ＝242++n n －n n 22+.20、解：设轮船航行的速度为x ，则每小时的燃料费用为y ＝k ·x 3，把x ＝10，y ＝6代入得：k ＝0.006，∴y ＝0.006·x 3，∵每千米所用时间为：x1∴每千米的费用总和为：)(x f ＝(0.006·x 3＋96)·x1＝0.006x 2＋x96， ∴由)(x f '＝0.012x －296x>0得：x >20；∴当0<x <20时，)(x f '<0，)(x f 为减函数； 当x >20时，)(x f '>0，)(x f 为增函数，∴当x ＝20时，)(x f 取最小值， ∴轮船以20km /h 的速度航行时，能使每千米的费用总和最小.21、证明：（1）过点M 作MN ⊥BE 于N ，则N 为BE 的中点， 且MN ∥CB ∥DA ，连结AN ，∵EA=AB 且EA ⊥AB ，又N 为BE 的中点， ∴AN ⊥BE ，又∵DA ⊥平面EAB ，∴DA ⊥BE ， ∴BE ⊥面ANMD ，∴BE ⊥DM ，即DM ⊥EB.（2）以A 为原点，AE ，AB ，AD 分别为x ，y ，z 轴，建立空间直角坐标系，A —xy z ，设AB=2，则A （0，0，0），B （0，2，0），D （0，0，2）， M （1，1，21），MB =（－1，1，－21），MD =（－1，－1，23），显然，AE =（2，0，0）为平面ABD 的法向量，设平面MBD 的法向量为1n =（x ，y ，z ），由⎪⎩⎪⎨⎧=⋅=⋅0011n MD n MB ，得⎪⎩⎪⎨⎧=+--=-+-023021z y x z y x ，令z=2，得x =1，y =2，∴取1n =（1，2，2） 设二面角M —BD —A 的平面角大小为θ，∵θ∈（0，90°）， ∴cos θ=<1,n AE cos 31.22、解：（1）∵)(x f '＝2)1(1xx ln x x +-+（x >0），令)(x g ＝)1(1+-+x ln x x （x >0），则DAE BCMN)(x g '＝2)1(1x x x +-+－11+x ＝2)1(x x +-≤0，∴)(x g 在（0，＋∞）上单调递减，∴)(x g <)0(g ＝0，∴)(x f '<0，∴)(x f 在（0，＋∞）上为减函数.（2）∵ln (1＋x )<ax 在（0，＋∞）上恒成立⇔ln (1＋x )－ax <0在（0，＋∞）上恒成立. 令)(x h ＝ln (1＋x )－ax ，则)(x h '＝11+x －a .①若a ≥1，则)(/x h <0，∴)(x h 单调递减，∴)(x h <)0(h ＝0，即ln (1＋x )<ax 恒成立； ②若a ≤0，则)(/x h >0，∴)(x h 单调递增，∴)(x h >)0(h ＝0，∴ln (1＋x )>ax ，即ln (1＋x )<ax 不恒成立；③若0<a <1，则由)(x h '＝0⇒x ＝a 1－1，当x ∈(0，a 1－1]时，)(x h '≥0，∴)(x h 在(0，a1－1]上单调递增，故有)(x h ＝ ln (1＋x )－ax >)0(h ＝0，即ln (1＋x )>ax ，∴0<a <1时，ln (1＋x )<ax 在（0，＋∞）上不恒成立。

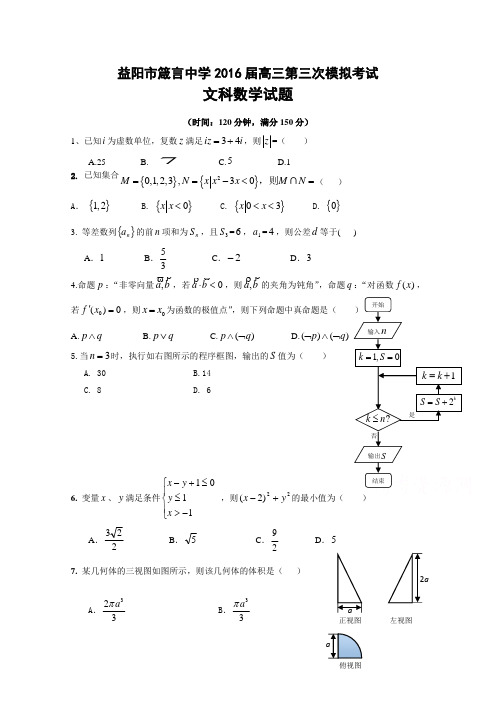
益阳市箴言中学2016届高三第三次模拟考试文科数学试题（时间：120分钟，满分150分）1、已知i 为虚数单位，复数z 满足i iz 43+=，则z =（ ）A.25B. 7C.5D.12. 已知集合{}{}20,1,2,3,30M N x x x M N ==-<=，则∩（ ）A ． {}1,2 B. {}0x x < C. {}3x x 0<< D. {}0 3. 等差数列{}n a 的前n 项和为n S ，且3S =6，1a =4，则公差d 等于( )A ．1B ．35C ．2-D ．3 4.命题p ：“非零向量b a,，若0<⋅b a ，则b a ,的夹角为钝角”，命题q ：“对函数)(x f ，若0)(0='x f ，则0x x =为函数的极值点”，则下列命题中真命题是（ A.q p ∧ B.q p ∨ C.)(q p ⌝∧ D.)()(q p ⌝∧⌝5.当3n =时，执行如右图所示的程序框图，输出的S 值为（ ） A. 30 B.14 C. 8 D. 66. 变量x 、y 满足条件⎪⎩⎪⎨⎧->≤≤+-1101x y y x ，则22)2(y x +-的最小值为（ ）A ．223 B ．5C ．29D ．57. 某几何体的三视图如图所示，则该几何体的体积是（ ）A ．323a π B ．33a πa正视图左视图俯视图C ．3a π D.36a π8. 将函数()()ϕ+=x x f 2sin 的图象向左平移8π个单位，所得到的函数图象关于y 轴对称，则ϕ的一个可能取值为( )A ．43π B ．4π C ．2πD ．4π- 9. 定义在R 上的函数f (x )满足f (－x )＝－f (x )，f (x )＝f (x ＋4)，且当x ∈(－1，0)时，f (x )＝2x ＋15，则f (log 220)＝( )A ．1 B.45 C ．－1 D ．－4510. 已知△ABP 的顶点A ，B 分别为双曲线x 216－y 29＝1的左、右焦点，顶点P 在双曲线上，则|sin A －sin B|sin P的值等于( )A.45B.74C.54D.7 11. 已知抛物线24y x =，过焦点且倾斜角为60°的直线与抛物线交于A 、B 两点，则△AOB 的面积为（ ） ABCD12、已知函数()(sin cos ),(02015)xf x e x x x π=-<≤，则()f x 的各极小值之和为（ ）A.20142(1)1e e e πππ--B. 20162(1)1e e e πππ--C. 220142(1)1e e e πππ--D. 220162(1)1e e e πππ--二．填空题;13. 设(2,4),(,2),(,0),(0,0)OA OB a OC b a b =-=-=>>，O 为坐标原点，若A,B,C 三点共线，则11a b+的最小值为 14.若sin cos θθ+=tan()3πθ+的值是 ___________.15. 已知点F 为椭圆C ：x 22＋y 2＝1的左焦点，点P 为椭圆C 上任意一点，点Q 的坐标为(4,3)，PA DM则|PQ |＋|PF |取最大值时，点P 的坐标为________．16.已知函数f (x )＝⎩⎪⎨⎪⎧x －[x ]，x ≥0，f （x ＋1），x <0，其中[x ]表示不超过x 的最大整数．若直线y ＝k (x ＋1)(k >0)与函数y ＝f (x )的图象恰有三个不同的交点，则实数k 的取值范围是_______三．解答题： 17．某城市持续性的雾霾天气严重威胁着人们的身体健康,汽车的尾气排放是造成雾霾天气的重要因素之一，为此该城市实施了机动车尾号限行政策。

湖南省益阳市箴言中学2009届高三摸底考试试卷文科数学时间 120分钟 总分 150分一、选择题（本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确的选项填入后面的表格内，否则不给分） 1、在R 上定义运算⊗为：x ⊗y =x (1－y )，若不等式(x －a ) ⊗(x +a )<1，对任意实数x 成立，则（ ）A 、－1<a <1 B 、0<a <2 C 、－21<a <23 D 、－23<a <212、已知函数f (x )定义域为[a ，b ]，函数f (x )的图象如图所示，则函数f (|x |)的图象是（ ）3、两直线L 1与L 2关于直线L ：y =－x +1对称，且L 1的方程为y =3x +4，则L 2的方程为（ ） A 、y =31x +6 B 、y =31x +2 C 、y =31x －6 D 、y =31x －24、在等差数列{a n }中，前n 项和S n =n m，m mS n =，其中m ≠n ，则S m +n 的值（ ）A 、大于4B 、等于4C 、小于4D 、大于2且小于45、已知集合M={|=(1，2）+λ(3，4)，λ∈R }，N={|=(－2，－2）+λ(4，5)，λ∈R }则M∩N=（ ） A 、{（1，2）} B 、{（1，2），（－2，－2）} C 、{（－2，－2）} D 、φ6、若f (x )=2cos (ωx +φ）+m ，对任意实数t 都有f (t +4π)=f (－t )，且f (8π=)=－1，则实数m 的值等于（ ） A 、±1 B 、±3 C 、－3或1 D 、－1或37、单位圆x 2+y 2=1上的点到直线3x +4y －25=0的距离的最小值为（ ）A 、0B 、1C 、4D 、58、已知O 为△ABC 的外心，=++，=31(++)，则点P 、Q 分别是△ABC 的（ ）A 、P 是重心，Q 是垂心B 、P 是重心，Q 是内心C 、P 是内心，Q 是重心D 、P 是垂心，Q 是重心9、已知O 为原点，点P （x ，y ）在单位圆x 2+y 2=1上，点Q （2cos θ，2sin θ），且=(34，－32)，则·的值是（ ）A 、1825 B 、925 C 、2 D 、91610、已知函数f (x )=ax 2+bx +c （a >0），α，β是方程f (x )=x 的两根，且0<α<β<1a，0<x <α，给出下列不等式：①x >f (x )；②α>f (x )；③x <f (x )；④α<f (x )， 其中正确的不等式是（ ）二、填空题：（每小题5分，共25分，把答案填在题中横线上）11、使关于x 的不等式|x +1|+k <x 有解的实数k 的取值范围是 . 12、若函数f (x )是奇函数，g (x )是偶函数，且f (x )+g (x )=11-x ，则f (x )= .13、已知方程x 2+(a +2)x +1+a +b 的两根为x 1，x 2，且0<x 1<1<x 2，则ab 的取值范围是 .14、已知直线ax +by +c =0被圆M ：⎩⎨⎧==θθsin 2cos 2y x 所截得的弦AB 的长为23（其中点M 为圆心），那么·的值等于 . 15、已知函数f (x )=x 21log ，g (x )=x －1，设h (x )=⎩⎨⎧<≥)()(),()()(),(x g x f x g x g x f x f ，则使h (a )≥2成立的a 的范围是 .三、解答题（本大题共6小题，共75分，解答应写出文字说明，证明过程或演算步骤） 16、（本题满分12分）如图，某建筑物的基本单元可近似地按以下方法构作：先在地平面α 内作菱形ABCD ，边长为1，∠BAD ＝60°，再在面α的上方，分别以△ABD 与△CBD 为底面安装上相同的正棱锥P -ABD 与Q -CBD ，∠APB ＝90°． （Ⅰ）求证：PQ ⊥BD ；（Ⅱ）求二面角P -BD -Q 的余弦值； （Ⅲ）求点P 到平面QBD 的距离；17、（本题满分12分）已知向量=(cosx，sinx)，=(sin2x，1－cos2x)，=（0，1），x∈（0， ）.（1）向量a，b是否是共线？证明你的结论；（2）若函数f(x)=|b|－(a+b)·c，求f(x)的最小值，并指出取得最小值时的x的值.18、(本题满分12分)在某次空战中，甲机先向乙机开火，击落乙机的概率为0.2；若乙机未被击落，就进行还击，击落甲机的概率为0.3；若甲机未被击落，则再进攻乙机，击落乙机的概率为0.4，求在这个三个回合中：（1）甲机被击落的概率；（2）乙机被击落的概率.19、（本题满分13分）已知函数f(x)=x3－ax2+bx+c的图象为曲线E.（1）若曲线E上存在点P，使曲线E在P点处的切线与x轴平行，求a，b的关系；（2）说明函数f(x)可以在x=－1和x=3时取得极值，并求此时a，b的值；（3）在满足（2）的条件下，f(x)<2C在x∈[－2，6]恒成立，求c的取值范围.20、（本小题满分13分）如图，已知圆C ：（x －1)2+y 2=r 2（r >1），设M 为圆C 与x 轴负半轴的交点，过M 作圆C 的弦MN ，并使它的中点P 恰好在y 轴上.（1）当r =2时，求满足条件的P 点的坐标； （2）当r ∈（1，+∞）时，求点N 的轨迹G 的方程；（3）过点P （0，2）的直线l 与（2）中轨迹G 相交于两个不同的点E 、F ，若·>0，求直线l 的斜率的取值范围.21、（本小题满分13分）设函数f (x )定义域为R ，当x <0时，f (x )>1，且对于任意的x ，y ∈R ，有f (x +y )=f (x )·f (y )成立，数列{a n }满足a 1=f (0)，且f (a n +1)=)2(1n a f --，(n ∈N *)（Ⅰ）求数列{a n }的通项公式并证明；（Ⅱ）是否存在正数k ，使(1+11a )·(1+21a ）·…·（1+na 1）≥k 12+n 对一切n ∈N *均成立，若存在，求出k 的最大值，并证明，否则说明理由 .参 考 答 案一、选择题：CBBAC CCDAB 二、填空题：（每小题5分，共25分，把答案填在题中横线上）11、【k <－1】； 12、【f (x )=12-x x 】； 13、【（－2，－32）】； 14、【－2】； 15、【（0，41]∪[3，+∞）】.三、解答题（本大题共6小题，共75分，解答应写出文字说明，证明过程或演算步骤） 16、（本小题满分12分） 解：（Ⅰ）由P -ABD ，Q -CBD 是相同正三棱锥，可知△PBD 与△QBD 是全等等腰△．取BD 中点E ，连结PE 、QE ，则BD ⊥PE ，BD ⊥QE ．故BD ⊥平面PQE ， 从而BD ⊥PQ ． …………………………4分 （Ⅱ）由（1）知∠PEQ 是二面角P -BD -Q 的平面角，作PM ⊥平面α，垂足为M ，作QN ⊥平面α，垂足为N ，则PM ∥QN ，M 、N 分别是正△ABD 与正△BCD 的中心，从而点A 、M 、E 、N 、C 共线，PM 与QN 确定平面P ACQ ，且PMNQ 为矩形．可得ME ＝NE ＝63，PE ＝QE ＝21，PQ ＝MN ＝33， ∴ cos ∠PEQ ＝312222=-+⋅QE PE PQ QE PE ，即二面角为31arccos ．……………………8分（Ⅲ） 由（1）知BD ⊥平面PEQ ．设点P 到平面QBD 的距离为h ，则h h S V Q B D Q B D P 12131==⋅⋅∆-∴ 11sin 32436P QBD PEQ V S BD PEQ -∆==∠==． ∴362121=h ． ∴ 32=h ． ……………12分 17、已知向量a =(cosx ，sinx )，b =(sin 2x ，1－cos 2x )，c =（0，1），x ∈（0，π）. （1）向量，是否是共线？证明你的结论；（2）若函数f (x )=||－(+)·，求f (x )的最小值，并指出取得最小值时的x 的值.解：（1）a ∥b 共线.（2）∵f (x )=sinx －2sin 2x =－2(sinx －41)2+81.，又x ∈(0，π)，∴sinx ∈(0,1]∴当sinx =1，即x =2π时，f (x )取最小值－1.18、在某次空战中，甲机先向乙机开火，击落乙机的概率为0.2；若乙机未被击落，就进行还击，击落甲机的概率为0.3；若甲机未被击落，则再进攻乙机，击落乙机的概率为0.4，求在这个三个回合中：（1）甲机被击落的概率；（2）乙机被击落的概率. 解：（1）设A 表示“甲机被击落”这一事件，则A 发生只可能在第2回合中发生，而第2回合又只能在第1回合甲失败了才可能进行，用A i 表示第i 回合射击成功（i =1，2，3），B 表示“乙机被击落”的事件，则A=21A A ，B=A 1+1A ·32A A .∴（1）P （A ）=0.8×0.3=0.24； （2）P （B ）=0.2+0.8×0.7×0.4=0.424.19、已知函数f (x )=x 3－ax 2+bx +c 的图象为曲线E.（1）若曲线E 上存在点P ，使曲线E 在P 点处的切线与x 轴平行，求a ，b 的关系； （2）说明函数f (x )可以在x =－1和x =3时取得极值，并求此时a ，b 的值； （3）在满足（2）的条件下，f (x )<2C 在x ∈[－2，6]恒成立，求c 的取值范围. 解：（1）f ′ (x )=3x 2－2ax +b ，设切点为P （x 0，y 0），则曲线y =f (x )在点P 的切线的斜率k =f ′（x 0）=3x 02－2ax 0+b ，由题意知： f ′（x 0）=3x 02－2ax 0+b =0有解，∴△=4a 2－12b ≥0，即a 2≥3b . （2）若函数f (x )可以在x =－1和x =3时取得极值，则f ′ (x ) =3x 2－2ax +b =0有两个解x =－1，x =3，易得a =3，b =－9.（3）由（2）得f (x )=x 3－3x 2－9x +c ，根据题意：c > x 3－3x 2－9x （x ∈[－2，6]）恒成立，∵函数g (x )= x 3－3x 2－9x （x ∈[－2，6]）在x =－1时有极大值5（用求导的方法）且在端点x =6处的值为54，∴函数g (x )=x 3－3x 2－9x （x ∈[－2，6]）的最大值为54，∴c >54.20、如图，已知圆C ：（x －1)2+y 2=r 2（r >1），设M 为圆C 与x 轴负半轴的交点，过M 作圆C 的弦MN ，并使它的中点P 恰好在y 轴上.（1）当r =2时，求满足条件的P 点的坐标； （2）当r ∈（1，+∞）时，求点N 的轨迹G 的方程；（3）过点P （0，2）的直线l 与（2）中轨迹G 相交于两个不同的点E 、F ，若·>0， 求直线l 的斜率的取值范围. 解：（1）当r =2时，M （－1，0），设P （0，b ）由MP ⊥CP ⇒b 2=1，∴b =±1，∴P （0，±1）.（2）设N （x ，y ），∵M （1－r ，0），设P （0，b ）由MP ⊥CP ⇒PO 2=MO·OC⇒b 2=(r －1)·1，又⎩⎨⎧-==-=)1(44122r b y r x ，消去r －1得：y 2=4x （x ≠0）（3）由题意知直线l 的斜率存在且不为0，设该直线l 的方程为：y =kx +2，E （x 1，y 1）、F （x 2，y 2）由⎩⎨⎧=+=xy kx y 422⇒k 2x 2+(4k －4)x +4=0，由△=－32k +16>0⇒k <21又∵CE ·CF >0，∴(x 1－1)(x 2－1)+y 1y 2>0，∴(k －2+1)x 1x 2+(2k －1)(x 1+x 2)+5>0⇒k 2+12k >0，∴k >0或k <－12，综上可得：0<k <21或k <－12.21、设函数f (x )定义域为R ，当x <0时，f (x )>1，且对于任意的x ，y ∈R ，有f (x +y )=f (x )·f (y )成立，数列{a n }满足a 1=f (0)，且f (a n +1)=)2(1n a f --，(n ∈N *)（Ⅰ）求数列{a n }的通项公式并证明；（Ⅱ）是否存在正数k ，使(1+11a )·(1+21a ）·…·（1+na 1）≥k 12+n 对一切n ∈N *均成立，若存在，求出k 的最大值，并证明，否则说明理由 . 解：（Ⅰ）令x =－1，y =0，则f (－1)=f (－1)·f (0)，∵f (－1)>1≠0，∴f (0)=1，令y =－x ⇒f (0)=f (x )·f (－x )，∴f (x )·f (－x )=1⇒f (x )=)(1x f -，∵当x <0时，f (x )>1，∴x <0时，)(1x f ->1，∴0<f (－1)<1，又f (0)=1， ∴x ∈R 时，f (x )>0恒成立.设x 1，x 2∈R ，且x 1<x 2，则x 1－x 2<0，∴f (x 1－x 2)>1， ∴f (x 1)·f (x 2)>1⇒)()(21x f x f >1⇒f (x 1)>f (x 2)，∴f (x )在R 上是减函数. 由f (a n +1)=)2(1n a f --，(n ∈N *)⇒f (a n +1)·f (－2－a n )=1⇒f (a n +1－2－a n )=f (0)， 在f (x )为单调函数情况下，必有a n +1－2－a n =0，即a n +1－a n =2且a 1=f (0)=1， ∴a n =2n －1（n ∈N *）.（Ⅱ）记F(n )=12)11()11)(11(21++⋅⋅⋅++n n，则)()1(n F n F +=321222+⋅++n n n=38448422++++n n n n >1，∴F(n )为关于n 的单调递增函数， ∴F(1)为F(n )的最小值，由F(n )≥k 恒成立知：只需F(1)≥k ， ∴k ≤332，∴k max =332.。

湖南省益阳市箴言中学2018-2019学年高三（上）第三次模拟数学试卷（文科）注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔在答题卡上填写自己的准考证号、姓名、试室号和座位号。

用2B型铅笔把答题卡上试室号、座位号对应的信息点涂黑。

2．选择题每小题选出答案后，用2B型铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4．考生必须保持答题卡整洁。

考试结束后，将试卷和答题卡一并交回。

一、选择题（本大题共12小题，共60.0分）1.已知全集U=R，集合A={x|lg（x+1）≤0}，B={x|3x≤1}，则∁U（A∩B）=（）A. B.C. ，D.2.设i是虚数单位，若复数a-（a∈R）是纯虚数，则a的值为（）A. B. C. 1 D. 33.下列命题为真命题的是（）A. 若为真命题，则为真命题B. “”是“”的充分不必要条件C. 命题“若，则”的否命题为“若，则”D. 已知命题p：∈，使得，￢：∈，使得4.设函数f（x）=x3+（a-1）x2+ax．若f（x）为奇函数，则曲线y=f（x）在点（0，0）处的切线方程为（）A. B. C. D.5.长方形ABCD中，AB=4，BC=3，O为AB中点，在长方形ABCD内随机取一点P，则点P到点O的距离大于2的概率为（）A. B. C. D.6.设等比数列{a n}满足a1+a2=-1，a1-a3=-3，则a4=（）A. 8B.C. 4D.7.若平面向量满足，，则，的夹角θ为（）A. B. C. D.8.已知函数f（x）的定义域为R．当x＜0时，f（x）=x3-1；当-1≤x≤1时，f（-x）=-f（x）；当x＞时，f（x+）=f（x-）．则f（6）=（）A. B. 1 C. 0 D. 29.三棱锥D-ABC中，底面是等腰直角三角形ABC，∠A=90°，BC=，DA AC，DA AB，E，F分别为DA，BC的中点，且直线DF与平面ABC所成角的正切值为，则异面直线BE与CD所成角的余弦值为（）A. B. 0 C. D.10.已知点（，）是f（x）=sin（2x+φ）+cos（2x+φ），（0＜φ＜π）图象的一个对称中心，将函数y=f（x）图象向左平移个单位，得到函数y=g（x）的图象，则函数y=g（x）在[，]上的最小值为（）A. B. C. D.11.已知函数f（x）=sinωx cosωx+cos2ωx-，（ω＞0，x∈R），若函数f（x）在区间（，）内没有零点，则ω的取值范围（）A. B. C. D.12.已知函数y=f（x）是定义域为R的偶函数．当x≥0时，f（x）=，，＞，若关于x的方程[f（x）]2+af（x）+b=0（a，b∈R），有且仅有6个不同实数根，则实数a的取值范围是（）A. B.C. D.二、填空题（本大题共4小题，共20.0分）13.若实数x，y满足约束条件，则Z=2x+y的最大值为______14.已知a，b，c分别为△ABC的三个内角A，B，C的对边，a=2且（2+b）（sin A-sin B）=（c-b）sin C，则△ABC面积的最大值为______．15.已知双曲线：＞，＞的右焦点为F，过点F作圆的切线，若该切线恰好与C的一条渐近线垂直，则双曲线C的离心率为______．16.设A，B，C，D是同一个半径为4的球的球面上四点，△ABC为等边三角形且其面积为9，则三棱锥D-ABC体积的最大值为______．三、解答题（本大题共7小题，共82.0分）17.已知等差数列{a n}的首项为a，公差为d，且不等式ax2-3x+2＜0的解集为（1，d）．（1）求数列{a n}的通项公式a n；（2）若b n=+a n-1，求数列{b n}前n项和T n．18.如图，四棱锥P-ABCD中，侧面积PAD为等边三角形且垂直于底面ABCD，AB=BC=，∠BAD=∠ABC=90°．（1）证明：直线AD∥平面PBC（2）若△PCD的面积为，求四棱锥-ABCD的体积．19.某工厂有25周岁以上（含25周岁）工人300名，25周岁以下工人200名．为研究工人的日平均生产量是否与年龄有关．现采用分层抽样的方法，从中抽取了100名工人，先统计了他们某月的日平均生产件数，然后按工人年龄在“25周岁以上（含25周岁）”和“25周岁以下”分为两组，在将两组工人的日平均生产件数分成5组：[50，60），[60，70），[70，80），[80，90），[90，100）分别加以统计，得到如图所示的频率分布直方图．（1）从样本中日平均生产件数不足60件的工人中随机抽取2人，求至少抽到一名“25周岁以下组”工人的概率．（2）规定日平均生产件数不少于80件者为“生产能手”，请你根据已知条件完成2×2的列联表，并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”？．20.已知抛物线C：y2=4x的焦点为F，平行于x轴的两条直线l1，l2分别与抛物线C交于A，B两点，与抛物线的准线交于D，E两点．（1）若F在线段AB上，点P为DE的中点，求证：PA PB（2）若AB过点（2，0），求AB中点M的轨迹方程．21.设函数f（x）=e x-1-x-ax2．（1）若a=0，求f（x）的单调区间；（2）若当x≥0时f（x）≥0，求a的取值范围．22.已知直线l的参数方程是（t是参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系．曲线C的极坐标方程为ρ=4cos（θ+）．（1）判断直线l与曲线C的位置关系；（2）过直线l上的点作曲线C的切线，求切线长的最小值．23.已知不等式2|x-3|+|x-4|＜2a．（Ⅰ）若a=1，求不等式的解集；（Ⅱ）若已知不等式的解集不是空集，求a的取值范围．答案和解析1.【答案】C【解析】解：全集U=R，集合A={x|lg（x+1）≤0}={x|-1＜x≤0}，B={x|3x≤1}={x|x≤0}，则A∩B={x|-1＜x≤0}，所以∁u（A∩B）={x|x≤-1或x＞0}故选：C．通过对数的性质求出集合A，指数的性质求出集合B，然后求出A∩B，再求解∁u（A∩B）本题考查不等式的求法，集合的基本运算，考查计算能力．2.【答案】D【解析】解：∵=（a-3）-i是纯虚数，∴a-3=0，解得a=3．故选：D．利用复数的运算法则把a-（a∈R）可以化为（a-3）-i，再利用纯虚数的定义即可得到a．熟练掌握复数的运算法则和纯虚数的定义是解题的关键．3.【答案】B【解析】解：A，由复合命题真值表知：若p q为真命题，则p、q至少有一个为真命题，有可能一真一假，也可能两个都真，推不出p q为真命题，∴选项A错误；B，由x=5可以得到x2-4x-5=0，但由x2-4x-5=0不一定能得到x=5，也可以是x=-1，∴选项B成立；C，选项C错在把否命题写成了命题的否定，∴选项C错误；D，选项D错在没有搞清楚特称命题的否定既要在量词上否定，且要在结论处否定（符号应为≤）．故选：B．A，利用复合命题真值表可判断A的正误；B，利用充分必要条件的概念可判断B的正误；C，搞清楚命题的否定与否命题的概念可判断C的正误；D，明确特称命题的否定既要在量词上否定，又要在结论处否定，可判断D的正误．本题考查命题的真假判断与应用，着重考查易混淆的概念的理解与应用，如否命题与命题的否定、特称命题的否定全称命题的关系及复合命题真值表的应用，属于中档题．4.【答案】D【解析】解：函数f（x）=x3+（a-1）x2+ax，若f（x）为奇函数，f（-x）=-f（x），-x3+（a-1）x2-ax=-（x3+（a-1）x2+ax）=-x3-（a-1）x2-ax．所以：（a-1）x2=-（a-1）x2可得a=1，所以函数f（x）=x3+x，可得f′（x）=3x2+1，曲线y=f（x）在点（0，0）处的切线的斜率为：1，则曲线y=f（x）在点（0，0）处的切线方程为：y=x．故选：D．利用函数的奇偶性求出a，求出函数的导数，求出切线的向量然后求解切线方程．本题考查函数的奇偶性以及函数的切线方程的求法，考查计算能力．5.【答案】D【解析】解：S ABCD=4×3=12，长方形内，半圆外的面积为12-×π×22=12-2π，根据几何概型得所求概率为：=1-．故选：D．根据几何概型概率公式可得．本题考查了几何概型，属基础题．6.【答案】B【解析】解：设等比数列{a n}的公比为q，∵a1+a2=-1，a1-a3=-3，∴a1（1+q）=-1，a1（1-q2）=-3，解得：q=-2，a1=1．则a4=（-2）3=-8．故选：B．利用等比数列的通项公式即可得出．本题考查了等比数列的通项公式，考查了推理能力与计算能力，属于中档题．7.【答案】C【解析】解析：，所以，故选：C．由向量垂直转化为向量点乘是0，得到向量a，b的关系式，由模相等，平方处理，得到向量a，b模的关系，由向量数量积的变形，得到夹角．本题考查向量数量积的变形公式，以及向量模的处理方式--平方处理．属于基础题目．8.【答案】D【解析】解：∵当x＞时，f（x+）=f（x-），∴当x＞时，f（x+1）=f（x），即周期为1．∴f（6）=f（1），∵当-1≤x≤1时，f（-x）=-f（x），∴f（1）=-f（-1），∵当x＜0时，f（x）=x3-1，∴f（-1）=-2，∴f（1）=-f（-1）=2，∴f（6）=2．故选：D．求得函数的周期为1，再利用当-1≤x≤1时，f（-x）=-f（x），得到f（1）=-f（-1），当x ＜0时，f（x）=x3-1，得到f（-1）=-2，即可得出结论．本题考查函数值的计算，考查函数的周期性，考查学生的计算能力，属于中档题．9.【答案】C【解析】解：如图，由DA AC，DA AB，得DA平面ABC，又AF=，直线DF与平面ABC所成角的正切值为，∴DA=1．以A为坐标原点，分别以AB，AC，AD所在直线为x，y，z轴建立空间直角坐标系，则B（1，0，0），E（0，0，），C（0，1，0），D（0，0，1），∴，，∴cos＜＞=．∴异面直线BE与CD所成角的余弦值为．故选：C．由已知可得DA平面ABC，并求得AD=AB=AC=1，以A为坐标原点，分别以AB，AC，AD所在直线为x，y，z轴建立空间直角坐标系，再由空间向量求解．本题考查空间角的求法，训练了利用空间向量求解空间角，是中档题．10.【答案】D【解析】解：∵已知点（）是f（x）=sin（2x+φ）+cos（2x+φ）=2sin（2x+φ+），（0＜φ＜π）图象的一个对称中心，∴-+φ+=kπ，k∈Z，∴φ=，故f（x）=2sin（2x+）．将函数y=f（x）图象向左平移个单位，得到函数y=g（x）=2sin（2x++）=2cos（2x+）的图象，则在[]上，2x+∈[-，]，故当2x+=时，g（x）取得最小值为-1，故选：D．利用两角和差的三角公式化简函数的解析式，利用函数y=Asin（ωx+φ）的图象变换规律求得g（x）的解析式，再利用余弦函数的定义域和值域求得y=g（x）在[]上的最小值．本题主要考查两角和差的三角公式，函数y=Asin（ωx+φ）的图象变换规律，余弦函数的定义域和值域，属于基础题．11.【答案】B【解析】解：函数f（x）=sinωcosωx+cos2ωx-，=，=，函数f（x）在区间（）内没有零点，所以：，即：，所以：①，解得：，②，解得：ω∈[]，综上所述：：ω∈（0，][]，故选：B．直接利用三角函数关系式的恒等变换，函数的零点的应用求出结果．本题考查的知识要点：三角函数关系式的恒等变换，函数的零点的应用，主要考察学生的运算能力和转换能力，属于基础题型．12.【答案】C【解析】解：作出函数f（x）的图象如图：则f（x）在（-∞，-2）和（0，2）上递增，在（-2，0）和（2，+∞）上递减，当x=±2时，函数取得极大值f（2）=；当x=0时，取得极小值0．要使关于x的方程[f（x）]2+af（x）+b=0，a，b∈R有且只有6个不同实数根，设t=f（x），则当t＜0，方程t=f（x），有0个根，当t=0，方程t=f（x），有1个根，当0＜t≤1或t=，方程t=f（x），有2个根，当1＜t＜，方程t=f（x），有4个根，当t＞，方程t=f（x），有0个根．则t2+at+b=0必有两个根t1、t2，则有两种情况符合题意：①t1=，且t2∈（1，），此时-a=t1+t2，则a∈（-，-）；②t1∈（0，1]，t2∈（1，），此时同理可得a∈（-，-1），综上可得a的范围是（-，-）（-，-1），故选：C．根据函数的奇偶性作出函数f（x）的图象，利用换元法判断函数t=f（x）的根的个数，利用数形结合即可得到结论．本题主要考查分段函数的应用，利用换元法结合函数奇偶性的对称性，利用数形结合是解决本题的关键．综合性较强．13.【答案】4【解析】解：作出实数x，y满足约束条件，表示的平面区域，如图所示：由z=2x+y可得y=-2x+z，则z表示直线y=-2x+z在y轴上的截距，截距越大，z越大作直线2x+y=0，然后把该直线向可行域平移，当直线经过A时，z最大由可得A（2，0），此时z=4．故答案为：4．作出不等式组表示的平面区域，由z=2x+y可得y=-2x+z，则z表示直线y=-2x+z在y轴上的截距，截距越大，z越大，结合图象即可求解z的最大值．本题主要考查了线性规划知识的应用，求解的关键是明确目标函数中z的几何意义．14.【答案】【解析】解：因为：（2+b）（sinA-sinB）=（c-b）sinC⇒（2+b）（a-b）=（c-b）c⇒2a-2b+ab-b2=c2-bc，又因为：a=2，所以：，△ABC面积，而b2+c2-a2=bc⇒b2+c2-bc=a2⇒b2+c2-bc=4⇒bc≤4所以：，即△ABC面积的最大值为．故答案为：．由正弦定理化简已知可得2a-b2=c2-bc，结合余弦定理可求A的值，由基本不等式可求bc≤4，再利用三角形面积公式即可计算得解．本题主要考查了正弦定理，余弦定理，基本不等式，三角形面积公式在解三角形中的应用，考查了计算能力和转化思想，属于中档题．15.【答案】2【解析】解：由双曲线的一条渐近线y=x，由题意可知该切线方程为y=-（x-c），即ax+by-ac=0，由圆的圆心为C（a，0）到切线的距离d===，由e=，则e2-4e+4=0，解得：e=2，双曲线C的离心率e=2，故答案为：2．求得切线方程，利用点到直线的距离公式，求得圆心到切线的距离d=，利用椭圆的离心率公式即可求得双曲线的离心率．本题考查双曲线的简单性质，点到直线的距离公式，考查计算能力，属于中档题．16.【答案】18【解析】解：设A，B，C，D是同一个半径为4的球的球面上四点，△ABC为等边三角形且其面积为9，∴=9，解得AB=6，球心为O，三角形ABC 的外心为O′，显然D在O′O的延长线与球的交点如图：O′C=×=2，OO′==2，则三棱锥D-ABC高的最大值为：6，则三棱锥D-ABC体积的最大值为：=18．故答案为：18．求出△ABC为等边三角形的边长，画出图形，判断D的位置，然后求解即可．本题考查球的内接多面体，棱锥的体积的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，考查数形结合思想，是中档题．17.【答案】解：（1）∵不等式ax2-3x+2＜0的解集为（1，d）．∴，解得a=1，d=2．＞∴a n=2n-1；（2）由（I）知b n=32n-1+2n-2，∴T n=（3+33+35+…+32n-1）+（2+4+6+8+…+2n）-2n=+-2n=+n2-n．【解析】（1）根据利用根与系数的关系求出a，d，代入等差数列的通项公式即可；（2）使用分组法把T n转化为等差数列，等比数列的前n项和计算．本题考查了方程与不等式的关系，等差数列，等比数列的求和公式，属于中档题．18.【答案】（1）证明：在平面ABCD内，∵∠BAD=∠ABC=90°，∴BC∥AD，又AD⊄面PBC，BC⊂平面PBC，∴AD∥平面PBC；（2）解：取AD的中点M，连接PM，CM．∵AB=BC=，BC∥AD，且∠ABC=90°，∴四边形ABCM为正方形，得CM AD．又侧面PAD为等边三角形且垂直底面ABCD，交线为AD，∴PM AD，PM平面ABCD，∵CM⊂平面ABCD，∴PM CM，设BC=x则CM=x，CD=，PM=，PC=PD=2x，取CD的中点N，连接PN，则PN CD，∴PN=，又△PCD的面积为，∴，解得x=1．∴AB=BC=1，AD=2，PM=，∴．【解析】（1）在平面ABCD内，由已知证明BC∥AD，再由线面平行的判定证明AD∥平面PBC；（2）取AD的中点M，连接PM，CM．证明CM AD．再由已知证明PM AD，PM平面ABCD，可得PM CM，设BC=x 则CM=x，CD=，PM=，PC=PD=2x，取CD的中点N，连接PN，得PN CD，且PN=，由△PCD的面积为求得x=1．即可得到AB=BC=1，AD=2，PM=，然后代入棱锥体积公式求解．本题考查直线与平面平行的判定，考查空间想象能力与思维能力，训练了多面体体积的求法，是中档题．19.【答案】解：（1）由已知得：样本中有25周岁以上组工人60名，25周岁以下组工人40人，所以样本中日平均生产件数不足60件的工人中25周岁以上组有60×0.05=3人，分别记为：A1，A2，A3，25周岁以下组有工人40×0.05=2人，分别记为B1，B2，从中随机抽取2人，所有可能的结果共10种，他们分别是（A1，A2），（A1，A3），（A2，A3），（A1，B1），（A1，B2），（A2，B1），（A2，B2），（A3，B2），（A3，B2），（B1，B2），其中“至少有1名”，25周岁以下组的结果有7种，故所求概率为P=；（2）由频率分别直方图可知：在抽取的100名工人中，“25周岁以上组”中的生产能手60×0.25=15人，“25周岁以下组”中的生产能手40×0.375=15人，2×2所以K2==≈1.786＜2.706．所以没有90%的把握认为“生产能手与工人所在的年龄组有关”．【解析】（1）根据分层抽样，求得样本中有25周岁以上组工人60名，25周岁以下组工人40人，由频率分布直方图日平均生产件数不足60件的工人中25周岁以上组有3人，25周岁以下组有2人，随机抽取2人，求得所有可能的结果，根据古典概型公式求得至少抽到一名“25周岁以下组”工人的概率；（2）据2×2列联表，代入求临界值的公式，求出观测值，利用观测值同临界值表进行比较，K2≈1.786＜2.706，没有90%的把握认为“生产能手与工人所在的年龄组有关”．本题考查根据频率分布直方图的应用，考查独立性检验的概率情况，以及随机分布的概率的计算，考查运算能力，属于中档题．20.【答案】（1）证明：设A（x1，y1），B（x2，y2）．则P（-1，），设直线AB的方程为：x=my+1，代抛物线方程得：y2-4my-4=0，∴y1+y2=4m，y1y2=-4，∴P（-1，2m），∴=（x1+1，y1-2m）•（x2+1，y2-2m）=x1x2+（x1+x2）+1+y1y2-2（y1+y2）+4m2，又x1x2=，x1+x2=m（y1+y2）+2=4m2+2，∴∴=1+4m2+2+1-4-8m2+4m2=0，∴PA PB．（2）解：若AB斜率不存在，则M（2，0），若AB斜率存在，=4x1，=4x2，∴（y1+y2）（y1-y2）=4（x1-x2），∴k AB==．设点M（x，y），则=，可得y2=2（x-2），又（2，0）满足y2=2（x-2），∴AB中点轨迹方程为y2=2（x-2）．【解析】（1）设A（x1，y1），B（x2，y2）．则P（-1，），设直线AB的方程为：x=my+1，代抛物线方程得：y2-4my-4=0，利用根与系数的关系、数量积运算性质证明=0即可得出PA PB．（2）若AB斜率不存在，则M（2，0），若AB斜率存在，=4x1，=4x2，作差可得 k AB=．设点M（x，y），可得AB中点轨迹方程．本题考查了抛物线的定义标准方程及其性质、中点坐标公式、一元二次方程的根与系数的关系、向量垂直与数量积的关系，考查了推理能力与计算能力，属于中档题．21.【答案】解：（1）a=0时，f（x）=e x-1-x，f′（x）=e x-1．当x∈（-∞，0）时，f'（x）＜0；当x∈（0，+∞）时，f'（x）＞0．故f（x）在（-∞，0）单调减少，在（0，+∞）单调增加（II）f′（x）=e x-1-2ax由（I）知e x≥1+x，当且仅当x=0时等号成立．故f′（x）≥x-2ax=（1-2a）x，从而当1-2a≥0，即时，f′（x）≥0（x≥0），而f（0）=0，于是当x≥0时，f（x）≥0．由e x＞1+x（x≠0）可得e-x＞1-x（x≠0）．从而当＞时，f′（x）＜e x-1+2a（e-x-1）=e-x（e x-1）（e x-2a），故当x∈（0，ln2a）时，f'（x）＜0，而f（0）=0，于是当x∈（0，ln2a）时，f（x）＜0．综合得a的取值范围为 ，．【解析】（1）先对函数f（x）求导，导函数大于0时原函数单调递增，导函数小于0时原函数单调递减．（2）根据e x≥1+x可得不等式f′（x）≥x-2ax=（1-2a）x，从而可知当1-2a≥0，即时，f′（x）≥0判断出函数f（x）的单调性，得到答案．本题主要考查利用导数研究函数性质、不等式恒成立问题以及参数取值范围问题，考查分类讨论、转化与划归解题思想及其相应的运算能力．22.【答案】解：（1）直线l方程：y=x+4，ρ=4cos（θ+）=2cosθ-2sinθ，∴ρ2=2ρcosθ-2sinθ，∴圆C的直角坐标方程为x2+y2-2x+2y=0，即+=4，∴圆心（，-）到直线l的距离为d=6＞2，故直线与圆相离．（5分）（2）直线l的参数方程化为普通方程为x-y+4=0，则圆心C到直线l的距离为=6，∴直线l上的点向圆C引的切线长的最小值为=4．（10分）【解析】（1）分别求出直线和曲线的普通方程，根据点到直线的距离，求出直线l与曲线C的位置关系；（2）根据点到直线的距离求出直线l上的点向圆C引的切线长的最小值即可．本题考查了参数方程、极坐标方程转化为普通方程，考查直线和圆的位置关系，考查切线问题，是一道中档题．23.【答案】解：（Ⅰ）对于不等式2|x-3|+|x-4|＜2，①若x≥4，则3x-10＜2，x＜4，∴舍去．②若3＜x＜4，则x-2＜2，∴3＜x＜4．③若x≤3，则10-3x＜2，∴＜x≤3．综上，不等式的解集为＜＜．…（5分）（Ⅱ）设f（x）=2|x-3|+|x-4|，则f（x）=，，＜＜，，∴f（x）≥1．要使不等式的解集不是空集，2a大于f（x）的最小值，故2a＞1，∴＞，即a的取值范围（，+∞）．…（10分）【解析】（Ⅰ）对于不等式2|x-3|+|x-4|＜2，分x≥4、3＜x＜4、x≤3三种情况分别求出解集，再取并集，即得所求．（Ⅱ）化简f（x）的解析式，求出f（x）的最小值，要使不等式的解集不是空集，2a 大于f（x）的最小值，由此求得a的取值范围．本题主要考查绝对值不等式的解法，体现了分类讨论以及转化的数学思想，属于中档题．。

益阳市箴言中学2017-2018学年高三第三次模拟考试语文试题第Ι卷阅读题甲必考题一、现代文阅读（9分，每小题3分）文学与地理环境的关系我国南北文化的差异很大，东西文化的差异同样显著。

即便是在南北两个区域内部，也存在不同的东西文化。

例如在黄河流域，由西向东，依次就有关陇文化、三晋文化、中原文化和齐鲁文化。

文化的地域差异，是由不同的自然地理环境以及在此基础上形成的不同的人文地理环境所决定的，而地域文化的多样性又影响了文学的多样性。

文学与地理环境之间的关系是一种互动的、辩证的关系。

一方面，地理环境会对文学家的文化心理结构造成影响，进而对文学家的创作造成影响，这些影响的表现形态或者载体，便是文学的地域性或者地域的文学；另一方面，这种文学的地域性或者地域的文学，久而久之会融进当地的地域文化，成为当地的人文地理环境的一个有机组成部分，这样的人文地理环境又反过来对文学家的文化心理结构的形成产生影响。

一个地方的文学家愈多，文学作品的质量愈高，对一个地方的文化贡献就愈大，这个地方的文化土壤就愈厚实，它对新一代文学家的成长就愈有利。

一个文学家迁徙流动到一个新的地方，他的感受、体验、思维方式、审美倾向等等可能会发生某些变化，其作品的主题、题材、体裁、语言等等也可能会发生相应的变化，也就是说，他的作品的本籍文化色彩会有所减弱，会融进客籍文化的某些成分。

另一方面，一个文学家迁徙流动到新的地方，除了有选择地吸收、消化当地的人文养料，他在当地的文学创作和文学活动，也会对当地人文环境的总体构成产生或多或少的影响，即反哺于当地文化。

还应该注意的是，地理环境对文学的影响虽然大量存在，但不会是，也不应是种瓜得瓜、种豆得豆那么单纯。

大量情形下，这种影响并不是显在的，而是隐性的。

浙东农村的目连戏这种文艺形态对鲁迅的创作不能说没有影响，有时还相当明显，但更多的时候，还是浙东那个“报仇雪耻之乡”的精神文化因素潜在地影响着他，影响着他那辛辣、冷峻的精神气质与文学风格。

学必求其心得，业必贵于专精箴言中学2017届高三第三次模拟考试试卷语文注意事项：1.本试卷分第I卷（阅读题）和第II卷（表达题)两部分，共150分.考试时间150分钟。

2.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。

作答时请认真阅读答题卡上的注意事项，将答案写在答题卡上,在本试卷上答题无效。

3.考生请使用黑色中性笔和2B铅笔作答。

第Ⅰ卷阅读题一、论述类文本阅读（9分,每小题3分)宋王朝在中国历史上存在了三百余年.这段时期的文学以词为极盛，其艺术成就亦最突出，因而被誉为“时代文学”。

词调今存八百余调,其中百分之八十是宋人创制和使用的。

宋代词人一千四百余家,词存两万余首。

宋词的作家作品的数目与唐诗相比约少一半,若与宋诗相比则少得更多.它是倚声而作的，要求作者精通音律，否则便可能遭到“不当行"之讥，而那种不谐音律的作品就被视为“句读不葺之诗”了。

所以像词这样精巧严密的古典格律诗体能有如此众多的作家作品，在世界文学史上都属罕见的文学现象.词之为时代文学，虽然因体性的局限，不可能像宋诗那样反映广阔的社会现实生活而获得重大的意义，但仍有不少言志遣怀、登临怀古、感时伤事或歌颂升平的题材,也有表达林泉逸兴、美好祝愿、情操高尚、人格伟大的作品，尤其当汉民族国家处于危难之时，词人发出了悲壮激烈的时代强音，汇为一股振奋人心的爱国思想的潮流。

在宋词里，估计最少有百分之六十的作品都属艳科，即涉及恋情的。

我们对于这部分作品应当怎样认识呢？我以为应从文化的意义上去理解。

爱情是文学中的永恒主题，各个时代的人们却赋予它特定的内容与色彩,因此我们可以从中见到那个时代人们情感的一般历史，还可见到一种很真实的时代精神。

宋人多在词里赞赏女性的形态之美，大胆地描述男欢女爱,表现心灵的颤动,歌颂甜蜜的幸福.正因宋人在词里写出了个体生命的真实，服从了新的规律，词才成为时代文学的。

在艳科题材里，作者流露了真实情感,于是往往不自觉地表现了主体的精神品格.因此这类作品就其品格而言，是存在各种等级的。

益阳市箴言中学2016届高三第三次模拟考试 语文试题 第Ι卷 阅读题 甲 必考题 一、现代文阅读（9分，每小题3分） 文学与地理环境的关系 我国南北文化的差异很大，东西文化的差异同样显著。

即便是在南北两个区域内部，也存在不同的东西文化。

例如在黄河流域，由西向东，依次就有关陇文化、三晋文化、中原文化和齐鲁文化。

文化的地域差异，是由不同的自然地理环境以及在此基础上形成的不同的人文地理环境所决定的，而地域文化的多样性又影响了文学的多样性。

文学与地理环境之间的关系是一种互动的、辩证的关系。

一方面，地理环境会对文学家的文化心理结构造成影响，进而对文学家的创作造成影响，这些影响的表现形态或者载体，便是文学的地域性或者地域的文学；另一方面，这种文学的地域性或者地域的文学，久而久之会融进当地的地域文化，成为当地的人文地理环境的一个有机组成部分，这样的人文地理环境又反过来对文学家的文化心理结构的形成产生影响。

一个地方的文学家愈多，文学作品的质量愈高，对一个地方的文化贡献就愈大，这个地方的文化土壤就愈厚实，它对新一代文学家的成长就愈有利。

一个文学家迁徙流动到一个新的地方，他的感受、体验、思维方式、审美倾向等等可能会发生某些变化，其作品的主题、题材、体裁、语言等等也可能会发生相应的变化，也就是说，他的作品的本籍文化色彩会有所减弱，会融进客籍文化的某些成分。

另一方面，一个文学家迁徙流动到新的地方，除了有选择地吸收、消化当地的人文养料，他在当地的文学创作和文学活动，也会对当地人文环境的总体构成产生或多或少的影响，即反哺于当地文化。

还应该注意的是，地理环境对文学的影响虽然大量存在，但不会是，也不应是种瓜得瓜、种豆得豆那么单纯。

大量情形下，这种影响并不是显在的，而是隐性的。

浙东农村的目连戏这种文艺形态对鲁迅的创作不能说没有影响，有时还相当明显，但更多的时候，还是浙东那个“报仇雪耻之乡”的精神文化因素潜在地影响着他，影响着他那辛辣、冷峻的精神气质与文学风格。

益阳市箴言中学高三第三次模拟考试理科数学试卷一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的1）A．1 B．-1 C D2）A B C．2D3．某班的元旦晚会安排6个节目，为考虑整体效果，作如下要求：节目甲必须排在前三位，且节目乙、丙必须连排，则演出顺序编排方案共有种（）A．120 B．156 C．188 D．2404大的项为（）A C D5.定义的偶函单调递增，则满足）6.）7.某空间几何体的三视图如图所示，则该几何体的体积是（）8.过抛焦于）9.在边长为2的正方体内部随机取一个点，则该点到正方体8个顶点的距离都不小于1的概率为（）A. B C. D .10.已知函数与11.如图,A,它关于原点的对称点为B,点F为双曲线的右焦点,设则双曲线离心率e的取值范围为()A. BC D12.外接球表面积为（A二、填空题：本题共4小题，每小题5分，共20分。

13.已知变量恒成立，则实数的取值范围为________．14．我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”意思是：一座7层塔共挂了381盏灯，且相邻两层中的下一层灯数是上一层灯数的2倍，则塔的顶层灯数为_____________15．的三个交点的横坐标分别为，那么的值是__________.16__________三、解答题：共70分。

解答应写出文字说明、证明过程或演算步骤。

第17~21题为必考题，每个试题考生都必须作答。

第22、23题为选考题，考生根据要求作答。

（一）必考题：共60分(12×5=60)。

17.在平面四边形ABCD 中，DA →·DC →=0，∠A=450，AB=32，BD=5， (1)求△ABD 的面积；(2)若DC=1，求△BCD 的外接圆的面积.18．如图，四棱锥P−ABC 中，P A ⊥底面ABCD ，AD ∥BC ，AB=AD=AC =3，P A=BC =4，M 为线段AD 上一点，AM=2MD ，N 为PC 的中点. （1）证明：MN ∥平面P AB ;（2）求直线AN 与平面PMN 所成角的正弦值.19．如图，O1（a>b>0）的短轴长为A(a，0)，线段OA的垂直平分线恰过椭圆的右焦点F，且交椭圆于第一象限的点B. （1）求椭圆的标准方程；（2）若M，N为椭圆上的不同的两点，且直线BM与BN关于直线BF对称，试问：直线MN的斜率是否为定值？若是，求出这个值，若不是，请说明理由.规定对岁的人群随机抽取人进行了每天使用手机时间，是否符合“手机控”的调查，若每天平均使用手机超过（1（221.（1.（2恒成立， 求ɑ 的取值范围.（二）选考题：共10分。

2016—2017学年湖南省益阳市桃江一中高三（上)第三次月考数学试卷(文科)一、选择题:本大题共12小题，每小题5分,共60分,在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合A={x｜x2﹣2x﹣3＜0｝，B=｛y｜y=，x∈R｝，则（∁R B)∩A=（)A．｛x|﹣1＜x＜1}B．｛x|﹣1＜x≤1｝C．{x｜1≤x＜3} D．{x｜﹣1＜x＜0｝2．已知复数z=，则|z｜=（）A．B．1 C．D．23．已知命题p和命题q中有且仅有一个真命题，则下列命题中一定为假命题的是（）A．p∨q B．￢p∨q C．￢p∧￢q D．p∨￢q4．设x,y∈R，则“x﹣y＞1"是“x＞y”的（）A．充分不必要条件B．必要不充分条件C．充要条件 D．既不充分也不必要条件5．指数函数f(x）=（2﹣a）x是单调函数，则a的取值范围是()A．（1,2）∪（﹣∞,1) B．(1，2）C．（﹣∞，1）D．（1，2）∪（﹣∞，1)∪（﹣1,1）6．若sin（2x+）=a（|a|≤1),则cos(﹣2x）的值是（）A．﹣a B．a C．|a｜D．±a7．已知|｜=1,||=2，|﹣|=，则与的夹角为（）A．0 B．C．D．8．一个由半球和四棱锥组成的几何体，其三视图如图所示．则该几何体的体积为(）A． +πB． +π C． +π D．1+π9．中国古代有计算多项式值的秦九韶算法，如图是实现该算法的程序框图．执行该程序框图，若输入的x=2,n=2，依次输入的a为2,2,5，则输出的s=()A．7 B．12 C．17 D．3410．等差数列｛a n｝满足a n﹣1+a n+a n+1=3n（n≥2）,函数f(x）=2x，则log2［f（a1）•f(a2）…f(a n）]的值为（）A．B．C．D．11．已知函数f（x)=，若方程f(x）+x﹣k=0，恰有两个实数根,则k的取值范围是（)A．k＞1 B．k≤1 C．k＜1 D．k≥112．函数y=2x2﹣e|x|在［﹣2,2]的图象大致为()A．B．C．D．二、填空题13．已知矩形ABCD中，AB=，AD=1，则•=．14．如图，在平面直角坐标系xOy中,F是椭圆+=1（a＞b＞0）的右焦点，直线y=与椭圆交于B,C两点，且∠BFC=90°,则该椭圆的离心率是．15．设f（x）是定义在R上且周期为2的函数,在区间[﹣1，1）上，f（x)=,其中a∈R,若f(﹣)=f（），则f（5a）的值是．16．已知不等式+＞1对x∈[，］恒成立,则a的取值范围是．三、解答题（共5小题，满分50分)17．在△ABC中,角A，B,C所对的边分别是a，b，c，且+=．（Ⅰ）证明：sinAsinB=sinC;（Ⅱ)若b2+c2﹣a2=bc，求tanB．18．已知向量=（2sinωx，sinωx），=(cosωx,﹣2sinωx）（ω＞0），函数f（x）=•+,直线x=x1，x=x2是函数y=f（x）的图象的任意两条对称轴，且|x1﹣x2|的最小值为．（I）求ω的值；（Ⅱ）求函数f（x）的单调增区间；（Ⅲ）若f（a）=，求sin（4a+）的值．19．如图，在直三棱柱ABC﹣A1B1C1中，D1E分别为BB1和CC1的中点，AF⊥平面A1DE，其垂足F落在直线A1D上．(1）求证：BC⊥A1D；（2）若A1D=，AB=BC=3，G为AC的中点，求三棱锥G﹣A1DB1的体积．20．已知单调递增的等比数列｛a n｝满足a2+a3+a4=28，且a3+2是a2,a4的等差中项．(I)求数列｛a n｝的通项公式；(Ⅱ）设b n=a n•log2a n，其前n项和为S n，若（n﹣1)2≤m（S n﹣n﹣1）对于n≥2恒成立，求实数m的取值范围．21．设函数f（x)=lnx+a（1﹣x）．(Ⅰ）讨论：f（x）的单调性；（Ⅱ）当f(x）有最大值，且最大值大于2a﹣2时，求a的取值范围．［选做题]22．已知直线C1（t为参数)，C2(θ为参数），（Ⅰ）当α=时，求C1与C2的交点坐标;（Ⅱ）过坐标原点O做C1的垂线，垂足为A，P为OA中点，当α变化时，求P点的轨迹的参数方程，并指出它是什么曲线．[选做题]23．已知函数f（x）=|2x﹣1|+｜2x+a｜，g（x）=x+3．（Ⅰ）当a=1时，求不等式f(x）＜g（x）的解集;（Ⅱ)设a＞﹣1,且当x∈［﹣，) 时，f（x）≤g（x）,求a的取值范围．2016—2017学年湖南省益阳市桃江一中高三（上）第三次月考数学试卷（文科）参考答案与试题解析一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合A={x｜x2﹣2x﹣3＜0}，B={y|y=，x∈R}，则（∁R B)∩A=(）A．｛x｜﹣1＜x＜1｝B．｛x|﹣1＜x≤1}C．{x|1≤x＜3｝ D．｛x|﹣1＜x＜0}【考点】交、并、补集的混合运算．【分析】解一元二次不等式x2﹣2x﹣3＜0即可得出集合A，容易得出，从而可求出集合B，然后进行补集、交集的运算便可求出（∁R B)∩A．【解答】解：A=｛x｜﹣1＜x＜3};x2+1≥1，∴；∴B=｛y｜y≥1｝；∴∁R B={y｜y＜1｝=｛x|x＜1｝；∴（∁R B）∩A={x｜﹣1＜x＜1}．故选A．2．已知复数z=，则|z|=(）A．B．1 C．D．2【考点】复数求模．【分析】利用复数模的运算性质即可得出．【解答】解:|z｜===．故选：C．3．已知命题p和命题q中有且仅有一个真命题，则下列命题中一定为假命题的是（）A．p∨q B．￢p∨q C．￢p∧￢q D．p∨￢q【考点】复合命题的真假．【分析】根据命题p，q的真假，判断复合命题的真假即可．【解答】解:∵命题p和命题q中有且仅有一个真命题，∴￢p∧￢q是假命题，故选:C．4．设x，y∈R,则“x﹣y＞1”是“x＞y"的（）A．充分不必要条件B．必要不充分条件C．充要条件 D．既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断．【分析】根据充分必要条件的定义以及不等式的性质判断即可．【解答】解:由x﹣y＞1，能推出x＞y，是充分条件，而x＞y推不出x﹣y＞1,不是必要条件,故选：A．5．指数函数f（x)=(2﹣a)x是单调函数，则a的取值范围是（）A．（1，2)∪（﹣∞，1) B．(1,2）C．(﹣∞,1）D．（1,2）∪（﹣∞，1）∪（﹣1，1）【考点】指数函数的单调性与特殊点．【分析】根据指数函数f(x）=（2﹣a）x在R内为增函数或为减函数，即可求出a的范围【解答】解：当指数函数f（x）=（2﹣a）x在R内为增函数，∴2﹣a＞1，解得a＜1，当指数函数f（x）=（2﹣a）x在R内为减函数，∴0＜2﹣a＜1，解得1＜a＜2，综上所述a的取值范围为(﹣∞，1）∪（1,2)，故选：A6．若sin（2x+）=a(|a|≤1），则cos（﹣2x）的值是（）A．﹣a B．a C．|a｜D．±a【考点】三角函数的化简求值．【分析】根据（2x+）+（﹣2x）=，利用诱导公式进行化简即可．【解答】解：∵sin（2x+）=a（｜a｜≤1），∴cos（﹣2x)=sin［﹣（﹣2x）]=sin（+2x）=a．故选：B．7．已知||=1,｜｜=2，｜﹣|=，则与的夹角为（）A．0 B．C．D．【考点】数量积表示两个向量的夹角．【分析】根据条件对两边平方即可求出，从而得出，进而便得出与的夹角．【解答】解:根据条件：==5；∴；∴；∴的夹角为．故选:B．8．一个由半球和四棱锥组成的几何体，其三视图如图所示．则该几何体的体积为（）A． +πB． +π C． +π D．1+π【考点】由三视图求面积、体积．【分析】由已知中的三视图可得：该几何体上部是一个半球，下部是一个四棱锥，进而可得答案．【解答】解：由已知中的三视图可得：该几何体上部是一个半球，下部是一个四棱锥，半球的直径为棱锥的底面对角线，由棱锥的底底面棱长为1，可得2R=．故R=,故半球的体积为：=π，棱锥的底面面积为：1，高为1，故棱锥的体积V=，故组合体的体积为： +π，故选：C9．中国古代有计算多项式值的秦九韶算法，如图是实现该算法的程序框图．执行该程序框图，若输入的x=2，n=2,依次输入的a为2,2，5,则输出的s=()A ．7B ．12C ．17D ．34【考点】程序框图．【分析】根据已知的程序框图可得，该程序的功能是利用循环结构计算并输出变量S 的值，模拟程序的运行过程，可得答案． 【解答】解：∵输入的x=2，n=2，当输入的a 为2时,S=2，k=1，不满足退出循环的条件；当再次输入的a 为2时，S=6，k=2，不满足退出循环的条件; 当输入的a 为5时,S=17,k=3，满足退出循环的条件； 故输出的S 值为17， 故选：C10．等差数列｛a n ｝满足a n ﹣1+a n +a n +1=3n （n ≥2），函数f （x ）=2x ,则log 2［f （a 1）•f （a 2)…f （a n ）]的值为（ ) A ．B ．C ．D ．【考点】数列递推式．【分析】等差数列｛a n ｝满足a n ﹣1+a n +a n +1=3n （n ≥2）,可得a n =n ，f （a n )=2n ．再利用指数函数与对数函数的运算性质、等差数列的求和公式即可得出． 【解答】解:∵等差数列{a n }满足a n ﹣1+a n +a n +1=3n （n ≥2），∴3a n =3n ，即a n =n ． ∵函数f(x)=2x ，∴f(a n ）=2n ． 则log 2［f （a 1）•f(a 2）…f （a n )］= ==1+2+…+n=．故选：B ．11．已知函数f（x）=，若方程f(x）+x﹣k=0，恰有两个实数根,则k的取值范围是（）A．k＞1 B．k≤1 C．k＜1 D．k≥1【考点】根的存在性及根的个数判断．【分析】方程f(x)+x﹣k=0，恰有两个实数根，转化为两个函数的图象的交点个数，利用数形结合求解即可．【解答】解：函数f（x）=，若方程f（x）+x﹣k=0，恰有两个实数根，就是f（x）=﹣x+k有两个实数根，也就是y=f（x)与y=﹣x+k由两个不同的交点，在坐标系中画函数y=f(x）与y=k﹣x的图象，如图：由图象可知，两个函数有两个交点,k＜1．故选：C．12．函数y=2x2﹣e|x｜在［﹣2，2]的图象大致为()A．B．C．D．【考点】函数的图象．【分析】根据已知中函数的解析式，分析函数的奇偶性，最大值及单调性，利用排除法，可得答案．【解答】解：∵f（x）=y=2x2﹣e｜x|，∴f(﹣x）=2（﹣x)2﹣e|﹣x｜=2x2﹣e|x|，故函数为偶函数，当x=±2时，y=8﹣e2∈（0，1)，故排除A，B;当x∈[0，2］时，f（x)=y=2x2﹣e x，∴f′（x）=4x﹣e x=0有解，故函数y=2x2﹣e|x｜在［0,2］不是单调的，故排除C，故选：D二、填空题13．已知矩形ABCD中,AB=,AD=1,则•=3．【考点】平面向量数量积的运算．【分析】由题意画出图形，把转化为，代入后展开得答案．【解答】解：如图，∵AB=,AD=1，∴•==．故答案为：3．14．如图，在平面直角坐标系xOy中,F是椭圆+=1（a＞b＞0）的右焦点，直线y=与椭圆交于B，C两点，且∠BFC=90°，则该椭圆的离心率是．【考点】直线与椭圆的位置关系．【分析】设右焦点F（c,0）,将y=代入椭圆方程求得B，C的坐标，运用两直线垂直的条件：斜率之积为﹣1，结合离心率公式，计算即可得到所求值．【解答】解：设右焦点F（c,0），将y=代入椭圆方程可得x=±a=±a,可得B(﹣a，），C(a，），由∠BFC=90°,可得k BF•k CF=﹣1，即有•=﹣1，化简为b2=3a2﹣4c2，由b2=a2﹣c2,即有3c2=2a2，由e=,可得e2==，可得e=,故答案为：．15．设f(x）是定义在R上且周期为2的函数，在区间［﹣1,1）上,f（x）=，其中a∈R，若f（﹣）=f(），则f（5a）的值是﹣．【考点】分段函数的应用；周期函数．【分析】根据已知中函数的周期性，结合f（﹣)=f（)，可得a值，进而得到f（5a）的值．【解答】解：f(x）是定义在R上且周期为2的函数，在区间［﹣1，1）上,f（x）=,∴f（﹣）=f(﹣）=﹣+a,f（)=f(）=｜﹣|=，∴a=,∴f（5a)=f（3）=f(﹣1)=﹣1+=﹣，故答案为：﹣16．已知不等式+＞1对x∈［,]恒成立，则a的取值范围是a＞．【考点】三角函数的最值．【分析】根据x∈[，]时sinx＞0，cosx＞0,原不等式化为a＞对x∈[,]恒成立;设f(x）=,求出它的最大值即可．【解答】解：当x∈［，］时，sinx＞0，cosx＞0；∴不等式+＞1可化为a＞=对x∈［，]恒成立;设f（x）=，x∈［，］，令t=sinx+cosx，x∈[，],∴t=sin(x+）；∵x∈[，]，∴x+∈[，］，∴sin（x+）∈[，];令sinxcosx=，则y==（t﹣）在（0,+∞）上是单调增函数，当t=时，y max=×（﹣）=，∴a的取值范围是a＞．故答案为：a＞．三、解答题(共5小题，满分50分）17．在△ABC中,角A,B,C所对的边分别是a，b，c，且+=．（Ⅰ）证明：sinAsinB=sinC;（Ⅱ）若b2+c2﹣a2=bc，求tanB．【考点】余弦定理的应用；正弦定理；余弦定理．【分析】（Ⅰ）将已知等式通分后利用两角和的正弦函数公式整理，利用正弦定理,即可证明．（Ⅱ）由余弦定理求出A的余弦函数值，利用（Ⅰ)的条件，求解B的正切函数值即可．【解答】(Ⅰ)证明:在△ABC中，∵ +=,∴由正弦定理得：,∴=，∵sin（A+B)=sinC．∴整理可得：sinAsinB=sinC，（Ⅱ）解:b2+c2﹣a2=bc,由余弦定理可得cosA=．sinA=,=+==1,=，tanB=4．18．已知向量=（2sinωx,sinωx）,=（cosωx,﹣2sinωx）（ω＞0）,函数f（x)=•+，直线x=x1，x=x2是函数y=f（x）的图象的任意两条对称轴，且|x1﹣x2｜的最小值为．（I）求ω的值；（Ⅱ）求函数f（x）的单调增区间;（Ⅲ)若f（a)=，求sin(4a+）的值．【考点】平面向量数量积的运算;三角函数的化简求值；正弦函数的图象．【分析】（I)利用数量积化简函数的表达式,通过函数的周期求ω的值；(Ⅱ）利用正弦函数的单调增区间，即可求函数f（x）的单调增区间;（Ⅲ）利用已知条件，通过两角和与差的三角函数化简求解即可．【解答】解:（Ⅰ）向量=（2sinωx，sinωx），=（cosωx，﹣2sinωx）(ω＞0）,函数f(x）=•+,所以，直线x=x1，x=x2是函数y=f（x）的图象的任意两条对称轴，且|x1﹣x2｜的最小值为．可得T=π，,∴ω=1．（Ⅱ)，可得2x∈，可得x∈（k∈Z ），函数的单调增区间：（k∈Z)（Ⅲ)，sin（4α+）=﹣cos（4α+）=﹣1+2sin2（2）=﹣1+=﹣．19．如图，在直三棱柱ABC﹣A1B1C1中,D1E分别为BB1和CC1的中点，AF⊥平面A1DE,其垂足F落在直线A1D上．（1）求证：BC⊥A1D；（2）若A1D=，AB=BC=3,G为AC的中点，求三棱锥G﹣A1DB1的体积．【考点】棱柱、棱锥、棱台的体积；空间中直线与直线之间的位置关系．【分析】（1）利用线面垂直的判定定理，证明BC⊥平面AA1B1B，即可证明BC⊥A1D；（2)利用三棱锥的体积公式，即可求三棱锥G﹣A1DB1的体积．【解答】（1）证明：∵在直三棱柱ABC﹣A1B1C1中，AA1⊥平面ABC，又∵BC⊂平面ABC，∴AA1⊥BC．…又∵AF⊥平面A1DE，DE⊂平面ADE，∴AF⊥DE．…又∵D,E分别为BB1和CC1的中点，∴DE∥BC，∴AF⊥BC．…而AA1∩AF=A，∴BC⊥平面AA1B1B．又∵A1D⊂平面AA1B1B,∴BC⊥A1D．…（2）解：∵AB=BC=3，∴A1B1=B1C1=DE=3,则由Rt△A1B1D≌Rt△C1DE,知C1D=，∴C1E==2，则B1D=2．…由（1）知BC⊥平面AA1B1B,则由G为AC的中点，知G到平面AA1B1B的距离为C到平面AA1B1B的距离的，即为=,…∴==．…20．已知单调递增的等比数列｛a n}满足a2+a3+a4=28，且a3+2是a2,a4的等差中项．（I）求数列｛a n}的通项公式；（Ⅱ)设b n=a n•log2a n,其前n项和为S n,若(n﹣1）2≤m（S n﹣n﹣1）对于n≥2恒成立，求实数m的取值范围．【考点】数列的求和;对数的运算性质；数列递推式．【分析】（Ⅰ）设出等比数列{a n}的首项和公比,由已知列式求得首项和公比，则数列｛a n｝的通项公式可求；（Ⅱ）把（Ⅰ)中求得的通项公式代入b n=a n•log2a n，利用错位相减法求得S n，代入(n﹣1）2≤m（S n﹣n﹣1）,分离变量m，由单调性求得最值得答案．【解答】解：(Ⅰ）设等比数列的{a n｝首项为a1，公比为q．由题意可知：，解得：或，∵数列为单调递增的等比数列,∴a n=2n；（Ⅱ）b n=a n•log2a n =n•2n，∴S n=b1+b2+…+b n=1•21+2•22+…+n•2n，①2S n=1•22+2•23+3•24+…+n•2n+1，②①﹣②,得：﹣S n=2+22+23+…+2n﹣n•2n+1=﹣n•2n+1=2n+1﹣2﹣n•2n+1，∴S n=（n﹣1）•2n+1+2,若（n﹣1）2≤m（S n﹣n﹣1）对于n≥2恒成立，则（n﹣1）2≤m［（n﹣1）•2n+1+2﹣n﹣1]=m[（n﹣1）•2n+1+1﹣n]对于n≥2恒成立，即=对于n≥2恒成立，∵=,∴数列｛}为递减数列，则当n=2时，的最大值为．∴m≥．则实数m得取值范围为［，+∞)．21．设函数f(x）=lnx+a（1﹣x）．（Ⅰ）讨论：f(x)的单调性;（Ⅱ）当f（x）有最大值，且最大值大于2a﹣2时，求a的取值范围．【考点】利用导数研究函数的单调性；导数在最大值、最小值问题中的应用．【分析】（Ⅰ）先求导，再分类讨论，根据导数即可判断函数的单调性;（2）先求出函数的最大值，再构造函数（a）=lna+a﹣1，根据函数的单调性即可求出a的范围．【解答】解：（Ⅰ）f（x)=lnx+a（1﹣x）的定义域为（0,+∞）,∴f′（x）=﹣a=,若a≤0，则f′（x）＞0，∴函数f（x）在(0，+∞）上单调递增，若a＞0，则当x∈（0,）时，f′（x)＞0，当x∈（，+∞）时，f′（x)＜0，所以f（x）在（0，）上单调递增，在(，+∞）上单调递减，（Ⅱ），由(Ⅰ）知，当a≤0时，f（x）在（0，+∞)上无最大值；当a＞0时,f(x）在x=取得最大值，最大值为f（）=﹣lna+a﹣1，∵f（）＞2a﹣2，∴lna+a﹣1＜0，令g（a)=lna+a﹣1,∵g（a）在（0，+∞）单调递增,g（1）=0,∴当0＜a＜1时,g（a）＜0，当a＞1时，g（a）＞0,∴a的取值范围为(0,1）．［选做题］22．已知直线C1(t为参数），C2（θ为参数），（Ⅰ）当α=时,求C1与C2的交点坐标；（Ⅱ）过坐标原点O做C1的垂线，垂足为A，P为OA中点，当α变化时,求P点的轨迹的参数方程，并指出它是什么曲线．【考点】简单曲线的极坐标方程；轨迹方程；直线和圆的方程的应用;直线的参数方程；圆的参数方程．【分析】（I)先消去参数将曲线C1与C2的参数方程化成普通方程，再联立方程组求出交点坐标即可,（II）设P（x，y）,利用中点坐标公式得P点轨迹的参数方程，消去参数即得普通方程，由普通方程即可看出其是什么类型的曲线．【解答】解：(Ⅰ)当α=时，C1的普通方程为，C2的普通方程为x2+y2=1．联立方程组，解得C1与C2的交点为（1，0)．（Ⅱ)C1的普通方程为xsinα﹣ycosα﹣sinα=0①．则OA的方程为xcosα+ysinα=0②，联立①②可得x=sin2α，y=﹣cosαsinα；A点坐标为（sin2α,﹣cosαsinα),故当α变化时，P点轨迹的参数方程为:，P点轨迹的普通方程．故P点轨迹是圆心为,半径为的圆．［选做题］23．已知函数f（x）=｜2x﹣1|+｜2x+a｜，g(x)=x+3．（Ⅰ）当a=1时，求不等式f(x）＜g（x）的解集；(Ⅱ）设a＞﹣1，且当x∈［﹣，) 时，f(x）≤g(x),求a的取值范围．【考点】绝对值三角不等式;绝对值不等式的解法．【分析】（I）对x分类讨论，去掉绝对值符号解出即可得出．（Ⅱ）当x∈［﹣,）时，f（x)=1+a，不等式f（x）≤g（x）化为1+a≤x+3，化简利用a的取值范围、函数的单调性即可得出．【解答】解:(Ⅰ）由|2x﹣1｜+|2x+1|＜x+3，得:①或②或③由①得：;由②得：;由③得：，综上,原不等式的解集为｛x｜}．（Ⅱ）当x∈[﹣，）时，f(x）=1+a，不等式f（x）≤g(x）化为1+a≤x+3，∴x≥a﹣2对x∈[﹣，）都成立，故≥a﹣2，即a,又由已知a＞﹣1,∴a的取值范围为（﹣1,]．2016年12月29日。